Filtry cyfrowe 8

FILTRY CYFROWE

Wstęp

Filtry cyfrowe są często spotykanymi algorytmami cyfrowego przetwarzania sygnałów, spotykanymi w prawie wszystkich układach DSP.

N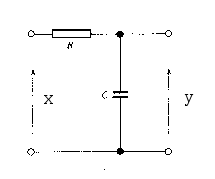 a przykładzie analogowego filtra dolnoprzepustowego RC przedstawiono wyprowadzenie podstawowych zależności dla filtra cyfrowego.

Prądy i napięcia w tym układzie można powiązać przy pomocy równania:

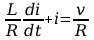
gdzie 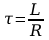-stała czasowa obwodu, ,

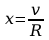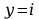
(po podstawieniu) 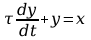. Przyjmujemy, że y jest próbkowany z częstotliwością 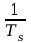, a okres próbkowania jest mały w porównaniu ze stałą czasową obwodu. W tym przypadku można zastosować przybliżenie różniczkowania w postaci: 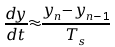, gdzie 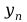-jest n-tą próbką mierzonej na wyjściu filtra wartości a 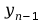-poprzednią próbką. Można zastąpić równanie różniczkowe filtra równaniem różnicowym:

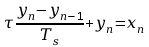
przekształconym do postaci:

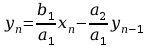
Równanie to opisuje filtr cyfrowy pierwszego rzędu.

Uogólnienie powyższego równania prowadzi do zależności opisującej przekształcenie danego wektora x w nowy wektor y przez przekształcenie dane wzorem:

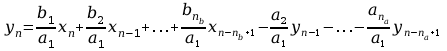
Równanie to opisuje filtr cyfrowy N-tego rzędu, gdzie .

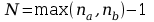Taki filtr może być reprezentowany przez schemat pokazany poniżej:

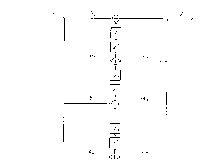
Współczynniki 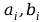są znormalizowane przez podzielenie ich przez 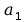. Moduł 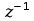oznacza jednostkowe przesunięcie w czasie. W każdym etapie obliczeń należy zapamiętać wartości .

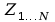IMPLEMENTACJA filtra przebiega następująco:

1. INICJALIZACJA

   1. Wektor wartości początkowych jest zapamiętywany w komórkach 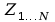. Jeśli wartości początkowe nie są znane wpisuje się wartości zerowe.

   2. Wartości współczynników 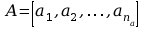i 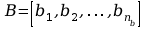są normalizowane przez podzielenie ich przez .

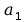2. GŁÓWNA PĘTLA

   1. Obliczenie wartości

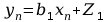
   2. Aktualizacja wartości 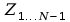zgodnie z zależnością: 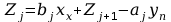a

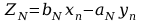
   3. Pętla jest wykonywana dopóki nie skończy się wektor wejściowy x.

3. KONIEC. Wartości Z_j są kopiowane do wektora wartości wyjściowych.

Obliczenia przy pomocy funkcji filter

FILTER (help filter)

Jednowymiarowy filtr cyfrowy. Y = FILTER(B,A,X) filtruje dane z wektora X przy pomocy filtra opisanego wektorami A i B i tworzy wektor wyjściowy Y.

Jest to implementacja równania różnicowego:

a(1)*y(n) = b(1)*x(n) + b(2)*x(n-1) + ... + b(nb+1)*x(n-nb)

• a(2)*y(n-1) - ... - a(na+1)*y(n-na)

[Y,Zf] = FILTER(B,A,X,Zi) umożliwia dostęp do wartości początkowych Zi i końcowych Zf.

Przykład 1

x=[1,2,1,2,1,2,1,2,1,2];

B=[0.5];

A=[1,-0.25,-0.25];

[y,Zf]=filter(B,A,x)

y(:)=0.5000

1.1250

0.9063

1.5078

1.1035

1.6528

1.1891

1.7105

1.2249

1.7338

Zadanie: Przeprowadzić kilka obliczeń przy pomocy funkcji filter z dowolnymi danymi.

Przykład 2

Przeprowadzamy filtrację sygnału losowego – szumu przy pomocy filtra Butterwortha piątego rzędu dolnoprzepustowego o częstotliwości odcięcia 30 Hz. Sygnał jest próbkowany z częstotliwością 100 Hz.

help butter

BUTTER Wyznaczenie współczynników filtra Butterwortha

[B,A] = BUTTER(N,Wn) wylicza filtr N-tego rzędu dolnoprzepustowy. Częstotliwość odcięcia musi być 0.0 < Wn < 1.0, gdzie 1.0 odpowiada połowie częstotliwości próbkowania.

X=rand(1000,1); sygnał

[b,a]=butter(5,30/50); obliczenia współczynników

b =

0.1084 0.5419 1.0837 1.0837 0.5419 0.1084

a =

1.0000 0.9853 0.9738 0.3864 0.1112 0.0113

Y=filter(b,a,X); przeprowadzamy filtrację

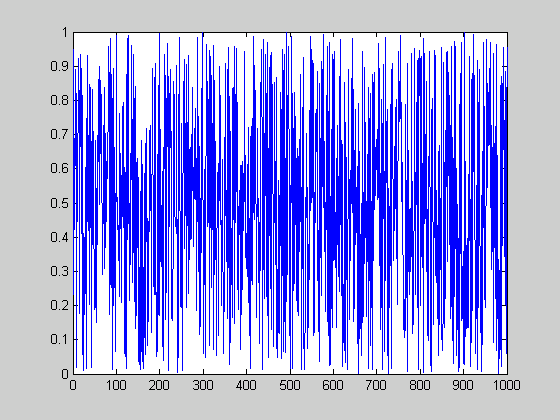
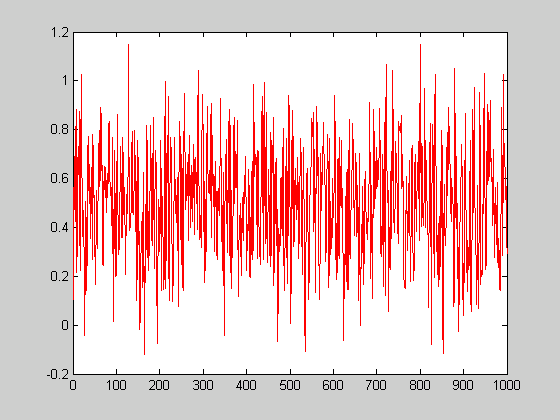
sygnał wejściowy sygnał wyjściowy

Zadanie: Przeprowadzić filtrację sygnału X filtrami o różnych rzędach, typach, dolno- górnoprzepustowy (patrz help butter) i różnych częstotliwościach odcięcia. Wykreślić sygnał Y [plot(Y)], podać wnioski.

Projektowanie filtrów cyfrowych

Zadaniem jest zaprojektowanie filtra cyfrowego o zadanej charakterystyce amplitudowej. W toolboxie Signal Processing jest wiele narzędzi do projektowania filtrów. Omówimy dwie funkcje yulewalk i fir2.

Przy pomocy operatora opóźnienia jednostkowego z^-1 można przedstawić filtr H przy pomocy zależności:

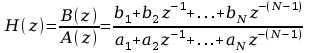
g dzie 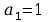i co najmniej jeden ze współczynników 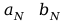jest różny od zera.

Jeśli wszystkie współczynniki 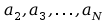śą zerowe to filtr jest określany jako FIR (Finite Impulse Response = SOI –Skończonej Odpowiedzi Impulsowej)

w przeciwnym wypadku IIR (Infinite Impulse response =NOI Nieskończonej Odpowiedzi Impulsowej)

Funkcja yulewalk służy do syntezy filtrów IIR a funkcja fir2 do syntezy filtrów FIR.

Definiowanie charakterystyki filtra

Charakterystyka częstotliwościowa filtra cyfrowego zależy od częstotliwości próbkowania. W wielu funkcjach MATLABa jest wymagane podanie częstotliwości w jednostkach bezwymiarowych tzn. częstotliwości w Hz podzielonej przez częstotliwość Nyquista (połowę częstotliwości próbkowania). Czyli jeśli częstotliwość próbkowania wynosi 1000 Hz to częstotliwość 50 Hz odpowiada częstotliwości unormowanej

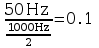
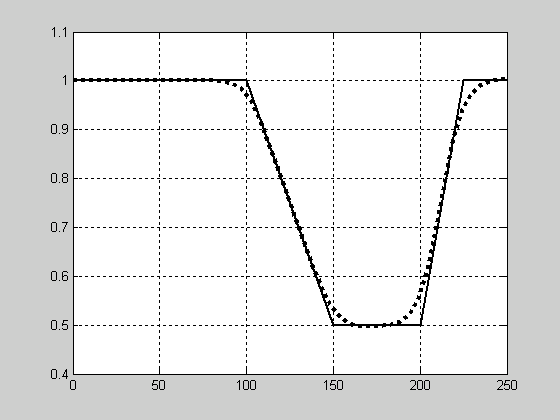
Aby zdefiniować charakterystykę projektowanego filtra, trzeba utworzyć dwa wektory określające częstotliwości (unormowanej) i odpowiadające im amplitudy.

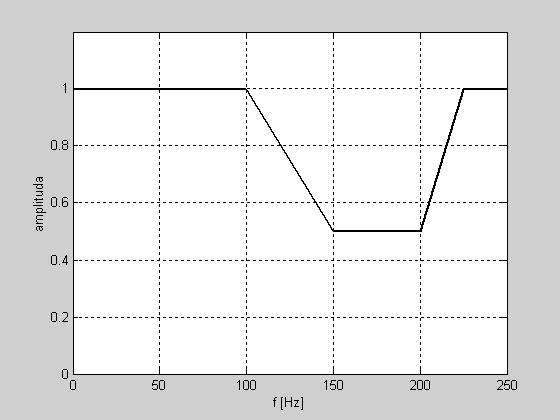
Przykład

Sygnał je próbkowany z częstotliwością 500 Hz.

Od Hz	Do Hz	amplituda
0	100	Stała 1.0
100	150	Liniowo malejąca się od 1 do 0,5
150	200	Stała 0,5
200	225	Liniowo rosnąca od 0,5 do 1
225	250	Stała 1.0

Wprowadzamy założoną charakterystykę do MATLABa

fHz0=[0 100 150 200 225 250]

m0=[1 1 0.5 0.5 1 1]

plot(fHz0,m0);

fs=500; częstotliwość próbkowania

f0=fHz0/(fs/2); normalizacja

[bIIR,aIIR]=yulewalk(6,f0,m0); filtr 6 rzędu

bIIR =

0.7977 1.0451 1.1993 0.9520 0.7048 0.3119 0.1364

aIIR =

1.0000 1.0900 1.0755 0.9712 0.6448 0.2489 0.1171

Charakterystykę amplitudową i fazową otrzymanego filtra można wykreślić przy pomocy freqz

freqz(bIIR,aIIR,250)

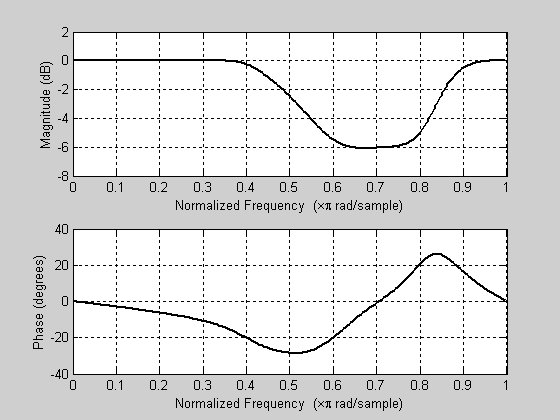
Charakterystykę amplitudową można porównać z założoną:

fHz1=linspace(0,250,50); oś x

om1=2*pi*fHz1; konwersja do rad/s

z=exp(sqrt(-1)*om1/fs);

mIIR=abs(polyval(bIIR,z)./polyval(aIIR,z));

plot(fHz0,m0,fHz1,mIIR);

Zadanie:

Opracował dr inż. Zbigniew Leonowicz na podstawie: A. Biran, M. Breiner: Matlab 5 for Engineers, Addison-Wesley, 1999, str. 567-600.

© Zakład Elektrotechniki Teoretycznej – Politechnika Wrocławska 2001