MATEMATYKA FINANSOWA - prof. Zawadzki
WYKŁAD 1
Egzamin pisemny - 5 zadań rachunkowych
Symbol sumowania
C - zbiór liczb całkowitych
C = {0,+-1,+-2,…}
Dla dowolnych dwóch liczb n, p ![]()
C takich, że p ≤ n, symbol sumowania
![]()
Gdzie:
i - bieżący wskaźnik sumowania
p - dolna granica sumowania
n - górna granica sumowania
a) ![]()
b) dla każdego r ![]()
C, że p ≤ r < n
![]()
![]()
c) ![]()
d) ![]()
Symbol mnożenia
![]()
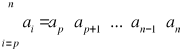
a) dla każdego r ![]()
C, p ≤ r < n
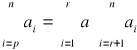
b) dla dowolnej liczby rzeczywistej C
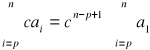
Ciąg geometryczny
Ciąg (an) nazywamy geometrycznym jeśli istnieje liczba q![]()
0 taka dla każdego n
![]()
Przykład:
(1,2,4,8,16) a=1, q=2
![]()
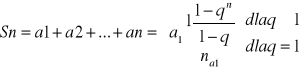
Gdy ![]()
to:
![]()
Ciąg arytmetyczny
Ciąg nazywamy arytmetycznym jeśli istnieje liczba r taka, że dla każdego n
![]()
Przykład:
(2,4,6,8) a1=2, r=2
Dla każdego ciągu arytmetycznego zachodzą wzory:
![]()
![]()
Liczba „е” i logarytm naturalny
![]()
![]()
![]()
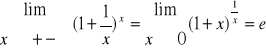
![]()
![]()
Wartość pieniądza w czasie
Zmiana wartości pieniądza czasie powoduje konieczność porównania kwot pieniężnych pochodzących z różnych okresów
Punkt odniesienia:
- przyszła wartość pieniądza [future value, FV]
- bieżąca wartość pieniądza [prezent value, PV]
Z porównywanie wiąże się:
Oprocentowanie - wyznaczanie przyszłej wartości na podstawie znajomości wartości obecnej
Dyskontowanie - wyznaczanie aktualnej wartości na podstawie znajomości przyszłej wartości
Przyszła wartość pieniądza
Odsetki Z - [ang. interest] - są opłatą za prawo użytkowania kapitału pieniężnego.
Dla wierzyciela są dochodem otrzymanym za odstąpienie prawa do dysponowania posiadanym kapitałem.
Dla dłużnika są kosztem uzyskania pożyczki.
Wartość przyszła:
![]()
Gdzie:
![]()
- wartość przyszła
![]()
- wartość początkowa
Odsetki:
![]()
Wysokość odsetek zależy od:
- wysokości pożyczonej kwoty
- długości okresu spłaty
- ryzyka niewypłacalności dłużnika
- ogólnej sytuacji panującej na rynku finansowym
Przedmiotem umowy może być:
stopa procentowa
sposób obliczania procentu
sposób płacenia odsetek
sposób spłaty kapitału
Sposoby spłacania odsetek:
- wypłacane na koniec okresu
- wypłacane na początku okresu
- wypłacane w podokresach
Sposoby spłaty kapitału:
- kapitał spłacany na końcu okresu
- kapitał spłacany w ratach
Stopa procentowa r - stosunek odsetek do początkowej wartości kapitału
Stopa procentowa:
![]()
![]()
![]()
![]()
- czynnik procentowy q
![]()
- zawsze dotyczy ustalonego czasu [okresu stopy procentowej]
Oprocentowanie złożone [składane]
Oprocentowanie złożone stosuje się w transakcjach średnio- i długoterminowych.
Odsetki o które powiększa się po każdym okresie kapitał obliczane są od całego dotychczas zgromadzonego kapitału.
![]()
- kapitał początkowy
![]()
- czas oprocentowania w latach
![]()
- roczna stopa procentowa
![]()
kapitał końcowy - wartość kapitału po upływie czasu n
![]()
- odsetki po upływie czasu n
Wartość kapitału końcowego
![]()
![]()
![]()
![]()
Całkowite odsetki:
![]()
![]()
WYKŁAD 2
Dokończenie wykładu 1:
Jak widać ze wzoru przy oprocentowaniu złożonym, przyszła wartość kapitału…
![]()
![]()
![]()
UWAGA: Zamiast logarytmu naturalnego możemy dać dowolny logarytm.
Przykład 1:
Ile lat musi upłynąć, aby podwoił się kapitał złożony w banku, jeśli przyjmiemy że roczna stopa procentowa r=0,03 (3%) i nie ulega ona zmianie.
![]()
![]()
Kapitalizacja w podokresach - kapitalizacja śródroczna
Załóżmy, że podstawowy okres oprocentowania [rok] podzielona na m równych podokresów. W każdym podokresie nagromadzony dotychczas kapitał zostaje powiększony zgodnie ze stopą procentową [względna stopa procentowa]
![]()
![]()
Wzór na kapitał ![]()
po k podokresach (k=1,2,3…):
![]()
![]()
![]()
UWAGA: Zwiększenie m, czyli skracanie podokresów kapitalizacji odsetek zwiększa przyszłą wartość kapitału
Przykład 2:
Kapitał ![]()
złożono na lokacie w banku, który oferuje roczną stopę kapitału r=3%. Oblicz wartość tego kapitału po 4 latach w przypadku kapitalizacji rocznej, półrocznej, kwartalnej, miesięcznej.
![]()
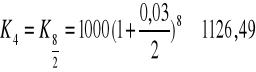
![]()
![]()
Przykład 3:
VW Bank oferuje lokatę „overnight Plus”. Minimalna wpłata wynosi 500 000 zł, a oprocentowanie 3%.
![]()
Kapitalizacja ciągła
Kapitalizacja ciągła - jest to graniczny przypadek kapitalizacji w podokresach, gdy liczba podokresów m, na które został podzielony rok dąży do nieskończoności.
![]()
![]()
Przykład:
Dla danych z przykładu 2
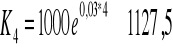
Równoważność warunków oprocentowania złożonego
Często spotykamy sytuację, gdy:
bank A oferuje oprocentowanie lokat 24 miesięcznych równe r=4% w stosunku rocznym z kwartalną kapitalizacją odsetek [m=4]
bank B oferuje oprocentowanie lokat 24 miesięcznych równe r=5% z półroczną stopa kapitalizacji odsetek [m=2]
dla A: ![]()
dla B: ![]()
Odp. Lepsza jest oferta banku B.
Można też obliczyć:
A ![]()
B ![]()
Zachodzi więc potrzeba porównania wariantów
P.S. Dwa warianty oprocentowania złożonego są równoważne, gdy dla obu wariantów ten sam kapitał początkowy ![]()
osiąga po tym samym czasie identyczną wartość !!!
Dwa warianty oprocentowania złożonego są równoważne, gdy:
![]()
czyli
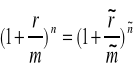
Efektywna stopa oprocentowania
Przy kapitalizacji w podokresach wartość kapitału końcowego jest rosnącą funkcją liczby podokresów n
Dla każdego n oraz m=1,2,4,12 prawdziwa jest nierówność:
![]()
![]()
- jest to efektywna stopa. Efektywną stopą nazywamy stopę procentową ![]()
równą stopie ![]()
. Może ona być wykorzystywana do porównywania różnych wariantów oprocentowania złożonego
Wzór na efektywną stopę oprocentowania:
![]()
![]()
W Excelu można to zrobić za pomocą formuły: EFFECT(stopa_nominalna;npery)
Przeciętna stopa procentowa
Obliczając wartość końcową kapitału musimy uwzględnić ewentualne zmiany warunków procentowania
Założenia:
okres kapitalizacji 1 rok
w ciągu kolejnych n lat roczna stopa procentowa była równa
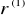
,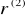
,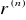
… przy czy, w sytuacji, gdy odsetki kapitalizuje się w podokresach krótszych niż rok w obliczeniach przyjmujemy: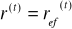
gdzie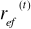
(i=1,2,…n)
![]()
Wartość kapitału w kolejnych latach nie będzie ciągiem geometrycznym !!!
![]()
- stopa przeciętna
![]()
można wyliczyć z:
![]()
Wyraża się ona wzorem:
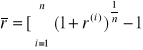
lub:
![]()
„Uśredniony” czynnik procentowy ![]()
jest średnią geometryczną czynników procentowych ![]()
, …, ![]()
Inflacja - wzór Fishera
Duża inflacja może spowodować, że rzeczywista wartość złożonego na lokacie bankowej kapitału zamiast rosnąć, będzie maleć.
Oznaczenia:
![]()
nominalna stopa procentowa
![]()
stopa inflacji [względny przyrost ceny]
![]()
rzeczywista [realna] stopa procentowa uwzględniająca zjawisko inflacji
![]()
kapitał początkowy
![]()
początkowa cena wzorcowego koszyka dóbr
![]()
siła nabywcza kapitału ![]()
Gdyby nie było inflacji dla ![]()
siła nabywcza ![]()
byłaby równa:
![]()
W przypadku inflacji siła nabywcza będzie równa:
![]()
Stopa wzrostu siły nabywczej:
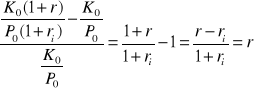
Wzór na realną stopę inflacji ma zatem postać:
![]()
Dodatkowo dla niewielkiego ![]()
zachodzi równość: ![]()
![]()
wzór Fishera:
![]()
Łączna stopa inflacji w k-okresach wynosi: 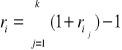
Przeciętna stopa inflacji: 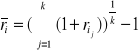
Oprocentowanie proste
O oprocentowaniu prostym mówimy wtedy, gdy odsetki obliczane są jedynie od początkowej wartości kapitału ![]()
Oprocentowanie to stosuje się przy obliczaniu odsetek an czas krótszy od okresu ich kapitalizacji.
Oznaczenia:
![]()
kapitał początkowy
![]()
czas oprocentowania
![]()
roczna stopa procentowa
![]()
wartość kapitału końcowego
![]()
odsetki skumulowane
![]()
Przyszła wartość kapitału:
![]()
Wzór na odsetki skumulowane: ![]()
Porównanie oprocentowania prostego i złożonego
Oprocentowanie proste stosuje się przy obliczaniu odsetek za czas krótszy od okresu ich kapitalizacji.
Dla każdego ![]()
zachodzi:
![]()
![]()
czas oprocentowania kapitału w latach [nie musi być liczbą całkowitą!]
![]()
największa liczba całkowita nie większa niż ![]()
(np. dla 1,5 = 1 dla 2,1 =2 dla 5=5)
![]()
cześć ułamkowa liczby ![]()
W przypadku gdy ![]()
nie jest liczbą całkowitą, obliczanie przyszłej wartości odbywa się dwuetapowo:
![]()
Natomiast gdyby w całym okresie ![]()
obowiązywało oprocentowanie złożone to ![]()
byłoby równe:
![]()
Ponieważ dla ![]()
oraz ![]()
zachodzi ![]()
to:
![]()
WYKŁAD 3
Dyskontowanie
Z porównywaniem wartości pieniądza w czasie wiążą się dwie operacje finansowe:
Oprocentowanie
Dyskontowanie
Oprocentowanie - polega na obliczeniu kwoty do jakiej wzrośnie po określonym czasie początkowy kapitał
Dyskontowanie - jest operacją odwrotną do oprocentowania. Polega na wyznaczeniu bieżącej wartości pieniądza na podstawie przyszłej wartości.
W przypadku oprocentowania złożonego:
![]()
Lub
![]()
![]()
- roczna stopa procentowa ![]()
- roczny czynnik dyskontujący
różnica
![]()
Nazywa się dyskontem złożonym przy stopie procentowej ![]()
Ze wzoru na wartość kapitału końcowego przy kapitalizacji w podokresach otrzymujemy:
![]()
lub ![]()
Gdzie:
![]()
- lata
![]()
- podokresy kapitalizacji
W przypadku kapitalizacji ciągłej otrzymujemy formułę:
![]()
Dyskontowanie pozwala na porównywanie kapitałów w różnych momentach czasu.
Równoważność kapitałów w różnych momentach czasu:
![]()
Czyli ![]()
i ![]()
są równoważne gdy bieżące wartości tych kapitałów obliczone na ten sam moment są sobie równe !
Przykład 1
Pan X chce sprzedać dom i zgłosiło się do niego dwóch potencjalnych kupców.
Jeden z nich jest gotowy zapłacić natychmiast 400 000 zł, a drugi proponuje 405 000 zł za 3 miesiące - będąc przy tym wiarygodnym.
Która z ofert jest dla Pana X korzystniejsza jeśli przyjąć:
Tzw. Rynkowa stopa procentowa wynosi 0,5% miesięcznie
Nie ma istotnych powodów dla których Pan X nie mógłby czekać na pieniądze
Rozwiązanie:
Bieżąca wartość 2 oferty: ![]()
Wartość przyszła 1 oferty: ![]()
Odp. Propozycja pierwszego kupującego jest korzystniejsza.
Strumienie pieniędzy i ich wartość bieżąca
Cash flow - wpływy i wypływy pieniędzy, które mają miejsce w jednakowych odstępach czasu np. spłaty kredytów, regularne wpłaty na lokatę bankową, renty, przychody osiągane w kolejnych latach przez inwestora
Gdzie:
CF0 - płatność [przychód lub wydatek] w chwili początkowej
CFi (i=1,2,3…n) - płatność przypadająca na koniec i-tego okresu
Wartość bieżąca strumienia pieniędzy
Musimy każdy element tego strumienia sprowadzić do chwili obecnej [zdyskontować] a następnie zsumować otrzymane w ten sposób wielkości.
![]()
Gdzie:
![]()
- stopa procentowa
UWAGA !!!
![]()
rozumiemy tu jako wielkość która mówi o ile procent wzrasta zaangażowany kapitał na koniec każdego okresu niezależnie od przyczyny tego wzrostu np. oprocentowanie lokaty, rentowność przedsięwzięcia, stopa zysku
Przykład 2
Pan LM wygrał na loterii 1 000 000 $. Zgodnie z regulaminem kwota została wypłacona w 9 ratach:
1 rata w wysokości 200 000 $ została wypłacona zaraz
Reszta wygranej zostanie wypłacona w 8 rocznych ratach po 100 000 $ [pod koniec każdego roku]
Rozwiązanie:
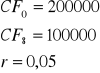
Otrzymujemy:
![]()
Cash flow z jednakowymi strumieniami płatności
Wzór na bieżącą wartość strumienia:
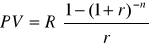
![]()
Która wyraża aktualną wartość strumienia jednostkowych płatności dokonywanych w momentach 1,2,3…n przy stopie procentowej ![]()
.
Wzór możemy zapisać w postaci
![]()
Analogicznie dla strumienia ![]()
jednakowych płatności „z góry”
![]()
![]()
Otrzymujemy wzór:
![]()
Gdzie:
![]()
oraz ![]()
Zachodzi wzór:
![]()
Definicja:
Przy oprocentowaniu złożonym dwa strumienie płatności nazywamy równoważnymi, gdy ich wartości aktualne obliczone na ten sam, dowolny moment są sobie równe.
Przykład 3
Strumień płatności złożonych z 12 rat po 200 zł chcemy zastąpić równoważnym mu strumieniem 4 rat kwartalnych przy oprocentowaniu rocznym 12%. Obliczyć wielkość rat kwartalnych
Rozwiązanie:
![]()
![]()
![]()
Ponieważ:
![]()
To aktualna zdyskontowana wartość strumienia 12 rat wynosi:
![]()
Raty kwartalne:
![]()
Z definicji równoważności strumieni płatności otrzymujemy:
![]()
Ten sam wynik otrzymalibyśmy wybierając inny moment aktualizacji
Dynamiczne metody oceny inwestycji
Metoda NPV [wartość bieżąca netto]
Gdzie:
![]()
- liczba rozważanych okresów czasu - czas zużycia ekonomicznego inwestycji
![]()
- jest stała
![]()
- nakłady, które musimy ponieść aby uruchomić inwestycję
![]()
- przewidywane przychody lub wydatki w kolejnych okresach
Definicja
Wartość bieżąca netto inwestycji:
![]()
Czyli wartość bieżąca strumienia przepływów pieniężnych ![]()
Jeśli ![]()
to inwestycja jest opłacalna
Jeśli ![]()
to inwestycja jest nieopłacalna
Przy porównywaniu kilku wariantów inwestycji stosujemy zasadę maksymalizacji NPV tzn. realizujemy projekt, dla którego NPV przyjmuje największą wartość dodatnią.
Przykład 4
Planujemy zakup nowego urządzenia. Przepływy podane są w tabelce.
Stopa procentowa [kwartalna] jest równa r=0,01. Stosując NPV oceń opłacalność inwestycji.
Nr kwartału |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
CFi |
-10 |
-5 |
-1 |
-1 |
-1 |
-1 |
7 |
8 |
9 |
10 |
12 |
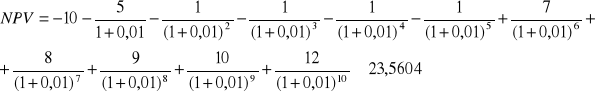
Odp. Ponieważ ![]()
można zdecydować się na kupno nowego urządzenia.
Przykład 5
Oprócz zakupu nowej maszyny bierzemy pod uwagę modernizację posiadanego urządzenia. Oceń opłacalność inwestycji.
Nr kwartału |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
CFi |
-5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
![]()
Odp. Stosując maksymalizację NPV powinniśmy wybrać pierwszy wariant, czyli zakup nowego urządzenia.
Metoda IRR [wewnętrzna stopa zwrotu]
Jest to stopa % przy której w zakładanym okresie eksploatacji inwestycji zwróci się zainwestowany kapitał. Przy założeniu, że przepływy środków pieniężnych są realizowane wg stopy IRR.
IRR jest stopa spełniającą równanie:
![]()
Kryterium:
(k- koszt uzyskania kapitału Np. oprocentowanie pożyczki bankowej]
Jeśli
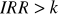
to inwestycja jest realizowanaJeśli

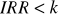
to inwestycja nie jest realizowana
Wzór stosowany do obliczenia przybliżonej wartości IRR:
![]()
Gdzie:
![]()
- wyznaczane są za pomocą metody prób i błędów wartości stopy procentowej dla których ![]()
i ![]()
W Excelu liczymy to z pomocą formuły IRR(wartość;wynik)
Przykład 6
Dla danych z przykładów 4 i 5
![]()
![]()
Odp. W tym przypadku zgodnie z kryterium maksymalizacji IRR należałoby wybrać wariant modernizacji urządzenia, podczas gdy z NPV wynikałoby, ze należy zakupić nowe urządzenie.
WYKŁAD 4
Podstawy wyceny obligacji
Akcje i obligacje są podstawowymi instrumentami rynku kapitałowego.
Obligacja [ang. Bond] - papier wartościowy potwierdzający nabycie przez jego posiadacza prawa do otrzymywania w określonym terminie sumy pieniężnej określonej w obligacji.
Termin wykupu - dzień, od którego poczynając obligacja podlega wykupowi.
Wartość nominalna [face value] - wartość, którą posiadacz otrzymuje od emitenta po upływie terminu wykupu.
Obligacje o stałym oprocentowaniu
Wycena obligacji pozwala na:
Określenie stopy zwrotu
Ile jest warta obligacja
Cena obligacji zależy głownie od wielkości odsetek.
Dwa rodzaje cen obligacji:
Cena czysta - nie uwzględnia odsetek, które narosły od momentu ostatniej płatności
Cena brudna - uwzględnia odsetki które narosły od ostatniej płatności
Cena brudna = cena czysta + odsetki
Cena brudna ![]()
cena czysta
Cena czysta i brudna obligacji 3-letnich o wartości nominalnej 100 i oprocentowaniu 10%
Notowania giełdowe cen obligacji podawane są zazwyczaj jako ceny „czyste” w procentach ceny nominalnej.
Podstawowy wzór stosowany do wyceny obligacji:
![]()
Gdzie:
P - wartość obligacji
Ct- dochód uzyskany w okresie t-tym
r - wymagana stopa dochodu inwestora
n - liczba okresów, które pozostały do terminu wykupu obligacji
Wymagana stopa dochodu inwestor r ustalana jest na podstawie stóp dochodu obligacji podobnego typu, podawanych w środkach masowego przekazu.
Wartość obligacji P jest tzw. „wartością wewnętrzną” obligacji. Porównuje się ją z wartością rynkową [ceną] obligacji i dokonuje zakupu gdy jest większa niż cena lub sprzedaży, gdy jest mniejsza.
Przykład 1
Dana jest obligacja o stałym oprocentowaniu z 3-letnim terminem wykupu o wartości nominalnej 100, a odsetki płacone są co roku. Oprocentowanie wynosi 10% a zatem roczne odsetki wynoszą 10.
Wiedząc, że wymagana stopa dochodu inwestora wynosi 8% oblicz wartość obligacji.
![]()
Odp. Inwestor może kupić obligacje, gdy jej cena nie przekracza 105,15
Stopa dochodu w okresie od wykupu [YTM].
Jest ona dodatnim rozwiązaniem równania:
![]()
Jest to stopa dochodu obligacji przy znajomości wartości rynkowej obligacji
YTM jest szczególnym przypadkiem IRR dla inwestycji polegającej na kupnie obligacji.
YTM -jest to stopa dochodu jaką otrzyma inwestor, który zakupi obligacje po cenie P.
Przykład 2
Dana jest obligacja z 2-letnim terminem wykupu o wartości nominalnej 100 i cenie 92 i oprocentowaniu 10%. Przy czym odsetki płacone są co roku. Oblicz YTM.
![]()
![]()
W przypadku kiedy odsetki są wyznaczane częściej niż raz w roku to YTM wyznacza się wzorem:
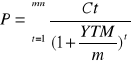
Renty
Renta [annuity] - ciąg płatności okresowych długoterminowych. To ciąg wpłat lub wypłat płaconych w równych odstępach czasu.
Emerytura
Renta [inwalidzka]
Wypłata odsetek z ulokowanego w banku kapitału
Ratalne spłaty kredytu lub pożyczki
Rodzaje rent:
Renty pewne - wypłacane przez uzgodniony z góry okres, niezależnie od tego czy rentobiorca żyje
Renty życiowe - wypłacane do momentu śmierci rentobiorcy
Renty czasowe - gdy liczba rat jest skończona
Renty wieczyste - gdy liczba rat jest nieskończona
Renty proste - kapitalizacja jest równoczesna z wypłatami renty
Renty uogólnione - okresy płatności są krótsze lub dłuższe od okresów kapitalizacji odsetek
Renty płatne natychmiast
Renty odroczone
Renty płatne z dołu
Renty płatne z góry
Renty pewne n-letnie [czasowe, proste, różne]
Renty wypłacane z dołu [coroczne w stałej wysokości równej R]
Wzór na obecną i przyszłą wartość takie renty:
![]()
![]()
Gdzie:
![]()
oznacza przyszłą wartość strumieni n-jednakowych wpłat [z dołu przy stopie procentowe r]
Między funkcjami ![]()
i ![]()
zachodzi związek:
![]()
Renty wypłacane z góry [coroczne i w stałej wysokości równej R]
Wzór na obecną i przyszłą wartość takiej renty:
![]()
![]()
Gdzie:
![]()
![]()
Zachodzi wzór:
Uwagi
Aby móc pobierać [z dołu] przez okres n-lat rentę w wysokości R rocznie, należy zgromadzić kapitał rentowy w wysokości danej wzorem
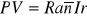
Aby móc pobierać analogiczną rentę z góry, trzeba zgromadzić kapitał określony wzorem
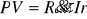
Renty wieczyste
Renty wieczyste to ciąg płatności dokonywanych okresowo na rzecz rentobiorcy.
Ze wzorów ![]()
i ![]()
wynika, że gdy ![]()
to wartość aktualna renty wieczystej
wypłacanej z dołu wynosi:
![]()
A wypłacanej z góry wynosi:
![]()
Wniosek: Jeśli dysponujemy kapitałem rentowym w wysokości S to wysokość rat
wypłacanych z dołu:
…………………………………
Wypłacanych z góry:
![]()
Renty tworzące ciąg asymetryczny
![]()
Renty wypłacane z dołu:
![]()
Wartość aktualna takiej renty jest równa:
![]()
Renty tworzące ciąg geometryczny
![]()
dla ![]()
![]()
dla ![]()
![]()
![]()
Renta pewna n-letnia, płatna m-razy w roku
W przypadku, gdy ![]()
to mamy do czynienia ze śródroczną kapitalizacją odsetek
Gdy renta wypłacana jest z dołu w wysokości ![]()
wtedy wzór na aktualną wartość takiej renty wynosi:
![]()
Stopa:
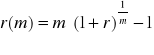
Która dla ![]()
przybiera postać ![]()
WYKŁAD 5
Rozliczenia związane ze spłatą długów
Spłata długu - jest to spłata kredytu lub pożyczki
Kredyt:
Udzielają go tylko banki
Umowa w formie pisemnej
Udzielany na określony cel
Udzielany jest odpłatnie [prowizje, odsetki]
Operacje są bezgotówkowe
Pożyczka:
Przeniesienie własności określonej kwoty pieniężnej na pożyczkobiorcę
Każdy może pożyczyć pieniądze innej osobie
Umowa przy kwocie powyżej 500 zł
Cel nie musi być określony
Można pożyczać pieniądze nieodpłatnie
Gotówka do ręki
S- wielkość zaciągniętego długu
N - liczba rat
r - roczna stopa procentowa
1+r lub (q) - czynnik procentowy
Dług został spłacony jeśli w określonym czasie suma spłaconych rat jest równa zaciągniętej kwocie wraz z odsetkami z tytułu użytkowania wypożyczonego kapitału
Oznaczenia:
An- wysokość n-tej raty
Tn - kwota długu zawarta w n-tej racie
Zn - odsetki spłacane w n-tej racie
Sn - reszta długu, która została dopłacenia po wpłacie n-tej raty
Z - suma wszystkich odsetek [odsetki skumulowane]
Wzór na wysokość n-tej raty:
![]()
Raty mogą być spłacane:
Zgodnie z okresem stopy procentowej lub w podokresach
Z dołu lub z góry
Raty mogą być jednakowych wysokości lub różnych
Odsetki mogą być doliczane zgodnie z okresem stopy procentowej lub w podokresach
Istnieje wiele różnych planów spłaty długu
(An), (Tn), (Zn), (Sn)
Oraz
![]()
Ciągi powyższe nie są niezależne!!!
Schematy spłaty długów
Schemat 1
Znane są wysokości rat ![]()
Pozostałe elementy planu spłaty długu wyznacza się z poniższych wzorów:
![]()
- reszta długu która pozostała do zapłacenia po wpłacie n-tej raty
![]()
![]()
- odsetki
![]()
- kwota długu zawarta w n-tej racie
![]()
- suma wszystkich odsetek
Schemat 2
Znany jest ciąg ![]()
Wtedy:
![]()
- reszta długu, która pozostała do zapłacenia po wpłacie n-tej raty
![]()
- odsetki
![]()
- wysokość n-tej raty
![]()
- suma wszystkich odsetek
Problem 1
Dług S mamy spłacić w N ratach.
Zakładamy, że wysokość rat: ![]()
zostały uzgodnione z wierzycielem. Obliczyć wysokość ![]()
ostatniej raty oraz ciąg.
Przykład 1 [będzie na egzaminie]
Wyznaczyć plan spłaty kredytu konsumpcyjnego w wysokości S=100 000 zł zaciągniętego na okres 5 lat znając wysokość 4 pierwszych rat.
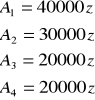
I wiedząc, ze oprocentowanie wynosi 10%.
Pominąć koszty prowizji i ubezpieczenia.
Rozwiązanie:
Mamy:
N= 5 lat
r=0,1 (10%)
q lub 1+r =1,1
![]()
oznaczamy ![]()
= 100 [tysięcy]
Korzystając ze wzorów ze schematu 1 otrzymujemy:
![]()
[tysięcy zł]
![]()
[tysięcy zł]
![]()
[tysięcy zł]
Odp. Do spłacenia zostało 70 000 zł
![]()
[tysięcy zł]
![]()
[tysiące zł]
![]()
[tysięcy zł]
![]()
[tysiąca zł]
![]()
[tysiąca zł]
![]()
[tysiąca zł]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Tabelka
n |
An |
Tn |
Zn |
Sn |
1 2 3 4 5 |
40 30 20 20 16,357 |
30 23 15,3 16,83 14,87 |
10 7 4,7 3,17 1,487 |
70 47 31,7 14,87 0 |
suma |
126,357 |
100 |
26,357 |
|
Problem 2
Raty o równych częściach długu. Dług S chcemy spłacić w N ratach, z których każda zawiera równą [jednakową] cześć długu
![]()
Przypadek 1
[spłaty zgodne z okresem stopy procentowej i okresem kapitalizacji]
Ciągi ![]()
można wyznaczyć posługując się wzorami ze schematu II
![]()
![]()
![]()
![]()
![]()
Przypadek 2
spłaty w podokresach stopy procentowej. Rok został podzielony na ![]()
równych podokresów.
Dług S ma być spłacony w mN ratach
w tym przypadku:
![]()
gdzie (k=1,2,3…., mN)
Każdy z pozostałych ciągów:
![]()
![]()
![]()
również liczby mN elementów.
W zależności od sposobu w jaki doliczane są odsetki otrzymujemy różne plany spłaty długów. Odpowiednio mamy:
Plan 1
Odsetki doliczane SA w podokresach
- zamiast ![]()
przyjmujemy ![]()
- zamiast ![]()
otrzymujemy ![]()
- liczba rat jest równa ![]()
Dla każdego ![]()
otrzymujemy:
![]()
![]()
![]()
![]()
![]()
Gdy m=1 wzory powyższe są takie same jak w przypadku 1
Dla m>1 natomiast
![]()
Dokładne [skumulowane odsetki]: ![]()
Przykład 2
Kredyt 70 000 zł ma być spłacony w ciągu 10 lat w miesięcznych ratach zawierających równą część długu. Roczna stopa r=0,06 (6%) oraz odsetki doliczane są wg opisanego wyżej planu.
Obliczyć wysokość skumulowanych odsetek
Rozwiązanie:
S= 70 000 ZŁ
N=10
m=12
R=0,06
Ze wzoru otrzymujemy:
![]()
Problem 3
Raty o równych wysokościach. Dług chcemy spłacić w równej wysokości np. A
Spłata zgodna z okresem stopy procentowej i okresem kapitalizacji:
![]()
W którym wystarczy przyjąć:
![]()
Otrzymujemy równanie:
![]()
![]()
Otrzymujemy:
![]()
Pozostałe elementy planu:
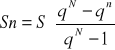
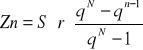
![]()
![]()
Spłaty w podokresach stopy procentowej.
Rok dzielimy na ![]()
podokresów i w każdym z tych podokresów dokonuje się spłaty długu w równych ratach i wielkości a. Łączna liczba rat wynosi mN.
odsetki doliczane są zgodnie z okresem stopy procentowej, raty spłacane z góry:
![]()
![]()
odsetki doliczane są w podokresach na postawie stopy procentowej. Raty spłacane są z góry.
![]()
![]()
Gdzie: ![]()
WYKŁAD 6
Elementy matematyki ubezpieczeniowej
Rozkład czasu trwania życia - zakłada się, ze czas życia ludzkiego jest zmienną losową o rozkładzie ciągłym
(x) - osoba, która obecnie ma x lat
(0) - noworodek
X- długość życia ludzkiego
W - maksymalny czas trwania życia dla danej generacji
![]()
Funkcja trwania życia [funkcja przeżycia]: ![]()
Czas dalszego trwania życia: ![]()
![]()
Prawdopodobieństwo, ze x-latek dożyje wieku x+1 lat: ![]()
Prawdopodobieństwo, ze x-latek nie osiągnie wieku x+t lat: ![]()
![]()
- prawdopodobieństwo, ze x-latek umrze w ciągu roku
![]()
- prawdopodobieństwo, ze x-latek przeżyje kolejny rok
![]()
Prawdopodobieństwo, że x-latek przeżyje t lat i umrze w ciągu następnych u lat:
![]()
Intensywność umieralności
Prawdopodobieństwo zgonu dokładnie w wieku x lat: ![]()
Siła życia: ![]()
![]()
Hipotezy dotyczące rozkładu trwania życia ludzkiego
Hipoteza de Maivera:
![]()
![]()
Hipoteza Kompertza:
![]()
gdzie ![]()
![]()
Hipoteza W.M. Makehama:
![]()
![]()
Całkowity czas trwania życia: ![]()
liczba pełnych lat jakie przeżyje x-latek
Rozkład zmiennej skokowej K(x)
Dla k=0,1,2,……
![]()
Dystrybuanta zmiennej k(x)
![]()
dla k=0,1,2,3,…..
![]()
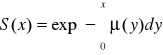
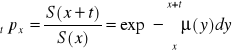
Tablice trwania życia [wymieralności]:
![]()
- przeciętna liczba zgonów w przedziale lx-lx+1
![]()
- prawdopodobieństwo zgonu w przeciągu roku
![]()
- prawdopodobieństwo przeżycia roku przez x-latka
![]()
- przeciętna liczba osób dożywających wieku ![]()
![]()
![]()
Ubezpieczenie na życie
Ubezpieczeniem na życie nazywamy umowę [kontrakt ubezpieczeniowy] miedzy ubezpieczonym, a ubezpieczycielem, w której:
ubezpieczony zobowiązuje się uiścić opłatę [składkę ubezpieczeniową] na rzecz ubezpieczyciela
ubezpieczyciel zobowiązuje się do wypłacenia sumy ubezpieczenia jednorazowo lub ratalnie na rzecz określonych w umowie osób lub spadkobierców w razie śmierci osoby ubezpieczonej jeśli nastąpiła ona w ściśle określonym czasie [terminie]
Rodzaje ubezpieczeń na życie:
ubezpieczenia życiowe - są to jednorazowe płatności dokonywane przez ubezpieczyciela w określonej wysokości następujące w przypadku śmierci ubezpieczonego
renty życiowe - są to ciągi płatności dokonywane przez ubezpieczyciela w ustalonych terminach na rzecz ubezpieczonego w sytuacji gdy osoba ta żyje
Składka ubezpieczeniowa brutto i netto
Składka ubezpieczeniowa brutto jest sumą:
składki ubezpieczeniowej netto, która jest równa oczekiwanej wypłacie
składki na pokrycie kosztów administracyjnych
składki za ryzyko, które jest nagrodą dla ubezpieczyciela, ze bierze ryzyko na siebie
Dożywotnie ubezpieczenie na wypadek śmierci - ubezpieczenie, którym płatność sumy ubezpieczenia na rzecz spadkobierców występujących w umowie ubezpieczeniowej następuje po śmierci ubezpieczonego
WYKŁAD 7
Osoba ubezpieczona ma w momencie zawierania umowy ubezpieczeniowej x lat [wiek wstępny]
Suma ubezpieczenia zostaje wypłacona na końcu roku w którym nastąpi śmierć osoby ubezpieczonej
Suma wypłaty wynosi 1 jednostkę pieniężną (1jp) [suma ubezpieczenia]
S- zmienna losowa określająca wysokość przyszłych świadczeń zdyskontowana na moment zawierania ubezpieczenia [aktualna wartość przyszłych świadczeń]
Jednorazową składkę netto obliczamy przyjmując, ze jest ona równa wartości oczekiwanej zmiennej losowej S
Ax - jednorazowa składka
![]()
Dożywotnie ubezpieczenie na wypadek śmierci:
![]()
![]()
![]()
![]()
Wysokość składki Ax można obliczyć także za pomocą liczb komutacyjnych, które można znaleźć w tablicach ubezpieczeniowych: ![]()
![]()
![]()
![]()
![]()
![]()
Przykład 1
Obliczyć jednostkową składkę netto w ubezpieczeniu na wypadek śmierci na kwotę 10 000 zł mężczyzny 50-letniego z miasta.
Przyjmując, ze r=0,1 (10%)
![]()
![]()
Terminowe ubezpieczenie na wypadek śmierci
Czasowym [n-letnim] ubezpieczeniem na wypadek śmierci nazywamy umowę na mocy, której wypłata sumy ubezpieczenia na rzecz spadkobierców dokonuje się po śmierci ubezpieczonego, jeśli nastąpi ona n-lat od momentu ubezpieczenia.
Jeśli ubezpieczony przeżyje n-lat wówczas ubezpieczyciel nie wypłaca sumy ubezpieczenia. - wypłata sumy ubezpieczenia może w ogóle nie nastąpić!!!
![]()
gdy k=0,1,2,…,n-1
![]()
gdy ![]()
![]()
![]()
![]()
Czyste ubezpieczenie na dożycie
Jest to ubezpieczenie, w którym suma ubezpieczenia jest wypłacana w końcu n-tego roku, jeżeli ubezpieczony będący w wieku x-lat w momencie zawierania ubezpieczenia dożyje wieku x+n lat
![]()
gdy k=0,1,2,,… n-1
![]()
gdy ![]()
![]()
![]()
![]()
Ubezpieczenie na dożycie [n-letnie]
Jest to ubezpieczenie na mocy którego suma ubezpieczenia wypłacana jest w wypadku śmierci ubezpieczonego jeśli nastąpi ona w ciągu n-pierwszych lat od momentu zawarcia ubezpieczenia lub na koniec roku n, jeśli ubezpieczony będący w wieku x- lat dożyje x+n lat
![]()
gdy k=0,1,2,…,n-1
![]()
gdy ![]()
![]()
![]()
26
wydatki
przychody
CF1
CF0
CF2
CFn-1
CFn
Wyszukiwarka
Podobne podstrony:
Prawo Finansowe prof Lemmonier id 386615
Opracowanie z prawa finansowego, Prawo finansowe - prof
Podstawy Audytu Finansowego prof UE dr hab J Pfaff
Prawo Finansowe prof Lemmonier id 386615
ANATOMIA wykład 7 układ limfatyczny; prof Łakomy
Wykład 1 - Terapia Manualna (prof. Śliwiński), fizjo
Metodologia - wykład 5.12.2010 - prof. Urbaniak - Zając, Metodologia nauk społecznych
Biomedyczne wyklady dawne lata prof J Cieslik, biomedyczne podstawy rozwoju i wychowania ( Anita Szw
ochrona zdrowia wykład, ISNS, od prof Hrynkiewicz
Wyklady ochrona srodowiska prof Gollinger, Study, Ochrona srodowiska, ochrona środowiska
WYKLAD~1, FIZYKA (W1 prof
notatki z wykładów - 2013-2014 - prof. Dąbrowski - KOMPARATYSTYKA, wprowadzenie do komparatystyki
03 134356 Negocjacje w biznesie (wyklady), Negocjacje w biznesie Prof
ANATOMIA wykład 6 układ krwionośny; prof Łakomy
więcej podobnych podstron