Akademia Górniczo-Hutnicza

Im. Stanisława Staszica w Krakowie

Wydział IMiR

Metody numeryczne - laboratorium

Maciej Maciejewski gr.7 IMIR

Interpretacja geometryczna metody Newtona:

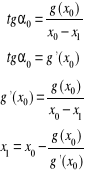
Stąd wzór iteracyjny:

Cel ćwiczenia:

Celem ćwiczenia było napisanie programu obliczającego wartość pierwiastka równania.

Wybrane równanie nieliniowe: y=2x²-8x-1

Przedział: <2;7>

Punkt startowy: x₀=3

Program liczący wartość pierwiastka równaia:

x=3; %Punkt od które zaczynamy poszukiwanie pierwiastka (x0)

z=0; %Zmienna do zliczania ilości kroków

p=1;

while abs(p)>=0.001 %Początek pętli liczącej pierwiastek funkcji

if (x>=2) & (x<=7) %sprawdzającej dokładność przybliżenia

p=(2.*x.^2-8.*x-1);

q=(4.*x-8);

p=p/q;

x=x-p;

z=z+1;

end

x

end

z

Wnioski:

W zakresie dużych przybliżeń ich zmiana powoduje zwiększenie dokładności wyniku, jednak dla pewnego odpowiednio małego przybliżenia dalsze zwiększanie dokładności nie wpływa na otrzymany wynik. Dlatego warto określać możliwie małą dokładność dla uzyskania wyniku z satysfakcjonującym przybliżeniem przy jednoczesnej oszczędności czasu działania programu.

---