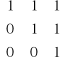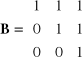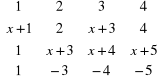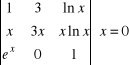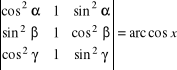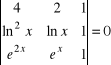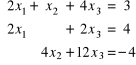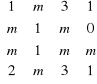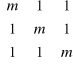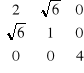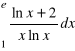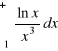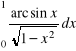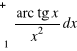Zestaw powtórzeniowy

(przygotowanie do egzaminu z matematyki)

Algebra liniowa

1.	Wyznacz macierz X z równania dla A = , B = .
2.	Wyznacz macierz X z równania dla A = , B = .
3.	Znajdź wszystkie macierze skośno-symetryczne A, dla których spełniony jest warunek , gdzie .
4.	Wykaż, że zbiór macierzy symetrycznych przemiennych z macierzą A = jest zamknięty ze względu na dodawanie i mnożenie.
5.	Znaleźć macierz X spełniającą równania: a) . b) , gdzie A = i B = .
6.	Dla jakich wartości zmiennej x macierz A = jest nieosobliwa?
7.	Rozwiązać równania: , , ..
8.	Ustal wartość i znak składnika wyznacznika macierzy A stopnia n wiedząc, że i .
9.	Oblicz det A dla A = , gdzie .
10.	Oblicz det A dla A = , gdzie .
11.	Ustal wartość i znak składnika wyznacznika macierzy A stopnia n wiedząc, że i n = 2k.
12.	Utwórz macierz A = , gdzie dla , punktu i oblicz jej wyznacznik.
13.	Oblicz wyznacznik macierzy , gdzie dla w punkcie x = (1, 2, 3, 4).
14.	Znajdź macierz przekształcenia liniowego, które każdemu punktowi płaszczyzny przyporządkowuje jego rzut prostokątny na prostą .
15.	Znajdź macierz przekształcenia liniowego na płaszczyźnie, w którym obrazem punktu x jest punkt x' taki, że .
16.	Dla jakich wartości parametru m obrazem punktu x = (1, m, m) w przekształceniu zadanym macierzą A jest punkt b = (2, -3, 5) , gdzie A = .
17.	Znajdź przeciwobraz punktu (1, 2) w przekształceniu liniowym zadanym macierzą A = .
18.	Rozwiąż układy równań: , . Znajdź wektory generujące zbiór rozwiązań układu .
19.	Przedstaw wektor x = (1, 1, -3) jako kombinację liniową wektorów a = (1, 2, 0), b = (1, 3, 3), c = (0, 2, 4).
20.	Zbadaj położenie punktu x = (1, 1, -3) względem trójkąta o wierzchołkach a = (1, 2, 0), b = (1, 3, 3), c = (0, 2, 4).
21.	Rozwiąż metodą eliminacji układ równań liniowych
22.	Zbadaj położenie punktu x = (3, 4, -4)) względem trójkąta o wierzchołkach (2, 2, 0), (1, 0, 4), (4, 2, 12).
23.	Wyznacz jądro przekształcenia liniowego określonego macierzą A. , gdzie .
24.	Zbadaj ilość rozwiązań układu równań w zależności od parametru m. , , .
25.	Ustal, dla jakich wartości parametru m zbiór rozwiązań jednorodnego układu równań liniowych określonego macierzą A = jest zbiorem jednoelementowym?
26.	Dla jakich wartości parametru m przeciwobraz punktu y = (m, m, m) w przekształceniu liniowym określonym macierzą A = jest zbiorem pustym ?
27.	Ustal, dla jakich wartości parametru a przeciwobraz punktu b = (4, 4, a) w przekształceniu liniowym określonym macierzą A = jest zbiorem pustym?
28.	Znajdź wartości własne i wektory własne macierzy A = . Zapisz formę kwadratową w postaci kanonicznej w bazie wektorów własnych.
29.	Znajdź wartości własne i wektory własne macierzy formy kwadratowej .
30.	Znajdź wartości własne i wektory własne macierzy przekształcenia liniowego A = .
31.	Zbadaj określoność formy kwadratowej w zależności od parametru m.

Funkcje jednej zmiennej

32.	Ustal liczbę pierwiastków równania a) . b) . Oszacuj pierwiastki kolejnymi liczbami całkowitymi.
33.	Naszkicuj wykresy funkcji: , , .
34.	Ustal, dla jakich wartości parametru m równanie ma jedno rozwiązanie.
35.	Dla jakich wartości parametru m równanie ma dwa rozwiązania?
36.	Ustal, dla jakiej wartości parametru a funkcja funkcja ma ekstremum maksimum równe 8.
37.	Ustal, dla jakiej wartości parametru a funkcja funkcja ma ekstremum maksimum równe 325.
38.	Wykorzystując różniczkę drugiego rzędu funkcji oblicz wartość tej funkcji dla .
39.	Znajdź wielomian trzeciego stopnia przybliżający funkcję w otoczeniu liczby i oblicz wartość tej funkcji dla .
40.	Znajdź wielomian stopnia trzeciego przybliżający funkcję w otoczeniu . Wykorzystaj otrzymany wielomian do obliczenia .
41.	Znajdź wielomian stopnia trzeciego przybliżający funkcję w otoczeniu . Wykorzystaj otrzymany wielomian do obliczenia .
42.	Za pomocą wielomianu trzeciego stopnia przybliżającego funkcję w otoczeniu punktu oblicz .
43.	Dla jakich wartości parametrów a i b funkcja jest różniczkowalna dla każdego ?
44.	Dla jakich wartości parametrów a i b funkcja jest różniczkowalna dla każdego ?
45.	Napisz równania stycznej do wykresu funkcji w podanym punkcie: a) w . b) w .
46.	Oblicz koszt krańcowy i przeciętny produkcji dla x =100 wiedząc, że funkcja kosztów całkowitych produkcji wyraża się wzorem .
47.	Wyznacz elastyczność funkcji . Oblicz , , .
48.	Dana jest funkcja kosztów całkowitych produkcji: . Cena zbytu danego wyrobu jest stała i wynosi 70 zł za jednostkę. Przy jakiej wielkości produkcji zysk jest największy? Wyznacz przedział opłacalności produkcji.
49.	Dana jest funkcja kosztów przeciętnych produkcji . Oblicz przyrost kosztów produkcji przy zwiększeniu produkcji z poziomu 100 do 101 sztuk wyrobu.
50.	W nagrodę za zaliczenie roku student dostanie od rodziców 1200 zł , które przeznaczy na wakacje. Planuje pojechać nad morze, gdzie średnia cena noclegu wynosi 25 zł za dobę, koszt wyżywienia 15 zł dziennie a na „przyjemności” planuje wydawać również 15 zł. dziennie. Bilet kolejowy w jedną stronę kosztuje 50 zł. Zapisz i narysuj wykres funkcji kosztów wakacji studenta oraz wykres zasobności jego portfela w zależności od ilości dni pobytu. Po ilu dniach najpóźniej mogą się go spodziewać rodzice?
51.	Aby pojechać na zasłużone wakacje, student zamierza wziąć kredyt wysokości 800 zł i spłacić go w ciągu czterech miesięcy. Podpisując umowę kredytową należy wpłacić 5% pożyczanej kwoty, a miesięczne raty składają się z kwoty kredytu i niespłaconego kapitału oprocentowanego na 5%. Tak więc, pierwsza rata jest równa 200 + . Oblicz koszt kredytu.
52.	Królewna Śnieżka zebrała w lesie pewną ilość orzechów i postanowiła rozdać je krasnoludkom. Najstarszy - Mędrek dostał połowę wszystkich orzechów, Wesołek - połowę tego co zostało, Apsik , Nieśmiałek, Śpioch i Gburek - każdy dostawał połowę tych orzechów, które zostawały Śnieżce po obdarowaniu poprzednich. W rezultacie dla Gapcia został jeden orzech. Ile było orzechów? Czy dla Śnieżki coś zostało?

Funkcje wielu zmiennych

53.	Oblicz wartość sumy dla funkcji .
54.	Oblicz wartość wyrażenia dla funkcji .
55.	Znajdź wielomian drugiego stopnia przybliżający funkcję w otoczeniu punktu (0, 0) i oblicz przybliżoną wartość tej funkcji w punkcie .
56.	Oblicz przybliżoną wartość funkcji w punkcie wykorzystując wielomian Taylora stopnia drugiego.
57.	Ustal znak różniczki drugiego rzędu funkcji w punkcie (2, 2).
58.	Dana jest funkcja . Ustal dla jakich wartości parametru m różniczka drugiego rzędu tej funkcji jest dodatnio określona.
59.	Ustal znak różniczki drugiego rzędu funkcji w punkcie dla n = 4.
60.	Ustal, dla jakich wartości parametru a funkcja ma ekstremum lokalne. Oblicz wartość ekstremum.
61.	Ustal, dla jakiej wartości parametru a funkcja ma ekstremum lokalne równe 27 ?
62.	Na krzywej, będącej wykresem funkcji , znajdź punkt leżący najbliżej prostej . Oblicz odległość tego punktu od prostej.
63.	Na krzywej będącej wykresem funkcji znajdź punkt leżący najbliżej prostej . Oblicz odległość tego punktu od prostej.
64.	Na krzywej będącej wykresem funkcji , znajdź punkt leżący najbliżej prostej . Oblicz odległość tego punktu od prostej.
65.	Znajdź wartości ekstremów lokalnych funkcji dla punktów leżących na krzywej .
66.	Znajdź ekstrema funkcji dla punktów leżących na paraboli .
67.	W trójkącie o wierzchołkach A (-4, 0), B (0, 8), C (0, 0) znajdź punkt, dla którego suma odległości od boków jest najmniejsza.
68.	W trójkącie o wierzchołkach A (-4, 0), B (0, 8), C (0, 0) znajdź punkt, dla którego suma kwadratów odległości od boków jest najmniejsza.
69.	Znajdź ekstrema funkcji określonej na zbiorze .
70.	a) Znajdź globalne ekstrema funkcji , której dziedziną jest zbiór .
	b) Znajdź globalne ekstrema funkcji , której dziedziną jest zbiór .
71.	Wyznacz wierzchołki tego prostokąta wpisanego w elipsę , którego pole jest największe.
72.	Wyznacz wymiary tego walca o objętości 128 , którego powierzchnia jest najmniejsza.
73.	Długość przekątnej prostopadłościanu jest równa , a stosunek długości krawędzi podstawy 1:3. Wyznacz wymiary prostopadłościanu o największej objętości.
74.	Na kuli o promieniu R opisano stożek o najmniejszej objętości. Podaj wymiary tego stożka.
75.	Wyznacz współrzędne punktu należącego do paraboli tak, aby jego odległość od punktu A(0, 10) była najmniejsza.

Całki

76.	Oblicz całki oznaczone:
a) .	b) .	c) .	d) .
77.	najdź tę funkcję pierwotną funkcji , której wykres przechodzi przez punkt .
78.	Wiadomo, że do wykresu funkcji należą punkty (0, 0) i (1, 1), oraz że jej druga pochodna . Wyznacz F.
79.	Znajdź tę funkcję pierwotną funkcji , której wykres przechodzi przez punkt .
80.	Wiadomo, że do wykresu funkcji należą punkty (0, -2) i , oraz że jej druga pochodna . Wyznacz F.
81.	Znajdź funkcję wiedząc, że i i .
82.	Znajdź funkcję wiedząc, że , i .
83.	Oblicz pole obszaru ograniczonego wykresem funkcji i prostymi .
84.	Oblicz pole obszaru ograniczonego krzywymi i .
85.	Oblicz pole obszaru ograniczonego wykresami funkcji i .
86.	Obliczyć pole obszaru ograniczonego wykresami funkcji i .
87.	Oblicz pole obszaru ograniczonego wykresem funkcji i osią OX w całej jej dziedzinie.
88.	Obliczyć pole obszaru ograniczonego krzywą i stycznymi do tej krzywej przechodzącymi przez początek układu współrzędnych.
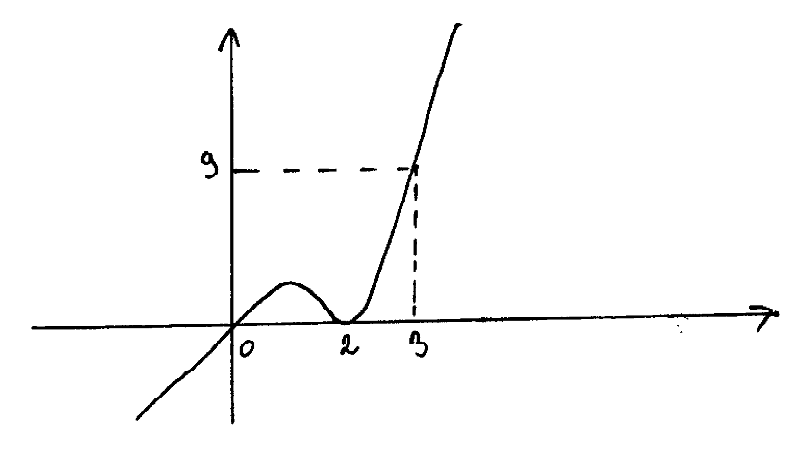
89.	Rysunek przedstawia wielomian trzeciego stopnia, który jest wykresem pochodnej funkcji . Znajdź funkcję wiedząc, że .
90.	Oblicz objętość bryły powstałej w wyniku obrotu wokół osi OX krzywej w przedziale .
91.	Oblicz objętość bryły powstałej w wyniku obrotu wokół osi OX krzywej w przedziale .
92.	Dana jest funkcja kosztów krańcowych: .Wyznacz funkcję kosztów całkowitych, jeżeli wiadomo, że koszt przeciętny przy produkcji 20 sztuk wyrobu wynosi 60 zł.
93.	Dana jest funkcja kosztów krańcowych produkcji: . Oblicz przeciętny koszt wyprodukowania jednej sztuki wyrobu przy produkcji 100 jednostek, wiedząc, że koszty stałe tej produkcji wynoszą 8 000.
94.	Dana jest funkcja kosztów krańcowych: .Wyznacz koszty stałe produkcji, jeżeli wiadomo, że koszt przeciętny przy produkcji 10 sztuk wyrobu wynosi 240 zł.

---