Wydział mechatroniki politechniki warszawskiej

Laboratorium Fizyki I			Ćwiczenie nr: 37
						Data: 2.11.2005
Wydział: MCHTR	Grupa: 23	Zespół: 8	Punktacja	Przygotowanie: 4
Nazwisko i imię: Owczarek Marcin
Temat ćwiczenia: Falowe własności mikrocząsteczek					Sprawozdanie:
Prowadzący: M. Ćwil					Suma punktów:

1. Wiadomości wstępne:

Wszystkie rodzaje obiektów mikroświata (kwanty pola sił, cząstki elementarne itp.) w pewnych warunkach eksperymentalnych (np. zjawisko dyfrakcji) manifestują właściwości pozwalające na opis ich jako fale (tj. np. fale świetlne, de Brogila fale), w innych (np. w zderzeniach sprężystych) daje się je lepiej opisywać jako cząstki (np. fotony, cząstki elementarne).

Również fale akustyczne w sieci krystalicznej manifestują czasem właściwości korpuskularne (fotony). Dualizm korpuskularno-falowy jest jednym z "dogmatów" współczesnej fizyki, koncepcja ta pojawiła się w pierwszych latach XX w. Wcześniej istniał spór o naturę promieniowania (głównie światła).

Spór istniał od czasów I. Newtona, który uważał światło za rój cząstek, a polemizował z nim Ch. Huygens, który rozpatrywał światło jako falę.

Broglie fale, inaczej fale materii to jeden z aspektów istnienia materii. Cząstki elementarne i inne obiekty mikroświata w pewnych warunkach wykazują właściwości typowe dla fal (np. ulegają zjawisku dyfrakcji). Każdej cząstce swobodnej o pędzie p można przypisać długość fali

 = h/p,

gdzie h - stała Plancka.

W ćwiczeniu wykorzystaliśmy także zjawisko dyfrakcji na sieci krystalicznej. Polega ono na tym, iż każdy atom z płaszczyzny atomowej kryształu staje się źródłem nowej fali, które interferując ze sobą tworzą falę odbitą. Kryształ posiada oczywiście wiele płaszczyzn stąd zjawisko to może zachodzić w różny sposób. Jeśli kryształ zaczniemy obracać to zaobserwujemy na ekranie ustawionym za nim okręgi. Aby uniknąć obracania stosujemy polikryształy złożone z wielu krystalitów w których zawsze znajdzie się płaszczyzna atomowa spełniająca warunek Bragga:

2d sinΘ=n λ

Gdzie d - odległość między pł. at. ;

Θ - kąt pomiędzy promieniem padającym a płaszczyzną at.

2. Przebieg i cel ćwiczenia.

W ćwiczeniu wykorzystaliśmy doświadczenie Thomsona, który umieścił w lampie oscyloskopowej, za układem anod ogniskujących, cienką złotą folię (w naszym przypadku aluminiowej i grafitowej, folia taka ma budowę polikrystaliczną).

Wiązka elektronów trafiając na folię podlega zjawisku opisanemu we wstępie, co ostatecznie obserwowaliśmy jako okręgi na ekranie. Gdybyśmy mieli możliwość zmniejszenia natężenia wiązki elektronów do takiej wartości, że w przybliżeniu emitowane byłyby pojedyncze elektrony, obserwowalibyśmy jedynie pojedyncze błyski. Jednak w naszym przypadku było to niemożliwe do uzyskania i mogliśmy jedynie uwierzyć w teorię.

W oscyloskopie mogliśmy regulować napięcie U, które przekładało się na zwiększenie energii przyspieszanych elektronów zgodnie z zależnością: E_k= e/U.

Biorąc pod uwagę fakt, że r>>D wzór Bragga w naszym przypadku wygląda trochę prościej:

dD/2r= nλ

gdzie D- śr okręgów; r- odl. folii od ekranu.

λ można obliczyć ze wzoru λ=h/p . Brakuje jeszcze pędu elektronu, który otrzymamy z zależności: eU= p²/2m skąd:

przekształcając wzór Bragga dochodzimy do zależności z której możemy wyznaczyć odległość międzyatomową d:

Pomiary przeprowadziliśmy dla sześciu różnych napięć i dla dwu różnych folii.

Dla folii aluminiowej o sieci kubicznej i powierzchni centrowanej (r=300±1mm) mierzyliśmy średnice czterech okręgów interferencyjnych. Oto wyniki pomiarów:

Lp.		D1 [m]	D2 [m]	D3 [m]	D4 [m]
1	0,2618	0,0245	0,0285	0,0400	0,0470
2	0,26612	0,0250	0,0290	0,0405	0,0485
3	0,27126	0,0255	0,0295	0,0420	0,0490
4	0,28583	0,0280	0,0315	0,0440	0,0515
5	0,29437	0,0285	0,0325	0,0465	0,0540
6	0,30802	0,0295	0,0340	0,0480	0,0560

Otrzymane wyniki wprowadziliśmy do programu Origin, za pomocą którego sporządziliśmy wykresy.

Program rozwiązał następujące równanie liniowe: Y = A + B * X,

gdzie Y to D, B to
, a X to
.

Dla D1:

Parameter Value Error

A -0,05354 0,02837

B 1,1445 0,10069

Dla D2:

A -0,03284 0,007

B 1,21312 0,02484

Dla D3:

A -0,07043 0,03093

B 1,7972 0,10979

Dla D4:

A -0,03116 0,02793

B 1,92425 0,09914

Dane z tablic:

r = 0.300m, odległość folia-ekran

h = 6.6261 10^-34 Js, stała Plancka

m = 9,1094 10^-31 [kg] masa elektronu

e = 1.6022 10^-19 [C] ładunek elektronu

odległości d w polikrysztale wyniosą:

Błąd systematyczny należy obliczyć z różniczki zupełnej biorąc pod uwagę fakt, że d zależy od r, D i U.

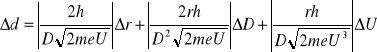
Błąd przypadkowy:

t-Studenta: t(β,k)=t(0,9;5)=2,02

Δd_przyp={error}*d*t-Studenta

Błąd całkowity:

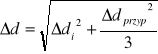
Wyniki przedstawia tabela:

Pierścień	B	di	Δdi	Δdprzyp	Δd
D1	1,1445	6,429*10^-10	0,061*10^-10	1,308*10^-10	0,757*10^-10
D2	1,21312	6,066*10^-10	0,047*10^-10	0,304*10^-10	0,182*10^-10
D3	1,7972	4,094*10^-10	0,025*10^-10	0,908*10^-10	0,525*10^-10
D4	1,92425	3,824*10^-10	0,019*10^-10	0,766*10^-10	0,443*10^-10

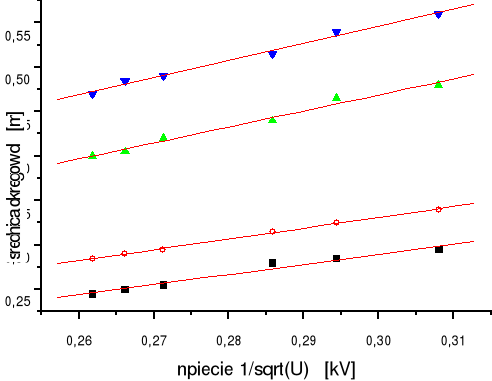
Wykresy dla D1, D2, D3 i D4 (licząc od dołu do góry):

Dla folii grafitowej o sieci heksagonalnej (r=127±1mm) wykonywaliśmy pomiary dwóch okręgów interferencyjnych. Oto wyniki pomiarów:

Lp.		D1 [m]	D2 [m]
1	0,33113	0,016	0,0265
2	0,35444	0,017	0,0285
3	0,37424	0,018	0,0300
4	0,39653	0,0185	0,0345
5	0,42295	0,020	0,0335
6	0,43644	0,0205	0,0350

Wyniki po wprowadzeniu danych do programu Origin i wykonaniu wykresów dla poszczególnych wartości:

Dla D1

Parameter Value Error

A 0,01947 0,00732

B 0,42456 0,01887

Dla D2

A 0,00727 0,00833

B 0,78006 0,02149

Dane z tablic:

r = 0.300m, odległość folia-ekran

h = 6.6261 10^-34 Js, stała Plancka

m = 9,1094 10^-31 [kg] masa elektronu

e = 1.6022 10^-19 [C] ładunek elektronu

odległości d w polikrysztale wyniosą:

Błąd systematyczny należy obliczyć z różniczki zupełnej biorąc pod uwagę fakt, że d zależy od r, D i U.

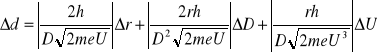
Błąd przypadkowy:

t-Studenta: t(β,k)=t(0,9;5)=2,02

Δd_przyp={error}*d*t-Studenta

Błąd całkowity:

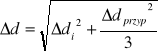
Wyniki przedstawia tabela:

Pierścień	B	di	Δdi	Δdprzyp	Δd
D1	0,42456	1,733*10^-9	0,014*10^-9	0,066*10^-9	0,041*10^-9
D2	0,78006	0,944*10^-9	0,006*10^-9	0,041*10^-9	0,025*10^-9

A oto wykresy dla D1 i D2

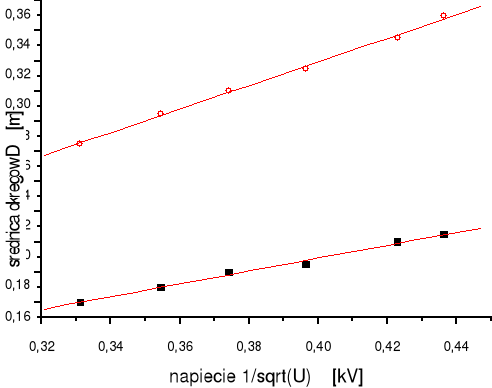
3. Wnioski:

Po wykonaniu ćwiczenia możemy stwierdzić, że średnice okręgów interferencyjnych są odwrotnie proporcjonalne do pierwiastka kwadratowego napięcia nadającego pęd elektronom, co jest zgodne ze wzorem, który otrzymaliśmy przekształcając wzór de Broglie`a i Bragga. Zatem założenia de Broglie`a są słuszne ponieważ elektrony uległy interferencji na użytych przez nas siatkach dyfrakcyjnych (polikryształach). Niestety użyte przyrządy pomiarowe nie pozwoliły na dokładne oszacowanie odległości między płaszczyznami atomowymi.. Jednak otrzymane wielkości są tego samego rzędu, co rzeczywiste wartości.

Marcin owczarek -laboratorium nr 2 - 2 -

---