Wiktor Andrzejkiewicz
OŚ, Gr. 1, Sem. 5
Dokumentacja dotycząca:
Szacowania zasobów energetycznych wiatru
Określenie przedmiotu projektu
Dokumentacja zawiera oszacowanie zasobów energetyczne wiatru według pomiarów ze stacji nr. 12385 w Siedlcach. Współrzędne geograficzne: N 52.18°, E 22.27°, 149m n.p.m. (http://cosmo.torun.pl/~tomlacz/meteo/kodymet.txt)
Opis metodyki, przyjętej w projekcie
Metodyka przyjeta w projekcie opiera się na statystycznym rozkładzie prędkości wiatru opisanym przy użyciu rozkladu Weibulla. Rozkład ten opisuje zmienność wiatru w jednym punkcie. Posiadając ciąg pomiarów prędkości wiatru można oszacować moc, którą otrzymamy z turbiny postawionej w tym punkcie.
Charakterystyka geograficzna miejsca, którego dotyczy projekt
Siedlce leżą na Wysoczyźnie Siedleckiej, która geograficznie jest częścią Niziny Południowopodlaskiej; między rzekami Muchawka Helenka, na wysokości 155 m n.p.m.
Klimatologia wiatru w miejscu, którego dotyczy projekt
Siedlce znajdują się w strefie klimatu umiarkowanego z przeważającymi wpływami klimatu kontynentalnego.
Średnie temperatury letnie kształtują się od 12,2°C do 23,9°C.
Zimą wynoszą one odpowiednio od -4°C do 1,2°C.
Średnie roczne opady w Siedlcach wynoszą 522 mml.
Kalisz - Prędkości wiatru (m/s) |
|||||
Wartość minimalna |
Pierwszy kwartyl |
Mediana |
Średnia |
Trzeci kwartyl |
Wartość maksymalna |
0,00 |
2,00 |
3,00 |
3,04 |
4,00 |
14 |
Histogram przedstawia częstość występowania wiatrów o danej prędkości. Oś OY przedstawia ilość godzin w roku, a oś OX przedstawia prędkość wiatru.
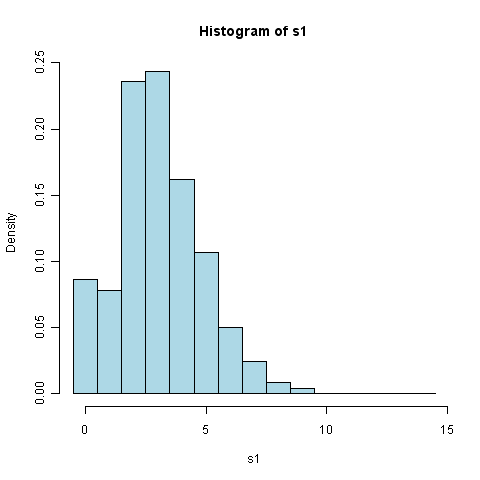
Ten histogram jest identyczny co poprzedni tylko przeskalowany na prawdopodobieństwo wystąpienia wiatru o danej prędkości.
Analiza histogramu
Minimalna prędkość wiatru dla turbiny musi wynosić 5m/s, Należy określić ile godzin w roku spełnia ten warunek. Na podstawie powyższego wykresu, stwierdza się, że jest ich około 1750 co stanowi 20% wszystkich godzin w roku. Należy pamiętać, że depesze SYNOP użyte do obliczeń zawierają pomiary przeprowadzane co 3 godziny.
Opis wykonanego ćwiczenia
Odpowiednie dane pobrane z serwera dla Stacji 12385 w Siedlcach dla zadanego roku. Dane połączono w ciąg a następnie przepisano do zbioru „s” za pomocą programu statystycznego „R”. Po wpisaniu komendy summary (s) otrzymano podstawowe dane statystyczne analizowanych danych. Dla pewności odfiltrowano możliwe wartości nonsensowne i przepisano dane do zbioru „s2”. Następnie określono progi dla histogramu prędkości wiatru (1). Przeskalowano go również na prawdopodobieństwo (2). Otrzymane wykresy (1) i (2) zamieszczono w punkcie 4. Automatyczne dobranie parametrów dla rozkładu Weibulla poleceniem fitdist(s2,”weibull”) nie powiodło się więc przystąpiono do ręcznego obliczania paramertów rozkładów prawdopodobieństa. Kożystając ze wzoru:
należy obliczyć parametr k, var(s2)/(mean(s2)^2)+1 otrzymano 1.342789. Należało doprowadzić do równości pomiedzy prawą a lewą strone równania. Lewą ujęto funkcją f po czym metodą iteracyjną określono parametr k= 1.764041. Obliczono parametr skali: mean(s1)/f1(1.342789) = 3.311971. Sporządzono wykres prawdopodobieństwa występowania prędkości wiatru z naniesionym rozkładem Weibulla:
Oszacowanie potencjału energetycznego
Obliczono go ze wzorów:
λ - parametr skal
> 0.5*1.27*3.311971^3*gamma(1+3/1.764041)
[1] 35.65293
Potencjał energetyczny
Gdzie:
Q - moc jaką można uzyskać z turbiny
X - powierzchnia zataczania turbiny
P - Potencjał energetyczny
W przypadku turbiny Vestas V -80, powierzchnia zataczania wynisi 5027 m2, zatem:
Uwagi i wnioski
Dane wykorzystane do obliczeń pochodzą z pomiarów wykonywanych co 3 godz. negatywnie wpływając na precyzję otrzymanych wyników. Chwilowe (któtsze niż 3 godzinne) podmuchy wiadru nie będą uwzględnione. Model statystyczny uśrednienia posiadane dane do średniej rocznej prędkości wiatru. Parametr skali został obliczony z przybliżeniem. Pomiary prędkości wiatru były zaokrąglane do liczb całkowitych. Rozkład Weibulla przeszacowuje częstość występowania wiatru o prędkościach 1m/s i niedoszacowywuje wartości 2-5m/s. Te czynniki powodują niedoszacowanie mocy jąką można uzyskać z turbiny.
„Błąd wstępnego szacowania warunków wiatrowych dla danego miejsca tylko na podstawie średniej rocznej prędkości wiatru. Mimo,że wielkość ta jest taka sama, rozkład prędkości jest zdecydowanie odmienny. Różnice w gęstości energii dla skrajnych przypadków się siegają ponad 2,5-krotności. Nieuwzględnienie rozkładu Weibulla w ocenie warunków wiatrowych prowadzić może do zdecydowanego niedoszacowania potencjału energetycznego wiatru, a tym samym do poważnego ryzyka inwestycyjnego. W analizie warunków wiatrowych niezbędne jest prześledzenie sytuacji ekstremalnych. Dotyczy to w szczególności oceny prawdopodobieństwa wystąpienia maksymalnych prędkości wiatru oraz porywów wiatru, zagrażających pracy elektrowni wiatrowych, bądź nawet prowadzących do ich zniszczenia. Prawdopodobieństwo to określa się zwykle dla jednorocznego okresu pomiarowego oraz dla ostatnich 50 lat.” [„Analiza warunków wiatrowych dla potrzeb energetycznych” mgr Agnieszka Latko, dr inż. Andrzej Latko]
R version 2.8.1 (2008-12-22)
Copyright (C) 2008 The R Foundation for Statistical Computing
ISBN 3-900051-07-0
R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.
R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.
Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.
> library(ncdf)
> nc<-open.ncdf("c:/wyniki/010100_123121_12385.nc")
> s<-get.var.ncdf(nc,"SPD_ts")
> hist(s,col="light blue")
> summary (s)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 2.00 3.00 3.04 4.00 14.00
> s1<-s[!(s==-99999)]
> summary (s1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 2.00 3.00 3.04 4.00 14.00
> hist(s1,col="light blue")
> hist(s1,plot=FALSE)
$breaks
[1] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
$counts
[1] 449 655 672 448 294 139 67 23 10 0 1 0 0 1
$intensities
[1] 0.1627400907 0.2374048568 0.2435665096 0.1623776731 0.1065603480
[6] 0.0503805727 0.0242841609 0.0083363538 0.0036245016 0.0000000000
[11] 0.0003624502 0.0000000000 0.0000000000 0.0003624502
$density
[1] 0.1627400907 0.2374048568 0.2435665096 0.1623776731 0.1065603480
[6] 0.0503805727 0.0242841609 0.0083363538 0.0036245016 0.0000000000
[11] 0.0003624502 0.0000000000 0.0000000000 0.0003624502
$mids
[1] 0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5 12.5 13.5
$xname
[1] "s1"
$equidist
[1] TRUE
attr(,"class")
[1] "histogram"
> progi<-c(-0.5,0.5,1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5,10.5,11.5,12.5,13.5,14.5)
> hist(s1,col="light blue", breaks=progi)
> png()
> hist(s1,col="light blue", breaks=progi)
> dev.off()
> fitdistr(s1,"weibull")
Error in optim(x = c(3, 4, 4, 4, 3, 4, 4, 5, 3, 4, 4, 4, 3, 4, 3, 3, 3, :
non-finite value supplied by optim
> var(s1)
[1] 3.167842
> var(s1)/(mean(s1)^2)+1
[1] 1.342789
> f1<-function(k){return(gamma(1+1/k))}
> f1(1.3)
[1] 0.9235767
> f2<-function(k){return(gamma(1+2/k))}
> f<-function(k){return(f2(k)/((f1(k))^2))}
> f(1.855)
[1] 1.312964
> f(1.764041)
[1] 1.342789
> mean(s1)/f1(1.342789)
[1] 3.311971
> png()
> hist(s1,col="light blue",probability=TRUE,breaks=progi)
> w=rweibull(1000000,shape=1.764041,scale=3.311971)
> lines(density(w,bw=1),col="red",lwd=3)
> dev.off()
> png()
> hist(s1,col="light blue",probability=TRUE,breaks=progi)
> dev.off()
> png()
> hist(s1,col="light blue",probability=TRUE,breaks=progi)
> w=rweibull(1000000,shape=1.764041,scale=3.311971)
> lines(density(w,bw=1),col="red",lwd=3)
> dev.off()
> 0.5*1.27*3.311971^3*gamma(1+3/1.764041)
[1] 35.65293
> 5027*35.65293
[1] 179227.3
Wyszukiwarka
Podobne podstrony:
Szacowanie wiatru, Szacowanie zasobów energetycznych wiatru - Dokumentacja
Wiatrak … bez wiatru Wiktor Sklarow chce zaopatrywać Rosję w energię elektryczną
Wiatrak … bez wiatru Wiktor Sklarow chce zaopatrywać Rosję w energię elektryczną
Szacowanie zasobów st
metodologia badan wydatkow i szacowanie budzetu rekomowego
Energia wiatru(1)
pm 3 4 szacowanie niepewnosci
5 egzamin geo inz rzad i 2010 , Studia Geodezja i szacowanie nieruchomości, rok III, GI
Metody szacowania ryzyka zawodowego
Dane o przedmiocie i?lu szacowania
WPLYW WIATRU NA TRAJEKTORIE POCISKU
Obliczenia Wiktora
Budowa i szacowanie modeli ekonometrycznych
Odziaływanie wiatru, Studia, Sem 5, SEM 5 (wersja 1), Konstrukcje Metalowe II, Konstrukcje stalowe I
02-Karnawał w Wiktorii, J. Kaczmarski - teksty i akordy
Energia wiatru
Wnisek o ustalenie warunków zabudowy, Geodezja i szacowanie nieruchomości, Sem 4, PPPiPU
więcej podobnych podstron