Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (1)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

Organizacja zajęć

Wykład: 1h30' / tydzień

Ćwiczenia: 2 grupy 1h30' / tydzień

Rozliczenie zajęć: zaliczenie ćwiczeń (obecność + 2 projekty) + egzamin

Konsultacje: o każdej porze

Materiały do zajęć:

http://wmii.uwm.edu.pl/~kulesza/Cyfrowe_przetwarzanie_sygnałów/

Literatura

S. K. Mitra, Digital Signal Processing. A computer-based approach,
McGraw-Hill 2006

V. K. Ingle, J. G. Proakis, Digital Signal Processing using MatLab, ITP 1997

R. G. Lyons, Understanding Digital Signal Processing, Prentice Hall 2001

M. H. Hayes, Digital Signal Processingi, McGraw-Hill 1999

T. P. Zieliński, Cyfrowe przetwarzanie sygnałów: od teorii do zastosowań, WKŁ
Warszawa 2005

R. G. Lyons, Wprowadzenie do cyfrowego przetwarzania sygnałów, WKŁ
Warszawa 1999

J. Szabatin, Podstawy teorii sygnałów, WKŁ Warszawa 2002

S. W. Smith, The scientist's and engineer's guide to Digital Signal Processing,
California Technical Publishing, San Diego 1999, dostępne on-line:
http://www.dspguide.com/pdfbook.htm

Zawartość zajęć

1) Sygnały i ich przetwarzanie.

2) Cyfrowe przetwarzanie sygnałów czasu ciągłego – próbkowanie, przetwarzanie

A/C, C/A i rekonstrukcja sygnału.

3) Sygnały i układy czasu dyskretnego.

4) Analiza częstotliwościowa sygnałów - transformata Fouriera.

5) Analiza sygnałów – transformaty ortogonalne.

6) z-transformata.

7) Układy LTI (Linear Time-Invariant).

8) Projektowanie filtrów FIR, IIR.

9) Kodowanie i kompresja sygnałów multimedialnych.

10) Sygnały losowe czasu dyskretnego.

Czym jest DSP?

Digital Signal Processing – Cyfrowe przetwarzanie sygnałów

Sygnał: każda wielkość fizyczna zależna od czasu, położenia lub

też od innej niezależnej zmiennej lub zmiennych.

Sygnał jest nośnikiem informacji pomiędzy badanym układem

a obserwatorem.

Cyfrowy: odnoszący się do sygnałów zmieniających się skokowo

w dziedzinie czasu i amplitudy (spróbkowanych i skwantowanych).

Przetwarzanie sygnału: przekształcenie sygnału wejściowego

według zadanego algorytmu.

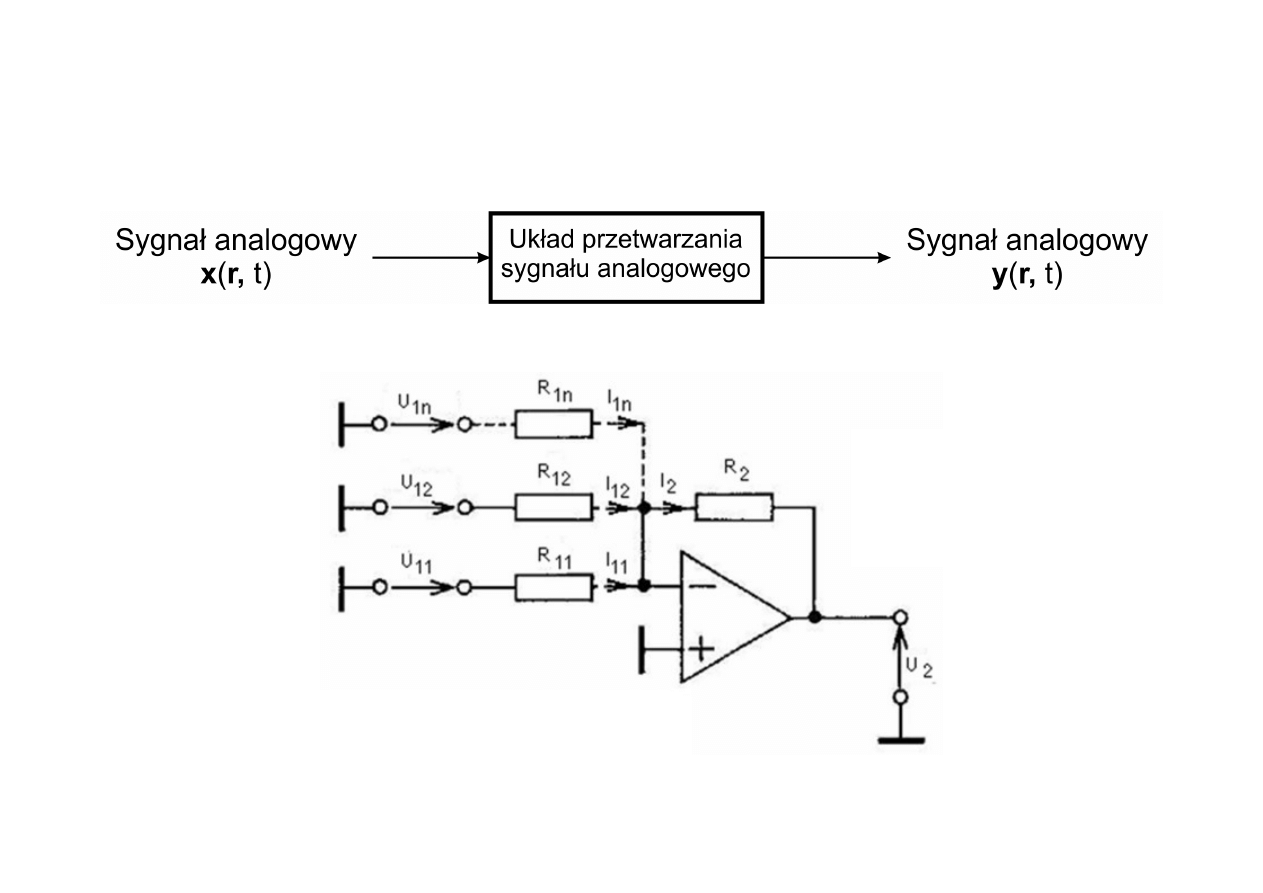
Metody przetwarzania sygnałów

Przetwarzanie analogowe (ASP)

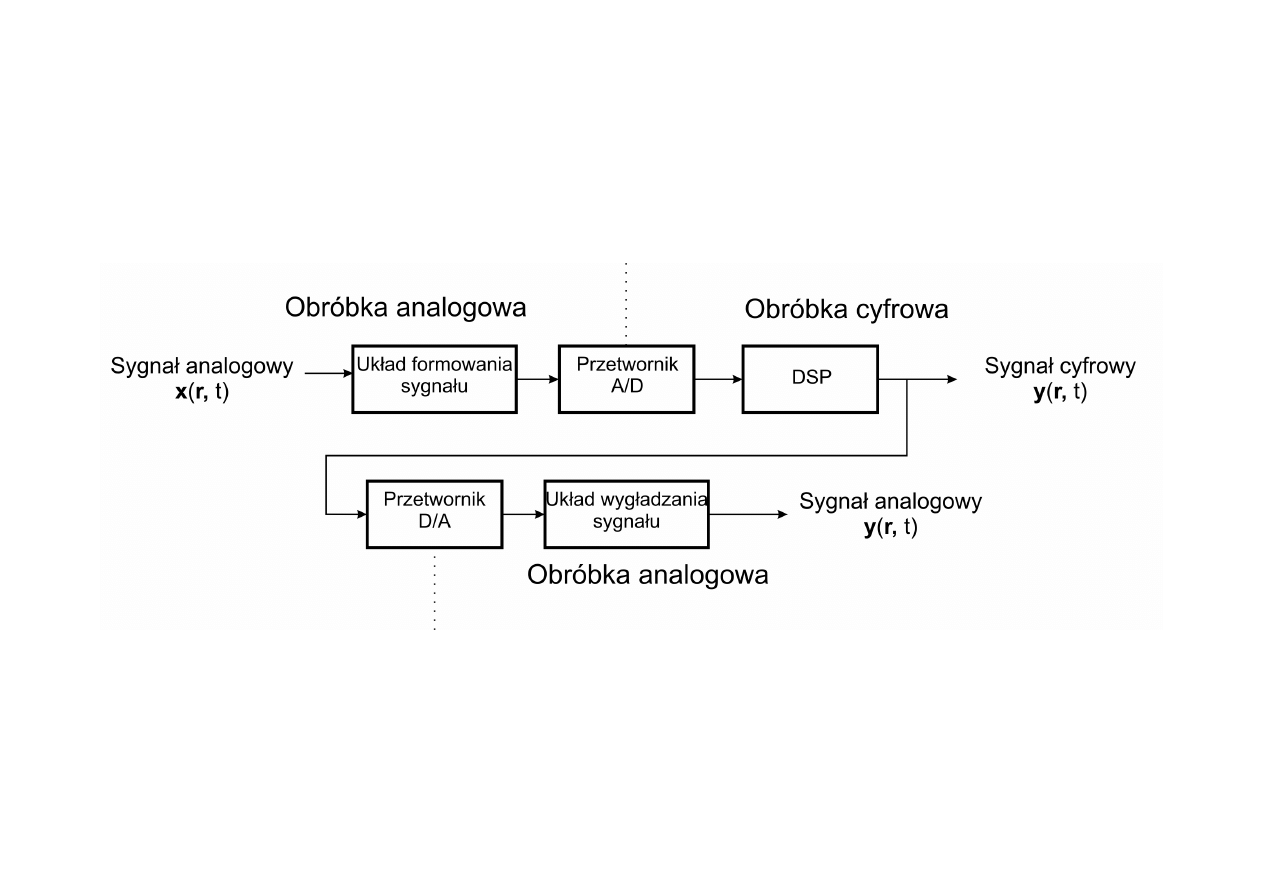
Przetwarzanie cyfrowe (DSP)

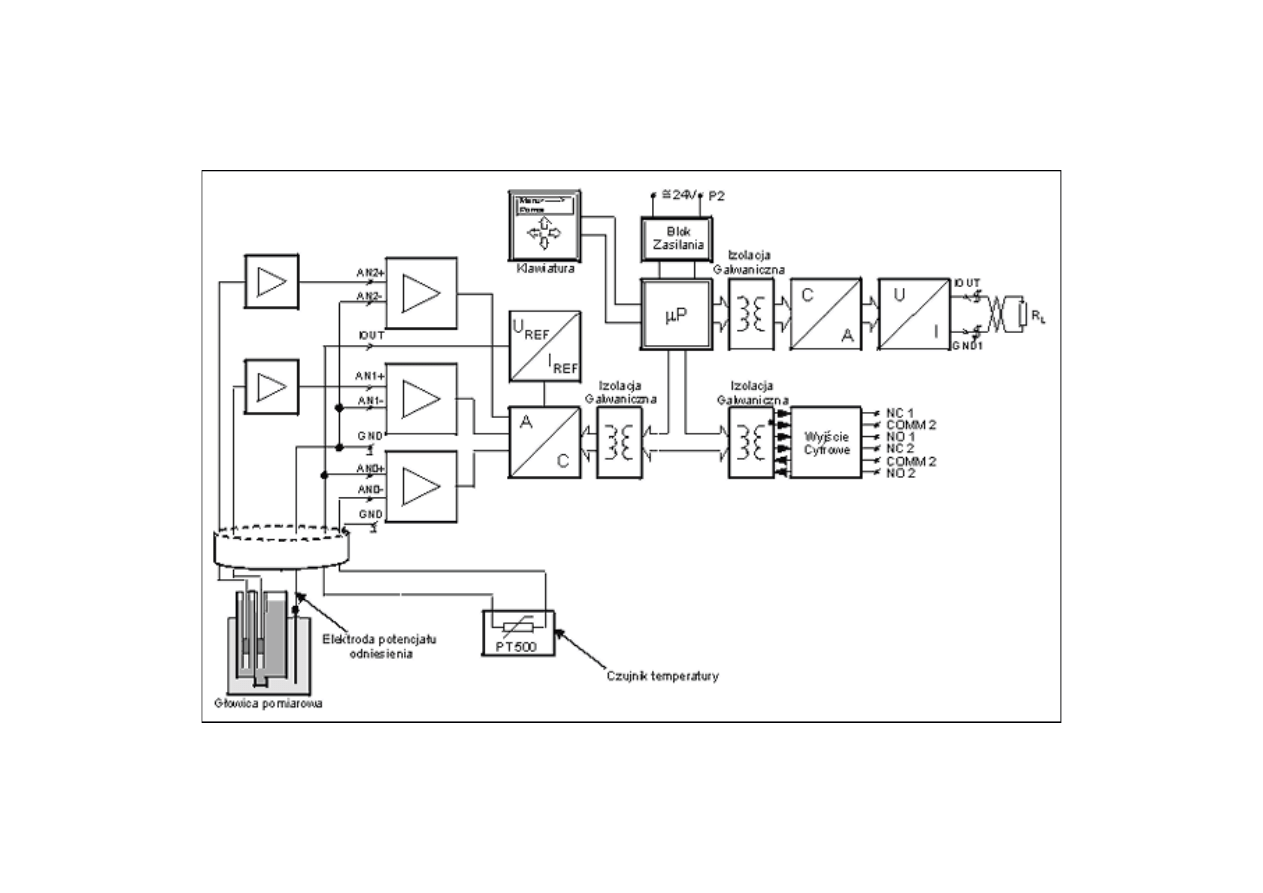
Schemat pH-metru z przetwarzaniem cyfrowym

ASP vs. DSP – porównanie

–

ASP ma ograniczone zastosowanie w zakresie skomplikowanych operacji na
sygnałach.

–

ASP jest mało elastyczna w zakresie przetwarzania oraz złożona w zakresie
projektowania niestandardowych układów przetwarzających, co składa się na
wysoką cenę układów ASP.

–

ASP nie daje się łatwo miniaturyzować – układom scalonym (wzm. operacyjne)
towarzyszą zwykle elementy dyskretne (cewki, kondensatory, oporniki).

–

DSP może być przeprowadzona nie tylko z użyciem specjalizowanych układów,
lecz także przy pomocy standardowego komputera.

–

Działanie układów DSP można względnie prosto symulować i testować przy
pomocy komputera, a otrzymane układy przetwarzające można łatwo przenosić
i powielać.

–

Dane w postaci cyfrowej łatwo przechowywać.

ASP vs. DSP – porównanie (cd.)

–

Przetwarzanie DSP jest całkowicie niewrażliwe na wpływ czynników
zewnętrznych, np. temperaturę, starzenie, tolerancję elementów itp. -
powtarzalność przetwarzania.

–

Operacje DSP można łatwo modyfikować poprzez zmiany w kodzie programu
sterującego.

–

DSP jest tańsze od ASP z uwagi na dalece większe zaawansowanie technologii
półprzewodnikowej.

–

DSP zwykle nieodwracalnie zniekształca pierwotny sygnał wejściowy podczas
próbkowania i kwantyzacji oraz dodatkowo wprowadza efekty skończonej
precyzji przetwarzania sygnałów cyfrowych (zaokrąglanie wyników obliczeń
matematycznych).

–

Szybkość współczesnych procesorów DSP jest wciąż niewystarczająca do
przetwarzania (w czasie rzeczywistym) przebiegów szybkozmiennych
(o szerokim widmie).

Modele DSP

Obszary zastosowań DSP

–

Przetwarzanie mowy: kodowanie i dekodowanie, szyfrowanie i deszyfrowanie
dźwięków, rozpoznawanie i synteza mowy, identyfikacja mówcy, usuwanie
echa, wspomaganie słuchu.

–

Przetwarzanie dźwięku: odszumianie sygnału, wyrównywanie charakterystyk,
symulowanie efektów otoczenia, synteza dźwięku, mieszanie i edycja
dźwięków.

–

Przetwarzanie obrazu: kompresja i dekompresja, rozpoznawanie obrazów,
wyostrzanie obrazów, wspomaganie widzenia.

–

Systemy informacyjne: poczta głosowa, fax, modemy, telefonia komórkowa,
szyfrowanie i deszyfrowanie wiadomości, komunikacja sieciowa, radio
i telewizja, obrazowanie biomedyczne.

–

Sterowanie: kontrola serwomechanizmów, robotyka, układy napędowe.

–

Wspomaganie badań i produkcji: generacja sygnałów, analiza stanów
nieustalonych, analiza stanów stacjonarnych.

DSP: zadania i narzędzia

Zadania:

–

Przewidywanie odpowiedzi układu na zadane pobudzenie.

–

Badanie cech posiadanego sygnału.

–

Wydobycie użytecznej informacji o badanym układzie.

Narzędzia:

–

Procesory ogólnego przeznaczenia, mikrokontrolery.

–

Procesory sygnałowe oraz procesory dźwięku.

–

Układy logiki programowalnej (PLD, FPGA).

–

Języki programowania wysokiego poziomu (Pascal, C, C++).

–

Języki specjalizowanych pakietów obliczeń matematycznych (MatLab, MathCAD,

Mathematica).

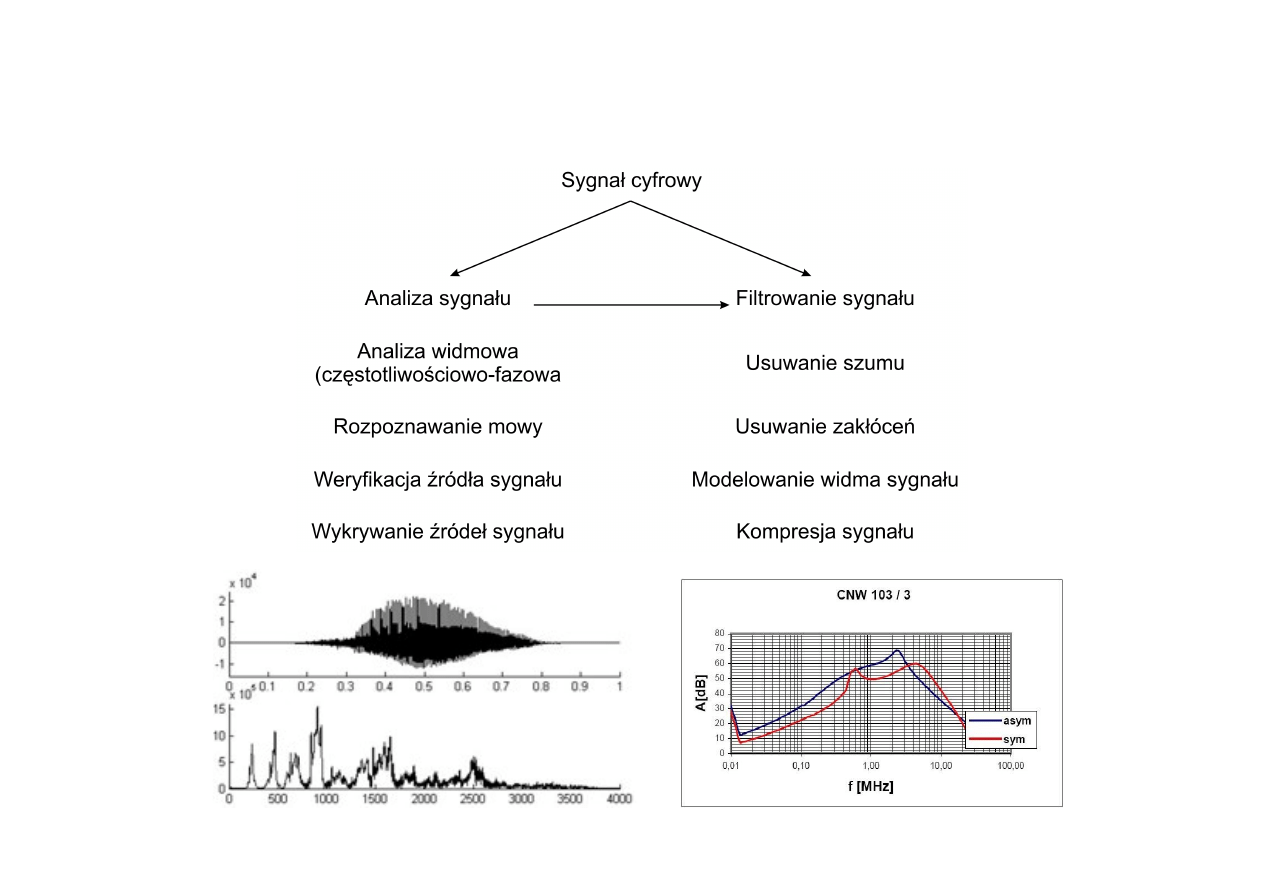
DSP: zadania i narzędzia (cd.)

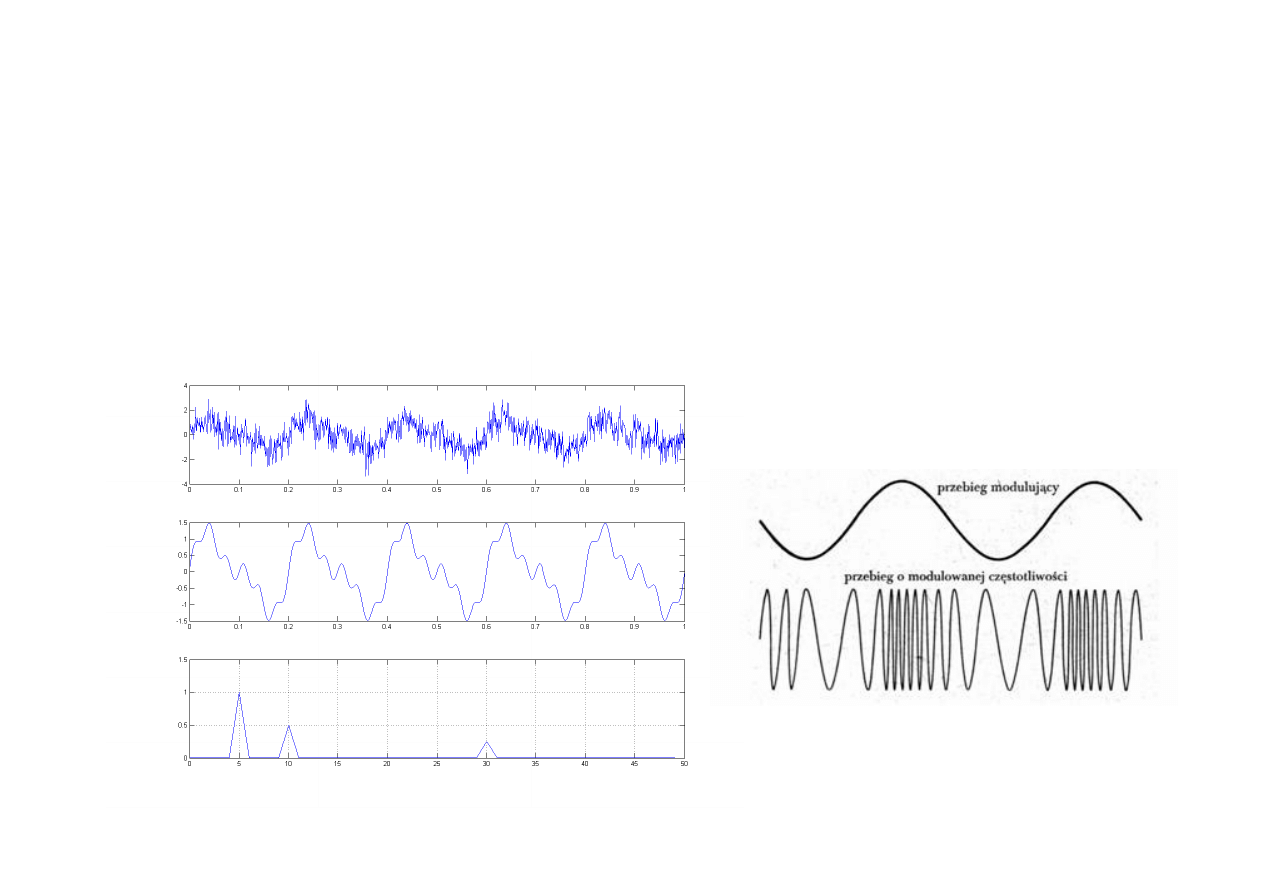
Uwypuklenie określonych cech sygnału.

Odzyskiwanie sygnału zakłóconego szumem lub bezużytecznym sygnałem tła

(demodulacja).

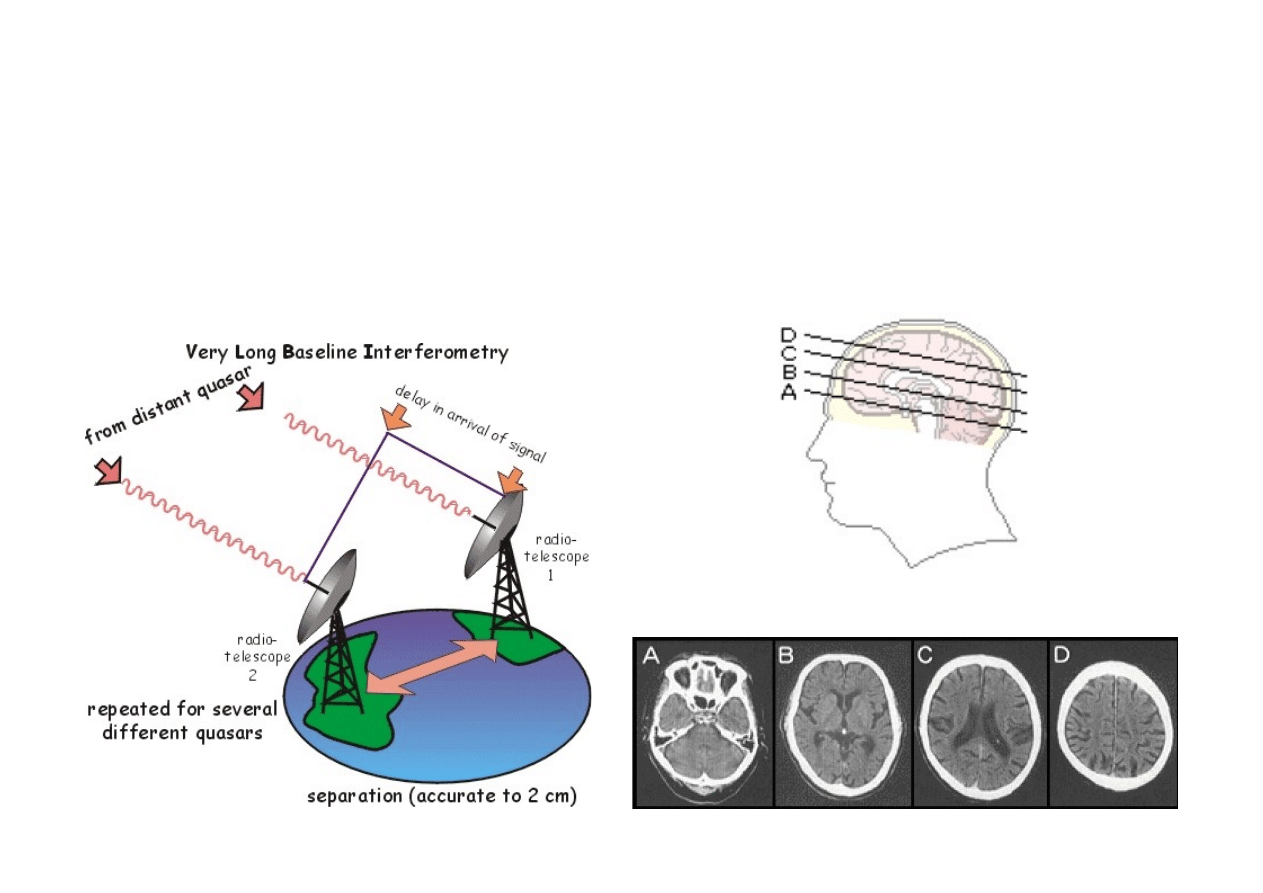
Rekonstrukcja sygnałów uzyskiwanych z różnych źródeł: diagnostyka medyczna

(tomografia rentgenowska, tomografia NMR, USG, EKG, EEG), echolokacja

(radar, sonar), interferometria (VLBI), pozycjonowanie (GPS) i in.

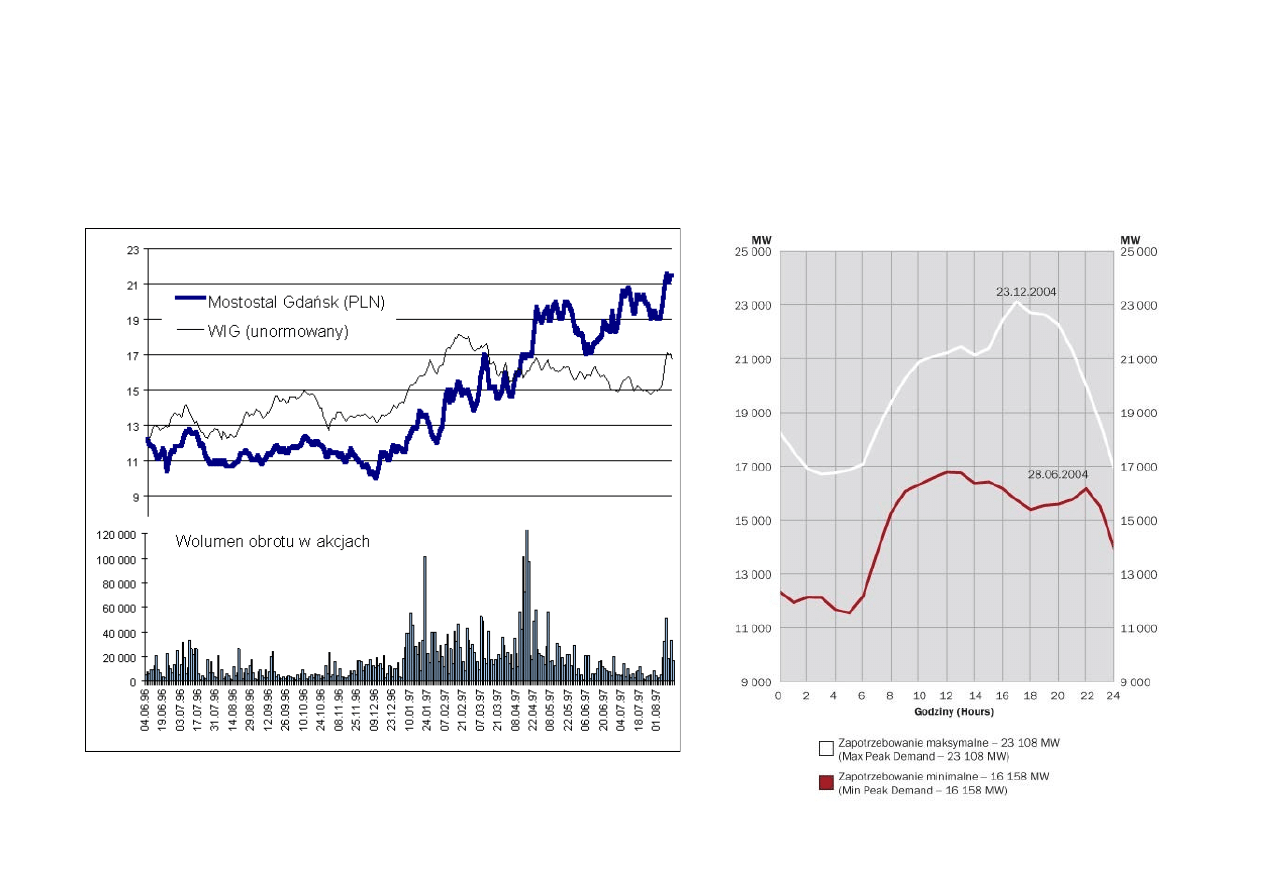
Przewidywanie trendów: analiza techniczna (giełda), prognozowanie zużycia

energii, kompresja sygnałów i in.

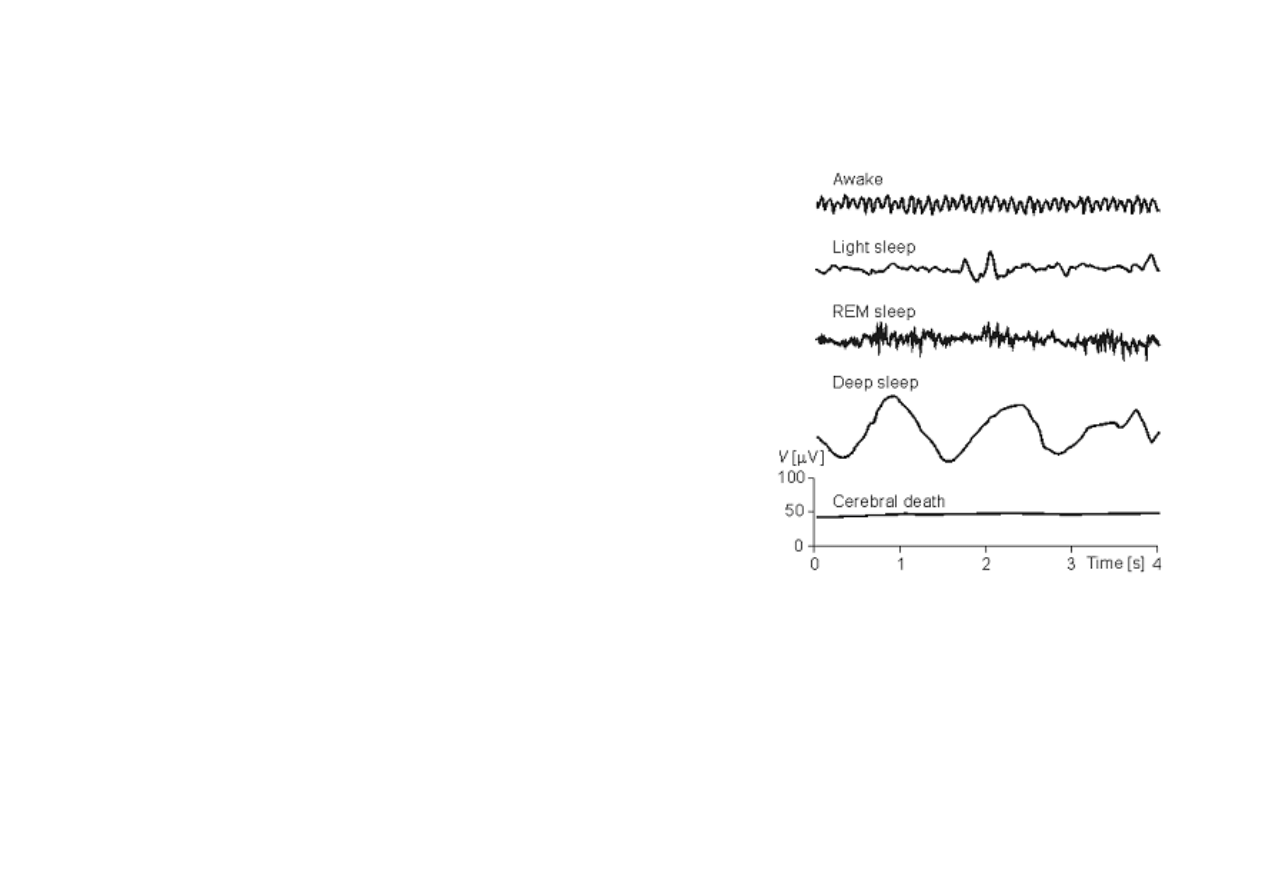
Sygnały

Sygnał – zależność dowolnej, dającej się zmierzyć

wielkości fizycznej od innej, niezależnej zmiennej

(zwykle czas t, położenie r).

W ogólności, sygnały mogą być zależne od n-parametrów, co określa ich wymiar,

oraz mogą posiadać k-niezależnych składowych, co określa ich liczbę kanałów:



A





x



=

[

A

1



x

1

, x

2

,..., x

n



, A

2



x

1

, x

2

,..., x

n



,..., A

k



x

1

, x

2

,..., x

n



]

Podział sygnałów

Z uwagi na model matematyczny danego sygnału wyróżnia się:

–

sygnały rzeczywiste,

–

sygnały zespolone,

–

sygnały dystrybucyjne.

Z uwagi na rodzaj nośnika wyróżnia się sygnały:

–

elektryczne,

–

akustyczne,

–

mechaniczne,

–

cieplne,

–

świetlne itd.

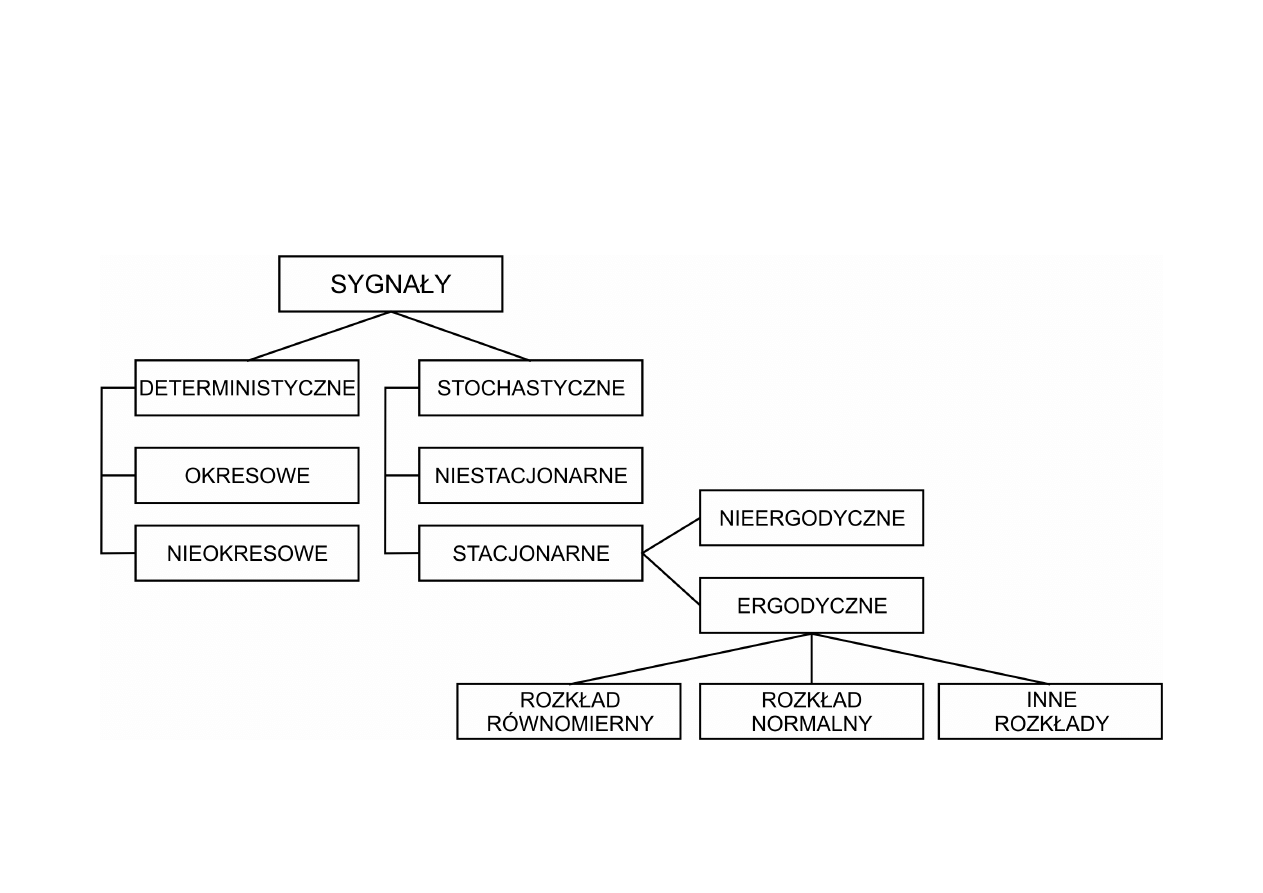
Podział sygnałów z uwagi na zdolność przewidywania

ich wartości chwilowej

Sygnał deterministyczny: każdy sygnał dający się jednoznacznie opisać jawną

formułą matematyczną, tzn. sygnał, którego przebieg daje się całkowicie

odtworzyć dowolnie daleko w przeszłości, jak i przewidzieć w dowolnie odległej

chwili w przyszłości.

Sygnał stochastyczny

(przypadkowy, losowy): sygnał, który

ewoluuje w czasie w sposób nie

dający się przewidzieć z pewnością.

Pomimo różnic chwilowych wartości

sygnałów stochastycznych, można je

analizować metodami statystycznymi

na gruncie teorii prawdopodobieństwa

i procesów stochastycznych.

Sygnał stochastyczny stacjonarny charakteryzuje niezależność od czasu jego

parametrów statystycznych (średnia, wariancja) – rzuty kostką o stałej geometrii.

Parametry statystyczne sygnału niestacjonarnego zmieniają się w czasie –

rzuty kostką o zmieniającym się położeniu środka ciężkości.

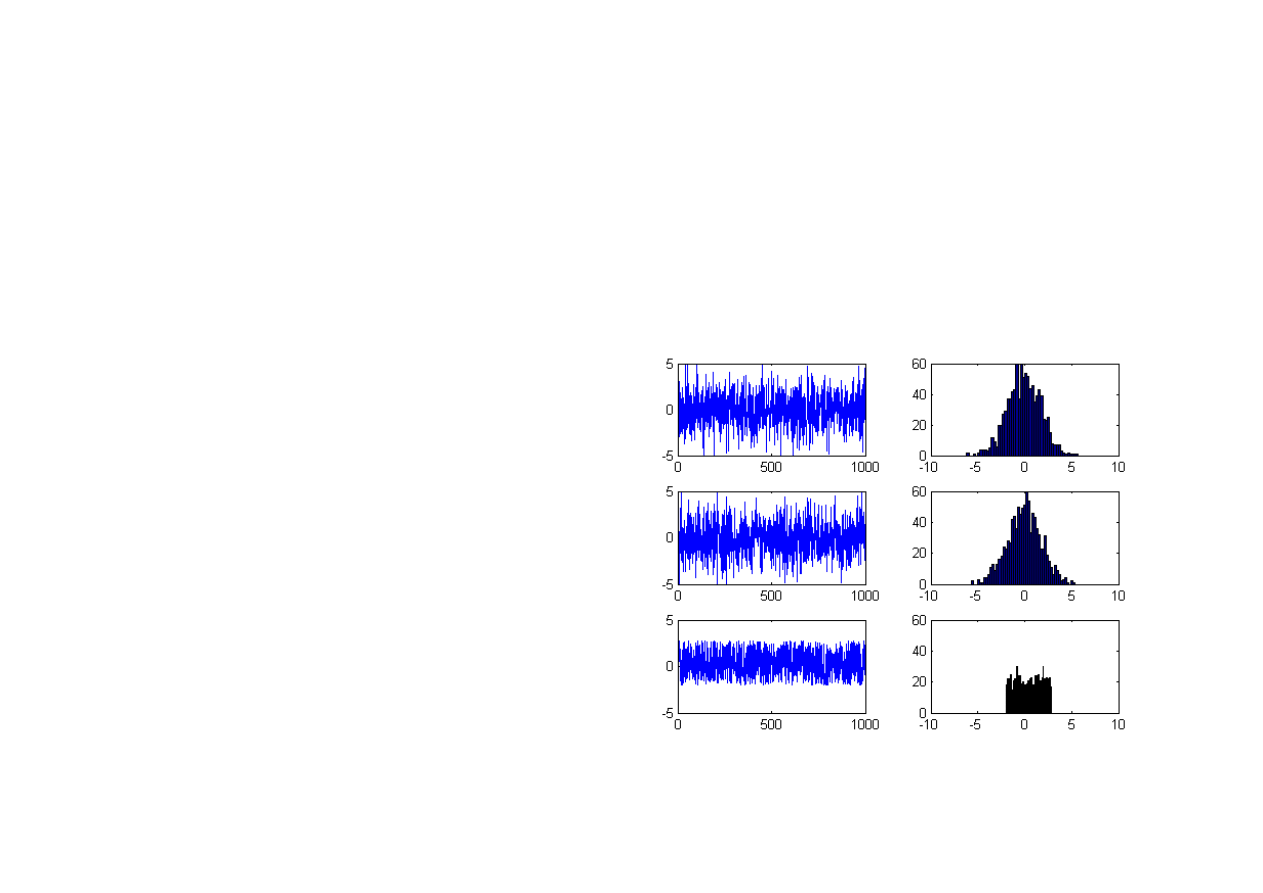
Jeśli parametry statystyczne jednej realizacji sygnału w długim okresie są takie

same jak zbioru wszystkich jego realizacji w dowolnej chwili, sygnał nazywamy

ergodycznym.

Sygnały deterministyczne a losowe

Jeśli przekazanie informacji jest aktem wypełnienia niewiedzy obserwatora,

sygnały deterministyczne nie niosą żadnej informacji

– wiedza o nich jest

pełna z założenia. Jedynie sygnały losowe, których zmiany można starać się

przewidywać z pewnym prawdopobieństwem, w akcie spełniania się określonej

realizacji przekazują obserwatorowi przenoszoną przez siebie informację.

Generalnie, wszystkie realne sygnały są sygnałami losowymi, które można

jedynie przybliżać przy pomocy modeli deterministycznych lub stochastycznych.

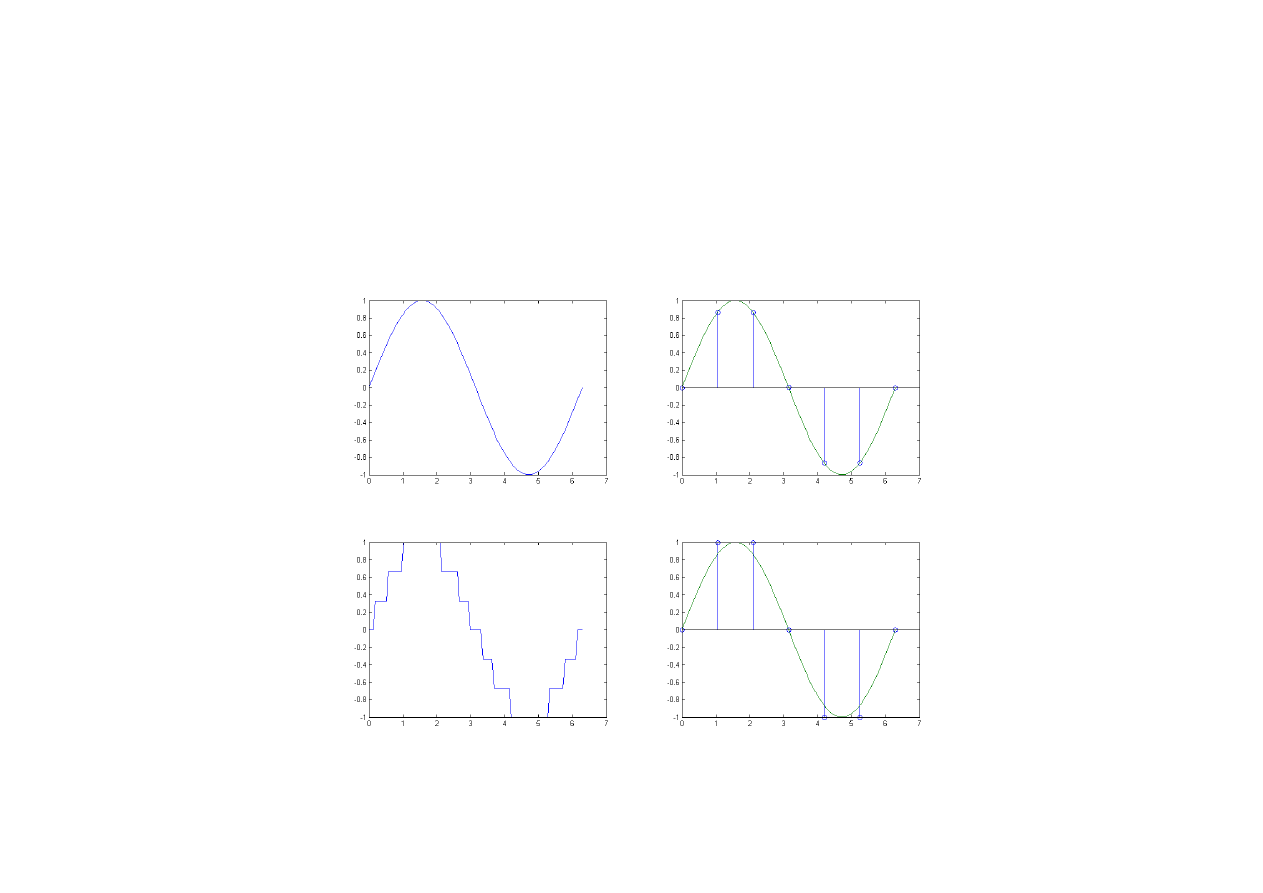
Podział sygnałów z uwagi na charakter ich dziedziny

i przeciwdziedziny

Sygnały ciągłe w czasie i amplitudzie
– sygnały analogowe

Sygnały dyskretne w czasie i ciągłe

w amplitudzie

Sygnały ciągłe w czasie i dyskretne
w amplitudzie

Sygnały dyskretne w czasie

i amplitudzie – sygnały cyfrowe

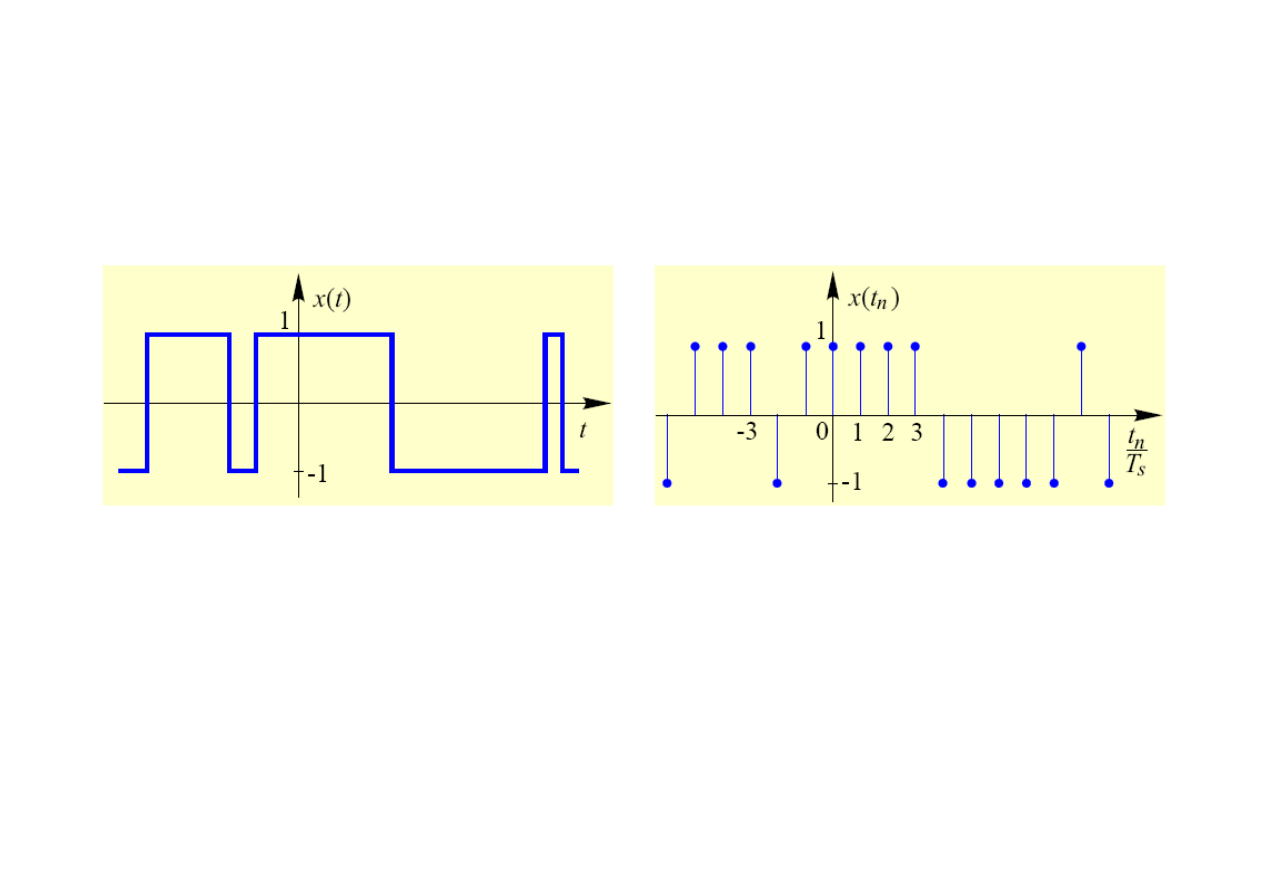
Sygnały dyskretne w amplitudzie – sygnały binarne

Sygnały binarne powstają na skutek binarnego (dwójkowego)

kodowania sygnałów cyfrowych.

Sygnały deterministyczne – parametry

Parametr

Sygnał analogowy

Sygnał dyskretny

Wartość średnia

sygnału

w przedziale

〈

x

〉

=

1

t

2

−

t

1

⋅

∫

t

1

t

2

x t ⋅dt

〈

x

〉

=

1

n

2

−

n

1



1

∑

n=n

1

n

2

x n

Wartość średnia

całego sygnału

〈

x

〉

=

lim

T ∞

1

2T

⋅

∫

−

T

T

x t⋅dt

〈

x

〉

=

lim

N ∞

1

2N1

∑

n=−N

N

x n

Wartość średnia

sygnału okresowego

〈

x

〉

=

1

T

⋅

∫

t

0

t

0



T

x t ⋅dt

〈

x

〉

=

1

N

∑

n=n

0

n

0



N 1

x n

Energia sygnału

E

x

=

∫

−∞

∞

x

2



t⋅dt

E

x

=

∑

n=−∞

∞

x

2



n

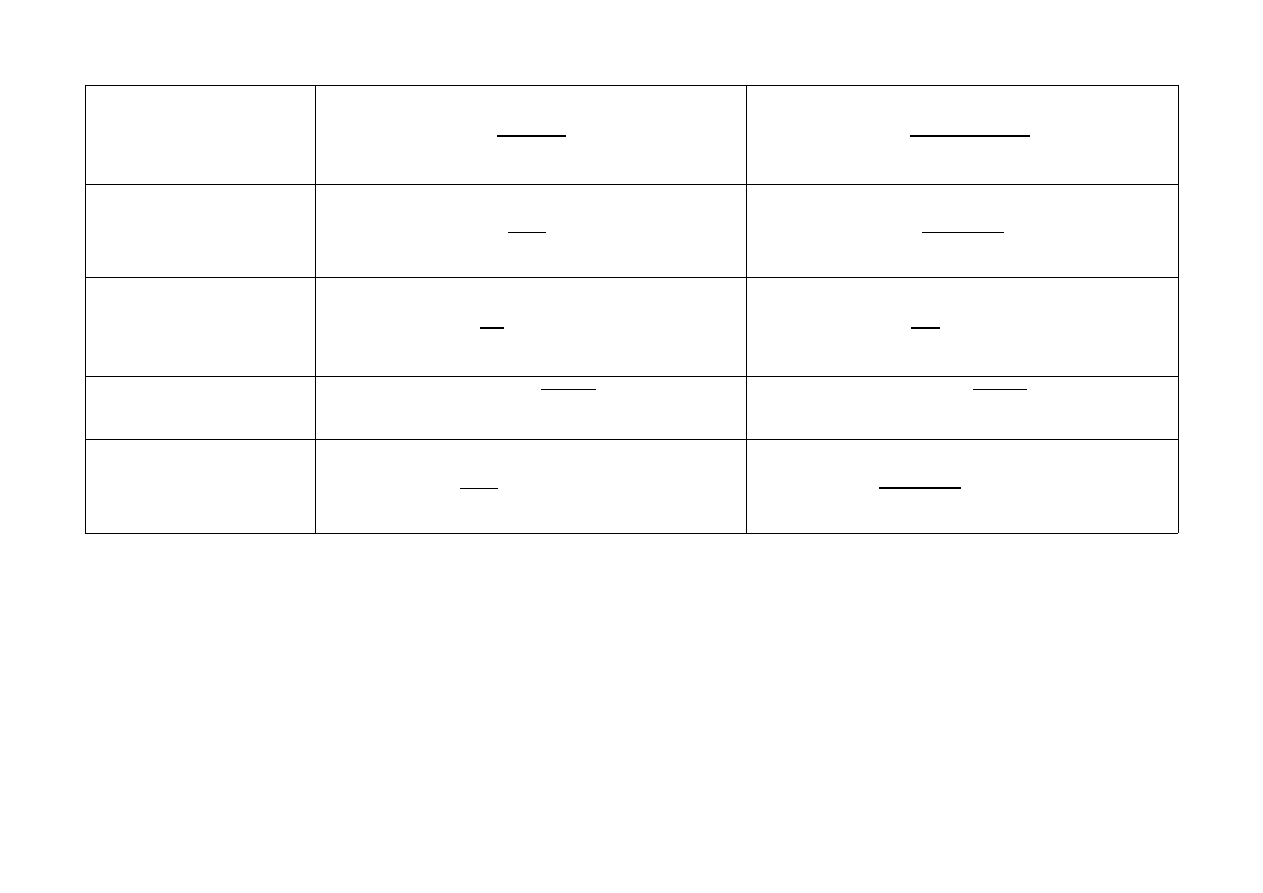
Moc średnia sygnału

w przedziale

P

x

=

〈

x

2

〉

=

1

t

2

−

t

1

⋅

∫

t

1

t

2

x

2



t ⋅dt

P

x

=

〈

x

2

〉

=

1

n

2

−

n

1



1

∑

n=n

1

n

2

x

2



n

Moc średnia

całego sygnału

〈

x

2

〉

=

lim

T ∞

1

2T

⋅

∫

−

T

T

x

2



t ⋅dt

〈

x

2

〉

=

lim

N ∞

1

2N1

∑

n=−N

N

x

2



n

Moc średnia

sygnału okresowego

〈

x

2

〉

=

1

T

⋅

∫

t

0

t

0



T

x

2



t⋅dt

〈

x

2

〉

=

1

N

∑

n=n

0

n

0



N 1

x

2



n

Wartość skuteczna

sygnału (RMS)

x

sk

=





P

x



x

sk

=





P

x



Wariancja sygnału



x

2

=

lim

T ∞

1

2T

⋅

∫

−

T

T

[

x t −

〈

x

〉

]

2

⋅

dt



x

2

=

lim

N ∞

1

2N1

∑

n=−N

N

[

x n−

〈

x

〉

]

2

Uwaga: Powyższe równania opisujące energię oraz moc sygnału nie mają

wymiaru energii i mocy, ale zależą od natury obserwowanych sygnałów. Służą

one jedynie opisowi 'wielkości' sygnału.

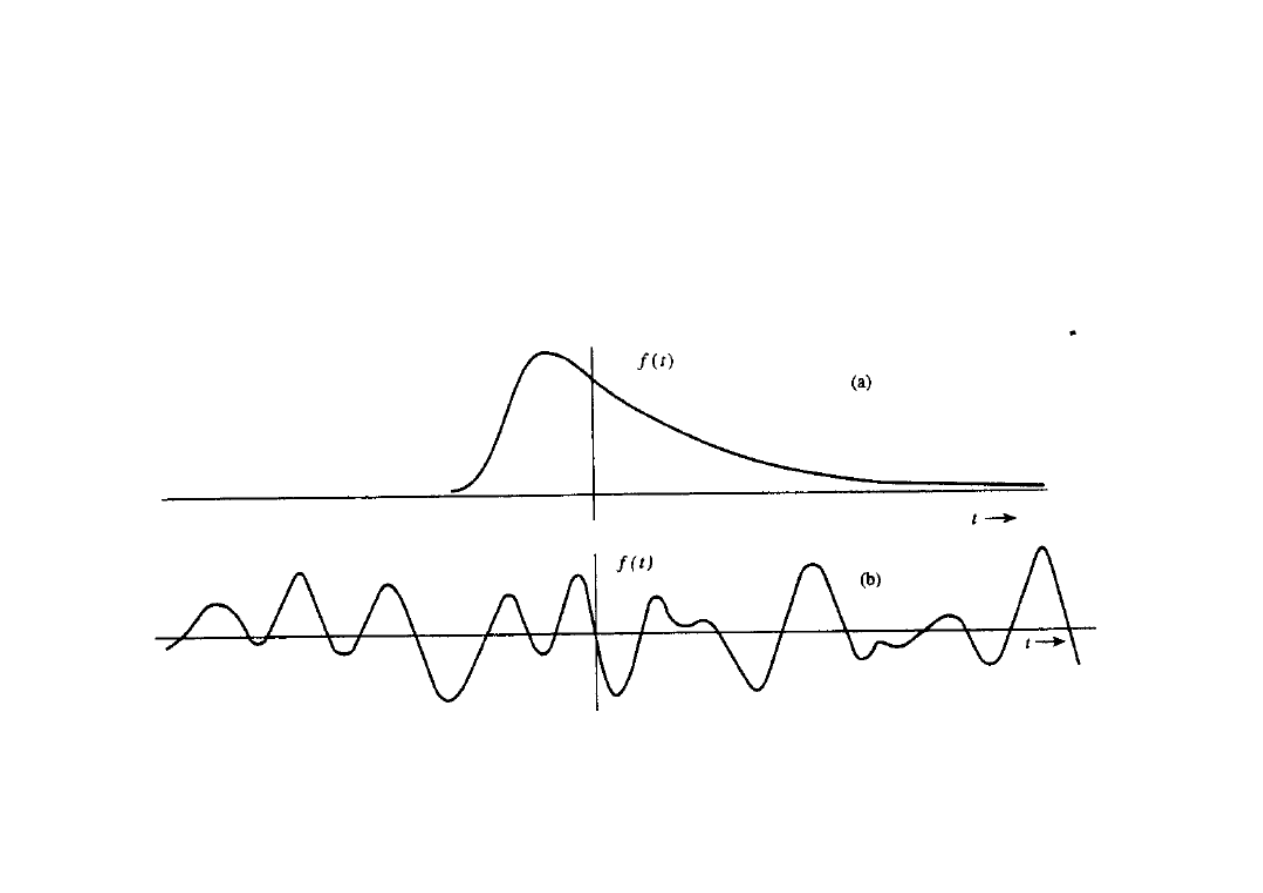
Użyteczne definicje:

a) Sygnał x(t) jest sygnałem o ograniczonej energii, gdy: 0 < E

x

< ∞.

b) Sygnał x(t) jest sygnałem o ograniczonej mocy, gdy: 0 < P

x

< ∞.

Moc sygnału o ograniczonej energii wynosi 0, a energia sygnału o ograniczonej

mocy jest nieskończona. Stąd, nie istnieje sygnał, który jest jednocześnie

sygnałem o skończonej mocy i energii. Analogicznie, istnieją sygnały, które nie są

jednocześnie ani sygnałami o skończonej energii, ani sygnałami o skończonej

mocy.

Wszystkie fizyczne sygnały nieokresowe są sygnałami o skończonej energii

z uwagi na ich skończony czas trwania. Z drugiej strony, sygnały okresowe f(t)

(nieskończone), dla których całka z f

2

(t) po okresie trwania ma skończoną

wartość, są sygnałami o skończonej mocy.

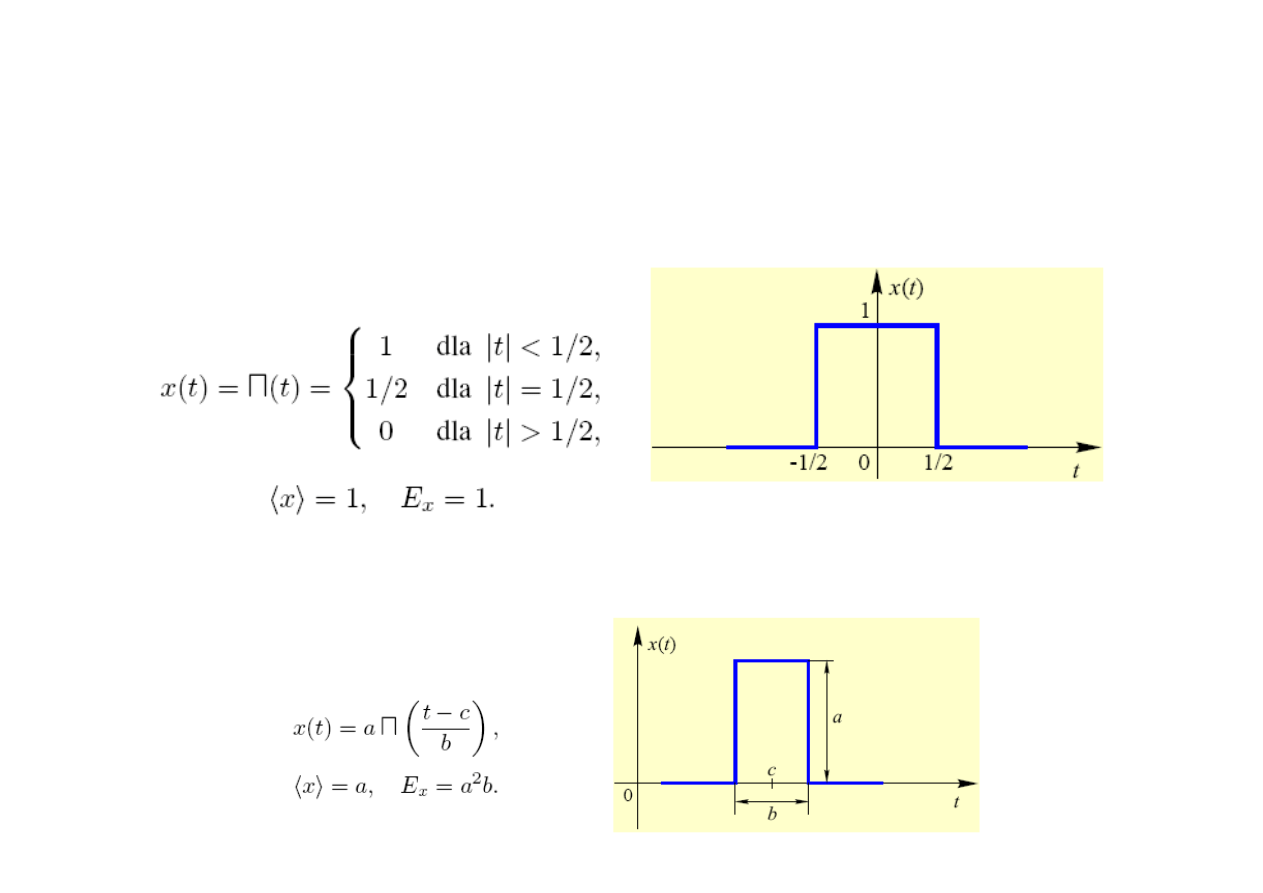
Sygnały analogowe o ograniczonej energii

i skończonym czasie trwania

Impuls prostokątny

Przesunięty w czasie impuls prostokątny

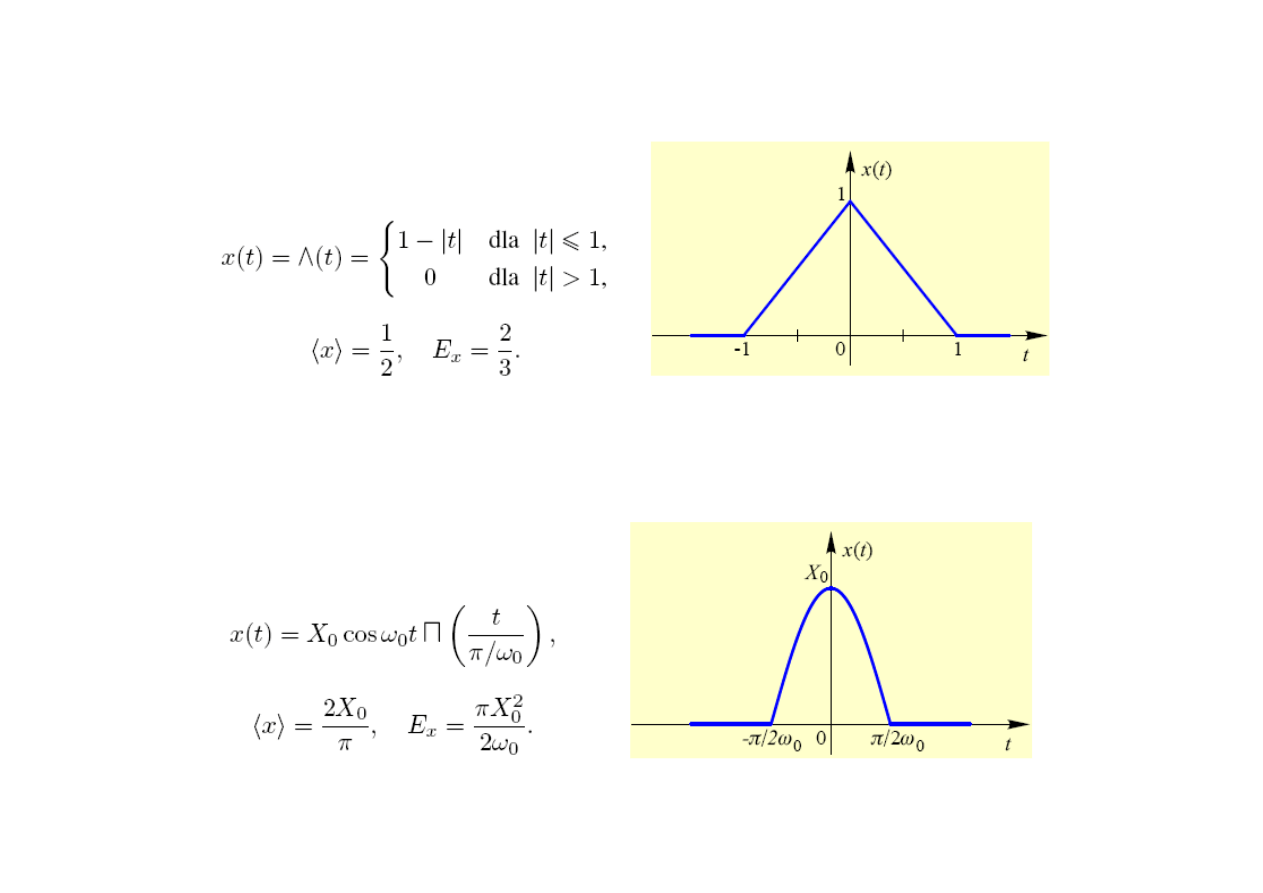
Impuls trójkątny

Impuls kosinusoidalny

Sygnały analogowe o ograniczonej energii

i nieskończonym czasie trwania

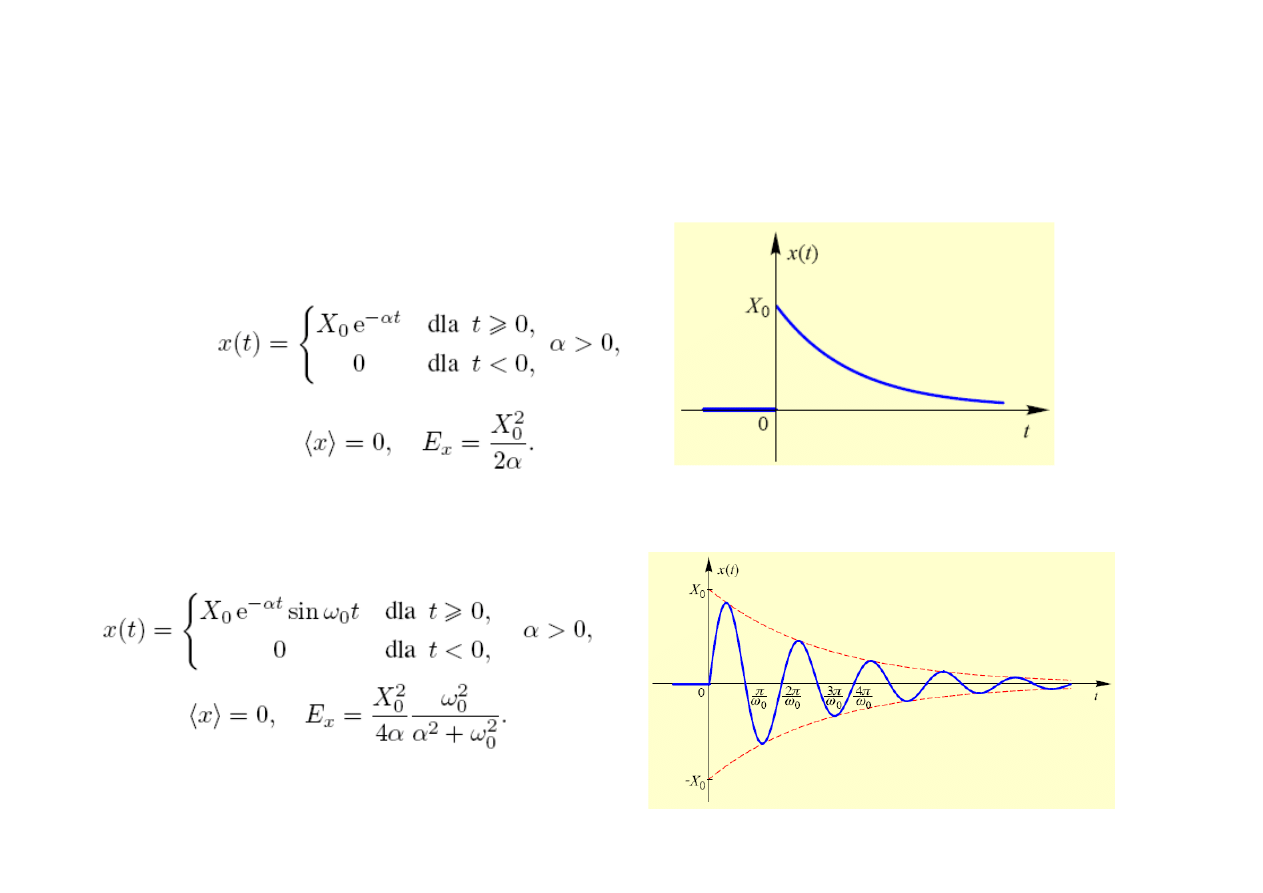
Impuls wykładniczy malejący

Sygnał sinusoidalny malejący wykładniczo

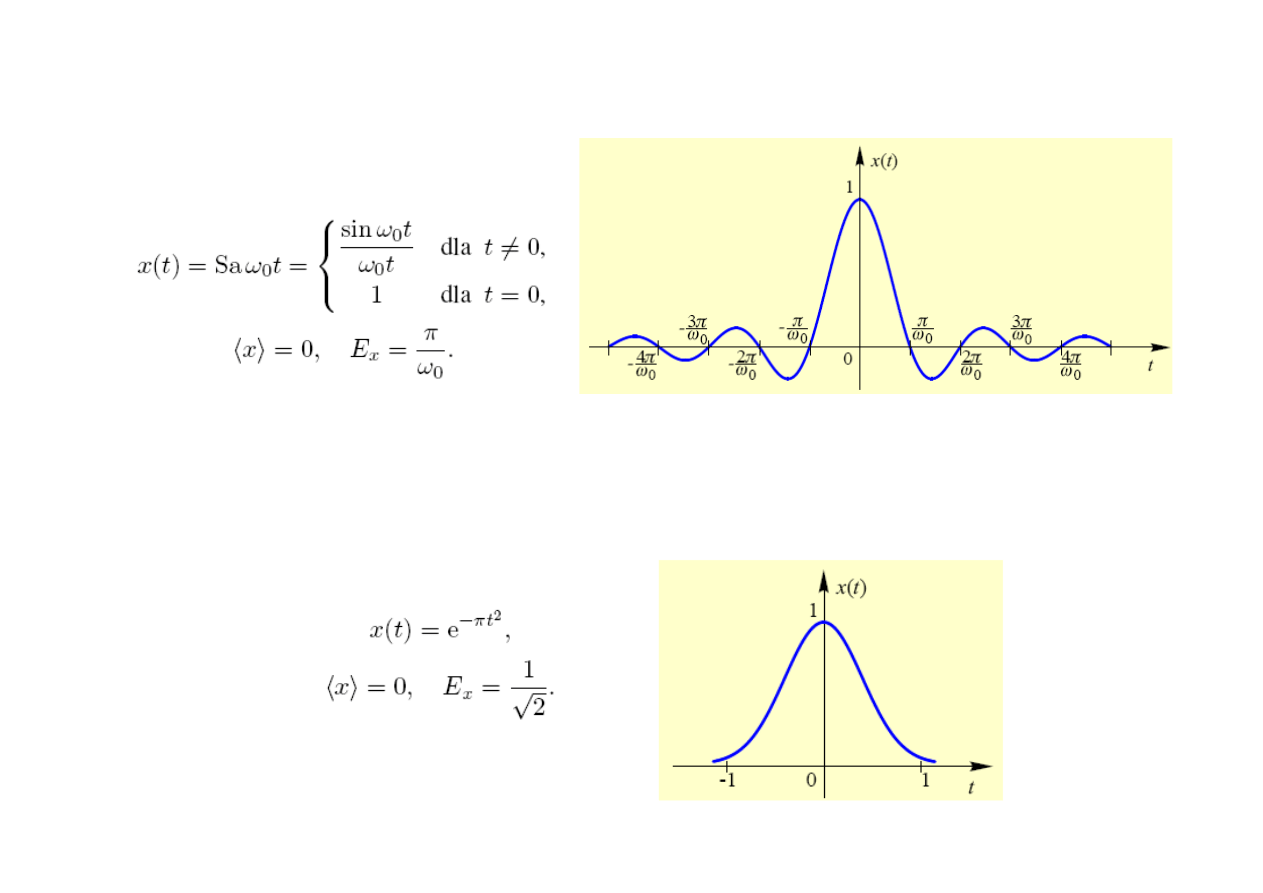
Sygnał sinc (Sa)

Sygnał Gaussa

Nieokresowe sygnały analogowe o ograniczonej mocy

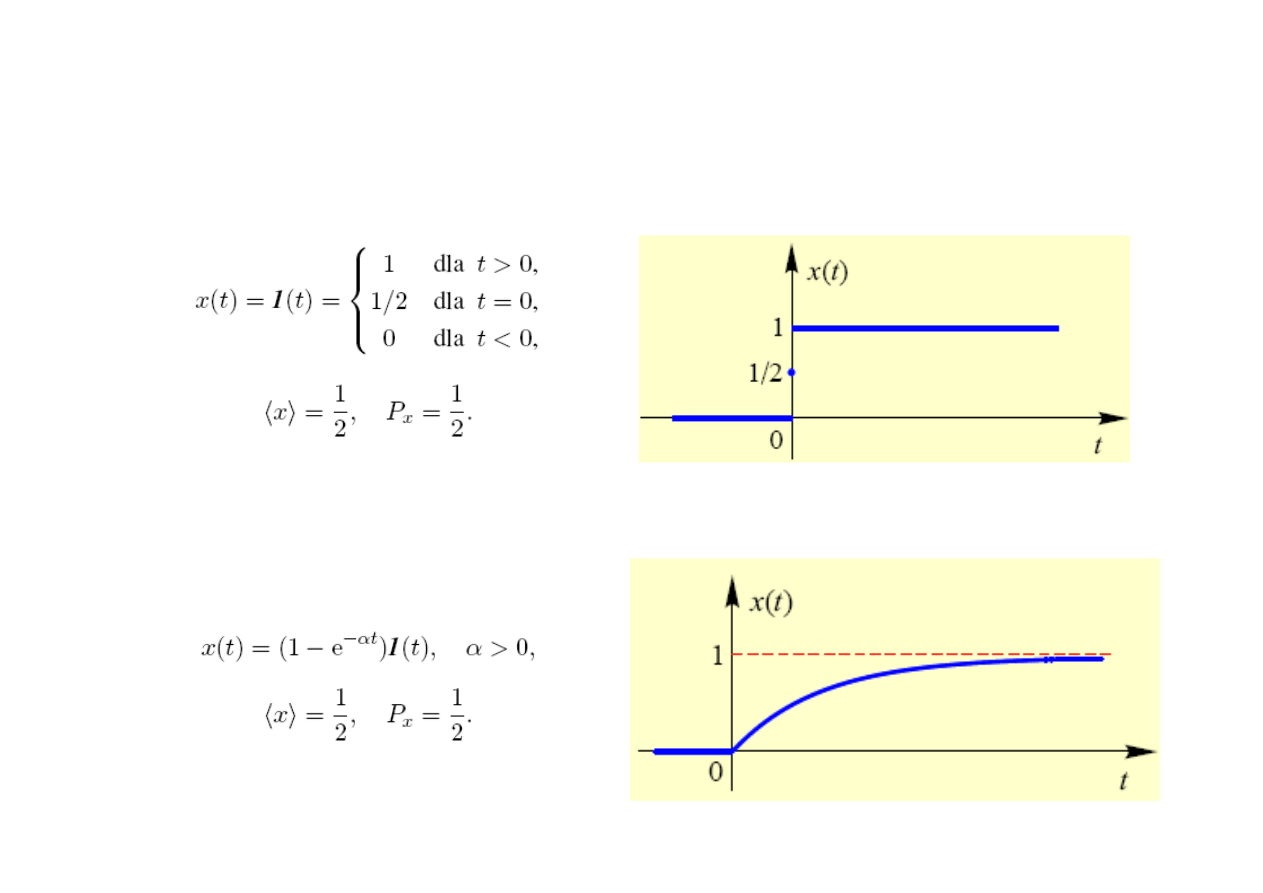
Skok jednostkowy u(t)

Sygnał wykładniczy narastający

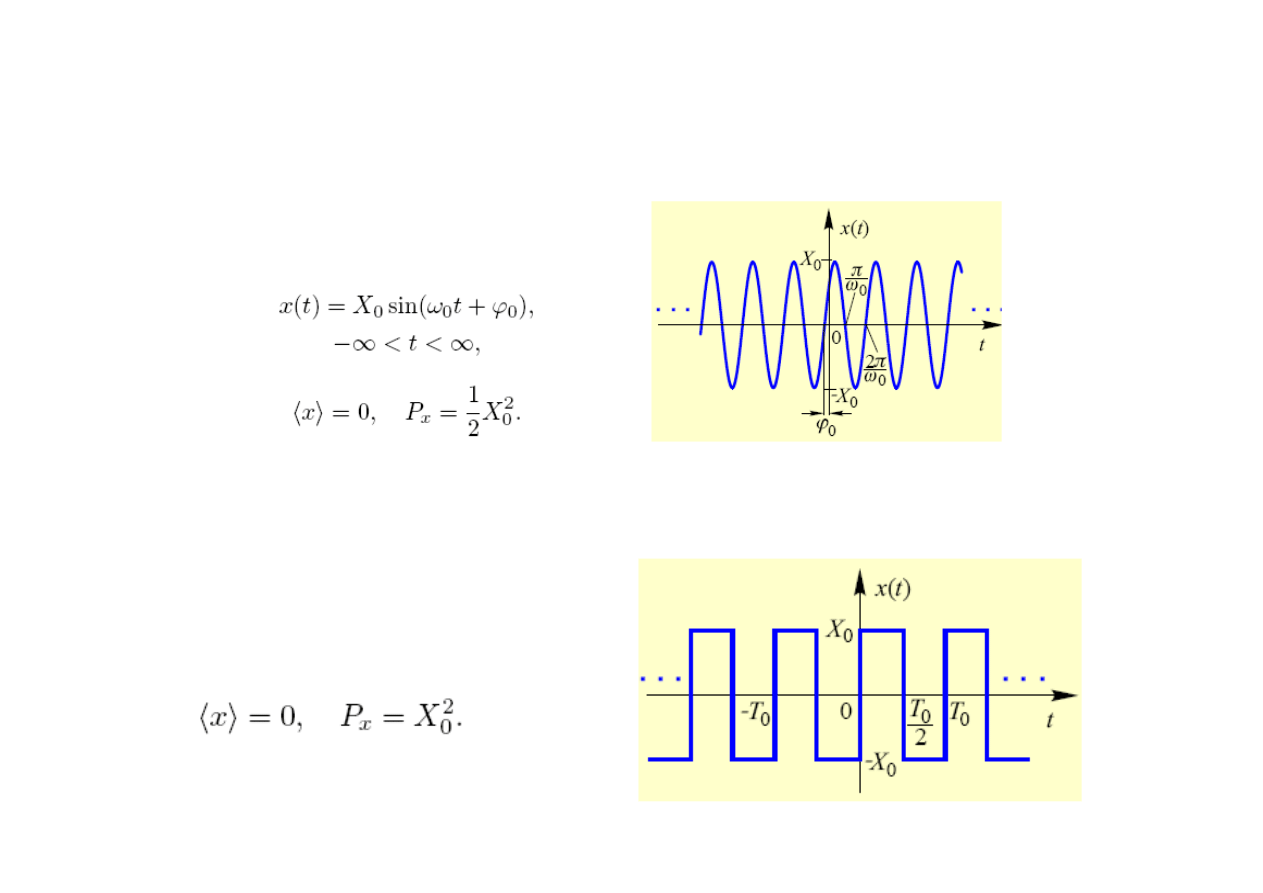
Okresowe sygnały analogowe o ograniczonej mocy

Sygnał harmoniczny

Fala prostokątna bipolarna

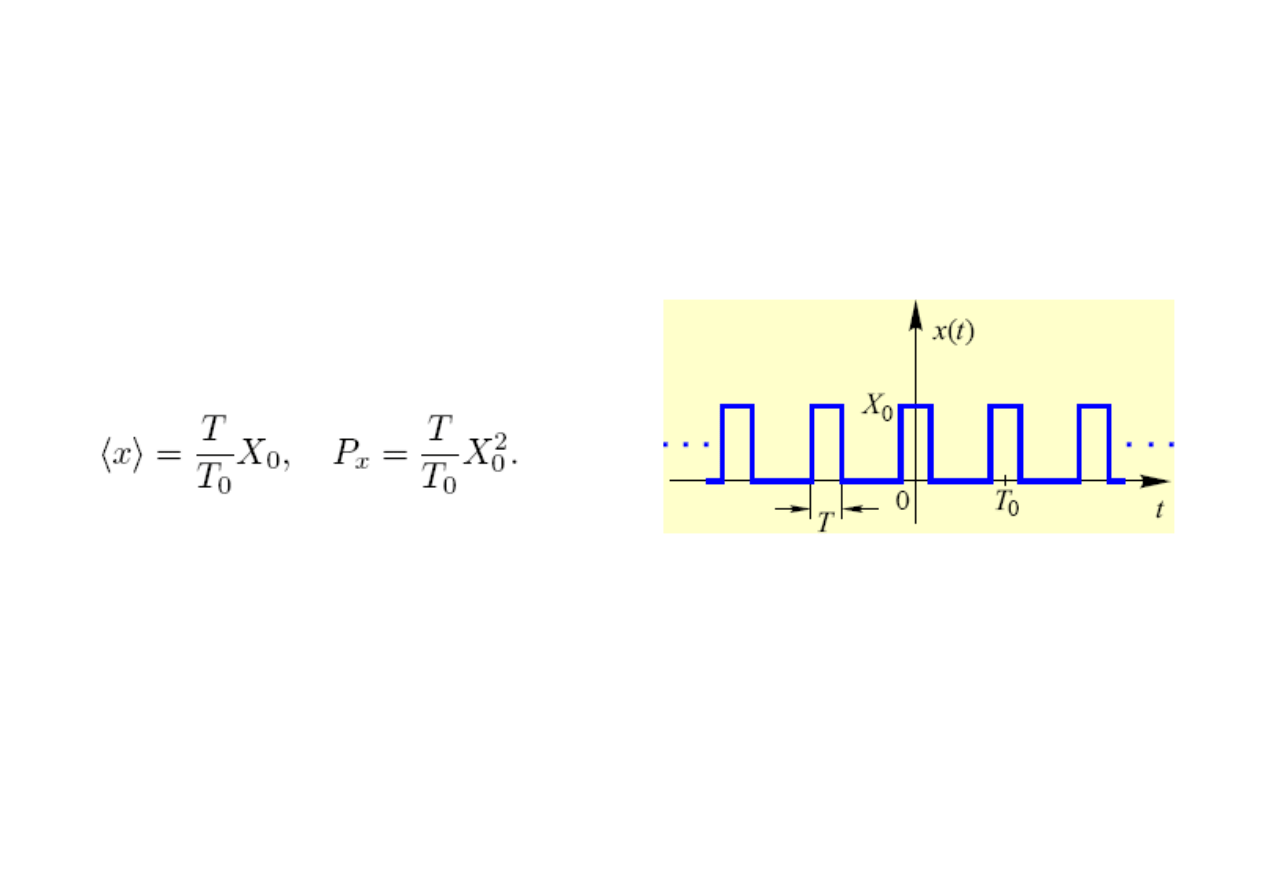
Fala prostokątna unipolarna

Współczynnik wypełnienia: n = T/T

0

Parametry sygnałów okresowych

Współczynnik szczytu:

Współczynnik kształtu:

Współczynnik zniekształceń nieliniowych:

Współczynnik zawartości harmonicznych:

k

s

=

X

maks

X

sk

k

ks

=

X

sk

X

srp

k

zn

=

1

X

sk

⋅





∑

n=2

∞

X

skn

2



k

zh

=

1

X

sk1

⋅





∑

n=2

∞

X

sk n

2



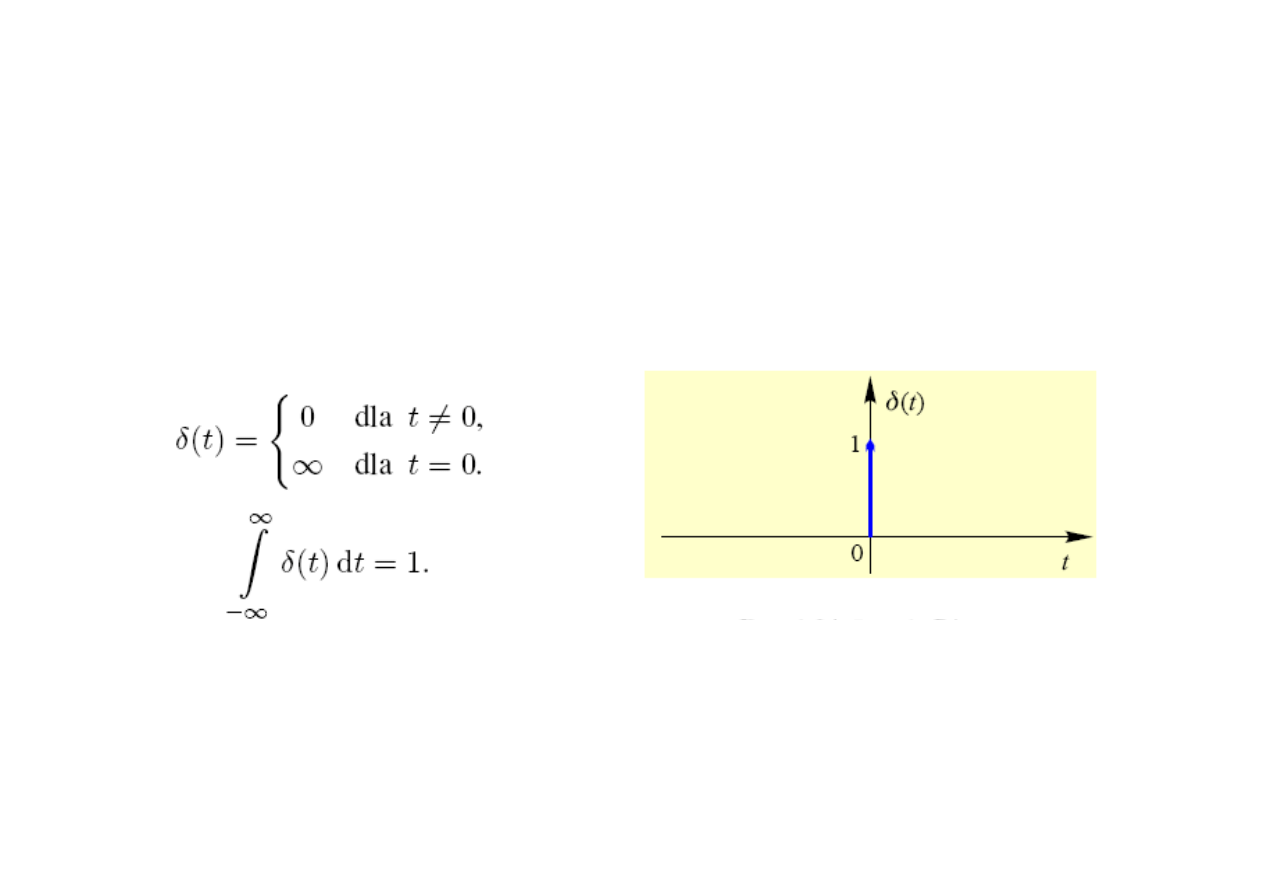
Sygnały dystrybucyjne

Impuls (dystrybucja, delta) Diraca – sygnał o nieskończonej mocy (gęstość

mocy na jednostkę czasu)

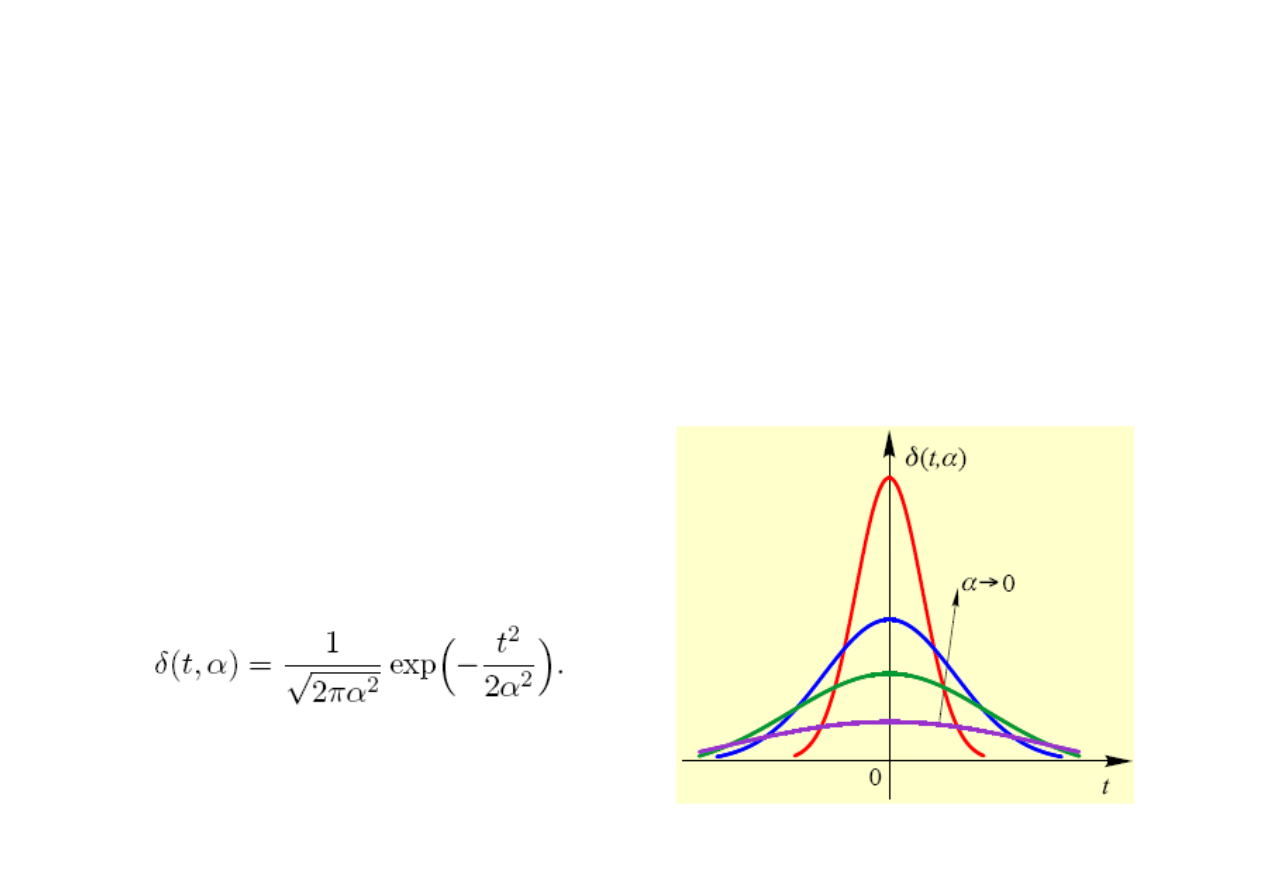
Impuls Diraca jest granicą ciągu funkcji aproksymujących δ(t, α):

Mogą to być np. funkcje Gaussa:

〚

∀



∫

−∞

∞



t ,⋅dt=1

〛



lim

  ∞



t ,=t 

Własności delty Diraca

1) Właściwość próbkowania sygnału:

2) Właściwość filtracji sygnału:

3) Związek ze skokiem jednostkowym u(t):

4) Niezmienniczość splotu:

x t⋅t−t

0

=

x t

0

⋅

t−t

0



∫

−∞

∞

x t⋅t−t

0

⋅

dt= x t

0



u t=

∫

−∞

t



t ' ⋅dt ' ,t=

d

dt

ut 

x t∗t =x t
x t∗t−t

0

=

x t−t

0



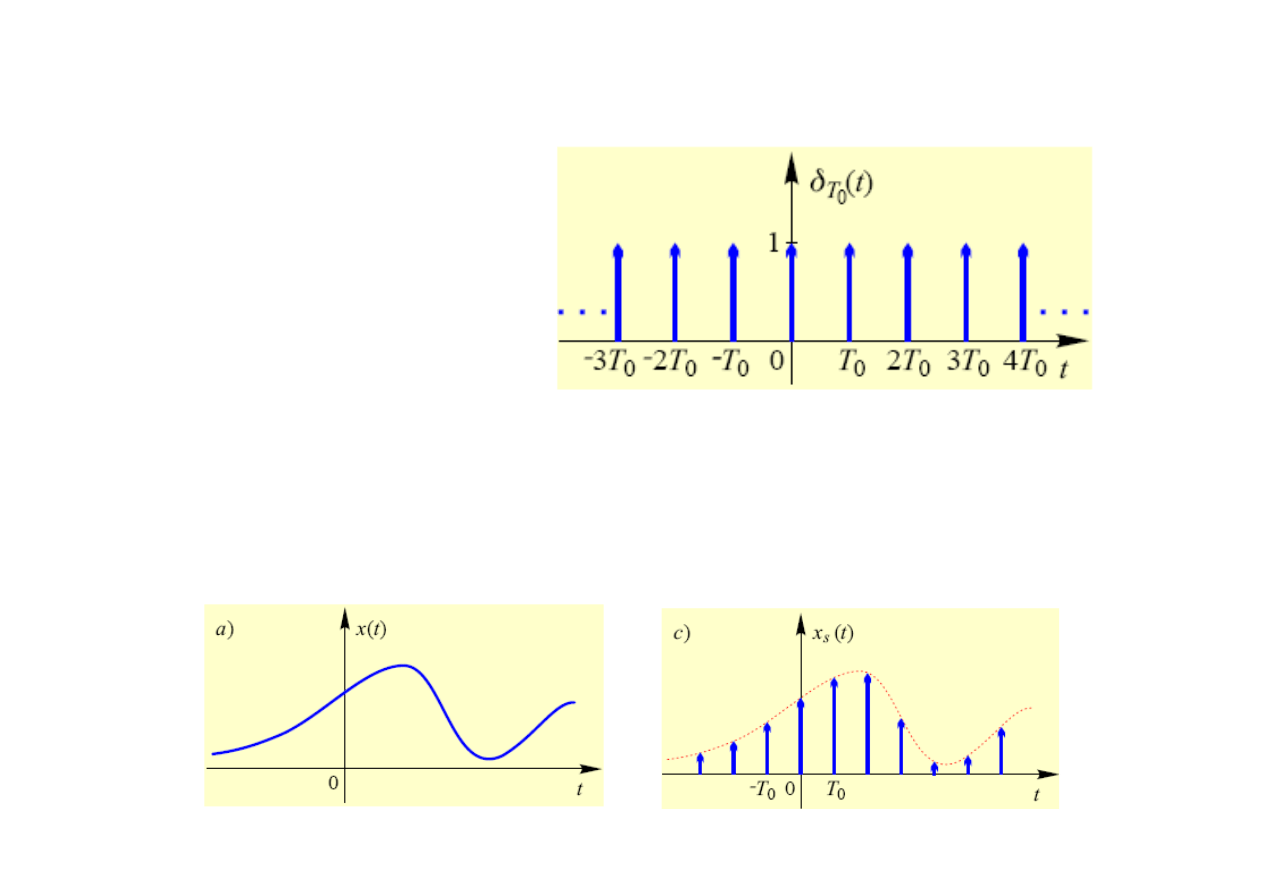
Dystrybucja grzebieniowa (okresowy ciąg szpilek Diraca – Dirac's comb):

Właściwości:

1) Próbkowanie (dyskretyzacja sygnału):



T



t =

∑

n=−∞

∞



t−n⋅T 

x t⋅

T



t =

∑

n=−∞

∞

x n⋅T ⋅t−n⋅T 

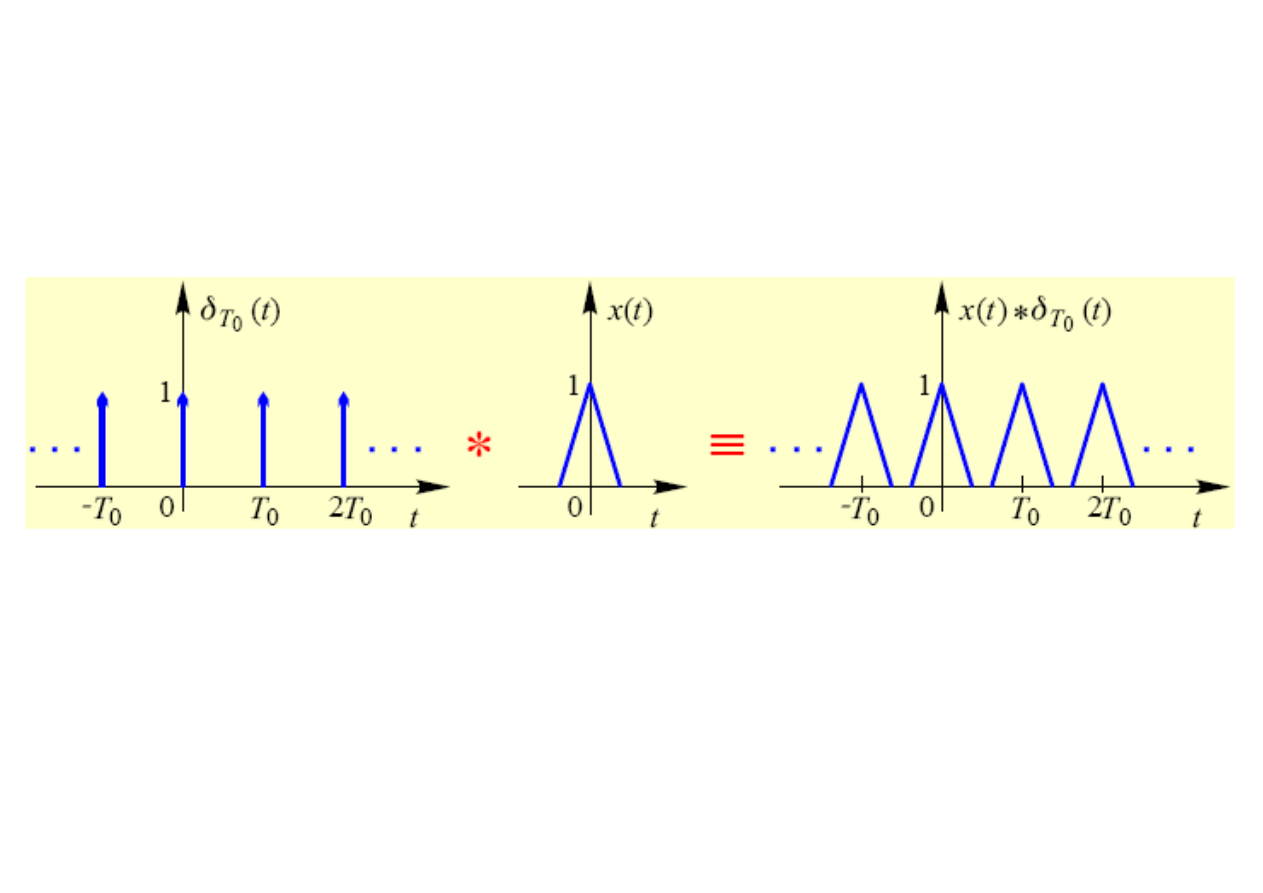
2) Powielanie okresowe:

x t∗

T



t=

∑

n=−∞

∞

x t−n⋅T 

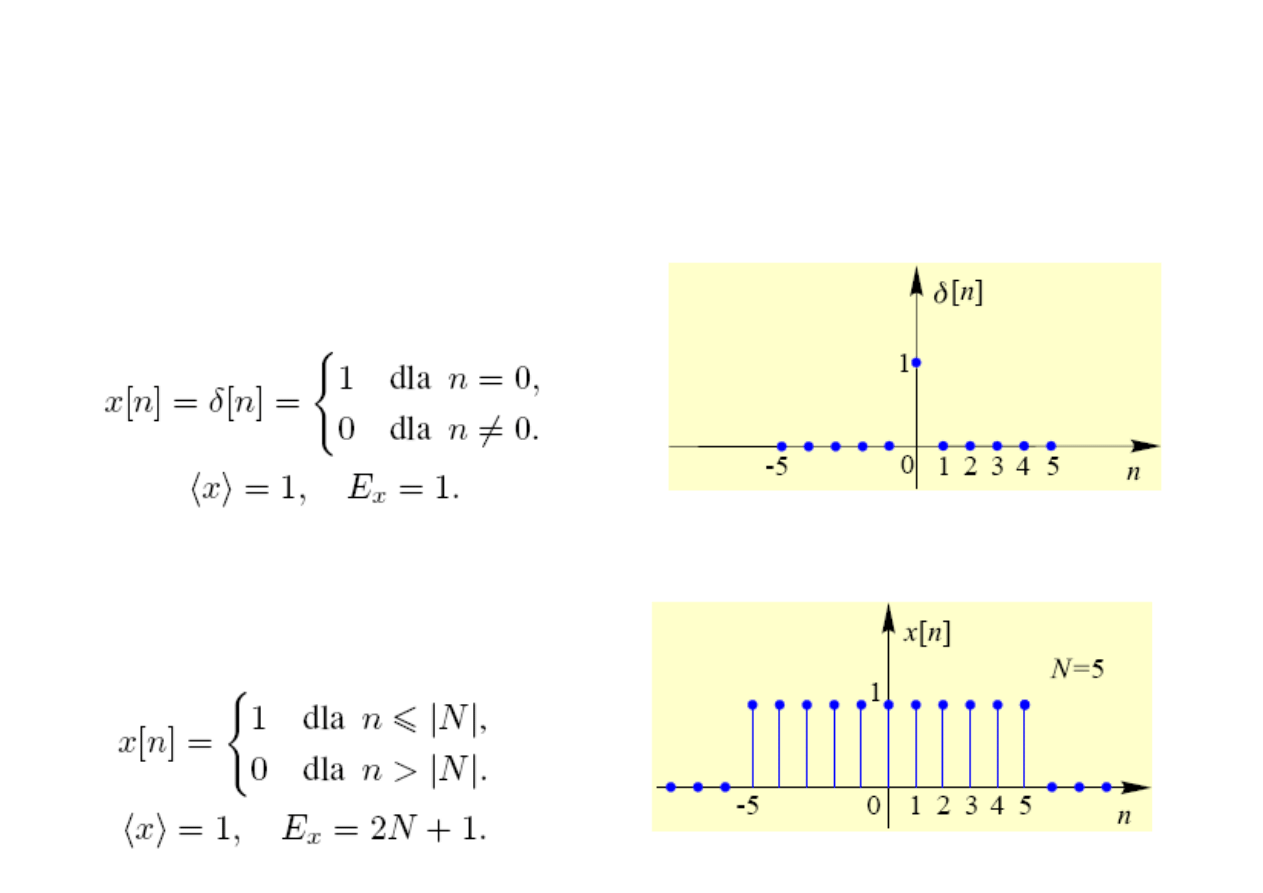
Wybrane sygnały dyskretne o ograniczonej energii

i skończonym czasie trwania

Impuls (delta) Kroneckera):

Impuls prostokątny:

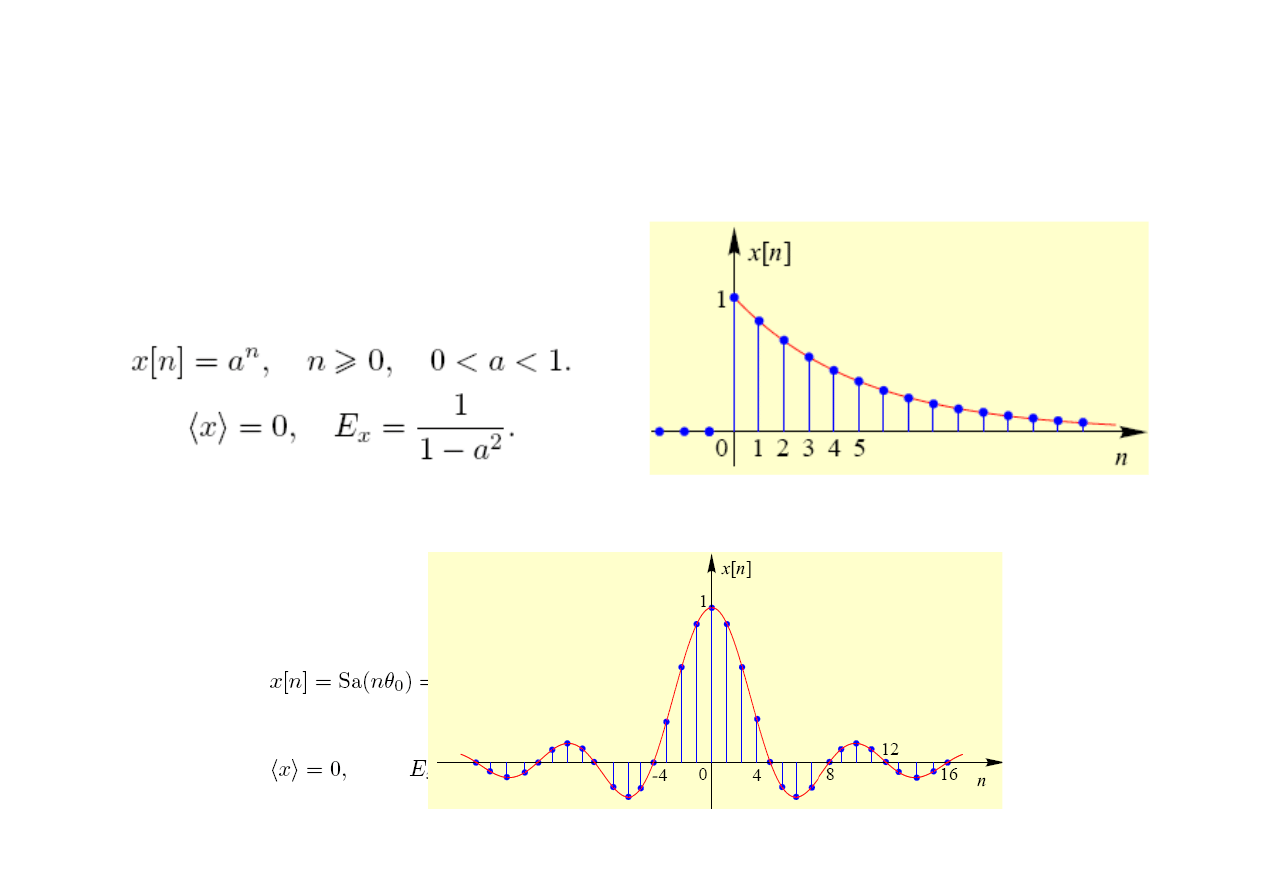
Wybrane sygnały dyskretne o ograniczonej energii

i nieskończonym czasie trwania

Sygnał wykładniczy:

Sygnał sinc:

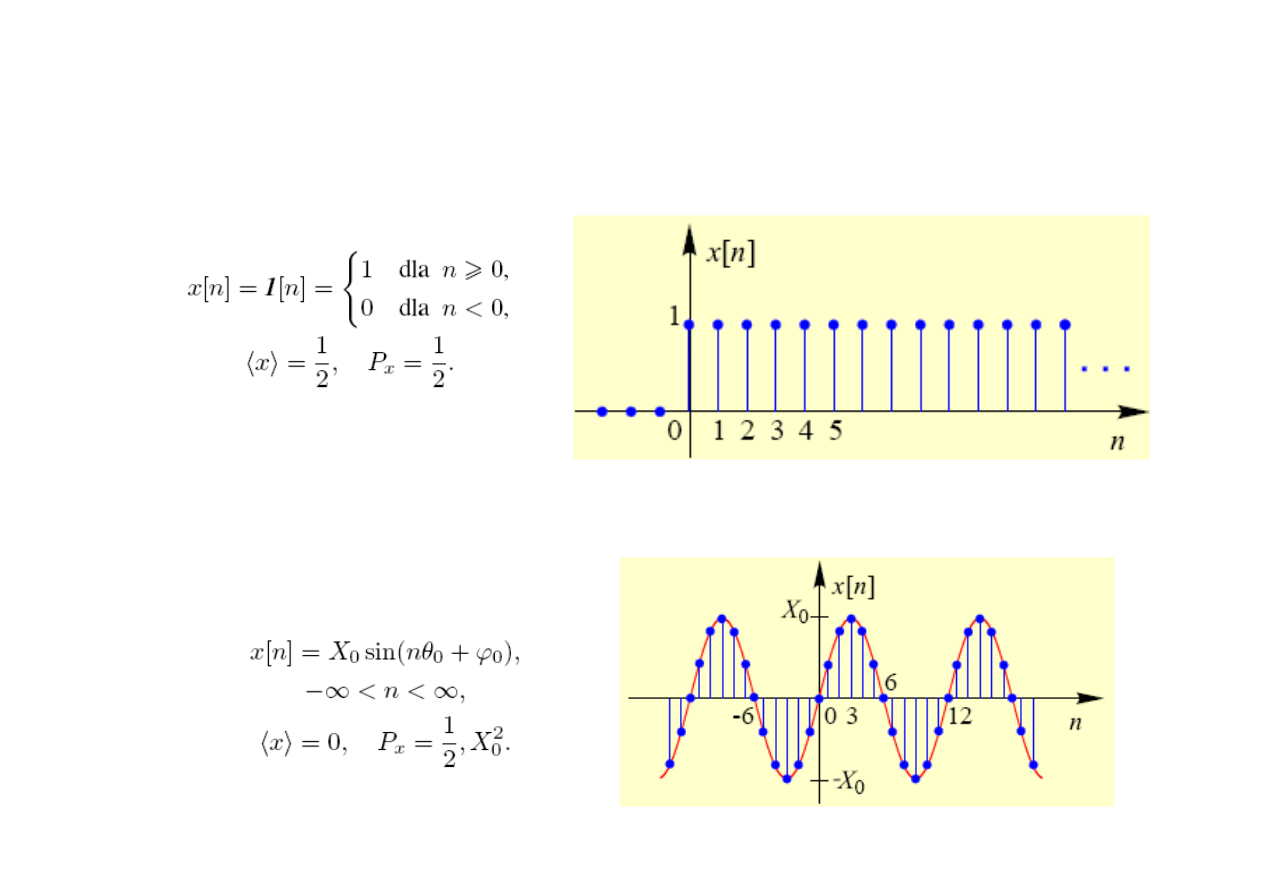
Wybrane sygnały dyskretne o ograniczonej mocy

Skok jednostkowy u(n):

Sygnał harmoniczny:

Warunek okresowości: 2π/θ

0

– wymierne, θ

0

= ω

0

T