Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (13)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

1 (26)

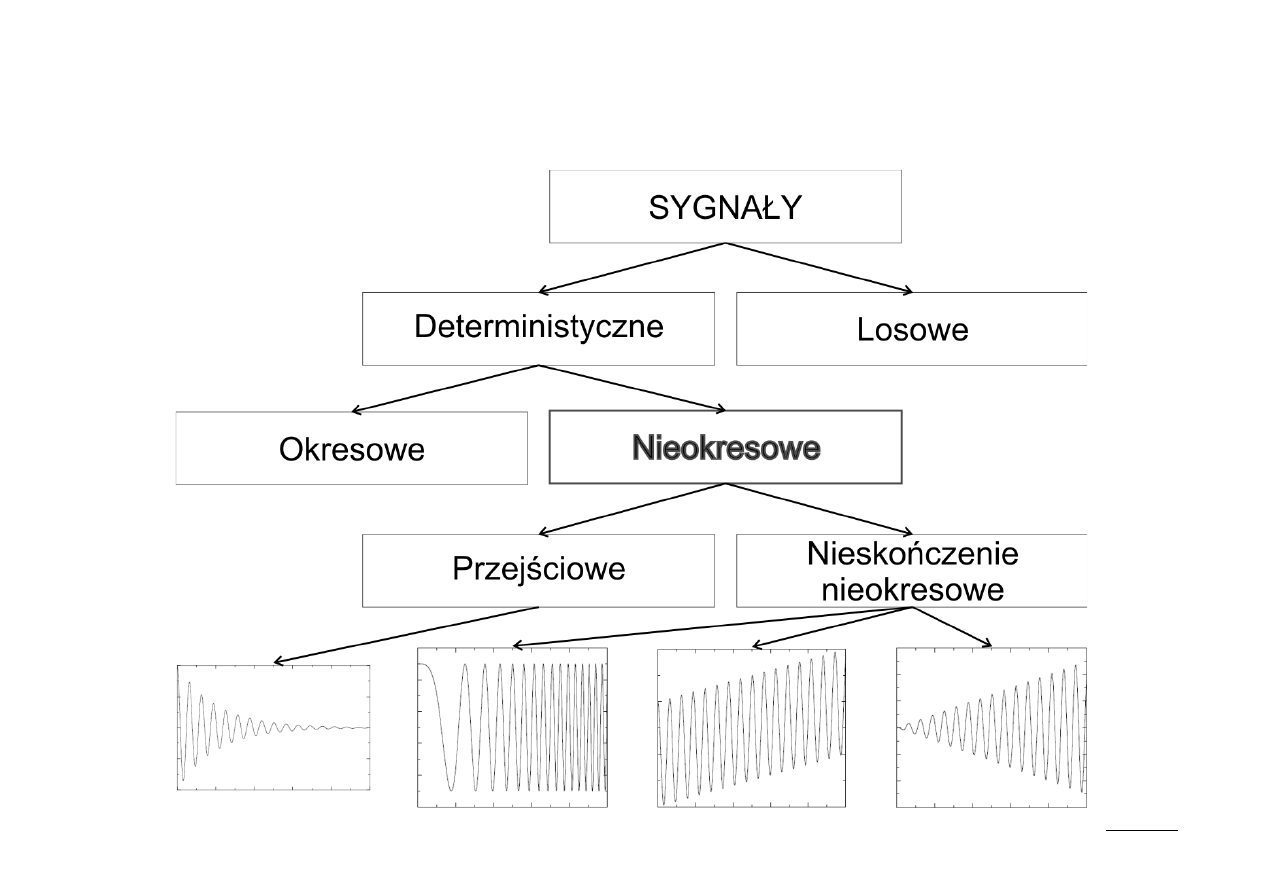
Podział sygnałów

2 (26)

Falki ciągłe – continuous wavelets

Transformata Fouriera zasadniczo służy do obróbki sygnałów stacjonarnych –

sygnałów, których parametry statystyczne (średnia, średnia kwadratowa (energia),

autokorelacja) nie zmieniają się w czasie. Biorąc pod uwagę fakt, że rzutuje ona

dany sygnał na idealne fale (ko-)sinusoidalne, które rozciągają się w czasie

w nieskończoność, jeśli rozwinięcie posiada pewną składową częstotliwościową

w określonej chwili, będzie ona stała przez cały czas.

W przypadku sygnałów niestacjonarnych powyższe założenie o stałości

rozwinięcia fourierowskiego jest absolutnie nieuzasadnione, czego dowodzi

następujący przykład:

3 (26)

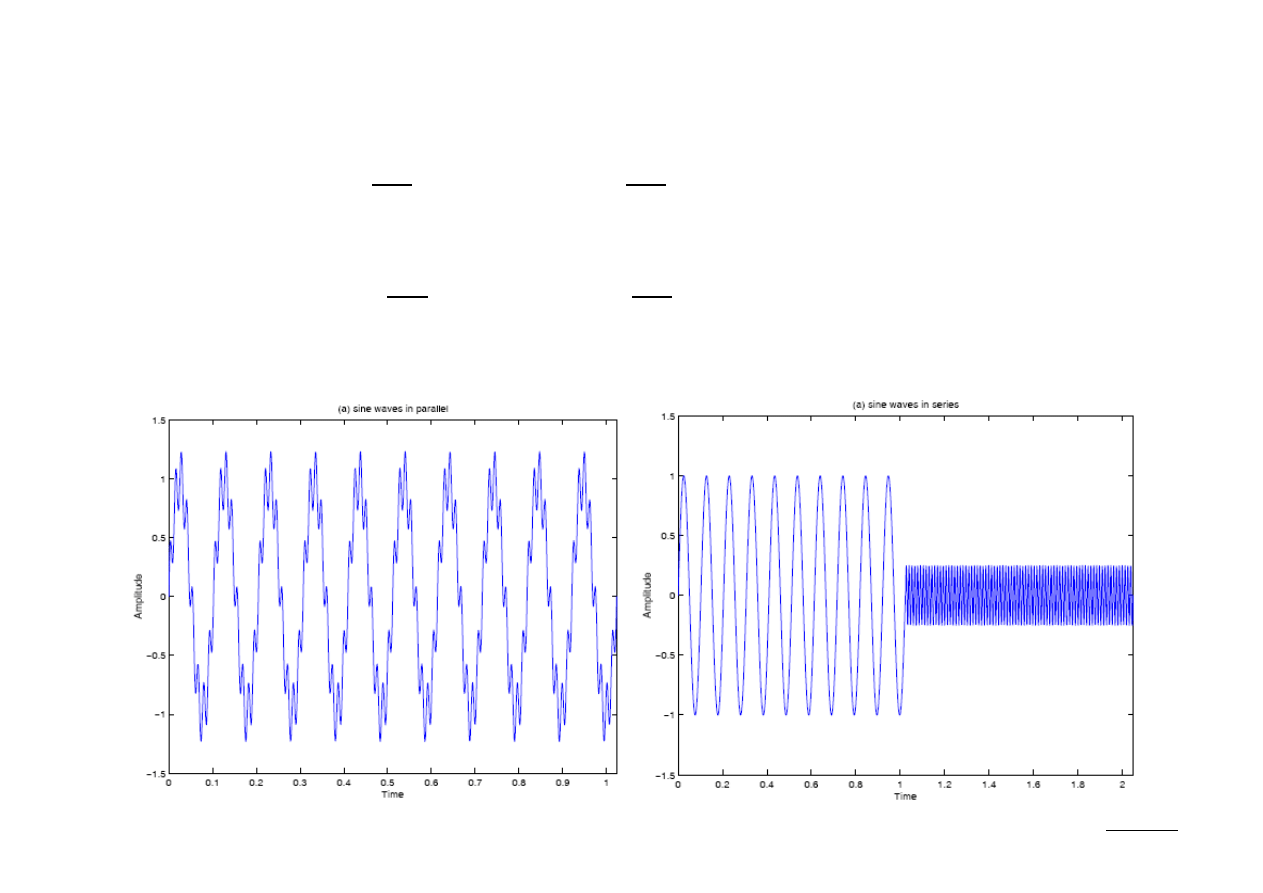
Rozważmy dwa sygnały:

-

x

1



t =sin 2 10

f

s

N

t sin 280

f

s

N

t

- sygnał stacjonarny,

-

x

2



t =

[

sin 2 10

f

s

N

t  , sin 2 80

f

s

N

t

]

- sygnał niestacjonarny,

gdzie: f

s

– jest częstotliwością próbkowania, zaś N – liczbą próbek.

4 (26)

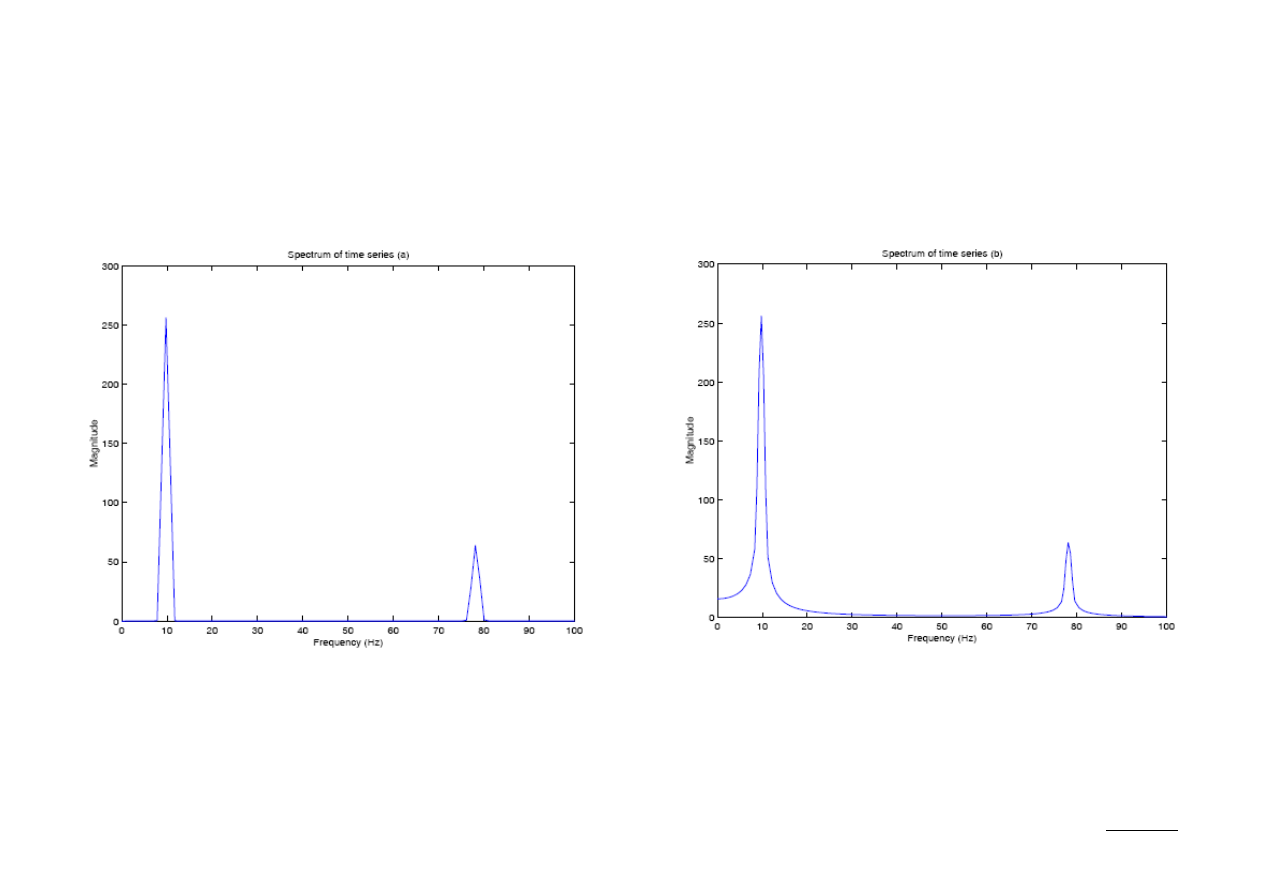
Porównanie widm fourierowskich:

Widma obu sygnałów są praktycznie nierozróżnialne (pomijając niewielkie

rozmycie widma sygnału x

2

spowodowane jego nieciągłością).

5 (26)

Krótkookresowa stacjonarność

Pomimo podobieństwa obu widm, transformata Fouriera nie jest w stanie

wyekstrahować informacji o tym, że w niestacjonarnym sygnale x

2

w pewnym

momencie składowa 10 Hz znika, a na jej miejsce pojawia się składowa 80 Hz.

Powyższa cecha transformaty Fouriera wynika z faktu, iż jej funkcje bazowe są

nieskończenie rozciągłe, a więc są one nielokalne w dziedzinie

czasoprzestrzennej.

Pewnym rozwiązaniem mogłoby być wprowadzenie do transformaty

zlokalizowanej funkcji okna czasowego (zakładając chwilową stacjonarność

sygnału w obrębie okna).

6 (26)

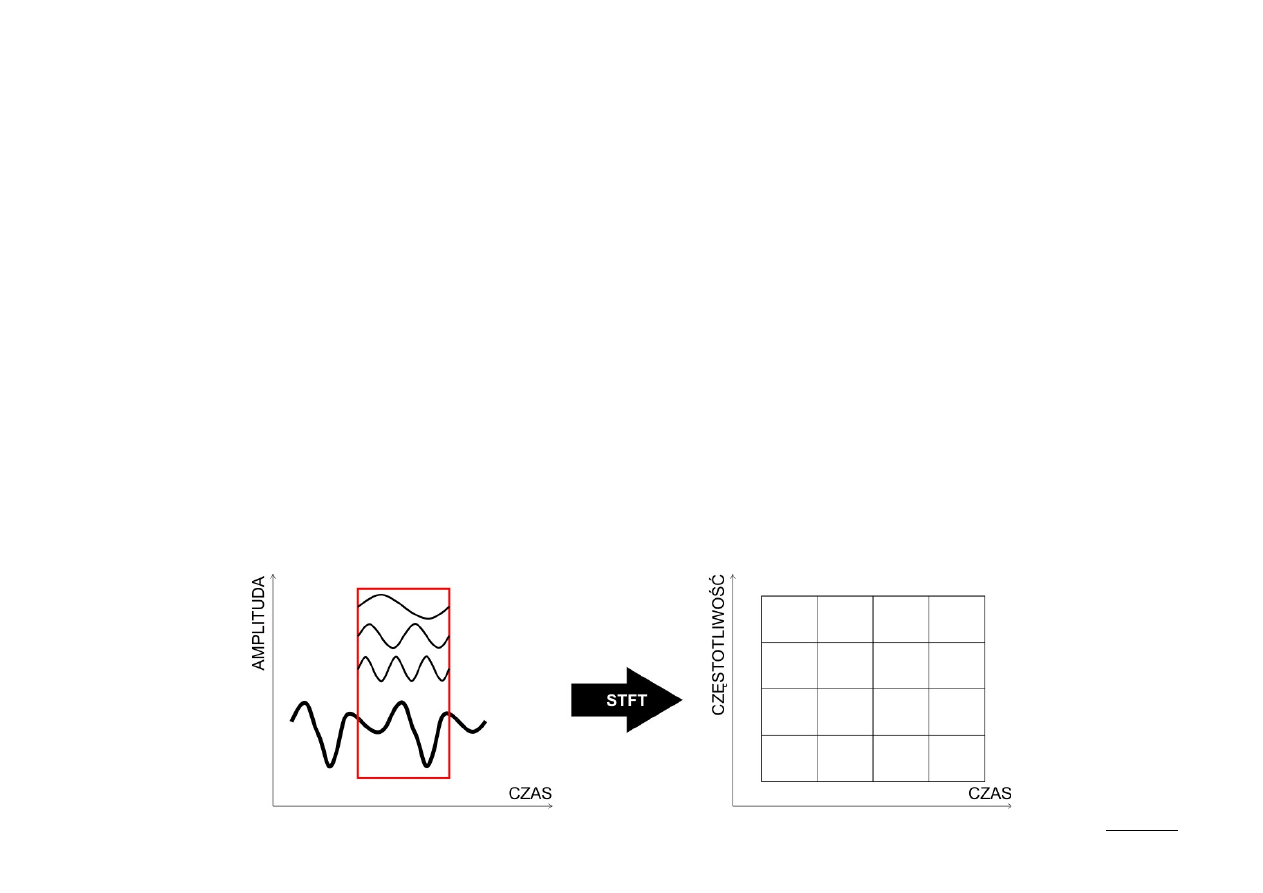
Krótkookresowa Transformata Fouriera (STFT)

Rozwińmy sygnał w bazie funkcji fourierowskich z nałożonym oknem:

X  ,=

∫

−∞

∞

x t  w t−e

i t

dt

gdzie funkcje zlokalizowanych w czasie składowych harmonicznych o czasie

trwania T wynoszą:

W



, 

=

w t−e

i t

Funkcje te nazywane są atomami czas-częstotliwość (TF), zaś powyższa

transformata – Krótkookresową Transformatą Fouriera (STFT).

7 (26)

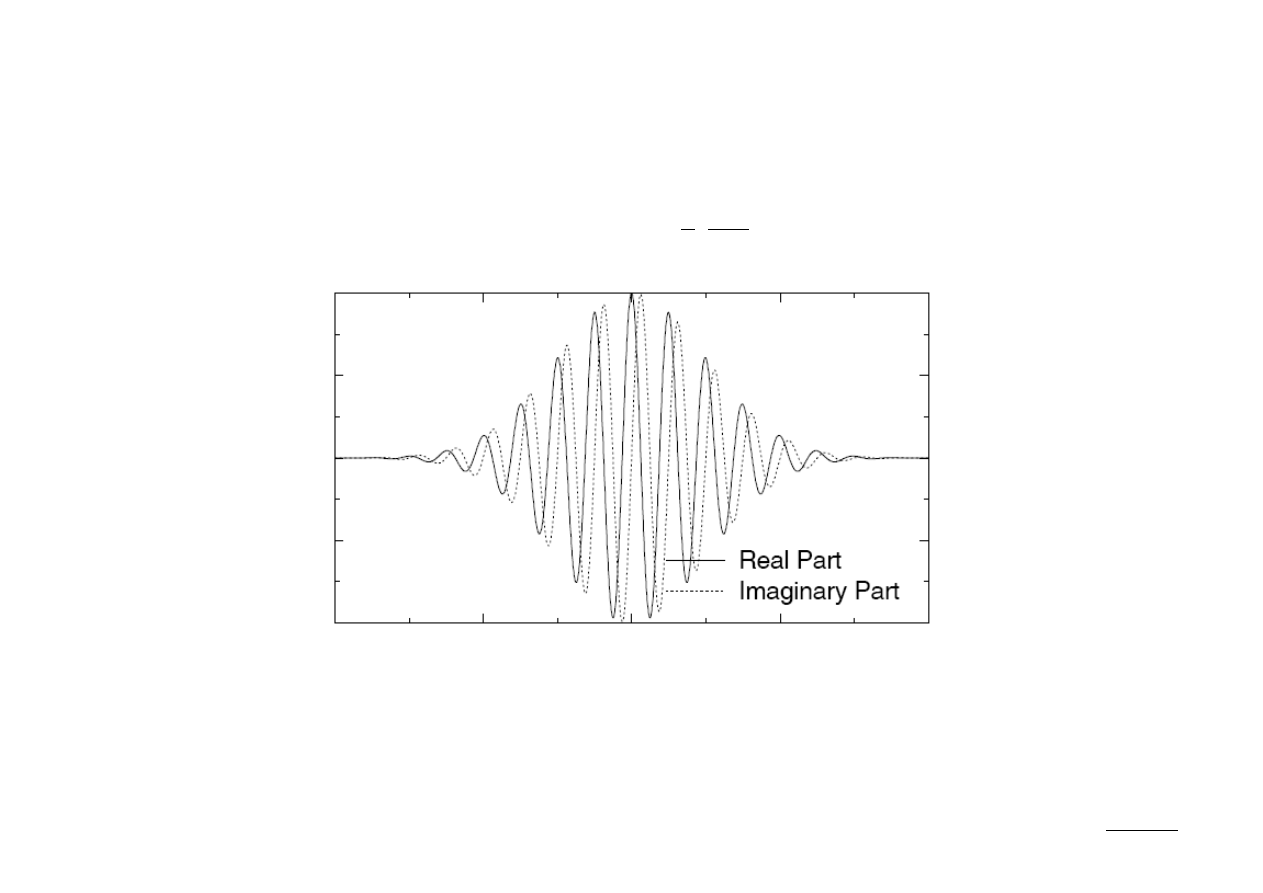
Lokalność STFT

Załóżmy, że funkcja okna ma charakter gaussowski (transformata Gabora):

w t−=e

−

1
2



t−





2

Powyższa funkcja jest istotnie niezerowa jedynie w obszarze o szerokości ± 3σ.

8 (26)

Pamiętajmy jednak o zasadzie nieoznaczoności:

 =

1

T

Powyższy wynik oznacza, że można albo dobrze zlokalizować składowe

czasoprzestrzenne sygnału (krótkie okno czasowe T) lub też dobrze zlokalizować

jego składowe częstotliwościowe (wysoka rozdzielczość widmowa Δω),

lecz nigdy nie można uzyskać obu efektów jednocześnie!

9 (26)

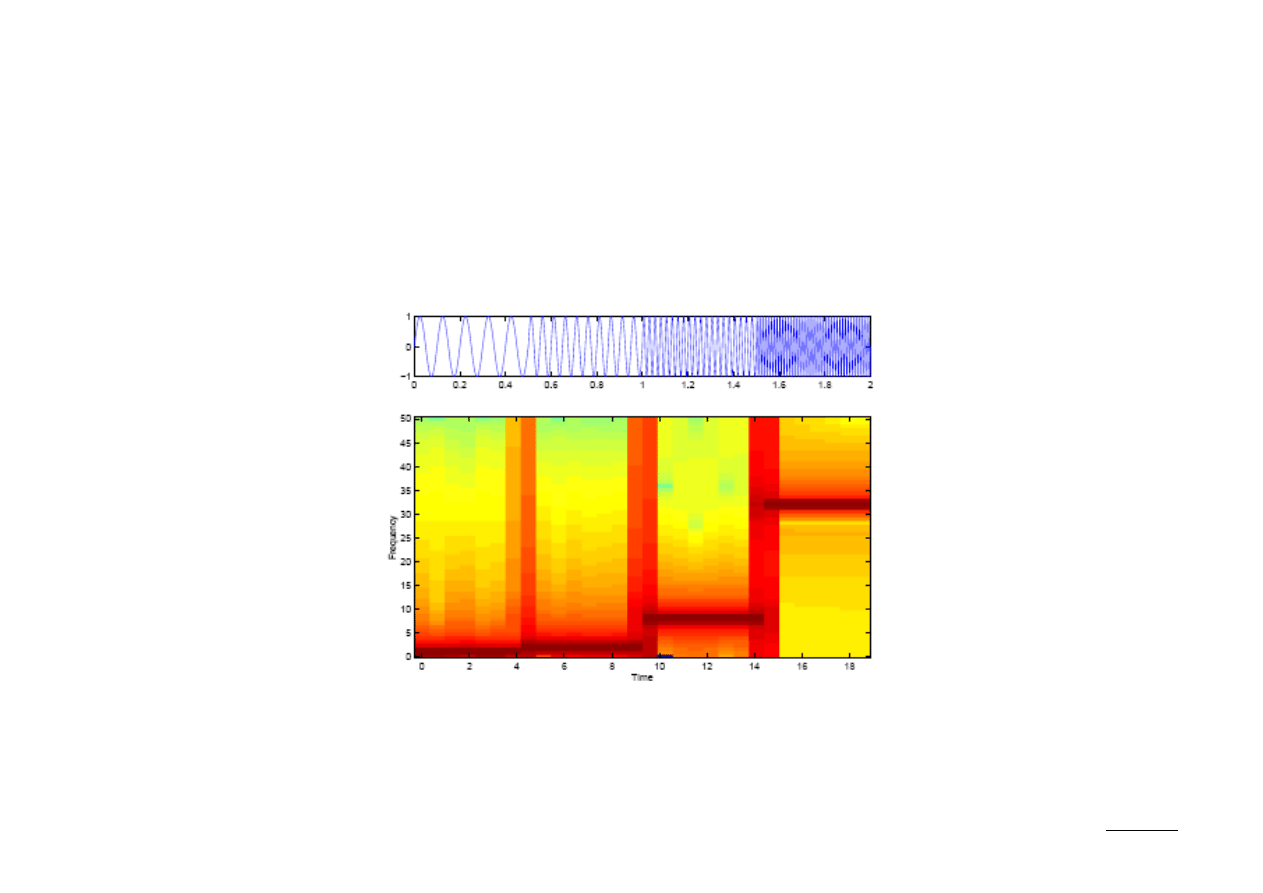
Spektrogram STFT

W przypadku STFT szerokość okna T można zmieniać w zależności od potrzeb,

jednak podczas analizy jest ona stała. Mapy zmian kształtu widm fourierowskich

w czasie nazywane są spektrogramami STFT:

Długie okno czasowe zwiększa rozdzielczość częstotliwościową, lecz pogarsza

lokalizację czasową i vice versa – pole każdego atomu TF jest stałe.

10 (26)

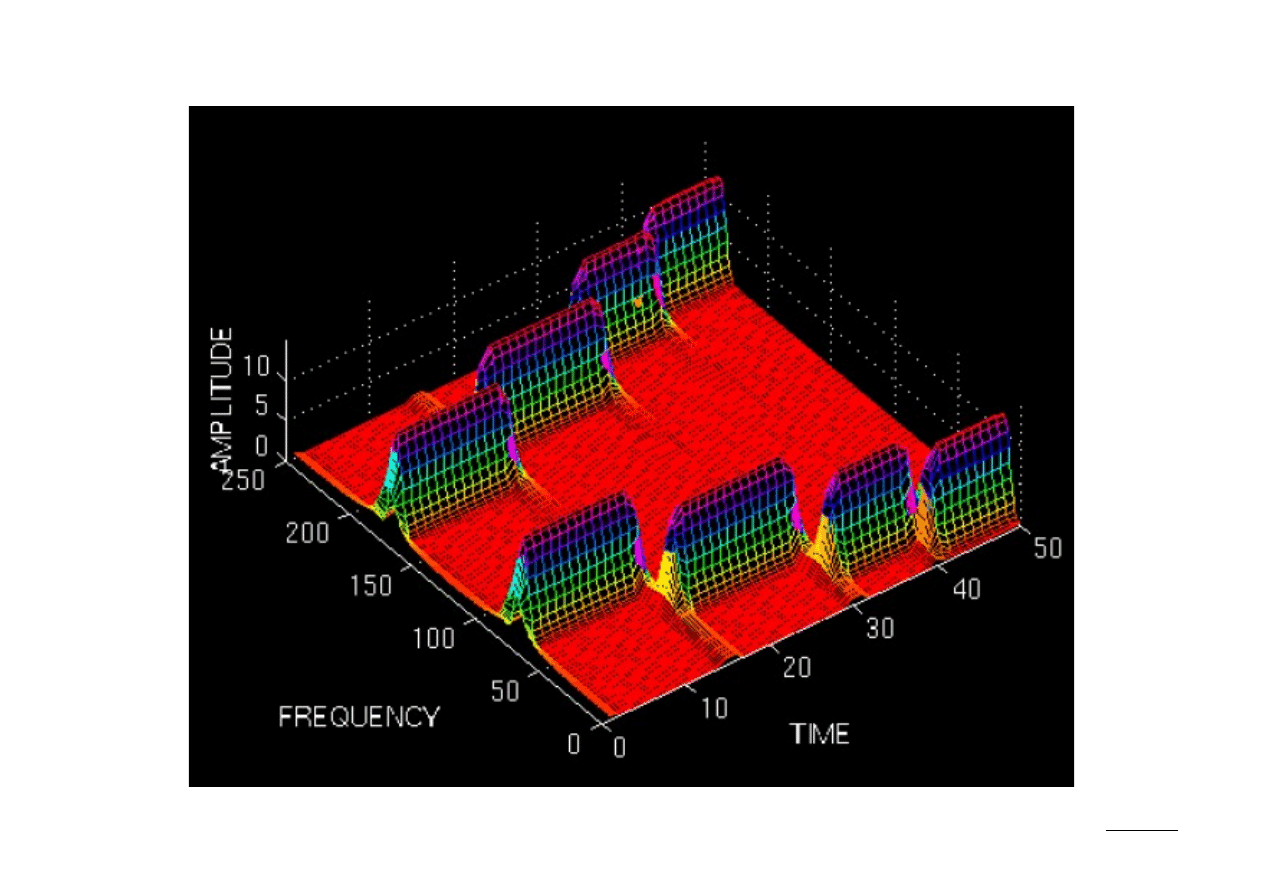
11 (26)

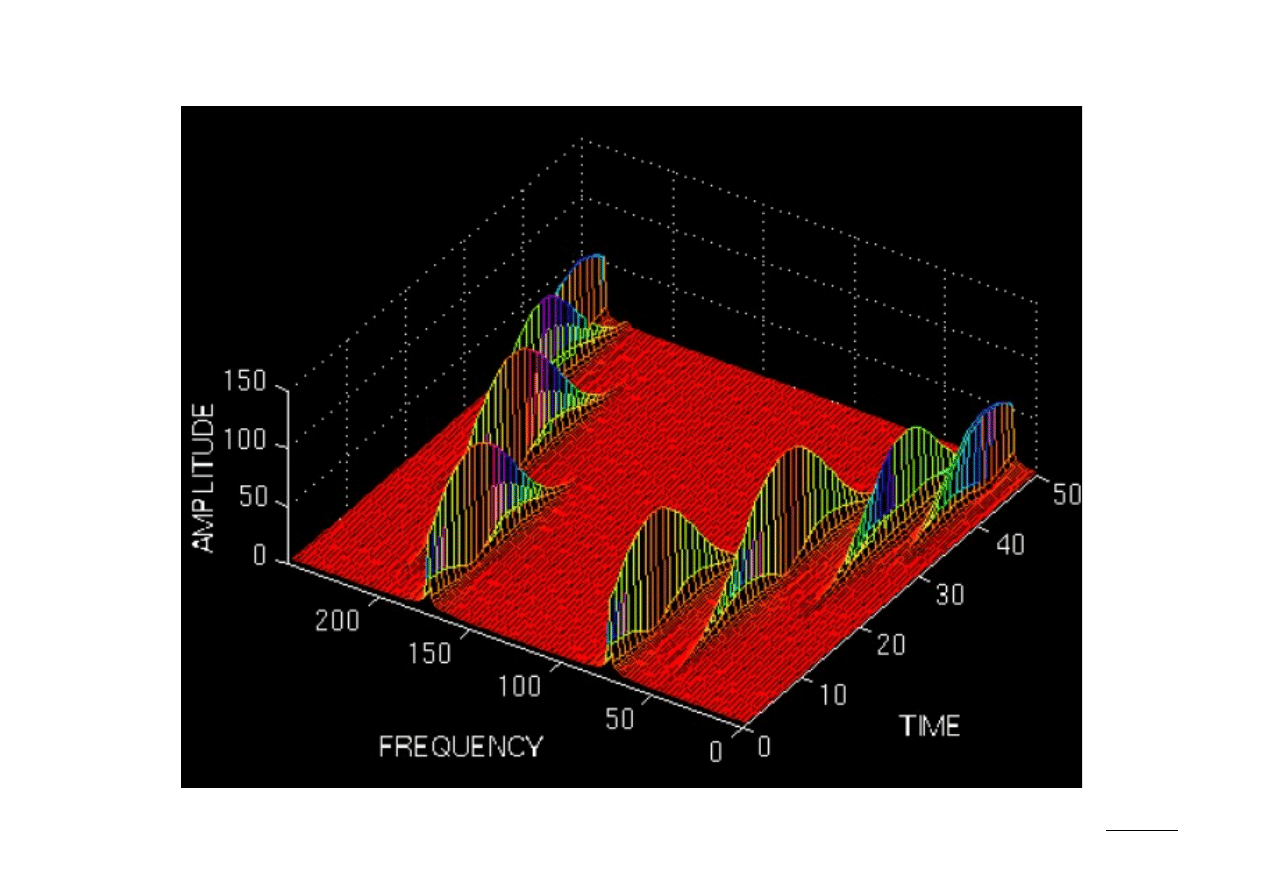
12 (26)

Ciągła transformata falkowa (CWT)

Transformata falkowa rozwiązuje problem sprzężenia lokalizacji sygnału

w dowolnej dziedzinie z rozdzielczością jego reprezentacji.

Ciągłe transformaty falkowe są pod pewnymi względami podobne do metody

STFT. Podobieństwo wynika z faktu, że w obu metodach w transformacji

całkujemy sygnał z pewna funkcja różną od zera w ograniczonym przedziale.

Transformatę falkową otrzymuje się jako całkę z iloczynu sygnału i pewnej funkcji

nazywanej falką pierwotną lub macierzystą (mother wavelet). Formalnie funkcja

ta zależy od trzech parametrów: czasu t, opóźnienia (przesunięcia) τ i skali s, ale

na ogół można ją przedstawić jako funkcję jednego parametru

u:

u=

t−

s

Odwrotna proporcjonalność u = f (s

-1

) oznacza, że składowym sygnału o wysokiej

częstotliwości odpowiadają krótkie skale i na odwrót.

13 (26)

Obrazem ciągłego sygnału

x(t) jest w CWT funkcja dwóch zmiennych (czasu

i skali):

CWT [ x ,] , s=

1



∣

s∣

∫

−∞

∞

x t 

∗



udt

gdzie: Ψ(u) jest zespoloną funkcją opisującą kształt falki (falką macierzystą).

Istotną różnicą w stosunku do tradycyjnych transformat Fouriera jest

występowanie parametru skali a nie częstości jako drugiej zmiennej. Jest to

podstawowy parametr analizy falkowej. Istnieje analogia między skalą

a częstością: duża skala (tzn. wartość tej zmiennej) odpowiada małym

częstościom, a wiec zjawiskom trwającym długi okres czasu. Z kolei mała skala

odpowiada wysokim częstościom i procesom krótkotrwałym.

14 (26)

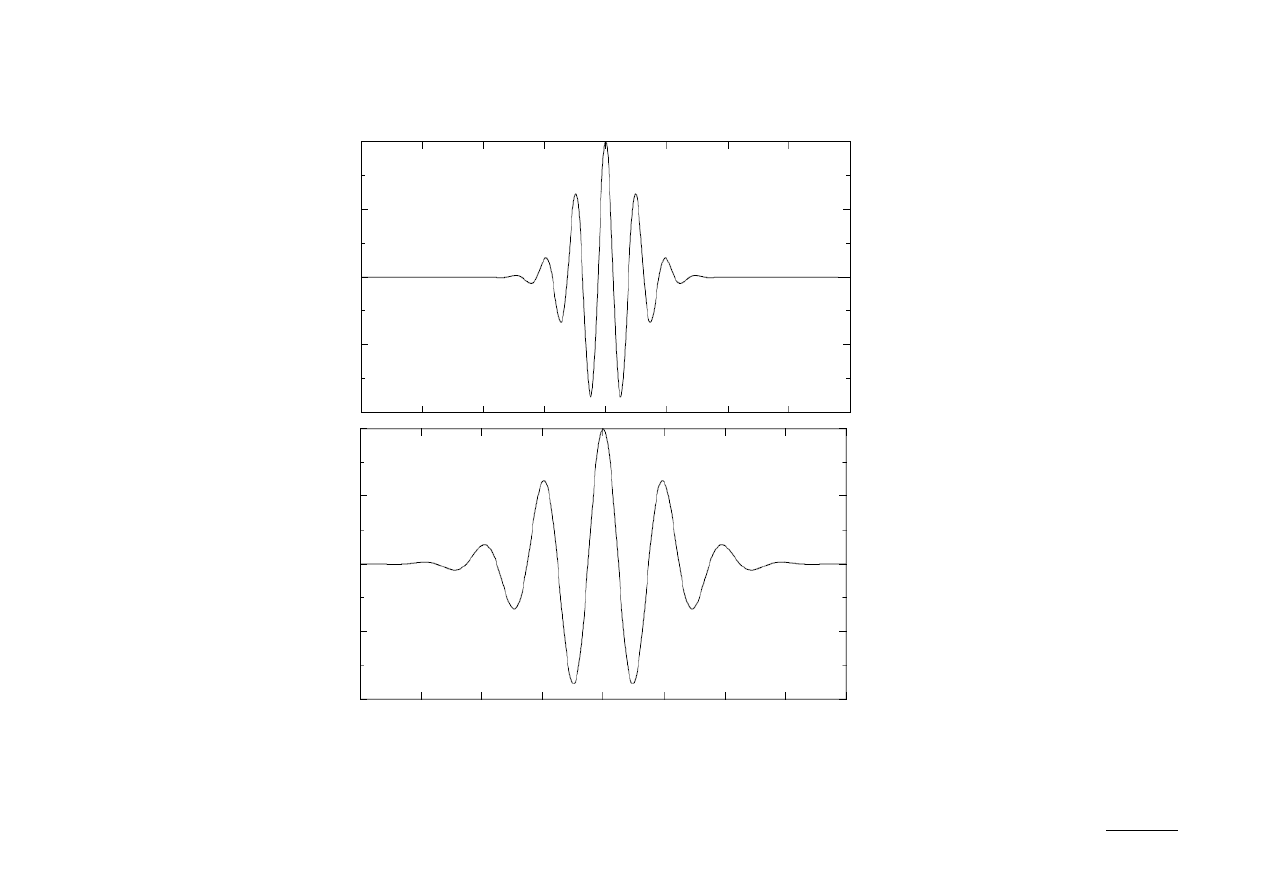
Przykłady falki macierzystej i jej przeskalowanej funkcji bazowej:

Zmieniając parametr skali można dopasować teraz potrzebną rozdzielczość do

długości okna.

15 (26)

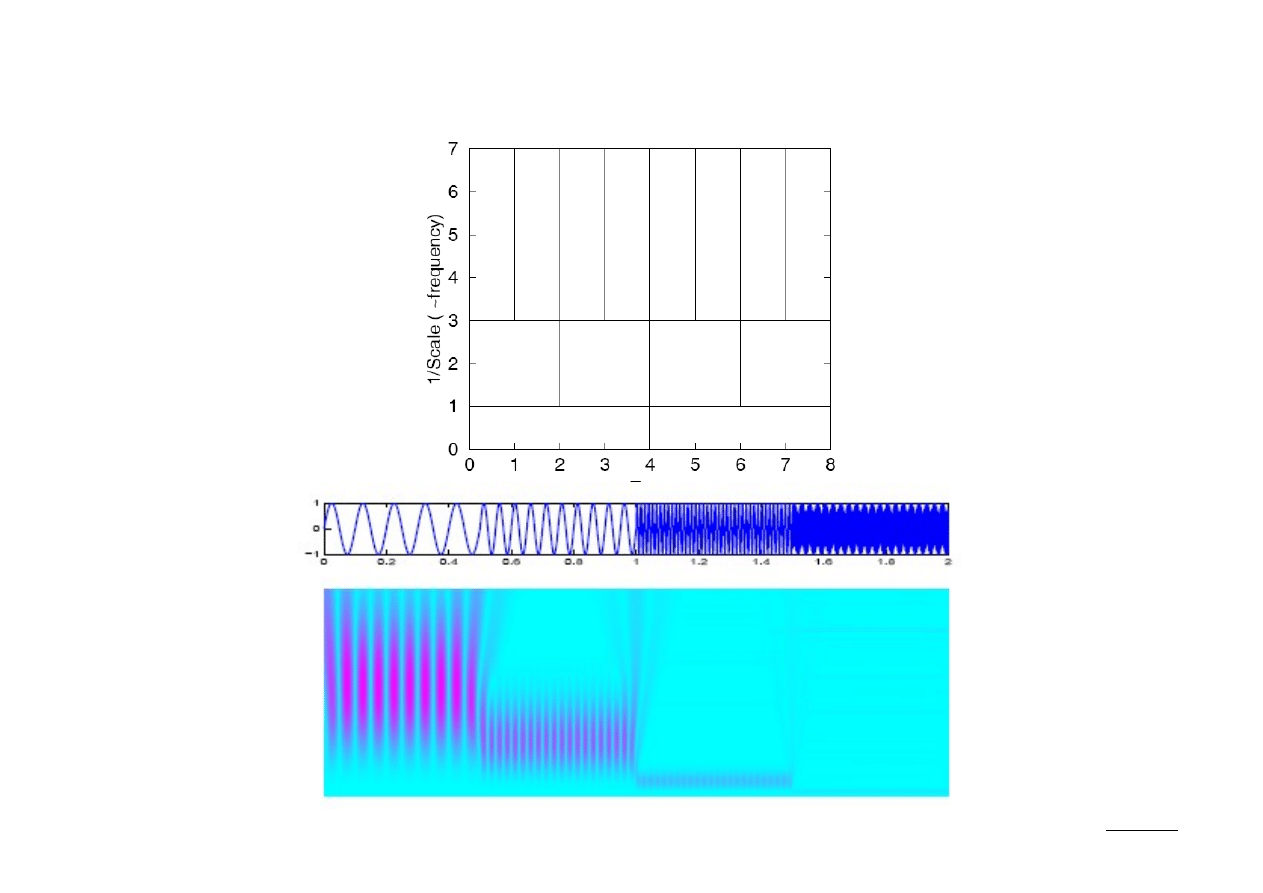
Mapa CWT

16 (26)

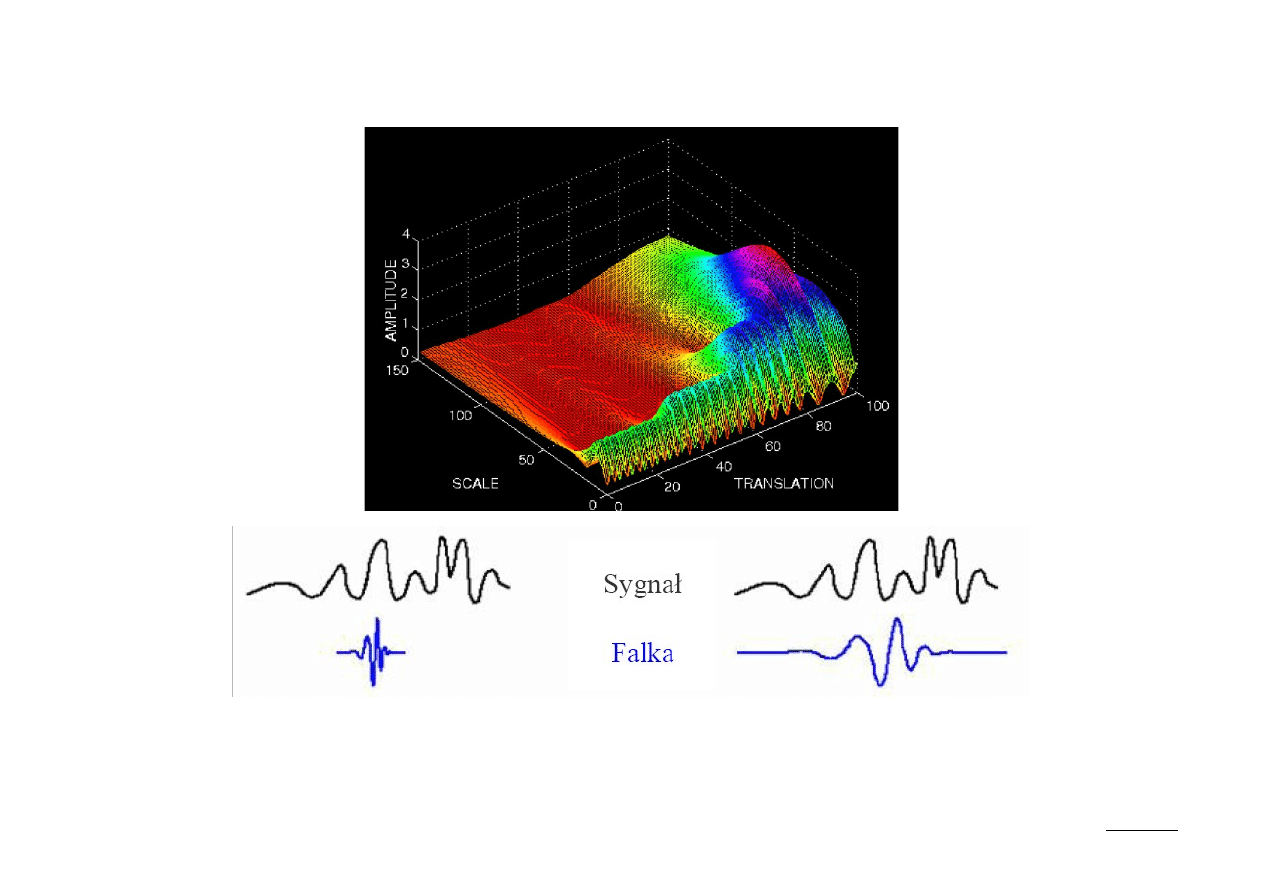
Mapa CWT

Długość skali jest odwrotnie proporcjonalna do szybkości zmian analizowanej

cechy sygnału.

17 (26)

Własności falki macierzystej

Falka macierzysta musi spełniać kilka własności:

(1) Aby funkcja była falką, musi mieć ona charakter zlokalizowanej w czasie

oscylacji, a więc jej wartość średnia musi być równa zero:

∫

−∞

∞



t dt=0

(2) Energia falki macierzystej musi być ograniczona:

lim

T  ∞

1

2T

∫

−

T

T

∣

t∣

2

dt=0

(3) Gęstość widmowa energii falki musi być skończona (warunek dopuszczalności

(odwracalności) CWT):

∫

−∞

∞

∣ ∣

2

∣∣

d =C



∞

18 (26)

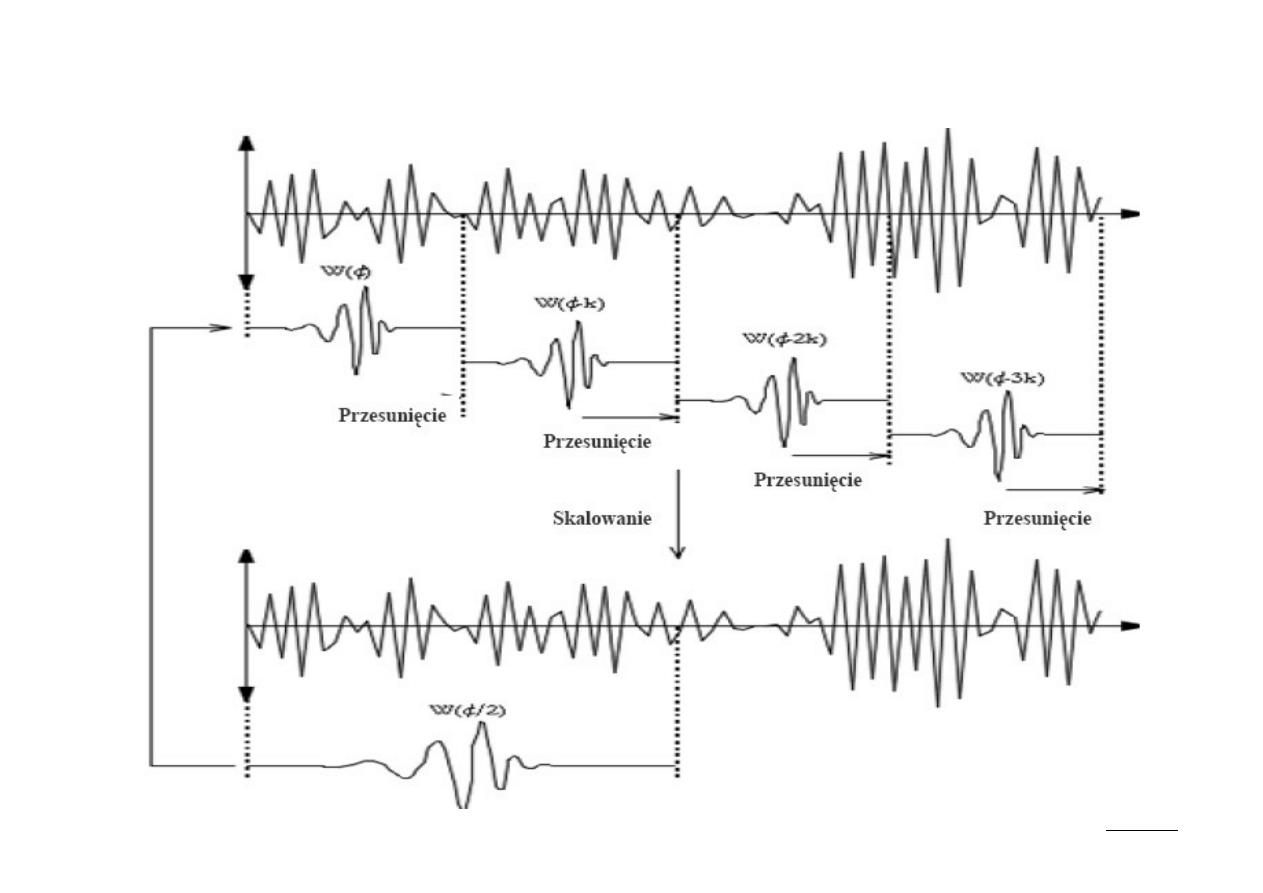
Wyznaczanie CWT

19 (26)

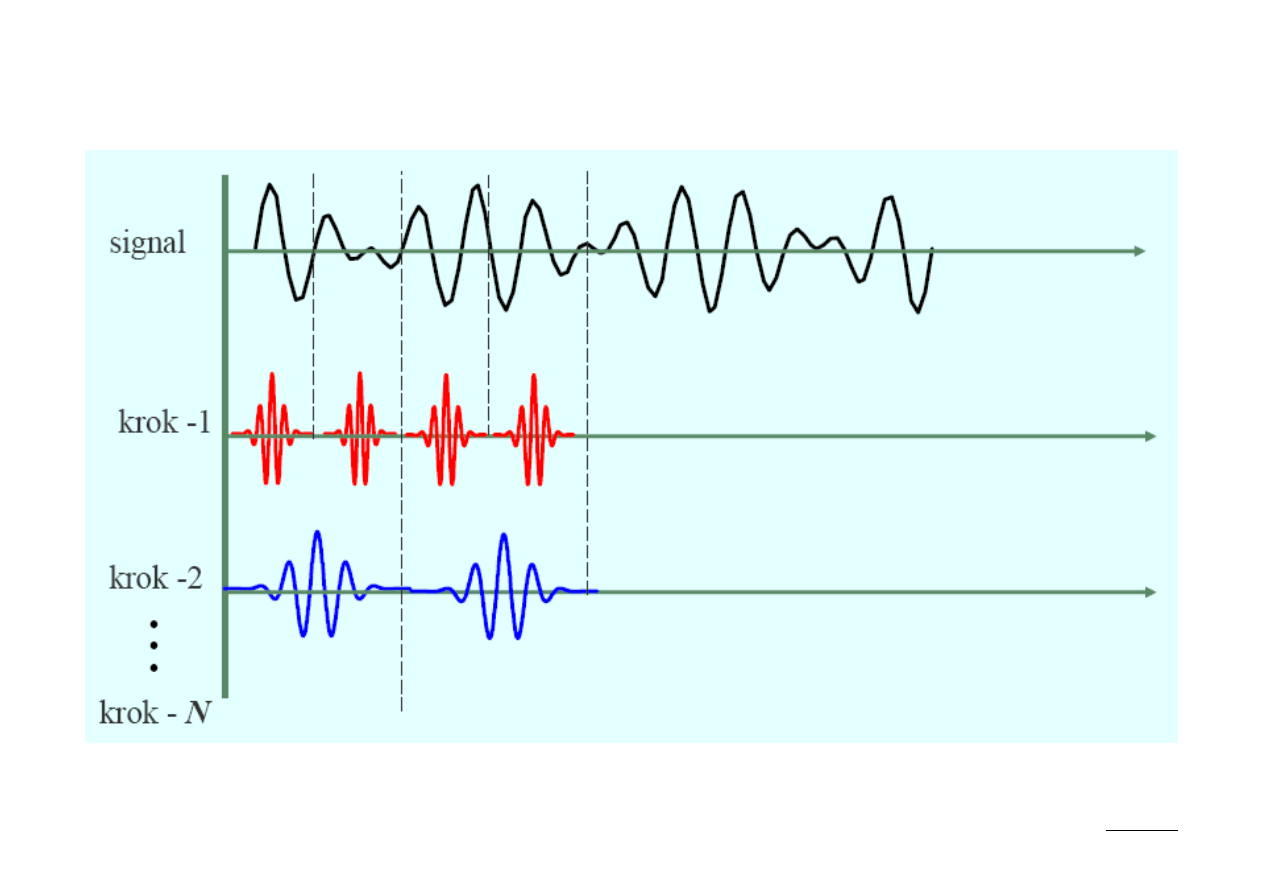
20 (26)

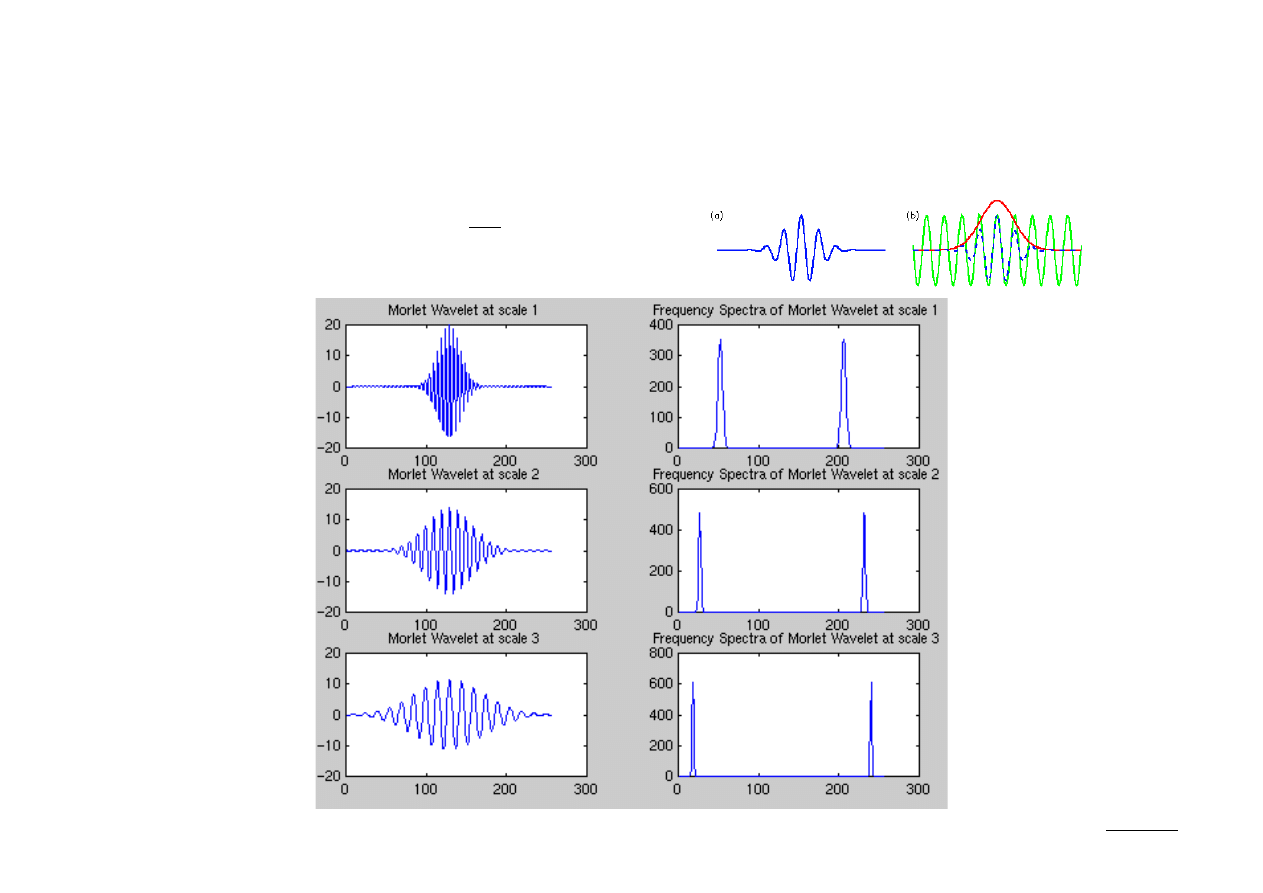
Falki Morleta

Falka Morleta jest funkcją zespoloną daną jako:



t =e

i 

0

t

e

−

t

2

2

21 (26)

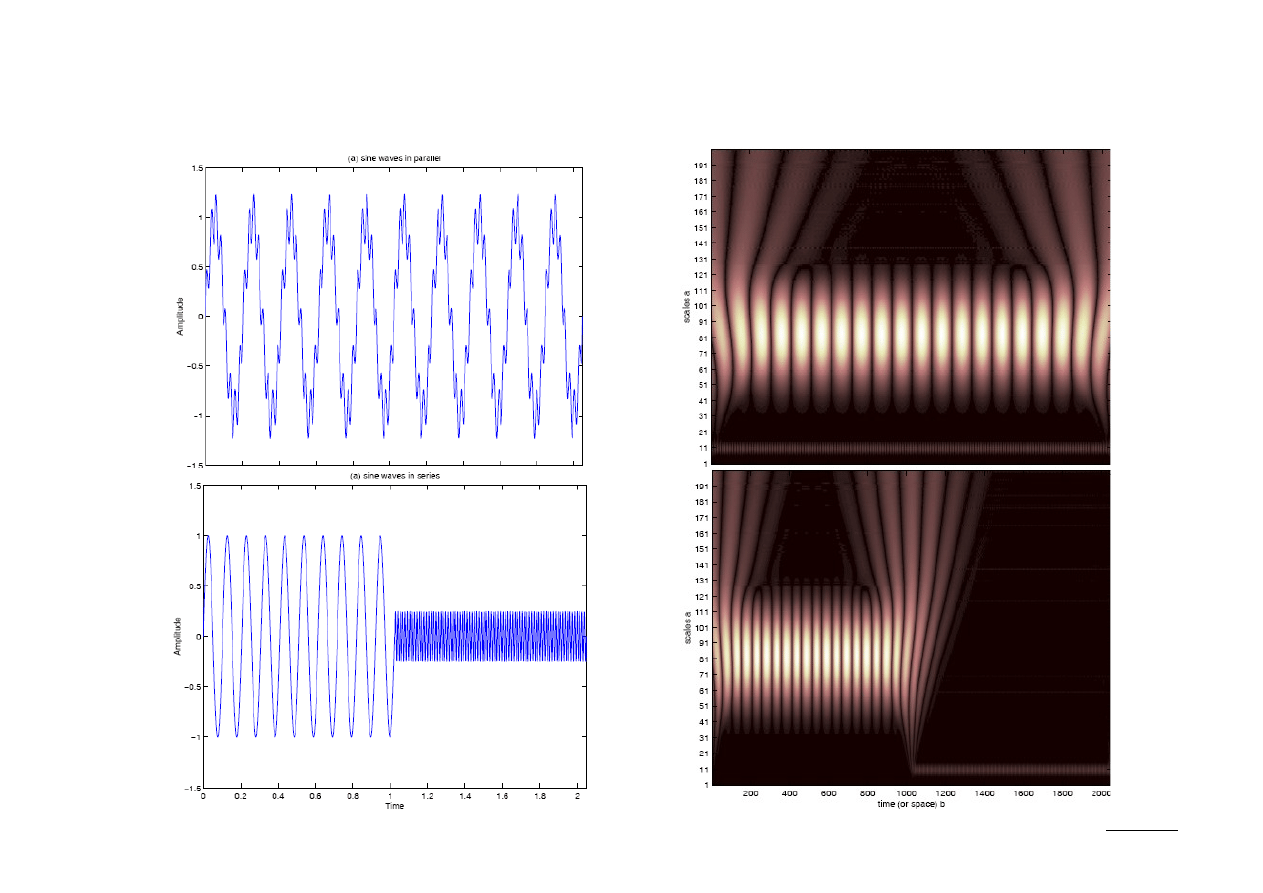
Wykorzystanie CWT

22 (26)

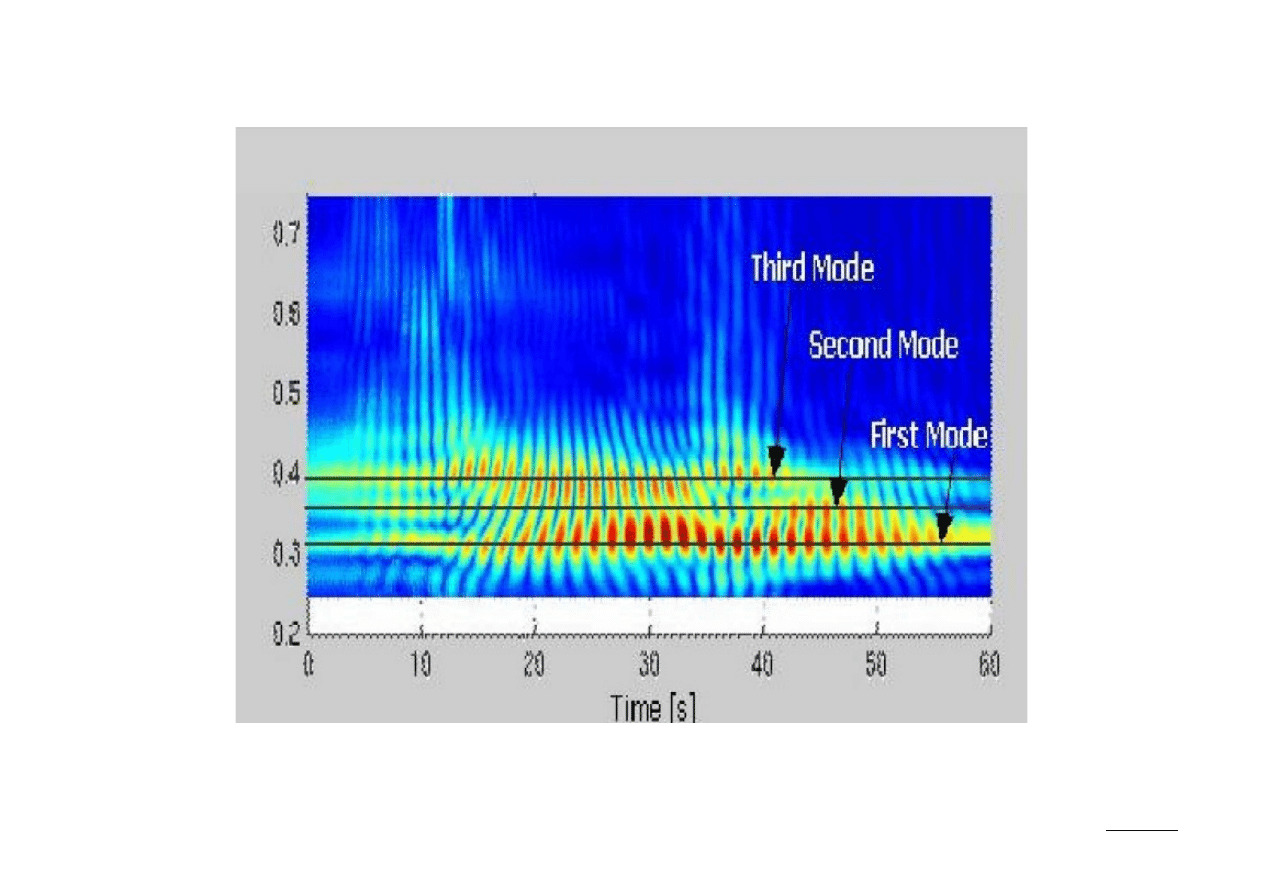
Wykorzystanie CWT

Analiza drgań budynku wywołanych trzęsieniem ziemi – widoczne mody drgań.

23 (26)

Dyskretna transformata falkowa (DWT)

Przez analogię do DFT, która liczona była jako dyskretna (spróbkowana

równomiernie) transformata DTFT, dokonajmy dyskretyzacji CWT.

Niech dana jest CWT:

CWT [ x ,] , s=

1



∣

s∣

∫

−∞

∞

x t 

∗



udt

Jeśli dane czasowe mają postać N-punktowego ciągu dyskretnego, wówczas:

CWT [ x ,] , s=



t



∣

s∣

∑

j=0

N −1

x

j



∗



t

j

−

s



gdzie przesunięcie oraz skala zmieniają się w sposób ciągły – nadmiarowość

danych.

24 (26)

Dyskretyzacja skali i przesunięcia

Problemem identycznym jak w przypadku DFT jest taka dyskretyzacja ciągłej

transformaty, aby możliwe było odtworzenie sygnału wyjściowego z jednoczesnym

usunięciem informacji nadmiarowej.

Dokonajmy najpierw dyskretyzacji skali: {s

j

| j = 0, 1, ..., L-1}, tak że: s

j

= 0.5 s

j-1

.

Wynika stąd, iż aby uzyskać stałą względną rozdzielczość skali (częstotliwości)

należy podwajać liczbę próbek przesunięcia w miarę wzrostu indeksu j (spadku

skali a wzrostu częstotliwości).

Poszukiwana dyskretna transformata falkowa ma postać:

DWT  s

m

,

m , n

=

1



s

m

∑

j=0

N −1

x

j



∗



t

j

−

m , n

s

m



gdzie:

s

m

=

2

−

m

, 

m , n

=

n⋅2

−

m

25 (26)

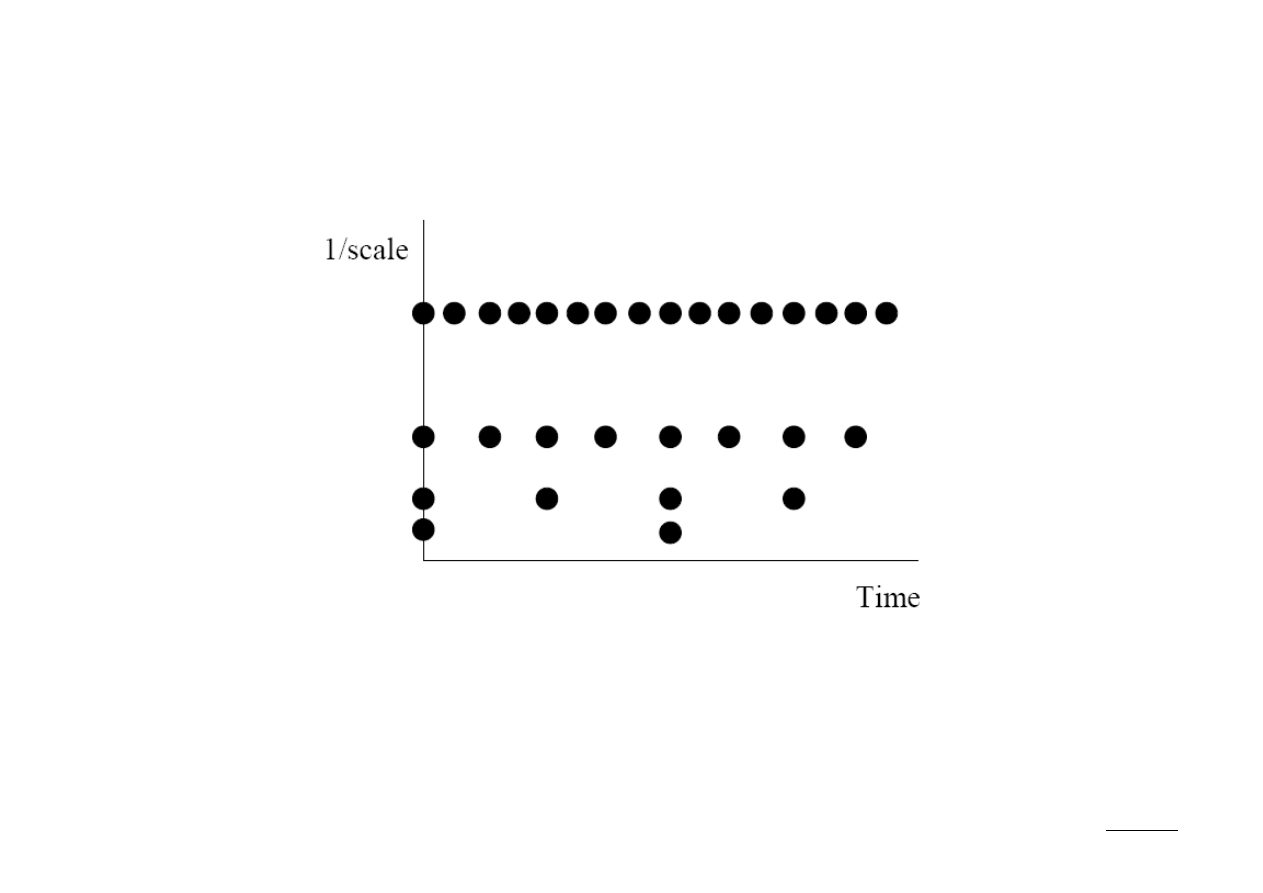
Siatka diadyczna

Wprowadzony typ dyskretyzacji określany jest mianem siatki diadycznej:

Dyskretyzacja skali wymaga, aby N = 2

L

, co jest zgodne z warunkiem dla DFT.

26 (26)