Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (7)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

1 (37)

Definicja z- transformaty

z-transformatą sygnału czasu dyskretnego x[n] nazywa się szereg potęgowy X[z]:

X  z=

∑

n=−∞

∞

x [n]⋅z

−

n

, z∈ℂ

Powyższy wzór definiuje tzw. prostą z-transformatę, zamieniającą sygnał x[n]

w jego reprezentację w dziedzinie liczb zespolonych X[z]. Procedura odwrotna,

tj. przekształcenie ciągu X[z] w x[n] nazywa się odwrotną z-transformatą.

Przyjmijmy następujące oznaczenia:

X  z =Z  x [n]

x [n]

z

X  z

Ponieważ z-transformata jest nieskończonym szeregiem potęgowym, jest istnienie

jest uwarunkowane zbieżnością z uwagi na z. Obszarem zbieżności (ROC –

Region of Convergence) jest zbiór wszystkich z, dla których X[z] jest skończona.

2 (37)

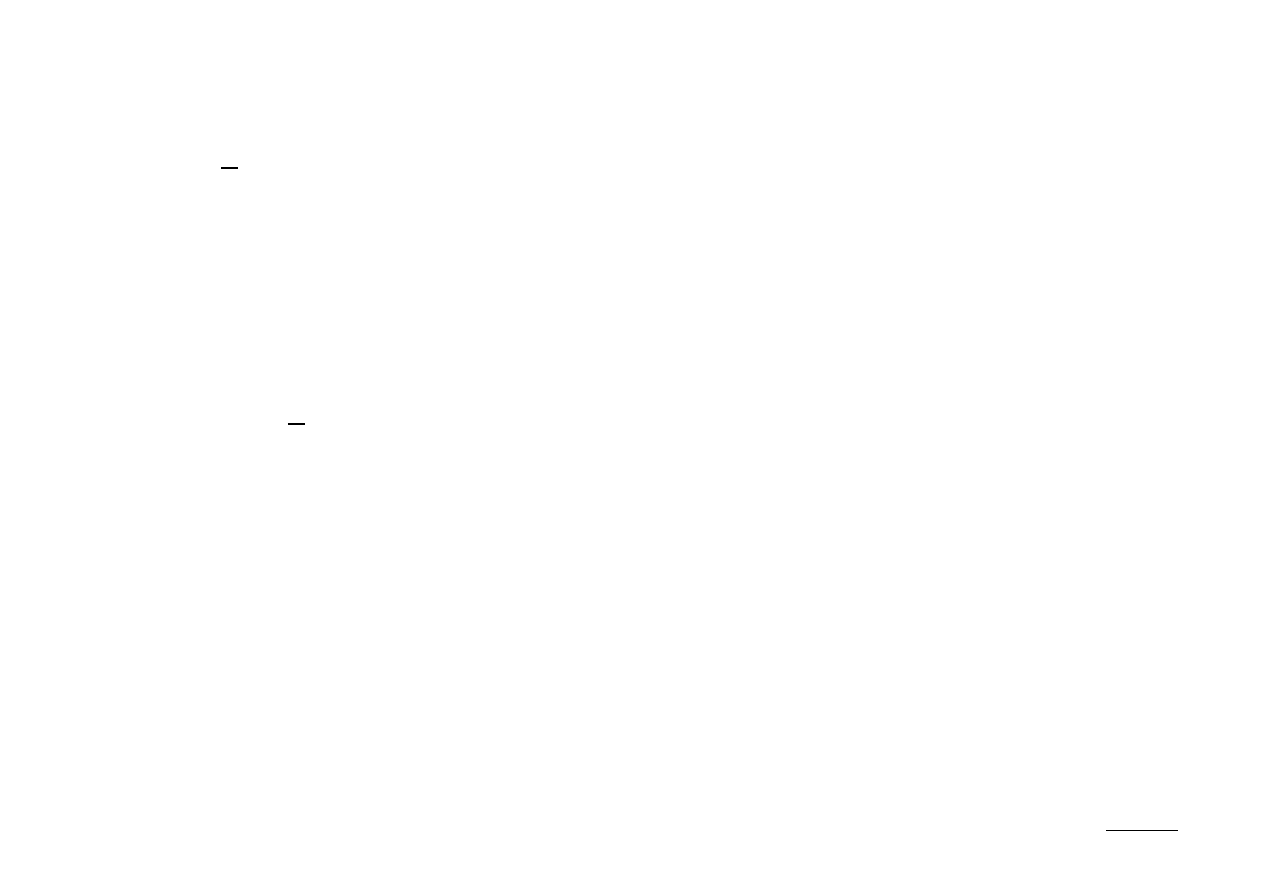
Ex.: Wyznaczyć z-transformatę następujących sygnałów:

(1) x[n] = [1, 2, 4, 5]

X  z =

∑

−∞

∞

x [n]⋅z

−

n

=

∑

0

3

x [n]⋅z

−

n

=

1⋅z

0



2⋅z

−

1



4⋅z

−

2



5⋅z

−

3

=

...

...=12⋅z

−

1



4⋅z

−

2



5⋅z

−

3

ROC =ℂ/{0}

(2) x[n] = [2, 4, 5, 7, 0, 1]

X  z =2⋅z

2



4⋅z57⋅z

−

1



z

−

3

; ROC=ℂ/{0,±∞}

(3) x[n] = δ[n]

X  z =1 ; ROC=ℂ

(4) x

1

[n] = δ[n - k], x

2

[n] = δ[n + k]; k>0

X

1



z =z

−

k

; ROC =ℂ/{0}; X

2



z = z

k

; ROC =ℂ/{±∞}

3 (37)

–

Z powyższych przykładów wynika, iż ROC sygnałów skończonych

(o skończonym czasie trwania) jest cała płaszczyzną liczb zespolonych za

wyjątkiem biegunów transformaty, w których jest ona rozbieżna.

–

Z matematycznego punktu widzenia z-transformata jest alternatywną

reprezentacją sygnału, w której współczynnik stojący przy z

-n

jest próbką

sygnału z chwili n.

–

W wielu przypadkach możemy wyrazić sumę skończonego lub nieskończonego

szeregu z-transformaty w postaci zamkniętego wyrażenia, co pozwala

w kompaktowy sposób reprezentować informację o sygnale.

4 (37)

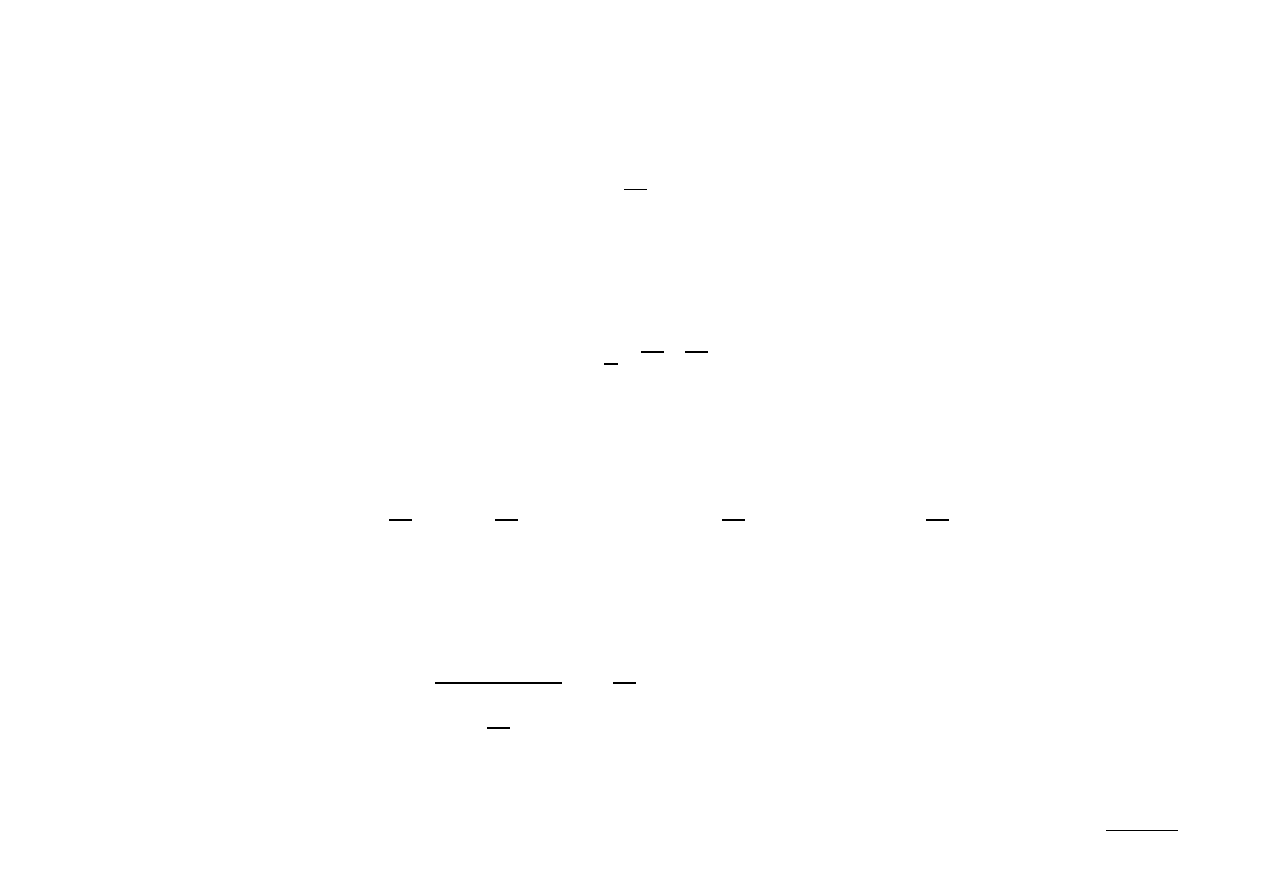
Ex.: Wyznaczyć z-transformatę sygnału:

x [n]=



1
2



n

⋅

u [n]

Przedstawmy sygnał x[n] w postaci jawnej:

x [n]=

[

1 ,

1
2

,

1
4

,...

]

Stąd jego z-transformata jest szeregiem:

X  z =1

1
2

z

−

1



1
4

z

−

2



...=

∑

n=0

∞



1
2



n

⋅

z

−

n

=

∑

n=0

∞



1

2

⋅

z

−

1



n

Granicą tego szeregu jest:

X  z =

1

1−

1
2

z

−

1

⇔

∣

1
2

z

−

1

∣



1 ; ROC :∣z∣1

5 (37)

Wyznaczanie ROC

Przedstawmy z-transformatę jako funkcję zmiennej z w postaci biegunowej:

z=r⋅e

i 

Wówczas:

X  z =

∑

n=−∞

∞

x [n]⋅r

−

n

⋅

e

−

i  n

W obszarze ROC X[z] jest zbieżna, tak więc:

∣

X  z ∣=

∣

∑

−∞

∞

x [ n]⋅r

−

n

⋅

e

−

i n

∣

≤

∑

n=−∞

∞

∣

x [n]∣⋅∣r

−

n

∣⋅∣

e

−

i n

∣=

∑

n=−∞

∞

∣

x [n]∣⋅∣r

−

n

∣

Zatem z-transformata jest ograniczona wtedy, gdy ciąg x[n]·r

-n

jest bezwględnie

sumowalny. Problem znajdowania ROC redukuje się zatem do problemu

wyznaczenia zakresu wartości r, dla których x[n]·r

-n

jest bezwględnie sumowalny.

6 (37)

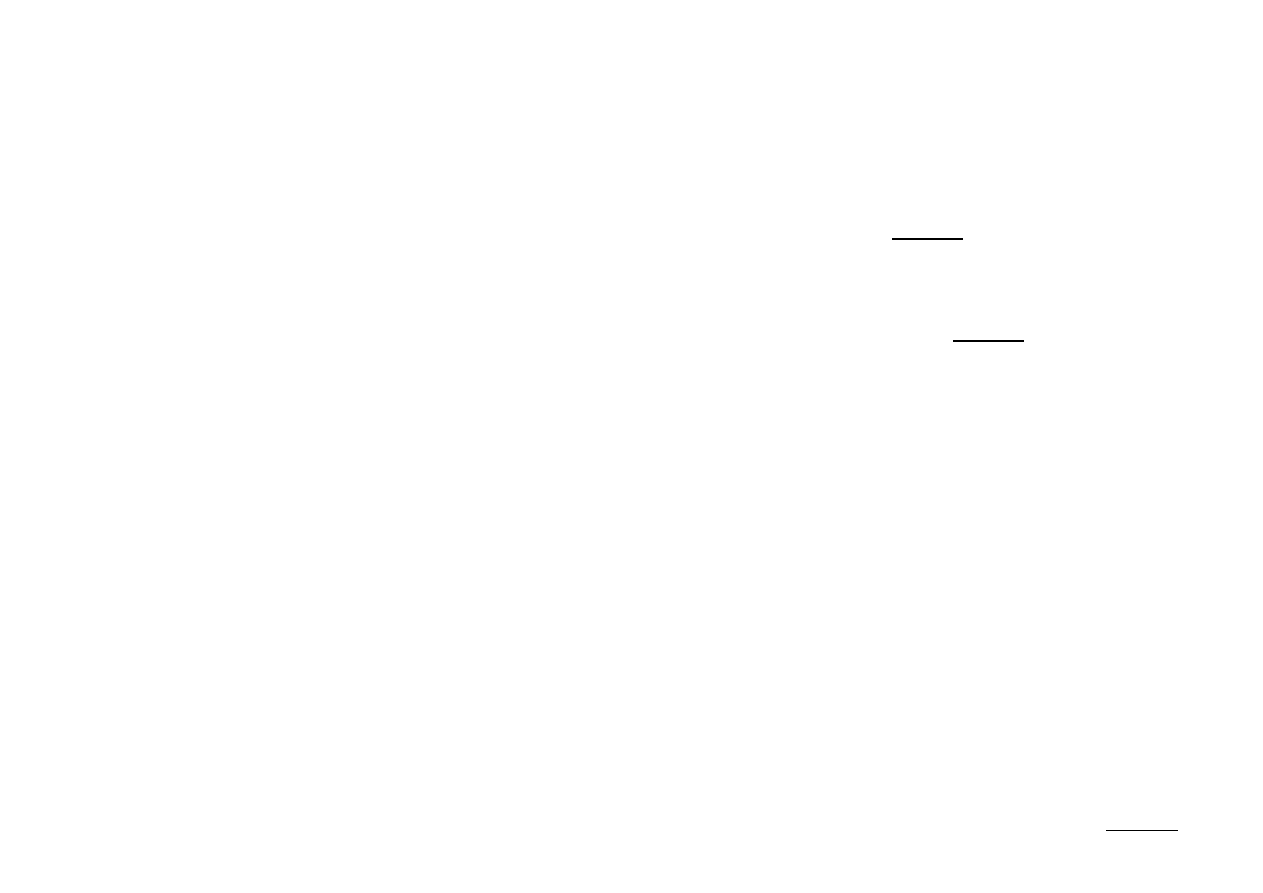
Przypomnijmy, że:

∣

X  z ∣=

∑

n=−∞

∞

∣

x [n]∣⋅∣r

−

n

∣=

∑

n=−∞

−

1

∣

x [n] r

−

n

∣

∑

n=0

∞

∣

x [n]

r

n

∣

=

...

...=

∑

n=1

∞

∣

x [−n] r

n

∣

∑

n=0

∞

∣

x [n]

r

n

∣

Z powyższego wzoru wynika, że ROC z-transformaty jest iloczynem dwóch

zbiorów z płaszczyzny liczb zespolonych:

–

punktów należących do wnętrza koła o promieniu r

1

na tyle małych, że pierwszy

szereg jest bezwzględnie sumowalny,

–

punktów leżących poza kołem o promieniu r

2

na tyle dużych, że drugi szereg

jest bezwzględnie sumowalny.

7 (37)

Ponieważ z-transformata ma być jednocześnie bezwzględnie sumowalna, ROC

musi być iloczynem (częścią wspólną) obu powyższych zbiorów:

8 (37)

Zbieżność

∑

n=0

∞

∣

x [n]

r

n

∣

Zbieżność

∑

n=1

∞

∣

x [−n]⋅r

n

∣

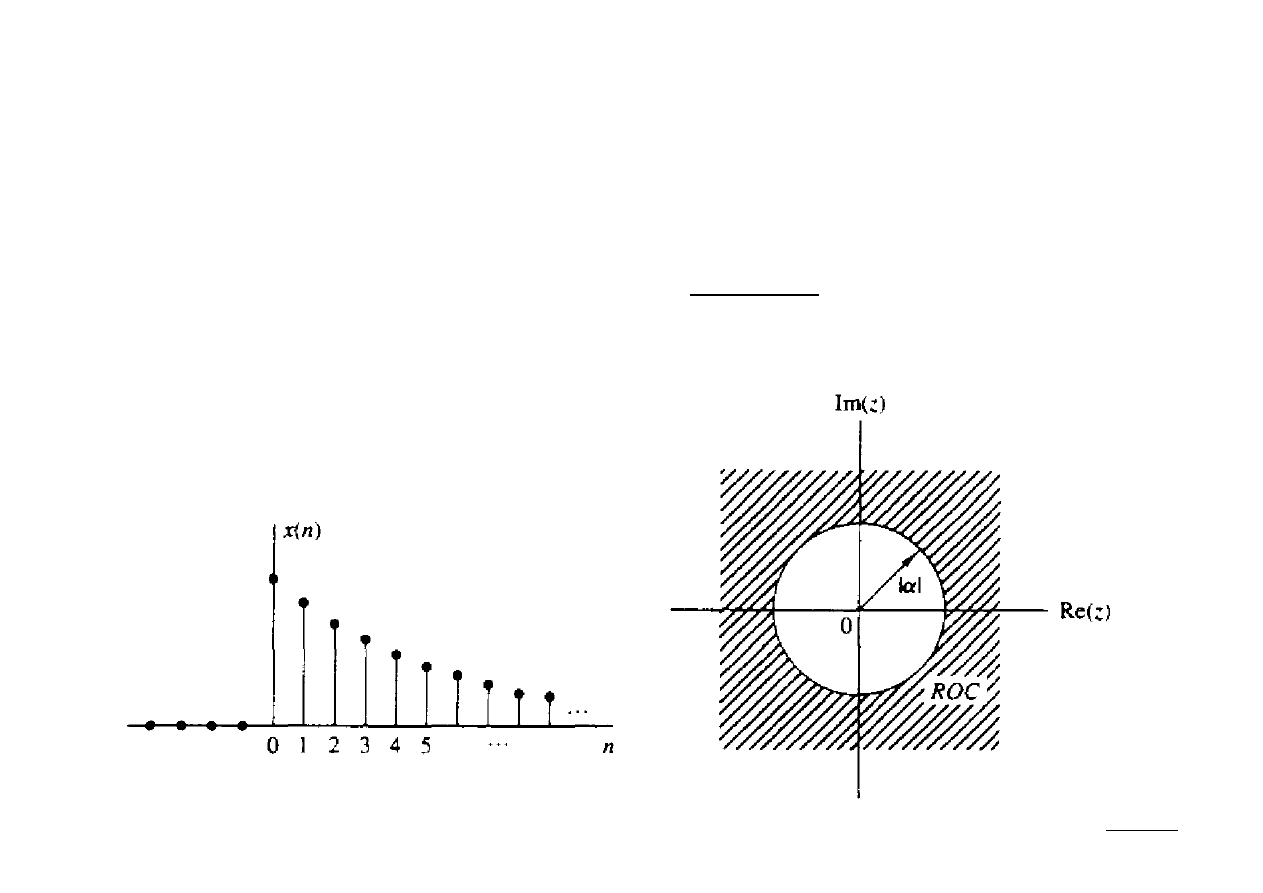
Ex.: Wyznaczyć z-transformatę sygnału:

x [n]=a

n

⋅

u[n]

Z definicji z-transformaty wynika, że:

X  z =

∑

n=0

∞

a

n

⋅

z

−

n

=

∑

n=0

∞



a⋅z

−

1



n

=

1

1−a⋅z

−

1

; ROC :∣z∣∣a∣

9 (37)

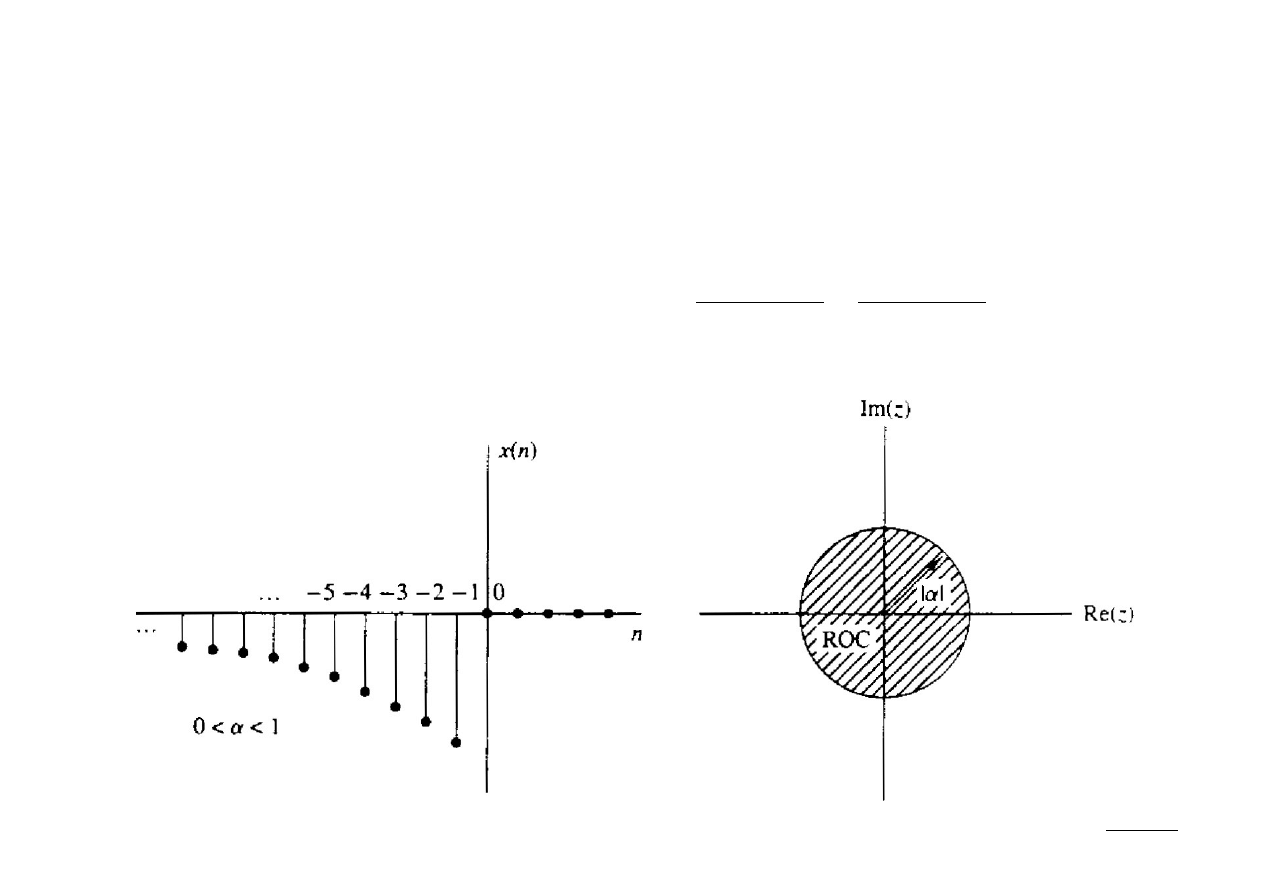
Ex.: Wyznaczyć z-transformatę sygnału:

x [n]=−a

n

⋅

u[−n−1]

Z definicji z-transformaty wynika, że:

X  z =

∑

n=−∞

−

1

−

a

n

⋅

z

−

n

=−

∑

n=1

∞



a

−

1

⋅

z

n

=−

a

−

1

⋅

z

1−a

−

1

⋅

z

=

1

1−a⋅z

−

1

; ROC :∣z∣∣a∣

10 (37)

Jednoznaczność z-transformaty

Powyższe przykłady pokazały, że w ogólności istnieją sygnały posiadające

identyczną z-transformatę, np. przyczynowy sygnał u[n] oraz antyprzyczynowy

u[-n-1]:

Z u[ n]=Z u[−n−1]=

1

1−z

−

1

Oznacza to, że zamknięta postać z-transformaty nie pozwala jednoznacznie

odtworzyć sygnału w dziedzinie czasu. Powyższej niejednoznaczności można

uniknąć wtedy, gdy oprócz z-transformaty wyspecyfikujemy także jej ROC.

11 (37)

Jednoznaczność z-transformaty

(1) Sygnały czasu dyskretnego x[n] są określone jednoznacznie poprzez podanie

ich z-transformaty X(z) oraz obszaru zbieżności ROC,

(2) ROC sygnałów antyprzyczynowych leży wewnątrz okręgu o promieniu r

1

, zaś

ROC sygnałów przyczynowych leży poza okręgiem o promieniu r

2

.

12 (37)

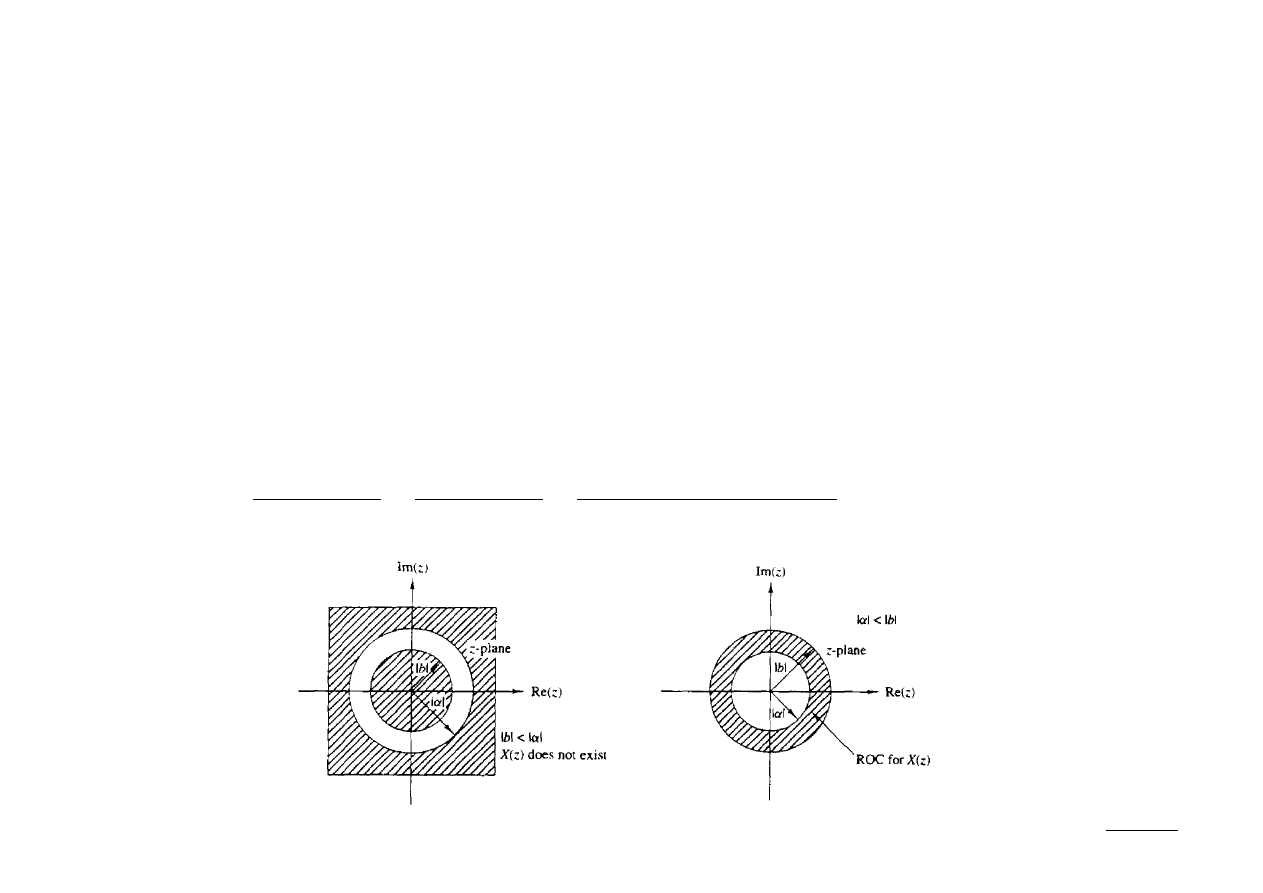
Ex.: Wyznaczyć z-transformatę sygnału:

x [n]=a

n

u[n]b

n

u[−n−1]

X  z =

∑

n=0

∞



a⋅z

−

1



n



∑

n=1

∞



b

−

1

⋅

z

n

; ROC :∣z∣∣a∣,∣z∣∣b∣

Rozpatrzmy 2 przypadki:

(1) |b| < |a|: obszary nie przekrywają się, więc X[z] nie istnieje,

(2) |b| > |a|:

X [ z ]=

1

1−a⋅z

−

1

−

1

1−b⋅z

−

1

=

b−a

ab−z−a⋅b⋅z

−

1

; ROC :∣a∣∣z∣∣b∣

13 (37)

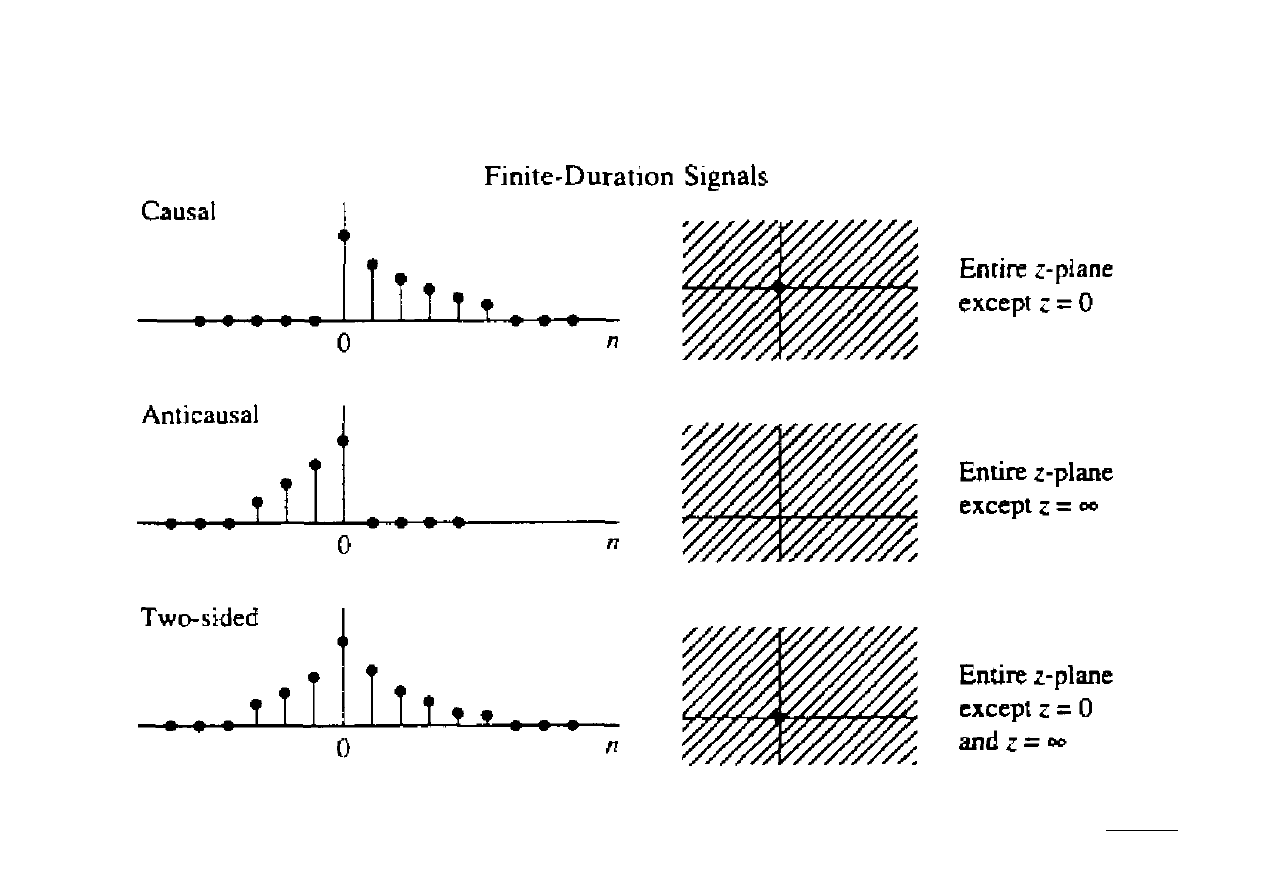
Rodziny charakterystycznych sygnałów i ich ROC

14 (37)

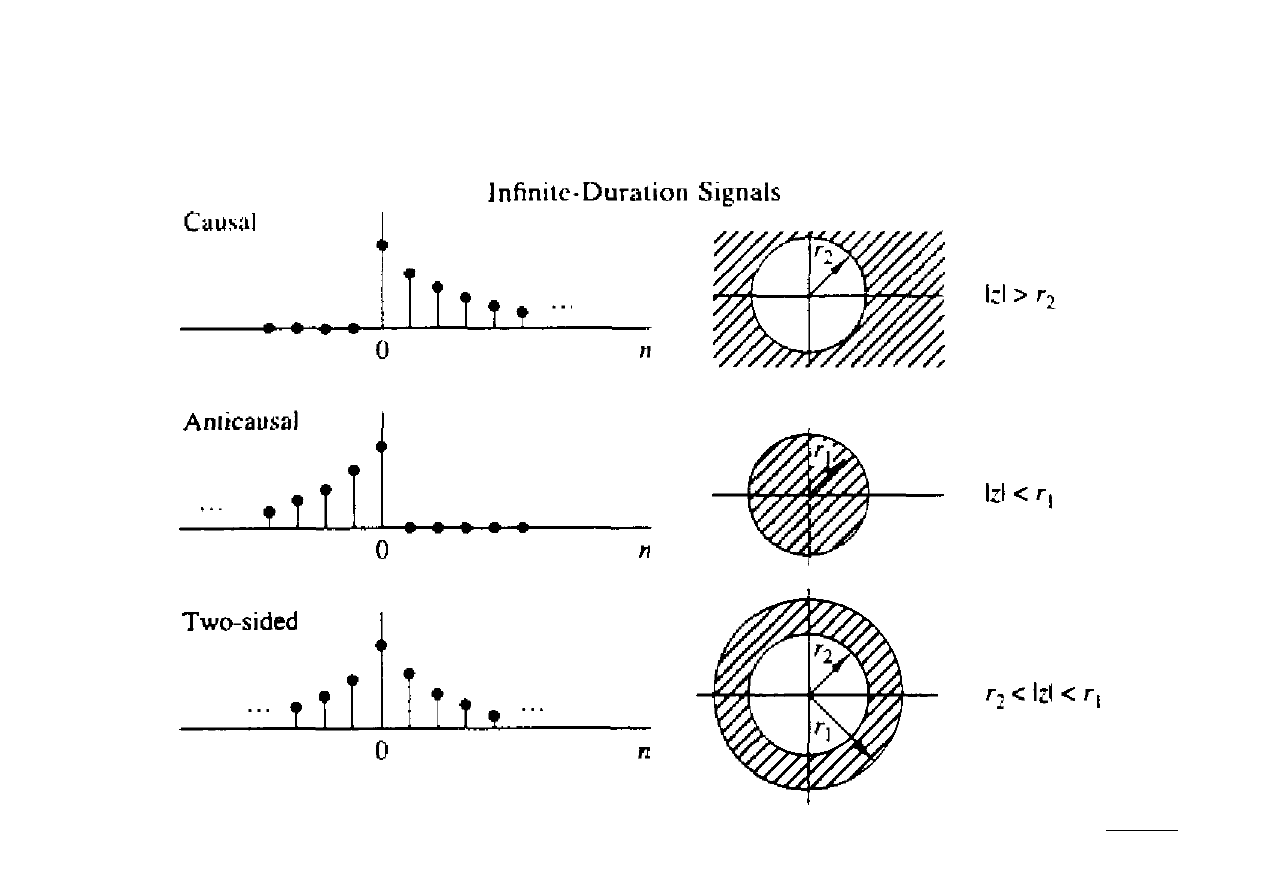
Rodziny charakterystycznych sygnałów i ich ROC

15 (37)

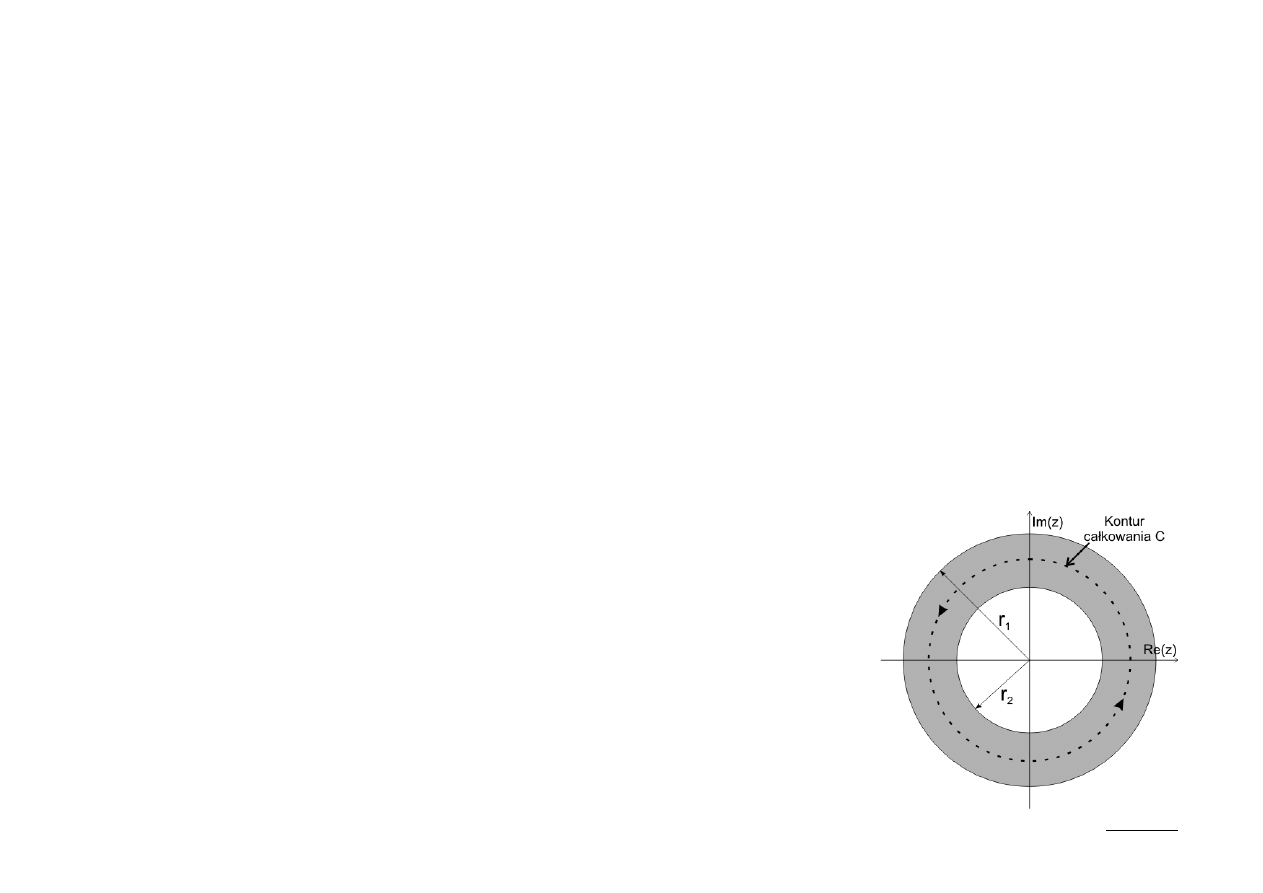
Odwrotna z-transformata

Proces obliczania odwrotnej z-transformaty pozwala z wyrażenia X(z) uzyskać

ciąg sygnałowy x[n], korzystając z teorii całek Cauchy'ego.

Przyjmijmy, że dana jest z-transformata (o znanym ROC) postaci:

X  z =

∑

k =−∞

∞

x [ k ]⋅z

−

k

Przemnóżmy obie strony powyższego wyrażenia przez z

n-1

i scałkujmy je po

dowolnym zamkniętym konturze C zawartym całkowicie wewnątrz ROC:

∮

C

X  z⋅z

n−1

dz=

∮

C

∑

k =−∞

∞

x [k ]⋅z

n−1−k

dz

Ponieważ szereg jest w ROC zbieżny, więc można

zamienić kolejność sumowania i całkowania:

∮

C

X  z ⋅z

n−1

dz=

∑

k =−∞

∞

x [ k ]

∮

C

z

n−1−k

dz

16 (37)

W teorii całek Cauchy'ego istnieje tożsamość:

∮

C

z

n−1−k

dz=2⋅⋅i⋅n−k 

Stąd mamy, że:

∮

C

X  z ⋅z

n−1

dz=

∑

k =−∞

∞

x [ k ]⋅2⋅⋅i⋅n−k =2⋅⋅i⋅x [ n]

Ostatecznie, poszukiwana odwrotna z-transformata ma postać:

x [n]=

1

2⋅⋅i

∮

C

X  z ⋅z

n−1

dz

17 (37)

Własności z-transformaty

(1) Liniowość z-transformaty:

Jeśli Z(x

1

[n]) = X

1

(z) oraz Z(x

2

[n]) = X

2

(z), to:

Z a

1

⋅

x

1

[

n]a

2

⋅

x

2

[

n]=a

1

⋅

X

1



a

2

⋅

X

2

Dowód:

Z a

1

⋅

x

1



a

2

⋅

x

2

=

∑

k =−∞

∞



a

1

⋅

x

1



a

2

⋅

x

2

⋅

z

−

n

=

...

...=a

1

∑

k =−∞

∞

x

1

⋅

z

−

n



a

2

∑

k =−∞

∞

x

2

⋅

z

−

n

=

a

1

⋅

X

1



z a

2

⋅

X

2



z

z-transformata dowolnego sygnału wyrażonego kombinacją liniową sygnałów

elementarnych jest kombinacją liniową z-transformat tychże sygnałów

elementarnych.

18 (37)

Ex.: Wyznaczyć z-transformatę sygnału:

x [n]=cos2 f n⋅u[n]

Skorzystajmy z tożsamości:

x [n]=cos2 f n⋅u[n]=

1
2

e

i 2 f n

u[n]

1
2

e

−

i 2 f n

u[n]=...

Korzystając z liniowości z-transformaty oraz wiedząc, że:

Z a

n

u[n]=

1

1−a⋅z

−

1

; ROC :∣z∣∣a∣

Otrzymamy:

Z  x [ n]=

1
2

⋅

1

1−e

i 2  f

⋅

z

−

1



1

2

⋅

1

1−e

−

i 2  f

⋅

z

−

1

; ROC :∣z∣∣e

±

i 2  f

∣=

1

Ostatecznie:

Z cos2  f n⋅u[ n]=

1−z

−

1

cos2 f n

1−2z

−

1

cos2  f nz

−

2

; ROC :∣z∣1

19 (37)

(2) Przesunięcie z-transformaty w czasie:

Jeśli Z(x[n]) = X(z), to:

Z  x [ n−k ]=z

−

k

X  z

Dowód:

Z  x [ n−k ]=

∑

n=−∞

∞

x [n−k ] z

−

n

=

∑

m=−∞

∞

x [m] z

−

mk 

=

...

...=z

−

k

∑

m=−∞

∞

x [m] z

−

m

=

z

−

k

X  z

ROC z-transformaty przesuniętej jest takie samo jak z-transformaty

nieprzesuniętej, oprócz z = 0, gdy k > 0 oraz z = ∞, gdy k < 0.

Skoro więc przy wyrazie z

-n

stoi wartośc n-tej próbki sygnału x[n], to opóźnienie

sygnału o k-próbek (k>0) oznacza przemnożenie z-transformaty przez z

-k

.

20 (37)

Ex.: Wyznaczyć z-transformatę sygnału:

x [n]=u[n]−u[n− N ]

Korzystając z przesuwalności z-transformaty w czasie:

Z u[ n]−u[n−N ]=Z u[n]−Z u[n− N ]=1−z

−

N

⋅

Z u[n]=...

...=



1− z

−

N

⋅

1

1−z

−

1

=

1−z

−

N

1−z

−

1

; ROC :∣z∣1

Z powyższego przykładu wypływa wniosek, iż jeśli kombinacja liniowa sygnałów

ma skończony czas trwania, wówczas ROC jej z-transformaty jest uwarunkowana

wyłącznie skończonym czasem trwania sygnału, a nie ROC poszczególnych

z-transformat.

21 (37)

(3) Skalowanie w domenie z-transformaty:

Jeśli Z(x[n]) = X(z) oraz ROC: r

1

< |z| < r

2

, to:

Z a

n

x [n]= X a

−

1

z; ROC :∣a∣r

1

∣

z∣∣a∣r

2

Dowód:

Z a

n

x [n]=

∑

n=−∞

∞

a

n

x [n] z

−

n

=

∑

n=−∞

∞

x [ n]a

−

1

z 

−

n

=

X a

−

1

z 

Ponieważ ROC z-transformaty wynosi r

1

< |z| < r

2

, zatem ROC z-transformaty

przeskalowanej:

ROC : r

1

∣

a

−

1

z∣r

2

ROC :∣a∣r

1

∣

z∣∣a∣r

2

22 (37)

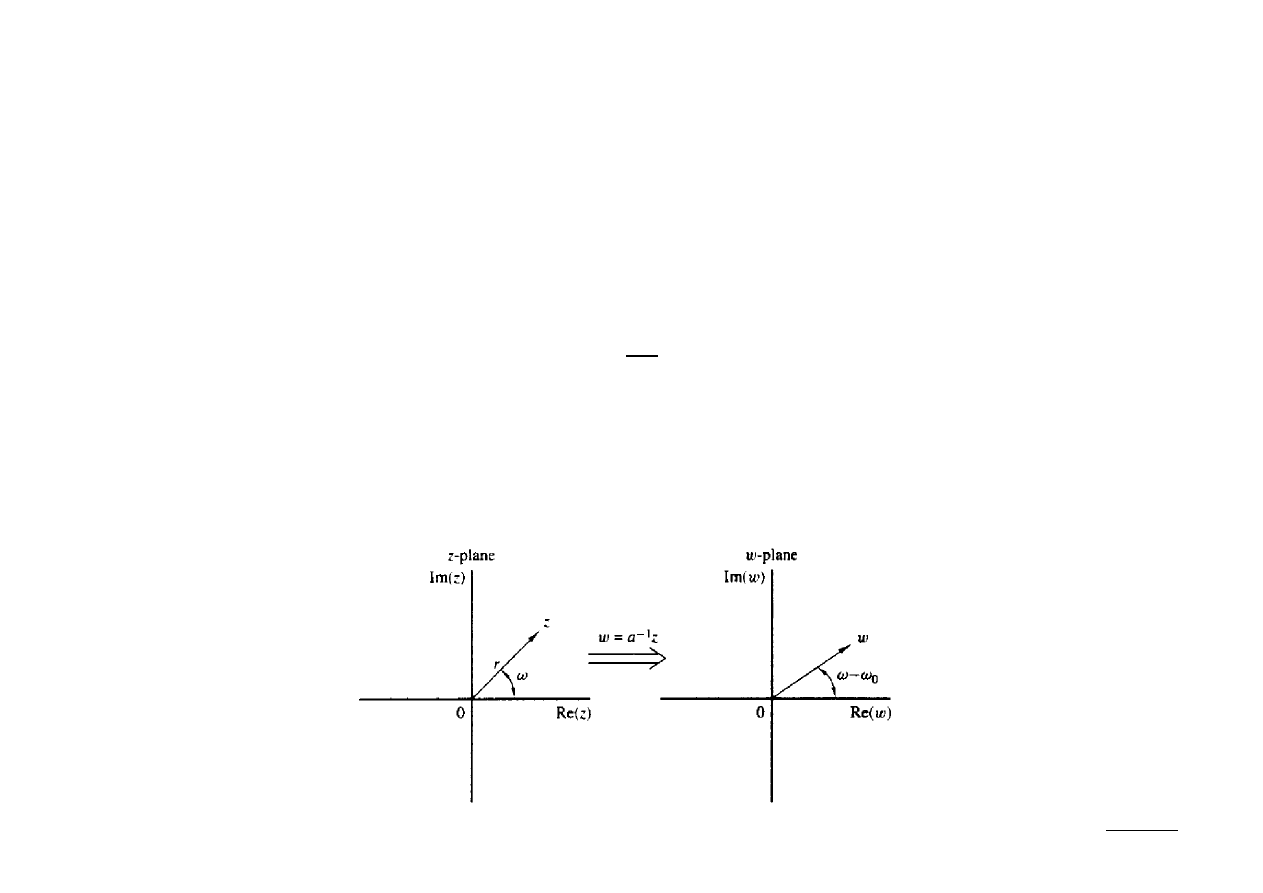
Aby lepiej zrozumieć powyższy wynik wyraźmy zmienne a oraz z we

współrzędnych biegunowych:

a=r

0

e

i 2 f

0

; z=r e

i 2  f

; w=a

−

1

⋅

z

Wówczas:

w=a

−

1

z=



r

r

0



e

i 2  f − f

0



Zamiana zmiennych prowadzi w efekcie do zwężenia bądź poszerzenia

płaszczyzny z w połączeniu z obrotem jej osi (jeśli f

0

≠ 2kπ).

23 (37)

Ex.: Wyznaczyć z-transformatę sygnału:

x [n]=a

n

cos2 f nu[n]

Korzystając ze skalowalności z-transformaty i wiedząc, że:

Z cos2  f n⋅u[ n]=

1−z

−

1

cos2 f n

1−2z

−

1

cos2  f nz

−

2

; ROC :∣z∣1

Otrzymujemy, że poszukiwana z-transformata ma postać:

Z a

n

cos2 f n⋅u[n]=

1−a⋅z

−

1

cos2  f n

1−2az

−

1

cos2 f na

2

z

−

2

; ROC :∣z∣a

24 (37)

(4) z-transformata zawinięcia sygnału:

Jeśli Z(x[n]) = X(z) oraz ROC: r

1

< |z| < r

2

, to:

Z  x [−n]= X  z

−

1



; ROC :

1

r

2

∣

z∣

1

r

1

Dowód:

Z  x [−n]=

∑

n=−∞

∞

x [−n] z

−

n

=

∑

k =−∞

∞

x [ k ] z

k

=

∑

k =−∞

∞

x [k ] z

−

1



−

k

ROC z-transformaty zawiniętej:

ROC : r

1

∣

z

−

1

∣

r

2

ROC :

1

r

2

∣

z∣

1

r

1

Powyższa własność wynika z faktu, iż zawinięcie sygnału powoduje zamianę

współczynników z → z

-1

w z-transformacie, a więc zawinięcie w dziedzinie czasu

wiąże się z odwrotnością w dziedzinie z-transformaty.

25 (37)

Ex.: Wyznaczyć z-transformatę sygnału: x[n] = u[-n]

Wiemy, że z-transformata skoku jednostkowego wynosi:

Z u[ n]=

1

1−z

−

1

Korzystając z twierdzenia o zawijalności z-transformaty:

Z u[−n]=

1

1− z

; ROC :∣z∣1

26 (37)

(5) różniczkowalność w dziedzinie z-transformaty:

Jeśli Z(x[n]) = X(z) oraz ROC: r

1

< |z| < r

2

, to:

Z n⋅x [n]=−z⋅

dX  z 

dz

; ROC : r

1

∣

z∣r

2

Dowód:

d

dz

X  z =

∑

k =−∞

∞

x [k ]⋅−n z

−

n−1

=−

z

−

1

∑

k=−∞

∞

n⋅x [ k ] z

−

k

=−

z

−

1

Z n⋅x [n]

Zauważmy, że obie z-transformaty mają identyczne ROC.

27 (37)

Ex.: Wyznaczyć z-transformatę sygnału x[n] = na

n

u[n].

Rozdzielmy sygnał x[n] na 2 części: x

1

[n] = a

n

u[n] oraz x

2

[n] = n x

1

[n].

z-transformata sygnału x

1

[n] ma postać:

Z a

n

⋅

u[n]=

1

1−a⋅z

−

1

; ROC :∣z∣∣a∣

Z twierdzenia o różniczkowalności w dziedzinie z-transformaty otrzymujemy, że:

Z n⋅x

1

[

n]=−z

−

1

d

dz



1

1−az

−

1



=

z

−

1

az

−

1



1−az

−

1



2

; ROC :∣z∣∣a∣

28 (37)

Ex.: Wyznaczyć sygnał x[n], którego z-transformata X(z) = log(1+az

-1

), |z| > |a|

Obliczmy pochodną X(z):

d

dz

ln 1az

−

1

=−

az

−

2

1az

−

1

Skąd otrzymujemy, że:

−

z

d

dz

X  z=−az

−

1

1

1az

−

1

=

az

−

1

1

1−−a z

−

1

Odwrotną z-transformatą (1-(-a)z

-1

)

-1

jest (-a)

n

u[n], ponieważ jednak wyrażenie to

jest mnożone przez z

-1

, więc musimy wziąć cofniętą odwrotną z-transformatę:

n⋅x [n]=a⋅−a

n−1

⋅

u[n−1]

Stąd ostatecznie:

x [n]=

a
n

−

a

n−1

⋅

u[n−1]=−1

n−1

a

n

n

⋅

u[n−1]

29 (37)

(6) z-transformata splotu sygnałów:

Jeśli Z(x

1

[n]) = X

1

(z), Z(x

2

[n]) = X

2

(z), to:

Z  x [ n]=x

1

[

n]∗x

2

[

n]= X

1



z⋅X

2



z 

Dowód:

X  z =

∑

k =−∞

∞

x [ k ] z

−

k

=

∑

k=−∞

∞

∑

j=−∞

∞

x

1

[

j ]⋅x

2

[

k− j] z

−

k

=

...

...=

∑

j=−∞

∞

x

1

[

j ]



∑

k =−∞

∞

x

2

[

k − j] z

−

k



=

∑

j=−∞

∞

x

1

[

j]⋅z

−

j

⋅

X

2



z = X

1



z ⋅X

2



z

Transformowalność splotu jest jedną z najważniejszych własności z-transformaty,

ponieważ pozwala zamienić operację obliczania splotu (w dziedzinie czasu) na

operację mnożenia z-transformat (przydatne np. przy filtracji sygnału).

30 (37)

Ex.: Wyznaczyć splot sygnałów:

x

1

[

n]=[1 ,−2,1]

x

2

[

n]=u[n]−u[n−6]

Wyznaczmy z-transformaty obu sygnałów:

X

1



z =1−2z

−

1



z

−

2

X

2



z =1z

−

1



z

−

2



z

−

3



z

−

4



z

−

5

Po wymnożeniu z-transformat otrzymujemy:

X  z = X

1



z⋅X

2



z=1−z

−

1

−

z

−

6



z

−

7

Stąd odwrotna z-transformata splotu ma postać:

x [n]=[1 ,−1,0,0 ,0 ,0 ,−1,1]

31 (37)

(6) z-transformata korelacji sygnałów:

Jeśli Z(x

1

[n]) = X

1

(z), Z(x

2

[n]) = X

2

(z), to:

Z r

x

1

x

2

=

X

1



z⋅X

2



z

−

1



Dowód:

Przypomnijmy, że:

r

x

1

x

2

=

x

1

[

n]∗x

2

[−

n]

Stąd:

Z r

x

1

x

2

=

Z  x

1

[

n]⋅Z  x

2

[−

n]= X

1



z⋅X

2



z

−

1



Podobnie jak w przypadku splotu, obliczenia korelacji są efektywniejsze

w dziedzinie z-transformaty niż w dziedzinie czasu.

32 (37)

Ex.: Wyznaczyć korelację własną sygnału:

x [n]=a

n

u[n] ;∣a∣1

Obliczmy z-transformatę korelacji własnej:

Z r

x x

=

X  z ⋅X  z

−

1

=

1

1−az

−

1

⋅

1

1−az

; ROC :∣a∣∣z∣

1

∣

a∣

Odwrotną z-transformatę obliczymy korzystając z wcześniejszych wyników, że:

Z



a

n

u[n]

1
a



n

u[−n−1]



=

Z



a

∣

n∣



=

1−a

2



1−az

−

1

⋅

1−az

Stąd otrzymujemy, że:

r

xx

[

n]=

a

∣

n∣

1−a

2

; n∈ℤ

33 (37)

(7) z-transformata iloczynu sygnałów:

Jeśli Z(x

1

[n]) = X

1

(z), Z(x

2

[n]) = X

2

(z), to:

Z  x

1

⋅

x

2

=

1

2 i

∮

C

X

1



v⋅X

2



z

v



v

−

1

dv

gdzie: C jest zamkniętym konturem leżącym wewnątrz ROC wspólnego dla X

1

(v)

oraz X

2

(1/v).

Twierdzenie pozostawiam bez dowodu.

Użyteczność tego wzoru wynika z jego stosowalności do sygnałów o skończonym

czasie trwania, których widma modyfikowane są skończonymi (z uwagi na

fizyczne ograniczenia czasu trwania sygnału) funkcjami okien.

34 (37)

(8) twierdzenie o wartości początkowej:

Jeśli x[n] jest sygnałem przyczynowym, to:

x [0]= lim

z ∞

X  z

Dowód:

Ponieważ x[n] jest sygnałem przyczynowym (x[n<0] = 0), to:

X  z =

∑

k =0

∞

x [k ]⋅z

−

k

=

x [0] x [1]⋅z

−

1



x [ 2]⋅z

−

2



... 

z ∞

x [0]

35 (37)

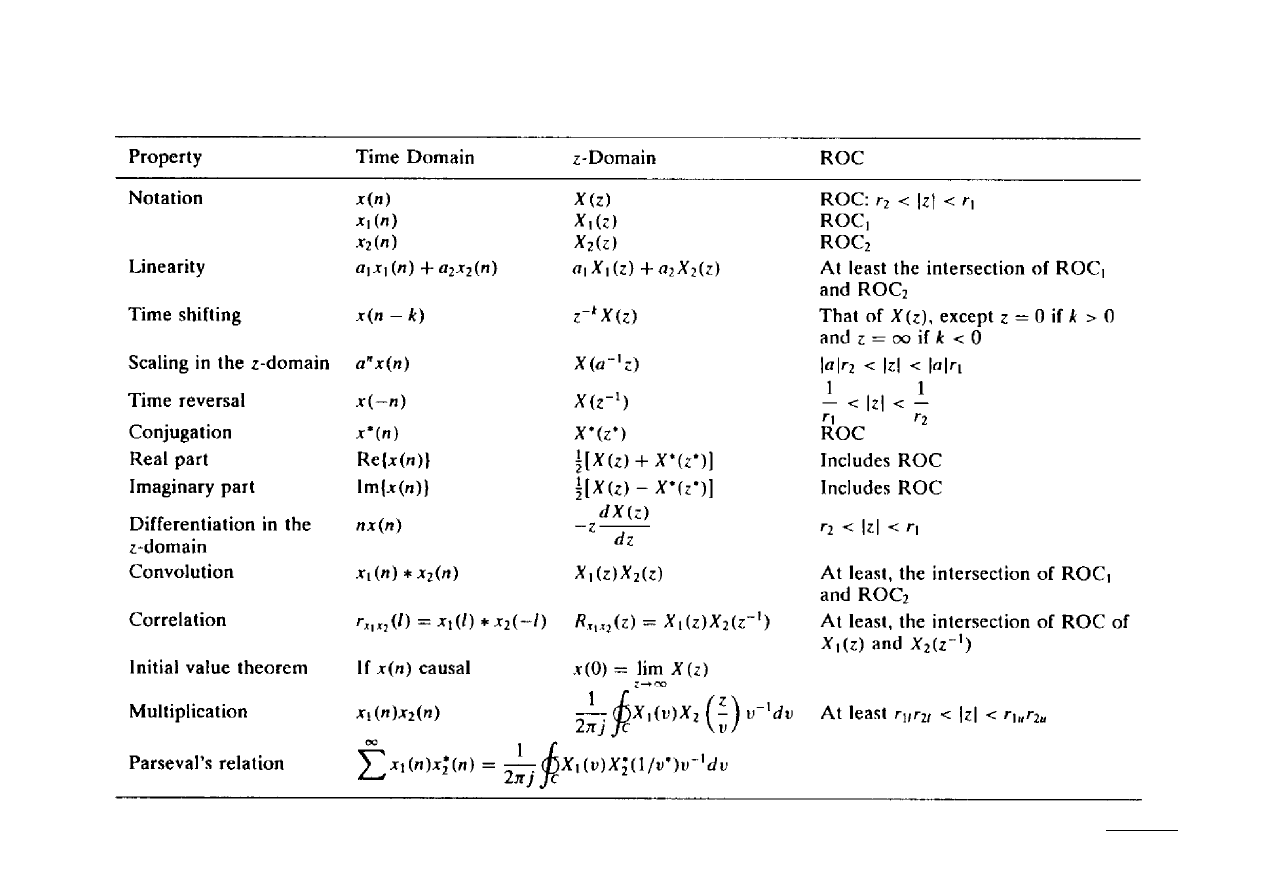
Podsumowanie: własności z-transformaty

36 (37)

Podsumowanie: wybrane pary z-transformat

37 (37)