Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (9)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

1 (46)

Analiza częstotliwościowa sygnałów i układów

Analiza częstotliwościowa sygnałów i układów LTI wykorzystuje transformatę

Fouriera (przekształcenie całkowe) oraz szereg Fouriera (okresowe sygnały czasu

ciągłego) do rozkładu danego sygnału na jego składowe sinusoidalne (ogólnie:

eksponencjalnie zespolone), reprezentując go w dziedzinie częstotliwości.

Rozkład na składowe sinusoidalne jest szczególnie istotny z uwagi na własności

układów LTI: ich odpowiedź na pobudzenie sinusoidalne jest sinusoidą o tej samej

częstotliwości, lecz zmienionej amplitudzie i fazie.

2 (46)

Rozszczepienie światła w pryzmacie

3 (46)

Szereg Fouriera sygnałów okresowych czasu ciągłego

Kombinacja liniowa sygnałów okresowych postaci:

x t =

∑

k =−∞

∞

c

k

e

i 2 k f

0

t

jest sygnałem okresowym o okresie podstawowym f

0

– szeregiem Fouriera.

Widać stąd, że sygnały sinusoidalne postaci:

{

e

i 2 k f

0

t

; k ∈ℤ}

tworzą bazę przestrzeni sygnałów okresowych.

Współczynniki rozwinięcia sygnału okresowego x(t) = x(t+T

p

) na szereg Fouriera

znajdziemy ze wzoru:

c

k

=

1

T

p

∫

0

T

p

x t e

−

i 2 k f

0

t

dt

4 (46)

Analiza a synteza sygnałów i układów

Równanie:

x t =

∑

k =−∞

∞

c

k

e

i 2 k f

0

t

jest równaniem syntezy sygnału, podczas gdy transformata całkowa:

c

k

=

1

T

p

∫

0

T

p

x t e

−

i 2 k f

0

t

dt

jest równaniem analizy.

Widmo sygnałów okresowych czasu ciągłego jest dyskretne, a odstęp

pomiędzy poszczególnymi prążkami widma jest równy częstotliwości

podstawowej f

0

lub odwrotności okresu sygnału T

p

.

5 (46)

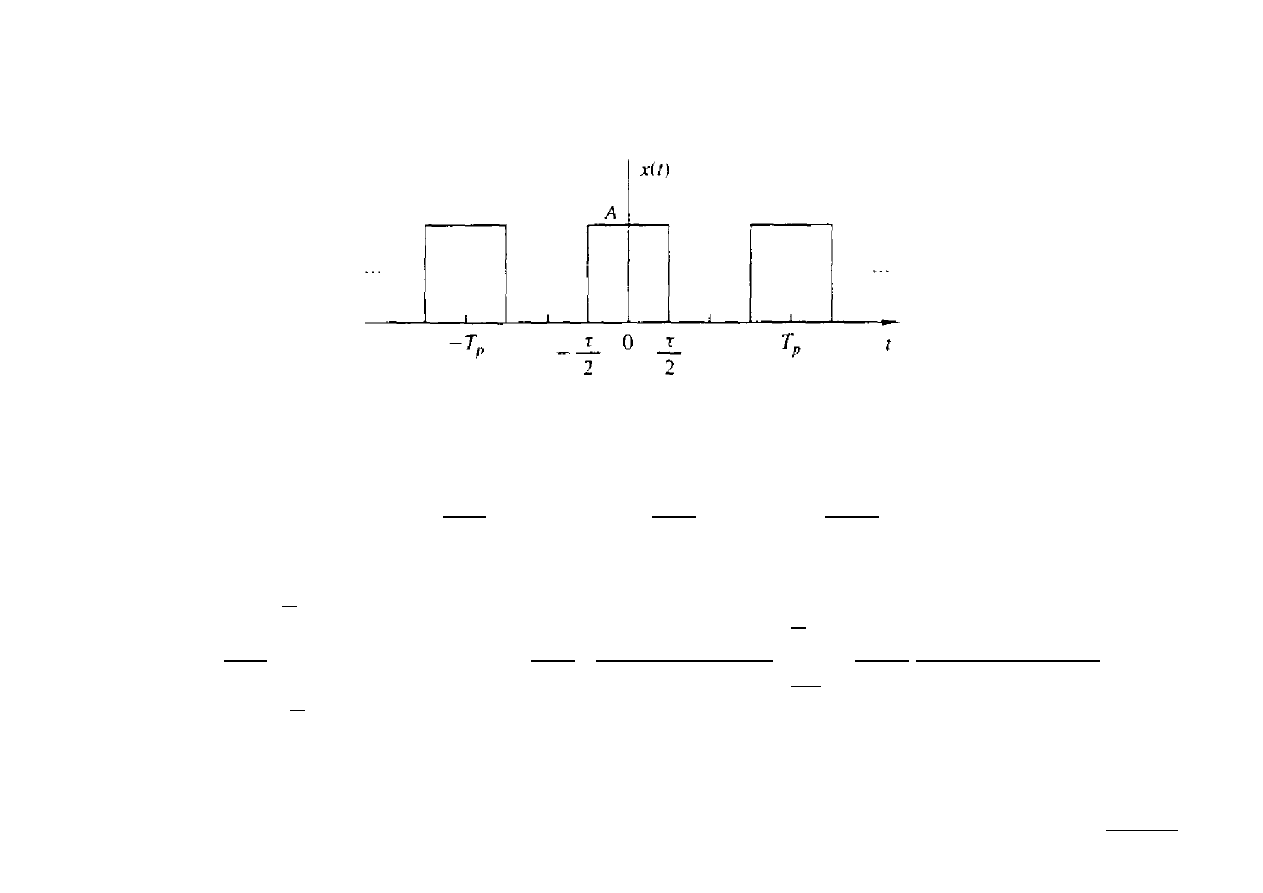
Ex.: Wyznaczyć szereg Fouriera ciągu impulsów prostokątnych:

Z równania analizy wynika, że:

c

0

=

1

T

p

∫

0

T

p

x t  dt=

1

T

p

∫

0

T

p

A dt=

A

T

p

c

k

=

1

T

p

∫

−



2



2

A e

−

i 2 k f

0

t

dt=

A

T

p



e

−

i 2  k f

0

t

−

i 2 k f

0

t



−

2



2

=

A

T

p

sin  k f

0

t



k f

0

t

6 (46)

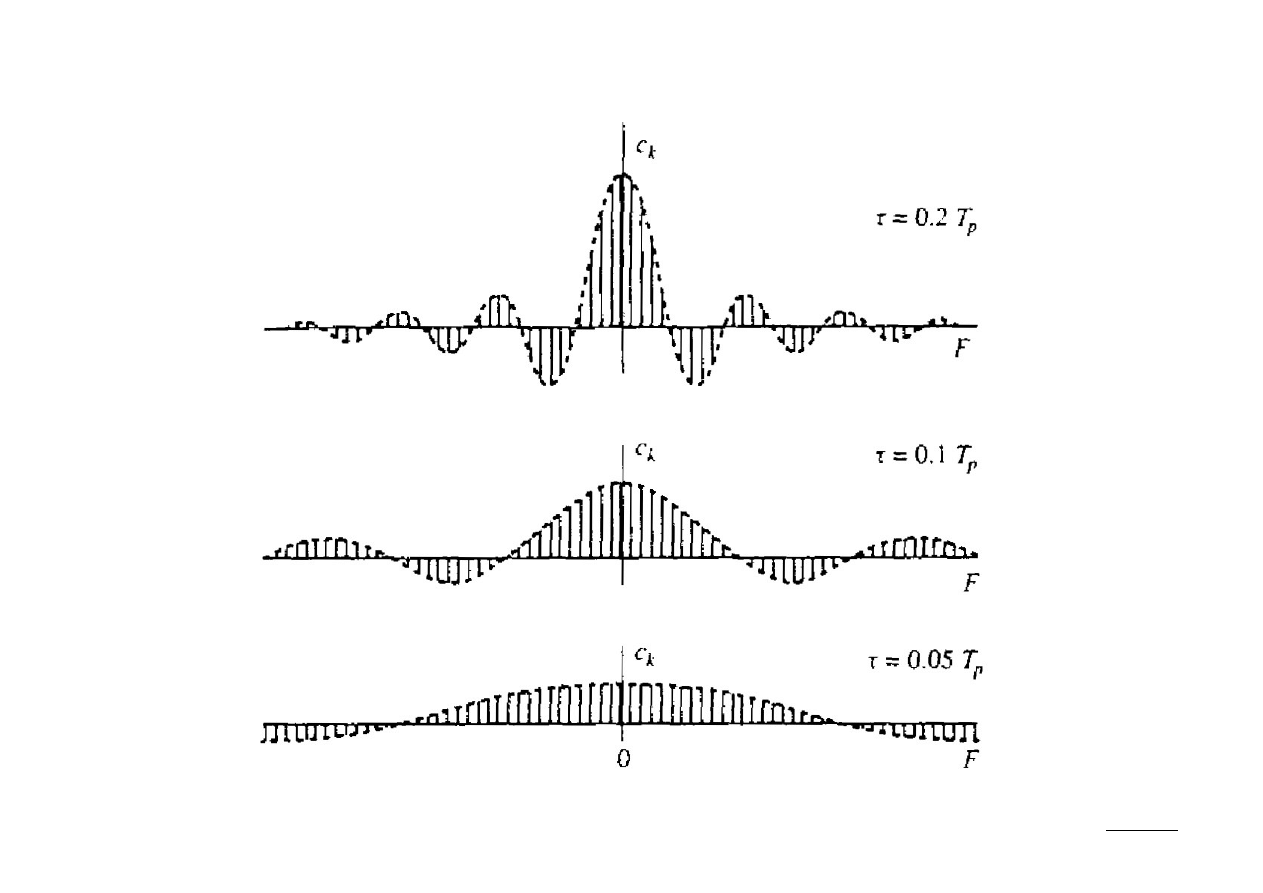
7 (46)

Analiza częstotliwościowa nieokresowych

sygnałów czasu ciągłego

Sygnały nieokresowe można uważać za sygnały okresowe o nieskończenie

długim okresie. W takim razie ich widma częstotliwościowe będą funkcjami

ciągłymi, jako że odstęp pomiędzy prążkami maleje ze wzrostem T

p

do 0.

Widmo sygnału jest wówczas analizowane zgodnie ze wzorem:

X  f =

∫

−∞

∞

x t e

−

i 2  f t

dt

Z kolei równanie syntezy przyjmuje postać:

x t=

∫

−∞

∞

X  f e

i 2  f t

df

8 (46)

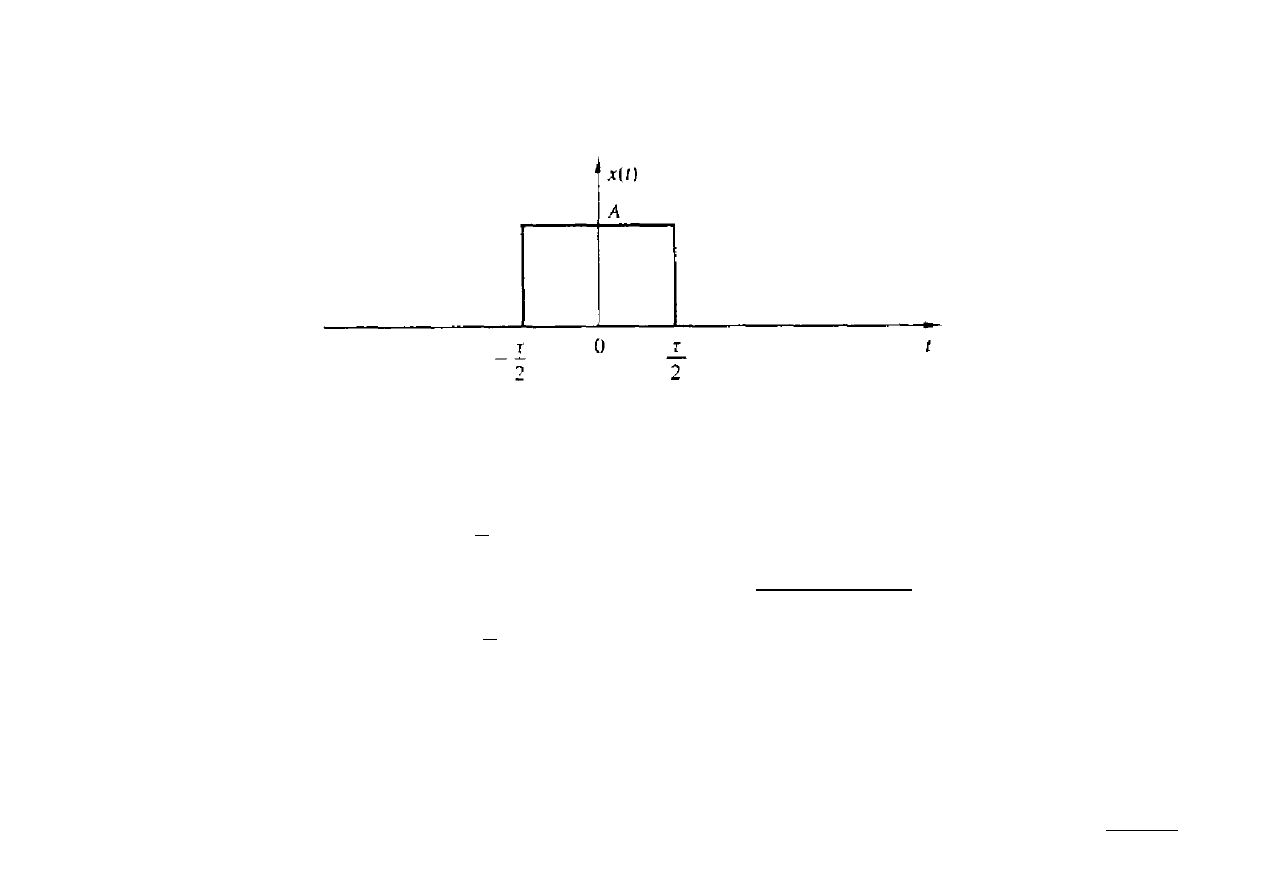
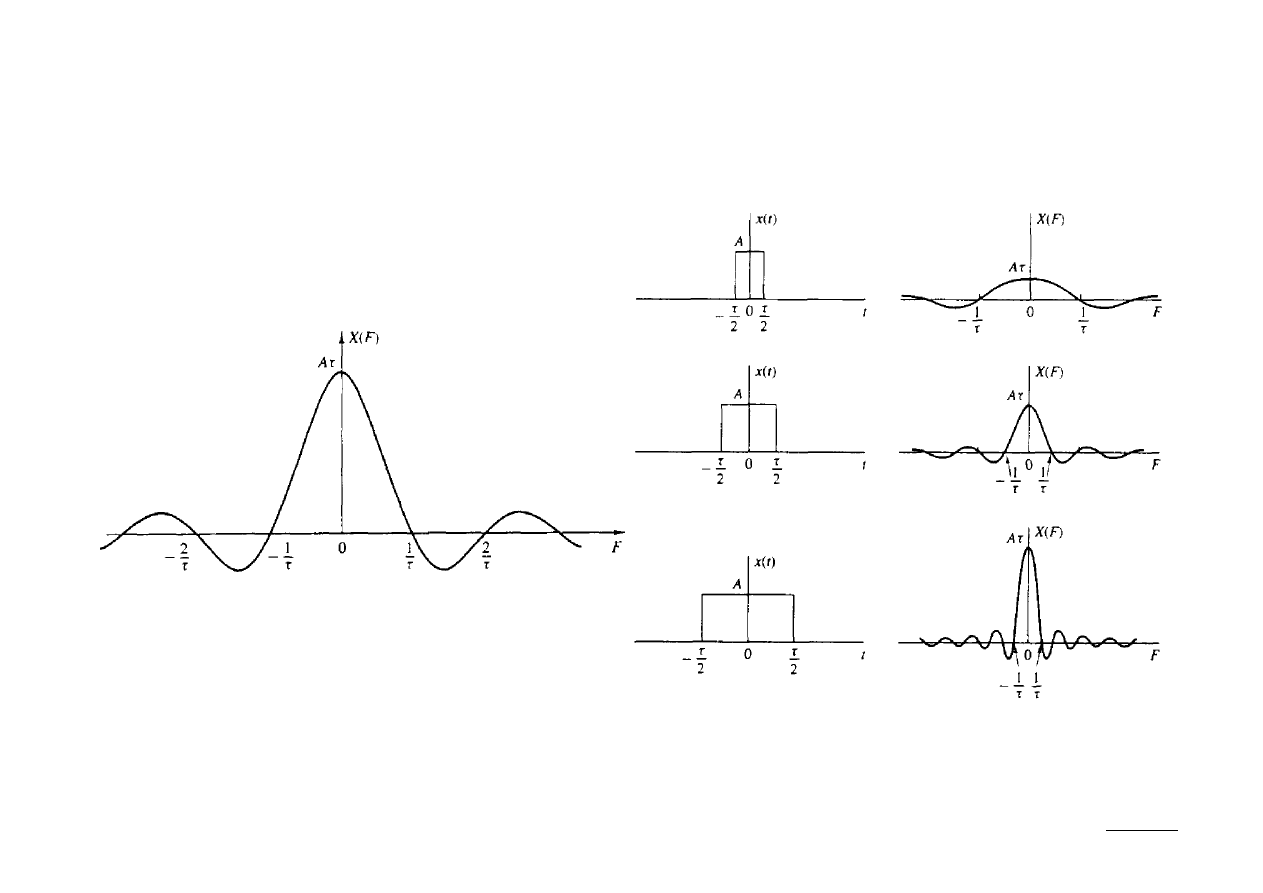
Ex.: Wyznaczyć transformatę Fouriera impulsu prostokątnego:

Transformata Fouriera tego sygnału ma postać:

X  f =

∫

−



2


2

A e

−

i 2  f t

dt=A 

sin  f 



f 

9 (46)

10 (46)

Analiza częstotliwościowa sygnałów czasu dyskretnego

Jak widzieliśmy wcześniej, widma sygnałów czasu ciągłego składają się

z nieskończonej ilości składowych harmonicznych o odstępach Δf = 1/T

p

, gdzie T

p

jest okresem podstawowym analizowanego sygnału x(t).

W przypadku sygnałów czasu dyskretnego występuje aliasing, stąd też sygnał

o okresie podstawowym N może zawierać co najwyżej N-składowych

o częstotliwościach: 0, 1/N, 2/N, ..., (N-1)/N.

11 (46)

Szereg Fouriera periodycznych sygnałów czasu dyskretnego

Szereg Fouriera sygnału okresowego (DTFS – Discrete-Time Fourier Series)

x[n] = x[n+N] ma postać:

x [n]=

∑

k=0

N −1

c

k

e

i 2 k

n

N

gdzie współczynniki szeregu c

k

dane są jako:

c

k

=

1

N

∑

n=0

N −1

x [n]e

−

i 2 k

n

N

Zauważmy, że:

c

k N

=

1

N

∑

n=0

N −1

x [n]e

−

i 2 k N 

n

N

=

1

N

∑

n=0

N −1

x [n]e

−

i 2 k

n

N

=

c

k

Widmo sygnału okresowego x[n] = x[n+N] jest sygnałem okresowym: c

k

= c

k+N

!

12 (46)

Ex.: Wyznaczyć szereg Fouriera sygnału o okresie podstawowym N = 4 takim,

że: x[n] = [1,1,0,0].

Z równania analizy otrzymujemy, że:

c

k

=

1
4

∑

n=0

3

x [n]e

−

i 2  k

n
4

=

1
4



1e

−

i 

k
2



; k=0,1, 2, 3.

Skąd mamy, że:

c

0

=

1

2,

c

1

=

1

4



1−i , c

2

=

0,c

3

=

1
4



1i

13 (46)

Transformata Fouriera nieokresowych

sygnałów czasu dyskretnego

Transformata Fouriera sygnału czasu dyskretnego (DTFT – Discrete-Time Fourier

Transform) dana jest wzorem:

X =

∑

n=−∞

∞

x [n]e

−

i n

Zauważmy, że w tym przypadku widmo X(ω) jest funkcją okresową:

X 2 k =

∑

n=−∞

∞

x [n]e

−

i 2  k n

=

∑

n=−∞

∞

x [n]e

−

i n

=

X 

Transformata odwrotna (iDTFT) dana jest wzorem:

x [n]=

1

2 

∫

0

2 

X e

i  n

d 

14 (46)

Zbieżność transformaty Fouriera czasu dyskretnego

Wyprowadzenie wzoru na odwrotną transformatę iDTFT wymaga założenia, aby:

lim

N ∞

X

N

=

lim

N ∞

∑

n=−N

N

x [n]e

−

i n

=

X 

tzn., aby szereg X

N

(ω) był jednostajnie zbieżny do X(ω).

Warunkiem jednostajnej zbieżności jest bezwzględna sumowalność x[n]:

∣

X ∣=∣

∑

n=−∞

∞

e

−

i  n

∣≤

∑

n=−∞

∞

∣

x [ n]∣∞

Zatem warunkiem wystarczającym istnienia DTFT danego sygnału jest:

∑

n=−∞

∞

∣

x [ n]∣∞

15 (46)

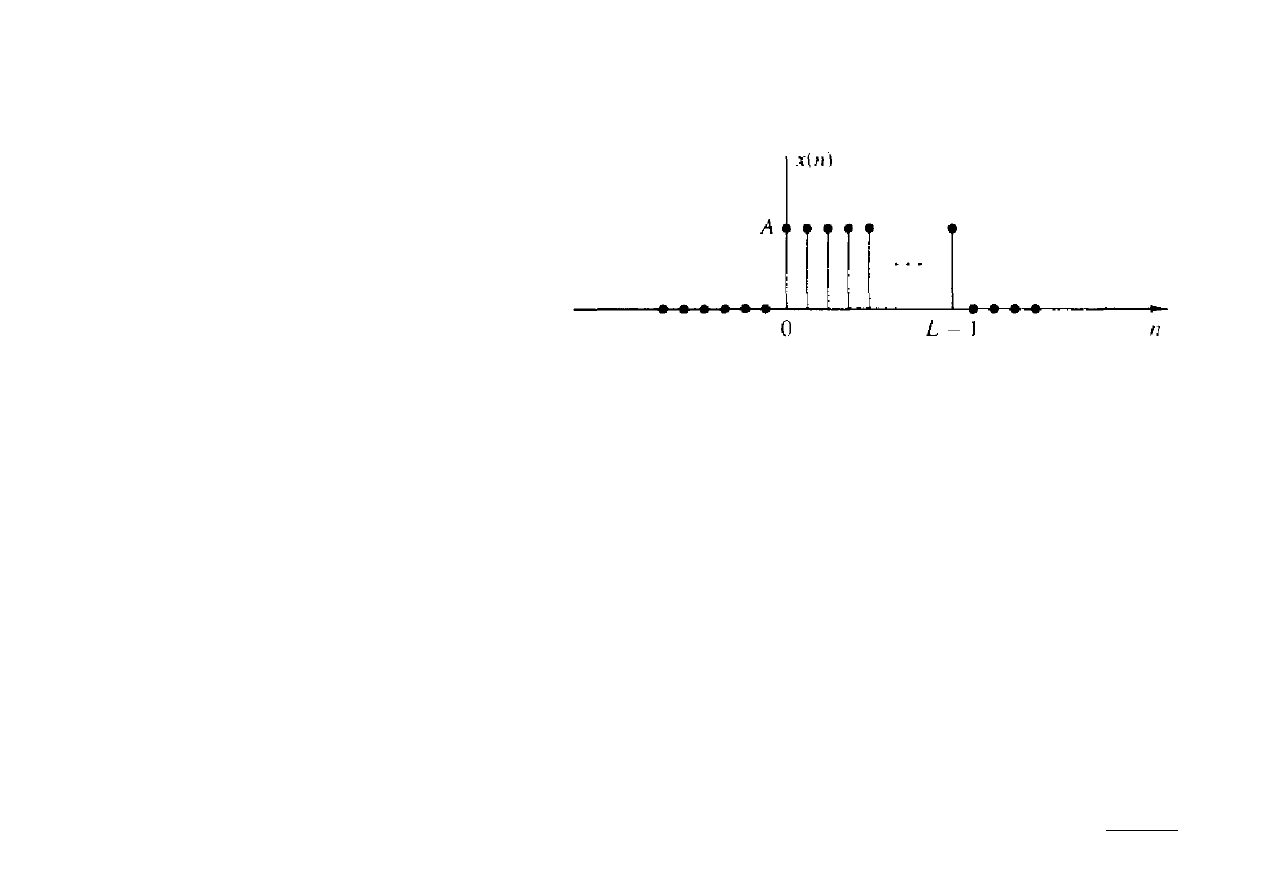
Ex.: Wyznaczyć DTFT sygnału:

Sprawdźmy najpierw warunek zbieżności transformaty:

∑

n=−∞

∞

∣

x [ n]∣=

∑

n=0

L−1

∣

A∣=L⋅∣A∣∞

Ponieważ x[n] jest bezwzględnie sumowalny, istnieje jego DTFT. Co więcej, jest to

sygnał o skończonej energii, ponieważ:

∑

n=0

L−1

∣

x [n]∣

2

=∣

A∣

2

⋅

L∞

16 (46)

x [n]=

{

A⇔0≤n≤ L−1

0 dla pozostałych n

}

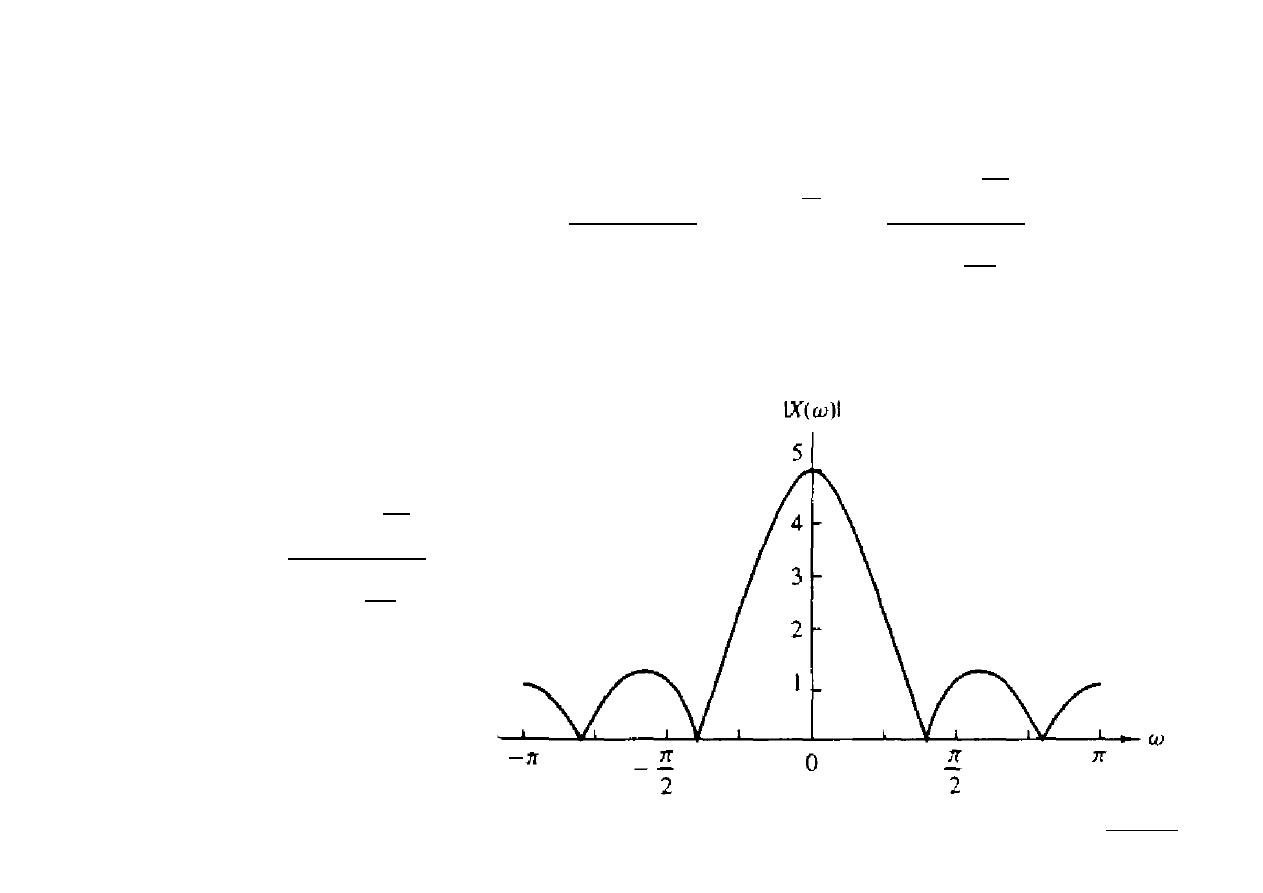
Transformata DTFT ma postać:

X =

∑

n=0

L−1

A e

−

i  n

=

A

1−e

−

i  L

1−e

−

i 

=

Ae

−

i 

2



L−1

sin 

L

2



sin 



2



Widmo amplitudowe DTFT ma postać:

17 (46)

∣

X ∣=∣A∣

∣

sin 

L

2



sin 



2



∣

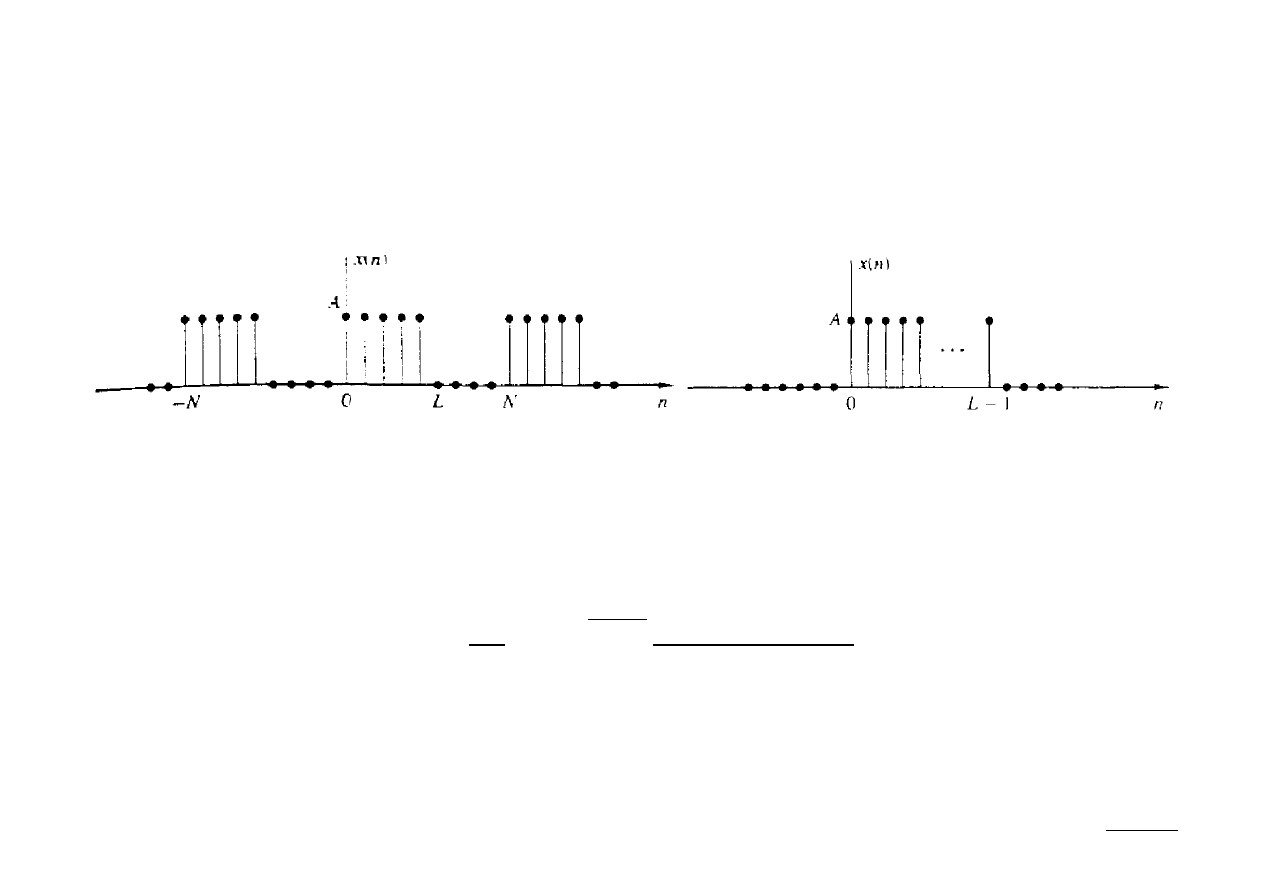
Istnieje interesujący związek pomiędzy współczynnikami szeregu Fouriera

prostokątnego sygnału czasu dyskretnego o okresie N, a widmem DTFT impulsu

prostokątnego czasu dyskretnego:

Współczynniki szeregu Fouriera DTFS dane są jako:

c

k

=

A

N

e

−

i k



L−1

N

sin  k L/ N 

sin  k / N 

18 (46)

Z drugiej strony, wartości transformaty DTFT dla równoodległych częstości

harmonicznych:



k

=

2

k

N

; k =0,1,2 ,... , N −1

wynoszą odpowiednio:

X 2

k

N

=

A e

−

i  k



L−1

N

sin  k L/ N 

sin  k / N 

Wynika stąd, że:

X 2

k

N

=

N⋅c

k

; k =0,1,2 , ... , N −1

Powyższa własność stwierdza, że widmo DTFS sygnału okresowego jest

dyskretną, przeskalowaną wersją widma DTFT pojedynczego okresu tego

sygnału. Powyższa zależność jest słuszna dla wszystkich sygnałów czasu

dyskretnego.

19 (46)

Związki łączące transformatę Fouriera i z-transformatę

z-transformata sygnału x[n] dana jest jako:

X  z =

∑

n=−∞

∞

x [n] z

−

n

; ROC : r

2

∣

z∣r

1

Jeśli zmienną zespoloną z wyrazimy w postaci wykładniczej z=re

iω

, wówczas:

X  z=r e

i 

=

∑

n=−∞

∞



x [n]r

−

n



e

−

i  n

Widać stąd, że X(z) jest transformatą Fouriera sygnału x[n]∙r

(-n)

.

Z drugiej strony, jeśli X(z) jest zbieżna dla |z| = 1, wówczas:

X  z=e

−

i 

=

∑

n=−∞

∞

x [n]e

−

i n

=

X 

Tak więc transformata Fouriera sygnału x[n] jest równoważna z-transformacie

obliczanej na obwodzie okręgu jednostkowego. Jeśli okrąg jednostkowy nie

należy do ROC, nie istnieje także transformata Fouriera X(ω) takiego sygnału x[n].

20 (46)

Przypomnijmy, że istnienie z-transformaty wymaga bezwzględnej sumowalności

ze względu na wartości r szeregu x[n] r

-n

:

∑

n=−∞

∞

∣

x [ n]r

−

n

∣∞

Jeśli więc powyższy szereg jest zbieżny dla pewnych wartości r > r

0

> 1, wówczas

z-transformata sygnału x[n] istnieje, lecz nie istnieje transformata Fouriera.

Przykładem jest przyczynowy sygnał x[n] = |a|

n

∙u[n], gdy |a| > 1.

21 (46)

Nie jest wszakże prawdą, iż istnienie transformaty Fouriera pociąga za sobą

istnienie z-transformaty. Sygnał postaci:

x [n]=

sin 2  f

c

n



n

; n∈ℤ

posiada transformatę Fouriera, która jest zbieżna w sensie średniej kwadratowej

(sygnał o skończonej energii) do nieciągłej funkcji X(ω):

X =

{

1⇔∣ f ∣ f

c

0⇔ f

c

∣

f ∣

1

2

}

Jednocześnie x[n] nie posiada z-transformaty.

22 (46)

Cepstrum

Niech dany jest sygnał x[n] o z-transformacie X(z) zbieżnej na obwodzie okręgu

jednostkowego. Zespolonym cepstrum sygnału x[n] jest ciąg c

x

[n] taki, że:

c

x

[

n]=Z

−

1



C

x



z=ln X  z

Zespolone cepstrum istnieje, gdy C

x

(z) jest zbieżne w obszarze: r

1

< |z| < r

2

, gdzie:

0 < r

1

< 1 oraz r

2

> 1. W tym obszarze zbieżności C

x

(z) można przedstawić

w postaci szeregu Laurenta:

C

x



z=ln X  z =

∑

n=−∞

∞

c

x

[

n] z

−

n

Jeśli zespolone cepstrum c

x

[n] istnieje, C

x

(z) jest zbieżne na okręgu

jednostkowym, tak więc:

C

x

=

ln X =

∑

n=−∞

∞

c

x

[

n]e

−

i n

23 (46)

Jeśli transformatę Fouriera wyrazimy w postaci:

X =∣X ∣e

i 

Wówczas:

ln X =ln∣X ∣i 

Stąd też zespolone cepstrum c

x

[n] przyjmie postać:

c

x

[

n]=iDTFT ln X =iDTFT ln∣X ∣iDTFT i 

c

x

[

n]=c

m

[

n]c



[

n]

W niektórych zastosowaniach zaniedbuje się obliczenia składowej fazowej

kosztem uproszczenia obliczeń, co uniemożliwia jednak odtworzenie sygnału x[n].

Analiza cepstralna jest stosowana obecnie przy analizowaniu sygnałów

akustycznych, w szczególności ludzkiej mowy.

24 (46)

Gęstość widmowa energii nieokresowych

sygnałów czasu dyskretnego

Energia sygnału czasu dyskretnego x[n] dana jest jako:

E

x

=

∑

n=−∞

∞

∣

x [n]∣

2

Spróbujmy teraz wyrazić E

x

jako funkcję X(ω):

E

x

=

∑

n=−∞

∞

x [n]⋅x

∗

[

n]=

∑

n=−∞

∞

x [n]



1

2 

∫

−



X

∗



e

−

i n



d =...

...=

1

2 

∫

−



X

∗





∑

n=−∞

∞

x [n]e

−

i n



d =

1

2

∫

−



∣

X ∣

2

d 

Wielkość |X(ω)|

2

opisuje rozkład energii sygnału w funkcji jego częstości i jest

nazywana widmem gęstości mocy sygnału x[n]. Nie zawiera ona żadnej

informacji o fazie sygnału.

25 (46)

Symetria widma gęstości mocy

Załóżmy, że sygnał x[n] jest rzeczywisty. Wówczas:

X

∗

=



∑

n=−∞

∞

x [n]e

−

i  n



∗

=

∑

n=−∞

∞

x [n]e

i  n

=

X −

Wynika stąd, że:

∣

X ∣=∣X −∣



X =− X −

∣

X ∣

2

=∣

X −∣

2

tak więc widmo gęstości mocy sygnału rzeczywistego jest funkcją parzystą.

Wynika stąd, że przedział częstotliwości, w którym sygnał czasu dyskretnego jest

opisywany jednoznacznie wynosi 0 ≤ f ≤ 0.5, gdyż znajomość X(ω) w tym

przedziale pozwala odtworzyć X(ω) w całym przedziale -0.5 ≤ f ≤ 0.5.

26 (46)

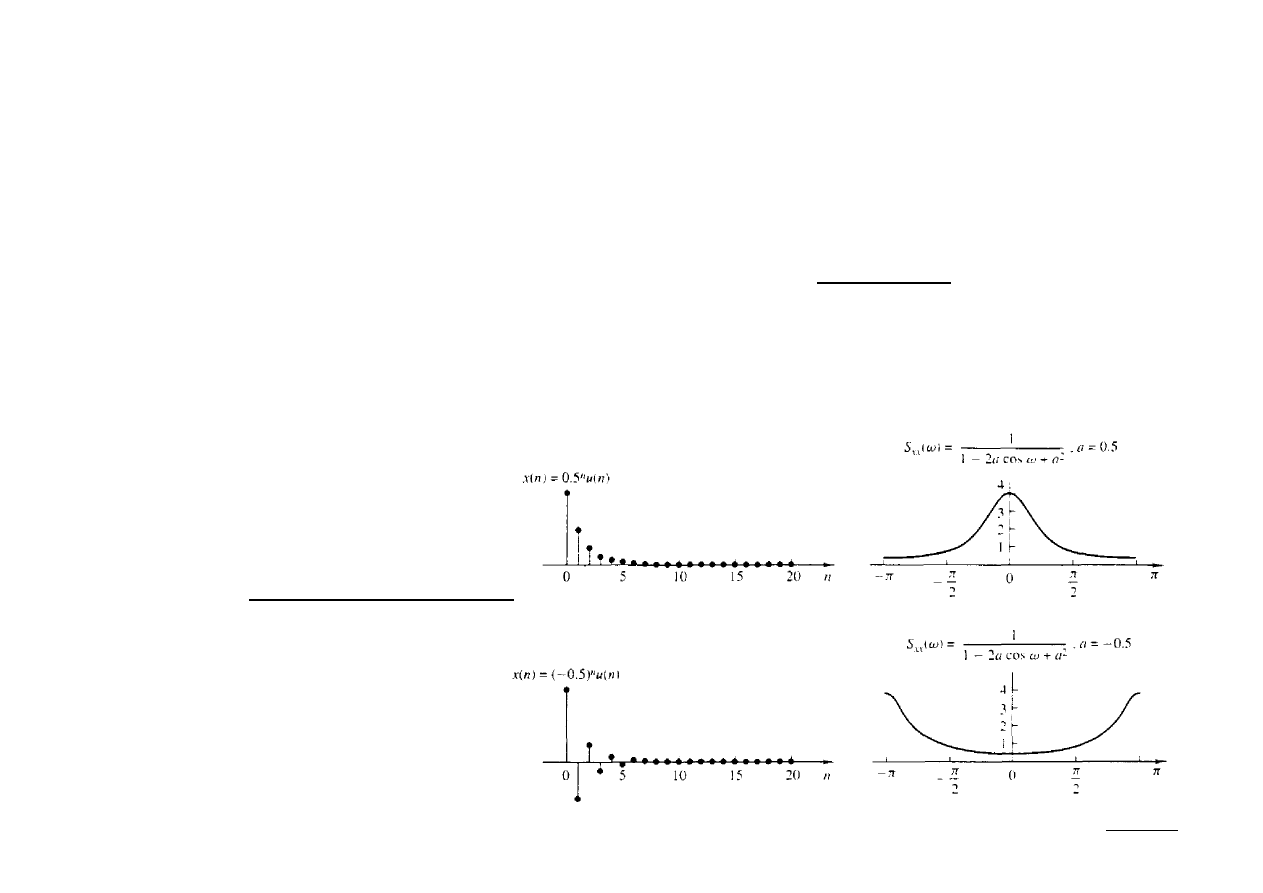
Ex.: Wyznaczyć widmo gęstości mocy sygnału x[n] = a

n

u[n], |a| < 1.

Przy założonej wartości a ciąg x[n] jest bezwzględnie sumowalny, więc jego

transformata Fouriera istnieje i wynosi:

X =

∑

n=0

∞

a

n

e

−

i  n

=

∑

n=0

∞



a e

−

i 



n

=

1

1−a e

−

i 

Widmo gęstości mocy wynosi:

27 (46)

∣

X ∣

2

=

1

1−2 a cosa

2

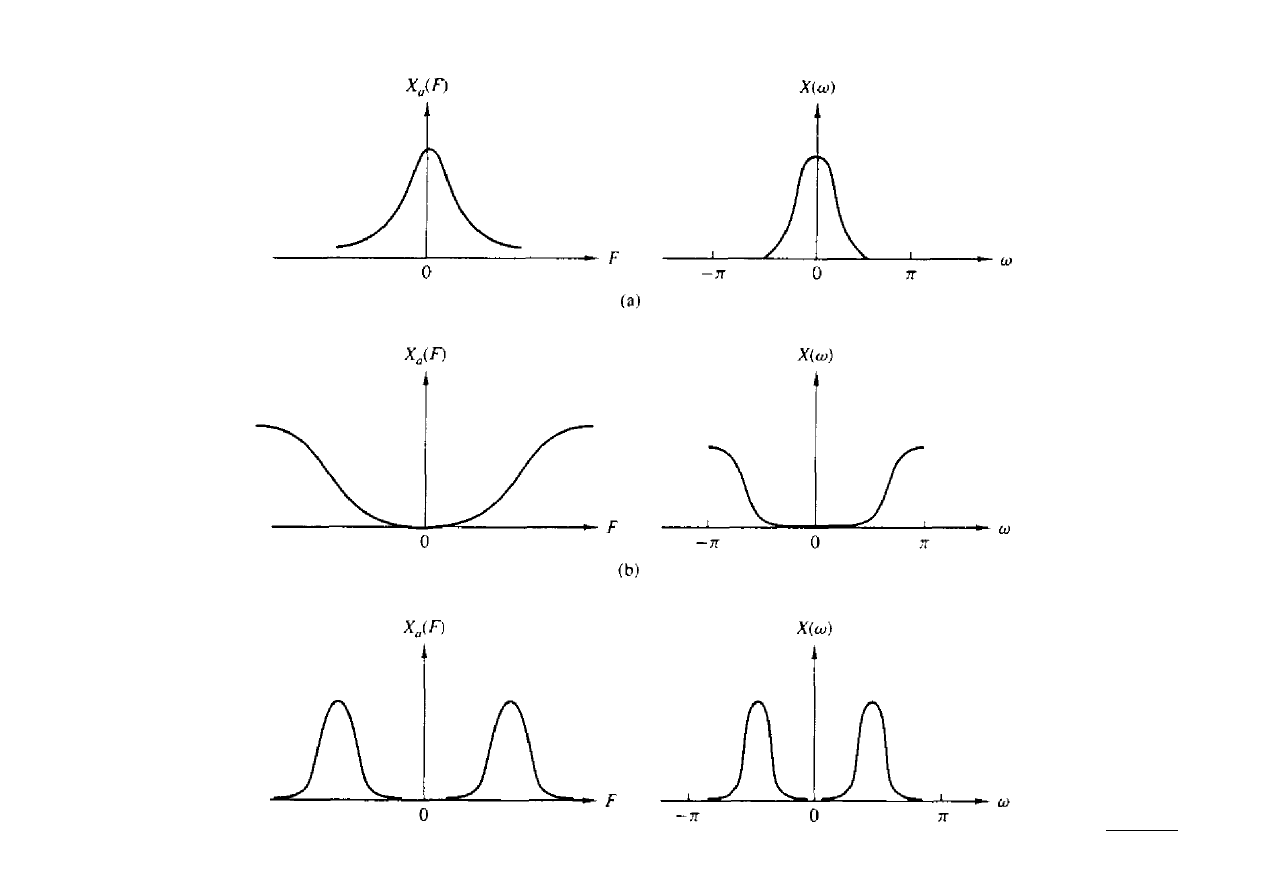
Podział sygnałów w dziedzinie częstotliwości.

Idea pasma częstotliwościowego

Do tej pory sygnały charakteryzowane były z uwagi na ich specyficzne cechy

występujące w dziedzinie czasu. W podobny sposób można stworzyć podział

sygnałów według ich charakterystyk w dziedzinie częstotliwości.

W szczególności, podział taki może zostać stworzony w oparciu o kształt widma

gęstości energii lub mocy sygnału:

–

sygnały o widmach skupionych wokół składowej DC to sygnały małej

częstotliwości,

–

sygnały o widmach skupionych wokół wysokich częstotliwości są sygnałami

wysokiej częstotliwości,

–

sygnały pośrednie nazywane są sygnałami pasmowymi.

28 (46)

29 (46)

Oprócz powyższego, dość ogólnego podziału, często używanym parametrem

charakteryzującym sygnał w dziedzinie częstotliwości jest szerokość jego

pasma, a więc zakres częstotliwości wokół których skupiona jest określona część

całego widma mocy lub energii.

Kryterium wyboru granic pasma jest umowne – może to być np. 95 % widma

gęstości mocy lub energii, lub np. zakres częstotliwości, dla których amplituda

sygnału spada o 3 dB w stosunku do amplitudy maksymalnej w danym pasmie

(tzw. pasmo 3-decybelowe – A

LIMIT

≈ 0.71 A

MAX

).

Sygnał jest wąskopasmowy, gdy szerokość jego pasma Δf = (f

2

-f

1

) jest znacznie

mniejsza niż częstotliwość środkowa pasma f

0

= (f

2

+f

1

)/2, w przeciwnym wypadku

sygnał jest szerokopasmowy.

Sygnał czasu dyskretnego x[n] ma ograniczone pasmo wtedy, gdy:

∣

X ∣=0⇔

0

∣∣

30 (46)

Pasma wybranych sygnałów naturalnych

31 (46)

32 (46)

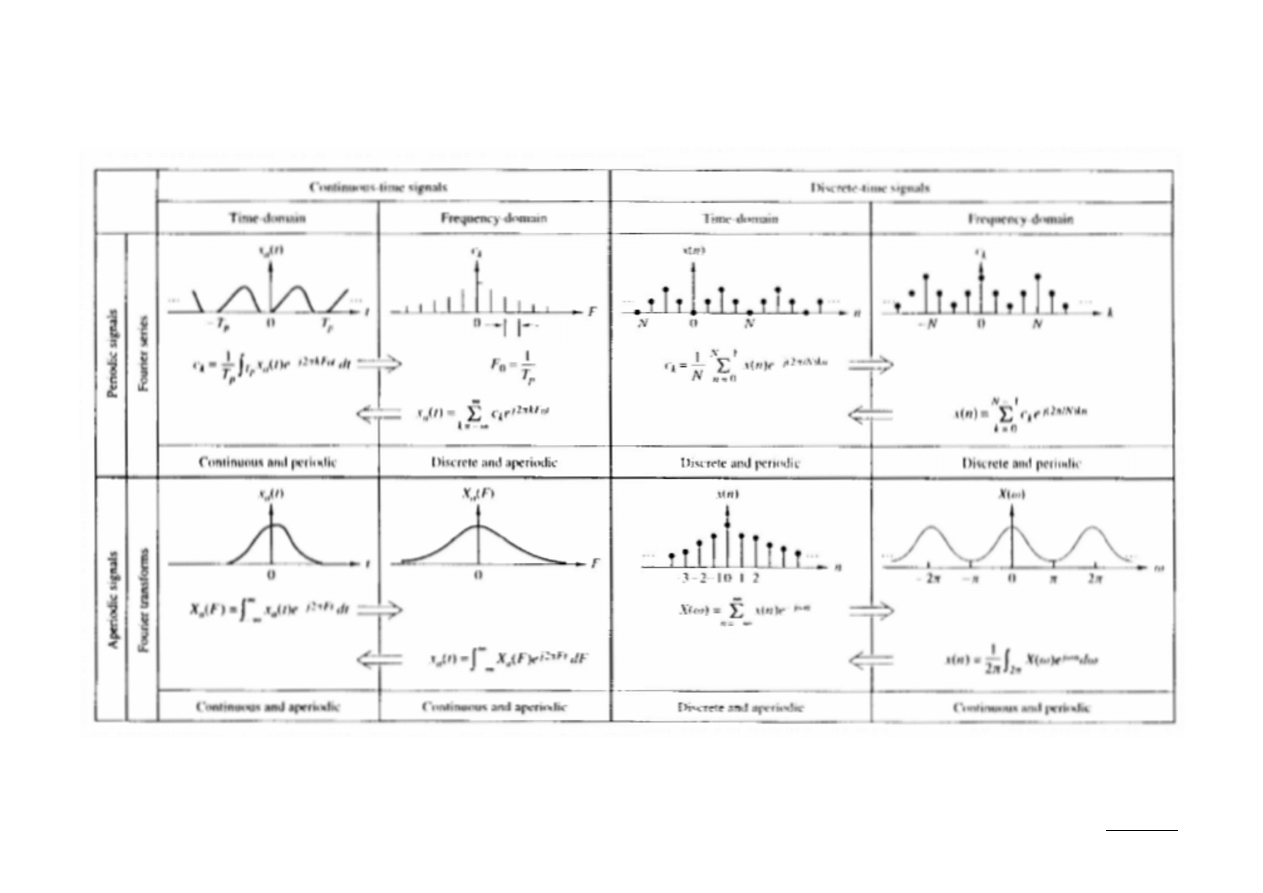
Podsumowanie równań syntezy i analizy fourierowskiej

33 (46)

Dualizm sygnałów w dziedzinie czasu i częstotliwości

Podsumujmy dotychczasowe spostrzeżenia na temat cech sygnałów i ich widm:

–

Sygnały czasu ciągłego mają widma nieokresowe,

–

Sygnały czasu dyskretnego mają widma okresowe,

–

Sygnały okresowe mają widma dyskretne,

–

Nieokresowe sygnały o skończonej energii mają widma ciągłe.

W sumie:

Okresowość sygnału w danej dziedzinie pociąga za sobą jego

dyskretność w przeciwdziedzinie:



f =

1

N

;T =

1

F

s

34 (46)

Własności transformaty Fouriera sygnałów czasu dyskretnego

Przyjmijmy następujące oznaczenia:

Prosta transformata Fouriera sygnału x[n] (DTFT) ma postać:

X =F  x [n]=

∑

n=−∞

∞

x [n]e

−

i  n

Odwrotna transformata Fouriera (iDTFT) ma postać:

x [n]=F

−

1



X =

1

2 

∫

2

X e

i  n

d 

Sygnały x[n] oraz X(ω) nazywane są parą transformat Fouriera oznaczaną jako:

x [n]⇔

F

X 

gdzie transformata X(ω) jest funkcją okresową o okresie 2π.

35 (46)

Symetria transformat Fouriera czasu dyskretnego

Wszelkie symetrie w dowolnej dziedzinie transformaty przenoszą się na

przeciwdziedzinę, co pozwala uprościć formuły obliczeniowe.

Załóżmy najpierw, że zarówno x[n], jak też jego widmo X(ω) są sygnałami

zespolonymi, a więc można je wyrazić jako:

x [n]=x

R

[

n]i x

I

[

n]

X =X

R



i X

I



Po podstawieniu powyższych wyrażeń do wzorów transformacyjnych otrzymamy:

X

R

=

∑

n=−∞

∞



x

R

[

n]cos n x

I

[

n]sin  n



X

I

=−

∑

n=−∞

∞



x

R

[

n]sin  n−x

I

[

n]cos n



36 (46)

Sygnały rzeczywiste

Jeśli x[n] jest sygnałem rzeczywistym, wówczas x

R

[n] = x[n] oraz x

I

[n] = 0, zatem:

X

R

=

∑

n=−∞

∞

x [n]cos n

X

I

=−

∑

n=−∞

∞

x [n]sin  n

Widać, że część rzeczywista transformaty jest funkcją parzystą, zaś część urojona

– nieparzystą:

X

R

=

X

R

−

X

I

=−

X

I

−

W sumie widmo sygnału rzeczywistego jest funkcją o symetrii:

X

∗

=

X −

Powyższa symetria oznacza parzystość widma amplitudowego oraz nieparzystość

widma fazowego sygnału x[n].

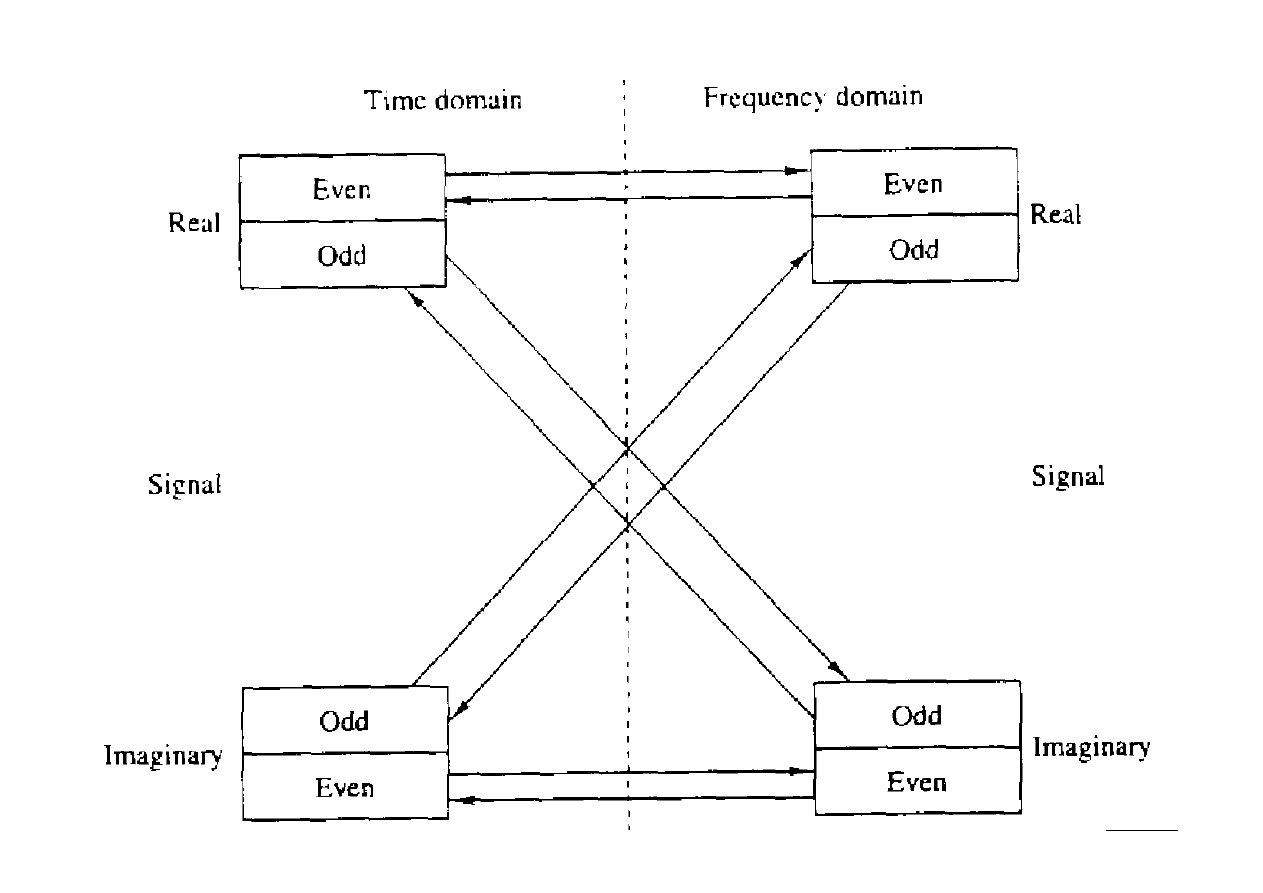
37 (46)

Parzyste sygnały rzeczywiste

Jeśli x[n] jest sygnałem rzeczywistym, parzystym, to:

X

R

=

x [0]2

∑

n=1

∞

x [n]cos n

X

I

=

0

Widma takich sygnałów są rzeczywiste i parzyste.

Nieparzyste sygnały rzeczywiste

Jeśli x[n] jest sygnałem rzeczywistym, nieparzystym, to:

X

R

=

0

X

I

=−

2

∑

n=1

∞

x [n]sin  n

Widma takich sygnałów są urojone i nieparzyste.

38 (46)

39 (46)

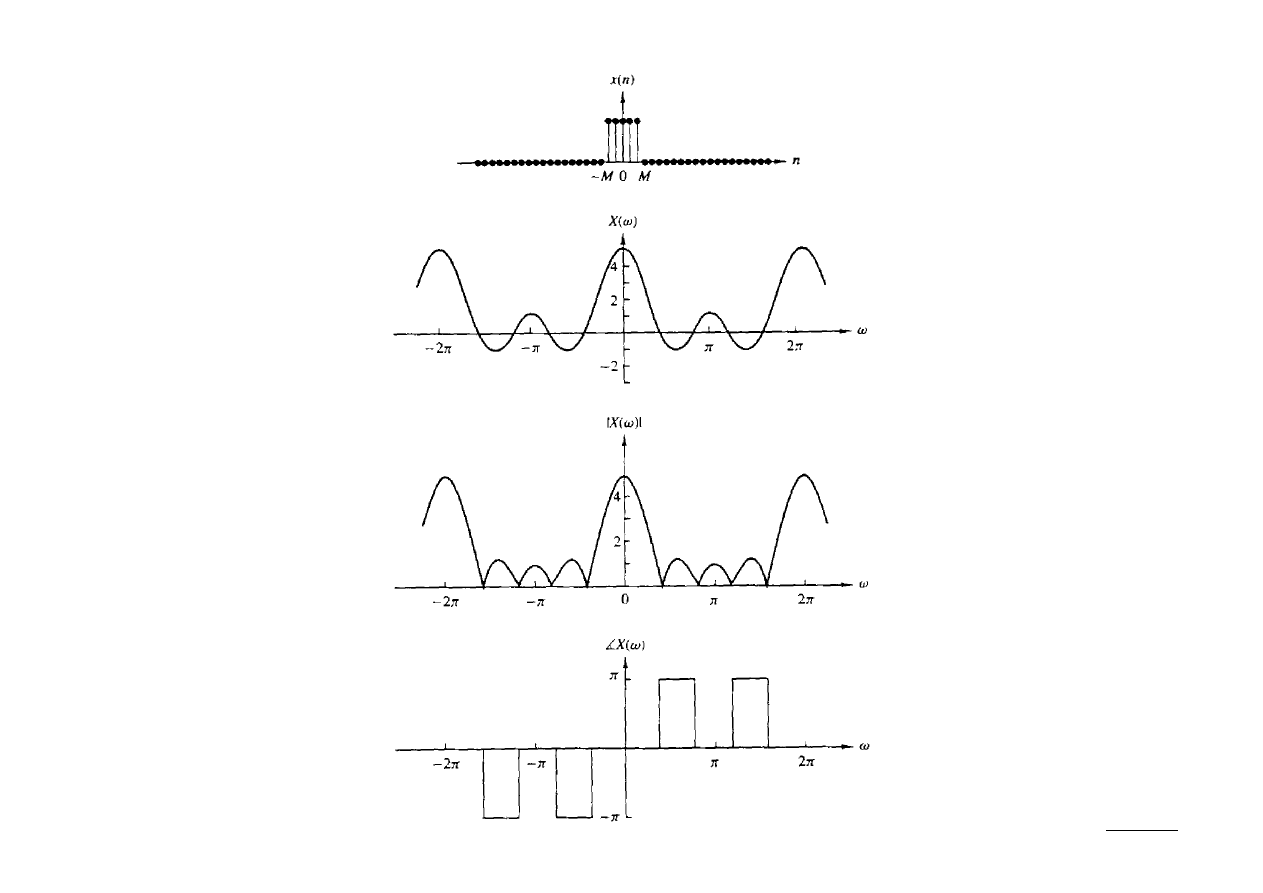
40 (46)

Ex.: Wyznaczyć transformatę Fouriera sygnału:

x [n]= Au[nM ]−u[ n−M −1]

Zauważmy, że: x[n] = x[-n], a więc jest rzeczywisty, parzysty. Stąd:

X = X

R

=

A



1

∑

n=1

M

cos n



=

A

sin  M 1/2

sin /2

Stąd:

∣

X ∣=∣A

sin  M 1/2

sin /2

∣



X =

{

0⇔ X 0

⇔

X 0

}

41 (46)

42 (46)

Własności transformat Fouriera

(1) Liniowość transformaty:



1

x

1

[

n]

2

x

2

[

n]⇔

F



1

X

1



2

X

2



(2) Przesuwanie w czasie:

x [n−k ]⇔

F

e

−

i  k

X 

(3) Zawijanie sygnału:

x [−n]⇔

F

X −

(4) Transformata splotu:

x

1

[

n]∗x

2

[

n]⇔

F

X

1

⋅

X

2



(5) Transformata korelacji:

r

x

1,

x

2

[

k ]⇔

F

X

1

⋅

X

2

−

43 (46)

Wynika stąd ważny wniosek: jeśli x[n] jest rzeczywisty, to:

r

xx

[

n]⇔

F

∣

X ∣

2

Widmo gęstości mocy jest transformatą funkcji autokorelacji rzeczywistego

sygnału x[n].

(6) Przesunięcie w dziedzinie częstotliwości:

e

i 

0

n

x [ n]⇔

F

X −

0



(7) Transformata iloczynu sygnałów (okienkowanie):

x

1

[

n]⋅x

2

[

n]⇔

F

X

1

∗

X

2



(8) Różniczkowanie w dziedzinie transformaty:

n x [n]⇔

F

i

d X 

d 

44 (46)

45 (46)

46 (46)