Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (3)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

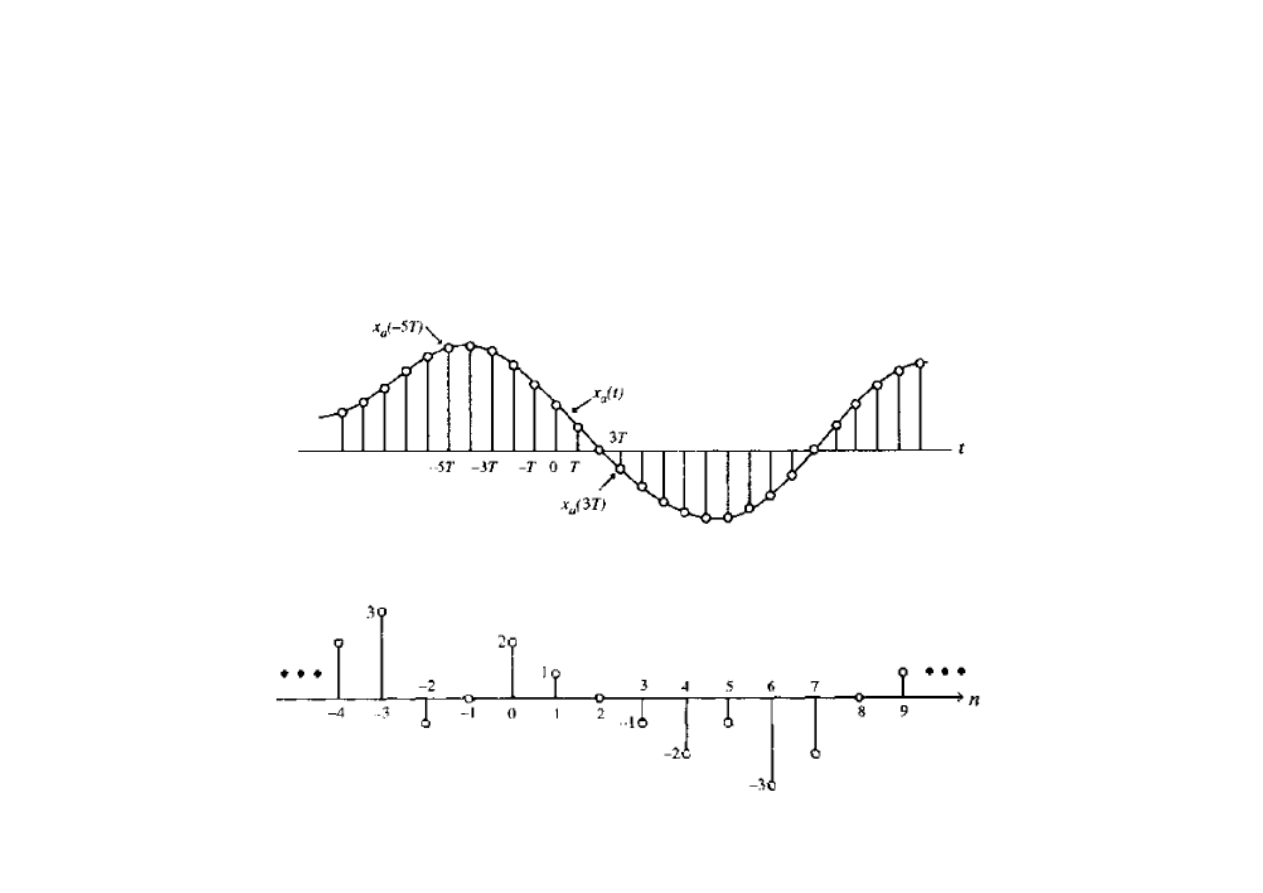
Sygnały dyskretne w czasie (Discrete-Time Signals)

Sygnałem dyskretnym w czasie określa się ponumerowany ciąg liczb

rzeczywistych lub zespolonych – jest to funkcja x[n], której argumentami są liczby

całkowite n. Do tej grupy należą sygnały próbkowane i sygnały cyfrowe:

Zmienna niezależna n nie musi reprezentować wyłącznie czasu (może np.

opisywać współrzędne przestrzenne) – ważne, iż ciąg x [n] jest zdefiniowany

wyłącznie dla całkowitych wartości n (nie znamy jego wartości między próbkami).

Wygodnie jest założyć, że ciąg x[n] jest zdefiniowany dla wszystkich liczb

całkowitych n

∈

(-

∞

,

∞

) oraz nazywać n-ty jego wyraz 'n-tą próbką', nawet jeśli

sygnał x[n] nie powstał przez próbkowanie sygnału analogowego.

Jeśli x(n) jest zbiorem próbek sygnału analogowego x

a

(t), wówczas zachodzi:

x [n]= x

a



t∣

t=n⋅T

=

x

a



n⋅T 

;

T =

1

F

s

gdzie: T [s] – jest okresem próbkowania (odstępem czasowym pomiędzy

kolejnymi próbkami sygnału – próbkowanie równomierne), zaś F

s

[Hz] – jest

częstotliwością próbkowania.

Reprezentacje czasowe sygnałów dyskretnych w czasie

1) Reprezentacja graficzna:

2) Reprezentacja funkcyjna:

x [n]=

{

1⇔n=−1,0,1

2⇔n=2, 3

0 dla pozostałych n

}

3) Reprezentacja tabelaryczna:

n

...

-2

-1

0

1

2

3

4

...

x[n]

...

0

1

1

1

2

2

0

...

4) Reprezentacja ciągowa:

–

ciąg nieskończony:

x [n]=

{

... 1 1 1 2 2 ...



}

–

ciąg skończony:

x [n]=

{

1 1 1 2 2



}

Długość sygnału dyskretnego w czasie

Sygnały dyskretne w czasie mogą być ciągami skończonymi lub nieskończonymi.

Ciąg skończony zdefiniowany jest dla liczb n z pewnego skończonego zakresu:

−∞

N

1

≤

n≤N

2

∞

Długość N tego ciągu wynosi:

N = N

2

−

N

1



1

Ciąg taki określa się jako N-punktowy. Każdy ciąg skończony można wydłużyć

przypisując próbkom o numerach spoza powyższego zakresu wartości zerowe.

Wydłużanie ciągu przez uzupełnianie próbkami zerowymi to tzw. zero-padding.

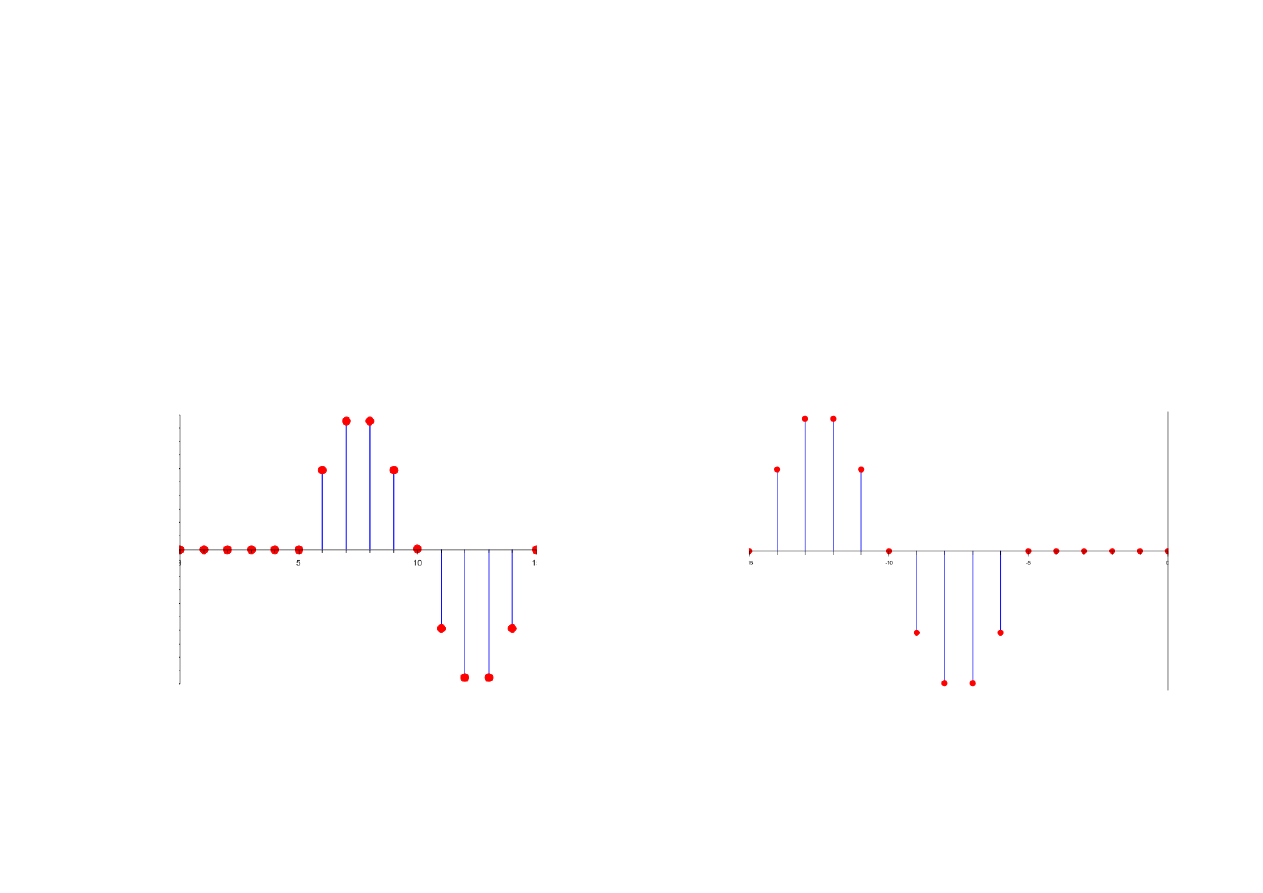
Ciągi przyczynowe i antyprzyczynowe

Zasadniczo wyróżnia się 3 typy ciągów nieskończonych:

–

ciągi prawostronne, dla których x [n < N

1

] = 0, w tym także ciągi przyczynowe

(causal sequences), dla których N

1

≥ 0.

–

ciągi lewostronne, dla których x [n > N

2

] = 0, w tym także ciągi

antyprzyczynowe (anti-causal sequences), dla których N

2

≤ 0.

–

ciągi obustronne, ograniczone próbkami o wartości zero z obu stron.

Wielkość sygnału dyskretnego w czasie

Zdefiniujmy L

p

- normę ciągu x[n] jako liczbę:

∥

x∥

p

=



∑

n=−∞

∞

∣

x [n]∣

p



1

p

, p∈ℤ

Zwykle używa się wartości p = 1, 2 lub ∞.

Z powyższej definicji wynika, że:

–

L

1

– norma (|| x ||

1

) jest równa średniej z wartości bezwzględnych ciągu x [n],

–

L

2

– norma (|| x ||

2

) jest równa pierwiastkowi średniej kwadratowej wartości ciągu

x [n] (tzw. wartość skuteczna, rms – root mean squared),

–

L

∞

– norma (|| x ||

∞

= | x |

max

) jest równa szczytowej wartości bezwzględnej ciągu

x [n].

Zastosowania L

p

– normy:

oszacowanie błędu aproksymacji sygnału

Zdefiniowana powyżej norma może służyć jako estymata wielkości sygnału.

Jeśli np. N-punktowy ciąg y[n] jest przybliżeniem N-próbkowego ciągu x[n]

(0 ≤ n ≤ N-1), to względny błąd tej aproksymacji jest równy stosunkowi L

2

– normy

sygnału różnicowego do L

2

– normy sygnału oryginalnego:



rel

=



∑

n=0

N −1

∣

y [ n]− x [n]∣

2

∑

n=0

N −1

∣

x [n]∣

2



1
2

Klasyfikacja sygnałów dyskretnych w czasie

Sygnały czasu dyskretnego mogą być klasyfikowane na wiele sposobów.

Wcześniej omówiony został podział ze względu na liczbę próbek definiujących

ciąg (ciągi skończone i nieskończone), ale możliwe są także podziały z uwagi na:

–

symetrię ciągu,

–

okresowość,

–

sumowalność,

–

wartość energii i mocy.

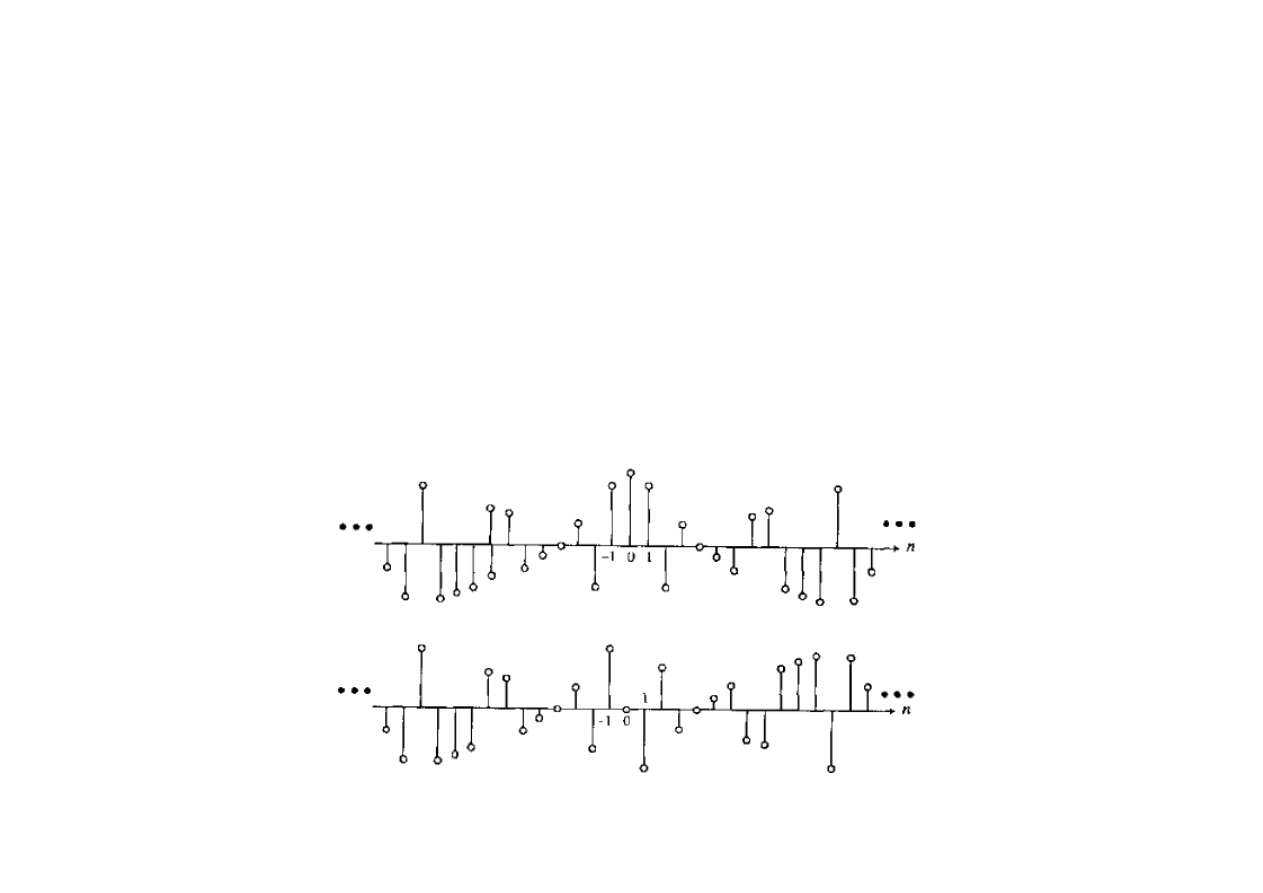
Podział sygnałów z uwagi na symetrię

Ciąg zespolony x[n] jest ciągiem sprzężonym symetrycznie (conjugate-

symmetric) wtedy, gdy: x[n] = x

*

[-n]. Ciąg rzeczywisty o takiej własności określa

się mianem ciągu parzystego (even sequence).

Ciąg zespolony x[n] jest ciągiem sprzężonym antysymetrycznie (conjugate-

antisymmetric) wtedy, gdy: x[n] = -x

*

[-n]. Ciąg rzeczywisty o takiej własności jest

ciągiem nieparzystym (odd sequence). W tym przypadku Re(x [0]) = 0.

Rozwijanie ciągów rzeczywistych

Dowolny rzeczywisty ciąg x[n] można wyrazić jako sumę jego części parzystej

x

parz

[n]

i nieparzystej x

np

[n]:

x [n]= x

parz

[

n] x

np

[

n]

x

parz

[

n]=

1
2



x [n] x [−n]



x

np

[

n]=

1
2



x [n]− x [−n]



Możliwość wydzielenia składowej parzystej i nieparzystej ciągu x[n] jest istotna

z punktu widzenia własności transformat (np. transformaty Fouriera).

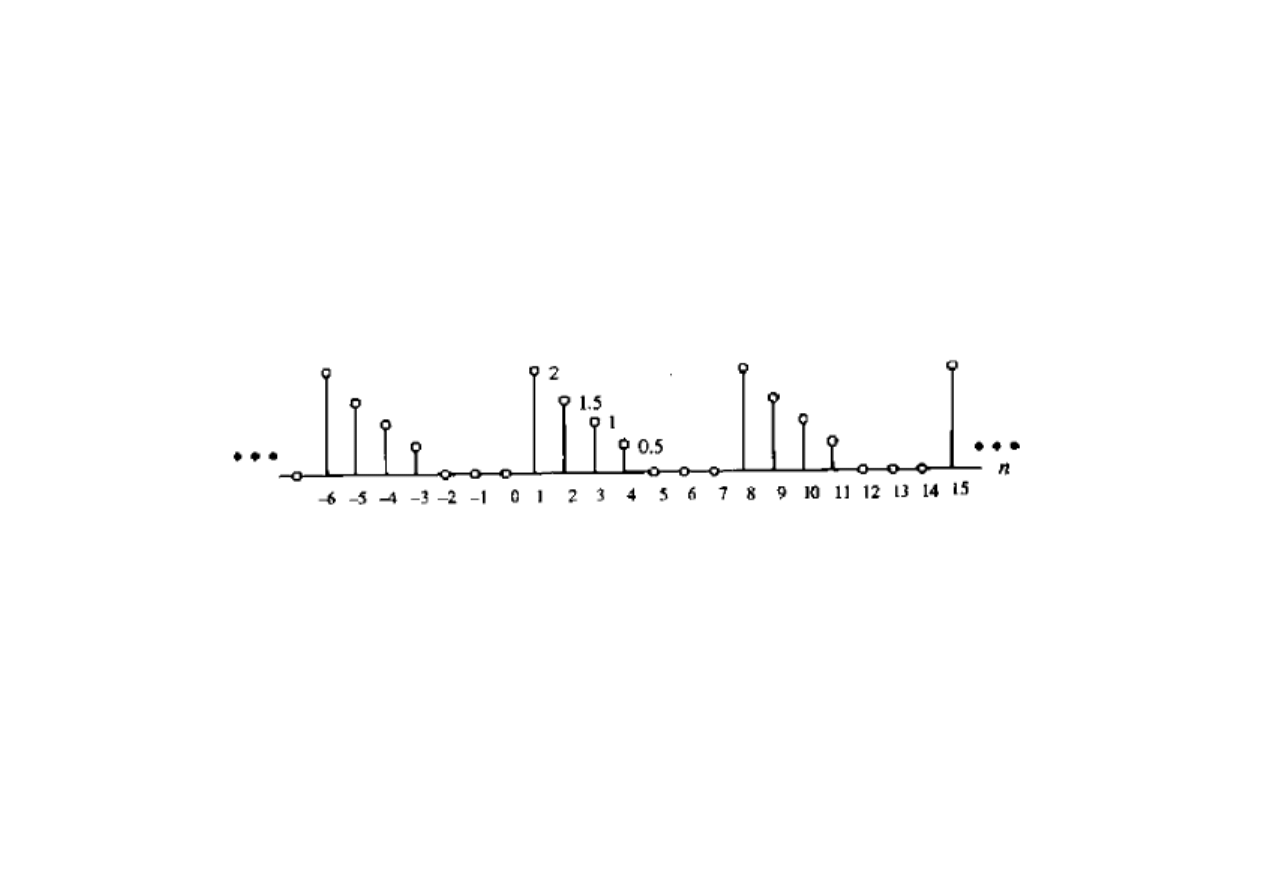
Sygnały periodyczne i aperiodyczne

Ciąg x[n] jest periodyczny z okresem N > 0 wtedy i tylko wtedy, gdy:

∀

N

x [ nN ]= x [n]

Najmniejszą wartość N, dla której powyższy warunek jest spełniony, nazywamy

okresem podstawowym sygnału periodycznego.

Sygnał, który nie spełnia powyższego warunku dla dowolnego N jest sygnałem

aperiodycznym (nieokresowym).

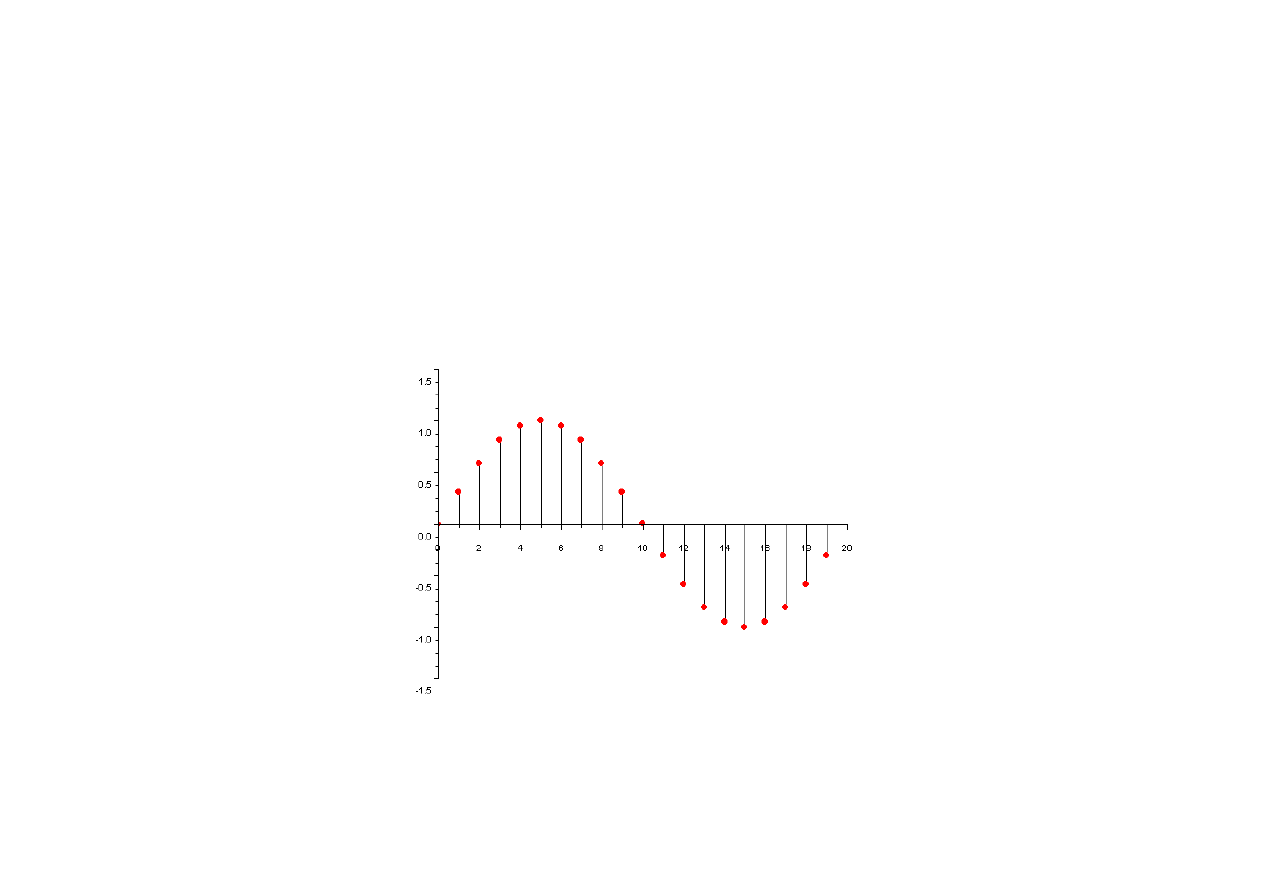
Sygnały sinusoidalne czasu dyskretnego

Dyskretny w czasie ciąg sinusoidalny można wyrazić w postaci:

x [n]= A⋅sin ⋅n=A⋅sin 2⋅⋅f ⋅n; n∈−∞ ,∞

gdzie: A – jest amplitudą ciągu, ω – jego częstością [rad/sample],

f - częstotliwością [cykli/sample] zaś φ – fazą początkową.

Sinusoida o f = 0.05 ckl/sam, ω = 0.1π rad/sam, φ = 0 rad.

Własności sygnałów sinusoidalnych czasu dyskretnego

Sygnały sinusoidalne czasu dyskretnego posiadają własności istotnie

odróżniające je od podobnych sygnałów czasu ciągłego.

(1) Sygnały sinusoidalne czasu dyskretnego są okresowe wtedy i tylko

wtedy, gdy ich częstotliwości f są ułamkami właściwymi:

Z definicji, sygnał czasu dyskretnego jest okresowy z okresem N > 0 wtedy i tylko

wtedy, gdy dla każdego n:

x [n + N] = x [n]

Najmniejsza wartość N spełniająca powyższy warunek to okres podstawowy.

Dowód:

Aby sinusoida o częstotliwości f była periodyczna, musi zachodzić:

sin 2⋅⋅f ⋅nN =sin 2⋅⋅ f ⋅n

Powyższy warunek jest prawdziwy, gdy istnieje taka liczba całkowita k, że:

2⋅⋅f ⋅N =2⋅k⋅

Skąd mamy, że:

f =

k

N

Aby wyznaczyć okres podstawowy N ciągu sinusoidalnego należy wyrazić jego

częstotliwość w postaci ułamka, w którym k i N są względnie pierwsze. Wówczas

okres podstawowy równy jest wartości N.

Uwaga! Niewielka zmiana częstotliwości może powodować silne zmiany okresu

podstawowego: por.: f

1

= 31/60 (N = 60) oraz f

2

= 30/60 (N = 2).

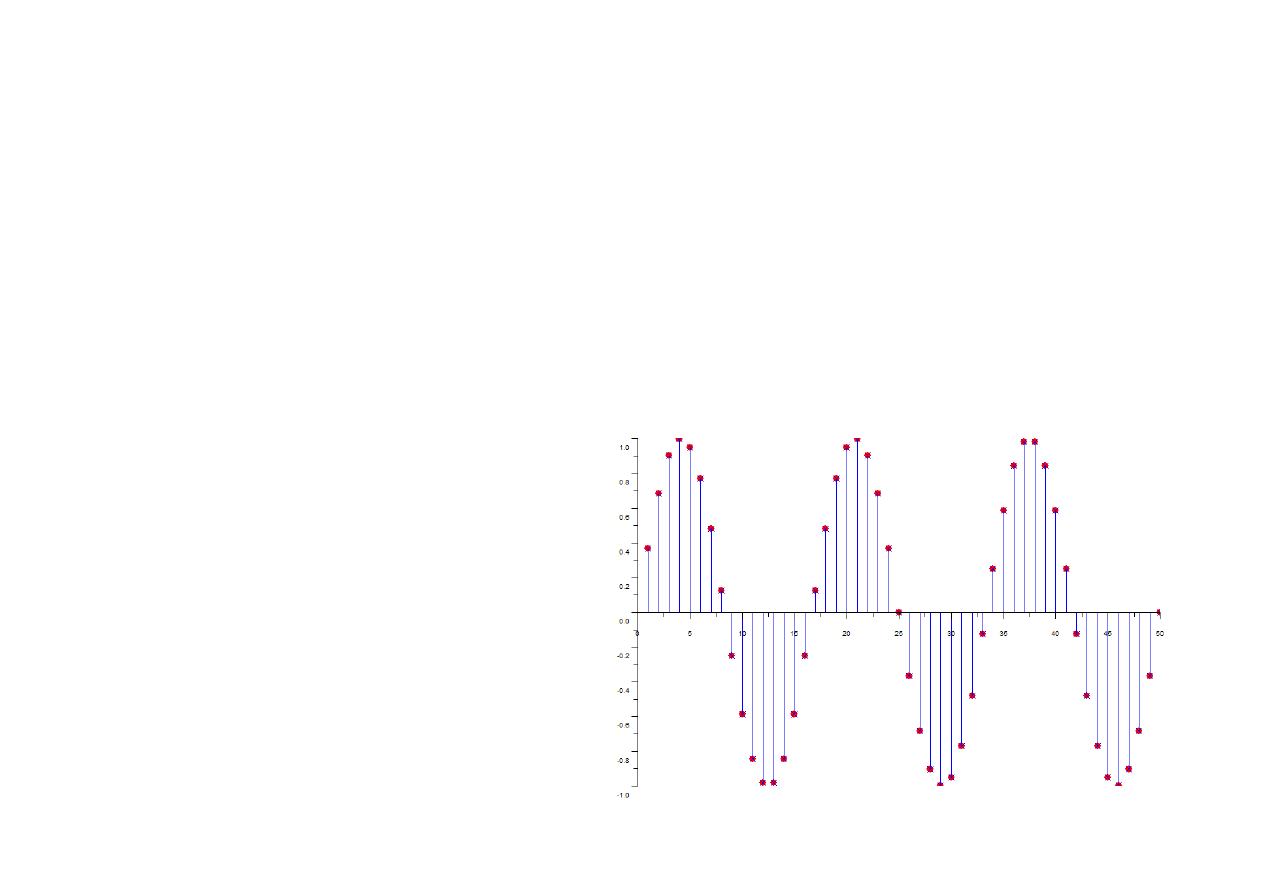
(2) Ciągi sinusoidalne czasu dyskretnego, których częstotliwości różnią się

pełną wielokrotnością 2π są identyczne:

Sprawdźmy identyczność dwóch ciągów sinusoidalnych:

sin





2⋅⋅n



=

sin



⋅

n2⋅⋅n



=

sin



⋅

n



Wynika stąd, że wszystkie ciągi sinusoidalne postaci:

x

k

[

n]=sin





k

⋅

n



; k =0,1, 2,...

gdzie:



k

=

02⋅k⋅ ,

0

∈[−

,]

są nierozróżnialne (identyczne).

Rys. Ciągi sinusoidalne o N = 50,

f

1

= 3/50, f

2

= 1 + 3/50.

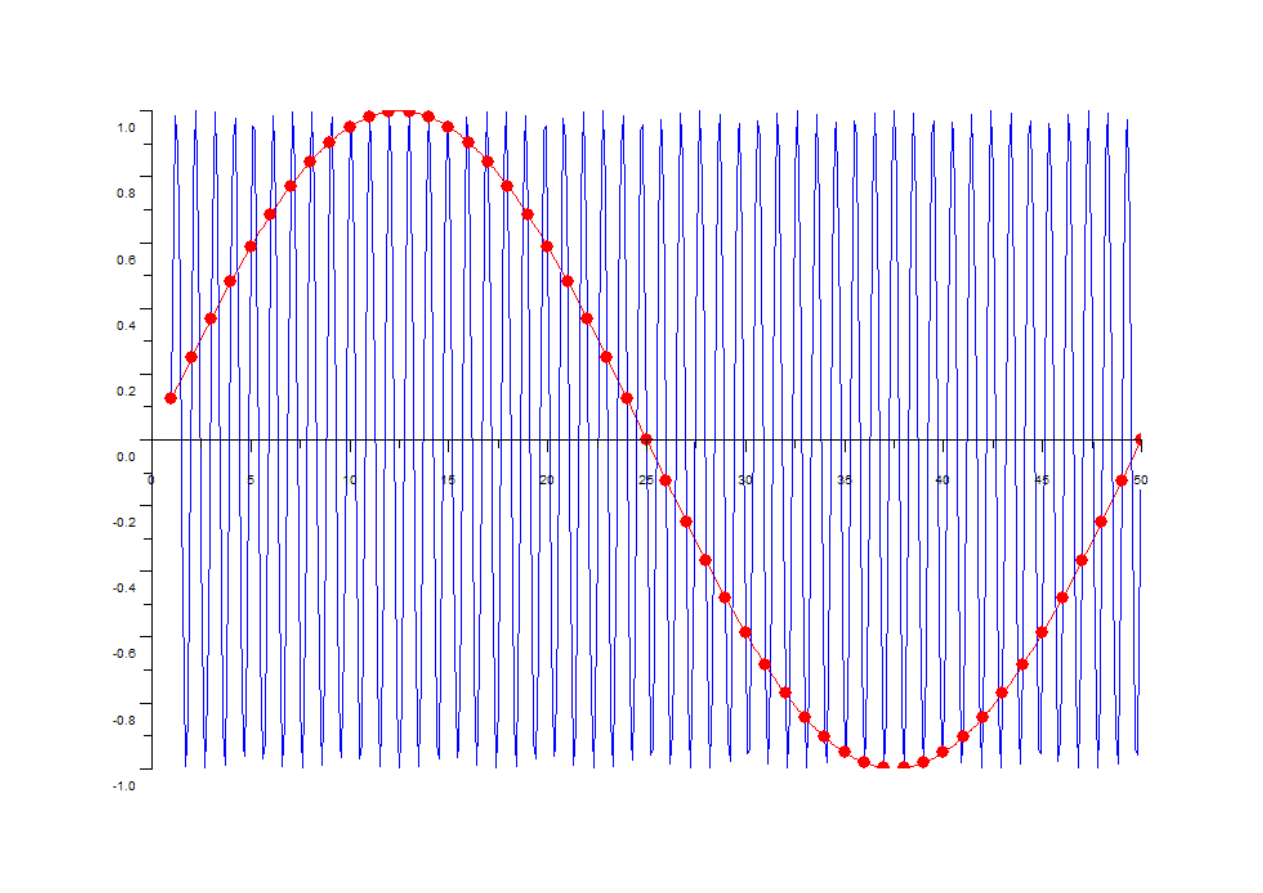
Aliasing

Z powyższej własności wynika, iż dwa ciągi sinusoidalne o częstościach

z przedziału: (- π ≤ ω ≤ π) lub (- 0.5 ≤ f ≤ 0.5) są rozróżnialne.

Wynika stąd, iż dla każdego ciąg sinusoidalnego o częstotliwości | f | ≥ 0.5 istnieje

ciąg o częstotliwości | f | ≤ 0.5. Z uwagi na opisywaną identyczność, ciąg

o częstotliwości | f | ≥ 0.5 jest nazywany aliasem odpowiadającego mu ciągu

o częstotliwości | f | ≤ 0.5. Jest to cecha istotnie odróżniająca sygnały sinusoidalne

czasu dyskretnego od sygnałów czasu ciągłego.

Oznacza to m.in., że próbkowanie sygnału nie jest procesem odwracalnym,

a więc nie zawsze jest możliwe odtworzenie oryginalnego sygnału analogowego

na podstawie jego próbek – próbkowanie powoduje w pewnych warunkach

częściową lub nawet całkowitą utratę informacji.

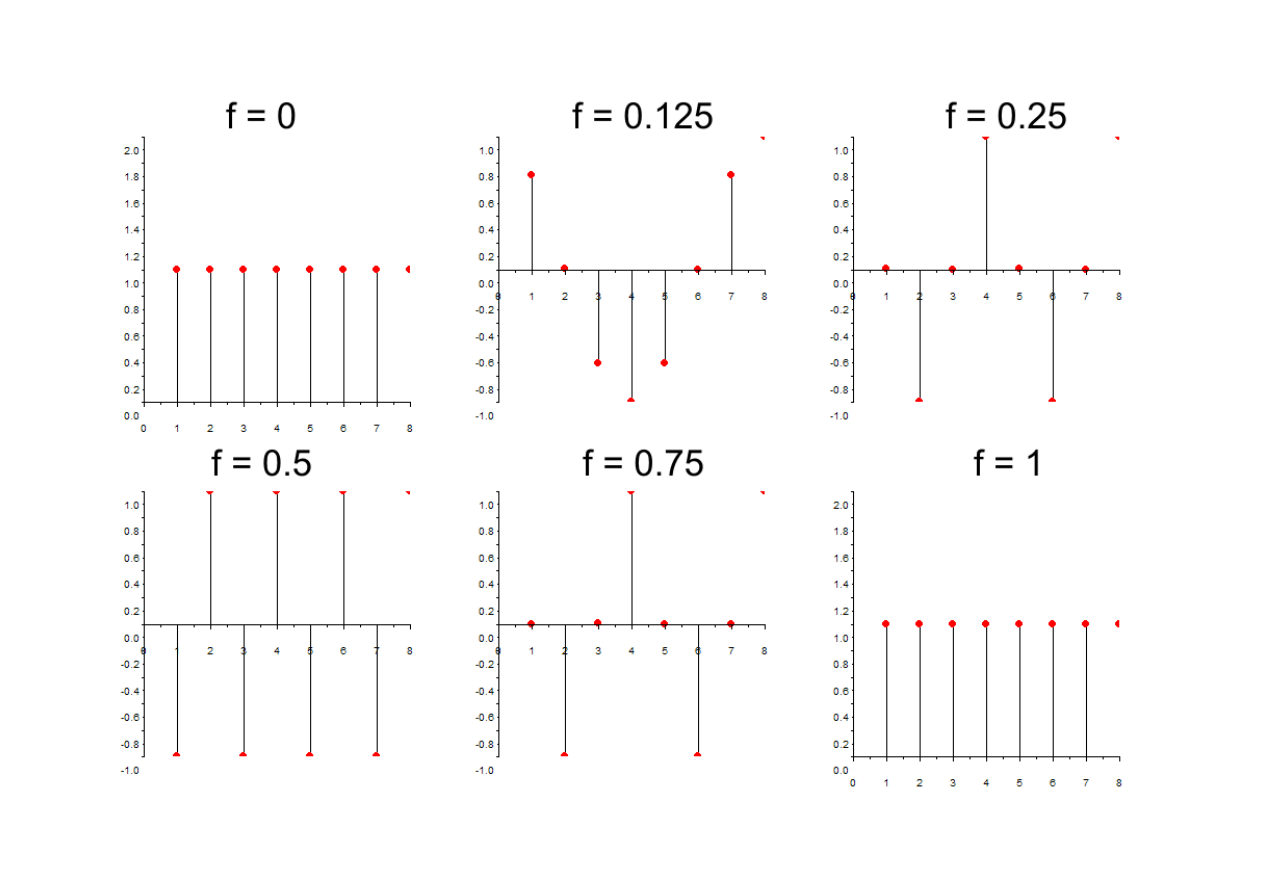
(3) Największa szybkość zmian sygnału sinusoidalnego czasu dyskretnego

odpowiada wartości | f | = 0.5:

Zbadajmy własności ciągu sinusoidalnego postaci:

x [n]=sin



2⋅⋅f ⋅n



gdzie:

f =0,

1

8,

1

4,

1

2,

3

4,

1

Aby sprawdzić zachowanie ciągu sinusoidalnego dla częstotliwości 0.5 ≤ f ≤ 1,

rozważmy dwie częstotliwości: f

0

oraz f

1

= (1 – f

0

) (| f

0

| ≤ 0.5):

x

0

[

n]=sin



2⋅⋅f

0

⋅

n



x

1

[

n]=sin



2⋅⋅f

1

⋅

n



=

sin



2⋅⋅1− f

0

⋅

n



=

sin



−

2⋅⋅f

0

⋅

n



=−

x

0

[

n]

Zespolone ciągi wykładnicze czasu dyskretnego

Podobnie jak ciągi sinusoidalne, zespolone ciągi wykładnicze czasu dyskretnego

są okresowe, gdy ich częstotliwość wyraża się ułamkiem właściwym. Wybierzmy

zatem częstotliwość podstawową f

0

= 1/N (N – liczba próbek ciągu) i zdefiniujmy

zbiór harmonicznych, zespolonych ciągów wykładniczych:

s

k

[

n]=e



i⋅2⋅⋅k⋅f

0

⋅

n



; k ∈ℤ

Zauważmy, że:

s

k N

[

n]=e



i⋅2⋅⋅k N ⋅f

0

⋅

n



=

e



i⋅2⋅⋅k⋅f

0

⋅

n



⋅

e



i⋅2⋅⋅N⋅f

0

⋅

n



=

e



i⋅2⋅⋅k⋅f

0

⋅

n



⋅

s

k

[

n]=s

k

[

n]

Oznacza to, że w zbiorze {s

k

[n]} istnieje dokładnie N-różnych zespolonych ciągów

eksponencjalnych, z których każdy posiada okres równy N.

Jeśli zatem wybierzemy zbiór ciągów:

s

k

[

n]=e



i⋅2⋅⋅k⋅n / N



; k =0,1, 2,... , N −1.

Wówczas kombinacja liniowa:

x [n]=

∑

k=0

N −1

c

k

⋅

s

k

[

n]=

∑

k =0

N −1

c

k

⋅

e

2⋅⋅k⋅n/ N

jest również ciągiem periodycznym o okresie podstawowym N. Ciąg ten jest

identyczny z dyskretnym szeregiem Fouriera o współczynnikach {c

k

}.

Ciągi aperiodyczne czasu dyskretnego

W dalszej części przedstawione zostaną wybrane aperiodyczne ciągi czasu

dyskretnego, które odgrywają istotną rolę w analizie i projektowaniu układów

z dyskretnym czasem. Możliwe jest np. wyrażenie dowolnego sygnału jako

kombinacji tychże sygnałów podstawowych lub poklasyfikowanie układów

z dyskretnym czasem w zależności od ich odpowiedzi na pewne ciągi

podstawowe.

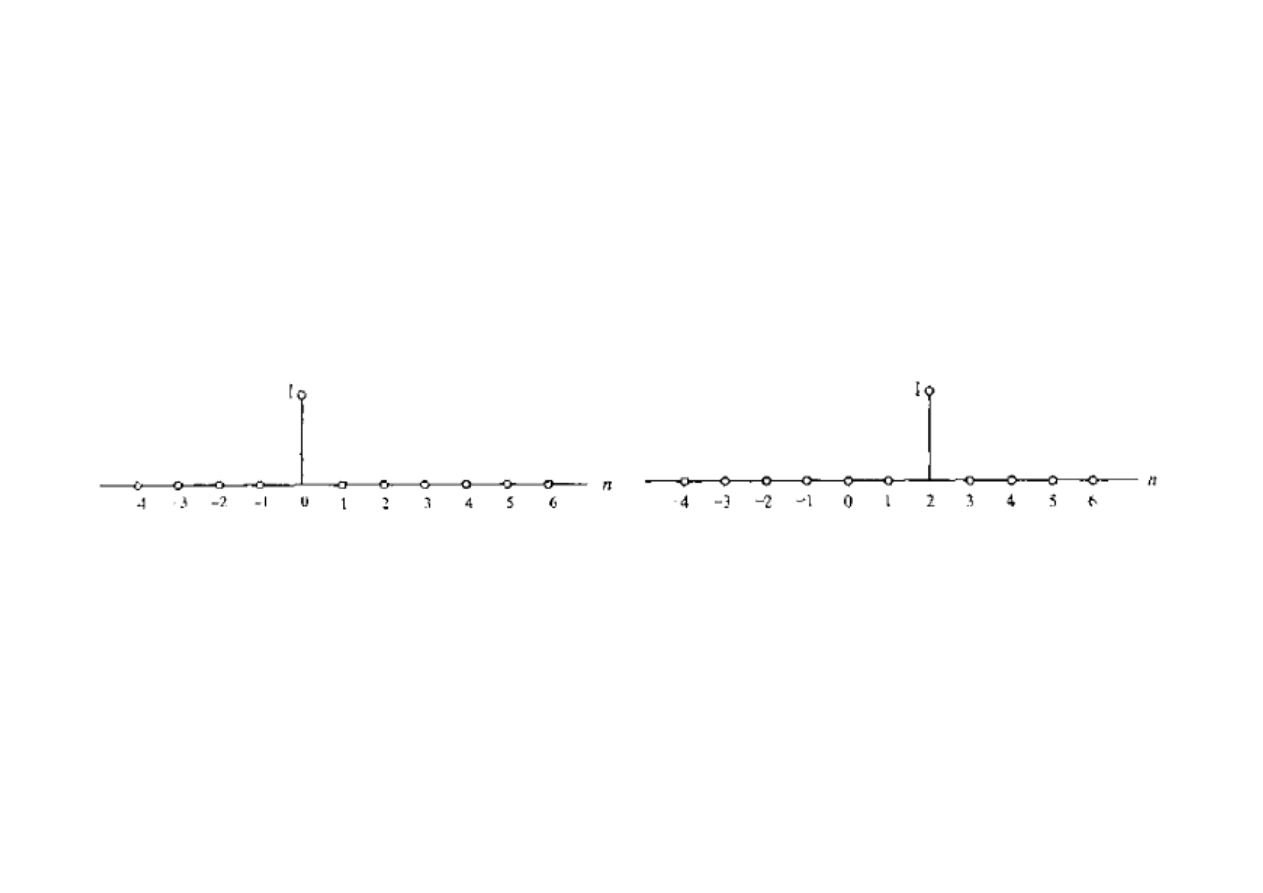
Impuls jednostkowy

Najprostszym i jednym z najbardziej użytecznych jest ciąg zwany impulsem

czasu dyskretnego lub impulsem jednostkowym δ[n]:

[

n]=

{

1⇔ n=0
0⇔ n≠0

}

,

[

n−k ]=

{

1⇔ n=k
0 ⇔n≠k

}

Dowodzi się, że każdy ciąg można przedstawić jako sumę ważoną przesuniętych

impulsów jednostkowych oraz, że istnieją układy całkowicie charakteryzowane w

dziedzinie czasu poprzez ich odpowiedź na pobudzenie impulsem

jednostkowym.Co więcej, na tej podstawie można przewidzieć odpowiedź układu

na dowolne inne pobudzenie.

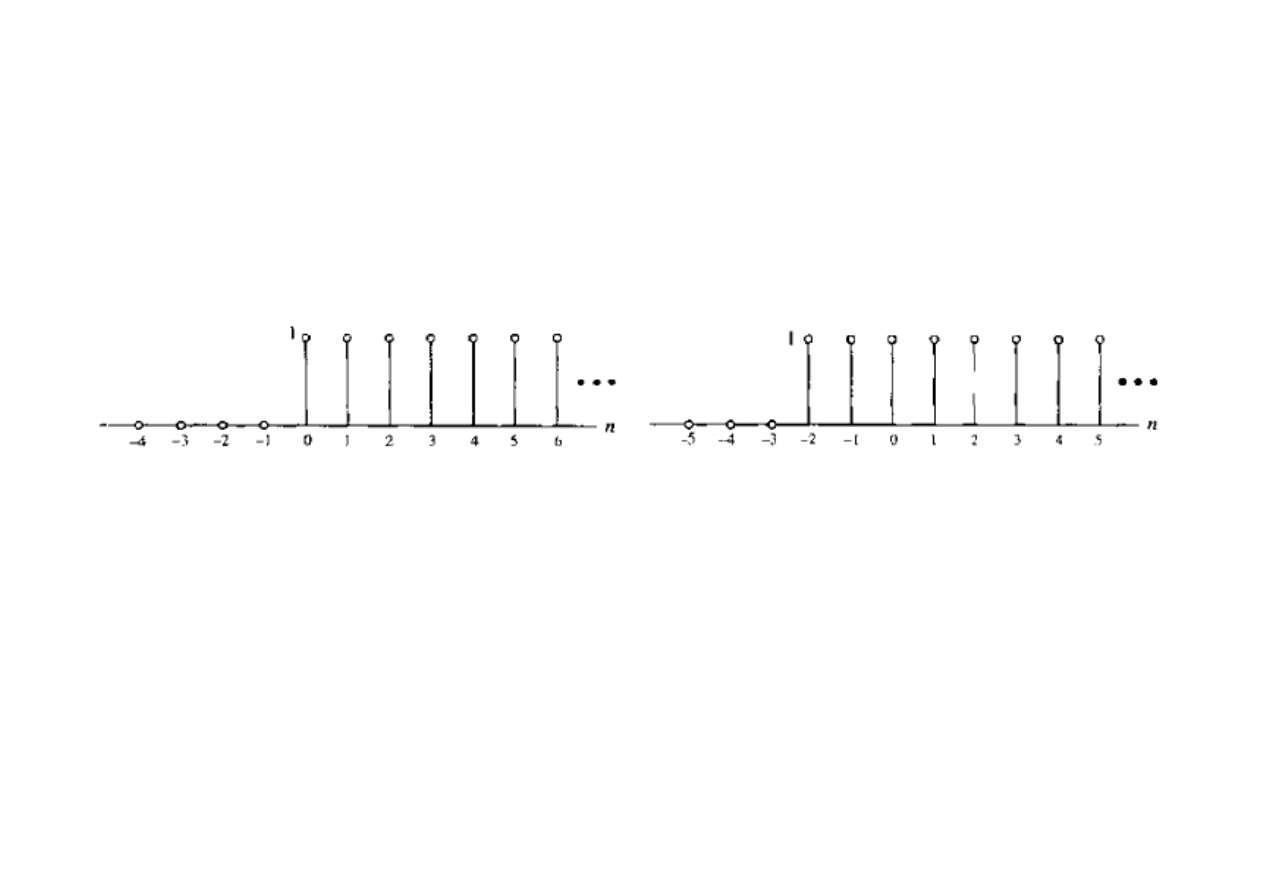
Skok jednostkowy

Skok jednostkowy μ[n] jest zdefiniowany jako:

[

n]=

{

1⇔ n≥0
0⇔ n0

}

,

[

n−k ]=

{

1⇔ n≥k
0⇔nk

}

Pomiędzy impulsem jednostkowym a skokiem jednostkowym istnieją następujące

zależności:

[

n]=

∑

m=0

∞

[

n−m]=

∑

k=−∞

n

[

k ]

[

n]=[n]−[ n−1]

Ciągi eksponencjalne czasu dyskretnego

Ciągi tego typu powstają po podniesieniu wartości n-tej próbki do n-tej potęgi

liczby rzeczywistej lub zespolonej:

x [n]= A⋅

n

; n∈−∞ ,∞ , A , ∈ℂ

W przypadku, gdy współczynniki α są liczbami zespolonymi postaci:

=

e

i⋅2⋅⋅k / N

ciągi eksponencjalne są wersjami ciągów sinusoidalnych czasu dyskretnego

uogólnionymi na przestrzeń liczb zespolonych.

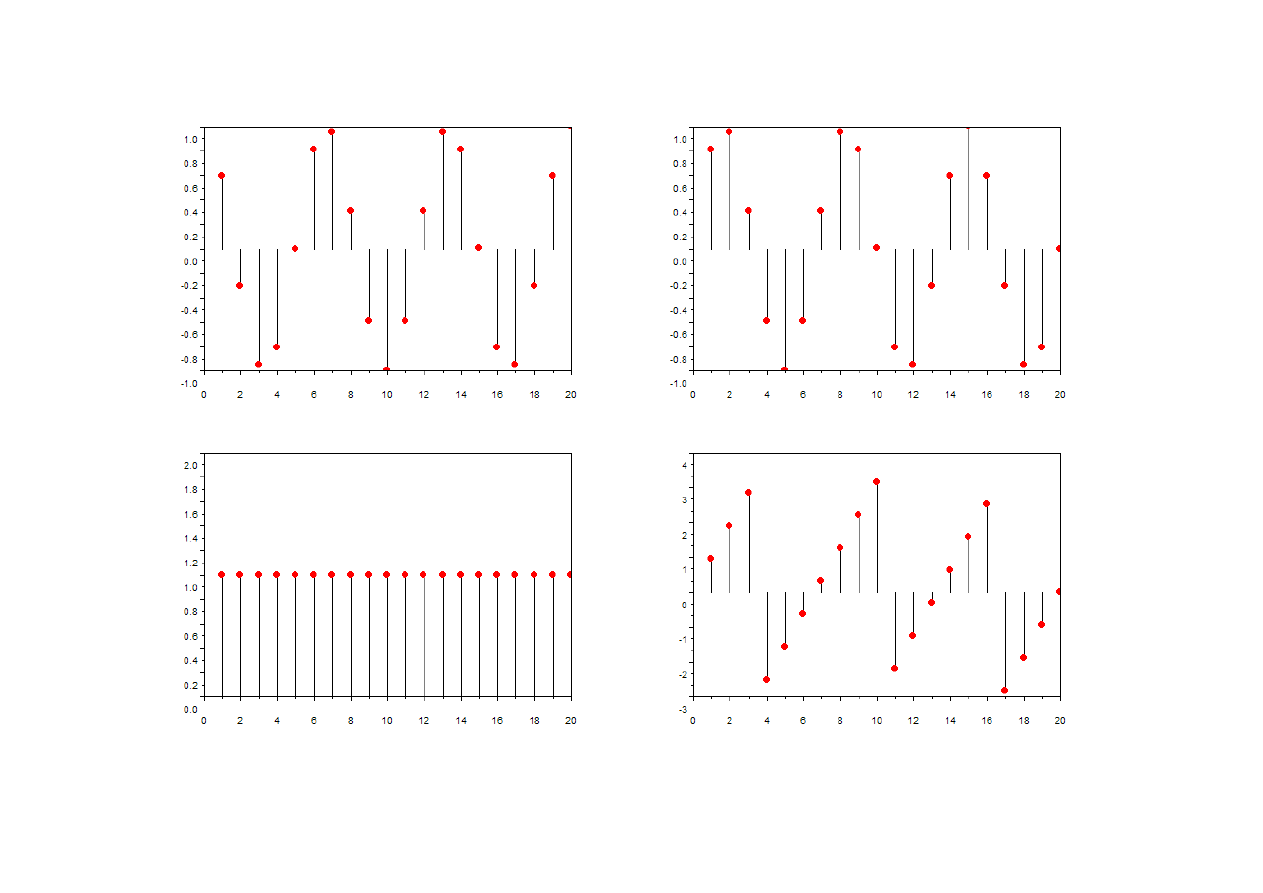
Wykresy Re(x), Im(x), Abs(x), φ(x) ciągu x[n] = exp(i·2·π·3·n/20)

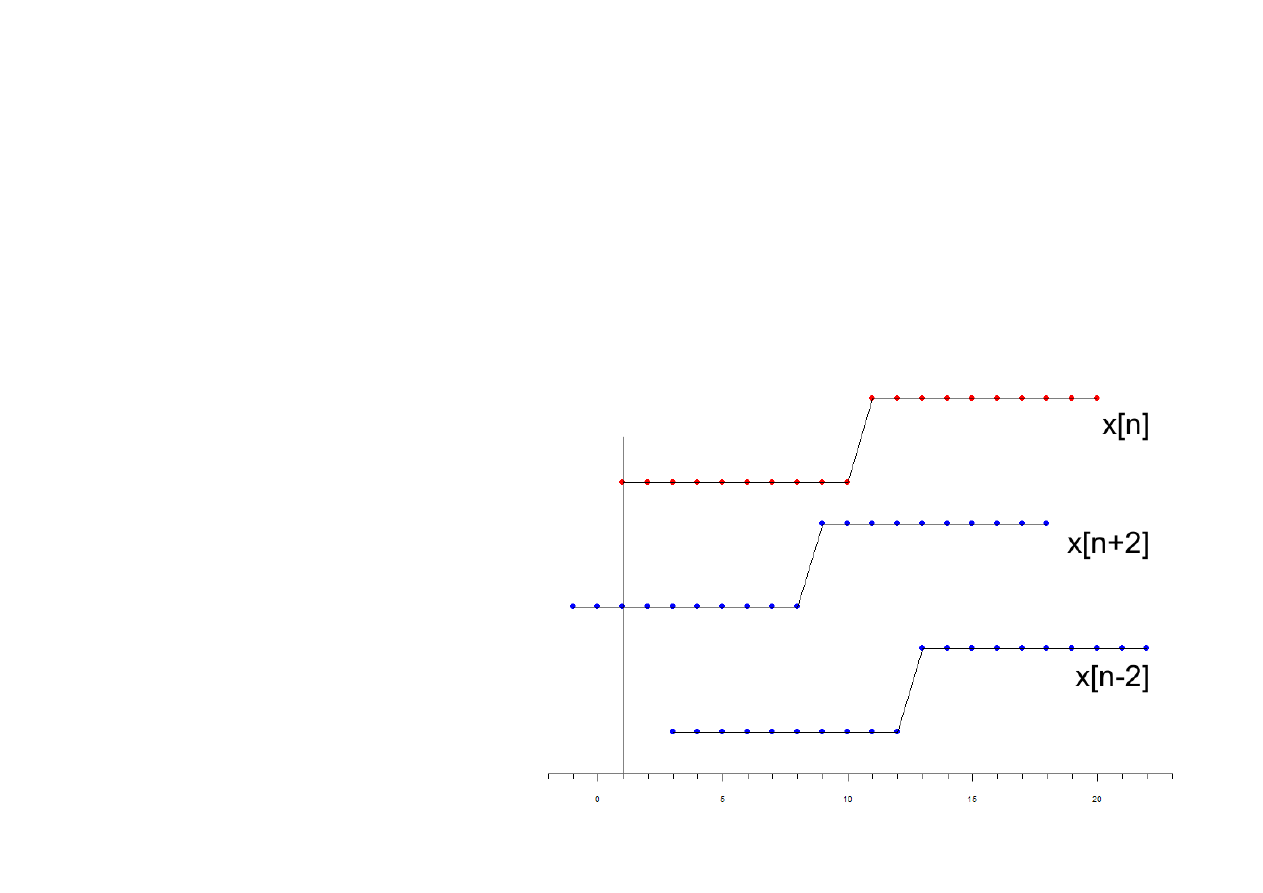
Podstawowe operacje na sygnałach czasu dyskretnego:

transformacje zmiennej niezależnej (t. czasu)

(1) Przesunięcie próbek w czasie:

Sygnał x[n] może zostać przesunięty w czasie po zamianie wartości zmiennej

n na (n-k), gdzie k jest liczbą całkowitą. Jeśli k>0, przesunięcie powoduje

opóźnienie sygnału o k-próbek,

jeśli zaś k<0 – sygnał ulega

przyspieszeniu o k-próbek.

W przypadku przetwarzania

sygnałów w czasie rzeczywis-

tym, operacja przyspieszania

podstawy czasu nie daje się

zrealizować fizycznie.

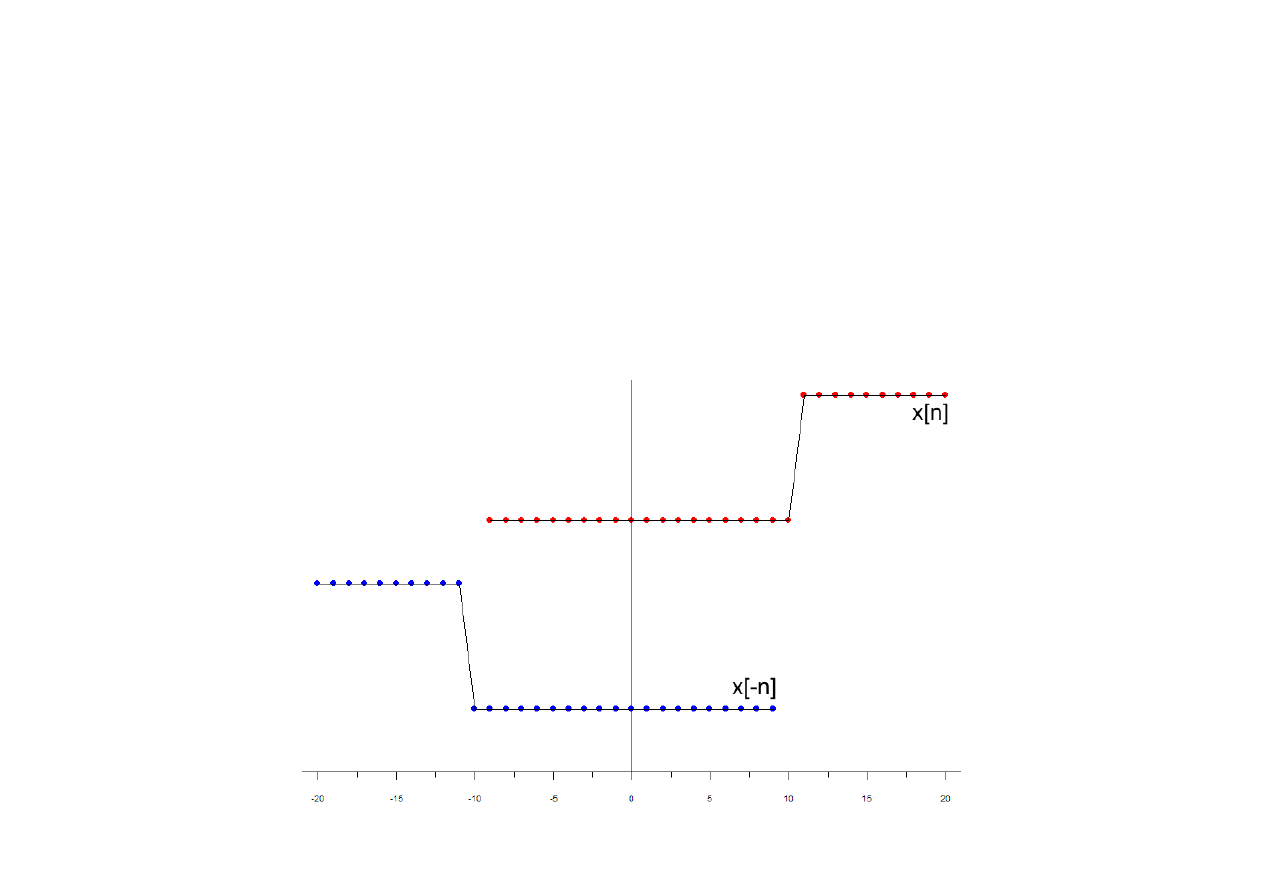
(2) Zawijanie ciągu próbek:

Zawijanie ciągu próbek (folding) polega na zamianie zmiennej n na (-n), skutkiem

czego sygnał ulega symetrycznemu odbiciu względem próbki n=0:

y [−1]= x [1] , y [0]=x [0] , y [1]= x [−1] ,...

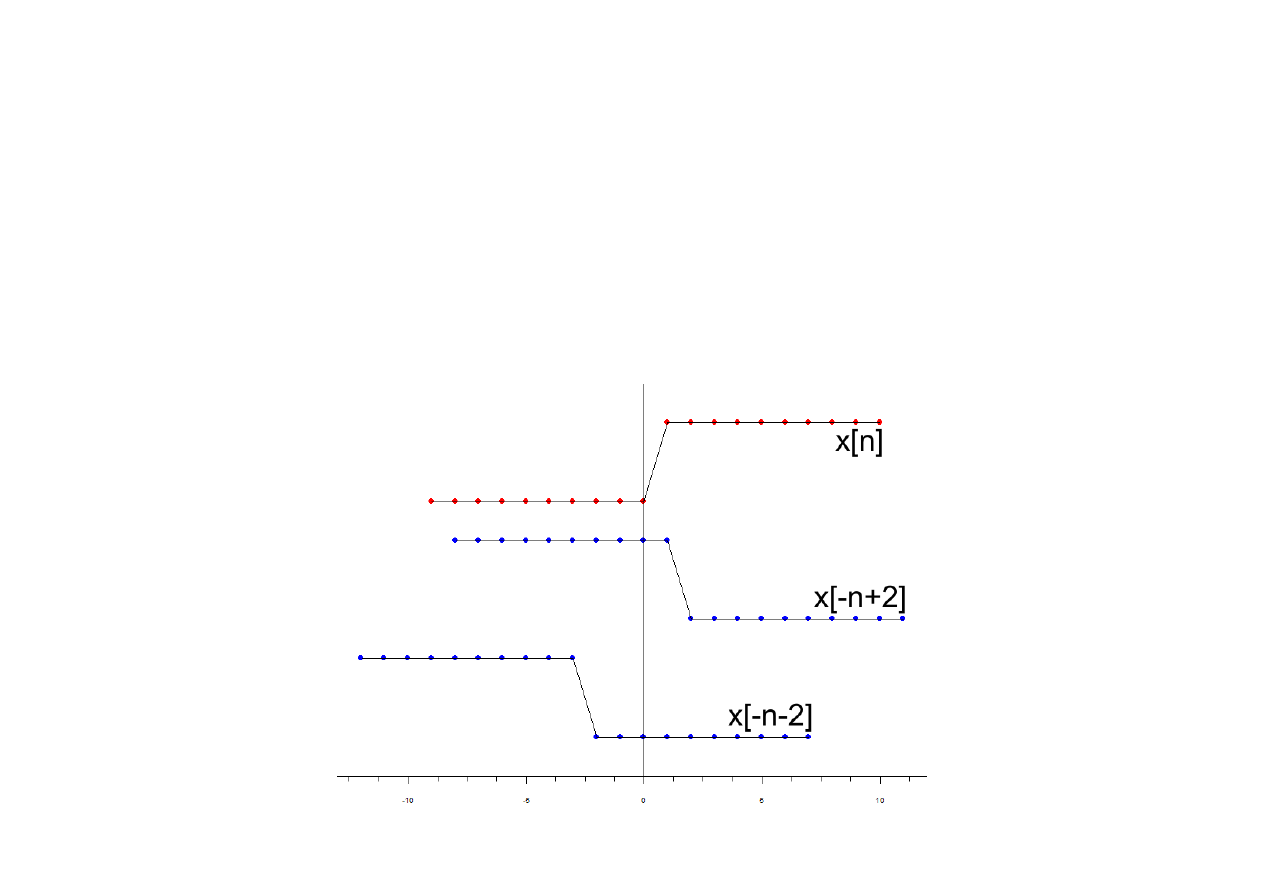
Przemienność operacji na zmiennej niezależnej

Zauważmy, iż operacje przesunięcia próbek sygnału w czasie (TS) oraz zawijania

sygnału (FD) nie są w ogólności przemienne. Zakładając, że k>0:

FDTS

k



x [n]=FD x [n−k ]= x [−nk ]

TS

k



FD x [n]=TS

k



x [−n]= x [−n−k ]

(3) Skalowanie podstawy czasu:

Skalowanie podstawy czasu powoduje zmianę częstotliwości próbkowania

sygnału, gdzie nowa częstotliwość próbkowania F

s

' dana jest jako:

F

s

' =R⋅F

s

, R∈ℤ

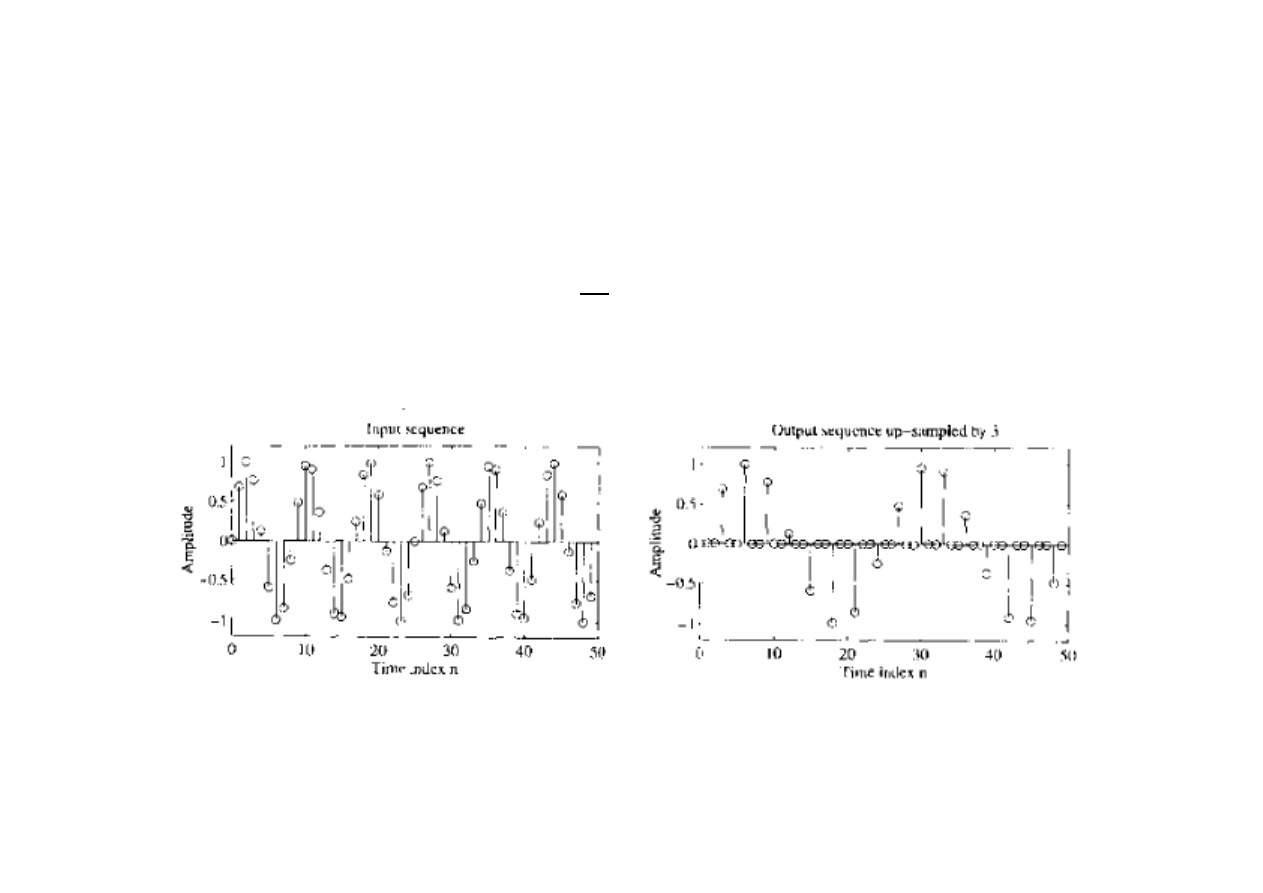
Jeśli R>1, mówimy o nadpróbkowaniu (up-sampling), kiedy to pomiędzy dwie

kolejne próbki ciągu x[n] wstawiane są (R-1) równoodległe próbki o wartościach

zero:

x

u

[

n]=

{

x

[

n

R

]

,∣n∣=0,1, 2,...

0∣n∣≠0,1, 2,...

}

Układ nadpróbkujący uzupełniony układem zamieniającym wstawiane próbki

zerowe na liniową kombinację próbek ciągu x[n] nazywa się interpolatorem.

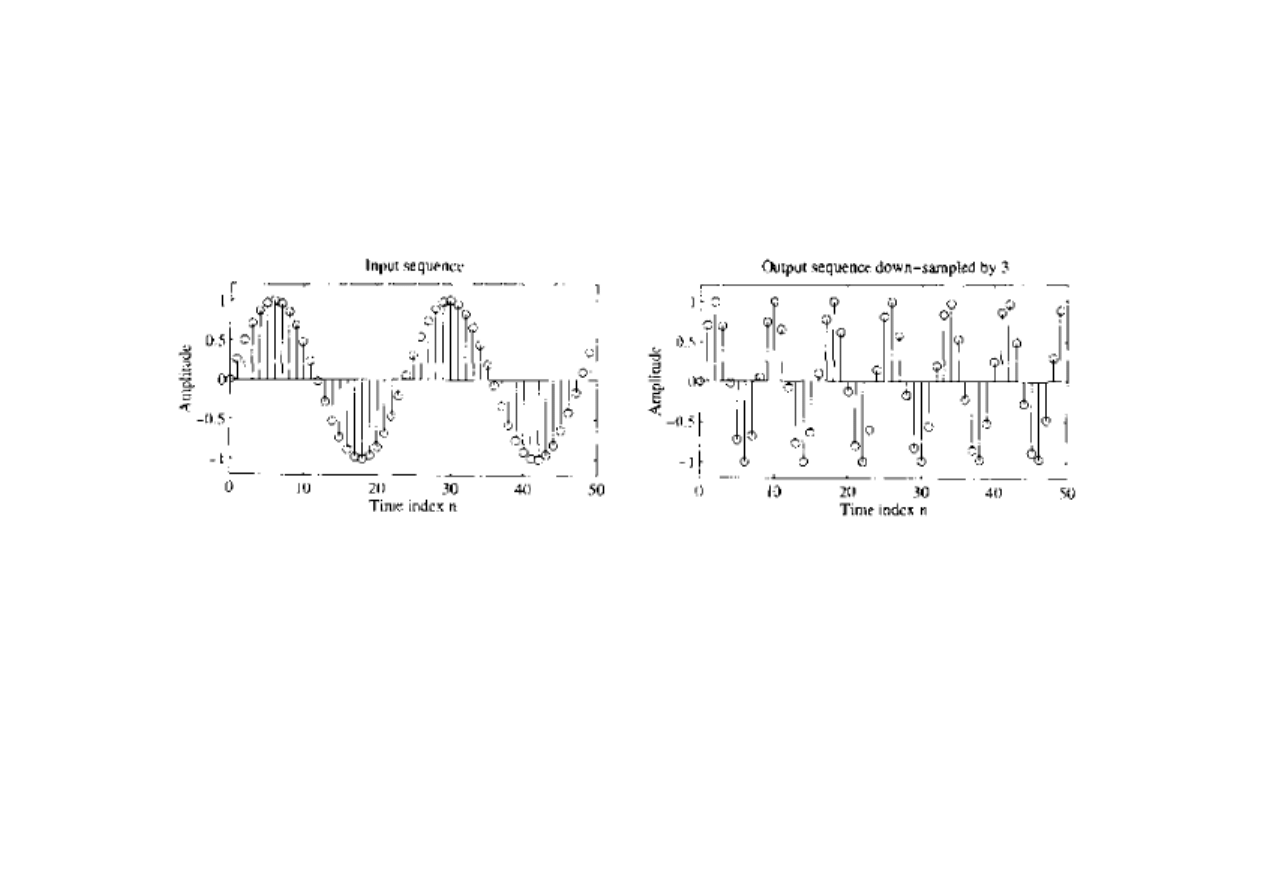
Jeśli R<1, mówimy o podpróbkowaniu (down-sampling), kiedy to z ciągu x[n]

wyjmowane są (R-1) próbki pozostawiając co R-tą próbkę oryginalną:

x

d

[

n]=x

[

n⋅R

]

Układ obniżający częstotliwość próbkowania sygnału nazywa się decymatorem.

Składa się on zwykle z modułu filtrującego, ograniczającego częstotliwość

sygnału podpróbkowanego (antyaliasing), który podaje następnie sygnał do

układu podpróbkującego.