Kolokwium I
rok 2007/2008
Zadanie 3:
Obliczyć
L
dy
y
xy
ydx
x
)
1
(
2
, jeżeli
L
jest krzywą
}
0
2
{
:
2
2
y
y
x
L
zoriento
waną
ujemnie względem swojego wnętrza.
Rozwiązanie:
:
Definicja
Całkę krzywoliniowa z funkcji
F
]
,
[
Q
P
ci
ągłej na łuku gładkim zorientowanym
,
)
(
:
t
dla
t
r
r
L
o parametryzacji zgodnej z orientacja, oznaczamy symbolem
L
P dx + Qdy
=
[ P (x(t), y(t)) · x’(t) + Q(x(t), y(t)) · y’(t))]
dt
1)
}
0
2
{
:
2
2
y
y
x
L
czyli
}
1
)
1
(
{
:
2
2
y
x
L
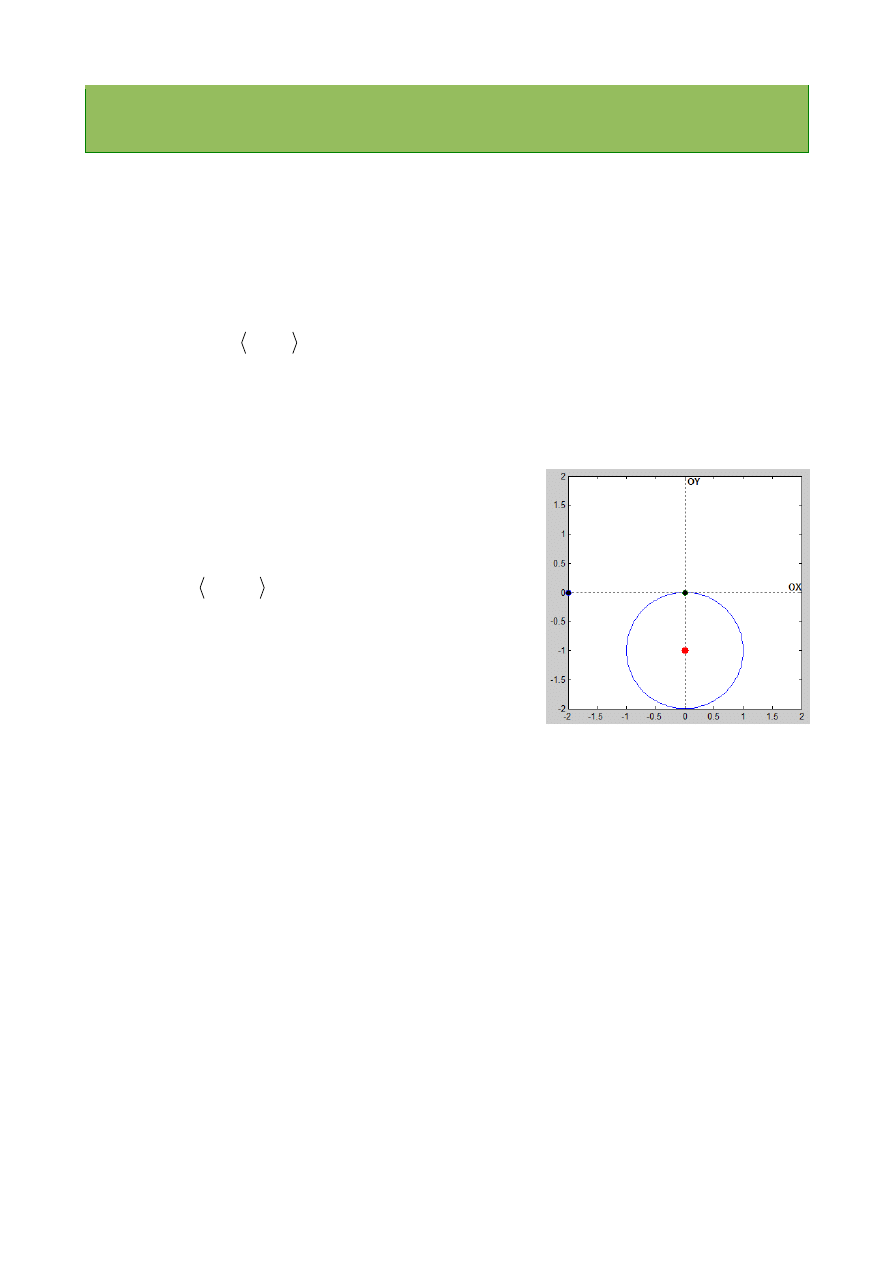
więc
L
jest okręgiem o środku
)
1
,
0
(
P
i
promieniu
1
r
. Pokzane jest to na wykresie:
2)
Paramatryzując okrąg otrzymamy:
2
;
0
1
sin
cos
t
dla
t
y
t
x
stąd:
t
y
t
x
cos
'
sin
'
3)
Podstawiając dane pod całkę obliczamy:
L
dy
y
xy
ydx
x
)
1
(
2
=
=
dt
t
t
t
t
t
t
t
)
cos
sin
)
1
(sin
cos
)
sin
)(
1
sin
(
(cos
2
0
2
=
=
dt
t
t
t
t
t
t
t
t
)
cos
sin
sin
cos
cos
sin
sin
cos
(
2
2
2
2
2
2
0
2
dt
2
0
0
0
Odpowiedź:
L
dy
y
xy
ydx
x
)
1
(
2
=
0
.
Autor: Dagmara Klos grupa 2
24.10.2013