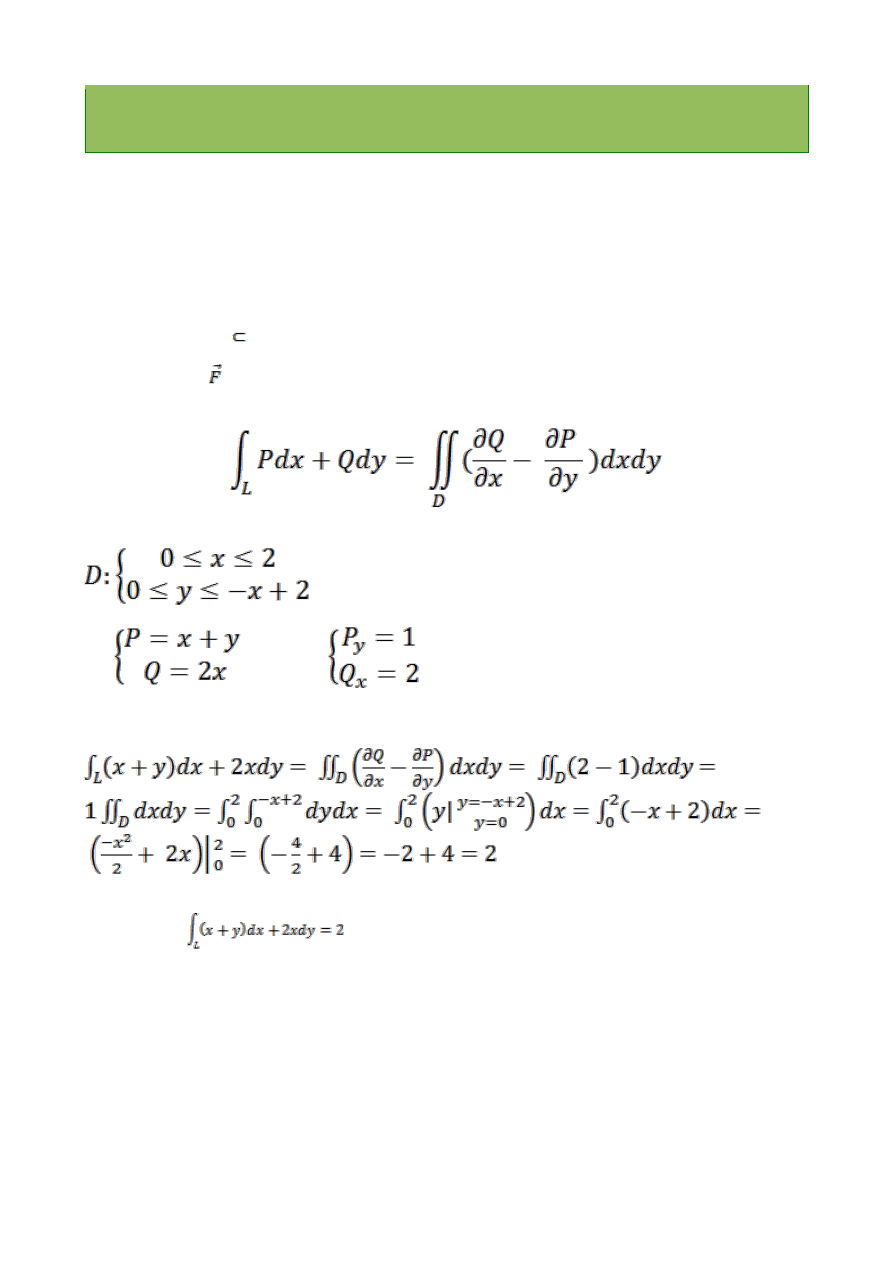
Kolokwium I 

 

 

 

 

 

 

 

 

rok 2007/2008

 

 

 

Zadanie 4:  

a) Podać twierdzenie Greena 

b) Korzystając z twierdzenia Greena obliczyć ∫

L

(x+y)dx+2xdy, jeżeli L jest trójkątem o wierzchołkach 

A(0,0), B(2,0), C(0,2) zorientowanym dodatnio względem swojego wnętrza.  

 
 

Rozwiązanie: 

 

a) Załóżmy, że: 

- obszar domknięty 

D R

2 

jest normalny względem o obu osi układu,

 

- brzeg L obszaru D jest łukiem zorientowanym dodatnio, 
- pole wektorowe 

=[P, Q]

 jest różniczkowalny w sposób ciągły na D.

 

 

Wówczas:  

 

 

b)   

                     

 

        

 

 
 
 

 

 

Odpowiedź:

  

 

 
 

 

Autor: Monika Ruchniewicz  grupa 10 

 

24.10.2013