1

Badaniem statystycznym nazywamy ogół prac mających na celu poznanie danego zjawiska i prawidłowości nim

rządzących. Badaniu podlegają zjawiska masowe czyli zjawiska, które badane w dużej ilości pojedynczych przypadków
wykazuje właściwą sobie prawidłowość, jakiej nie można zaobserwować przy analizie pojedynczego przypadku.

Etapy badania:
1. Przygotowanie badania statystycznego.
2. Zebranie materiału.
3. Opracowanie zebranego materiału.
4. Graficzne przedstawienie wyników.

Ad. 1:



Określenie celu badania.



Określenie przedmiotu badania.
Przedmiotem badania jest zbiorowość statystyczna (populacja generalna). Zbiorowością statystyczną nazywamy zbiór

elementów (osób, przedmiotów, faktów) podobnych pod względem określonych cech (lecz nie identycznych). Populacja
składa się z jednostek statystycznych. Jednostką statystyczną jest poszczególny element zbiorowości statystycznej mający te
same cechy stałe.
Cechy stałe dzielimy na rzeczowe (strukturalne) – określają kto lub co jest przedmiotem badania, przestrzenne – określają
gdzie odbywa się badanie, czasowe – określają jaki jest okres objęty badaniem lub w jakiej chwili się ono odbywa.



Określenie zakresu badania.
Zakres badania to zespół cech, które charakteryzują badane jednostki.

Cechami statystycznymi nazywamy własności, którymi odznaczają się jednostki wchodzące w skład badanej

zbiorowości.
Cechy zmienne ustalamy w zakresie badania (dzielą się one tak jak stałe).

Wyróżniamy cechy:

a. mierzalne (ilościowe) – dające się wyrazić za pomocą liczb- np. waga, wzrost, wysokość zarobków;
b. niemierzalne (jakościowe) – nie można ich wyrazić liczbowo – np. płeć, wykształcenie.

Cechy mierzalne dzielą się na:

a. ciągłe – mogą w zasadzie przyjąć każdą wartość z określonego skończonego przedziału (nieprzeliczalny zbiór

wartości) – np. wiek;

b. skokowe – przyjmują tylko niektóre wartości z określonego przedziału (zbiór przeliczalny lub skończony) – np.

liczba dzieci w rodzinie.

Cechy mierzalne można ująć w sposób niemierzalny – np. wzrost: niski, średni, wysoki (cecha porządkowa, quasimierzalna).
Cechy niemierzalne dzielą się na:

a. dwudzielne (2 warianty cechy – np. płeć),
b. wielodzielne (więcej niż dwa warianty cechy – np. kolor oczu.



Wybór rodzaju badania.

a. pełne – obejmuje wszystkie elementy zbiorowości generalnej – np. spisy powszechne, rejestracja zgonów, urodzeń;
b. częściowe – obejmuje pewną część elementów zbiorowości generalnej; podzbiór elementów populacji podlegających

badaniu określa się mianem próby.

Badania częściowe mają szersze zastosowanie, gdyż:

a. w przypadku populacji nieskończonej nie istnieje możliwość przeprowadzenia badania pełnego;
b. badanie statystyczne może mieć charakter niszczący;
c. w przypadku populacji skończonej ale bardzo licznej koszt badania pełnego byłby zbyt wysoki.

Ad. 2.: Zbieranie materiału statystycznego:

a. b. pełne – spisy, rejestracja bieżąca, bieżąca sprawozdawczość statystyczna;
b. b. częściowe – reprezentacyjne, monograficzne, ankietowe.

Ad. 3.: Po zebraniu materiału otrzymujemy tzw. surowy materiał statystyczny. Materiał ten podlega opracowaniu i analizie.
Analiza uzyskanych wyników idzie w trzech kierunkach:

1. analiza struktury badanego zjawiska z punktu widzenia jednej cechy;
2. analiza zmian w czasie na podstawie cech czasowych;
3. analiza zależności między cechami.

Podstawową formą prezentacji zebranego i opracowanego materiału jest szereg statystyczny. W zależności od rodzaju

cechy wg której grupujemy materiał statystyczny wyróżniamy szeregi terytorialne (przestrzenne), czasowe (dynamiczne) i
strukturalne (rzeczowe).

Podstawą analizy struktury badanego zjawiska z punktu widzenia jednej cechy jest szereg strukturalny (szczegółowy i

rozdzielczy).

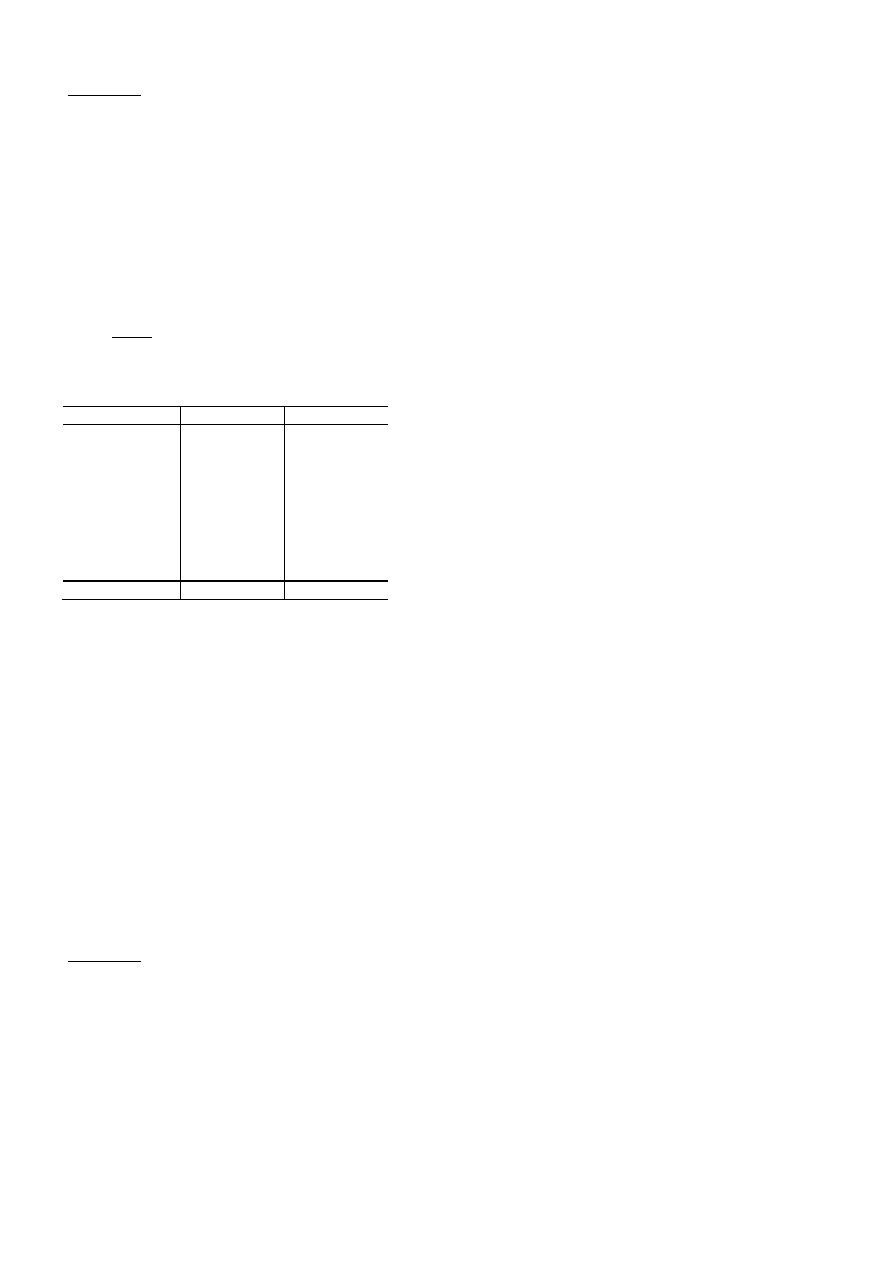
2

Przykład 1.
W grupie studentów zebrano informacje o ich wzroście (w cm). Uzyskano następujące wyniki: 175, 149, 150, 164, 150, 164,
164, 175, 170, 168, 167, 167, 150, 175, 170, 155, 166, 155, 164, 164.
Szereg szczegółowy przedstawia się następująco: 149, 150, 150, 150, 155, 155, 164, 164, 164, 164, 164, 166, 167, 167, 168,
170, 170, 175, 175, 175.

Szeregi rozdzielcze dzielimy na szeregi o klasach jednostkowych i szeregi o przedziałach klasowych.

Rozkład badanej zbiorowości wg danej zmiennej wyrażamy liczebnością poszczególnych wariantów badanej cechy

lub przy pomocy wskaźników struktury. Wskaźnikiem struktury nazywamy stosunek liczby jednostek z wyróżnionym
wariantem cechy do ogólnej liczby jednostek w danej zbiorowości.
Niech x

i

oznacza poszczególne wartości cechy (i=1, 2, ..., k) a n

i

liczbę jednostek charakteryzujących się daną wartością

cechy; n – oznacza liczebność badanej zbiorowości (







k

i

i

n

n

1

); w

i

– wskaźnik struktury dla i-tego wariantu cechy

(







k

i

i

i

i

n

n

w

1

(*100%)). Wskaźniki struktury należą do przedziału [0,1] ([0, 100%]). Suma wskaźników struktury wynosi 1

(100). W rozważanym przykładzie szereg rozdzielczy o klasach jednostkowych przyjmuje postać:

wzrost w cm - x

i

liczebność - n

i

w

i

149
150
155
164
166
167
168
170
175

1
3
2
5
1
2
1
2
3

0,05
0,15

0,1

0,25
0,05

0,1

0,05

0,1

0,15

razem

n=20

1,00

Przy badaniu cechy ciągłej możemy otrzymać, jeśli pomiary będą dostatecznie dokładne, liczbę różnych wyników

równą ogólnej liczbie pomiarów. Wtedy określenie rozkładu odbywa się poprzez przyporządkowanie liczebności (częstości)
odpowiednim przedziałom wartości cechy, a nie jej konkretnym wartościom. Takie przedziały nazywamy przedziałami
klasowymi. Różnicę między górną granicą danego przedziału a górną granicą poprzedniego przedziału nazywamy

rozpiętością przedziału i oznaczamy przez h

i

. Środek i-tego przedziału klasowego oznaczamy przez

i

o

x

i obliczmy jako

połowę sumy dolnej i górnej granicy danego przedziału. Z wielkości tej korzysta się przy różnych obliczeniach.

W kwestii ustalania rozpiętości i liczby przedziałów nie ma jednoznacznych reguł postępowania. Zwykle ustala się

je intuicyjnie w taki sposób, aby szereg rozdzielczy dawał w miarę przejrzysty obraz badanego rozkładu zbiorowości.

Przy zbyt małej liczbie przedziałów tracimy dużą liczbę informacji o badanej zbiorowości, a przy zbyt dużej liczbie

przedziałów tracimy przejrzystość danych. Przyjmuje się na ogół, że k (liczba przedziałów) nie powinno być mniejsze od 5 i
większe od 20.Przy dokładniejszym określeniu liczby przedziałów klasowych k może być pomocny warunek k



log n, gdzie n

jest liczebnością badanej zbiorowości.

Praktycznie pożądane jest, aby wszystkie przedziały klasowe były ograniczone (dotyczy to pierwszej i ostatniej

klasy), miały jednakową rozpiętość (co ułatwia analizę i prezentację rozkładu) oraz aby nie występowały (w miarę
możliwości) przedziały puste. Podział na klasy powinien być rozłączny (każda jednostka może trafić tylko do jednej klasy) i
wyczerpujący (wszystkie jednostki muszą być objęte klasyfikacją).

Przykład 2.

Zmierzono czas obsługi przy kasie sklepowej 25 klientów i uzyskano następujące wyniki (w s.): 15, 37, 34, 9, 61,

24, 56, 52, 6, 35, 21, 46, 86, 40, 74, 39, 48, 55, 73, 92, 43, 78, 67, 30, 29.

Pogrupujmy te dane w szereg rozdzielczy. Ze względu na małą liczebność zbioru danych przyjmijmy najmniejszą

polecaną liczbę klas czyli 5. Rozstęp dla danego szeregu (różnica między najdłuższym a najkrótszym czasem obsługi) wynosi
92-6=86 s., zatem 5 przedziałów o rozpiętości równej 20 s., z których pierwszy ma dolną granicę równą 0, obejmie wszystkie
obserwacje.

Zliczając jednostki w klasach przyjęto, że wszystkie przedziały w szeregu rozdzielczym są domknięte

prawostronnie.

3

Czas obsługi - x

i

Liczba klientów – n

i

Wskaźnik struktury - w

i

0-20

3

0,12

20-40

8

0,32

40-60

7

0,28

60-80

5

0,2

80-100

2

0,08

Ad. 4.: Wygodną formą prezentacji rozkładu badanej cechy jest forma graficzna.

Najbardziej popularne formy graficzne, za pomocą których przedstawia się szereg rozdzielczy to histogram,

wielobok liczebności, wielobok skumulowanych liczebności, krzywa liczebności.

Histogram to zbiór prostokątów, których podstawy wyznaczone są na osi odciętych przez poszczególne przedziały

klasowe, natomiast wysokości są określone na osi rzędnych przez liczebności odpowiadające poszczególnym przedziałom
klasowym. Histogram można też wykreślić przy użyciu częstości w

i

.

Dla danych z przykładu 2 histogram rozkładu czasu obsługi klientów wygląda następująco:

Dla szeregu rozdzielczego o klasach jednostkowych z przykładu 1 otrzymujemy następujący wykres:

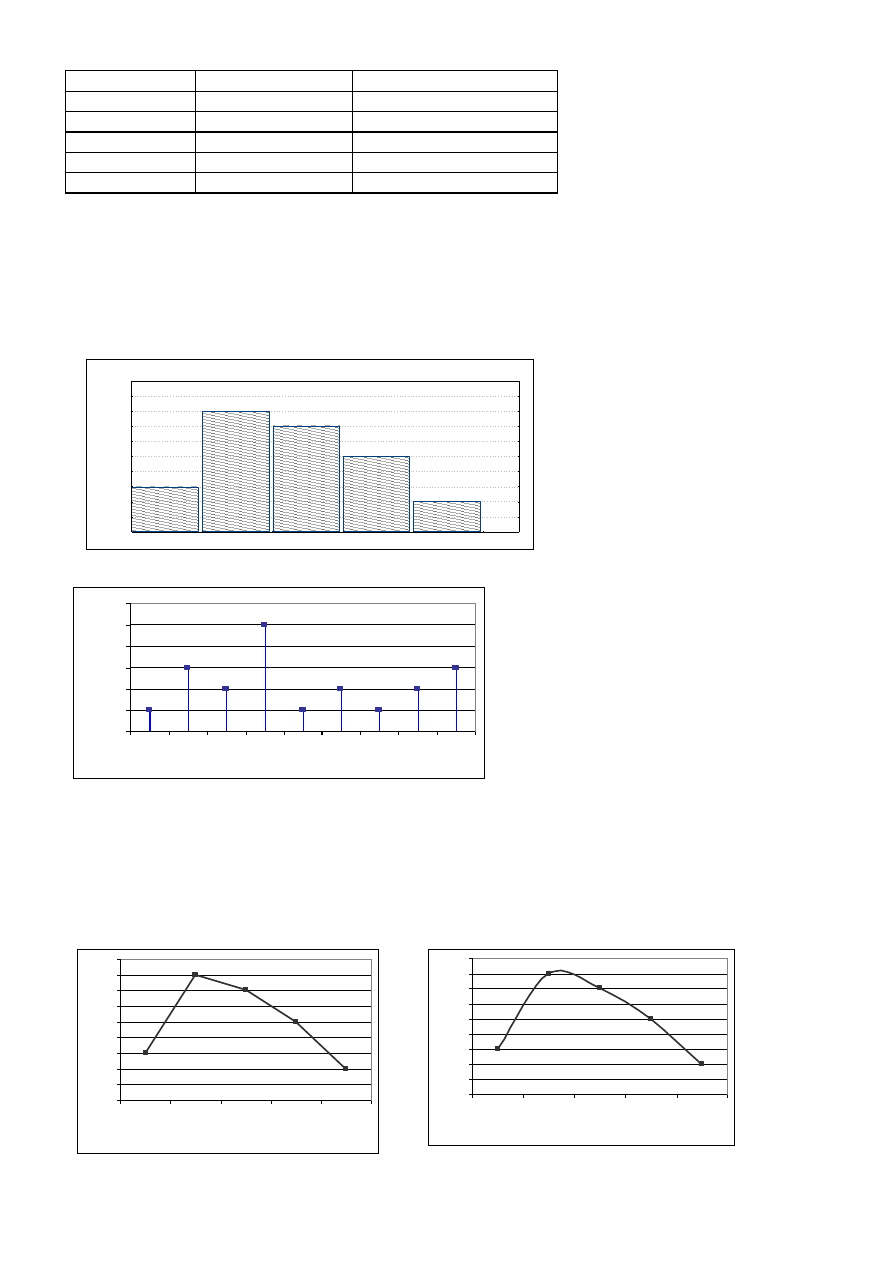
Inną formą graficznej prezentacji jest wielobok liczebności, który otrzymujemy przez połączenie punktów (

i

o

x

, n

i

)

lub (

i

o

x

, w

i

), w których odciętą jest środek i-tego przedziału, zaś rzędną liczebność (częstość) tego przedziału. Dla danych z

przykładu 2 wielobok liczebności przedstawia się następująco:

Dla zmiennej ciągłej – poprzez zmniejszenie rozpiętości przedziałów oraz zwiększenie ich liczby – możemy

otrzymać bardzo gęstą siatkę punktów wyznaczających wielobok liczebności i w konsekwencji – wygładzoną krzywą
prezentującą badany rozkład – tzw. krzywą liczebności. Schematycznie nakreślona krzywa dla danych z przykładu 2
przedstawia się następująco:

Szeregi skumulowane można przedstawić za pomocą skumulowanych histogramów lub wieloboku czy krzywej

skumulowanych liczebności (do własnoręcznego narysowania).

C

z

a

s

o

b

s

łu

g

i w

s

e

k

u

n

d

a

c

h

Liczba kl

ientów

0

1

2

3

4

5

6

7

8

9

1

0

0

2

0

4

0

6

0

8

0

1

0

0

0

1

2

3

4

5

6

149

150

155

164

166

167

168

170

175

Wzrost w cm

Li

cz

eb

no

ść

0

1

2

3

4

5

6

7

8

9

10

30

50

70

90

Czas obsługi

L

ic

zb

a

k

li

en

tó

w

0

1

2

3

4

5

6

7

8

9

10

30

50

70

90

Czas obsługi

L

ic

zb

a

kl

ie

nt

ów