
Olsztyn, 27th May, 2013
University of Warmia and Mazury in Olsztyn
Faculty of Geodesy and Land Management
Department of Satellite Geodesy and Navigation
ESSAY
Elementary rotation matrices in 3D space.
Daria Bruniecka
Geodesy and Satellite Navigation
1st year M.Sc. studies
Elementary rotation matrices in 3D space
a. Generated by modulo function
b. Prove that and check relation
( ) =
( ) =
(− ); = , ,
The elementary 3D rotation matrices are constructed to perform rotations individually about
the three coordinate axes.
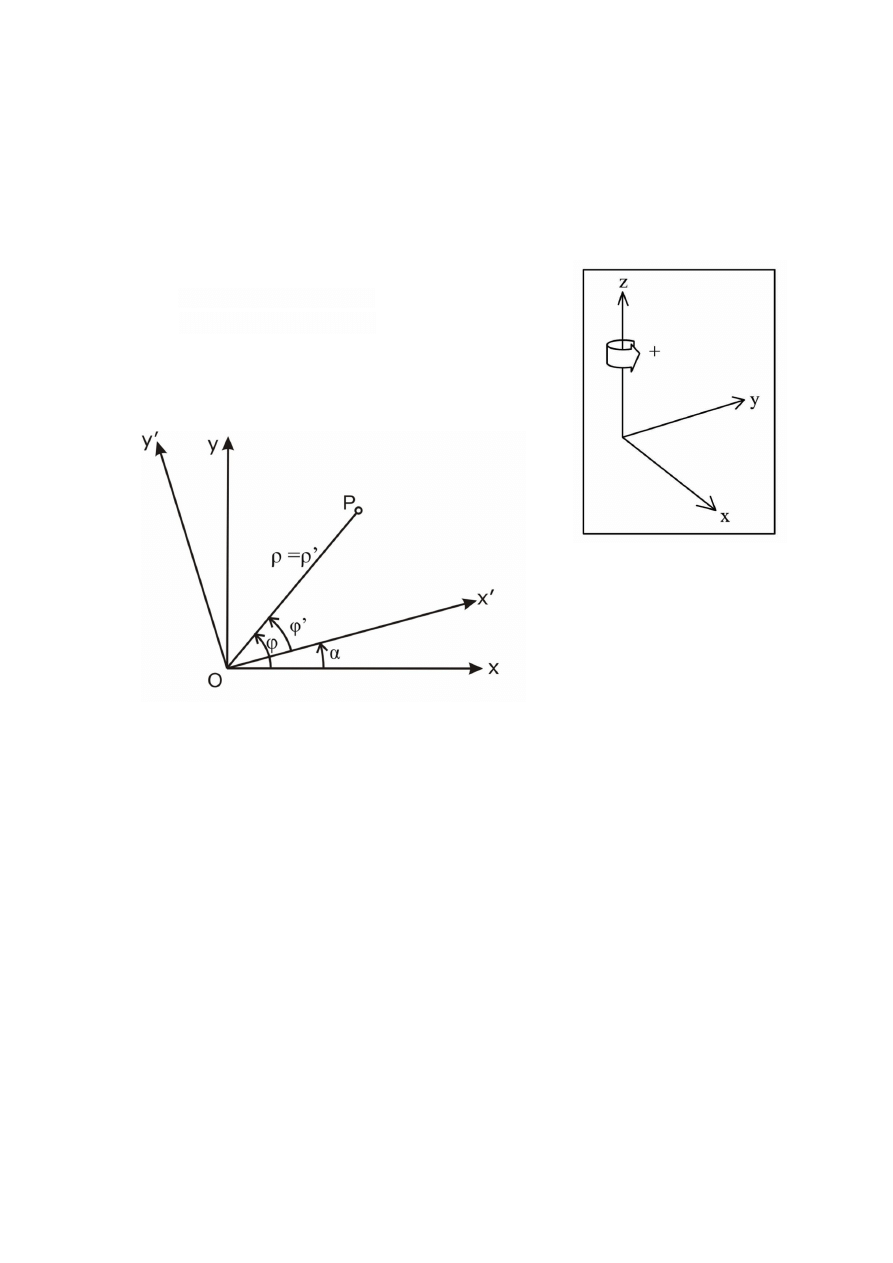
Rotation about
z-axis
(x, y, z = 1,2,3)
'
'
Z = Z’
- the angle of elementary rotation about z-axis
From Oxyz to Ox’y’z’ we have R
3
(+
)
From Ox’y’z’ to Oxyz we have R
3
(-
)
From above figure we have:
z
z
y
x
'
'
sin
'
'
cos
'
'
sin
cos
z
z
y
x
We calculate:
sin
cos
sin
sin
cos
cos
)
sin
sin
cos
(cos
)
cos(
'
cos
'
y
x
x
Therefore:
0
sin
cos
'
z
y
x
x
sin
cos
cos
sin
)
sin
cos
cos
(sin
)
sin(
'
sin
'
y
0
cos
sin
'
z
y
x
y
And
1
0
0
'
z
y
x
z
From the point of view of matrix calculations we have:
1
0
0
0
cos
sin
0
sin
cos
)
(
3
R
- for polar distances
- for polar angles
Analogical considerations give us:
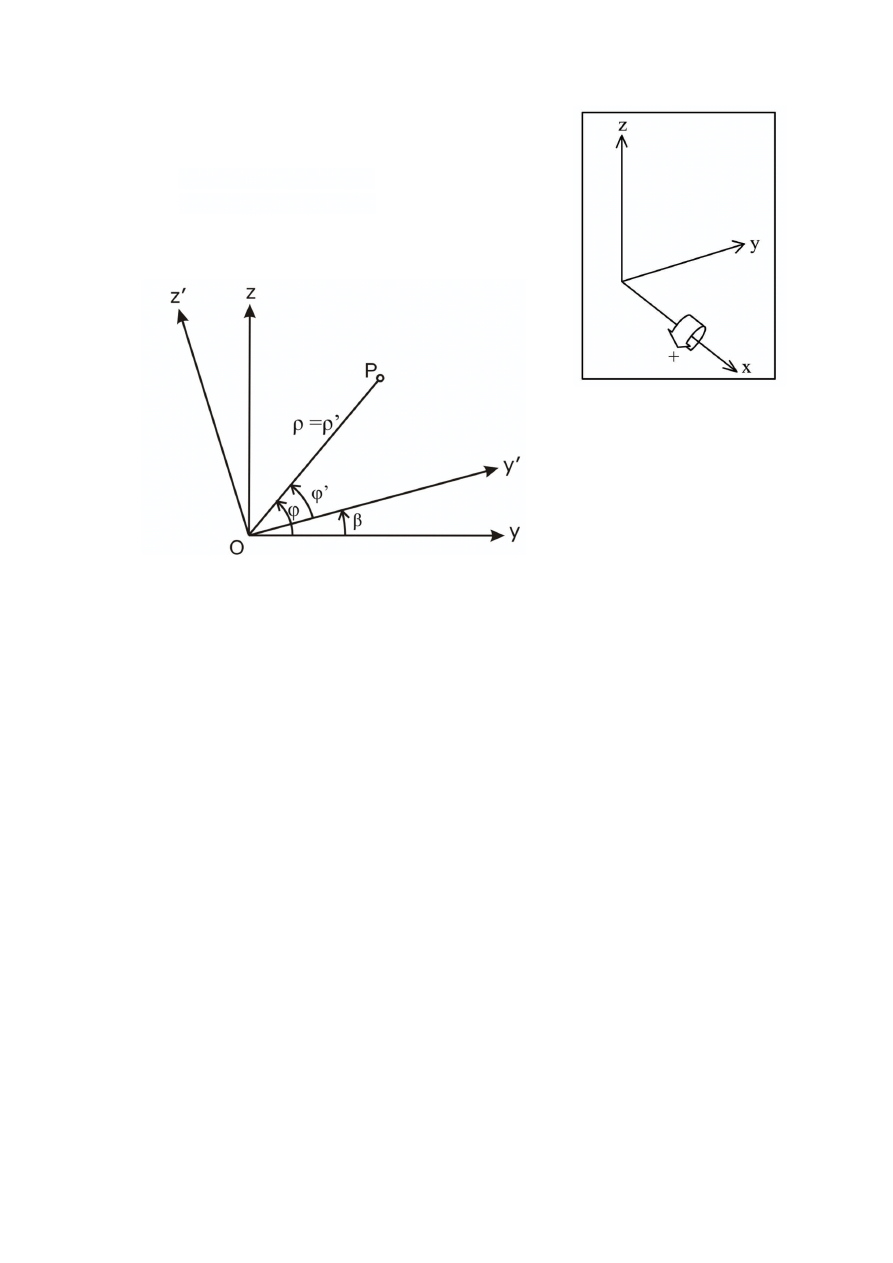
Rotation about
x-axis
(x, y, z = 1,2,3)
'
'
X = X’
- the angle of elementary rotation about x-axis
From Oxyz to Ox’y’z’ we have R
1
(+
)
From Ox’y’z’ to Oxyz we have R
1
(-
)
From above figure we have:
'
sin
'
'
cos
'
'
z
y
x
x
sin
cos
'
z
y
x
x
We calculate:
sin
sin
cos
cos
sin
sin
cos
cos
)
cos(
'
cos
'
y
Therefore:
sin
cos
0
'
z
y
x
y
And
cos
sin
0
'
sin
cos
cos
sin
)
sin
cos
cos
(sin
)
sin(
'
sin
'
z
y
x
z
z
0
0
1
'
z
y
x
x
The elementary rotation about x:
cos
sin
0
sin
cos
0
0
0
1
)
(
1
R
- for polar distances
- for polar angles
Analogical considerations give us:
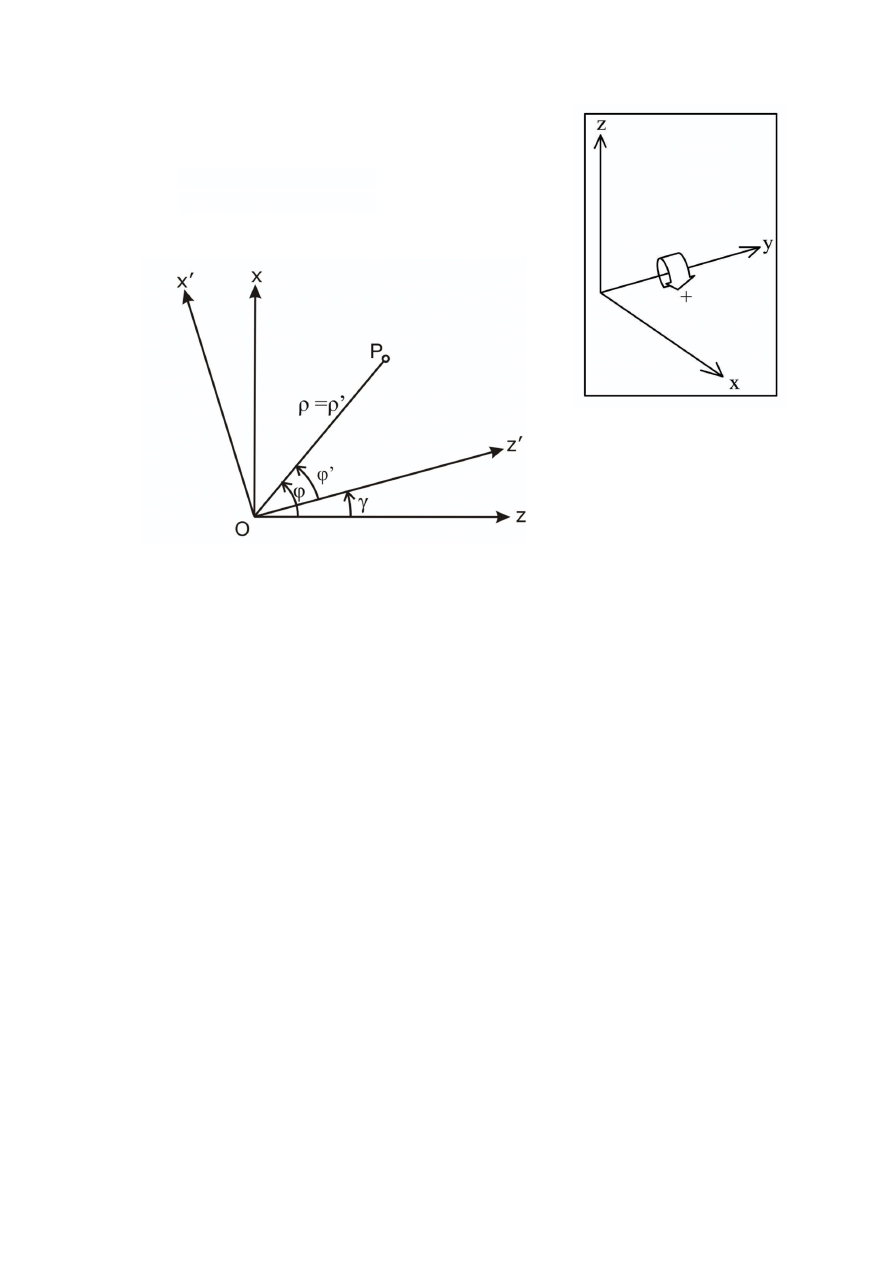
Rotation about
y-axis
(x, y, z = 1,2,3)
'
'
Y = Y’
- the angle of elementary rotation about y-axis
From Oxyz to Ox’y’z’ we have R
1
(+
)
From Ox’y’z’ to Oxyz we have R
1
(-
)
From above figure we have:
'
cos
'
'
'
sin
'
z
y
y
x
cos
'
sin
z
y
y
x
We calculate:
sin
0
cos
'
sin
cos
cos
sin
sin
cos
cos
sin
)
sin(
'
sin
'
z
y
x
x
x
cos
0
sin
'
sin
sin
cos
cos
)
sin
sin
cos
(cos
)
cos(
'
cos
'
z
y
x
z
z
And:
0
1
0
'
z
y
x
y
The elementary rotation about y:
cos
0
sin
0
1
0
sin
0
cos
)
(
2
R
- for polar distances
- for polar angles
Elementary rotation matrices in 3D space
a) Generated by modulo function
Common looking on elementary rotations:
Subroutine: (i, α, A
3x3
);
i = 1, 2, 3 = x, y, z
MOD(A,P) computes the remainder of the division of A by P
j = mod(i, 3) + 1
k = mod(j, 3) + 1
( , ) = −
, ∈
For i -th row
A (i,i)=1
A(i,j)=0
A(i,k)=0
For j -th row
A (j,i)=0
A(j,j)=
cos
A(j,k)=
sin
For k-th row
A(k,i)=0
A(k,j)= -A(j,k)
A(k,k)=A(j,j)
1) for x-azis:
i = 1
j = mod (1,3) + 1 = 2
k = mod (2,3) +1 = 3
For 1
st
(i) row:
0
)
3
,
1
(
)
,
(
0
)
2
,
1
(
)
,
(
1
)
1
,
1
(
)
,
(
A
k
i
A
A
j
i
A
A
i
i
A
For 2
nd
(j) row:
sin
)
3
,
2
(
)
,
(
cos
)
2
,
2
(
)
,
(
0
)
1
,
2
(
)
,
(
A
k
j
A
A
j
j
A
A
i
j
A
For 3
rd
(k) row:
cos
)
2
,
2
(
)
3
,
3
(
)
,
(
)
,
(
sin
)
3
,
2
(
)
2
,
3
(
)
,
(
)
,
(
0
)
1
,
3
(
)
,
(
A
A
j
j
A
k
k
A
A
A
k
j
A
j
k
A
A
i
k
A
cos
sin
0
sin
cos
0
0
0
1
)
(
1
R
given (input)
output

2) for y-azis:
i = 2
j = mod (2,3) + 1 = 3
k = mod (3,3) +1 = 1
For 1
st
(k) row:
sin
)
1
,
3
(
)
3
,
1
(
)
,
(
)
,
(
0
)
2
,
1
(
)
,
(
cos
)
3
,
3
(
)
1
,
1
(
)
,
(
)
,
(
A
A
k
j
A
j
k
A
A
i
k
A
A
A
j
j
A
k
k
A
For 2
nd
(i) row:
0
)
3
,
2
(
)
,
(
1
)
2
,
2
(
)
,
(
0
)
1
,
2
(
)
,
(
A
j
i
A
A
i
i
A
A
k
i
A
For 3
rd
(j) row:
cos
)
3
,
3
(
)
,
(
0
)
2
,
3
(
)
,
(
sin
)
1
,
3
(
)
,
(
A
j
j
A
A
i
j
A
A
k
j
A
cos
0
sin
0
1
0
sin
0
cos
)
(
2
R
3) for z-azis:
i = 3
j = mod (3,3) + 1 = 1
k = mod (1,3) +1 = 2
For 1
st
(j) row:
0
)
3
,
1
(
)
,
(
sin
)
2
,
1
(
)
,
(
cos
)
1
,
1
(
)
,
(
A
i
j
A
A
k
j
A
A
j
j
A
For 2
nd
(k) row:
0
)
3
,
2
(
)
,
(
cos
)
1
,
1
(
)
2
,
2
(
)
,
(
)
,
(
sin
)
2
,
1
(
)
1
,
2
(
)
,
(
)
,
(
A
i
k
A
A
A
j
j
A
k
k
A
A
A
k
j
A
j
k
A
For 3
rd
(i) row:
1
)
3
,
3
(
)
,
(
0
)
2
,
3
(
)
,
(
0
)
1
,
3
(
)
,
(
A
i
i
A
A
k
i
A
A
j
i
A
1
0
0
0
cos
sin
0
sin
cos
)
(
3
R

Elementary rotation matrices in 3D space
b) Prove that and check relation
( ) =
( ) =
(− ); = , ,
For i=1, x-axis:
R
1
(+β)=
1
0
0
0
0 −
The inverse matrix:
( ) =
1
det
( )
det R
1
(+β) - determinant of a matrix
M - matrix of cofactors
det R
1
(+β)=
1
0
0
0
0 −
= cos
2
β+ sin
2
β=1
M
11
=
(−1)
−
= cos
2
β+ sin
2
β=1 M
12
=
(−1)
0
0
=0 M
13
=
(−1)
0
0 −
=0
M
21
=
(−1)
3
0
0
−
=0 M
22
= (−1)
4
1
0
0
=cos M
23
=
(−1)
5
1
0
0 −
=sinβ
M
31
=
(−1)
0
0
=0 M
32
=
(−1)
5
1
0
0
= −sinβ M
33
=
(−1)
1
0
0
=cosβ
M=
1
0
0
0
0 −
The inverse matrix is as follows:
( ) =
1
det
( )
=
1
0
0
0
−
0
Transposed matrix is as follows:
( ) =
1
0
0
0
−
0
It is known that:
sin(− ) = − sin( ) and
cos(− ) = cos ( )
So:
(− ) =
1
0
0
0
−
0
To sum up the proof:
( ) =
( ) =
(− )

For i=2, y-axis:
R
2
(γ)=
0 −
0
1
0
0
det R
2
(γ)=
0 −
0
1
0
0
= cos
2
γ+ sin
2
γ=1
M
11
=
1
0
0
= cosγ M
12
=
0
0
=0 M
13
=
0
1
0
= −
M
21
=
0 −
0
=0 M
22
=
−
= 1 M
23
=
0
0
=0
M
31
=
0
−
1
0
=sinγ M
32
=
−
0
0
=0 M
33
=
0
0
1
=cosγ
M=
0 −
0
1
0
0
( ) =
1
det
( )
=
0
0
1
0
−
0
( ) =
0
0
1
0
−
0
(− ) =
0
0
1
0
−
0
To sum up the proof:
( ) =
( ) =
(− )

For i=3, z-axis:
R
3
(α)=
0
−
0
0
0
1
Det R
3
(
)=
0
−
0
0
0
1
= cos
2
α+ sin
2
α=1
M
11
=
0
0
1
= cosα M
12
=(-1)
3
−
0
0
1
=
M
13
=
−
0
0
=0
M
21
=(-1)
3
0
0
1
= −
M
22
=
0
0
1
=cos M
23
=
0
0
=0
M
31
=
0
0
=0 M
32
=
0
−
0
=0 M
33
=
−
= 1
M=
0
−
0
0
0
1
( ) =
1
det
( )
=
−
0
0
0
0
1
( ) =
−
0
0
0
0
1
(− ) =
−
0
0
0
0
1
To sum up the proof:
( ) =
( ) =
(− )
Wyszukiwarka
Podobne podstrony:
Esej Matrix rot
Esej Matrix rot
Esej o chrześcijaństwie
esej rodzina, Pedagogika, socjologia edukacji
esej z psychiatrii, PIELĘGNIARSTWO ROK 3 LICENCJAT
SKŁADANIE EWOLUCYJNEJ MOZAIKI esej
Dola ateisty esej
O zakładzie Pascala słów kilka esej
matrix, 5d , 2002 2010
Euro ratunek czy katastrofa esej id
Esej Współczesne Kierunki Wychowania
„Mądrość, która chadza w parze ze skromnością i poczuciem humoru” Esej Leszka Kołakowskiego O podróż
Esej - zaliczenie wersja robocza, ZARZĄDZANIE, Zarządzanie przedsiębiorstwem
esej manipulacja, Pedagogika, socjologia edukacji
Zasiłki w Polsce i w Wielkiej Brytanii - esej, Politologia - pliki
komunikacyjne esej, Studia, Sem 5, SEM 5 (wersja 1), Budownictwo Komunikacyjne, budownictwo komunika
esej rozwojowa film
więcej podobnych podstron