1

Prawo

Równanie

1

prawo Gaussa dla
elektryczno

ś

ci

2

prawo Gaussa dla
magnetyzmu

3

uogólnione prawo
Faradaya

4

uogólnione prawo
Ampère'a

∫

=

0

d

ε

ε

r

Q

S

E

∫

=

0

d S

B

∫

−

=

t

B

d

d

d

Φ

l

E

I

t

r

E

r

r

0

0

0

d

d

d

µ

µ

Φ

ε

ε

µ

µ

+

=

∫

l

B

Wszystkie powy

ż

sze prawa s

ą

słuszne zarówno w przypadku statycznym

(pola niezale

ż

ne od czasu) jak i w przypadku pól zale

ż

nych od czasu.

Równania Maxwella (1864)

∫

−

=

t

B

d

d

d

Φ

l

E

t

E

d

d

d

0

0

Φ

ε

µ

=

∫

l

B

Ka

ż

da zmiana w czasie pola elektrycznego wywołuje

powstanie zmiennego pola magnetycznego, które z kolei
indukuje wirowe pole elektryczne itd.
Taki ci

ą

g sprz

ęż

onych pól elektrycznych i magnetycznych

tworzy fal

ę

elektromagnetyczn

ą

.

s

m

.

8

0

0

10

9979

2

1

⋅

=

=

ε

µ

c

0

0

B

E

c

=

Pola E i B s

ą

do siebie prostopadłe i prostopadłe do

kierunku rozchodzenia si

ę

fali.

Fala poprzeczna

FALE ELEKTROMAGNETYCZNE

w pró

ż

ni:

2

2

2

2

2

1

t

B

c

x

B

z

z

∂

∂

∂

∂

=

2

2

2

2

2

1

t

E

c

x

E

y

y

∂

∂

∂

∂

=

fala elektromagnetyczna
(spolaryzowana):

2

2

2

2

2

1

t

y

x

y

∂

∂

∂

∂

v

=

struna:

Równanie falowe

2

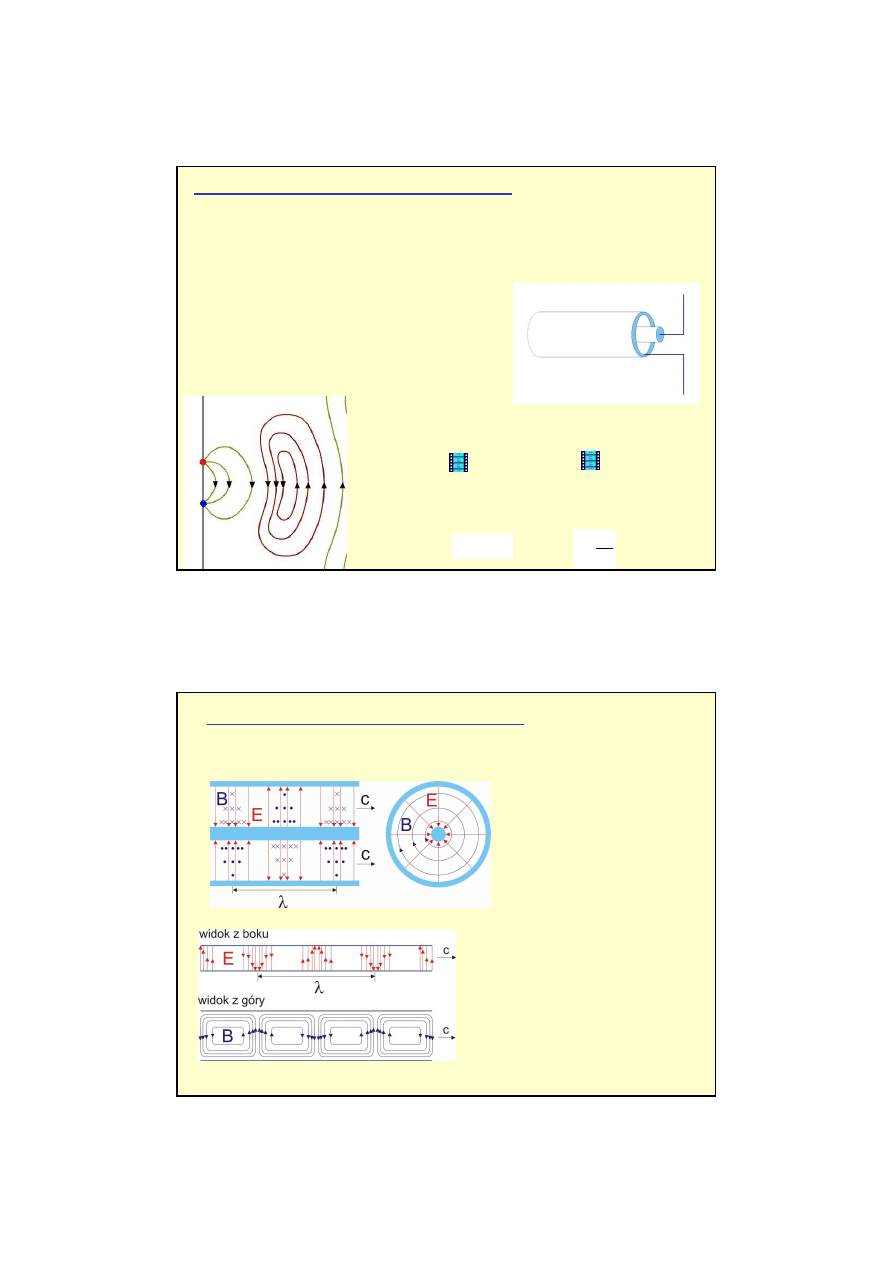
Antena słu

ż

y do wypromieniowanie energii elektromagnetycznej do otaczaj

ą

cej przestrzeni.

Je

ż

eli ró

ż

nica potencjałów pomi

ę

dzy mi

ę

dzy drutami

zmienia si

ę

sinusoidalnie to taka antena zachowuje si

ę

jak dipol elektryczny, którego moment dipolowy zmienia
si

ę

co do wielko

ś

ci jak i kierunku.

antena dipolowa

Fala elektromagnetyczna emitowana

przez drgaj

ą

cy dipol elektryczny

Energia jest wypromieniowywana przez anten

ę

w postaci fali elektromagnetycznej.

Fale elektromagnetyczne mog

ą

rozchodzi

ć

si

ę

w pró

ż

ni

λ

f

c

=

0

0

B

E

c

=

Rozchodzenie si

ę

fal elektromagnetycznych

W 1888 roku Hertz potwierdził do

ś

wiadczalnie prawdziwo

ść

istnienia hipotetycznie przyjmowanego

dot

ą

d promieniowania elektromagnetycznego, a w roku 1893 Tesla zaprezentował publicznie

eksperyment potwierdzaj

ą

cy istnienie fal radiowych.

Rozkład pola elektrycznego
i magnetycznego w kablu
koncentrycznym w danej
chwili t.

Przykładowy rozkład pól

E, B

dla

prostok

ą

tnego falowodu.

Rozkład pól nie musi by

ć

sinusoidalnie zmienny.

Rozchodzenie si

ę

fal elektromagnetycznych

3

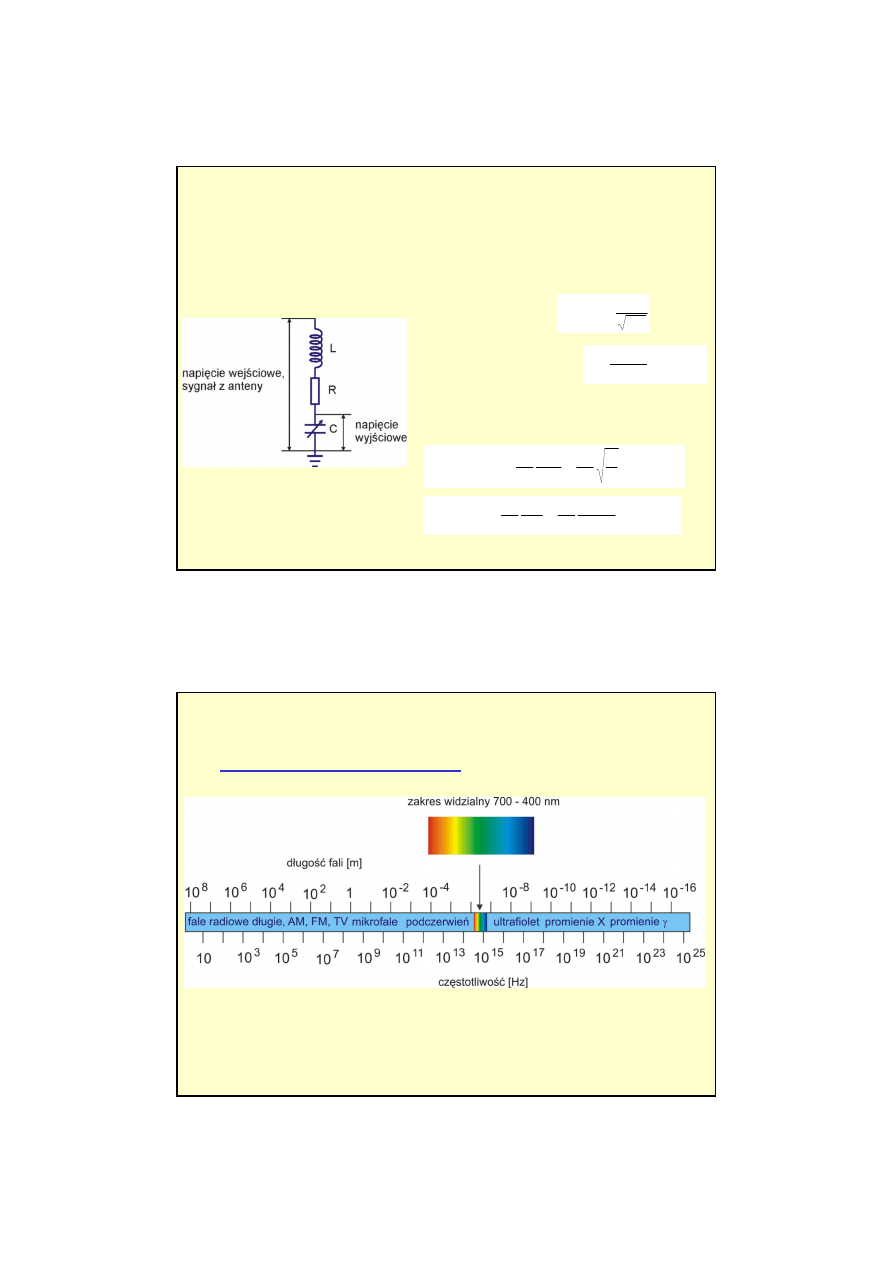
Przykład

:

Układ RLC w obwodzie wejściowym radioodbiornika (telewizora) zasilany sygnałem z

anteny. R = 10 Ω, a L = 1 µH. Szukamy pojemności C potrzebnej aby uzyskać dostrojenie
odbiornika (rezonans) do stacji nadającej z częstotliwością 101 MHz. Sygnał wejściowy z
anteny ma amplitudę 100 µV. Szukamy jakie jest napięcie na kondensatorze przy częstotliwości
rezonansowej i jakie napięcie na kondensatorze daje przy tych samych ustawieniach R, L, C
sygnał o tej samej amplitudzie ale o częstotliwości 96.0 MHz ?

warunek rezonansu

LC

1

0

=

=

ω

ω

Uwzgl

ę

dniaj

ą

c,

ż

e

ω

= 2

π

f

pF

48

.

2

4

1

2

=

=

L

f

C

π

Napi

ę

cie na kondensatorze przy

cz

ę

stotliwo

ś

ci rezonansowej (tj. gdy Z = R)

wynosi

mV

35

.

6

1

0

0

0

0

,

=

=

=

=

C

L

R

U

C

R

U

X

I

U

C

rez

C

ω

Gdy pozostawimy R, L, C, ale
zmienimy cz

ę

stotliwo

ść

f

mV

96

.

0

2

1

1

0

0

0

=

=

=

=

C

f

Z

U

C

Z

U

X

I

U

C

C

π

ω

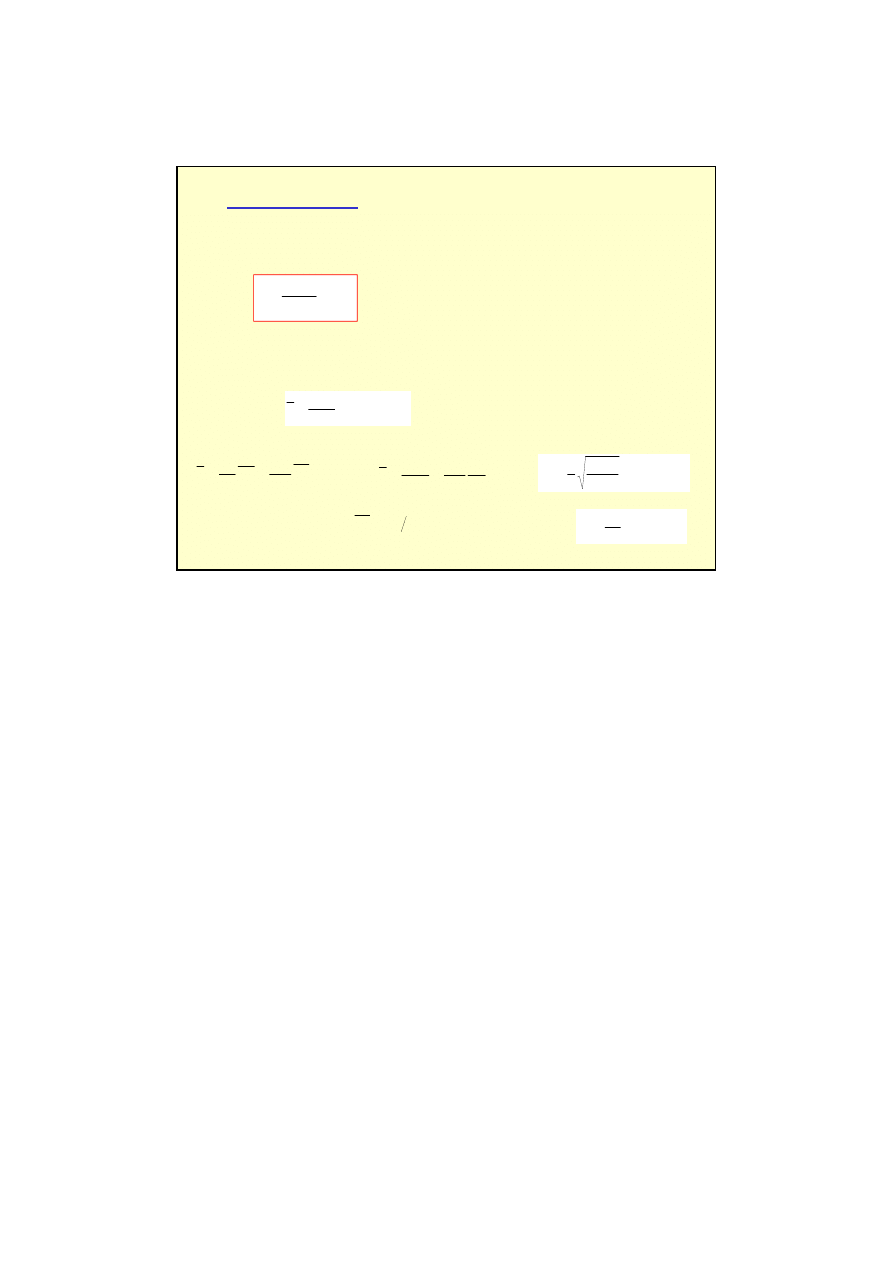
Widmo fal elektromagnetycznych

4

Szybko

ść

przepływu energii przez jednostkow

ą

powierzchni

ę

płaskiej fali

elektromagnetycznej opisujemy wektorem

S

zwanym wektorem Poyntinga

B

E

S

×

=

0

1

µ

µ

r

Kierunek wektora

S

pokazuje kierunek przenoszenia

energii. Wektory

E

i

B

s

ą

chwilowymi warto

ś

ciami pola

elektromagnetycznego w rozpatrywanym punkcie.

Przykład : Radiostacja o mocy P

0

= 30 kW wysyła fale EM izotropowo. Obliczamy nat

ęż

enie

sygnału (moc na jednostk

ę

powierzchni) w odległo

ś

ci r = 10 km od nadajnika.

ś

rednia warto

ść

wektora Poyntinga w

odległo

ś

ci r od

ź

ródła

2

2

0

m

/

µ

W

24

4

=

=

r

P

S

π

m

/

V

13

.

0

2

1

0

0

0

=

=

π

µ

cP

r

E

2

0

0

1

1

E

c

EB

S

µ

µ

=

=

cB

E

=

2

1

4

2

0

0

2

0

E

c

r

P

S

µ

π

=

=

2

2

0

2

E

E

=

fala sinusoidalna

T

10

4

10

0

0

−

⋅

=

=

c

E

B

Wektor Poyntinga