1

FUNKCJE DWÓCH ZMIENNYCH

Def.
Jeżeli każdemu punktowi (

x

,

y

) ze zbioru E

płaszczyzny 0XY przyporządkujemy pewną
liczbę rzeczywistą

z

, to mówimy, że na zbiorze E

określona została funkcja

z = f(x, y)

.

Gdy zbiór E nie jest wyraźnie podany,
sprawdzamy dla jakich par (x, y) funkcja
Z = f(x, y) ma sens, np.:

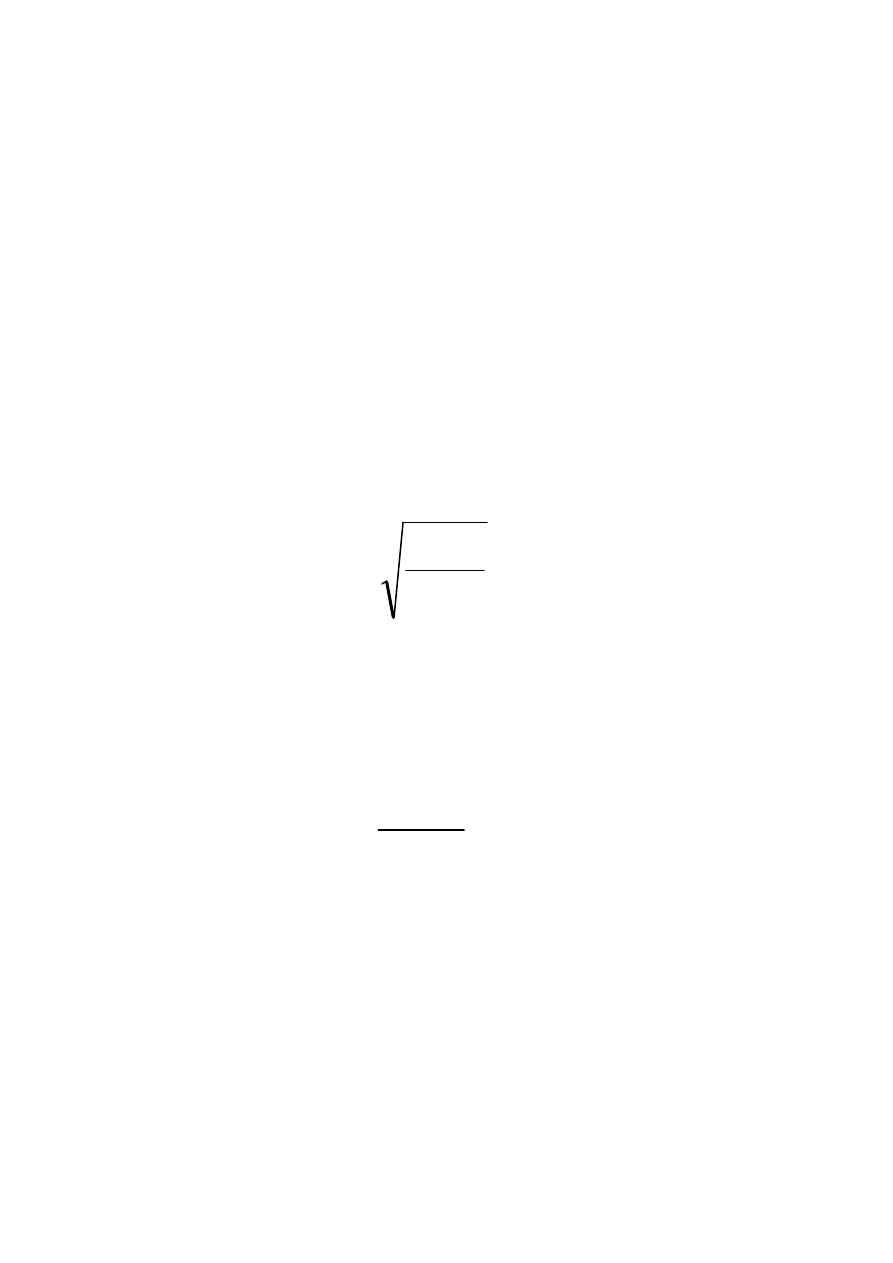
Funkcja

y

x

y

x

x

z

−

+

=

2

jest określona gdy:

1. pod pierwiastkiem jest liczba nieujemna tj.

0

≥

−

+

y

x

y

x

czyli :
(x +y)≥

≥≥≥0 i (x -y) ≥≥≥≥0 albo

(x +y)≤

≤≤≤0 i (x -y)≤≤≤≤0

2

Pole funkcji

y

x

y

x

x

z

−

+

=

2

2.wyrażenie w mianowniku jest różne od zera
tj. gdy (x -y)≠

≠≠≠0 to x≠≠≠≠y

Def.

Zbiór E to pole funkcji dwóch zmiennych,
inaczej zwany dziedziną funkcji. Jest to część
płaszczyzny.

3

Wykresem funkcji dwóch zmiennych
nazywamy zbiór W punktów w przestrzeni R

3

spełniających warunki:

(

) ( )

( )

(

)

y

x

f

z

E

y

x

z

y

x

W

,

,

:

,

,

=

∧

∈

=

Jest to zatem pewna powierzchnia w
przestrzeni R

3

.

Na przykład obrazem geometrycznym
funkcji:

( )

2

2

2

,

,

R

y

x

gdzie

y

x

z

∈

+

=

jest powierzchnia zwana paraboloidą
obrotową.

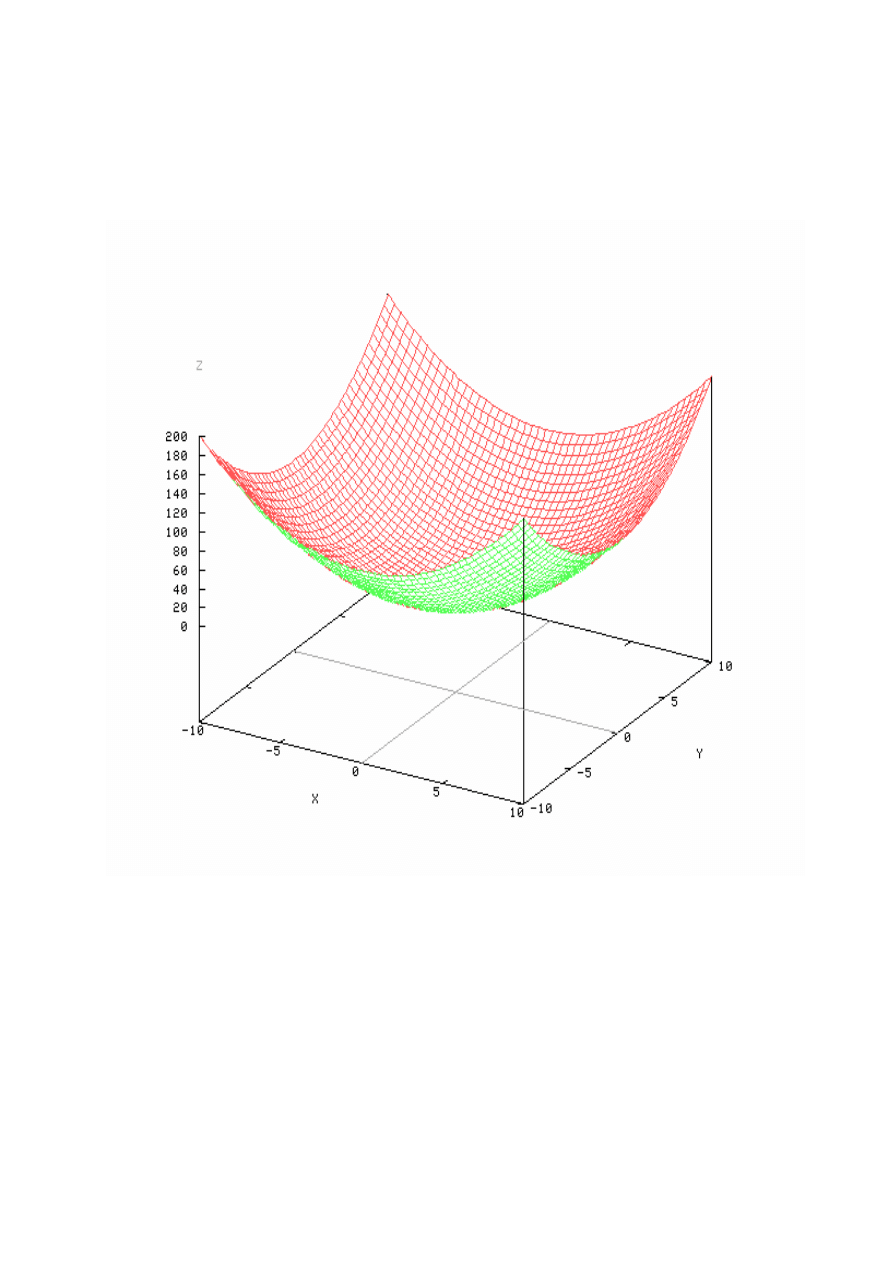
4

Paraboloida

2

2

y

x

z

+

=

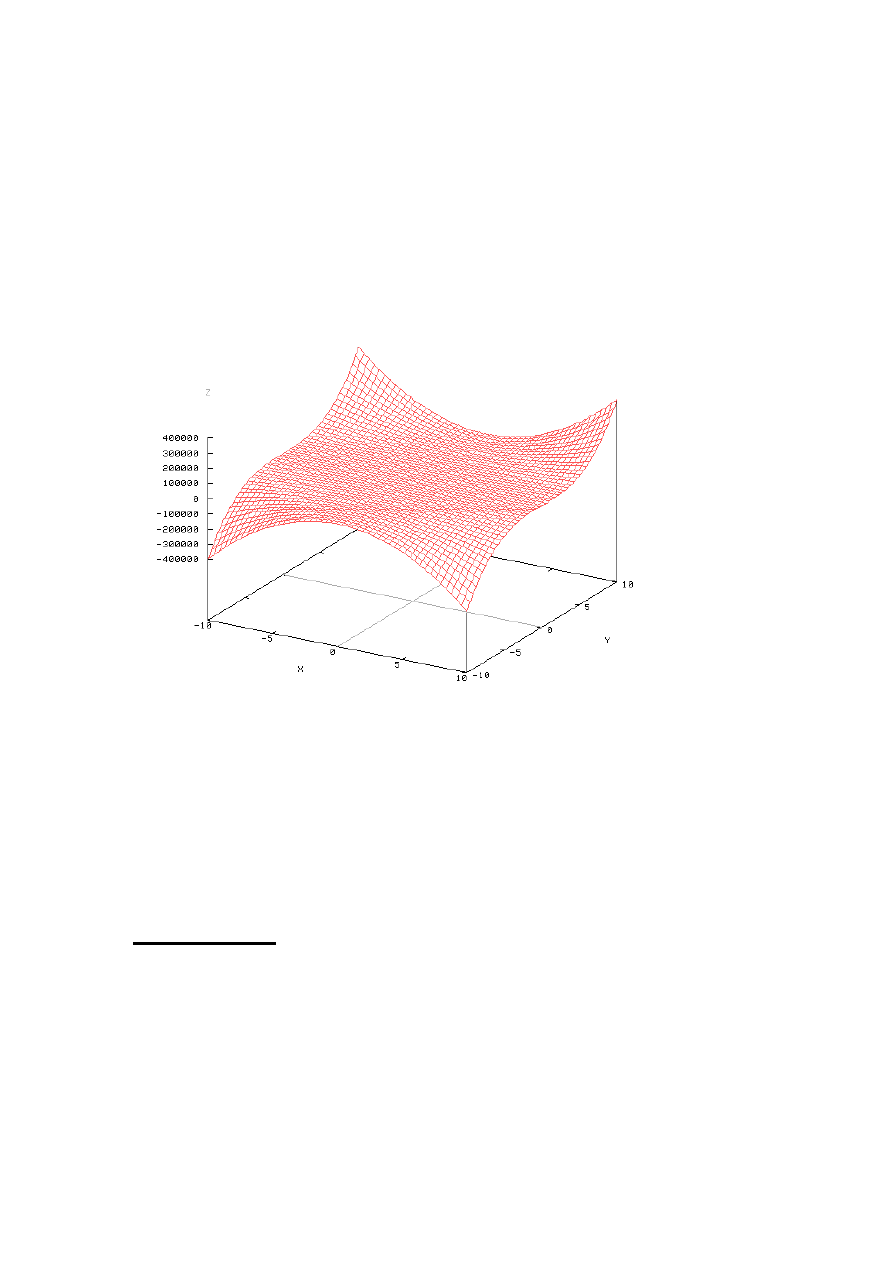
5

Funkcja potęgowa

3

2

4

y

x

z =

Def.
Rzut prostopadły na płaszczyznę OXY
przekroju powierzchni z = f(x, y) płaszczyzną
równoległą do płaszczyzny OXY nazywamy
warstwicą tej funkcji.
Jak wynika z definicji warstwice funkcji
dwóch zmiennych są pewnymi prostymi lub
krzywymi na płaszczyźnie OXY.

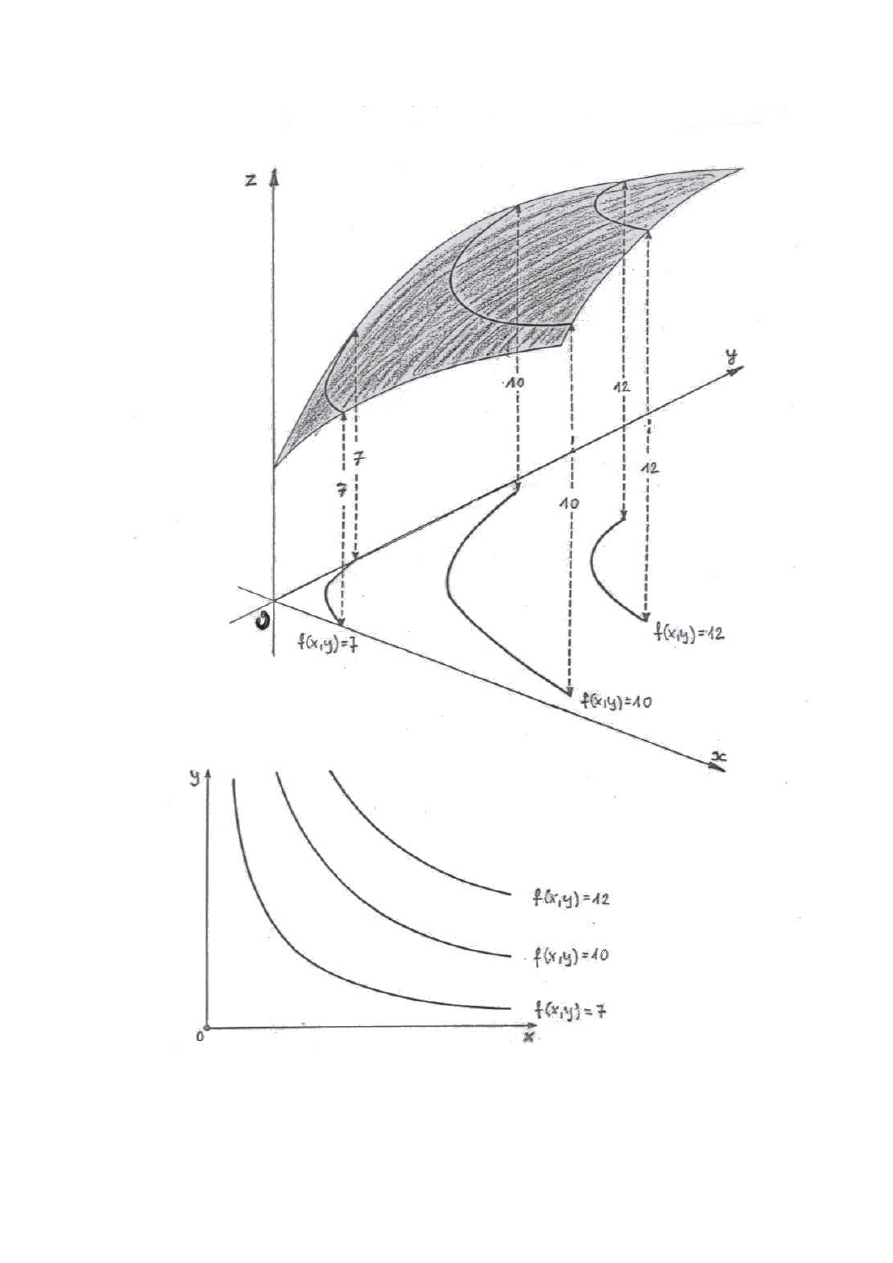
6

7

POCHODNA CZĄSTKOWA FUNKCJI

z =f(x, y)

Def.
Dana jest funkcja z= f (x, y). Zakładając, że
jedna ze zmiennych jest ustalona, np. zmienna
y=y

0

otrzymujemy w ten sposób funkcję jednej

zmiennej z=f(x, y

0

). Jeżeli funkcja f(x, y

0

)

posiada pochodną w punkcie x

0

, to pochodną tę

nazywamy pochodną cząstkową w punkcie (x

0

,

y

0

) funkcji f(x, y) względem zmiennej x i

oznaczamy przez

(

)

)

y

,

(

0

,

0

'

0

0

y)

,

(

lub

x

x

x

x

f

y

x

f

δ

δ

Analogicznie definiujemy pochodną
cząstkową względem zmiennej y f'

y

(x

0

, y

0

)

Analogicznie możemy definiować pochodną
pochodnej czyli drugą pochodną. Z tym, że w
tym przypadku mamy aż cztery pochodne
rzędu drugiego:
f´´

xx

, f´´

xy

, f´´

yx

, f´´

yy

Przykład:

8

6

3

2

+

−

+

=

y

x

y

x

z

3

1

2

2

'

'

−

=

+

=

x

f

xy

f

y

x

x

f

x

f

y

f

yx

xy

xx

2

2

0

f

2

''

''

yy

''

''

=

=

=

=

GRADIENT FUNKCJI z= f(x, y)

GRADIENTEM funkcji z nazywamy wektor,
którego składowymi są pochodne cząstkowe
rzędu pierwszego

(

)

(

)

(

)













=

0

0

'

0

,

0

'

0

0

,

,

y

x

f

y

x

f

y

x

gradf

y

x

W otoczeniu punktu (x

0

, y

0

) gradient wskazuje

kierunek w którym funkcja f wzrasta
najszybciej.
Przykład:
Wskaż kierunek najszybszego przyrostu
wartości funkcji

(

)

1

,

2

x

przy

5

6

0

0

2

3

=

=

+

−

=

y

x

xy

x

z

9

( )













−

+

−

=

2

3

15

2

5

6

,

xy

x

y

y

x

f

grad

( )













⋅

⋅

−

⋅

+

⋅

−

=

1

2

15

2

2

1

5

6

1

,

2

f

grad

( )













−

=

30

5

1

,

2

f

grad

Elastyczność cząstkowa funkcji z= f(x, y)

Elastyczności cząstkowe funkcji dwóch
zmiennych definiujemy:

( )

( )

( )

y

x

f

y

x

f

x

y

x

f

E

Ez

x

x

x

,

,

,

'

⋅

=

=

10

( )

( )

( )

y

x

f

y

x

f

y

y

x

f

E

Ez

y

y

y

,

,

,

'

⋅

=

=

Określamy w ten sposób % wzrost wartości
funkcji z= f(x, y), gdy jedna zmienna
niezależna (x lub y)wzrasta o 1%.

Przykład:
Obliczyć elastyczności cząstkowe funkcji

3

2

2

y

x

z =

3

'

4xy

z

x

=

2

2

'

6

y

x

z

y

=

stąd

3

6

2

Ez

2

4

2

2

2

3

2

y

3

3

2

=

=

=

=

y

x

y

x

y

xy

y

x

x

Ez

x

Z kolei dla funkcji

2

2

y

x

e

z

+

=

pochodne

cząstkowe i elastyczności wynoszą:

11

2

2

2

2

2

,

2

'

'

y

x

y

y

x

x

ye

z

xe

z

+

+

=

=

2

2

2

2

2

2

2

2

2

2

2

2

2

2

y

ye

e

y

Ez

x

xe

e

x

Ez

y

x

y

x

y

y

x

y

x

x

=

=

=

=

+

+

+

+

RÓśNICZKA ZUPEŁNA z= f(x, y)
Zakładamy, że funkcja z= f(x, y) jest
różniczkowalna w pewnym obszarze. Różniczki
cząstkowe tej funkcji względem zmiennej x i
zmiennej y są określone następującymi wzorami:

y

f

y

x

f

d

oraz

x

f

y

x

f

d

y

y

x

x

∆

=

∆

⋅

=

'

'

)

,

(

)

,

(

Jako, że różniczka zmiennej niezależnej jest po
prostu równa przyrostowi tej zmiennej to
powyższe wzory można zapisać:

dy

f

y

x

f

d

oraz

dx

f

y

x

f

d

y

y

x

x

'

'

)

,

(

)

,

(

=

⋅

=

Sumę różniczek cząstkowych nazywamy różniczką
zupełną funkcji f(x,y).

12

( )

dy

f

dx

f

y

x

f

d

y

x

f

d

y

x

df

y

x

y

x

'

'

)

,

(

)

,

(

,

+

⋅

=

+

=

Przykład:

Obliczyć przyrost funkcji

3

2

2

y

x

z

+

=

z

punktu (x

0

=2, y

0

=1) przy ∆x=∆y=0,01

( )

(

)

(

)

(

)

11

,

0

01

,

0

3

01

,

0

8

3

4

,

0

0

0

0

0

0

,

2

,

,

=

⋅

+

⋅

=

∆

⋅

+

∆

≈

∆

y

y

x

x

y

x

f

y

x

y

x

y

x

Przykład:
W badaniach ekonomicznych stosowana jest tzw
funkcja Cobb-Douglasa

β

α

Z

aM

D =

D- wielkość wytworzonego dochodu narodowego
M- wielkość produkcyjnego majątku trwałego
funkcjonującego w gospodarce narodowej
Z- wielkość zatrudnienia w produkcji materialnej
a, α, β- parametry (dodatnie)

średnie tempo wzrostu dochodu narodowego:

D

D

r

D

∆

=

13

ponieważ :

(

)

Z

M

f

D

,

=

to przyrost zupełny funkcji wynosi:

Z

D

M

D

D

Z

M

∆

′

+

∆

′

=

∆

β

α

α

Z

M

a

D

M

1

−

=

′

czyli:

Z

Z

aM

M

Z

aM

D

∆

+

∆

=

∆

−

−

1

1

β

α

β

α

β

α

stąd średnie tempo wzrostu dochodu narodowego
wynosi:

Z

Z

M

M

Z

aM

Z

Z

aM

M

Z

aM

D

D

∆

+

∆

=

∆

+

∆

=

∆

−

−

β

α

β

α

β

α

β

α

β

α

1

1

1

−

=

′

β

α

β

Z

M

a

D

Z

14

Uwzględniając inny zapis:

m

r

M

M =

∆

oznacza średnie tempo wzrostu produkcyjnego
majątku trwałego

Z

r

Z

Z =

∆

oznacza średnie tempo wzrostu zatrudnienia w
produkcji materialnej

średnie tempo wzrostu dochodu narodowego
wynosi:

Z

r

β

α

+

=

M

D

r

r

Na podstawie funkcji Cobb-Douglasa obliczamy
elastyczność dochodu narodowego względem
produkcyjnego majątku trwałego i zatrudnienia:

α

α

β

α

β

α

=

=

′

⋅

=

−

Z

M

a

Z

aM

M

D

D

M

ED

M

M

1

β

β

β

α

β

α

=

=

′

⋅

=

−1

Z

M

a

Z

aM

Z

D

D

Z

ED

Z

Z

15

EKSTREMA FUNKCJI DWÓCH ZMIENNYCH

Def.
F: D→ Z, D∈R

2

i (x, y)∈D

Funkcja f(x, y) ma w punkcie (x

0

, y

0

) maksimum,

jeżeli istnieje otoczenie tego punktu takie, że dla
każdego punktu (x, y) należącego do tego
otoczenia zachodzi nierówność:

( )

(

)

(

)

(

) (

)

( )

(

)

0

0

2

2

0

2

0

,

0

0

0

,

,

,

,

y

x

f

y

x

f

r

y

y

x

x

czyli

y

x

f

y

x

f

D

y

x

r

≤

⇒

≤

−

+

−

∧

∨

≤

∈

>

Def.
Funkcja f(x, y) ma w punkcie (x

0

,y

0

) minimum

jeżeli istnieje otoczenie tego punktu takie, że dla
każdego punktu (x, y) należącego do tego
otoczenia zachodzi nierówność:

16

( )

(

)

(

)

(

) (

)

( )

(

)

0

0

2

2

0

2

0

,

0

0

0

,

,

,

,

y

x

f

y

x

f

r

y

y

x

x

czyli

y

x

f

y

x

f

D

y

x

r

≥

⇒

≤

−

+

−

∧

∨

≥

∈

>

Maksima i minima funkcji to inaczej ekstrema
funkcji.
Tw. [WARUNEK KONIECZNY ISTNIENIA
EKSTREMUM]

Jeżeli funkcja F: D→Z, D∈R

2

ma w punkcie

(x

0

,y

0

)∈D ekstremum i obie pochodne cząstkowe

pierwszego rzędu, to pochodne te są w tym
punkcie równe zeru to jest:

(

)

(

)

0

,

'

0

,

'

0

0

0

0

=

=

y

x

f

i

y

x

f

y

x

Tw. [WARUNEK WYSTARCZAJACY
ISTNIENIA EKSTREMUM]

Załóżmy, że funkcja f(x, y) ma w otoczeniu punktu
(x

0

, y

0

) ciągłe pochodne cząstkowe drugiego rzędu

i oznaczmy:

17

(

)

(

)

(

)

(

)

(

)

yy

yx

xy

xx

yx

xy

yy

xx

f

f

f

f

y

x

f

y

x

f

y

x

f

y

x

f

y

x

w

=

=

⋅

−

⋅

=

,

,

,

,

,

wyrażenie W wyróżnik funkcji f
Zakładamy, że f

x

(x

0

, y

0

)=f

y

(x

0

, y

0

)=0

1

0

Jeżeli W(x

0

, y

0

)>0 i f

xx

>0 to funkcja ma w

punkcie (x

0

, y

0

) minimum.

2

0

Jeżeli W(x

0

, y

0

)>0 i f

xx

<0 to funkcja ma w

punkcie (x

0

, y

0

) maksimum

3

0

Jeżeli W(x

0

, y

0

)<0 to funkcja nie ma w punkcie

(x

0

, y

0

) ekstremum

4

0

Jeżeli W(x

0

, y

0

)=0 to funkcja może mieć lub nie

mieć w punkcie (x

0

, y

0

) ekstremum

Przykład:
Zbadać ekstrema funkcji

98

54

16

9

-4x

y)

,

(

2

2

−

−

+

−

=

y

x

y

x

f

54

18

16

8

−

−

=

′

+

−

=

′

y

f

x

f

y

x

0

=

′

=

′

y

x

f

f

18

-3

y

2

0

54

18

0

16

8

=

=

=

−

−

=

+

−

x

y

x

0

18

8

=

′′

=

′′

−

=

′′

−

=

′′

yx

xy

yy

xx

f

f

f

f

(

) ( )(

)

0

0

144

0

0

18

8

3

,

2

<

′′

>

=

⋅

−

−

−

=

−

xx

f

W

czyli funkcja f posiada w tym punkcie (2, -3)
maksimum.

19

W zastosowaniach matematyki do ekonomii
występuje problem wyznaczenia zależności
między wielkościami ekonomicznymi na przykład:
między dochodem narodowym, a inwestycjami,
popytem na dane dobro, a dochodami ludności.
Przez X określimy jedną z wielkości
ekonomicznych, a przez Y drugą oraz założymy,
że mamy odpowiednie informacje statystyczne o
tych wielkościach w ilości „n” danych.
Metoda najmniejszych kwadratów polega na
wyznaczeniu parametrów funkcji f(x), które
zapewniałyby, że suma kwadratów S odchyleń
przyjmowała wartość najmniejszą:

( )

(

)

∑

∑

=

=

−

=

=

n

i

i

i

n

i

i

x

f

y

e

S

1

2

1

2

Załóżmy, że zależność między zmiennymi ma
charakter liniowy:

b

aX

Y

+

=

Metoda najmniejszych kwadratów pozwala nam na
wyznaczenie parametrów a i b :

(

)

∑

=

−

−

=

n

i

i

i

b

ax

y

S

1

2

Jest to funkcja dwóch zmiennych a i b

20

Naszym zadaniem jest znalezienie minimum
funkcji dwóch zmiennych.
Pochodne cząstkowe funkcji S(a,b) określonej
wzorem:

(

)

∑

=

−

−

=

n

i

i

i

b

ax

y

S

1

2

wynoszą:

( )

(

) (

)

(

)

∑

∑

=

=

−

−

−

=

−

⋅

−

−

=

′

n

i

i

i

i

n

i

i

i

i

a

b

ax

y

x

x

b

ax

y

b

a

S

1

1

2

2

,

( )

(

) ( )

(

)

∑

∑

=

=

−

−

−

=

−

⋅

−

−

=

′

n

i

i

i

n

i

i

i

b

b

ax

y

b

ax

y

b

a

S

1

1

2

1

2

,

warunek konieczny na ekstremum przyjmuje
postać układu równań:

(

)

(

)

∑

∑

=

=

=

−

−

=

−

−

n

i

i

i

n

i

i

i

i

b

ax

y

b

ax

y

x

1

1

,

0

,

0

21

po przekształceniach równania przyjmują postać:

∑

∑

∑

∑

∑

=

=

=

=

=

=

+

=

+

n

i

i

n

i

i

i

n

i

i

n

i

i

n

i

i

y

nb

x

a

y

x

x

b

x

a

1

1

1

1

1

2

co daje rozwiązanie tego układu względem
zmiennych a i b:

2

1

1

2

1

1

1













−

−

=

∑

∑

∑

∑

∑

=

=

=

=

=

n

i

i

n

i

i

n

i

i

n

i

i

i

n

i

i

x

x

n

y

x

y

x

n

a

n

x

a

y

b

n

i

i

n

i

i

∑

∑

=

=

−

=

1

1

Zakładając, że:

0

2

1

1

2

≠













−

∑

∑

=

=

n

i

i

n

i

i

x

x

n

22

funkcja S może mieć ekstremum w punkcie o
współrzędnych określonych wzorami na a ib

Sprawdzimy jeszcze czy funkcja spełnia warunek
dostateczny istnienia ekstremum w tym punkcie:

(

)(

)

∑

∑

=

=

=

−

−

=

′′

n

i

n

i

i

i

i

aa

x

x

x

S

1

1

2

2

2

( )( )

n

S

n

i

bb

2

1

1

2

1

=

−

−

=

′′

∑

=

( )(

)

∑

∑

=

=

=

−

−

=

′′

n

i

n

i

i

i

ab

x

x

S

1

1

2

1

2

(

)( )

∑

∑

=

=

=

−

−

=

′′

n

i

i

n

i

i

ba

x

x

S

1

1

2

1

2

Wyróżnik:

( )



























−

=













−

⋅

=

∑

∑

∑

∑

=

=

=

=

n

i

n

i

i

i

n

i

i

n

i

i

x

x

n

x

n

x

b

a

W

1

2

1

2

2

1

1

2

4

2

2

2

,

Można udowodnić, że jeżeli x

i

(i=1, 2, 3, 4,…,n)

23

nie są wszystkie równe, (założenie to w metodzie
najmniejszych kwadratów jest spełnione), to

0

2

1

1

2

>













−

∑

∑

=

=

n

i

n

i

i

i

x

x

n

Z tego warunku wynika, że wyróżnik jest dodatni
w każdym punkcie (a, b). Jest on funkcją stałą
zmiennych a, b- jest więc dodatni w punkcie o
współrzędnych a, b wyznaczonych MNK. Zatem w
punkcie tym funkcja S ma ekstremum i jest to

minimum (

( )

0

,

>

′′

b

a

S

aa

dla każdego punktu (a, b).