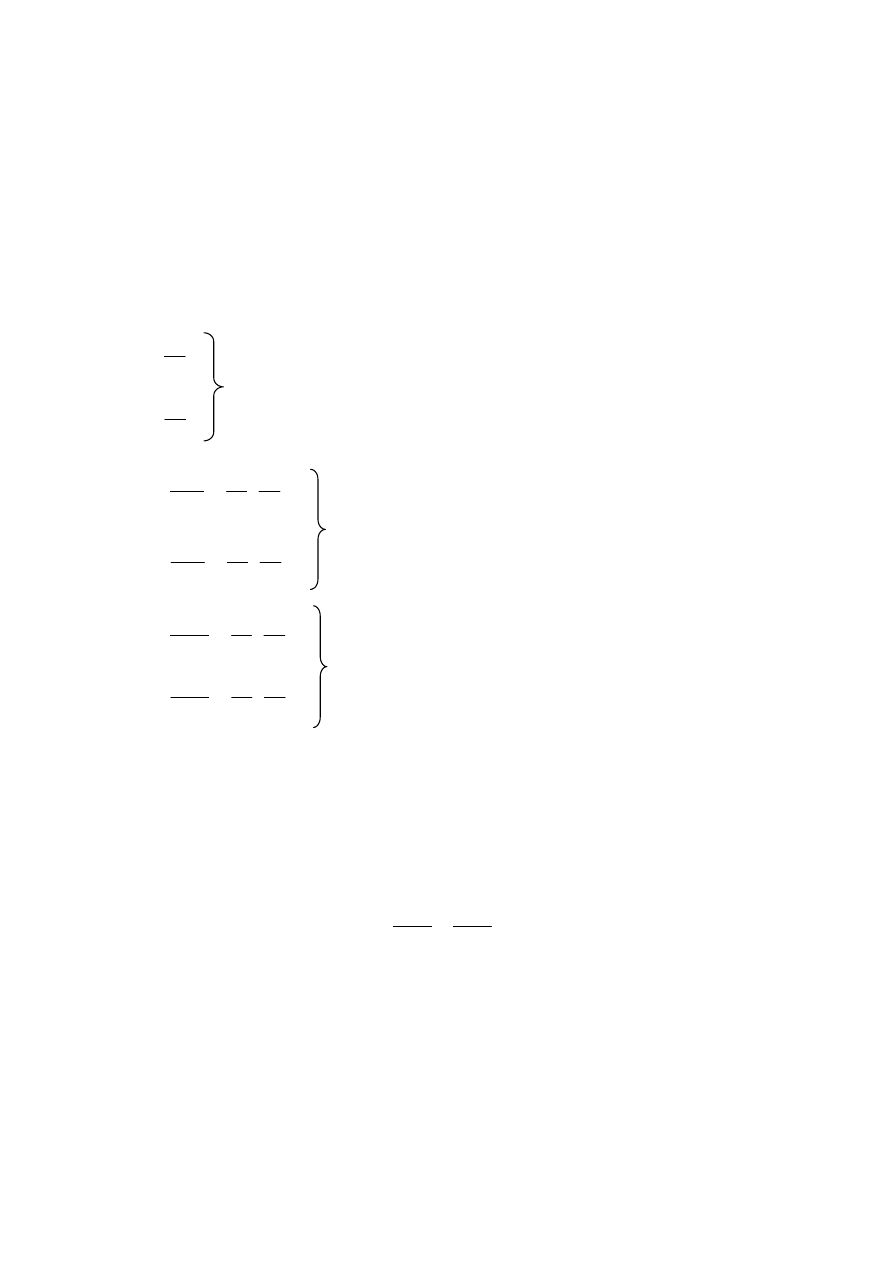
FUNKCJE DWÓCH ZMIENNYCH
POCHODNE CZĄSTKOWE
Niech
,
, gdzie
, będzie funkcją dwóch zmiennych (x,y).
( )
z
y
x
f
=
,
R
A
f
→
:
2
R
A
⊂
( )
x
f
y
x
f
x
∂
∂
=
,
'
pochodne cząstkowe rzędu 1-go
( )
y
f
y
x
f
y
∂
∂
=
,
'
( )
∂
∂
∂
∂
=
∂
∂
=
x
f
x
x
f
y
x
f
xx
2
2
''
,
czyste pochodne cząstkowe rzędu 2-go
( )
∂
∂
∂
∂
=
∂
∂
=
y
f
y
y
f
y
x
f
yy
2
2
''
,
( )
∂
∂
∂
∂
=
∂
∂
∂
=
y
f
x
y
x
f
y
x
f
xy
2
''
,
mieszane pochodne cząstkowe rzędu 2-go
( )
∂
∂
∂
∂
=
∂
∂
∂
=
x
f
y
x
y
f
y
x
f
yx
2
''
,
Twierdzenie Schwarza: Jeżeli pochodne mieszane funkcji f w punkcie (x
0
,y
0
) są ciągłe
i istnieją w pewnym otoczeniu tego punktu, to pochodne te w punkcie (x
0
,y
0
) są sobie
równe
x
y
f
y
x
f
∂
∂
∂
=
∂
∂
∂
2
2
.
Przykład:
y
x
xy
x
y
x
f
12
15
3
)
,
(
2
3
−
−
+
=
( )
15
3
3
,
2
2
'
−
+
=
y
x
y
x
f
x
,
( )
12
6
,
'
−
= xy
y
x
f
y
( )
x
y
x
f
xx
6
,
''
=
,
,
,
( )
x
y
x
f
yy
6
,
''
=
( )
y
y
x
f
xy
6
,
''
=
( )
y
y
x
f
yx
6
,
''
=
Arkadiusz Lisak
1
EKSTREMA FUNKCJI DWÓCH ZMIENNYCH
Niech funkcja f(x,y) będzie określona w pewnym obszarze D
⊂R
2
. Mówimy,
że funkcja f(x,y) ma w punkcie (x
0
,y
0
)
∈D maksimum lokalne (minimum lokalne),
jeżeli istnieje takie otoczenie S punktu (x
0
,y
0
), że dla każdego punktu (x,y) należącego
do otoczenia S spełniona jest nierówność
( )
(
0
0
,
,
y
x
f
y
x
f
≤
) ( )
(
0
0
,
,
y
x
f
y
x
f
≥
(
)
)
WARUNEK KONIECZNY
: Jeżeli funkcja dwóch zmiennych f(x,y) ma w punkcie
(x
0
,y
0
) ekstremum i ma w tym punkcie pochodne cząstkowe pierwszego rządu, to
(
)
0
,
0
0
'
=
y
x
f
x
i
(
)
0
,
0
0
'
=
y
x
f
y
Punkty (x
0
,y
0
), które spełniają powyższe warunki nazywamy punktami
stacjonarnymi.
WARUNEK WYSTARCZAJĄCY
: Jeżeli funkcja dwóch zmiennych f(x,y) ma
w pewnym otoczeniu punktu (x
0
,y
0
) ciągłe pochodne cząstkowe drugiego rzędu,
i
((x
(
)
0
,
0
0
'
=
y
x
f
x
(
)
0
,
0
0
'
=
y
x
f
y
0
,y
0
) jest punktem stacjonarnym) oraz
(
)
(
)
(
)
(
)
(
)
(
)
0
,
,
,
,
,
0
0
''
0
0
''
0
0
''
0
0
''
,
''
''
''
''
0
0
0
0
>
⋅
−
⋅
=
=
y
x
f
y
x
f
y
x
f
y
x
f
f
f
f
f
y
x
W
yx
xy
yy
xx
y
x
yy
yx
xy
xx
to f ma w punkcie (x
0
,y
0
) ekstremum lokalne.
Jeśli
W
, to powyższe kryterium nie rozstrzyga, czy funkcja f ma w punkcie
(x
(
)
0
,
0
0
=
y
x
0
,y
0
) ekstremum lokalne. Jeśli
, to funkcja f nie ma w punkcie (x
(
)
0
,
0
0
<
y
x
W
0
,y
0
)
ekstremum lokalnego.
Jeśli
>0, to f ma minimum lokalne, a jeśli
<0, to f ma maksimum
lokalne w punkcie (x
(
0
0
''
, y
x
f
xx
)
)
(
0
0
''
, y
x
f
xx
0
,y
0
).
Arkadiusz Lisak
2
Przykład: Dla funkcji
z wcześniejszego przykładu:
y
x
xy
x
y
x
f
12
15
3
)
,
(
2
3
−
−
+
=
=
=
0
0
'
'
y
x
f
f
⇔
=
−
=
−
+
0
12
6
0
15
3
3
2
2
xy
y
x
Rozwiązując ten układ otrzymamy cztery punkty stacjonarne: (1,2), (2,1), (-1,-2),
(-2,-1).
( )
( )
2
2
,
''
''
''
''
36
36
6
6
6
6
,
y
x
x
y
y
x
f
f
f
f
y
x
W
y
x
yy
yx
xy
xx
−
=
=
=
,
więc
( )
108
4
36
36
2
,
1
−
=
⋅
−
=
W
,
W
,
( )
108
36
4
36
1
,
2
=
−
⋅
=
(
)
108
4
36
36
2
,
1
−
=
⋅
−
=
−
−
W
,
W
.
(
)
108
36
4
36
1
,
2
=
−
⋅
=
−
−
Ponadto
0
12
)
1
,
2
(
''
>
=
xx
f
,
.
0
12
)
1
,
2
(
''
<
−
=
−
−
xx
f
Funkcja f ma minimum lokalne w punkcie (2,1) (
), zaś
w
punkcie (-2,-1) ma maksimum lokalne (
).
W punktach (1,2) i (-1,-2) funkcja nie ma ekstremów lokalnych.
( )
28
12
30
6
8
1
,
2
min
−
=
−
−
+
=
f
(
)
12
30
6
8
1
,
2
max
=
+
+
−
−
=
−
−
f
28
Arkadiusz Lisak
3