funkcje dwoch zmiennych

Określenie ciągu punktów na płaszczyźnie

Ciąg punktów na płaszczyźnie jest to przyporządkowanie każdej liczbie naturalnej dokładnie jednego punktu
płaszczyzny Oxy.

Ciąg punktów jest więc funkcją, której dziedziną jest zbiór liczb naturalnych N, a wartościami są punkty
płaszczyzny Oxy.

Punkt przyporządkowany liczbie naturalnej n oznaczamy zazwyczaj

i nazywamy n-tym wyrazem ciągu,

natomiast ciąg oznaczamy

 

albo





P P P

,...

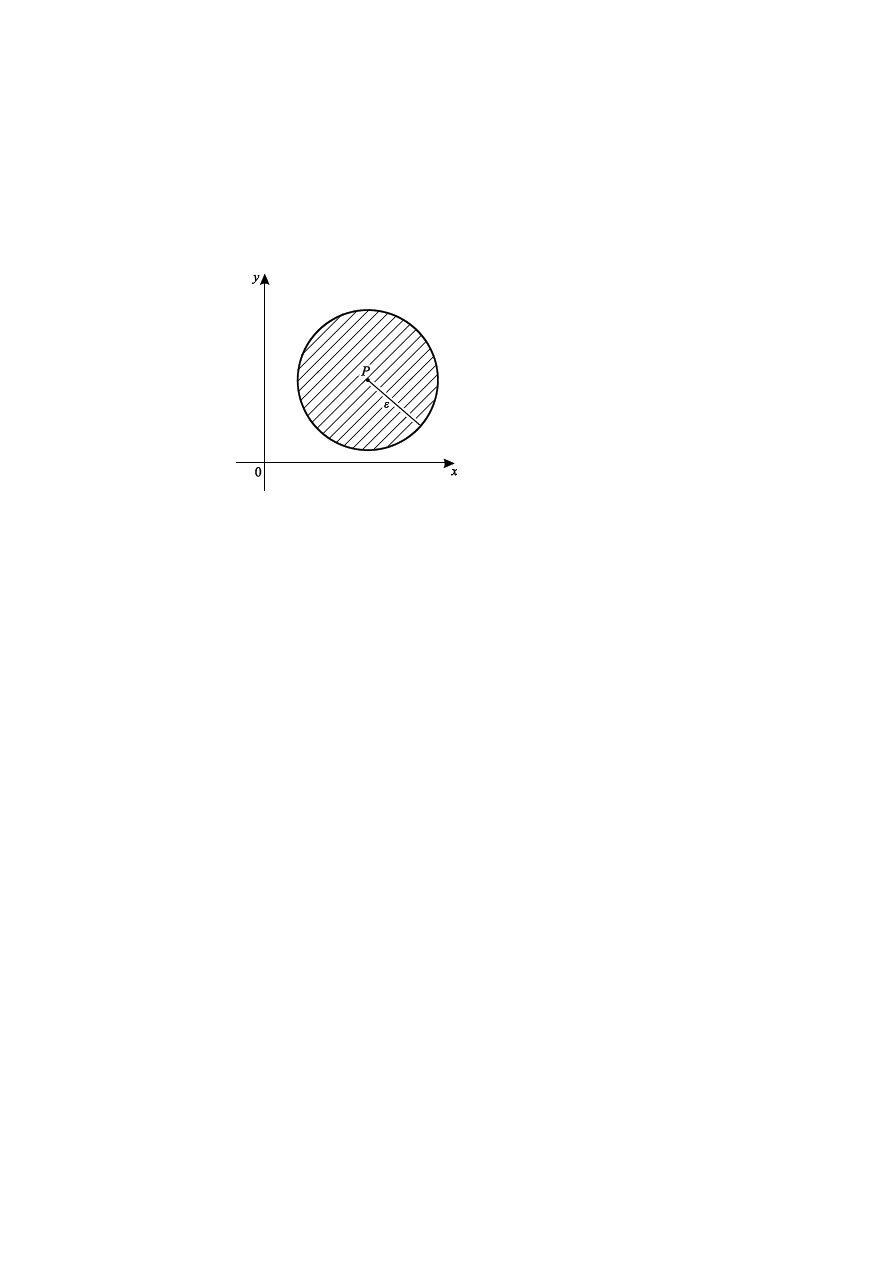
Otoczenie punktu na płaszczyźnie Oxy

Niech P będzie dowolnym punktem na płaszczyźnie Oxy, zaś



dowolną liczbą dodatnią.

Otoczeniem punktu P o promieniu



nazywamy zbiór punktów płaszczyzny Oxy, których odległość od

punktu P jest mniejsza niż



Otoczeniem punktu P o promieniu



jest więc wnętrze koła o środku P i promieniu



(rys. 5).

Granica ciągu punktów na płaszczyźnie Oxy

Granicą ciągu punktów

 

na płaszczyźnie Oxy jest punkt Q tej płaszczyzny, jeżeli ciąg odległości









d P Q

jest zbieżny do zera, tzn.





lim

d P Q





Uwaga 1

Ciąg









d P Q

jest ciągiem liczbowym.

Uwaga 2

Granicą ciągu punktów

 

jest punkt Q wtedy i tylko wtedy, gdy do każdego otoczenia punktu Q należą

prawie wszystkie wyrazy ciągu

 

Zdanie „ Granicą ciągu

 

jest punkt Q ” można zastąpić zdaniem „ Ciąg

 

ma granicę Q ”. Oba te

zdania zapisujemy symbolem

lim





Ciągi zbieżne i ciągi rozbieżne

Ciąg punktów

 

nazywamy ciągiem zbieżnym, jeżeli ten ciąg ma granicę. Ciąg punktów

 

nazywamy

ciągiem rozbieżnym, jeżeli ten ciąg nie ma granicy.

Twierdzenie 1.

Ciąg punktów

 

na płaszczyźnie Oxy , gdzie







jest zbieżny wtedy i tylko wtedy, gdy oba

ciągi liczbowe

 

są zbieżne. Wówczas granicą ciągu

 

jest punkt







, przy czym



lim

Pojęcie funkcji dwóch zmiennych

Dany jest niepusty podzbiór D płaszczyzny Oxy.

Funkcję f, która każdemu punktowi

x y



( , )

należącemu do zbioru D przyporządkowuje dokładnie jedną

liczbę rzeczywistą z nazywamy funkcją dwóch zmiennych rzeczywistych x i y (albo krótko: funkcją dwóch
zmiennych).

Liczbę z nazywamy wartością funkcji f w punkcie

x y



( , )

i oznaczamy

f P

( )

albo

f x y

( , )

Przykład

a) Niech f x y

( , )





3 . Dziedziną funkcji f jest cała płaszczyzna Oxy:



b) Niech f x y

( , )





. Dziedziną funkcji f jest płaszczyzna Oxy z usuniętą prostą



 





x y







c) Niech

f x y

( , )





. Dziedziną funkcji f jest płaszczyzna Oxy z usuniętym początkiem układu:

 





 

 

x y





  





0 0

d) Niech

f x y

( , )

ln (

)



. Dziedziną funkcji f jest wnętrze pierwszej i trzeciej ćwiartki układu

współrzędnych:

 





x y







Granica funkcji dwóch zmiennych

Będziemy zakładać, że istnieje co najmniej jeden ciąg

 

argumentów tej funkcji zbieżny do punktu

o wyrazach różnych od

Mówimy, że granica funkcji f dwóch zmiennych x i y w punkcie



(

)

jest równa g, jeżeli dla

każdego ciągu

 

argumentów tej funkcji zbieżnego do punktu

o wyrazach różnych od

, ciąg

 





f P

wartości funkcji jest zbieżny do g, tzn.

 

lim

f P





Jeżeli



(

)

, to powyższą równość można zapisać w postaci





lim

f x





Zdanie „ Granicą funkcji f w punkcie

jest g ” zapisujemy:

lim

( )

f P





albo

lim

( , )

(

)

x y

f x y





albo lim

( , )

f x y





Przykład

Pokażemy, że granica funkcji f określonej wzorem

f x y

x y

( , )





w punkcie

0 0



( , )

jest równa 0.

Weźmy dowolny ciąg

 

, gdzie



(

)

, argumentów tej funkcji zbieżny do punktu

(ponieważ

punkt (0, 0) nie jest argumentem funkcji f, zatem ciąg ten ma wyrazy różne od

). Mamy:

lim





Zauważmy, że

f x

x y

(

)

(

)
















Ponadto

f x

x y

(

)







Zatem: 0



f x

x y

(

)

Ponieważ

lim

x y







  

0 0

więc na mocy twierdzenia o trzech ciągach (część I, rozdz.1, tw.9) otrzymujemy:





lim

f x





0 .

Zatem: lim

x
y

x y







0
0

0 .

Przykład

Pokażemy, że granica funkcji f określonej wzorem

f x y

( , )





w punkcie

0 0



( , )

nie istnieje.

Weźmy ciąg

 

, gdzie

n n

 






1 1

. Jest to ciąg argumentów tej funkcji zbieżny do punktu

0 0



( , )

o wyrazach różnych od tego punktu. Dla ciągu

 

mamy:

 

lim

f P

n n











1 1

Weźmy teraz ciąg

 

gdzie

n n

 






2 1

. Jest to również ciąg argumentów tej funkcji zbieżny do punktu

0 0



( , )

o wyrazach różnych od tego punktu. Dla ciągu

 

mamy:

 

lim

f Q

n n











2 1

Gdyby granica danej funkcji w punkcie

0 0



( , )

istniała, to dla każdego ciągu argumentów tej funkcji

zbieżnego do punktu

o wyrazach różnych od punktu

powinniśmy otrzymać ten sam wynik. Zatem

rozpatrywana granica nie istnieje.

Granica niewłaściwa funkcji dwóch zmiennych

Mówimy, że granica niewłaściwa funkcji f dwóch zmiennych x i y w punkcie



(

)

jest równa



jeżeli dla każdego ciągu

 

argumentów tej funkcji zbieżnego do punktu

o wyrazach różnych od

ciąg

 





f P

wartości funkcji ma granicę niewłaściwą



, tzn.

 

lim

f P



 

Jeżeli



(

)

, to powyższą równość można zapisać w postaci





lim

f x



 

Zdanie „ Granicą niewłaściwą funkcji f w punkcie

jest



” zapisujemy:

lim

( )

f P



 

albo

lim

( , )

(

)

x y

f x y



 

albo

lim

( , )

f x y



 

W analogiczny sposób określamy granicę niewłaściwą lim

( )

f P



 

Przykład

Pokażemy, że funkcja f określona wzorem

f x y

( , )





ma w

punkcie

0 0



( , )

granicę niewłaściwą



Weźmy dowolny ciąg

 

, gdzie



(

)

, argumentów tej funkcji zbieżny do punktu

(ponieważ

punkt (0, 0) nie jest argumentem funkcji f, zatem ciąg ten ma wyrazy różne od

). Mamy:

lim





Zatem:





lim

f x



















  

więc lim

x
y





 

0
0

Ciągłość funkcji dwóch zmiennych

Dana jest funkcja dwóch zmiennych oraz punkt



(

)

należący do dziedziny tej funkcji.

Mówimy, że funkcja f jest ciągła w punkcie

gdy istnieje granica funkcji f w punkcie

i jest równa

wartości funkcji w tym punkcie, tzn.

lim

( , )

(

)

f x y

f x





Przykład

Rozważmy funkcję

f x y

x y

( , )


















0 0

gdy

We wcześniejszym przykładzie stwierdziliśmy, że

lim

( , )

x
y

f x y



0
0

nie istnieje, zatem ta funkcja nie jest ciągła

w punkcie (0, 0).

Ustalmy teraz zmienną



. Zbadamy ciągłość otrzymanej funkcji

f x

( )

( , )





























gdy

czyli

( )





dla

Podobnie stwierdzamy, że funkcja

( )

( , )





dla

Funkcje

są funkcjami stałymi. Są to funkcje ciągłe w każdym punkcie.

Wniosek

Funkcja dwóch zmiennych może być funkcją ciągłą ze względu na każdą ze zmiennych, ale nie być funkcją
ciągłą.

Określenie pochodnych cząstkowych funkcji dwóch zmiennych

Pochodna cząstkowa funkcji f względem zmiennej x w punkcie (x, y) jest to granica ilorazu różnicowego
względem zmiennej x, gdy przyrost tej zmiennej dąży do zera (o ile ta granica istnieje).

Pochodną tę oznaczamy symbolem

x y

( , )

. Zatem:

x y

f x

x y

f x y

( , )

lim

(

, )

( , )











Stosujemy także oznaczenia:



x y

( , )

albo

x y

( , )

Analogicznie określamy pochodną cząstkową funkcji f względem zmiennej y (oznaczenie:

x y

( , )

albo



x y

( , )

albo

x y

( , )

x y

f x y

( , )

lim

( ,

)

( , )











Obliczanie pochodnych cząstkowych

Obliczanie pochodnych cząstkowych należy wykonywać według reguł znanych z funkcji jednej zmiennej,
z tym, że przy obliczaniu pochodnych cząstkowych względem x należy uważać y za stałą, a przy obliczaniu
pochodnych cząstkowych względem y należy uważać x za stałą.

Przykład

Niech f x y

x y

( , )



2 5

. Wówczas:

 

x y

( , )











2 5

 

x y

( , )











2 5

Przykład

Niech f x y

( , )

sin







. Wówczas:





   

x y

( , )

sin

(sin )









  

 

1 5 3





sin y





   

x y

( , )

sin

cos









  



0 2 2





cos

Przykład 21

Niech f x y

( , )





. Wówczas:





   

x y

( , )















   

x y

( , )







 

  



1 0

Przykład 23

Niech f x y

x y

( , )





. Wówczas:

  











x y

x y x

( , )















 

 



 





























 



 















x x

x y

1 0

  











x y

x y x

( , )















 

 



 



























  



 

















x y

0 2

Pochodne cząstkowe drugiego rzędu

Pochodne cząstkowe funkcji dwóch zmiennych są także funkcjami dwóch zmiennych. Mogą więc istnieć ich
pochodne cząstkowe. Pochodne cząstkowe pochodnych cząstkowych nazywamy pochodnymi cząstkowymi
drugiego rzędu. Istnieją cztery pochodne cząstkowe drugiego rzędu, które oznaczamy:

symbole Newtona

lub



symbole Leibniza

lub

Pochodne te definiujemy następująco:





x y

( , )







x y

( , )







x y

( , )







x y

( , )



Stosując symbole Leibniza powyższe definicje można zapisać w postaci:









































































































Pochodne f

nazywamy pochodnymi czystymi.

Pochodne

nazywamy pochodnymi mieszanymi.

Przykład 28

Obliczymy wszystkie pochodne cząstkowe drugiego rzędu funkcji f x y

x y

( , )





Najpierw obliczamy pochodne f

   

x y

( , )







 



3 3

 

x y

( , )

( )





 





Obliczając pochodne cząstkowe powyższych pochodnych cząstkowych otrzymujemy:





 

x y

( , )

(

)













3 3





 

x y

( , )







 

3 3

3 2





 

x y

( , )







 

3 2





 

x y

( , )







 

Zauważmy, że w powyższym przykładzie pochodne mieszane są równe

x y

( , )



Nie jest to przypadkiem.

Twierdzenie (twierdzenie Schwarza o pochodnych mieszanych)

Jeżeli pochodne mieszane

funkcji f istnieją w obszarze D i są ciągłe w pewnym punkcie (x, y) tego

obszaru, to są one w tym punkcie równe

x y

( , )



Różniczka funkcji dwóch zmiennych

Założenia:

f jest funkcją dwóch zmiennych x i y określoną w otoczeniu punktu

(x, y),

istnieją pochodne cząstkowe

w tym otoczeniu,

dx oznacza przyrost zmiennej x (poprzednio oznaczany



dy oznacza przyrost zmiennej y (poprzednio oznaczany



punkt

(

)

dx y



należy do otoczenia, w którym jest określona funkcja f .

Różniczka df funkcji f dwóch zmiennych x i y jest to funkcja, której wartość w punkcie (x, y) wyraża się
wzorem:

df x y

x y dx

x y dy

( , )





Przykład 29

Dana jest funkcja

f x y

( , )





. Pochodne cząstkowe tej funkcji:

x y

( , )



Różniczka funkcji f :

df x y

x dx

y dy

( , )





Przykładowo, jeżeli



, to

( , )

2 3

3 2

2 3

 

 





Jeżeli ponadto przyjmiemy, że



0 02

0 05

, to

df ( , )

2 3

12 0 02 6 0 05

0 24 0 3

0 54





 







Jest to wartość różniczki funkcji f w punkcie (2, 3) odpowiadającej przyrostowi zmiennej x o 0,02
i przyrostowi zmiennej y o 0,05.

Różniczkowalność funkcji dwóch zmiennych

Przyrost funkcji f odpowiadający argumentowi (x, y) oraz przyrostom zmiennych o dx i dy jest równy

f x

dx y

f x y

(

)

( , )





. Oznaczmy ten przyrost symbolem



f x y

( , )

. Zatem:



f x y

f x

dx y

f x y

( , )

(

)

( , )







Jeżeli

lim

( , )

(

)

(

)

dx
dy

f x y

df x y









0
0



to mówimy, że funkcja f jest różniczkowalna w punkcie (x, y).

Wniosek

Jeżeli funkcja f jest różniczkowalna w punkcie (x, y), a przyrosty dx i dy zmiennych x i y są niewielkie, to



f x y

df x y

( , )



Twierdzenie

Jeżeli pochodne cząstkowe

funkcji f istnieją w pewnym otoczeniu punktu (x, y) i są ciągłe w tym

punkcie, to funkcja f jest różniczkowalna w punkcie (x, y).

Wniosek

Jeżeli pochodne cząstkowe

funkcji f istnieją w pewnym otoczeniu punktu (x, y) i są ciągłe w tym

punkcie, a przyrosty dx i dy zmiennych x i y są niewielkie, to



f x y

df x y

( , )



Zatem:

f x

dx y

f x y

x y dx

x y dy

(

)

( , )









(1)

f x

dx y

x y dx

x y dy

f x y

(

)

( , )







(2)

Przykład 30

We wcześniejszym przykładzie obliczyliśmy wartość różniczki funkcji

f x y

( , )





w punkcie (2, 3)

odpowiadającej przyrostowi zmiennej x o 0,02 i przyrostowi zmiennej y o 0,05. Wynosiła ona 0,54.

Obliczymy teraz przyrost tej funkcji w punkcie (2, 3) odpowiadający przyrostom



0 02

0 05

zmiennych x i y.

f ( , )

2 3

8 9





  









)

(

)

(

)

(

)

(







8 242408 9 3025 17 544908



( , )

(

)

( , )

2 3

17 544908 17

0 544908













Przyrost funkcji i różniczka w tym punkcie są w przybliżeniu równe, co jest ilustracją wzoru (1)

Przykład

Obliczymy przybliżoną wartość funkcji

f x y

( , )



w punkcie

(0,05 , 0,98). W tym celu korzystamy ze wzoru (2) przyjmując:



 

0 05

0 02

. Otrzymujemy:

( ,

, ,

)

(

)

( , )

( , ) (

)

0 05 0 98

0 0 05 1 0 02

0 1 0 05

0 1

0 02













 



f ( , )

0 1

Obliczamy kolejno:

x y

( , )



( , )

0 1

1 1 1



  

x y

( , )





( , )

0 1

2 1

0 5







f x y

( , )



  

1 1 1

W rezultacie:

f ( ,

, ,

)

, (

)

0 05 0 98

1 0 05 0 5

0 02

1 1 04

 



 

 

Maksimum i minimum funkcji dwóch zmiennych

Dana jest funkcja dwóch zmiennych f o dziedzinie D i punkt

(

)

należący do dziedziny D.

Mówimy, że funkcja f ma w punkcie

(

)

maksimum, jeżeli istnieje otoczenie U tego punktu, zawarte

w dziedzinie i takie, że

f x y

f x

( , )

(

)



dla

( , )

, ( , )

(

)

x y





Oznacza to, że w otoczeniu U największą wartością funkcji f jest

f x

(

)

Mówimy, że funkcja f ma w punkcie

(

)

minimum, jeżeli istnieje otoczenie U tego punktu, zawarte

w dziedzinie i takie, że

f x y

f x

( , )

(

)



dla

( , )

, ( , )

(

)

x y





Oznacza to, że w otoczeniu U najmniejszą wartością funkcji f jest

f x

(

)

Mówimy, że funkcja f ma w punkcie

(

)

ekstremum, jeżeli funkcja f ma w tym punkcie maksimum lub

minimum.

Uwaga

Podobnie jak w przypadku funkcji jednej zmiennej z faktu, że funkcja f ma w punkcie

(

)

maksimum

nie wynika, że

f x

(

)

jest największą wartością funkcji f w całej dziedzinie. Identyczna uwaga dotyczy

minimum i wartości najmniejszej funkcji f.

Warunek konieczny ekstremum funkcji dwóch zmiennych
Twierdzenie 4

Jeżeli funkcja f ma w punkcie

(

)

ekstremum i istnieją w tym punkcie pochodne cząstkowe

, to

są one w tym punkcie równe zeru

(

)

(

)



Uwaga 1

Twierdzenie odwrotne nie zachodzi. Funkcja f może nie mieć w punkcie

(

)

ekstremum mimo, że obie

pochodne cząstkowe są w tym punkcie równe zeru.

Uwaga 2

Funkcja, która nie ma w punkcie

(

)

jednej z pochodnych cząstkowych lub obu tych pochodnych, może

mieć w tym punkcie ekstremum.

Wniosek

Funkcja może mieć ekstremum tylko w takich punktach, w których obie pochodne cząstkowe są równe zeru
lub w których przynajmniej jedna z tych pochodnych nie istnieje.

Warunek wystarczający ekstremum funkcji dwóch zmiennych
Twierdzenie 5

Jeżeli

istnieją wszystkie pochodne cząstkowe rzędu pierwszego i drugiego funkcji f w pewnym otoczeniu

punktu

(

)

i są one w tym otoczeniu ciągłe,

obie pochodne cząstkowe rzędu pierwszego funkcji f są w punkcie

(

)

równe zeru, czyli:

(

)

(

)



wyrażenie





, y

)

(

)

(

)

(

)

(



jest dodatnie,

to funkcja f ma w punkcie

(

)

ekstremum.

Gdy

(

)



jest to maksimum, zaś gdy

(

)



jest to minimum.

Warunek wykluczający ekstremum funkcji dwóch zmiennych
Twierdzenie 6

Jeżeli spełnione są założenia 1

i 2

twierdzenia 5 i

W x

(

)



, to funkcja f nie ma w punkcie

(

)

ekstremum.

Uwaga

Twierdzenia 5 i 6 nie rozstrzygają, czy funkcja f ma ekstremum w punkcie

(

)

w przypadku, gdy

W x

(

)



Przykład

Wyznaczymy ekstrema funkcji

f x y

( , )







Dziedzina funkcji:



Pochodne cząstkowe funkcji:

x y

( , )

 



  

3 2

Miejsca zerowania się pochodnych cząstkowych:

3 2



 

 



Z pierwszego równania wyznaczamy

 

3 2

i wstawiamy do drugiego równania. Otrzymujemy:

2 3 2

 





(

)

6 4

  



 



Zatem

3 2 0

   

Stwierdzamy, że obie pochodne cząstkowe są równe zeru w punkcie



( , )

0 3

Pochodne cząstkowe rzędu drugiego:

x y

( , )

 


 

Wartość wyznacznika W w punkcie



( , )

0 3

W P

( )

( , )





   

0 3

4 1

Wniosek: W punkcie



( , )

0 3

funkcja f ma ekstremum. Jest to maksimum, gdyż

( , )

0 3

  

Wartość funkcji f w tym punkcie:

f ( , )

0 3

3 0 6 3 0

0 3 3

    

  



Odpowiedź. Funkcja f ma w punkcie (0, 3) maksimum równe 9.

Przykład

Wyznaczymy ekstrema funkcji

f x y

( , )







Dziedzina funkcji:



Pochodne cząstkowe funkcji:

x y

( , )









Miejsca zerowania się pochodnych cząstkowych:









Z pierwszego równania wyznaczamy



i wstawiamy do drugiego równania. Otrzymujemy:





 

x x

(

)

 



Zatem



Stwierdzamy, że obie pochodne cząstkowe są równe zeru w punktach

0 0

1 1



( , ) ,

( , )

Pochodne cząstkowe rzędu drugiego:

x y

( , )




 



Wartość wyznacznika W w punkcie

0 0



( , )

W P

(

)

( , )

0 0

6 0

3 6 0

3 0













  

Wniosek: W punkcie

0 0



( , )

funkcja f nie ma ekstremum.

Wartość wyznacznika W w punkcie

1 1



( , )

W P

(

)

( , )

1 1

6 1

3 6 1

3 6

36 9















 



Wniosek: W punkcie

1 1



( , )

funkcja f ma ekstremum. Jest to minimum, gdyż f

( , )

1 1

 

. Wartość

funkcji f w tym punkcie:

f ( , )

1 1

3 1 1





    

Odpowiedź. Funkcja f ma w punkcie (1, 1) minimum równe



Określenie gradientu funkcji dwóch zmiennych

Dana jest funkcja dwóch zmiennych f o dziedzinie D oraz punkt

( , )

x y

należący do dziedziny D.

Zakładamy, że istnieją pochodne cząstkowe funkcji f w punkcie

( , )

x y

Gradientem funkcji f w punkcie

( , )

x y

nazywamy wektor, którego składowymi są pochodne cząstkowe

funkcji f w tym punkcie.

Gradient funkcji f w punkcie

( , )

x y

oznaczamy

grad f x y

( , )

. Zatem:





grad f x y

x y

( , )

( , ) ,

( , )



Przykład 38

Obliczymy gradient funkcji f x y

x y

( , )



Pochodne cząstkowe:

x y

( , )




Gradient:





grad f x y

x y

( , )



2 2

Przykładowo, w punkcie (2, 1) jest to wektor









grad f ( , )

2 1

2 2 1

3 2

4 12

  





Interpretacja gradientu funkcji dwóch zmiennych

Gradient funkcji f w punkcie

( , )

x y

jest wektorem. Kierunek tego wektora jest kierunkiem najszybszych

zmian wartości tej funkcji. Zwrot tego wektora wyznacza najszybszy wzrost wartości tej funkcji.

Przykład

Wielkość produkcji zależy od zaangażowanego w produkcję kapitału x (w mln zł) oraz od pracy y
wydatkowanej w procesie produkcji (w liczbie etatów) i wyraża się wzorem:

f x y

x y



( , )

Dotychczas w produkcję zaangażowano kapitał x w wysokości 400 mln zł przy zatrudnieniu y 100 etatów.
Zamierzamy zwiększyć zatrudnienie o 10 etatów. Jaki dodatkowy kapitał zaangażować, aby wzrost produkcji
był największy?

Rozwiązanie.

Pochodne cząstkowe:

x y

( , )




Gradient:





grad f x y

( , )



Gradient w punkcie (x, y)=(400, 100) jest to wektor









grad f (

)

400 100

4 400 100 2 400

160000 320000

 





Druga współrzędna gradientu jest dwa razy większa niż pierwsza, zatem wzrostowi zatrudnienia y o 10
etatów powinien towarzyszyć wzrost nakładów x o 5 mln zł.

Wyszukiwarka

Podobne podstrony:
4 6 Różniczki funkcji dwóch zmiennych
1 funkcje dwoch zmiennych
09 Rozdział 07 Więcej o całce funkcji dwóch zmiennych
4 5 Ekstrema funkcji dwoch zmiennych
6 Funkcja dwóch zmiennych 2 zadania
Ekstrema lokalne funkcji dwóch zmiennych, Ekstrema lokalne funkcji dwóch zmiennych
sciaga18 ekstrema lokalne funkcji dwoch zmiennych, AGH górnictwo i geologia, I SEM, matematyka
Funkcje dwóch zmiennych
6 funkcje dwoch zmiennych
funkcje dwóch zmiennych wykład
sciaga18 ekstrema lokalne funkcji dwoch zmiennych[1], Analiza
8 Funkcje dwóch zmiennych
RACHUNEK?LKOWY FUNKCJI DWOCH ZMIENNYCH
Funkcje dwóch zmiennych
sciaga20 rozniczka zupelna funkcji dwoch zmiennych, Księgozbiór, Studia, Pozostałe
E3 Funkcje dwóch zmiennych rozwiązywanie zadań
AM23 w08 Ekstrema funkcji dwóch zmiennych
07 Rozdział 05 Całka funkcji dwóch zmiennych

więcej podobnych podstron