DWUWYMIAROWE ZMIENNE LOSOWE
Rozkład łączny pary zmiennych losowych
)
,
(
Y
X
określonych na tej samej przestrzeni zdarzeń
elementarnych:
)
)
,
((
A
Y
X
P
, A
- dowolny podzbiór zbioru par
wartości zmiennych X, Y.
Definicja.
Dystrybuantą zmiennej losowej
)
,
(
Y
X
nazywamy funkcję
)
,
(
)
,
(
y
Y
x
X
P
y
x
F
,
gdzie
,
x
.
y
Twierdzenie
. Łączny rozkład prawdopodobieństwa
zmiennej losowej
)
,
(
Y
X
określony jest jednoznacznie
przez jej dystrybuantę.
Zmienne dyskretne
Funkcja prawdopodobieństwa ( łącznego )
dwuwymiarowej zmiennej losowej dyskretnej:
)
,
(
)
,
(
y
Y
x
X
P
y
x
f
.
Własności:
(i)
0
)
,
(
y
x
f
, dla dowolnej pary wartości )
,
(
y
x
,
(ii)
x
y
y
x
f
1
)
,
(
,
(iii)
A
y
x
y
x
f
A
Y
X
P
)
,
(
)
,
(
)
)
,
((
,
(iv)
x
s
y
x
F
)
,
(
y
t
t
s
f
)
,
(
.
Przykład.
W każdym z dwóch etapów teleturnieju
można otrzymać 0, 1, lub 2 punkty. Niech zmienne
losowe X, Y oznaczają liczby punktów uzyskane w
etapie I i II, odpowiednio, przez losowo wybranego
uczestnika. Funkcję prawdopodobieństwa łącznego
określa tabela:
Y
X
0
1
2
0
0,5
0,05
0,01
1
0,2 0,1
0,06
2
0,02
0,03
A
Znaleźć:
(a)
)
2
,
2
(
)
2
,
2
(
Y
X
P
f
(b)
)
2
(
Y
P
(c)
)
1
,
1
(
F
.
(a)
2
0
2
0
)
,
(
x
y
y
x
f
= 1. Stąd
)
2
,
2
(
f
= A = 1 – ( 0,5 + 0,05 + 0,01 + 0,2 + 0,1 +
+ 0,06 + 0,02 + 0,03 ) = 1 – 0,97 = 0,03.
(b)
2
0
)
2
,
(
)
2
(
x
Y
x
X
P
Y
P
=
)
2
,
2
(
)
2
,
1
(
)
2
,
0
(
f
f
f
= 0,01 + 0,06 + 0,03 = 0,1.
(c)
)
1
,
1
(
F
=
)
1
,
1
(
Y
X
P
=
=
)
1
,
1
(
)
0
,
1
(
)
1
,
0
(
)
0
,
0
(
f
f
f
f
=
= 0,5 + 0,05 + 0,2 + 0,1 = 0,85.
Zmienne ciągłe
Zmienna losowa (
)
,Y
X
jest dwuwymiarową ciągłą
zmienną losową, jeśli jej łączny rozkład prawdopodo-
bieństwa określony jest przez funkcję gęstości łącznej
( łączną gęstość prawdopodobieństwa ), taką że
(i)
0
)
,
(
y
x
f
(ii)
1
)
,
(
dxdy
y
x
f
(iii)
A
dxdy
y
x
f
A
Y
X
P
)
,
(
)
)
,
((
W szczególności dla
]
,
(
]
,
(
y
x
A
:
)
,
(
y
x
F
=
x
y
dtds
t
s
f
y
Y
x
X
P
)
,
(
)
,
(
.
)
,
(
)
,
(
2
y
x
F
y
x
y
x
f
,
x
,
y
.
Przykład.
Zmienna losowa
)
,
(
Y
X
ma gęstość
prawdopodobieństwa
0
)
,
(
y
x
y
x
f
gdy
przeciwnie
y
x
1
0
,
1
0
.
Obliczyć
)
25
,
0
,
5
,
0
(
Y
X
P
=
5
,
0
0
1
25
,
0
)
(
dydx
y
x
=
dx
y
xy
1
25
,
0
5
,
0
0
2
)
2
/
(
=
5
,
0
0
)
2
/
625
,
0
25
,
0
5
,
0
(
dx
x
x
= ?
Rozkłady brzegowe
Niech )
,
(
Y
X
będzie dwuwymiarową zmienną losową o
rozkładzie prawdopodobieństwa określonym przez
funkcję
)
,
(
y
x
f
( funkcja prawdopodobieństwa lub
gęstość ).
Rozkład brzegowy = rozkład prawdopodobieństwa
zmiennej losowej X lub zmiennej losowej Y.
(a)
dla dyskretnych zmiennych X, Y , brzegowe
funkcje prawdopodobieństwa są postaci
y
X
y
x
f
x
X
P
x
f
)
,
(
)
(
)
(
x
Y
y
x
f
y
Y
P
y
f
)
,
(
)
(
)
(
(b)
dla ciągłych zmiennych X, Y , brzegowe gęstości
są postaci
dy
y
x
f
x
f
X
)
,
(
)
(
dx
y
x
f
y
f
Y
)
,
(
)
(
.
D.
(a)
)
(x
f
X
y
y
Y
x
X
P
x
X
P
})
,
(
)
(
=
y
y
y
x
f
y
Y
x
X
P
)
,
(
)
,
(
.
(b)
)
(
)
(
x
X
P
x
F
X
=
)
,
(
Y
x
X
P
=
x
dtds
t
s
f
)
,
(
. Stąd
)
(x
f
X
)
(x
F
dx
d
X
=
dt
t
x
f
)
,
(
.
Przykład.
Dwuwymiarowa zmienna losowa
)
,
(
Y
X
ma gęstość
0
8
/
)
(
3
)
,
(
2
y
x
y
x
f
gdy
przeciwnie
y
x
1
1
,
1
1
Znaleźć gęstość zmiennej losowej X.
Niech
1
1
x
.
dy
y
x
f
x
f
X
)
,
(
)
(
=
1
1
2
)
(
8
3
dy
y
x
1
1
2
2
)
2
(
8
3
dy
y
xy
x
=
1
1
]
3
/
[
8
3
3
2
2
y
xy
y
x
=
4
1
4
3
2
x
.
0
4
/
)
1
3
(
)
(
2
x
x
f
X
gdy
przeciwnie
x
1
1
.
Gęstość zmiennej losowej Y ma identyczną postać.
Rozkłady warunkowe
(a)
Niech )
,
(
Y
X
będzie
dyskretną
zmienną losową
mającą funkcję prawdopodobieństwa )
,
(
y
x
f
.
Niech y – ustalone oraz
0
)
(
y
f
Y
.
Rozkład
warunkowy
zmiennej losowej X pod
warunkiem, że Y = y określa
warunkowa funkcja
prawdopodobieństwa:
)
( y
x
f
=
)
(
)
,
(
y
f
y
x
f
Y
, x – dowolna wartość zmiennej X.
)
( y
x
f
=
)
(
)
,
(
y
Y
P
y
Y
x
X
P
)
(
y
Y
x
X
P
=
funkcja prawdopodobieństwa zmiennej X pod
warunkiem, że zmienna Y przyjęła wartość y.
Analogicznie:
)
( x
y
f
=
)
(
)
,
(
x
f
y
x
f
X
=
)
(
x
X
y
Y
P
, gdzie
0
)
(
x
f
X
.
Notacja:
)
(
)
(
y
x
f
y
x
f
Y
X
)
(
)
(
x
y
f
x
y
f
X
Y
(b)
Niech
)
,
(
Y
X
będzie ciągłą zmienną losową o
łącznej gęstości
)
,
(
y
x
f
.
Niech y – ustalone oraz
0
)
(
y
f
Y
.
Warunkową gęstością prawdopodobieństwa zmiennej
losowej X pod warunkiem, że
y
Y
nazywamy funkcję
)
( y
x
f
=
)
(
)
,
(
y
f
y
x
f
Y
,
x
.
Przykład.
(kontynuacja)
0
8
/
)
(
3
)
,
(
2
y
x
y
x
f
gdy
przeciwnie
y
x
1
1
,
1
1
)
( y
f
Y
0
4
/
)
1
3
(
2
y
gdy
przeciwnie
y
1
1
Niech
1
1
y
- ustalone.
)
( y
x
f
=
4
/
)
1
3
(
8
/
)
(
3
2
2
y
y
x
=
2
6
)
(
3
2
2
y
y
x
dla
]
1
,
1
[
x
)
( y
x
f
= 0 dla
].
1
,
1
[
x
Uwaga.
Analogicznie określamy rozkład warunkowy
zmiennej losowej Y pod warunkiem X = x. Zatem
)
( x
y
f
=
)
(
)
,
(
x
f
y
x
f
X
, gdzie y – dowolna wartość Y,
x - ustalone, takie że
0
)
(
x
f
X
.
Notacja:
)
(
)
(
x
y
f
x
y
f
X
Y
,
)
(
)
(
y
x
f
y
x
f
Y
X
Przykład. (kontynuacja)
(a) Znaleźć rozkład brzegowy zmiennej Y, liczby
punktów uzyskanych w II etapie teleturnieju przez
losowo wybranego uczestnika.
(b) Wyznaczyć rozkład warunkowy Y pod warunkiem,
że w I etapie uzyskano 2 punkty, tzn. X = 2.
Y
X
0
1
2
0
0,5
0,05
0,01
1
0,2 0,1
0,06
2
0,02
0,03
0,03
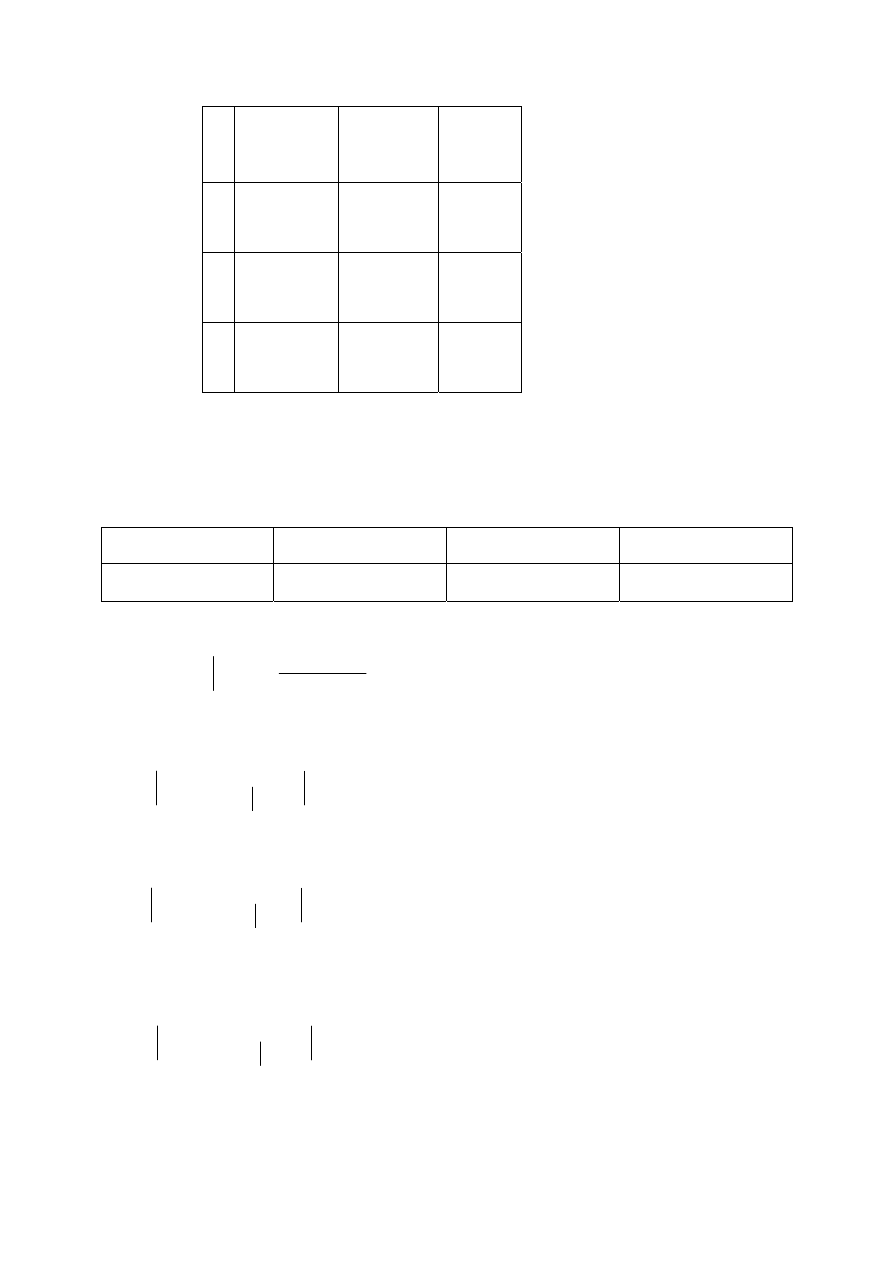
Y
X
0
1
2
0
0,5
0,05
0,01
1
0,2 0,1
0,06
2
0,02
0,03
0,03
(a)
)
( y
f
Y
=
)
,
2
(
)
,
1
(
)
,
0
(
y
f
y
f
y
f
. Stąd
Y
0
1 2
)
( y
f
Y
0,72
0,18
0,1
(b)
)
2
( y
f
=
)
2
(
)
,
2
(
X
f
y
f
= ?
)
2
0
(
f
=
)
2
0
(
X
Y
f
=
)
2
(
/
)
0
,
2
(
X
f
f
=
= 0,02/(0,02 + 0,03 + 0,03) =1/4,
)
2
1
(
f
=
)
2
1
(
X
Y
f
=
)
2
(
/
)
1
,
2
(
X
f
f
=
= 0,03/0,08 = 3/8,
)
2
2
(
f
=
)
2
2
(
X
Y
f
=
)
2
(
/
)
2
,
2
(
X
f
f
=
= 0,03/0,08 = 3/8.
Niezależne zmienne losowe
Definicja.
Niech )
,
(
Y
X
będzie dwuwymiarową
zmienna losową o dystrybuancie
)
,
(
y
x
F
oraz
dystrybuantach brzegowych
),
(x
F
X
)
( y
F
Y
,
)
,
(
,
y
x
. Zmienne losowe X, Y są niezależne,
jeśli
)
(
)
(
)
,
(
y
F
x
F
y
x
F
Y
X
,
dla wszystkich wartości x, y.
Twierdzenie
. Zmienne losowe X, Y są niezależne
wtedy i tylko wtedy gdy
)
(
)
(
)
,
(
y
f
x
f
y
x
f
Y
X
,
dla wszystkich wartości x, y.
Wniosek.
Poniższe warunki są równoważne:
(i) Zmienne losowe X, Y są niezależne.
(ii)
)
(
)
(
x
f
y
x
f
X
,
x
, dla wszystkich y,
takich że
0
)
(
y
f
Y
.
(iii)
)
(
)
(
y
f
x
y
f
Y
,
y
, dla wszystkich x,
takich że
0
)
(
x
f
X
.
Przykład.
( kontynuacja )
Czy liczby punktów uzyskane w I i II etapie teleturnieju
przez losowo wybranego uczestnika są niezależnymi
zmiennymi losowymi ?
Y
X
0
1
2
0
0,5
0,05
0,01
1
0,2 0,1
0,06
2
0,02
0,03
0,03
)
2
,
0
(
)
1
,
0
(
)
0
,
0
(
)
0
(
f
f
f
f
X
= 0,5 + 0,05 +
+ 0,01 = 0,56.
)
0
,
2
(
)
0
,
1
(
)
0
,
0
(
)
0
(
f
f
f
f
Y
= 0,5 + 0,2
+ 0,02 = 0,72.
Stąd
)
0
(
)
0
(
72
,
0
56
,
0
5
,
0
)
0
,
0
(
Y
X
f
f
f
,
Zmienne losowe
Y
X ,
są zależne.
Przykład.
( kontynuacja ). Czy X, Y są niezależnymi
zmiennymi losowymi, jeśli ich łączna gęstość ma
postać:
0
8
/
)
(
3
)
,
(
2
y
x
y
x
f
gdy
przeciwnie
y
x
1
1
,
1
1
Dla
]
1
,
1
[
,
y
x
:
4
/
)
1
3
(
)
(
2
x
x
f
X
oraz
4
/
)
1
3
(
)
(
2
y
y
f
Y
.
)
(
)
(
)
,
(
y
f
x
f
y
x
f
Y
X
.
Przykład.
Czasy poprawnej pracy dwu podzespołów są
niezależnymi zmiennymi losowymi X, Y o rozkładach
wykładniczych z parametrami
,
,
2
1
odpowiednio.
Średnie czasy pracy podzespołów wynoszą 1000
(godzin ) i 1200 ( godzin ). Obliczyć
prawdopodobieństwo zdarzenia takiego, że każdy
podzespół nie ulegnie awarii przed upływem 1500
godzin.
1000
/
1
)
(
1
X
E
(godz.),
1200
/
1
)
(
2
Y
E
(godz.)
Stąd
1000
/
1
1
(1/godz.)
1200
/
1
2
(1/godz.).
)
1500
,
1500
(
Y
X
P
=
)
1500
(
X
P
)
1500
(
Y
P
=
1500
1500
2
1
e
e
=
1200
/
1500
1000
/
1500
e
e
=
= 0,2231
0,2865 = 0,0639.
Wartość oczekiwana. Kowariancja.
)]
,
(
[
Y
X
g
E
=
x
y
y
x
f
y
x
g
)
,
(
)
,
(
,
gdy X, Y są dyskretne,
)]
,
(
[
Y
X
g
E
=
dxdy
y
x
f
y
x
g
)
,
(
)
,
(
,
gdy X, Y są ciągłe.
Uwaga
. Dla
X
Y
X
g
)
,
(
lub
Y
Y
X
g
)
,
(
otrzymujemy wartości oczekiwane brzegowych
zmiennych losowych X lub Y.
Np.
]
[
X
E
=
x
y
y
x
xf
)
,
(
=
x
y
y
x
f
x
)
,
(
=
=
x
X
X
x
xf
)
(
.
Stwierdzenie.
Niech c będzie dowolną stałą, a
)
,
(
Y
X
g
,
)
,
(
1
Y
X
g
,
)
,
(
2
Y
X
g
zmiennymi losowymi
jednowymiarowymi. Wówczas
)]
,
(
[
)
,
(
[
Y
X
g
cE
Y
X
cg
E
,
)]
,
(
[
)]
,
(
[
)]
,
(
)
,
(
[
2
1
2
1
Y
X
g
E
Y
X
g
E
Y
X
g
Y
X
g
E
.
D.
Dowód jest bezpośrednią konsekwencją definicji
wartości oczekiwanej oraz własności całki i sumowania.
Stwierdzenie.
Jeśli zmienne losowe X, Y są niezależne,
to
)
(
)
(
)
(
Y
E
X
E
XY
E
.
D. Niezależność zmiennych jest równoważna
)
(
)
(
)
,
(
y
f
x
f
y
x
f
Y
X
. Stąd i z definicji wartości
oczekiwanej mamy
(a) (zmienne dyskretne )
)]
,
(
[
Y
X
g
E
=
x
y
y
x
f
y
x
g
)
,
(
)
,
(
.
)
( XY
E
=
x
y
y
x
xyf
)
,
(
=
x
y
Y
X
y
f
x
xyf
)
(
)
(
=
x
y
Y
X
y
yf
x
xf
)
(
)
(
=
y
Y
y
yf
)
(
x
X
x
xf
)
(
=
)
(
)
(
)
(
)
(
Y
E
X
E
X
E
Y
E
.
(b) (zmienne ciągłe) Dowód analogiczny - Sumowanie
należy zastąpić całkowaniem.
Definicja.
Niech X i Y będą zmiennymi losowymi o
łącznej funkcji prawdopodobieństwa ( gęstości )
)
,
(
y
x
f
. Kowariancją zmiennych X i Y nazywamy
liczbę:
)]
)(
[(
Y
X
XY
Y
X
E
.
Uwaga.
Z definicji
XY
oraz
)]
,
(
[
Y
X
g
E
, przyjmując
)
)(
(
)
,
(
Y
X
y
x
y
x
g
, otrzymujemy wzory:
x
y
Y
X
XY
y
x
f
y
x
)
,
(
)
)(
(
,
gdy X, Y są dyskretne
dxdy
y
x
f
y
x
Y
X
XY
)
,
(
)
)(
(
,
gdy X, Y są ciągłe.
Notacja
: Zamiast
XY
często piszemy Cov (X,Y).
Interpretacja.
Kowariancja określa pewną
współzależność między zmiennymi losowymi:
(a)
Jeśli „dużym” wartościom zmiennej X
przewyższającym
X
towarzyszą zwykle „duże”
wartości zmiennej Y przewyższające
Y
, a wartościom
X mniejszym od
X
towarzyszą zwykle wartości Y
mniejsze od
Y
, to
XY
> 0.
(b)
Jeśli wartościom zmiennej X większym od
X
towarzyszą zwykle wartości Y mniejsze od
Y
wartościom X mniejszym od
X
towarzyszą zwykle
wartości Y większe od od
Y
, to
XY
< 0.
Stwierdzenie. Cov(X,Y) =
Y
X
XY
E
)
(
.
D.
Cov(X,Y) =
)]
)(
[(
Y
X
Y
X
E
=
=
)
(
Y
X
X
Y
Y
X
XY
E
=
=
Y
X
X
Y
Y
E
X
E
XY
E
)
(
)
(
)
(
=
=
Y
X
XY
E
)
(
.
Twierdzenie.
Jeśli zmienne losowe X i Y są
niezależne, to
Cov(X,Y) = 0.
D.
Dla niezależnych zmiennych losowych
)
(
)
(
)
(
Y
E
X
E
XY
E
. Stąd oraz wzoru na
kowariancję mamy:
Cov(X,Y) =
Y
X
XY
E
)
(
=
=
Y
X
Y
E
X
E
)
(
)
(
= 0.
Uwaga.
Twierdzenie odwrotne nie jest na ogół
prawdziwe.
Twierdzenie.
Dla dowolnych stałych a, b
Var(
)
bY
aX
=
2
a Var(X) +
2
b Var(Y) + 2ab Cov(X,Y).
D.
E{
2
)
(
)
(
Y
X
b
a
bY
aX
} =
E{
2
)
(
)
(
Y
X
Y
b
X
a
} = E{
2
))
(
X
X
a
}
+ E
)
)(
(
2
Y
X
Y
X
ab
+ E{
2
)
(
Y
Y
b
} =
=
2
a Var(X) + 2abCov(X,Y) +
2
b Var(Y). c.k.d.
Wniosek. Jeśli zmienne losowe X i Y są niezależne,
to
Var(
bY
aX
) =
2
a
Var(X) +
2
b
Var(Y).
Definicja.
Współczynnikiem korelacji między
zmiennymi losowymi X i Y nazywamy liczbę:
)
(
)
(
)
,
(
Y
Var
X
Var
Y
X
Cov
.
Przykład.
?
Y
X
0
1
2
0
0,5
0,05
0,01
1
0,2 0,1
0,06
2
0,02
0,03
0,03
)
( X
E
=
x
y
y
x
f
x
)
,
(
=
0(0,5 + 0,05 + 0,01) +
+ 1
(0,2 + 0,1 + 0,06) + 2(0,02+0,03+0,03) = 0,52.
)
(Y
E
=
x
y
y
x
f
y
)
,
(
= 0 (0,5 + 0,2 + 0,02) +
+ 1
(0,05 + 0,1 + 0,03) + 2(0,01+0,06+0,03) = 0,38.
Y
X
0
1
2
0
0,5
0,05
0,01
1
0,2 0,1
0,06
2
0,02
0,03
0,03
)
( XY
E
=
x
y
y
x
xyf
)
,
(
=
0 + 0 + 0 + 0 + 1 1
0,1 +
+
06
,
0
2
1
+
03
,
0
1
2
+
03
,
0
2
2
= 0,31.
Cov(X,Y) = 0,31 – 0,52
38
,
0
= 0,1124.
)
(
2
X
E
2
1
(0,2 + 0,1 + 0,06) +
+
)
03
,
0
03
,
0
02
,
0
(
2
2
= 0,68
)
(
2
Y
E
2
1
(0,05 +
0,1 + 0,03) +
+
)
03
,
0
06
,
0
01
,
0
(
2
2
=
0,58.
Var(X) =
2
2
2
52
,
0
68
,
0
)]
(
[
)
(
X
E
X
E
=
0,4096
Var(Y) =
2
2
2
38
,
0
58
,
0
)]
(
[
)
(
Y
E
Y
E
= 0,4356
.
2661
,
0
4356
,
0
4096
,
0
1124
,
0
Własności współczynnika korelacji
(i)
1
1
(ii)
Jeśli
a
i
b
są stałymi, oraz jeśli
Y
=
a
+
bX
,
to
1
1
gdy
0
0
b
b
(iii) Jeśli zmienne losowe
X
i
Y
są niezależne, to
.
0
(iv) Jeśli
1
, to między zmiennymi losowymi
X,
Y
istnieje liniowa zależność funkcyjna.
Interpretacja.
Współczynnik korelacji jest miarą
zależności liniowej między zmiennymi losowymi.
Dwuwymiarowy rozkład normalny
Zmienna losowa
)
,
(
Y
X
ma dwuwymiarowy rozkład
normalny, jeśli ma gęstość postaci:
Y
X
y
x
f
2
1
)
,
(
exp
)
,
(
)
1
(
2
1
2
y
x
q
,
gdzie
2
2
2
2
)
(
)
)(
(
2
)
(
)
,
(
y
Y
Y
X
Y
X
X
X
y
y
x
x
y
x
q
,
,
x
y
, stałe
X
,
Y
,
spełniają
warunki
X
> 0,
Y
> 0,
1
1
.
Notacja
:
)
,
,
,
,
(
~
)
,
(
Y
X
Y
X
N
Y
X
Twierdzenie.
Jeśli
)
,
,
,
,
(
~
)
,
(
Y
X
Y
X
N
Y
X
, to
(i)
X
~
)
,
(
X
X
N
,
Y
~
)
,
(
Y
Y
N
.
(ii) Cov(
X
,
Y
) =
.
(iii)
X
,
Y
są niezależne wtedy i tylko wtedy gdy
= 0.
Twierdzenie.
Zmienna losowa (
X
,
Y
) ma
dwuwymiarowy rozkład normalny wtedy i tylko wtedy
gdy zmienna losowa
aX
+
bY
ma rozkład normalny,
a
,
b
są dowolnymi stałymi.
CIĄGI ZMIENNYCH LOSOWYCH
Niech
n
X
X
X
,...,
,
2
1
będą zmiennymi losowymi
określonymi na tej samej przestrzeni zdarzeń
elementarnych
S
.
)
,...,
,
(
2
1
n
x
x
x
F
=
)
,...,
,
(
2
2
1
1
n
n
x
X
x
X
x
X
P
=
dystrybuanta wektora losowego (
n
X
X
X
,...,
,
2
1
).
)
,...,
,
(
2
1
n
x
x
x
f
= funkcja prawdopodobieństwa
łącznego lub funkcja gęstości łącznej wektora losowego
(
n
X
X
X
,...,
,
2
1
).
Definicja
. Zmienne losowe
n
X
X
X
,...,
,
2
1
są niezależne,
jeśli
)
,...,
,
(
2
1
n
x
x
x
F
=
)
(
...
)
(
)
(
2
1
2
1
n
X
X
X
x
F
x
F
x
F
n
,
gdzie
)
(
)
(
i
i
X
x
X
P
x
F
i
i
, i = 1,2,...,n.
Definicja.
)]
,
,
,
,
,
(
[
2
1
n
X
X
X
g
E
=
1
2
)
,...,
,
(
)
,...,
,
(
...
2
1
2
1
x x
x
n
n
n
x
x
x
f
x
x
x
g
,
lub
n
n
dx
dx
dx
x
x
x
f
x
x
x
g
n
...
)
,...,
,
(
)
,...,
,
(
...
2
1
2
1
2
1
.
Stwierdzenie.
)
...
(
2
2
1
1
n
n
X
a
X
a
X
a
E
=
)
(
...
)
(
)
(
2
2
1
1
n
n
X
E
a
X
E
a
X
E
a
.
Wniosek.
Niech
n
i
i
X
n
X
1
1
, ,
)
(
i
X
E
i = 1,2,..,n.
)
( X
E
=
.
D. W stwierdzeniu trzeba przyjąć
n
a
i
1
, i = 1,2,..,n.
Stwierdzenie.
Jeśli
n
X
X
X
,...,
,
2
1
są niezależnymi
zmiennymi losowymi, to
Var
)
...
(
2
2
1
1
n
n
X
a
X
a
X
a
=
2
1
a Var(
1
X ) +
2
2
a Var(
2
X ) + ... +
2
n
a
Var(
n
X ).
W szczególności, jeśli Var(
i
X
) =
2
oraz
n
a
i
1
,
i = 1,2,..,n, to
Var( X ) =
n
2
.
Przykład.
Dokonujemy n jednakowych, niezależnych
doświadczeń Bernoulli’ego o prawdopodobieństwie
sukcesu p,
1
0
p
. Znaleźć wartość oczekiwaną i
wariancję zmiennej losowej Y będącej liczbą sukcesów.
Niech
i
X
1, gdy sukces w i-tym doświadczeniu,
i
X
0, gdy porażka w i-tym doświadczeniu. Wówczas
n
X
X
X
,...,
,
2
1
są niezależnymi zmiennymi losowymi o
funkcjach prawdopodobieństwa:
p
f
i
X
)
1
(
,
p
f
i
X
1
)
0
(
.
Stąd:
p
X
E
i
)
(
,
Var(
i
X ) =
)
1
(
p
p
.
Liczba sukcesów =
.
...
2
1
n
X
X
X
Y
)
(Y
E
=
)
...
(
2
1
n
X
X
X
E
=
)
(
...
)
(
)
(
2
1
n
X
E
X
E
X
E
=
np .
Var(Y) =
Var(
)
1
X + Var(
)
2
X
+ ... + Var(
)
n
X
=
)
1
(
p
np
Definicja. Prostą próbą losową
o liczności n
nazywamy ciąg niezależnych zmiennych losowych
n
X
X
X
,...,
,
2
1
określonych na przestrzeni zdarzeń
elementarnych S i takich, że każda ze zmiennych ma
taki sam rozkład.
Twierdzenie. ( CENTRALNE TWIERDZENIE
GRANICZNE)
Niech
n
X
X
X
,...,
,
2
1
będzie prostą próbą losową z
rozkładu o średniej
i wariancji
2
. Wówczas dla
dużych liczności próby n rozkład prawdopodobieństwa
standaryzowanej średniej ( = standaryzowanej sumy
n
X
X
X
...
2
1
) jest bliski standardowemu
rozkładowi normalnemu
)
1
,
0
(
N
, dokładniej dla
dowolnych liczb a, b,
b
a
)
/
(
b
n
X
a
P
),
(
)
(
)
(
a
b
b
Z
a
P
przy
n
. Równoważnie rozkład średniej X
jest
bliski rozkładowi normalnemu
)
/
,
(
n
N
.
Przykład.
Załóżmy, że rozkład codziennego dojazdu do
pracy jest w przybliżeniu rozkładem jednostajnym na
przedziale [0,5 godz., 1 godz. ] i że czasy dojazdów w
różne dni są niezależne. Obliczyć przybliżone
prawdopodobieństwo zdarzenia, że średni dzienny
dojazd w ciągu 30 dni przekroczy 0,8 godz.
Niech
i
X oznacza czas dojazdu w i-tym dniu ,
30
,...,
2
,
1
i
.
4
3
2
1
5
,
0
)
(
i
X
E
,
48
1
12
)
5
,
0
1
(
)
(
2
2
i
X
Var
.
4
3
)
(
X
E
,
48
30
1
)
(
X
Var
)
8
,
0
(
X
P
=
)
)
48
30
/(
1
4
/
3
8
,
0
)
48
30
/(
1
4
/
3
(
X
P
03
,
0
)
89
,
1
(
1
)
89
,
1
(
Z
P
.