Zestaw 2
Trygonometria
Strona 1
yrażenia
Zadanie 1. Długość boku x, zaznaczonego na rysunku wynosi:
A. 8
B. 10
C. 12
D. 15
Zadanie 2. Wartość w
4
4
cos
sin
α
α
−
dla 30
α
=
D
wynosi:
A. 0
B.
1
2
C.
1
2
− D.
1
Zadanie 3. Punkt A leży na jednym ramieniu kąta o mierze
w odległości 1 dm od drugiego ramienia tego
kąta. Odległość punktu A od wierzchołka tego kąta wynosi:
30
D
A. 20 cm
B. 3 dm
C.
40
3
dm
D.
2
3
dm
Zadanie 4. Jeżeli
α
jest kątem ostrym i tg
2
α
= , to:
A.
3 5
sin
5
α
=
B.
5
n
5
si
α
=
C.
5
cos
α
=
D.
5
3
co
α
=
5
s
5
Zadanie 5. Wartość wyrażenia
(
)
2
2
2 sin 15
cos 15
3tg30
2sin 45
+
−
D
D
D
D
jest równa:
A.
2 2
6
2
−
B.
2 3 3
2
−
C.
2 3 3
2
+
D.
2 2
6
2
+
30
D
Zadanie 6. Samolot startuje z lotniska pod kątem
do poziomu. Po przebyciu 3 km w linii prostej samolot
znajdzie się na wysokości:
A. 6 km
B. 3 km
C. 3
km
D. 1,5 km
3
Zadanie 7. Wyrażenie
2
1 sin
cos
α
α
−
można zapisać w postaci:
A.
sin
α
B.
1
C.
cos
α
D.
1
cos
α
Zadanie 8. Jeśli
3
sin
5
α
= i
α
jest kątem ostrym, to cos
α
jest równy:
A.
2
5
B.
3
5
C.
4
D.
25
4
5
Zadanie 9. Cosinus pewnego kąta ostrego
α
wynosi
12
13
. Wówczas sin
α
wynosi:
A.
12
13
B.
1
C.
13
5
13
D.
5
12
2
2
2
sin 30
cos 60
tg 45
+
−
D
D
D
Zadanie 10. Wartość wyrażenia
jest równa:
A. 1
B.
1
2
− C.
0
D.
3
4
−
Zadanie 11. Jeżeli
α
jest kątem ostrym i
2
sin
3
α
= , to wartość
(
)
cos 90
α
−
D
jest równa:
A.
2
3
B.
1
C.
3
5
D.
3
2
3
45
Zadanie 12. Jacek, leżąc na łące, widzi wierzchołek drzewa pod kątem
D
w stosunku do poziomu. Drzewo
ma wysokość 16 metrów. W odległości ilu metrów od drzewa znajduje się Jacek?
A. 8 m
B. 32 m
C. 16 m
D. 16 3 m
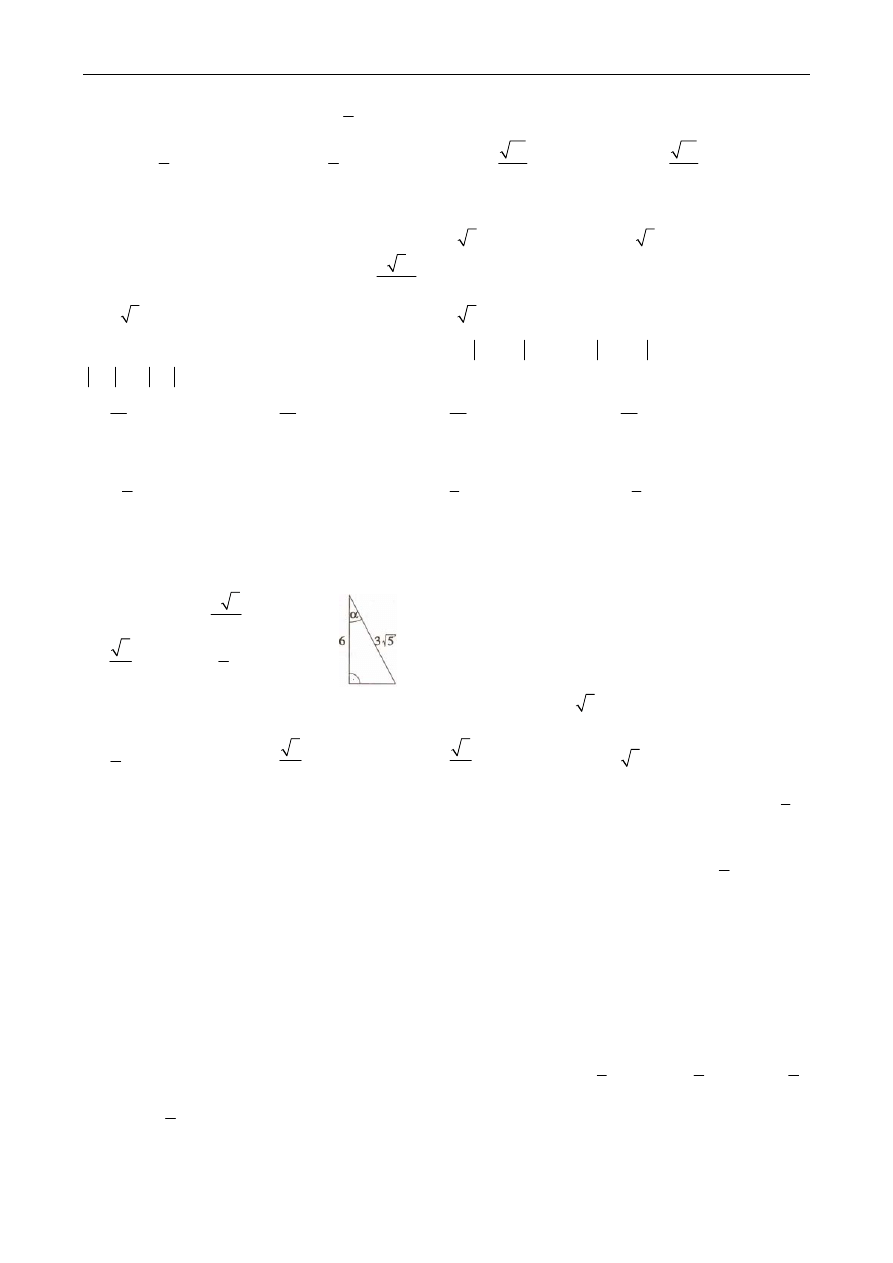
Zestaw 2
Trygonometria
Strona 2
Zadanie 13. Kąt
α
jest ostry i
1
cos
4
α
= . Wówczas:
A.
3
sin
4
α
< B.
3
sin
4
α
= C.
13
sin
4
α
>
D.
13
sin
4
α
=
Zadanie 14. Tymek leżąc w odległości 10 m od drzewa widzi jego wierzchołek pod kątem
. Drzewo ma
wysokość:
45
D
A. 5 m
B. 10 m
C. 5 3 m
D. 10 3 m
Zadanie 15. Wartość wyrażenia
3
2sin 30
tg 60
+
D
D
jest równa:
A. 2 3 B.
2
C.
3 3 D.
0
Zadanie 16. Dany jest trójkąt prostokątny ABC, w którym
90
ACB
∠
=
D
oraz
BAC
α
∠
= . Mając dane
5,
13
AC
AB
=
=
, wartość tg
α
wynosi:
A.
13
5
B.
5
13
C.
12
5
D.
5
12
Zadanie 17. Wartość wyrażenia
wynosi:
sin 30
cos30 tg 30
−
⋅
D
D
D
A.
1
2
− B.
0
C.
1
3
D.
1
3
−
Zadanie 18. Po uproszczeniu wyrażenia
2
sin
sin cos
α
α
−
α
otrzymujemy:
A.
3
sin
α
B.
2
cos
α
C.
2
s
1 co
α
D.
sin
α
−
Zadanie 19. W trójkącie prostokątnym (patrz rysunek) tg
α
wynosi:
A. 2
B.
2 5
5
C.
5
5
D.
1
2
Zadanie 20. Przyprostokątne w trójkącie prostokątnym mają długości 2,
2 3 . Tangens większego z kątów
ostrych w tym trójkącie wynosi:
A.
1
2
B.
3
C.
3
3
D.
2
3
Zadanie 21. Z dokładnością do jednego stopnia podaj miarę takiego kąta ostrego
α
, dla którego
1
23
α
=
D
D
D
67
α
=
D
tg
2
3
α
=
.
A.
B.
24
α
=
C.
66
α
=
D.
Zadanie 22. Z dokładnością do jednego stopnia podaj miarę takiego kąta ostrego
α
, że
2
41
α
=
D
D
D
23
α
=
D
D
43
40
D
cos
3
α
= .
A.
B.
42
α
=
C.
48
α
=
D.
49
α
=
D
Zadanie 23. W trójkącie prostokątnym przyprostokątne mają długość 3 cm i 7 cm. Podaj z dokładnością do
jednego stopnia miarę najmniejszego kąta tego trójkąta.
A.
B.
24
α
=
C.
42
α
=
D
D.
α
=
D
Zadanie 24. W trójkącie prostokątnym najdłuższy bok ma 10, a najmniejszy kąt ma miarę
. Długość
średniego boku najdokładniej określa liczba:
A. 6,4
B. 6,5
C. 7,6
D. 7,7
Zadanie 25. O pewnym kącie ostrym
α
podano cztery informacje: I.
3
sin
α
5
= , II.
5
cos
α
=
4
, III.
3
tg
α
4
= i
IV.
4
ctg
α
=
3
. Fałszywą informacją jest:
A. I
B. II
C. III
D. IV
Zestaw 2
Trygonometria
Strona 3
ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI
Zadanie 1. Oblicz wartość wyrażenia:
2
cos 30
3tg30 tg 60
1 3tg 45
−
⋅
−
D
D
D
D
.
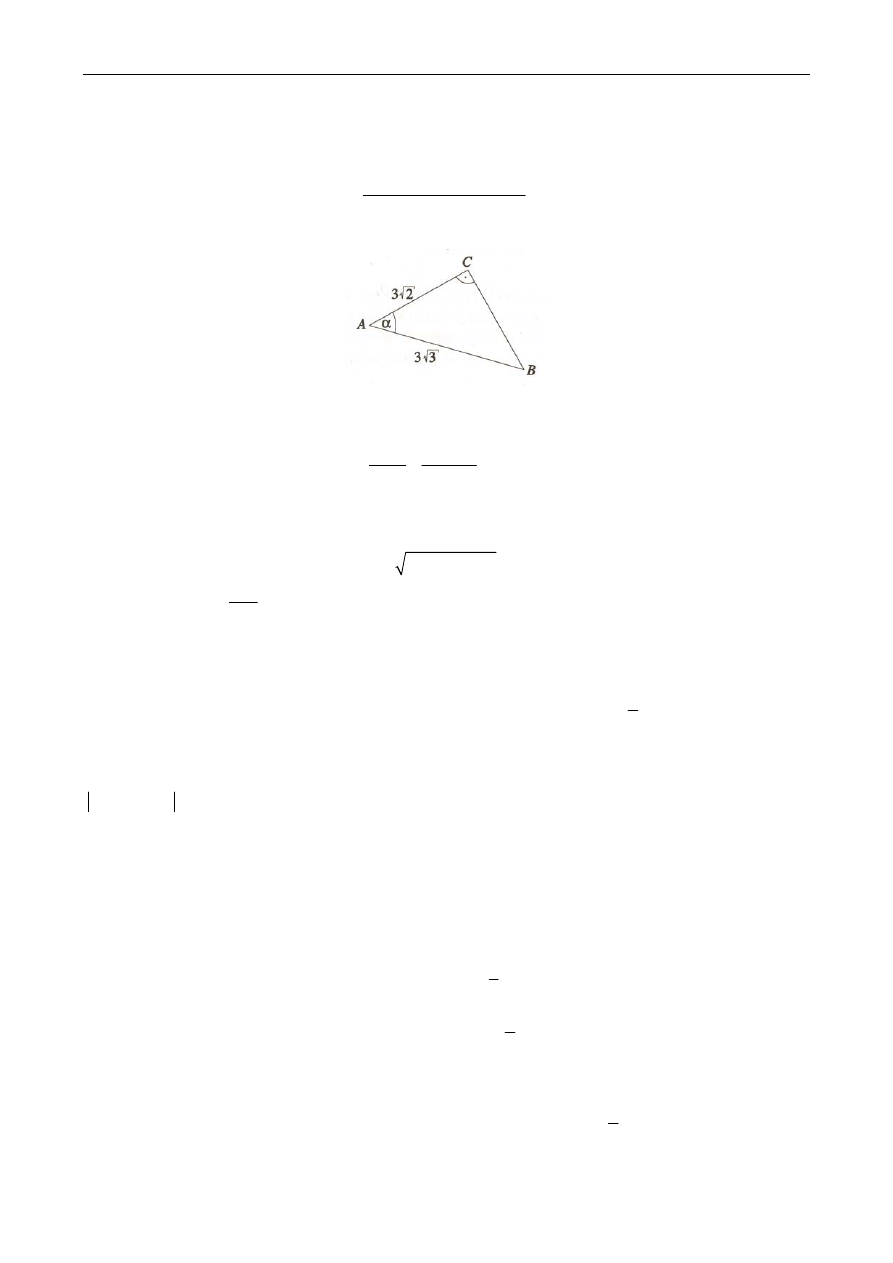
Zadanie 2. Oblicz
sin
α
(patrz rysunek).
Zadanie 3. Sprawdź, czy dla każdego kąta ostrego
α
zachodzi równość:
1
cos
tg
cos
1 sin
α
α
α
−
=
.
α
+
Zadanie 4. Wiadomo, że
α
jest kątem ostrym i tg
ctg
4
α
α
= . Oblicz
+
2
2
tg
ctg
α
α
+
Wskazówka:
1
ctg
tg
α
α
=
30
D
.
Zadanie 5. Drzewo rzuca cień długości 21 m. Oblicz wysokość drzewa wiedząc, że promienie słoneczne
padają na płaszczyznę poziomą pod kątem
. Wynik podaj z dokładnością do jednego metra.
Zadanie 6. W trójkącie prostokątnym sinus jednego z kątów ostrych ma wartość
4
5
. Oblicz długości
przyprostokątnych tego trójkąta wiedząc, że przeciwprostokątna ma długość 10 cm.
Zadanie 7. Boki trójkąta prostokątnego mają długości: 5, 12, 13. Jaką wartość przyjmuje wyrażenie
sin
cos
α
α
−
30
D
D
, jeżeli
α
jest najmniejszym kątem w tym trójkącie?
ZADANIA OTWARTE ROZSZERZONEJ ODPOWIEDZI
Zadanie 8. Na morzu widać z żaglówki światło latarni morskiej pod kątem o mierze
do poziomu. Po
przepłynięciu 50 m w kierunku latarni światło latarni widać pod kątem o mierze 60 do poziomu. Oblicz
wysokość latarni. Wynik podaj z dokładnością do 0,1 m.
Zadanie 9. Uzasadnij, że nie istnieje kąt ostry
α
taki, że:
5
sin
cos
3
α
α
.
+
=
Zadanie 10. Wiedząc, że
α
jest kątem ostrym i
1
sin
cos
4
α
α
oblicz
−
=
sin
cos
α
⋅
α
.
Zadanie 11. Długość boku równoległoboku jest o 3 większa od wysokości opuszczonej na ten bok. Wyznacz
długości boków równoległoboku wiedząc, że jego pole jest równe 10 i
3
sin
4
α
= , gdzie
α
jest kątem ostrym
równoległoboku.