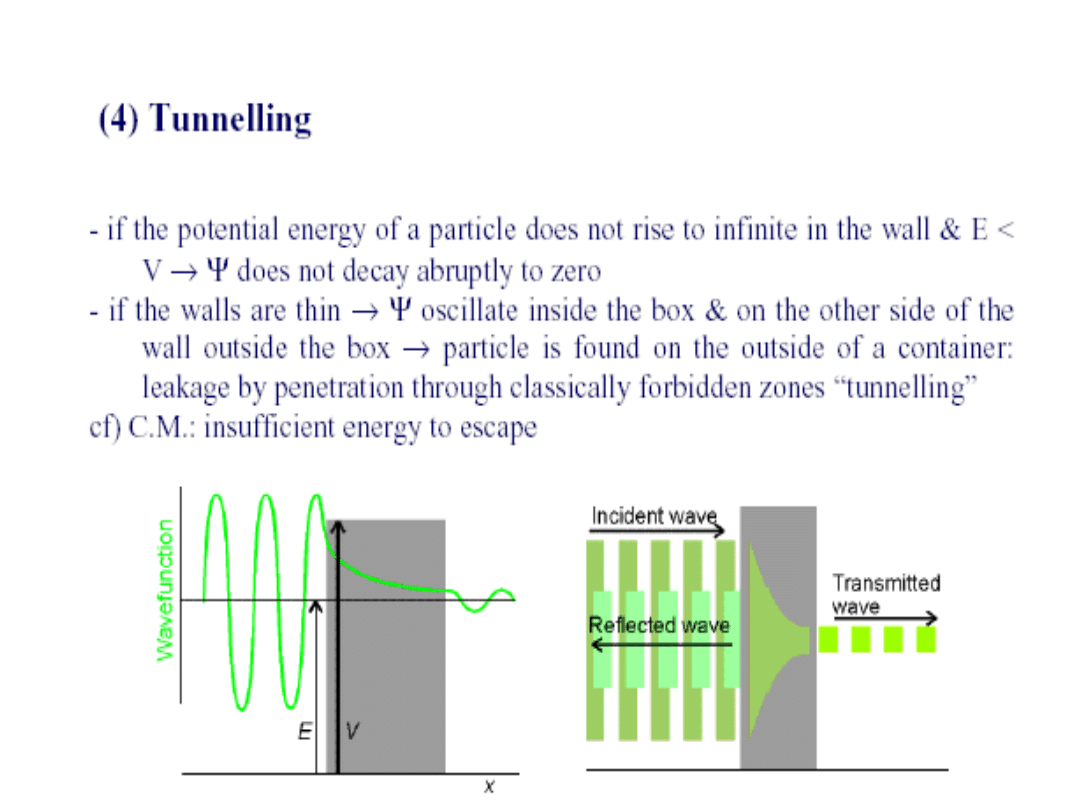
Tunelowanie przez barierę potencjału.

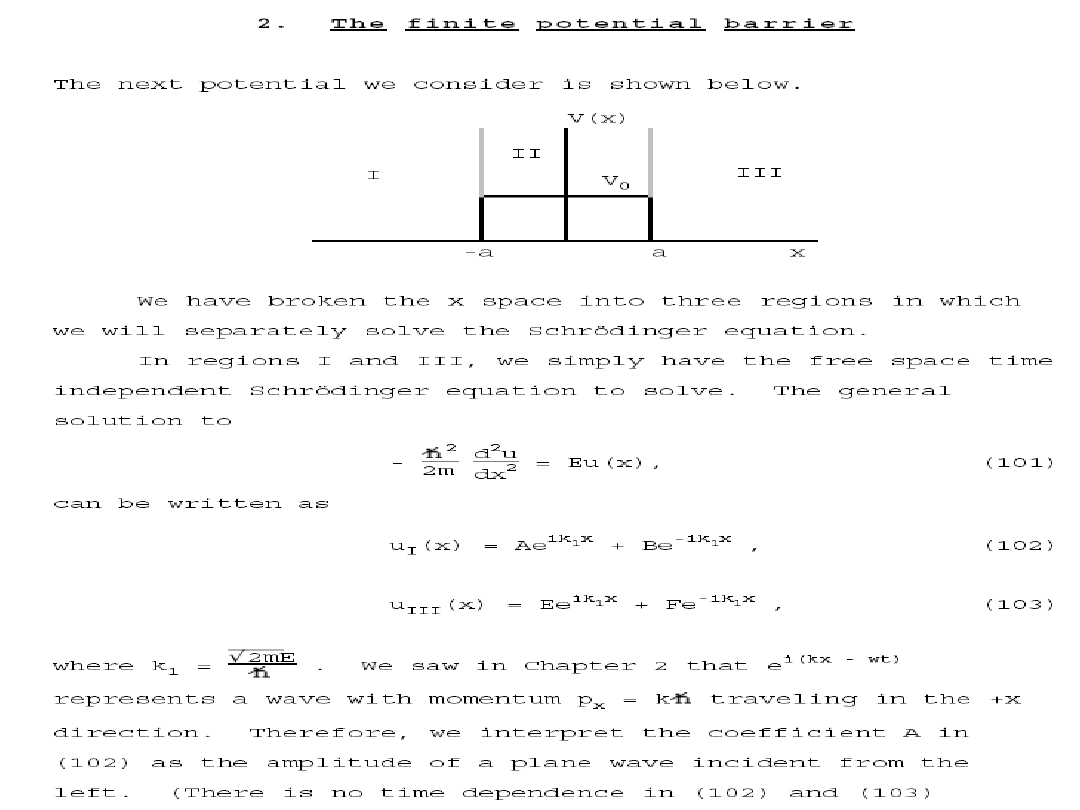
The quantum mechanical result is one of the most remarkable

features of modern physics. There is a finite probability that the particle

can penetrate the barrier and even emerge on the other side!

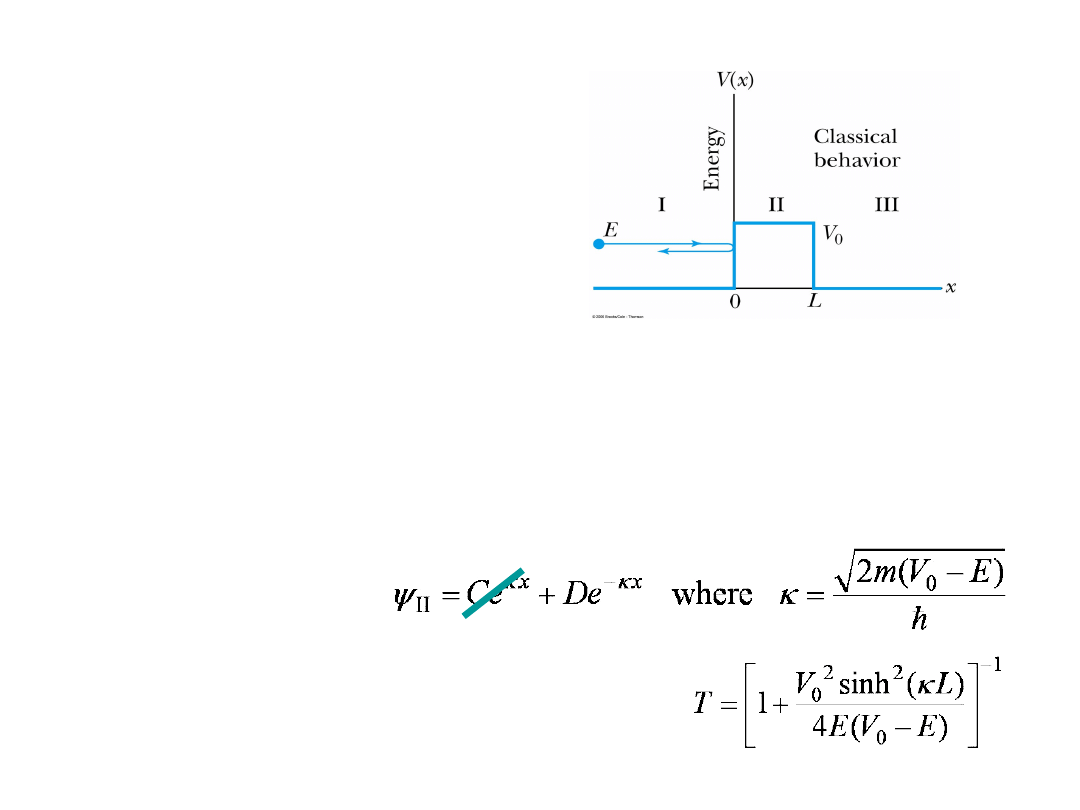
The wave function

in region II becomes:

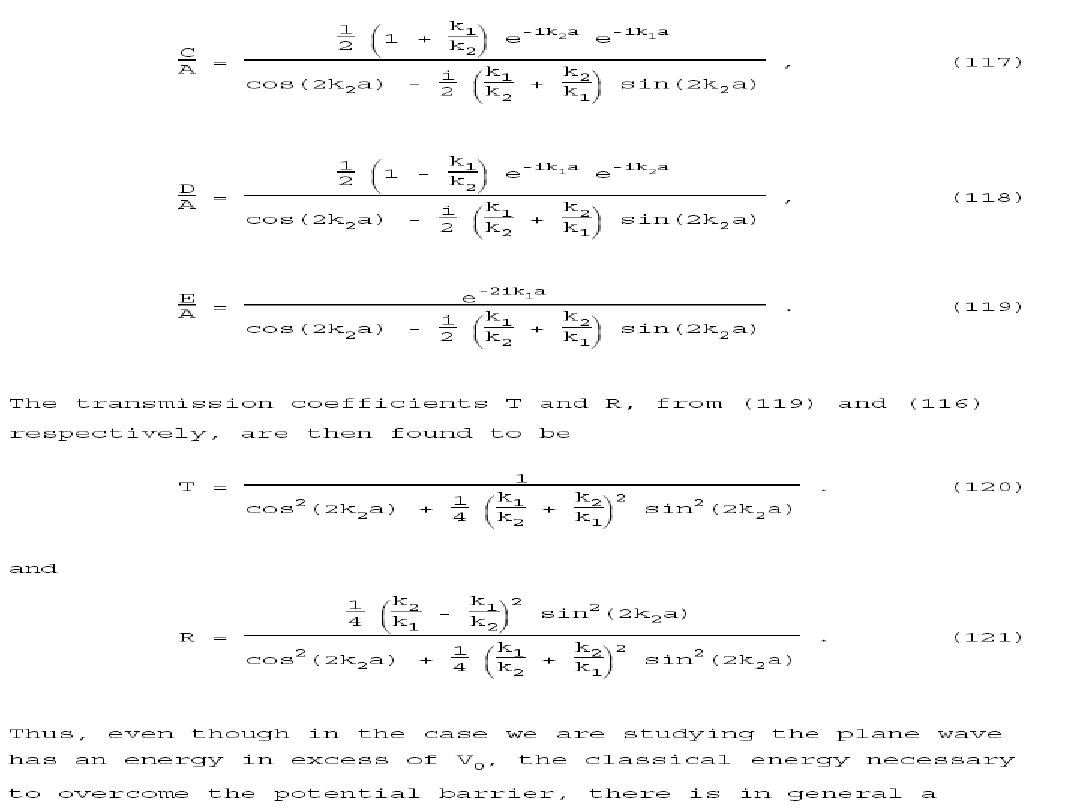
The transmission probability that

describes the phenomenon of tunneling is:

Tunelowanie

•Now we consider the situation
where classically the particle
doesn’t have enough energy to
surmount the potential barrier, E
< V

0

.

Reflection and Transmission

•The wave function will consist of an incident wave, a reflected wave, and a
transmitted wave.
•The potentials and the Schrödinger wave equation for the three regions are as
follows:
•
•
•
•
•The corresponding solutions are:
•
•

•

•As the wave moves from left to right, we can simplify the wave functions to:

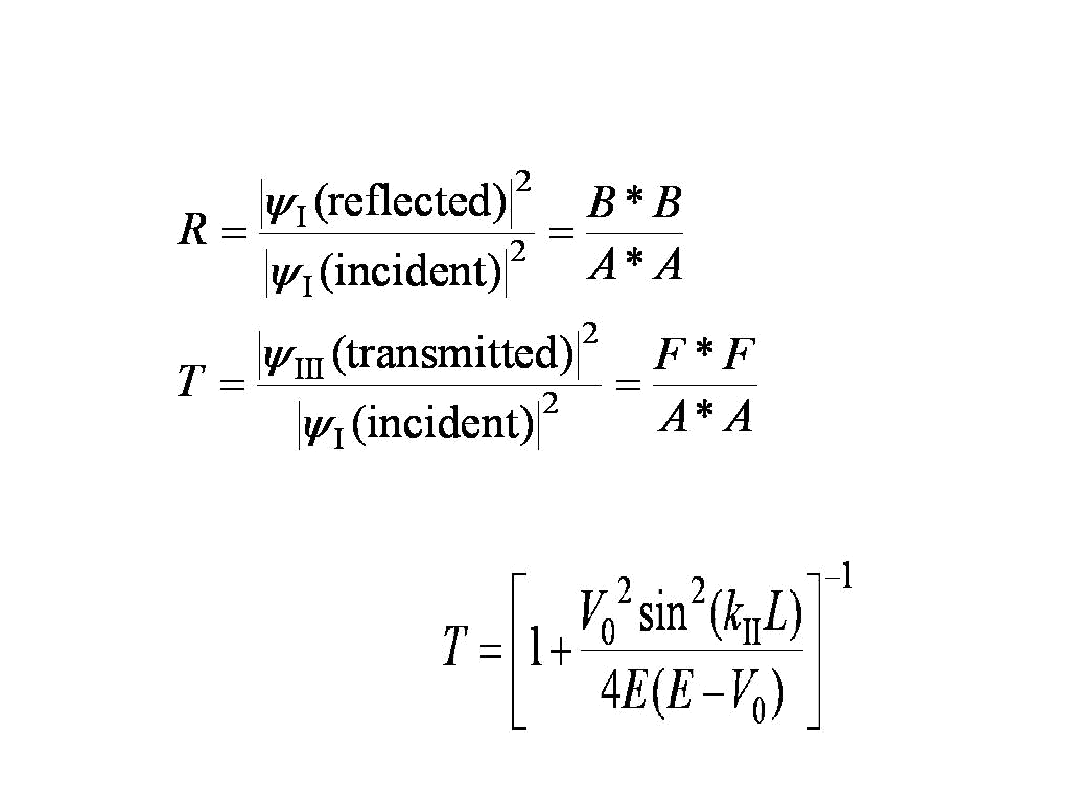
Współczynnik Odbicia i

Transmisji

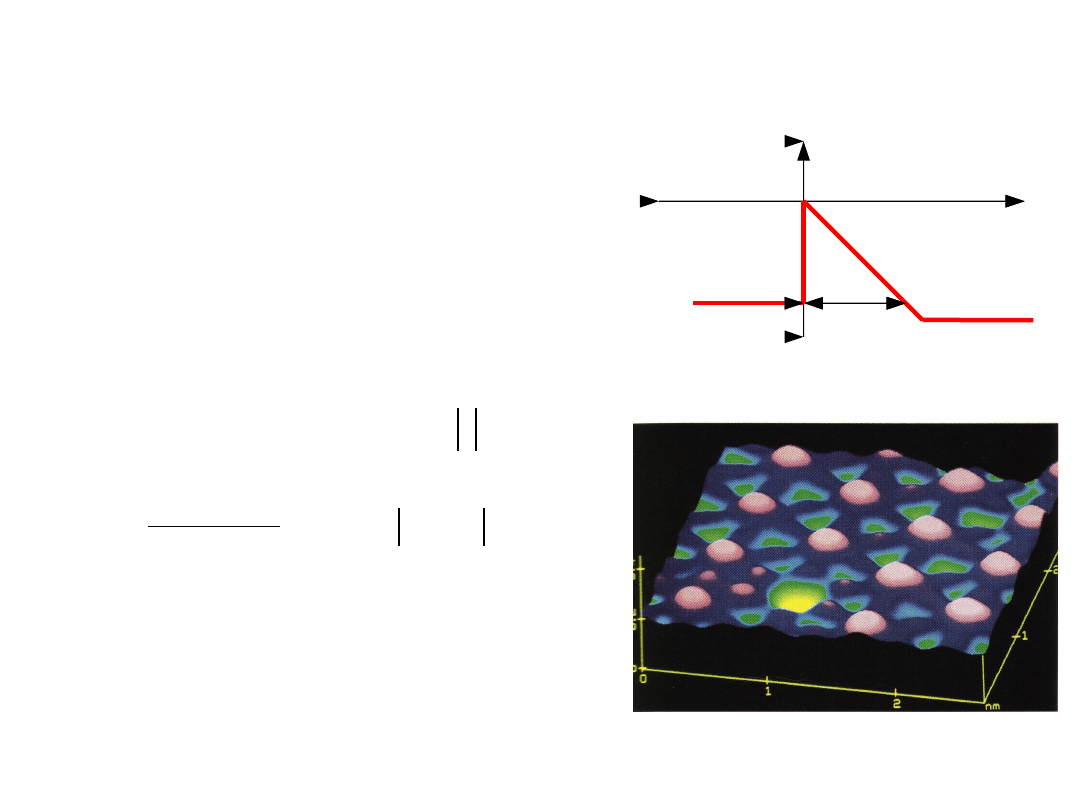
Examples of Tunnelling

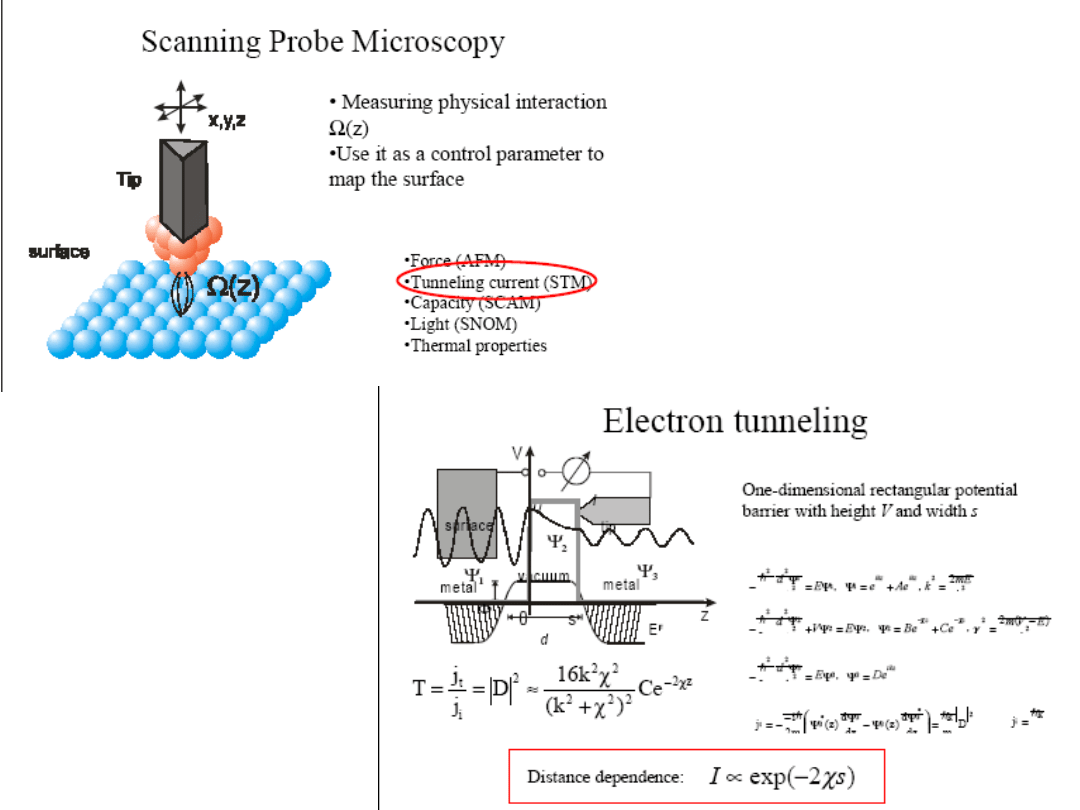
3. Scanning tunnelling microscope

STM image of Iodine atoms on platinum.
The yellow pocket is a missing Iodine atom

A conducting probe with a very sharp tip is
brought close to a metal. Electrons tunnel through
the empty space to the tip. Tunnelling current is so
sensitive to the metal/probe distance (barrier
width) that even individual atoms can be mapped.

0

4eV

E V

−

ﾻ

(

)

0

2

2

2m E V

q

−

=

h

( )

1

1 A

q

−

:

2

2qa

t

e

−

:

If a changes by 0.01A (~1/100

th

of the atomic size)

then current changes by a factor of 0.98,
i.e. a 2% change, which is detectable

Tunnelling current proportional to

and

so

Vacuum

Material

V

x

Probe

a

Wymyślony przez G. Binning’a i H. Rohrer’a w 1981r. Nagroda Nobla w 1986r.

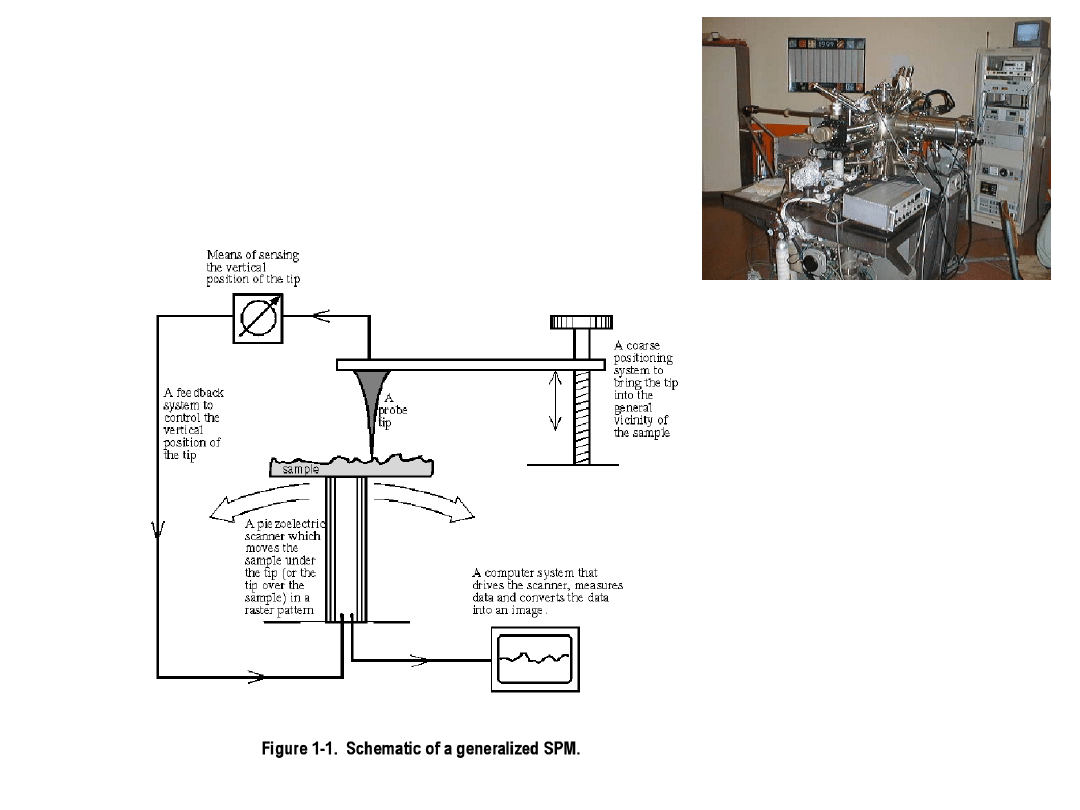
budowa

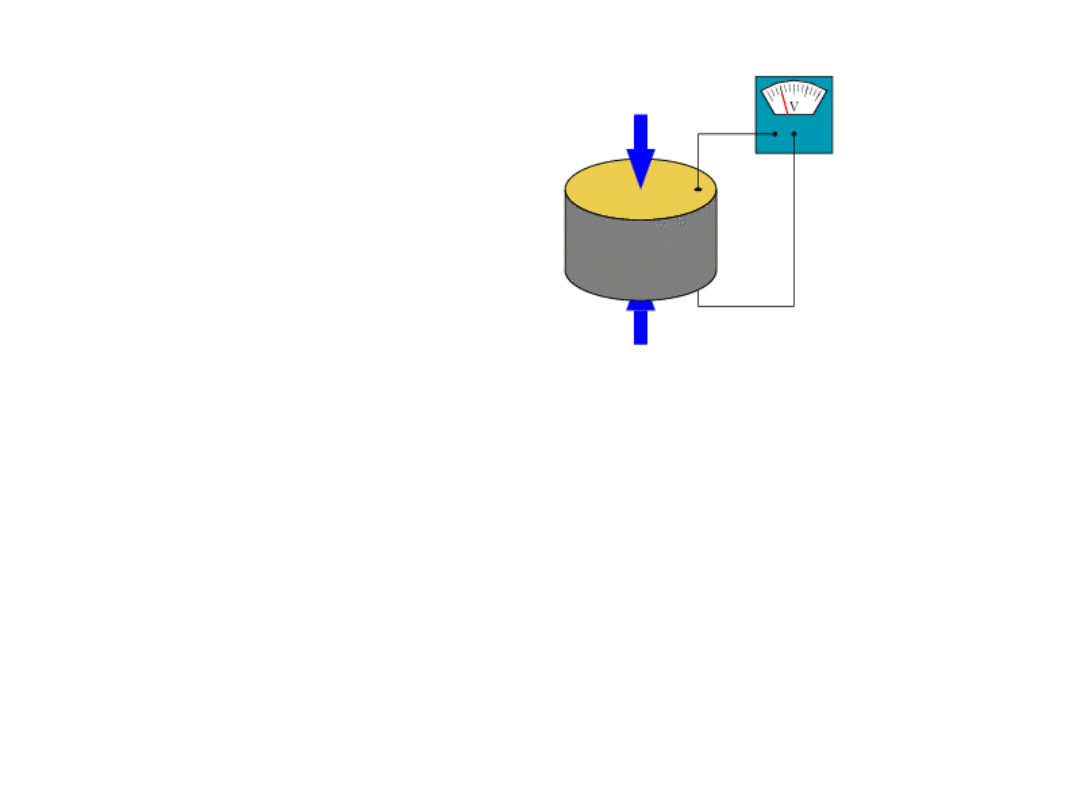
efekt piezoelektryczny

Aby skanować z wystarczająco dużą

rozdzielczością wymagane są

przesunięcia końcówki skanującej

rzędu 1A.

Przesunięcie tego typu zostało

osiągnięte dzięki materiałom

piezoelektrycznym.

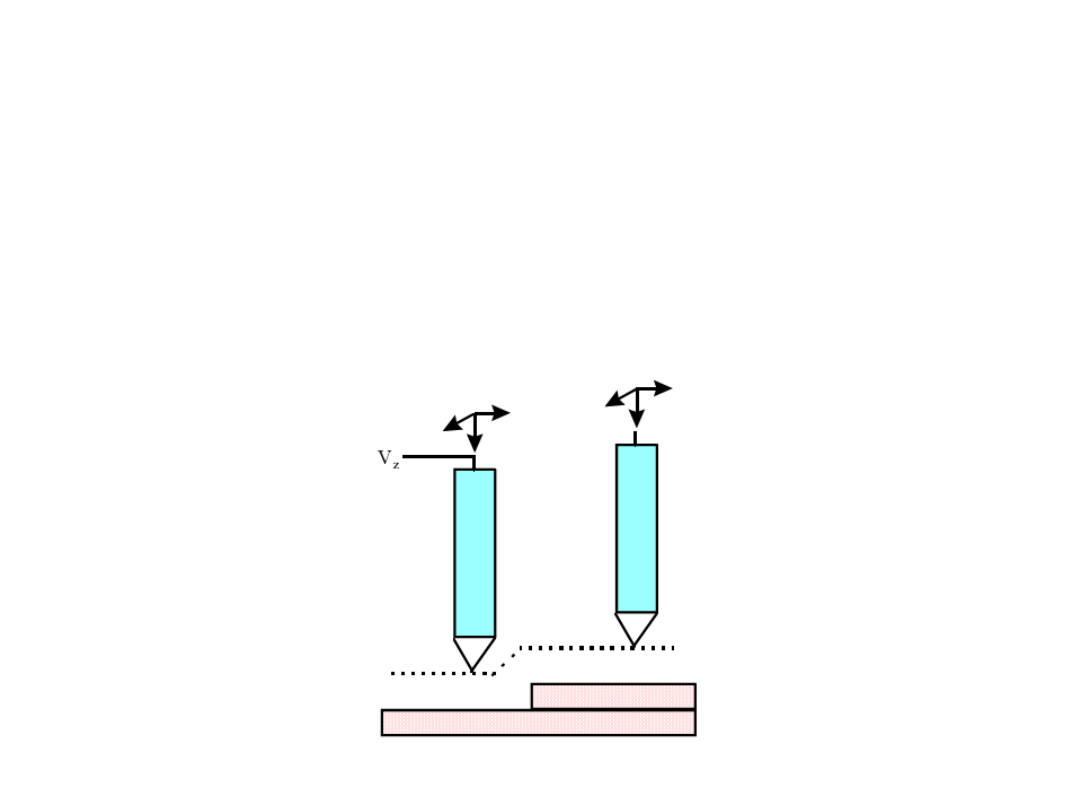
metody badania powierzchni



metoda stałego prądu – stała szerokość
przerwy

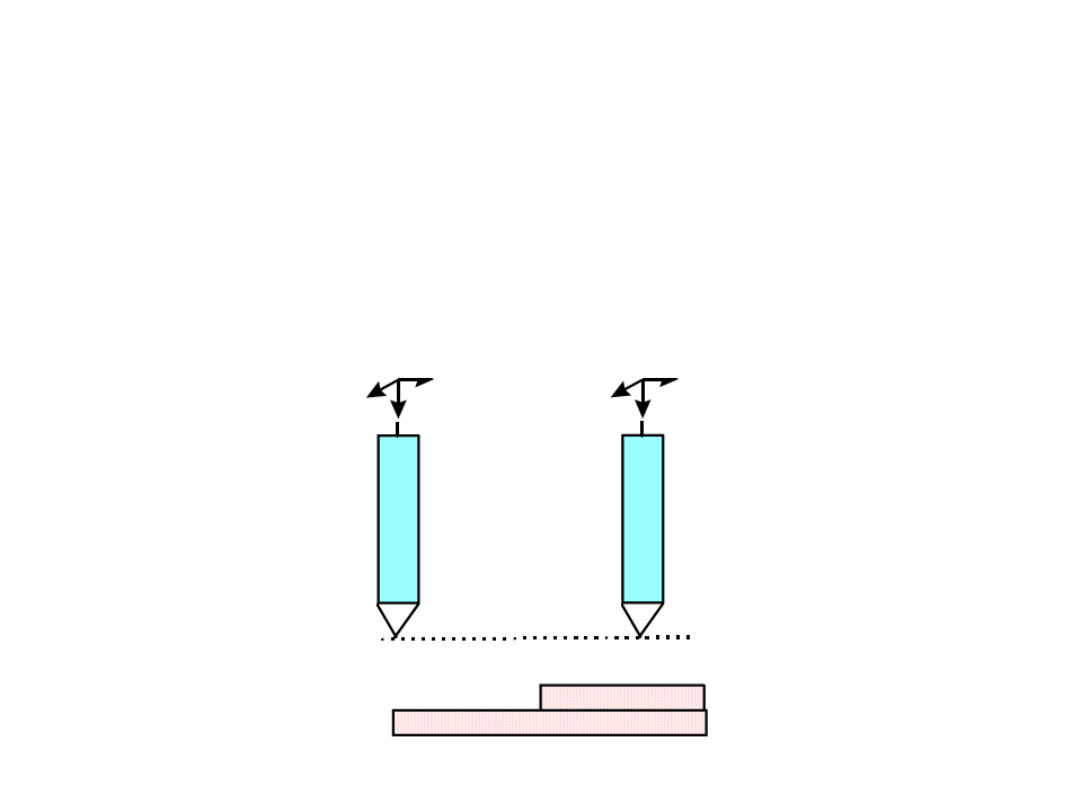
metody badania powierzchni



metoda stałej wysokości – położenie
końcówki skanującej się nie zmienia.

Particles can tunnel through classically forbidden regions.
Transmitted flux decreases exponentially with barrier height and width

Summary of Flux and Tunnelling

The

particle flux density

is

*

*

i

( , )

2

j x t

m

x

x

�

�

−

Ψ

Ψ

ﾻ

ﾻ

=

Ψ

− Ψ

�

�

ﾶ

ﾶ

�

�

h

(

)

0

2

2

2m E V

q

−

=

h

2

2qa

t

e

−

:

We get transmission and reflection at potential steps.
There is reflection even when E > V

0

.

Only recover classical limit for E >> V

0

(correspondence principle)

(

)

(

)

0

0

2

,

2

,

k K

k

E V

r

t

k K

k K

k iq

k

E V

r

t

k iq

k iq

−

>

=

=

ﾻ

+

+

−

<

=

=

ﾶ

+

+

2 2

2

2

2 2

0

0

0

0

,

(

),

(

)

2

2

2

k

K

q

E

E V

E V

V

E

E V

m

m

m

=

− =

>

− =

<

h

h

h

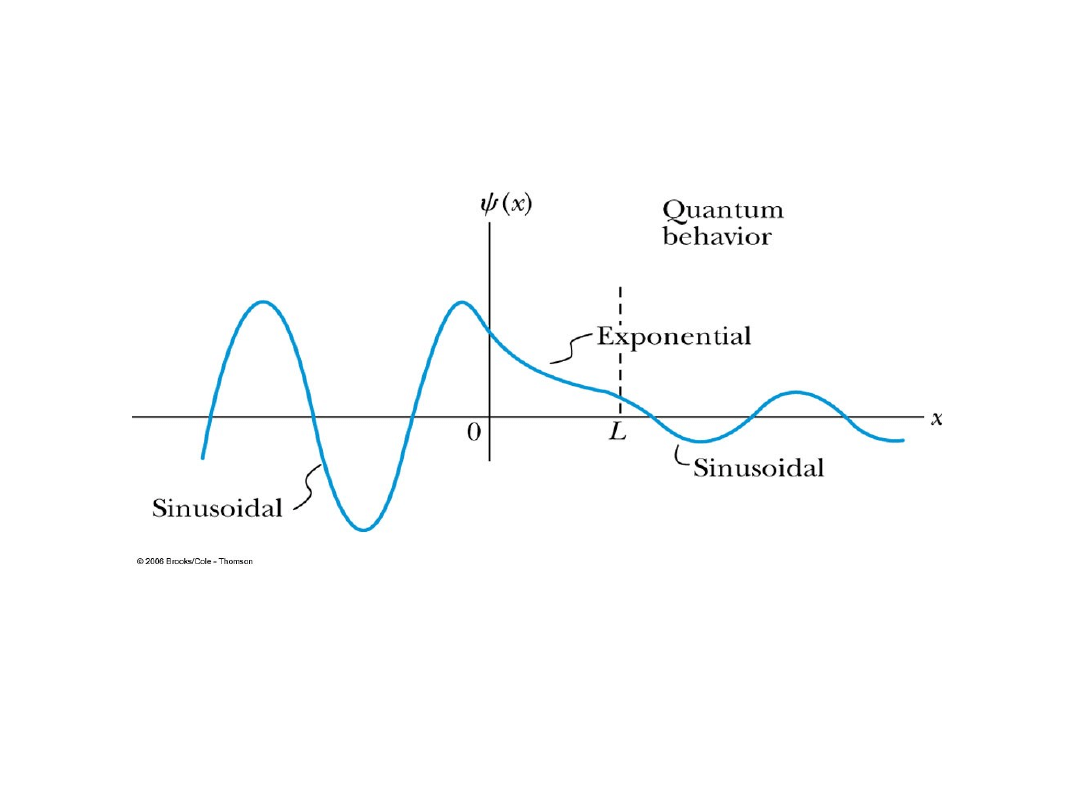
Tunelująca funkcja falowa

przed barierą, w barierze I po przejściu przez barierę.

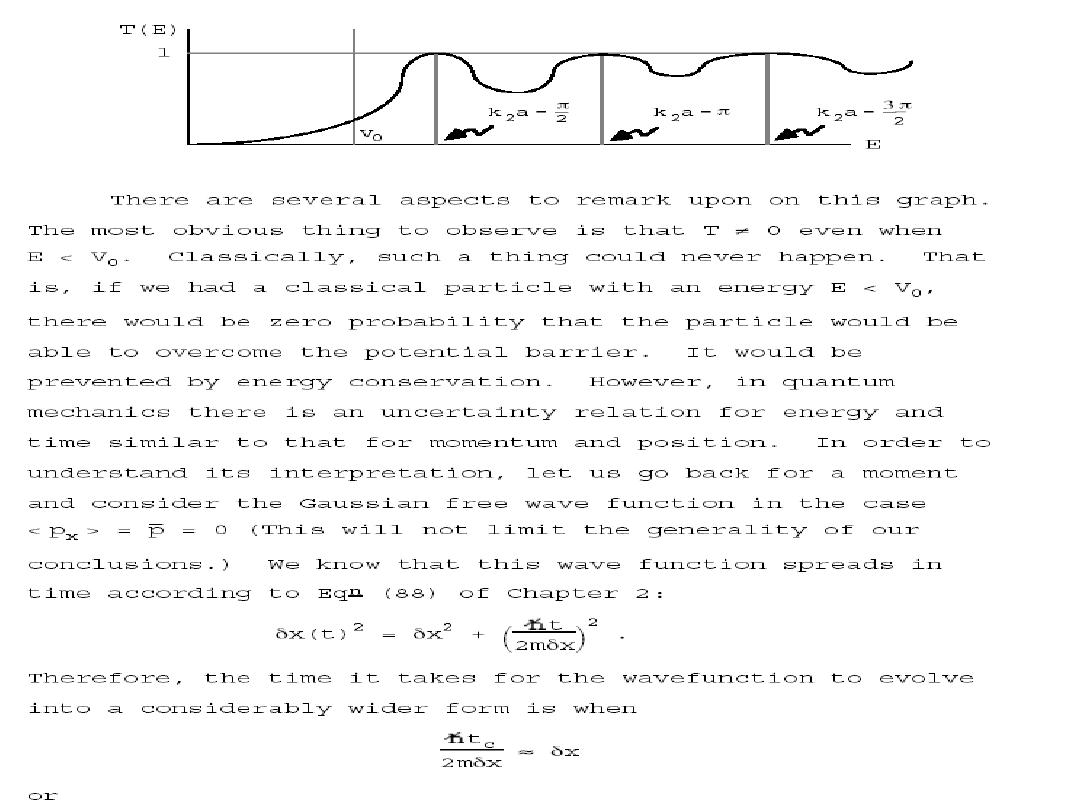
This violation of classical physics is allowed by the uncertainty principle.
The particle can violate classical physics by

E for a short time, ﾶt ~ ħ / ﾶE.

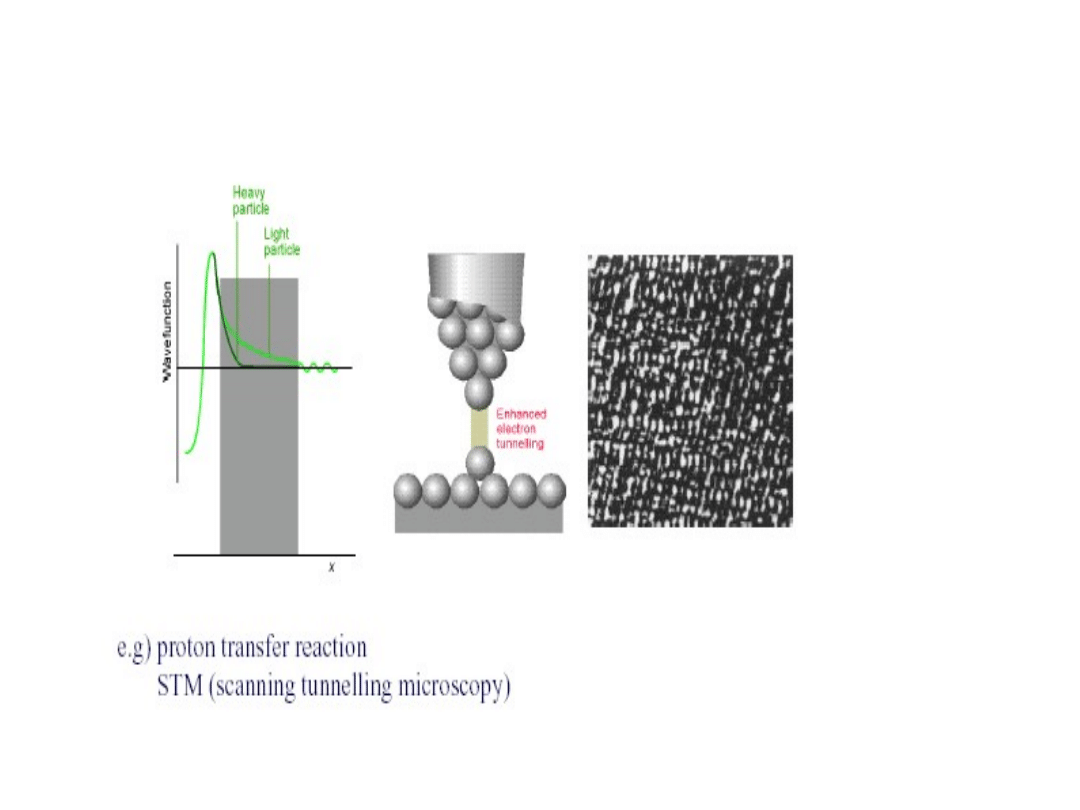
Zastosowanie efektu tunelowego w mikroskopie skaningowym STM

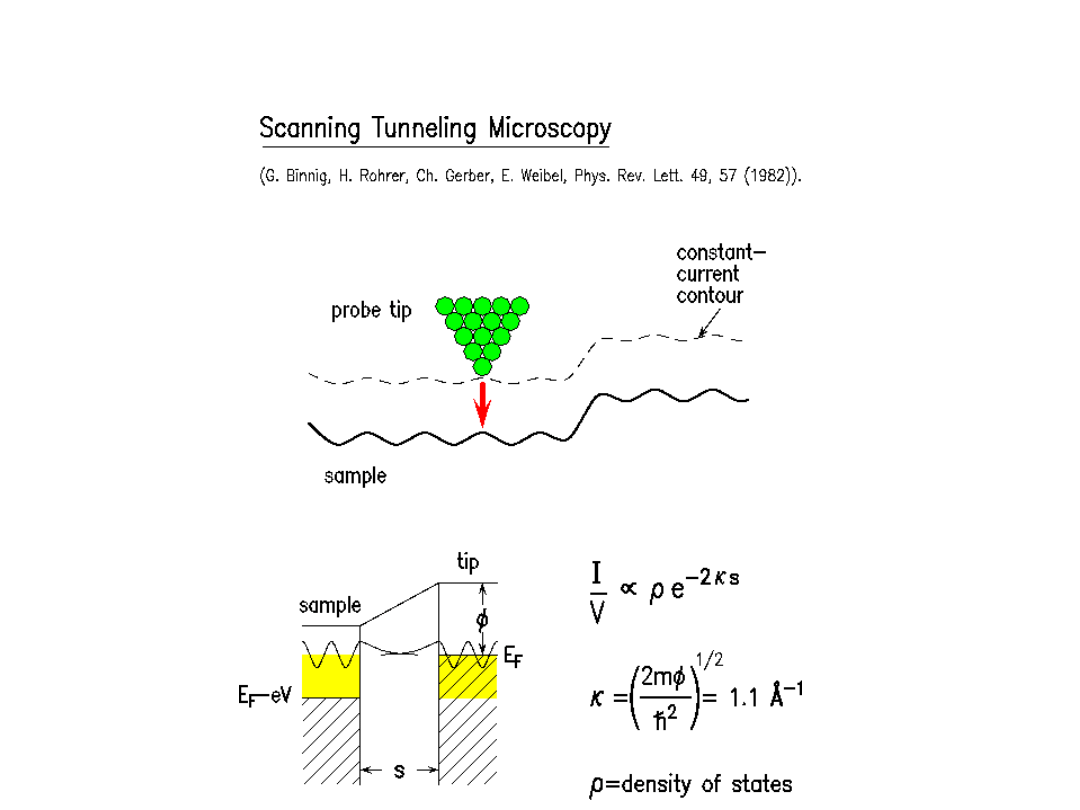
Schemat działania STM: płynący prąd tunelowy zależy od gęstości chmury
elektronowej, stąd jest wykorzystany do obrazowania powierzchni.

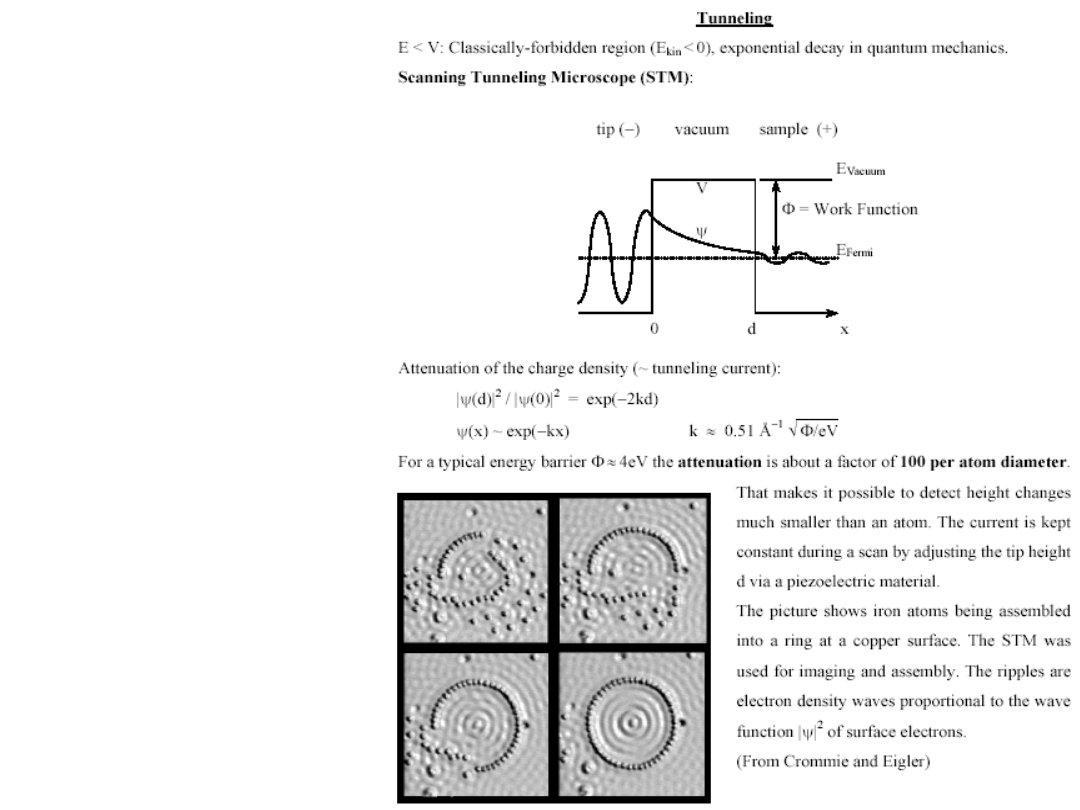
Zastosowanie
mikroskopu STM do
manipulacji pojedyńczymi
atomami (na rys. ułożony
okrąg z atomów żelaza
na podłożu miedzianym)

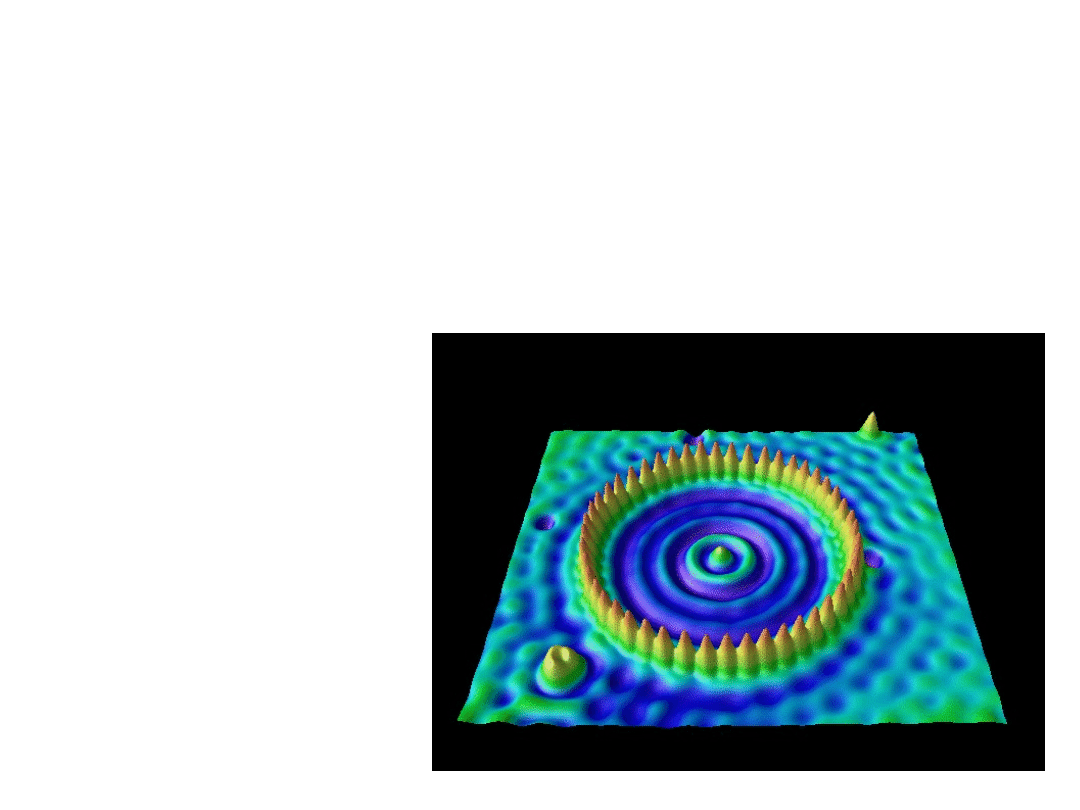
zdjęcia STM

Fala stojąca lokalnej
gęstości stanów na
powierzchni Cu jest wynikiem
rozpraszania dwu
wymiarowego
gazu elektronowego na
atomach Fe.

zdjęcia STM

powierzchnia metalu