Rotacje bryły sztywnej

H =

1
2

I 

2

=

L

2

2I

Energia kinetyczna ruchu
obrotowego bryły sztywnej dla
obrotu wokół osi głównej



H =



L

2

2I

Stąd operator hamiltona



L

2

=−ℏ

2

[

1

sin 

∂

∂ 



sin  ∂

∂ 



1

sin

2



∂

2

∂ 

2

]



H Y  ,=E Y  , 

−ℏ

2

2I

[

1

sin 

∂

∂ 



sin  ∂

∂ 



1

sin

2



∂

2

∂

2

]

Y  ,=E Y  ,



L

2

2I

Y  ,=E Y  ,

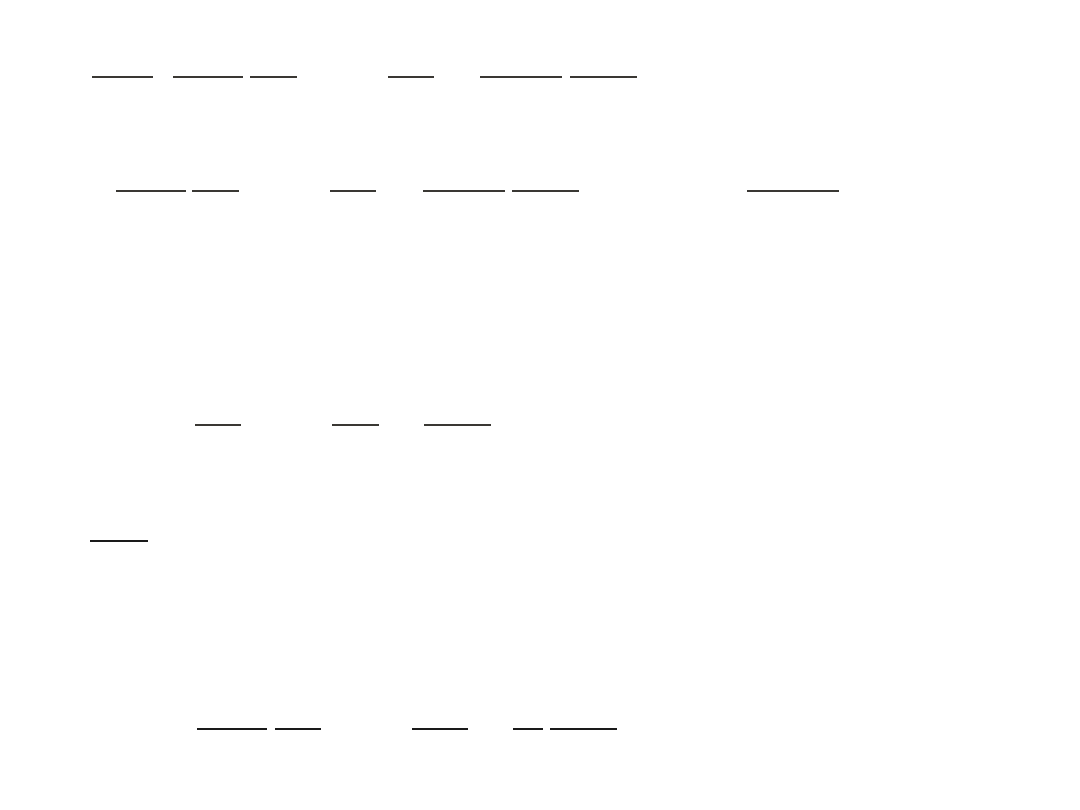
−ℏ

2

2I

[

1

sin 

∂

∂ 



sin  ∂

∂ 



1

sin

2



∂

2

∂

2

]

Y  ,=E Y  ,

[

1

sin 

∂

∂ 



sin  ∂

∂ 



1

sin

2



∂

2

∂ 

2

]

Y  , =

−

E 2I

ℏ

2

Y  , 

[

sin  ∂

∂ 



sin  ∂

∂ 

 ∂

2

∂ 

2

]

Y  ,=−⋅sin

2



Y  ,

//⋅sin

2



=

2IE

ℏ

2

Y  , =⋅=

// / 

sin 



∂

∂ 



sin 

∂

∂



1



∂

2



∂ 

2



sin

2

=

0

Szukamy rozwiązania w postaci:

sin 



∂

∂ 



sin 

∂

∂



sin

2

=−

1



∂

2



∂ 

2

−

1



∂

2



∂ 

2

=

m

2

sin 



∂

∂ 



sin 

∂

∂



sin

2

=

m

2

∂

2



∂ 

2



m

2

=

0

=

a expi m 



2 =

expi m =1

m=0,±1,±2,±3,⋯

L=P=constans=m

2

x=cos

x

2

=

cos

2



1−x

2

=

sin

2



dx

d 

=−

sin 



P x 



1−x

2



d

2

P

dx

2

−

2x

dP

dx

[−

m

2



1−x

2



]

P=0

po przekształceniach otrzymujemy

Ponieważ

jest stałą wyznaczyć ją można dla m=0

Drugie z równań po podstawieniu

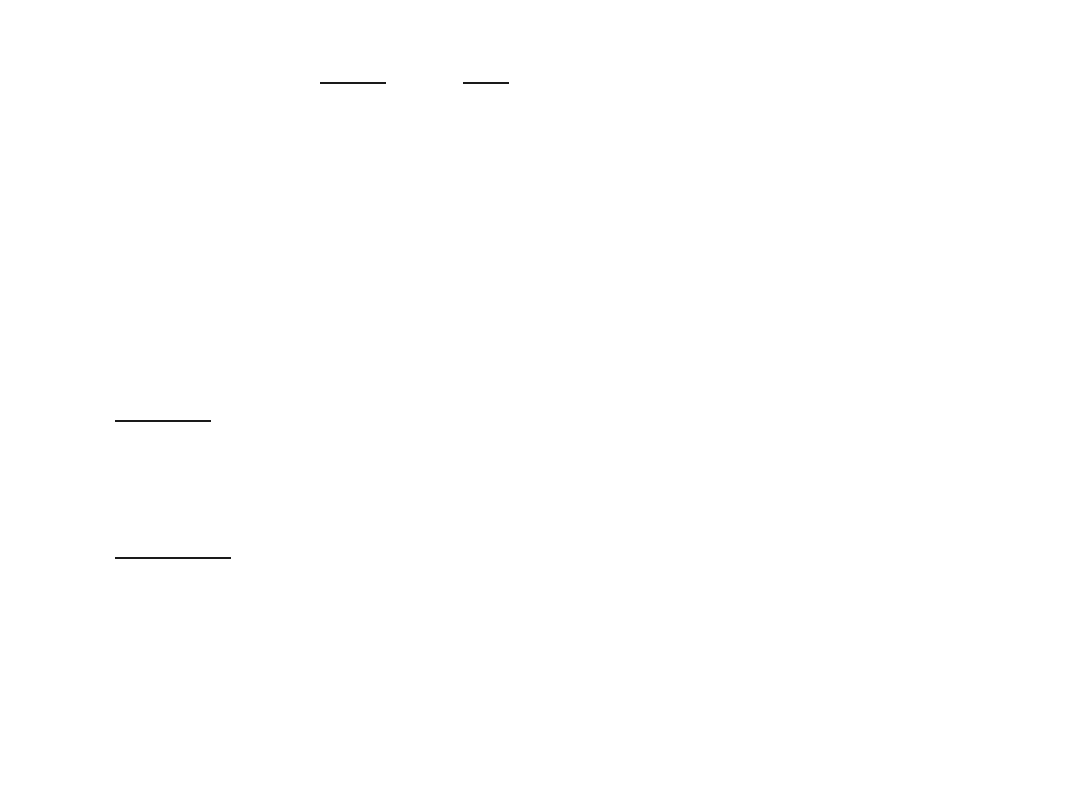
szukamy rozwiązania w postaci

P  x=

∑

k

a

k

x

k

k=0,1, 2,3,⋯, K



1−x

2



d

2

P

dx

2

−

2x

dP

dx



P=0

dP  x

dx

=

∑

k

a

k

k x



k−1

d

2

P  x

dx

2

=

∑

k

a

k

k k−1 x



k−2 

żeby istniało rozwiązanie trywialne x=0

współczynniki przy tej samej potędze

muszą dać 0

a

k2



k1k2−a

k

k k−1−2a

k

k a

k

=

0

a

k2



k1k2=a

k

[

k k1−]

a

k2

a

k

=

k



k2

−





k1k2

żeby szereg był zbieżny

a

k2

a

k



1

a

k2



0

=

k k1

=

l l1

Zamienimy oznaczenie

=

2IE

ℏ

2

E=

l l1 ℏ

2

2I

Y  , =Y

m

l



, =[

2l1

4 



l−∣m∣!



l∣m∣!

]

1
2

P

l

m



cos e

i m 

harmoniki sferyczne

P

l

m



cos=1−cos 

1
2

∣

m∣

d

∣

m∣

P

l



cos

d cos

2



∣

m∣

P

l



cos =

1

2

l

l !

d

l



cos

2

−

1

l

d cos

l

Stowarzyszona
funkcja

Legendre'a

Wielomian

Legendre'a

Ogólnie rozwiązanie obu równań możemy zapisać w
postaci

(

)

(

)

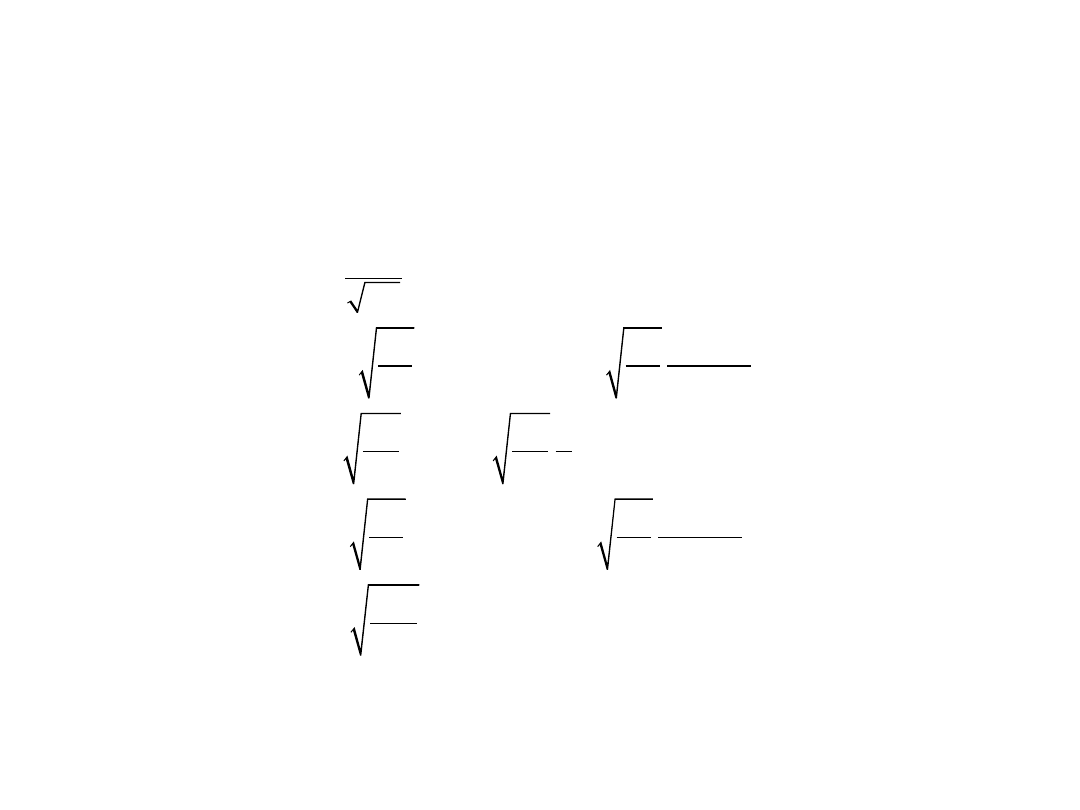
00

11

10

1 1

2

20

1

( , )

4

3

3 (

)

( , )

sin exp( )

8

8

3

3

( , )

cos

4

4

3

3 (

)

( , )

sin exp(

)

8

8

5

,

3cos

1

16

Y

x iy

Y

i

r

z

Y

r

x iy

Y

i

r

Y

θ φ

π

θ φ

θ

φ

π

π

θ φ

θ

π

π

θ φ

θ

φ

π

π

θ φ

θ

π

−

=

+

= −

= −

=

=

−

=

−

=

=

−

Ze względu na występujące we wzorach tych funkicj liczby kwantowe l I m
możemy te funkcje numerować tymi liczbami kwantowymi.

Przykładowe funkcje falowe dla początkowych liczb kwantowych l i m

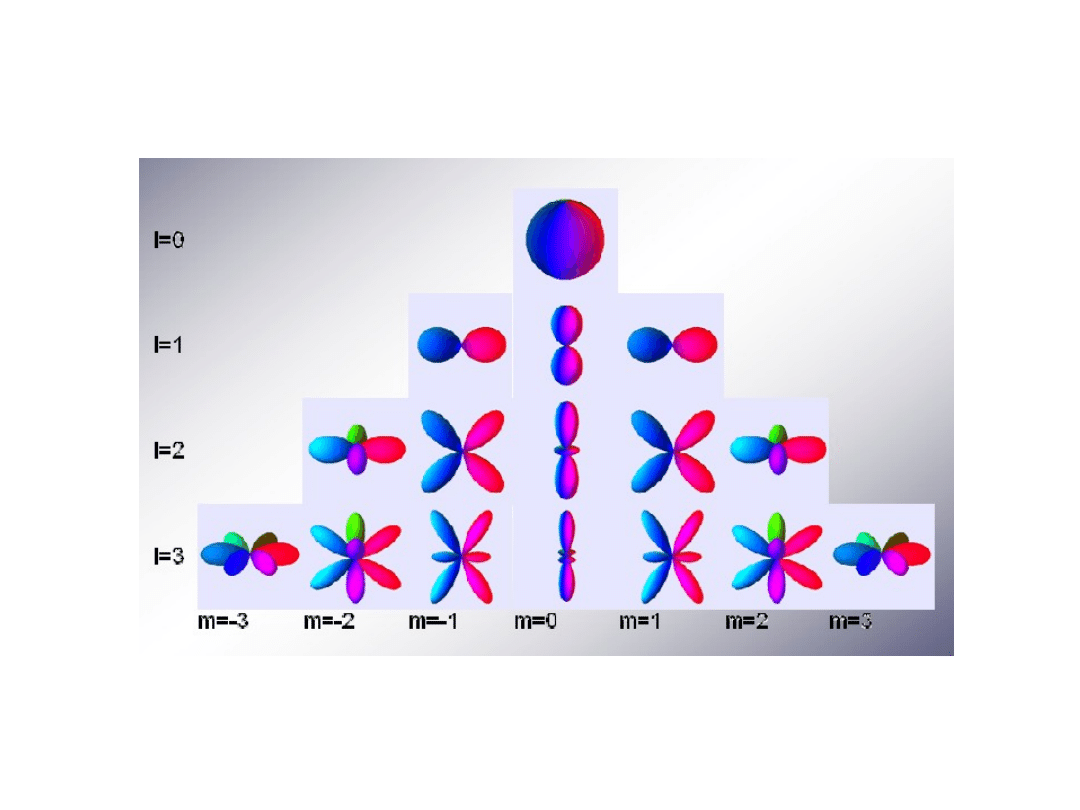
Shapes of the spherical harmonics

Model “planetarny” Bohra atomu wodoru (1913r)

Elektron krąży po orbitach kołowych wokół jądra atomowego. Rolę siły

dośrodkowej spełnia siła oddziaływania elektrycznego. Stabilne orbity to te, dla
których moment pędu elektronu jest całkowitą wielokrotnością h/2



mvr=n h

2 

=

n ℏ

e

2

4  

0

r

2

=

m 

2

r

Stąd

r

n

=

4  

0

ℏ

2

m e

2

n

2

E=E

kin



E

pot

=

m v

2

2



−

e

2

4  

0

r



E

n

=

−

e

2

8 

0

r

n

Atom promieniuje energię porcjami ( kwantami)

To wyjaśniało istnienie linii widmowych.

h =E

n

−

E

n '

=

Rc  1

n '

2

−

1

n

2



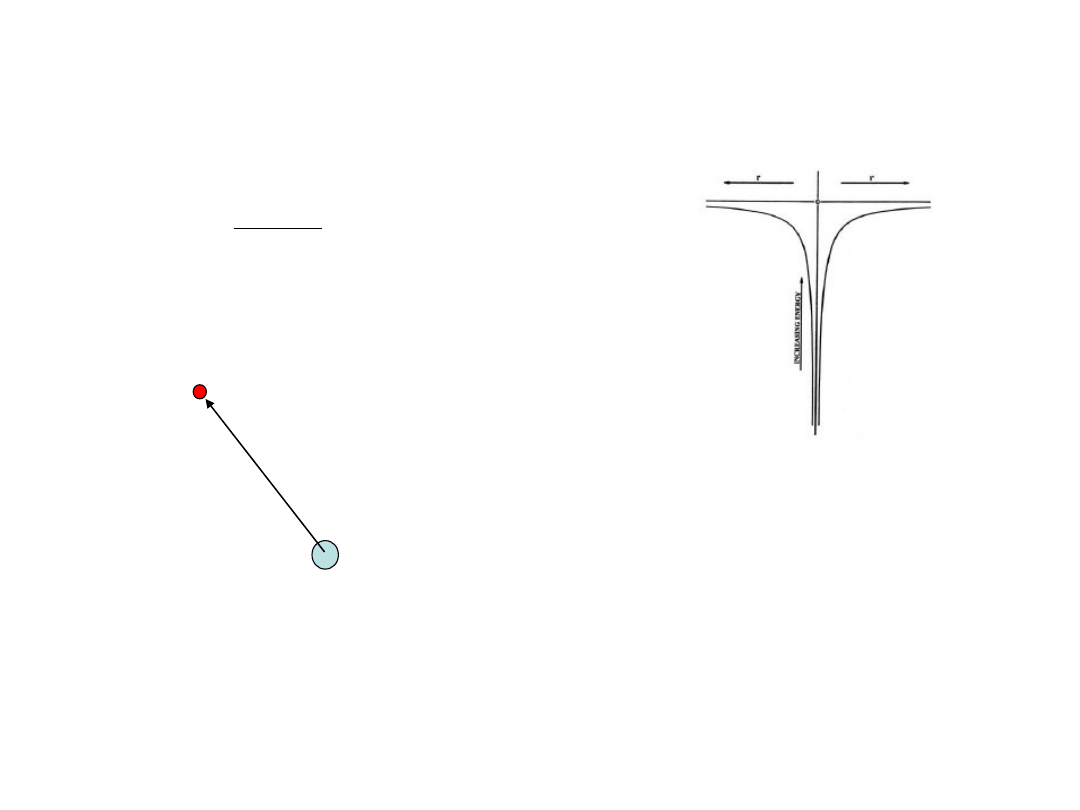
Atom wodoru

2

0

( )

4

Ze

V r

r

πε

= −

r

+Ze

-e

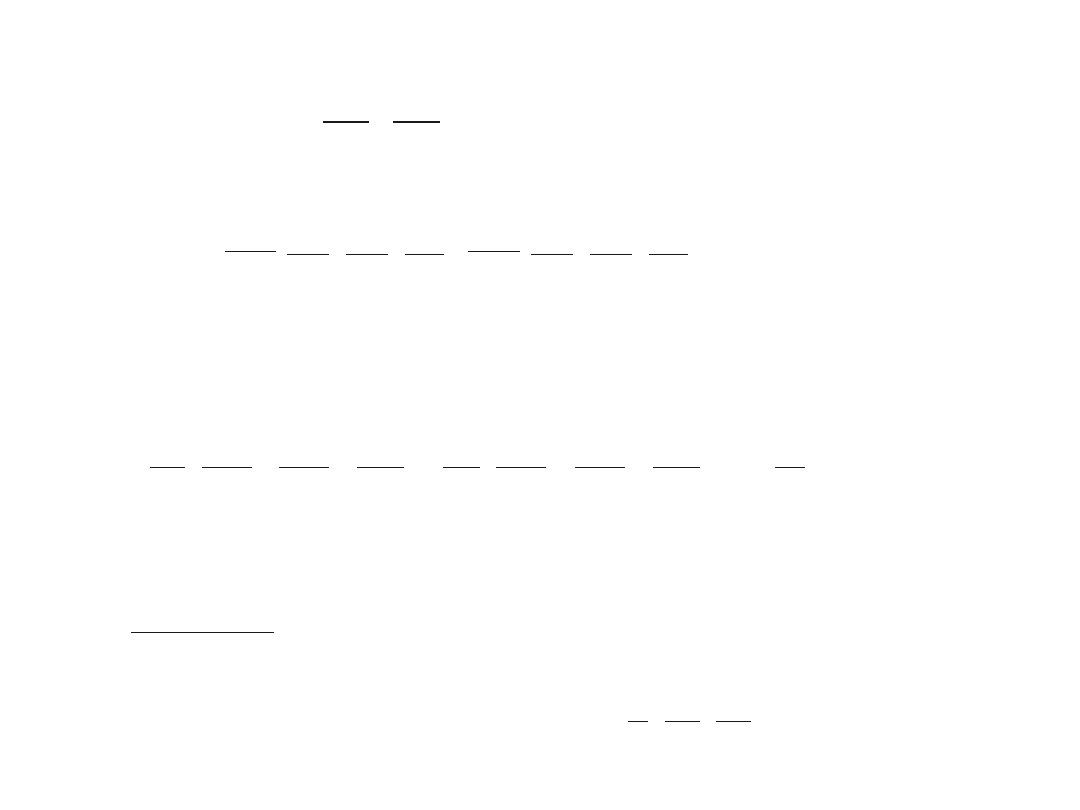
E

total

=

p

1

2

2m

1



p

2

2

2m

2



V  r

1

, r

2



Równanie Schrodingera dla atomu wodoru

p

1

2

=

p

1x

2



p

1y

2



p

1z

2

p

2

2

=

p

2x

2



p

2y

2



p

2z

2



H

=

−ℏ

2

2m

1



∂

2

∂

x

1

2



∂

2

∂

y

1

2



∂

2

∂

z

1

2

−

ℏ

2

2m

2



∂

2

∂

x

2

2



∂

2

∂

y

2

2



∂

2

∂

z

2

2



V

 

r

1,



r

2





H 

=

E 

[

1

m

1



∂

2

∂

x

1

2



∂

2

∂

y

1

2



∂

2

∂

z

1

2



1

m

2



∂

2

∂

x

2

2



∂

2

∂

y

2

2



∂

2

∂

z

2

2

]

2

ℏ

2



E−V  

r

1

, 

r

2

=

0

Wprowadzamy współrzędne środka masy: X, Y, Z i współrzędne względne: x, y, z

X

=

m

1

x

1

m

2

x

2

m

1

m

2

Y

=

...

Z

=

...

x

=

x

2−

x

1

y

=

...

z

=

...

r

2

=

x

2



y

2



z

2

1



=

1

m

1



1

m

2

Masa zredukowana

[

1

m

1



m

2



∂

2

∂

X

2



∂

2

∂

Y

2



∂

2

∂

Z

2



1





∂

2

∂

x

2



∂

2

∂

y

2



∂

2

∂

z

2

]

2

ℏ

2



E−V  

r

1

, 

r

2

=

0

V  r

1

, 

r

2

=

V

z



X ,Y ,Z V

w



x , y , z

  

r

1

, r

2

=

1



X ,Y , Z⋅ x , y ,z

1

m

1



m

2

1



1



∂

2

∂

X

2



∂

2

∂

Y

2



∂

2

∂

Z

2



1

−

2

ℏ

2

V

z



X ,Y , Z =

=−

1



1





∂

2

∂

x

2



∂

2

∂

y

2



∂

2

∂

z

2

−

2

ℏ

2



E−V

w



r 

L

=

P

=

const.

=

A

A

=

−

2

ℏ

2

E '

E

−

E '

=



Pierwszym równaniem nie będziemy się teraz zajmowac, gdyż opisuje oddziaływanie atomu z polem
zewnetrznym. Drugie opisuje oddziaływanie pomiędzy składnikami atomu – oddziawływania

wewnętrzne.

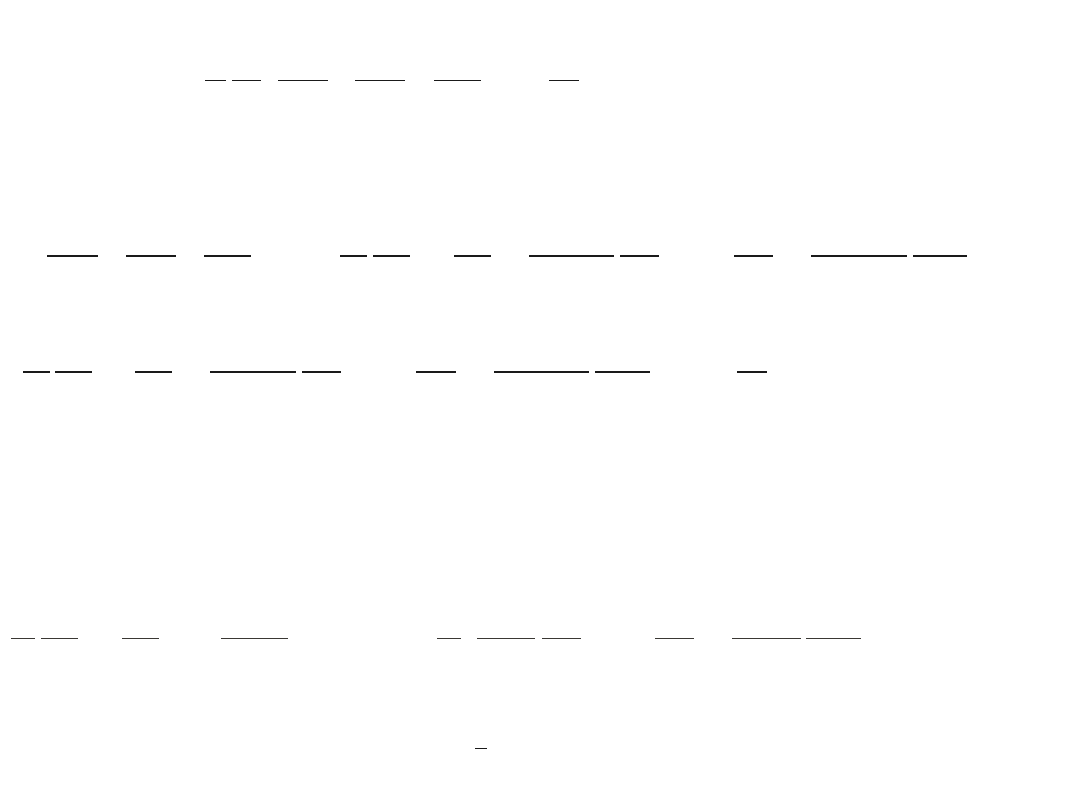
1



1





∂

2

∂

x

2



∂

2

∂

y

2



∂

2

∂

z

2

 

2

ℏ

2

−

V

w

=

0

Przechodzimy do współrzędnych sferycznych

∂

2

∂

x

2



∂

2

∂

y

2



∂

2

∂

z

2



1

r

2

∂

∂

r



r

2

∂

∂

r



1

r

2

sin 

∂

∂ 



sin  ∂

∂ 



1

r

2

sin

2



∂

2

∂ 

2

[

1

r

2

∂

∂

r



r

2

∂

∂

r



1

r

2

sin

∂

∂ 



sin ∂

∂ 



1

r

2

sin

2



∂

2

∂ 

2

]

2



ℏ

2

−

V

w

=

0

Rozdzielamy zmienne



r , ,=Rr Y  ,

1

R

∂

∂

r



r

2

∂

∂

r



R

2 r

2

ℏ

2

−

V

w

=−

1

Y

[

1

sin 

∂

∂ 



sin  ∂

∂ 



1

sin

2



∂

2

∂ 

2

]

Y

L=P=const.=



'

=−

ℏ

i



2



∂

∂

r



r

2

∂

∂

r



R

2 r

2

ℏ

2

−

V

w



R= R



ℏ

i



2

[

1

sin 

∂

∂ 



sin  ∂

∂ 



1

sin

2



∂

2

∂ 

2

]=

' 

Ostatnie równanie jest równaniem własnym dla kwadratu momentu pędu



L

2

Y =L

2

Y

∂

∂

r



r

2

∂

∂

r



R

2 r

2

ℏ

2

−

V

w



R= R



ℏ

i



2

[

1

sin 

∂

∂ 



sin  ∂

∂ 



1

sin

2



∂

2

∂ 

2

]

Y=' Y

1

R

∂

∂

r



r

2

∂

∂

r



R

2 r

2

ℏ

2

−

V

w

==

l l1

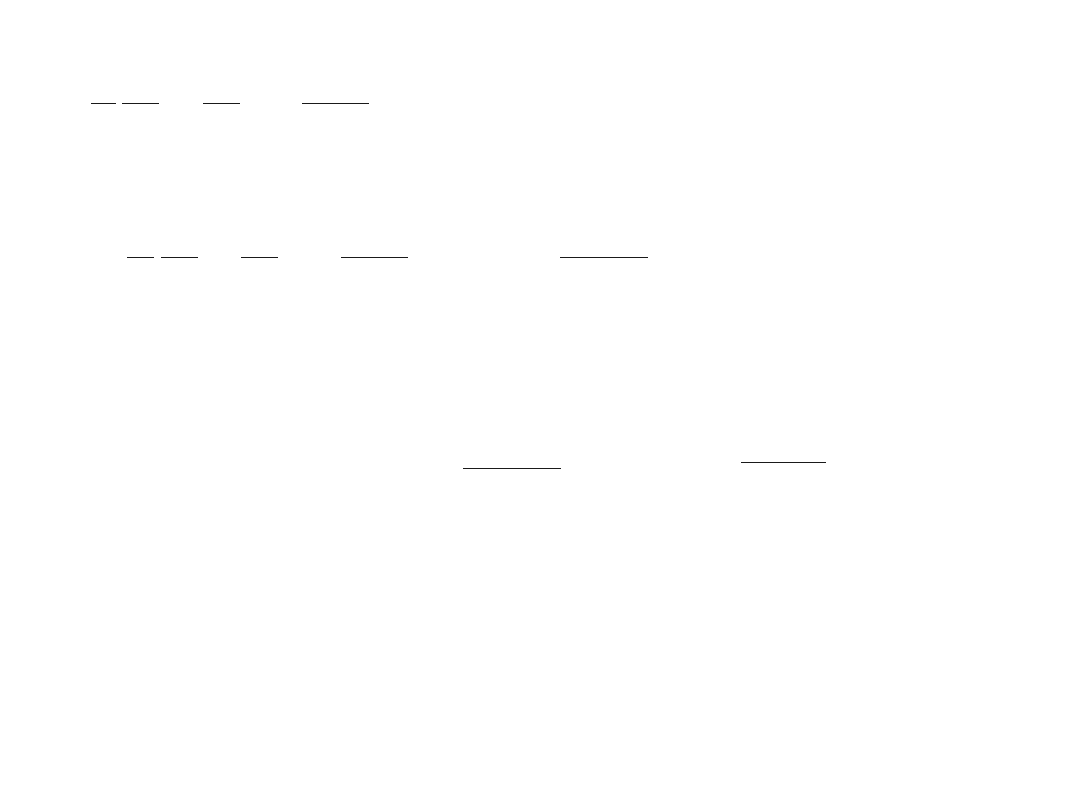
1

R

∂

∂

r



r

2

∂

∂

r



R

2 r

2

ℏ

2

−

V

w

==

l l1

1

r

2

∂

∂

r



r

2

∂

∂

r



R

2 r

2

ℏ

2

−

V

w



R−

l l1

r

2

R=0

Istnieje rozwiązanie tego równania dla

 < 0

takiego, że



n

=−

k



Z

2

e

4

2 ℏ

2

n

2

k=

1

4 

0

R r

nl

=

A

nl

e

−

r /2

r

l

L

2l1

n1



r

A

nl

=[

2Z

na

0



3



n−l−1!

2n [nl!]

3

]

1/2

n = 1,2,3,4, ...

l= 0, 1, 2, … , n-1

L

p

k

=

d

p

L

k



r

dr

p

Wielomian Laguerre'a stopnia k

L

k



r =e

r

d

k



r

k

e

−

r



dr

k

Stowarzyszony wielomian Laguerre'a

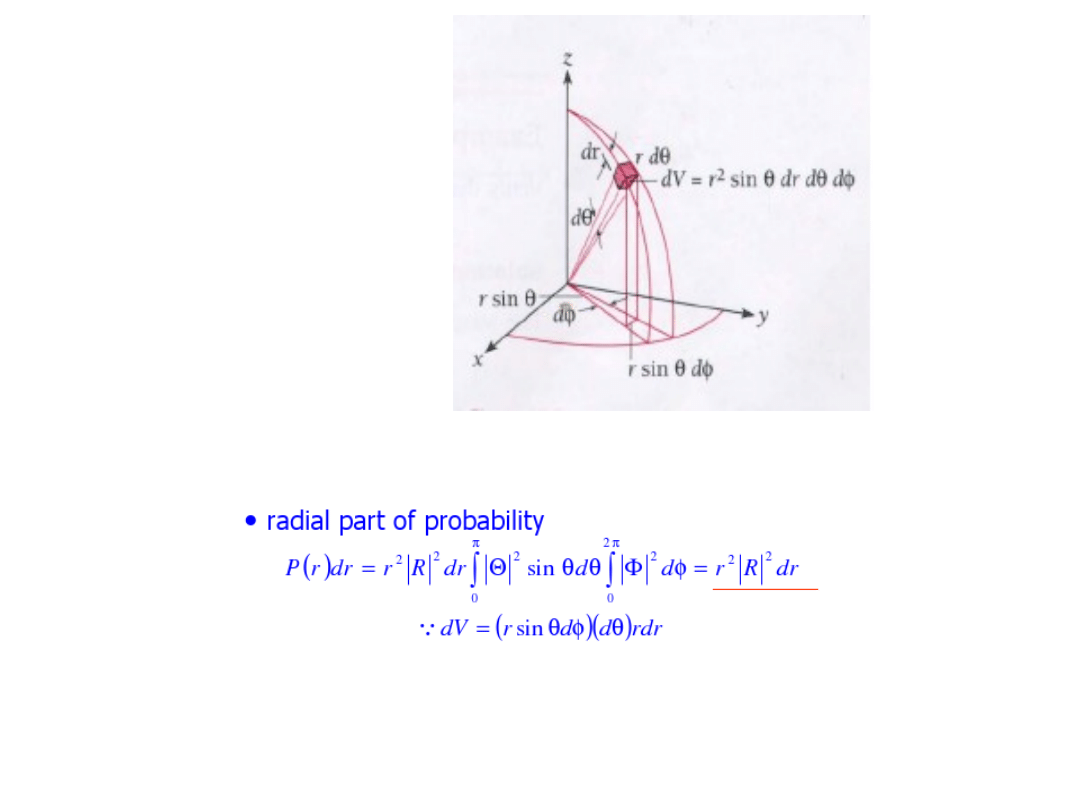
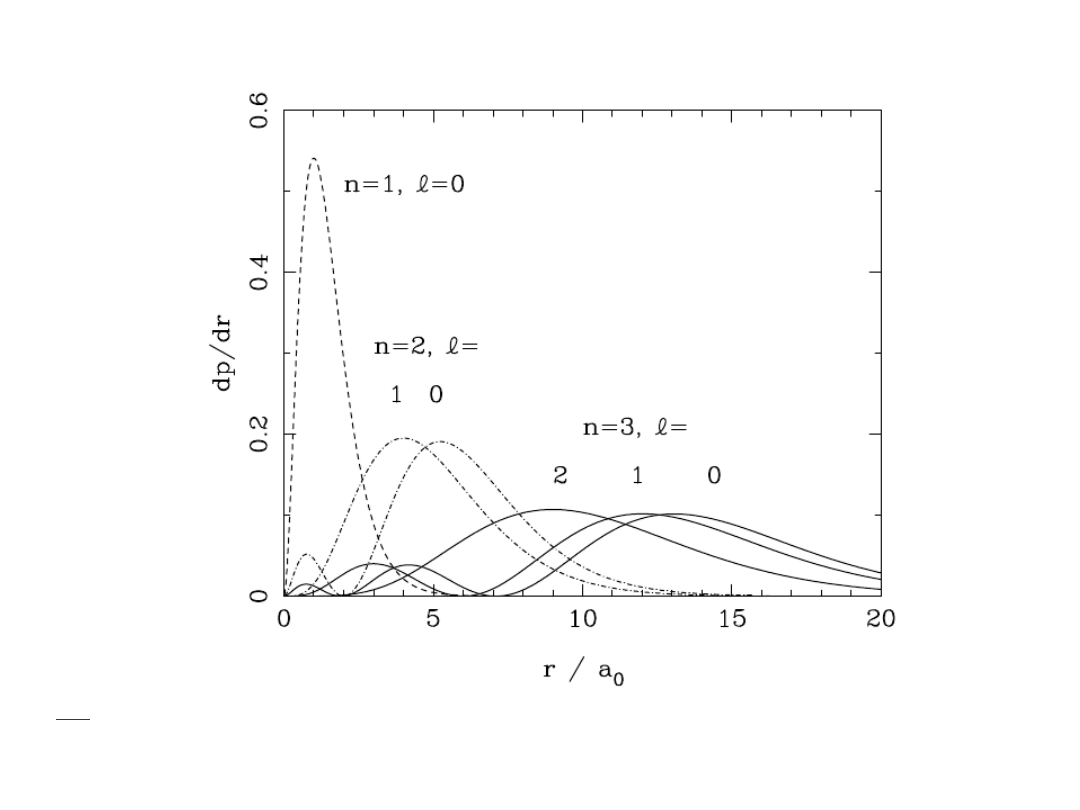
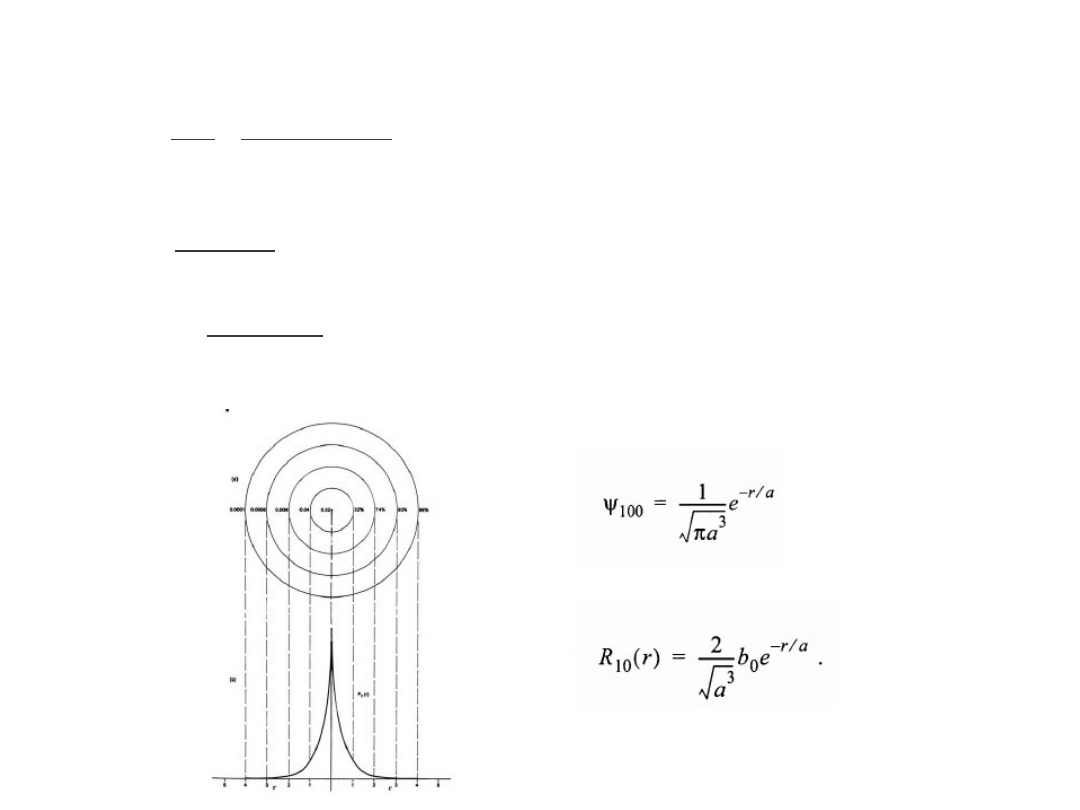
Prawdopodobieństwo znalezienia elektronu w odległości r od jądra atomowego

dp

dr

=

4 r

2

∣

R r∣

2

- rozkład radialny gęstości prawdopodobieństwa

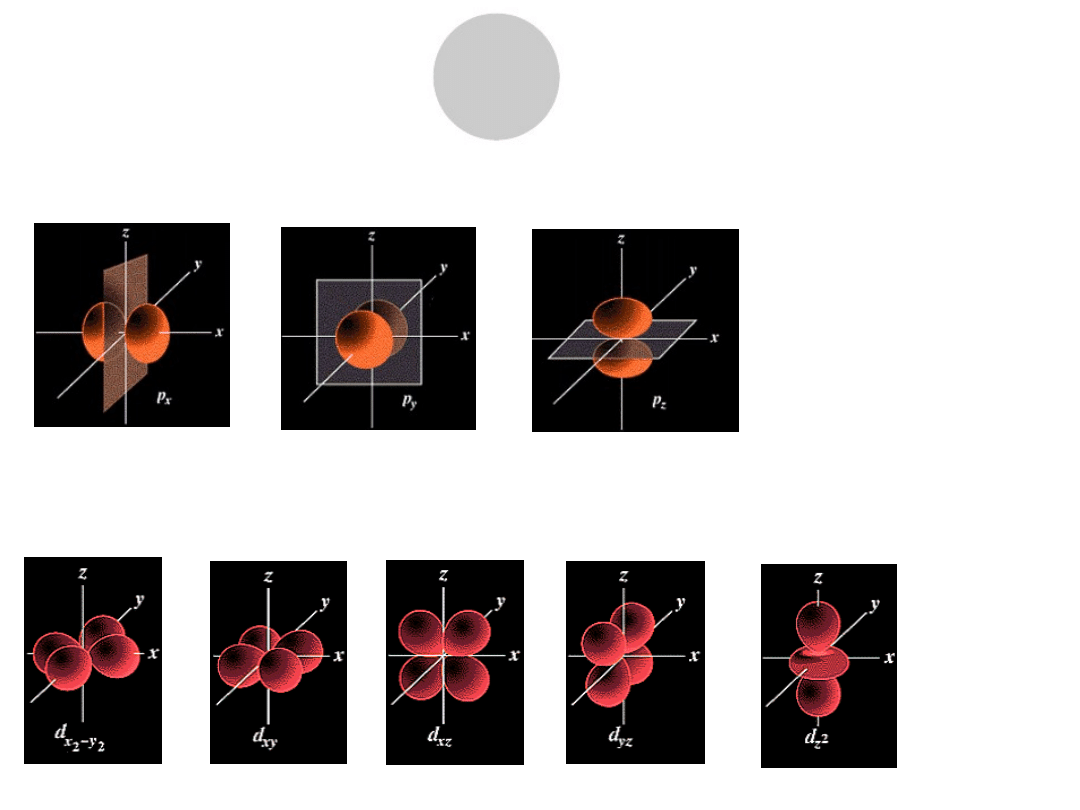
l = 1 orbital typu p ( 3 różne dla m = -1, 0 , 1) ozn. Px, py, pz

l = 0 orbital typu s

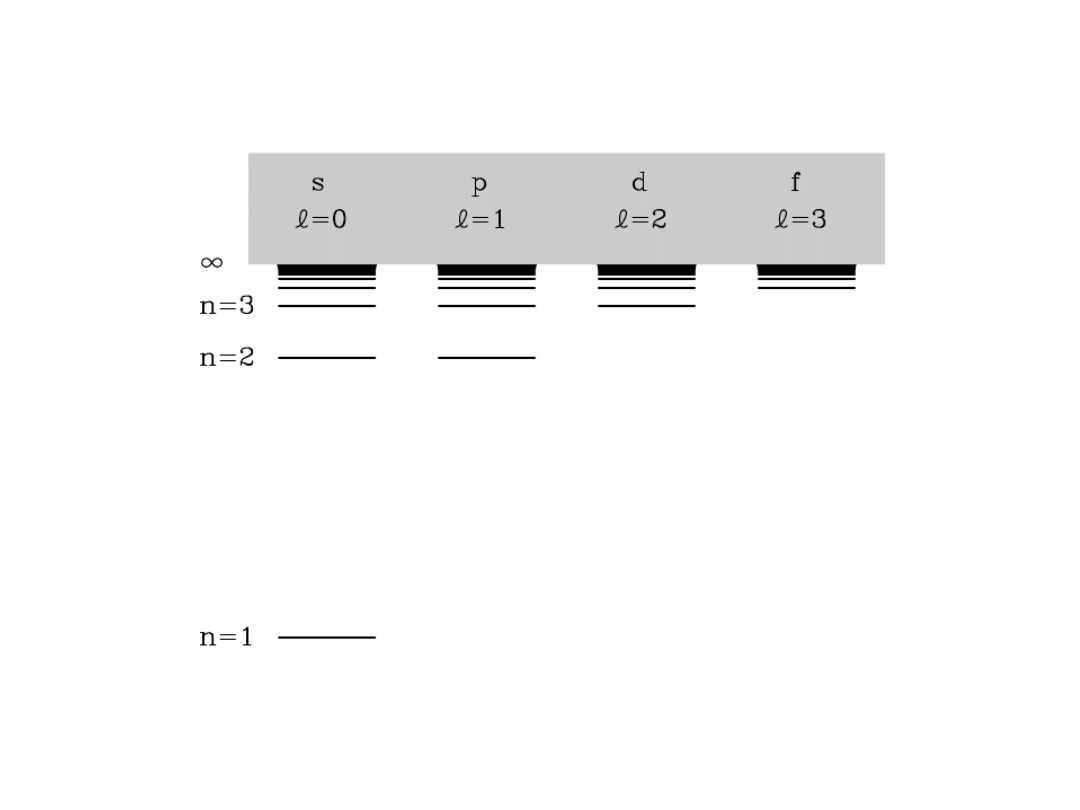
Poziomy energetyczne w atomie wodoru

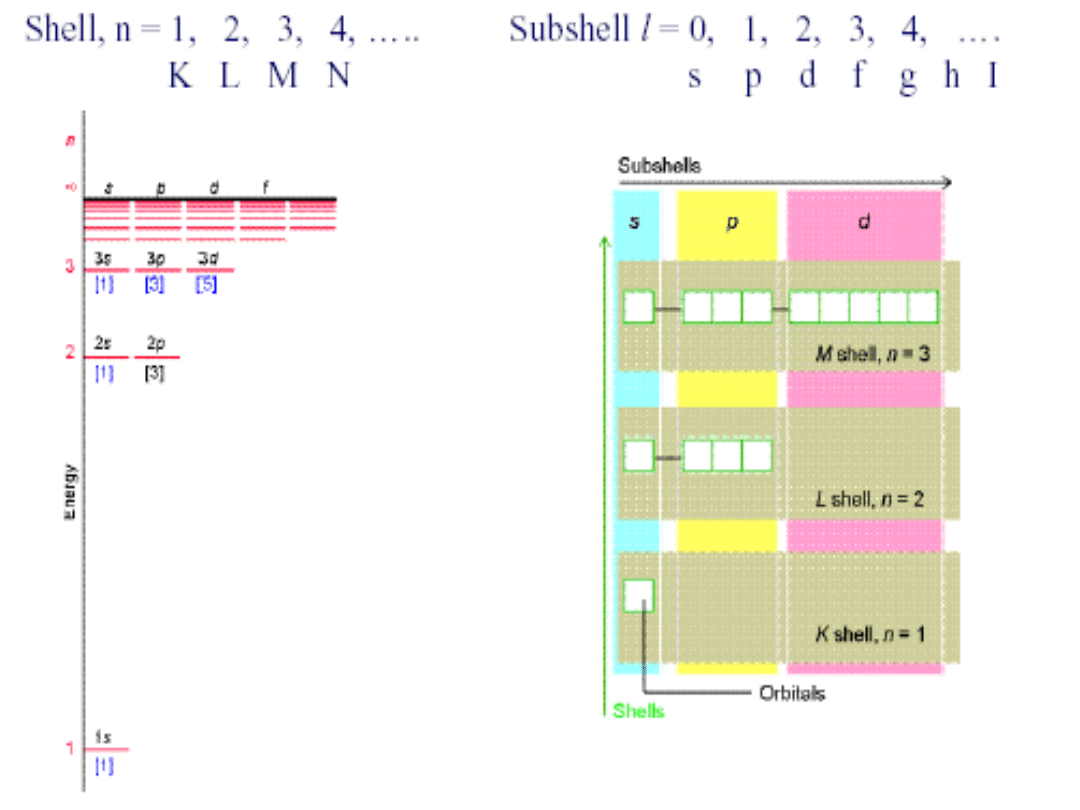
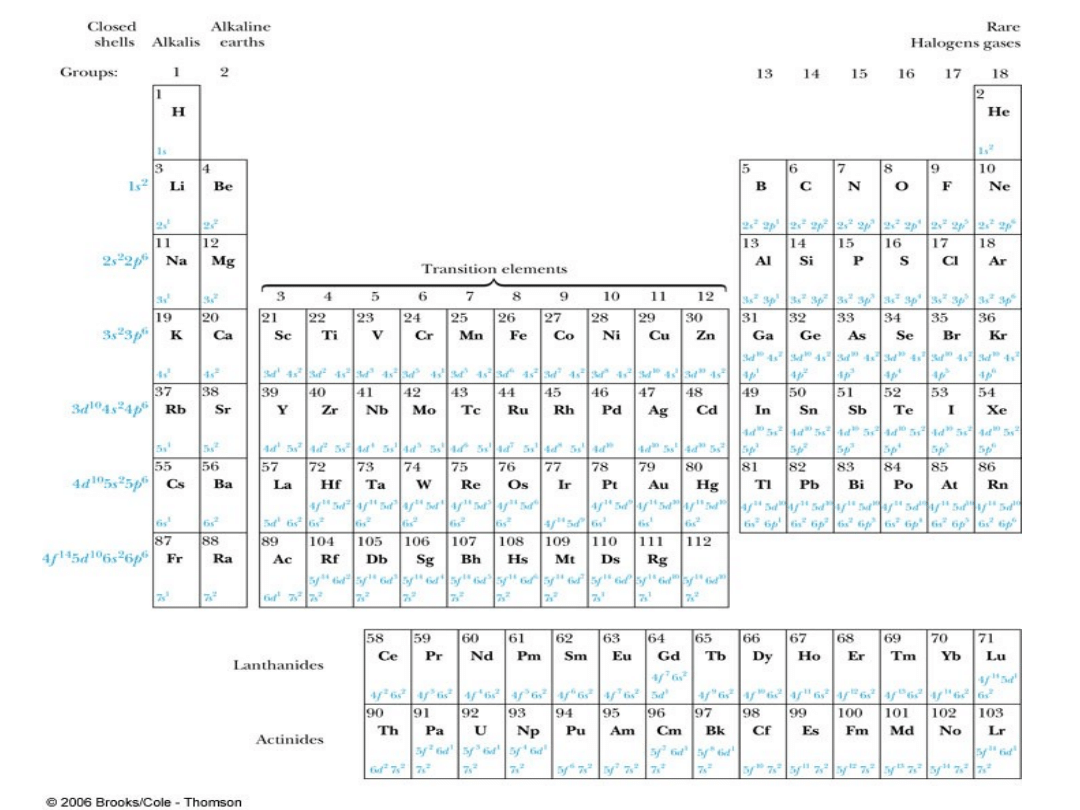
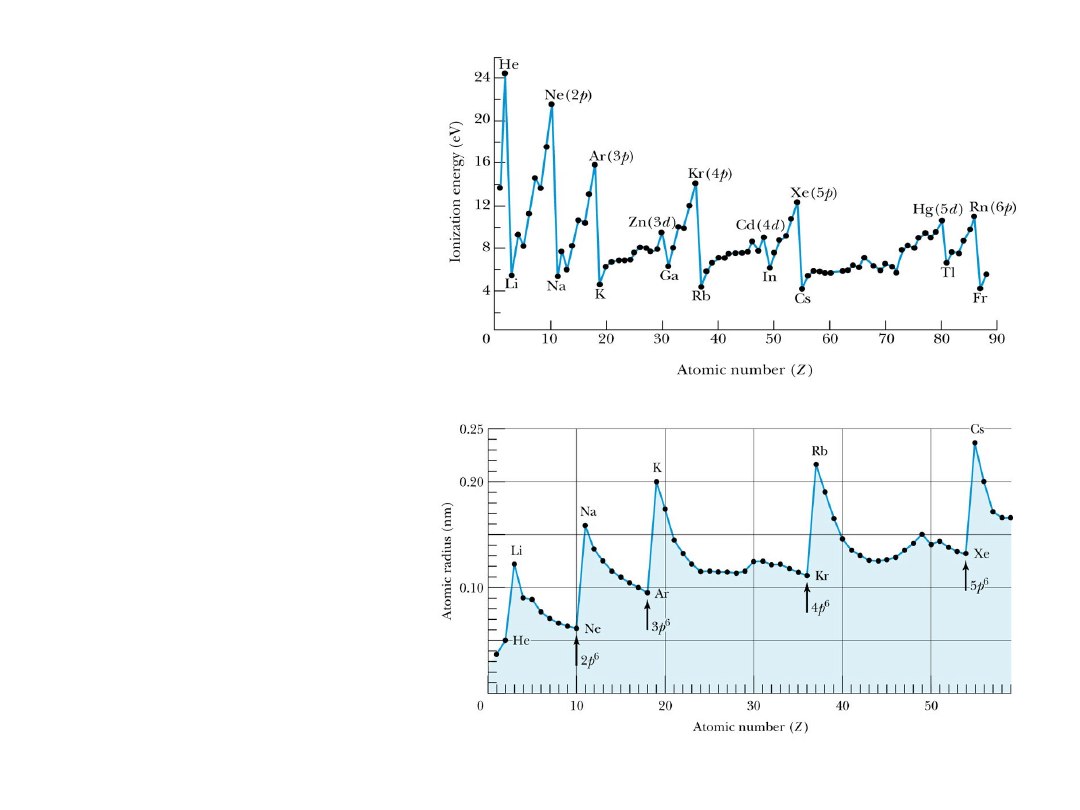
Groups and

Periods

• Groups:


Vertical columns.



Same number of
electrons in an ℓ
orbit.



Can form similar
chemical bonds.

• Periods:


Horizontal rows.



Correspond to filling
of the subshells.

The Periodic

Table

• Inert Gases:
• Last group of the periodic table
• Closed p subshell except helium
• Zero net spin and large ionization energy
• Their atoms interact weakly with each other

• Alkalis:
• Single s electron outside an inner core
• Easily form positive ions with a charge +1e
• Lowest ionization energies
• Electrical conductivity is relatively good

• Alkaline Earths:
• Two s electrons in outer subshell
• Largest atomic radii
• High electrical conductivity

The

Periodic

Table

• Lanthanides (rare earths):
• Have the outside 6s

2

subshell

completed

• As occurs in the 3d subshell, the

electrons in the 4f subshell have
unpaired electrons that align
themselves

• The large orbital angular

momentum contributes to the large
ferromagnetic effects

• Actinides:
• Inner subshells are being filled

while the 7s

2

subshell is complete

• Difficult to obtain chemical data

because they are all radioactive

• Have longer half-lives