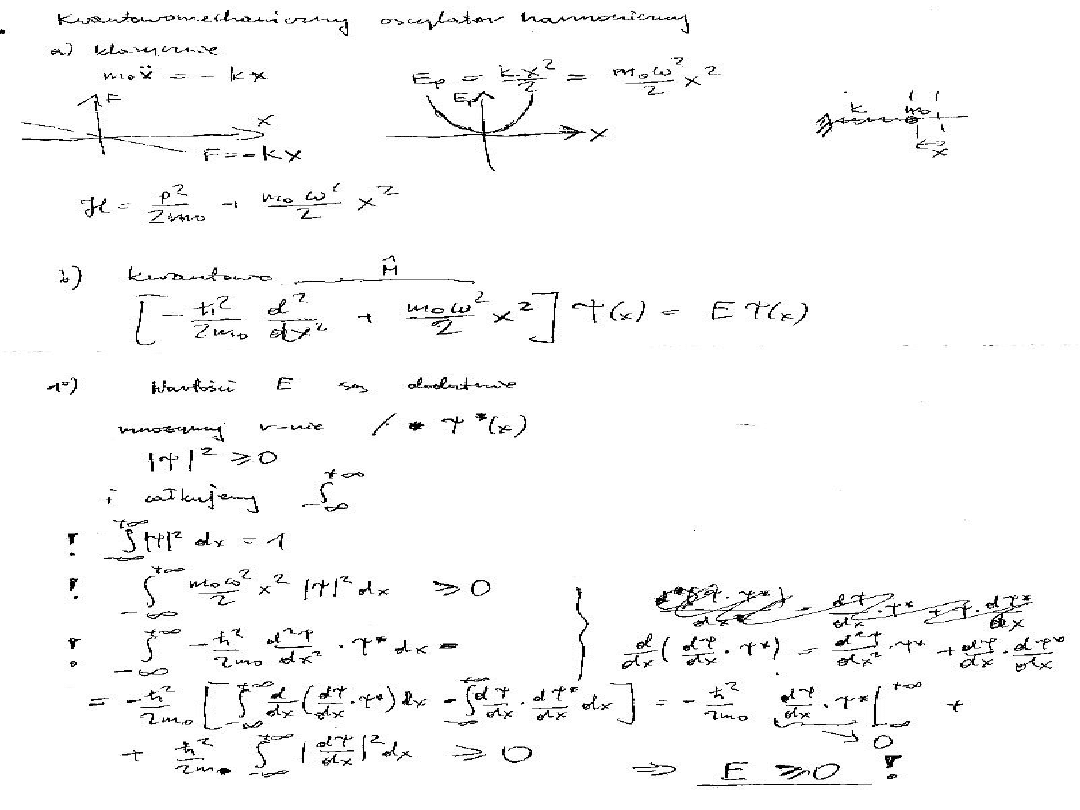
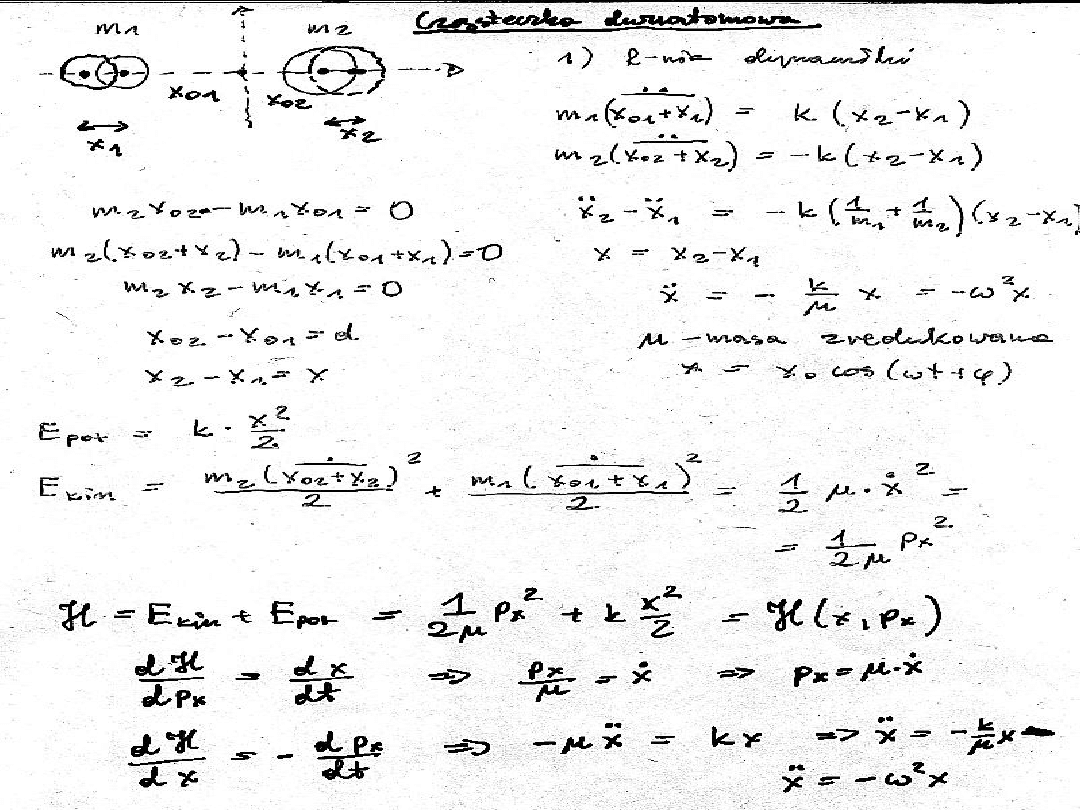
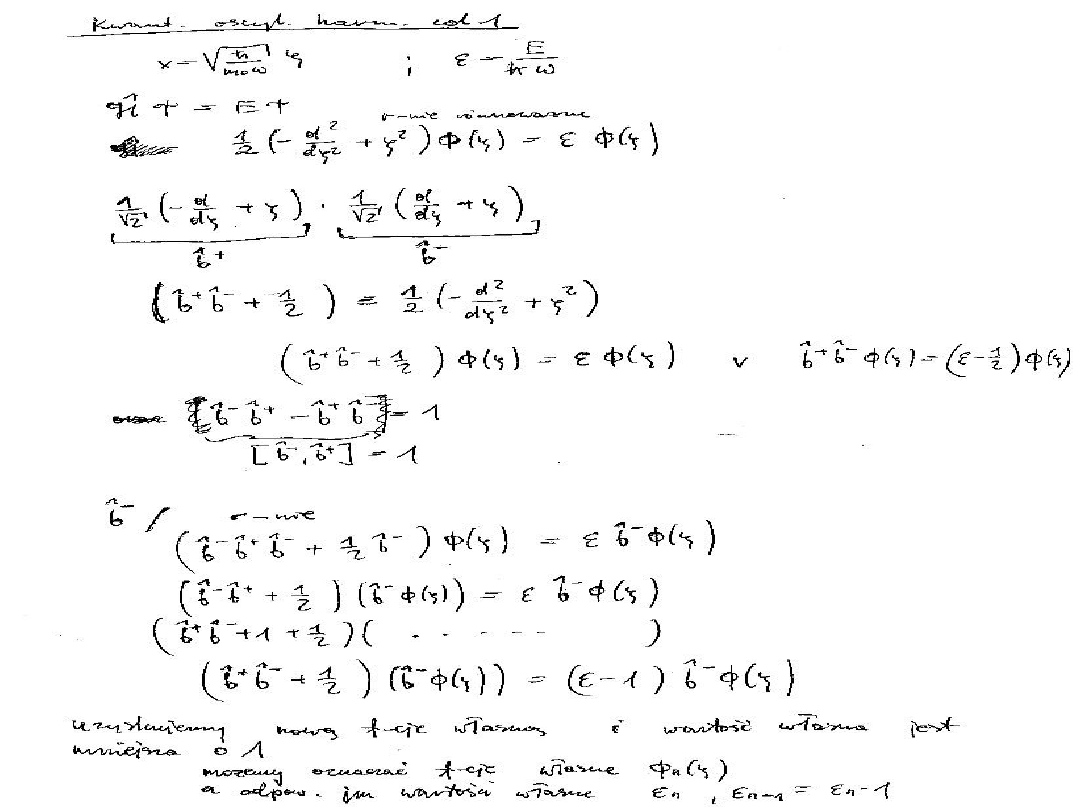
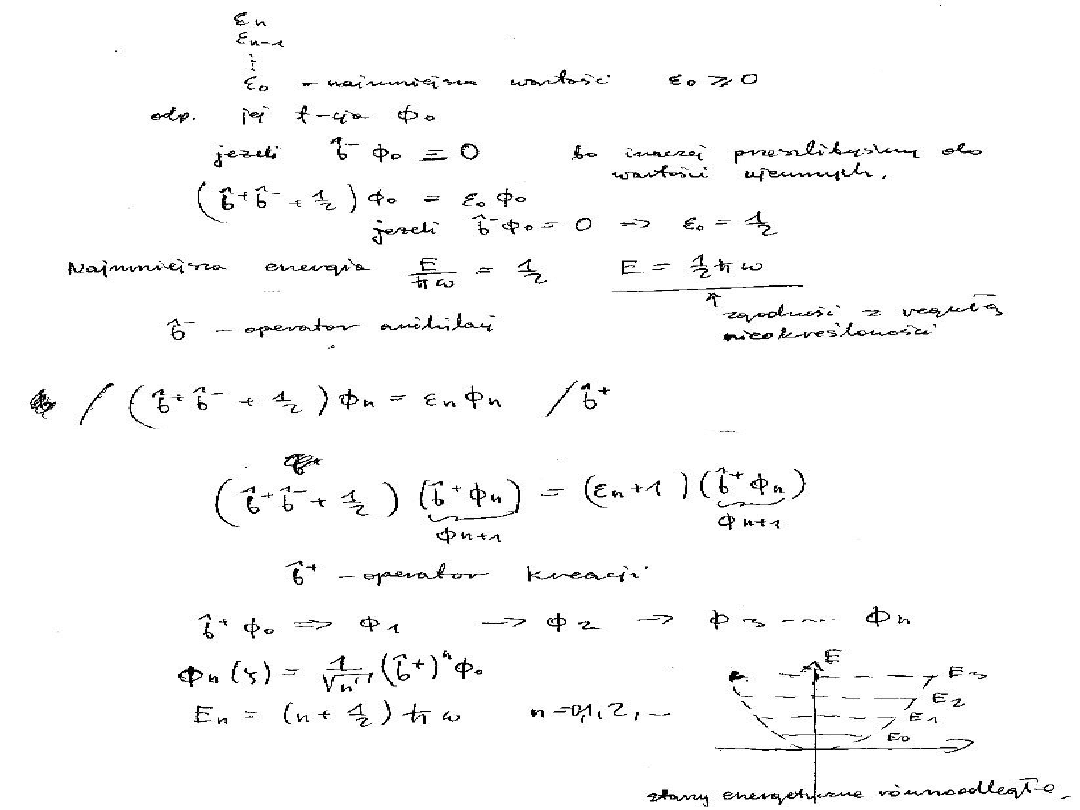
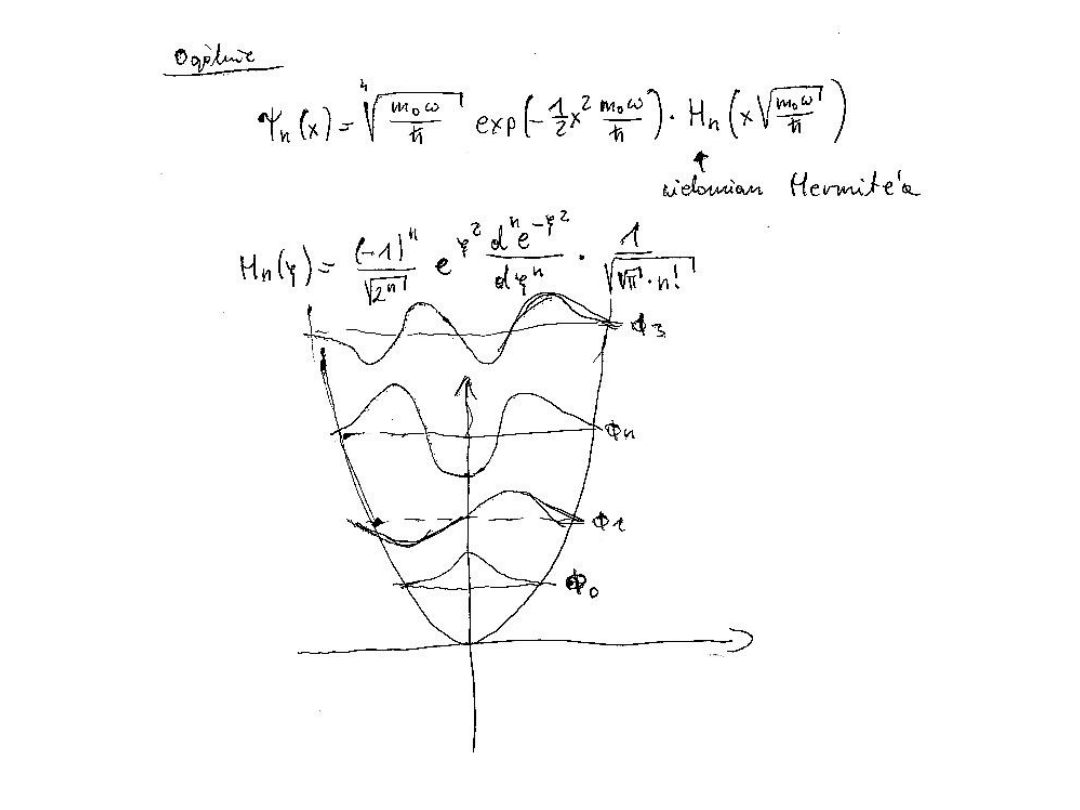
E

1

2

h

ϖ

3
2

h

ϖ

5
2

h

ϖ

7
2

h

ϖ

x

9
2

h

ϖ

11

2

h

ϖ

The

energy

levels of a

harmonic

oscillator

are evenly

spaced

with

separation

·

ω

, with 

ω

= (k/m)

1/2

.

Even in its

lowest

state, an

oscillator

has an

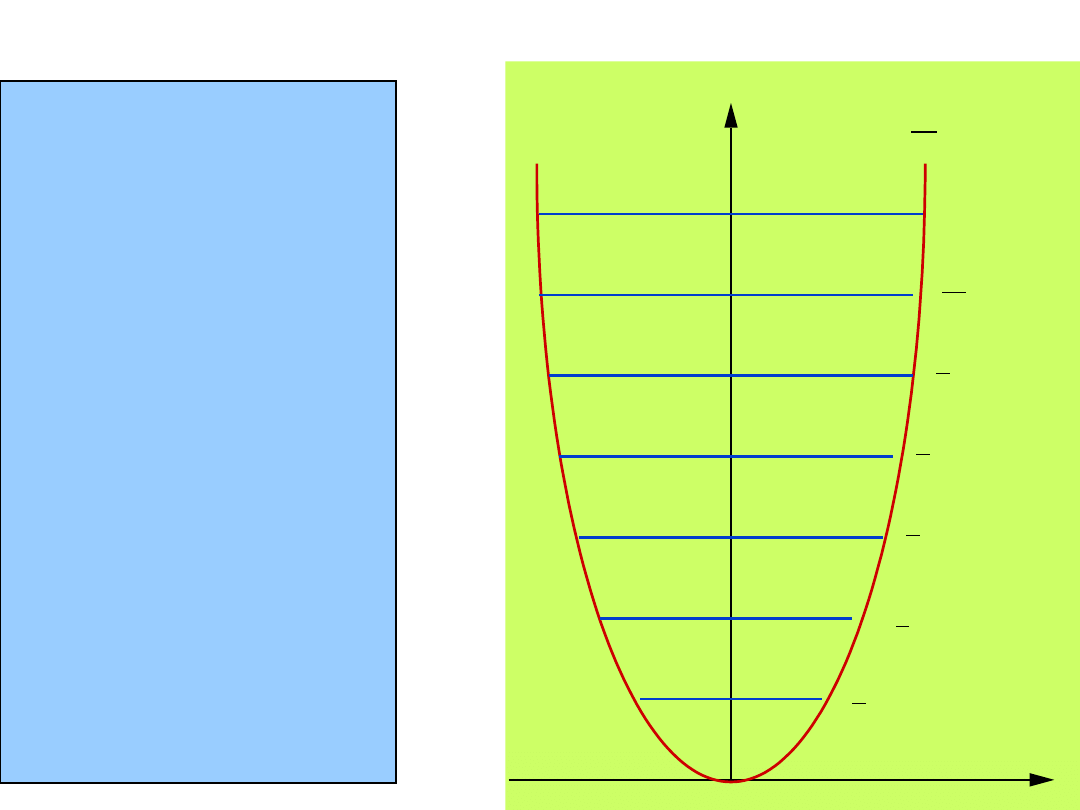
Harmonic oscillator . . . Quantum mechanically  . Energy levels

v=0

v = 1

v =2

v =3

v = 4

v =5

v=6

E=hv  1

2



v 

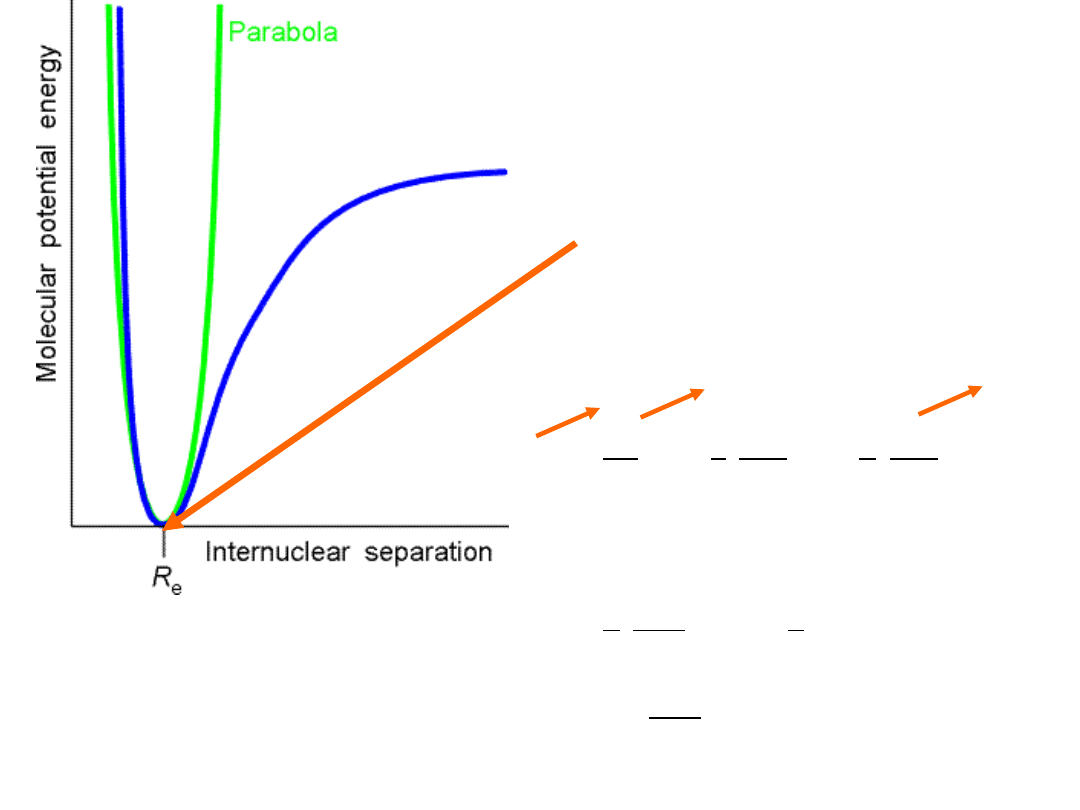
Harmonic oscillator Quantum mechanically Vibration Spectroscopy

V R=V R

e

dV

dR



dR

e

 1

2

 d

2

V

dR

2



dR

e

2

 1

8

 d

3

V

dR

3



dR

e

3



...

Taylor  expansion

0

small

0

V R= 1

2

 d

2

V

dR

2



dR

e

2

= 1

2

k⋅dR

e

2



d

2

V

dR

2

=

k

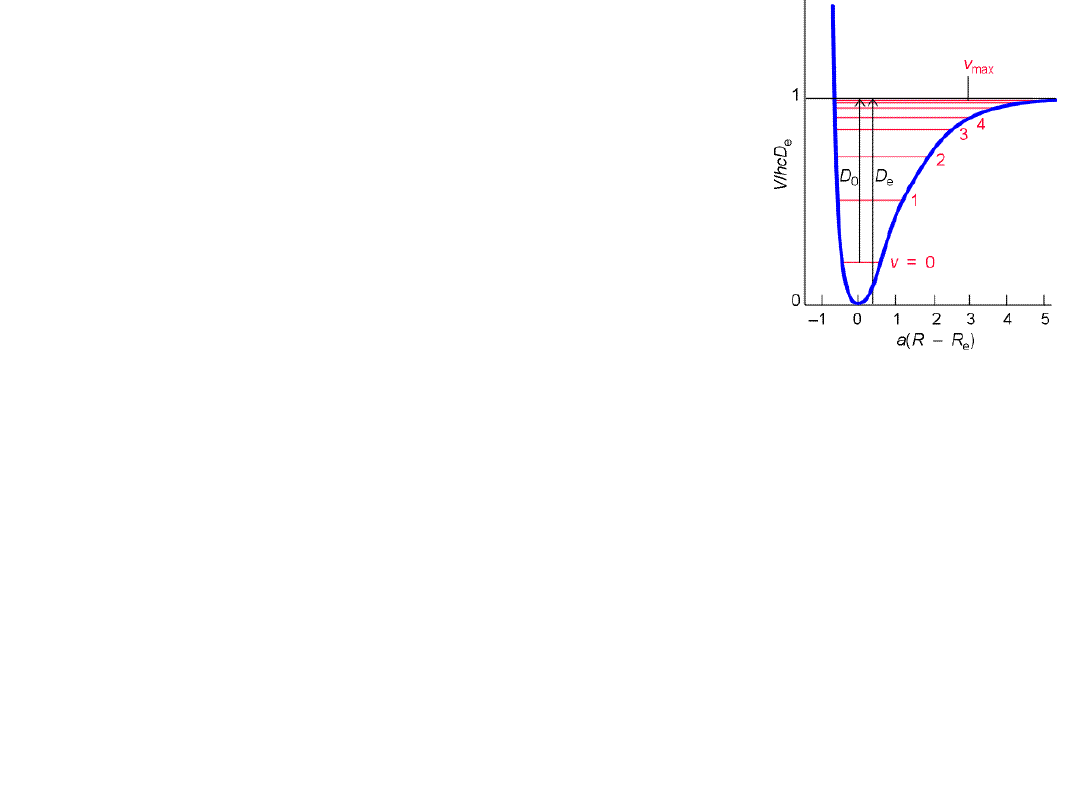
Harmonic oscillator . . . Quantum mechanically

We  note relation between bond energy D ;

 bond order and force constant k   

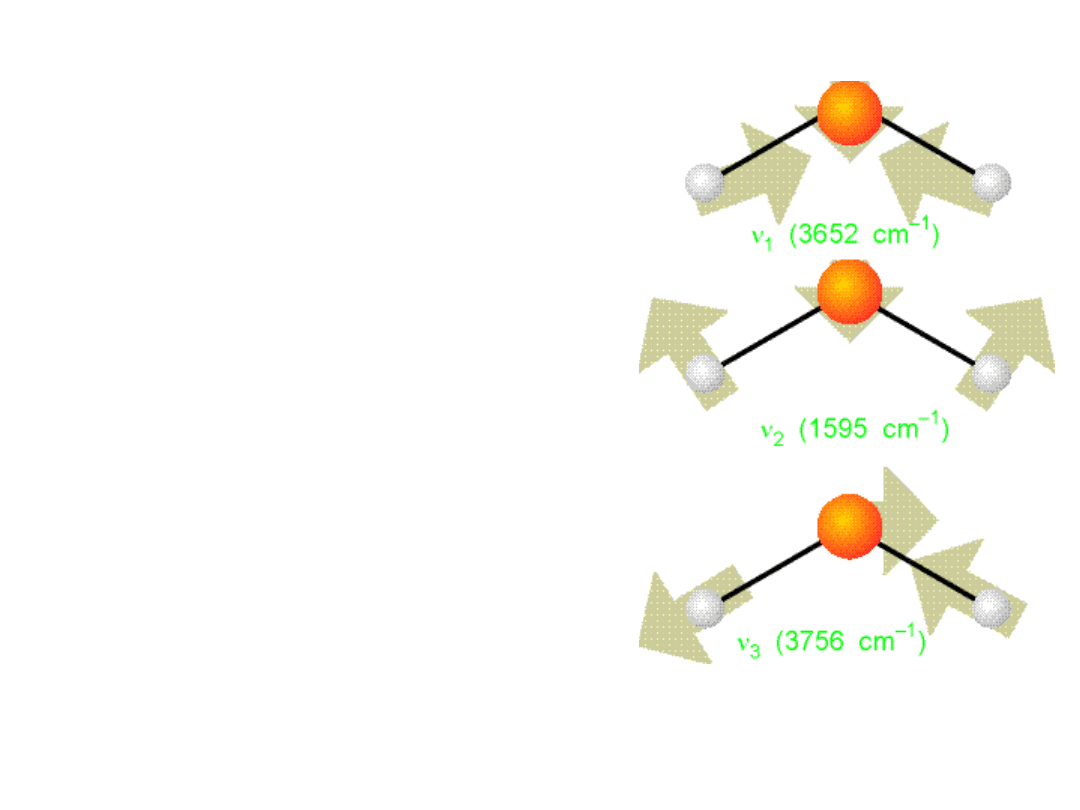
Harmonic oscillator . . . Quantum mechanically

The three

normal

modes of

H

2

O. The

mode v

2

 is

predomina

ntly

bending,

and occurs

at lower

wavenumb

er than the

other two.