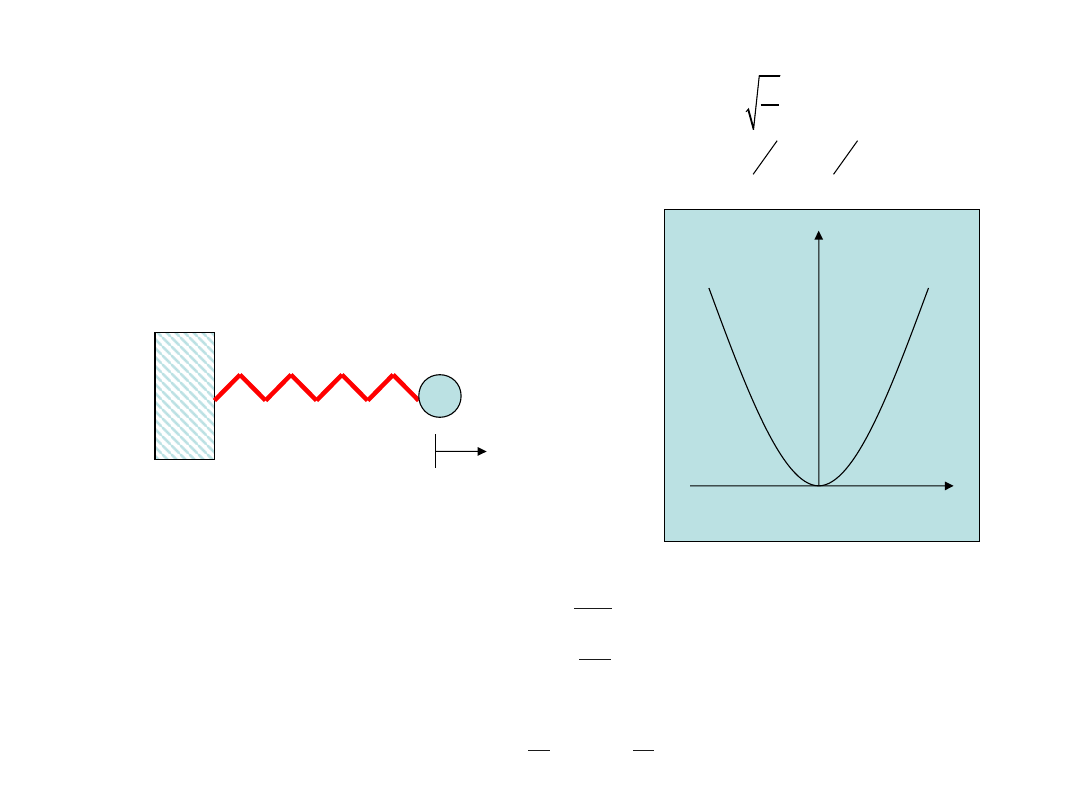
Kwantowy oscylator harmoniczny
a) klasyczny oscylator harmoniczny
b) Hamiltonian I operator Hamiltona
c) rozwiązanie równania Schrodingera
Mass m
x
V(x)
x
0
2
2 2
0
Force
Angular frequency =
1
1
Potential energy ( )
2
2
F
kx
k
m
V x
kx
m
x
ω
ω
= −
=
=
Siła harmoniczna
Częstość drgań własnych
Energia potencjalna
F=−kx
0
=
k
m
V x=
1
2
kx
2
=
1
2
m
0
2
x
2
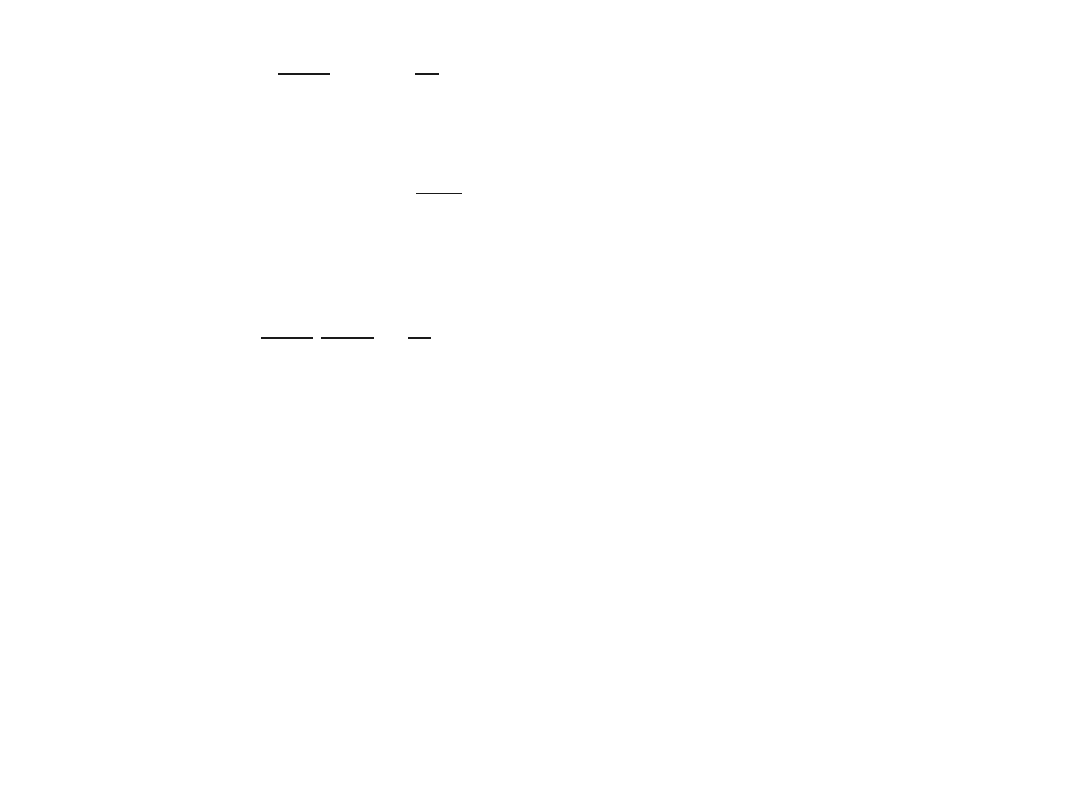
H =
1
2m
p
x
2
1
2
m
0
2
x
2
Hamiltonian
p
x
p
x
=−
i ℏ ∂
∂
x
H =
1
2m
p
x
2
1
2
m
0
2
x
2
H =−
ℏ
2
2m
d
2
dx
2
1
2
m
0
2
x
2
Operator Hamiltona
H =E
Można wykazać, że wartości własne E są nieujemne
i całkujemy
∫
−∞
∞
mnożymy przez
*
/
H =E
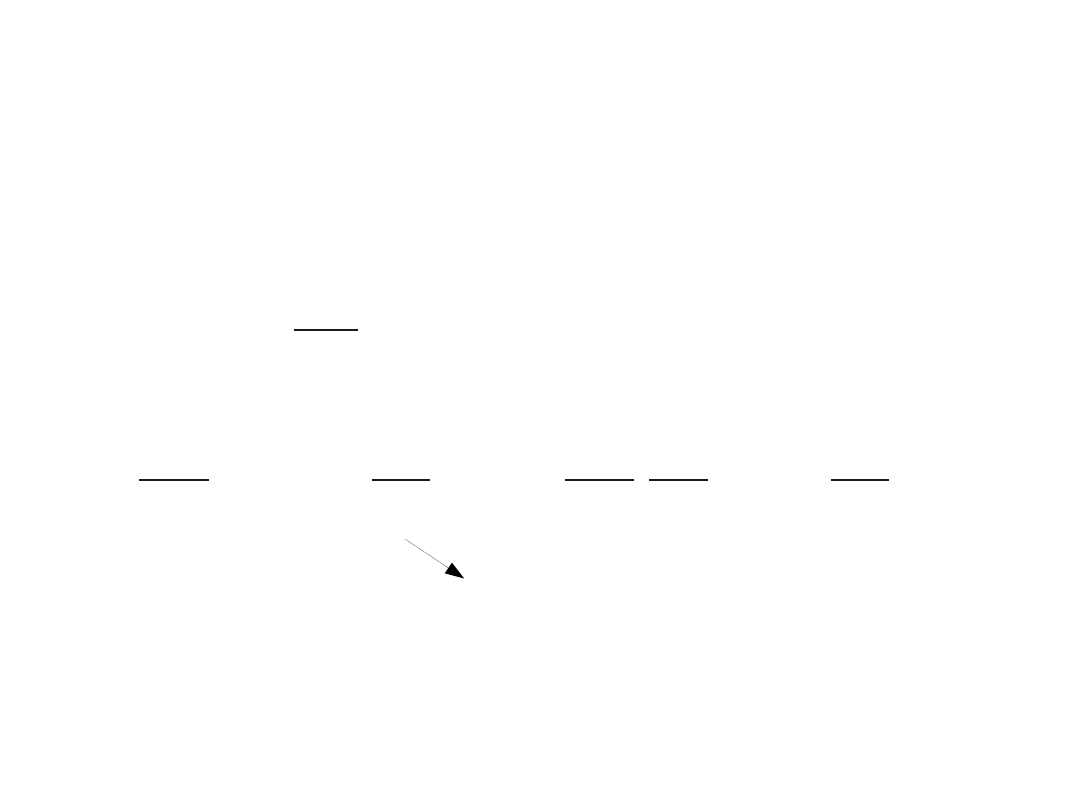
∫
−∞
∞
*
H dx=E
∫
−∞
∞
*
x
2
dx0
∫
−∞
∞
*
−
d
2
dx
2
dx ? 0
−
∫
−∞
∞
*
d
2
dx
2
dx= −
*
d
dx
∣
∞
−∞
∫
−∞
∞
d
*
dx
⋅
d
dx
dx=
∫
−∞
∞
∣
d
dx
∣
2
dx0
0
E0 ! ! !
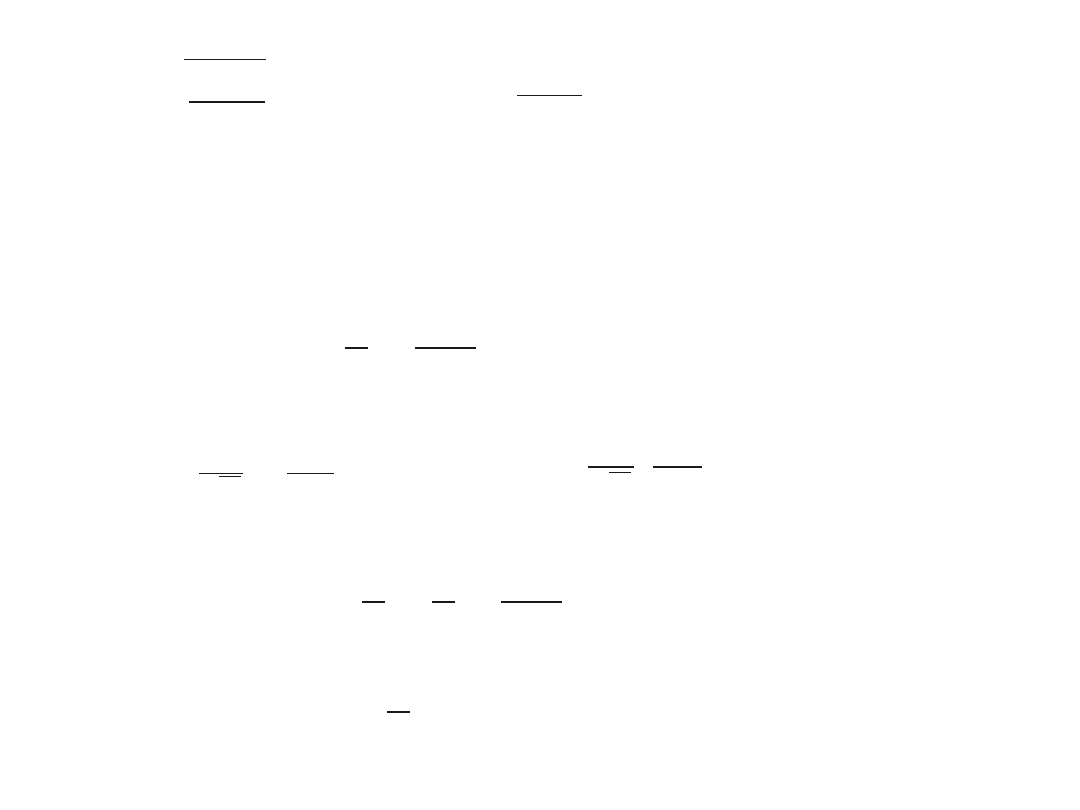
x=
ℏ
m
0
=
E
ℏ
0
H =E
Wtedy równanie
przyjmie postać
1
2
−
d
2
d
2
2
=
b
+
=
1
2
−
d
d
b
=
1
2
d
d
b
+
b
1
2
=
1
2
−
d
2
d
2
2
b
+
b
1
2
=
b
+
b
=−
1
2
b
b
+
−
b
+
b
=
1
Można wykazać, że
czyli
[
b
, b
+
]=
1
b
+
b
1
2
=
Działamy operatorem
b
na
b
b
+
b
1
2
b
=
b
b
b
+
1
2
b
=
b
1
b
+
b
1
2
b
=
b
b
+
b
1
2
b
=−
1 b
Uzyskujemy nową funkcję własną dla wartości własnej o 1 mniejszej
b
Działając wielokrotnie operatorem
Otrzymujemy coraz mniejsze wartości własne.
Ponieważ są one nieujemne, musi istnieć najmniejsza wartość własna
Oznaczmy ją
0
=
E
0
ℏ
0
0
b
0
≡
0
bo inaczej uzyskalibyśmy wartości własne
ujemne
b
+
b
1
2
0
=
0
0
1
2
0
=
0
0
⇒
0
=
1
2
E
0
=
1
2
ℏ
0
Najmniejsza energia drgań

Działamy teraz operatorem
b
+
na
b
+
b
1
2
=
b
+
b
1
2
b
+
=
1 b
+
Otrzymujemy
Dozwolone wartości energii możemy numerować liczbami naturalnymi
Tak samo odpowiadające im funkcje własne
n
=
0
n=
1
2
n
E
n
=
1
2
n ℏ
0
równoodległe
b
b
+
Operatory “drabinkowe” kreacji i anihilacji

Równanie dla H
Funkcje własne
Można pokazać, że rozwiązanie
asymptotyczne powinno być postaci
=
H exp
−
2
2
asymp
=
exp
−
2
2
d
2
H
d
2
−
2
dH
d
−
1 H =0
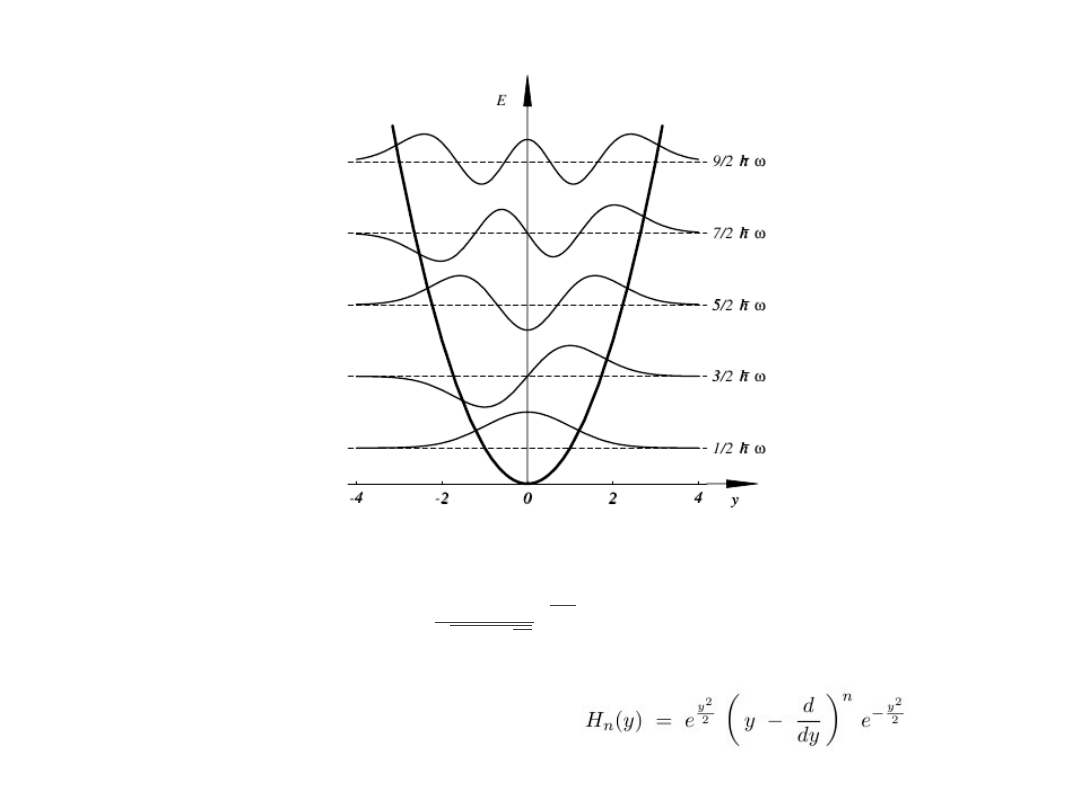
Stany stacjonarne oscylatora harmonicznego dla n = 0,1,2,3,4
n
=
1
2
n
n !
e
−
y
2
2
H
n
y
Gdzie H
n
(y) są to wielomiany Hermite'a
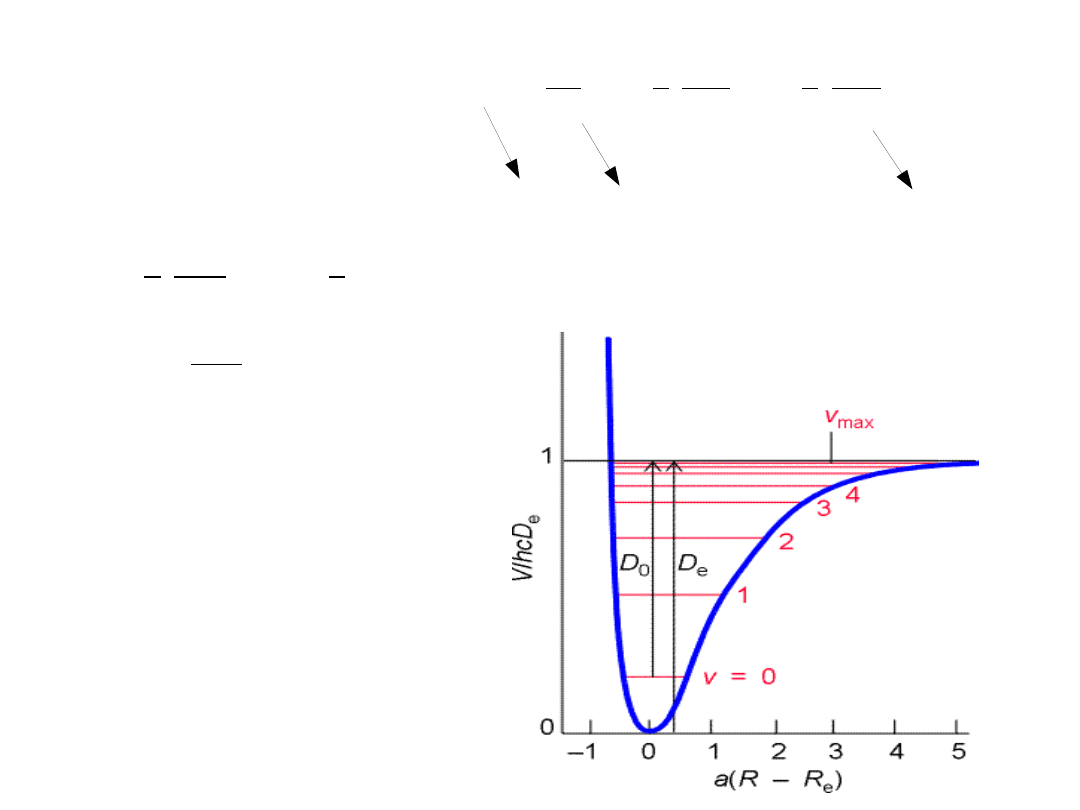
Energia potencjalna
drgającej cząsteczki
V R=V R
e
dV
dR
dR
e
1
2
d
2
V
dR
2
dR
e
2
1
8
d
3
V
dR
3
dR
e
3
...
V R= 1
2
d
2
V
dR
2
dR
e
2
=
1
2
k⋅dR
e
2
d
2
V
dR
2
=
k
0
0
małe
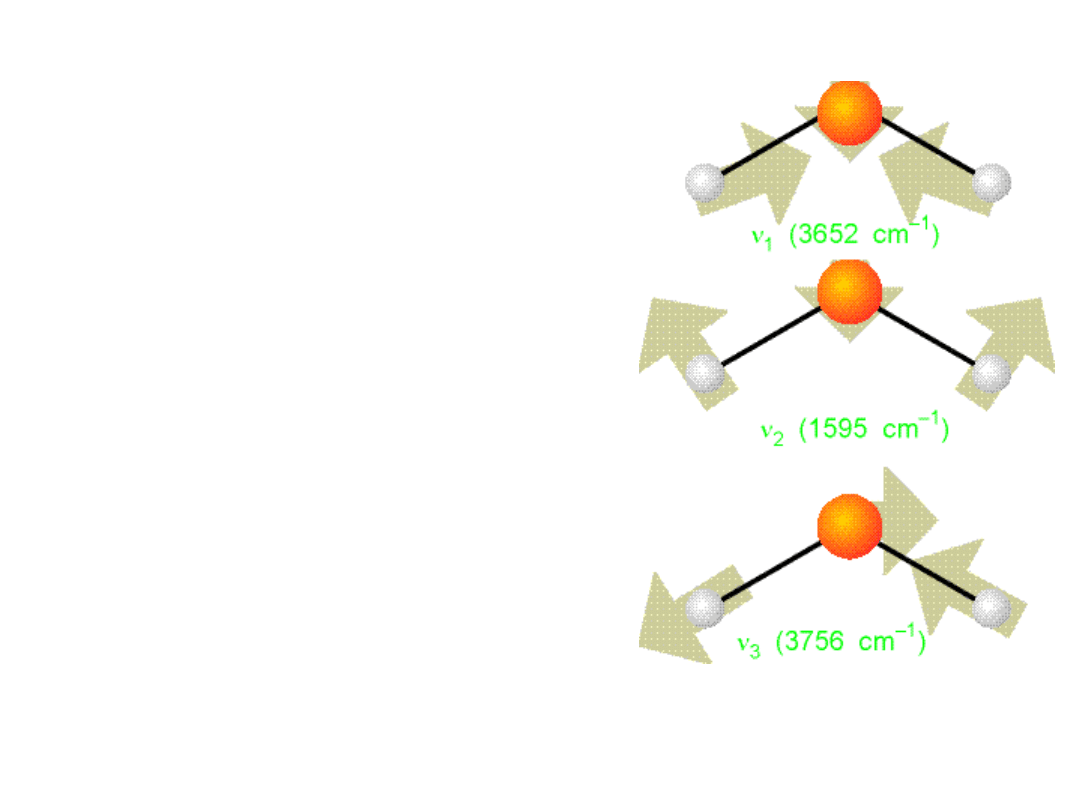
Częstości drgań własnych cząsteczki wody
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Simple Harmonic Oscillator (2)
- Slide 9
- Slide 10
- Slide 11
Wyszukiwarka
Podobne podstrony:
MechKw i07
MechKw i04
MechKw i03
MechKw i05
MechKw i11
MechKw i11
MechKw 03
MechKw 10
MechKw pytania
MechKw i12
MechKw 06
MechKw 07
MechKw i13
MechKw i09
MechKw i04
MechKw i01
MechKw i02 2011
więcej podobnych podstron