1 

ELEMENTY TEORII BŁĘDÓW 

2 

Informacje ogólne 

Każdy pomiar wielkości fizycznej dokonywany jest ze 

skończoną dokładnością co oznacza że wynik każdego 

pomiaru dokonywany jest z niepewnością pomiarową 

zwaną błędem pomiaru. Zasady obliczania jak również 

ocena błędów zawarte są w teorii błędów zwanej 

rachunkiem błędów. 

Wykonanie bezbłędnego pomiaru jest niemożliwe dlatego 

rzeczywistej wielkości pomiarowej nie poznamy nigdy. 

Wartość pomierzoną możemy zapisać: X = X

np 

+ m

x 

   

 

 

np – najbardziej prawdopodobny 

3 

Rodzaje błędów 

Błędy pomiarowe dzielą się na trzy zasadnicze grupy: 

•

błędy grube (omyłki), 

•

błędy systematyczne, 

•

błędy przypadkowe. 

Rachunek wyrównawczy zajmuje się jedynie błędami 

przypadkowymi. 

Błędy grube i systematyczne należy wyeliminować 

przed wyrównaniem wyników pomiarów. 

4 

Błędy grube i systematyczne 

Błędy grube to poważne odchylenia wyników 

pomiarów od wartości rzeczywistej mierzonej 
wielkości, powstają na skutek nieuwagi, pośpiechu. 
Wykrywa się je i eliminuje z pomiarów przez 
kilkakrotne obserwacje tej samej wielkości. 

Błędy systematyczne mają te same znaki, a 

czasami nawet te same wartości. Zdarza się, że 
wzrastają one proporcjonalnie do mierzonej 
wielkości. Źródłem tych błędów jest najczęściej 
niedoskonałość narzędzi pomiarowych. 

5 

Błędy przypadkowe 

Błędy przypadkowe obarczają wszystkie pomiary. 

Najczęściej spowodowane są one niedoskonałością 

wzroku obserwatora. Mają one niewielkie wartości, 

są nieuchwytne i mają różne znaki. Przyczyny ich 

powstania są przypadkowe i zmienne, zatem ich 

wartości i znaków nie można przewidzieć. Nie da 

się ich wyeliminować zupełnie, można jednak 

osłabić ich wpływ przez wykonanie pomiarów 

nadliczbowych i wyrównanie wyników pomiarów. 

6 

Wartość najbardziej prawdopodobna – średnia 

arytmetyczna 

n

]

l

[

n

l

...

l

l

x

n

2

1











l

1

, l

2

, ... – spostrzeżenia 

n – ilość spostrzeżeń 

Błąd prawdziwy – różnica między wartością 

prawdziwą X a i-tą wartością obserwowaną l

i

 

i

i

l

X







Spostrzeżenia bezpośrednie jednakowo 

dokładne 

7 

Błąd pozorny – różnica między średnią 

arytmetyczną x a i-tą wartością obserwowaną l

i

. 

i

i

l

x

v





0

[l]

–

[l]

l]

[

x

n 

]

v

[









Własność pierwsza: 

Własność druga: 

min.

]

vv

[



Na drugiej własności opiera się stosowana w 

rachunku wyrównawczym „metoda najmniejszych 

kwadratów” opracowana przez Gaussa. 

Spostrzeżenia bezpośrednie jednakowo 

dokładne 

8 

Błąd średni pojedynczego spostrzeżenia: 

• wyrażony przez błędy prawdziwe 

 

• wyrażony przez błędy pozorne 

 

Błąd średni średniej arytmetycznej (wartości 
wyrównanej): 

n

]

[

m





1

-

n

[vv]

m



 

1

-

n

n

[vv]

n

m

M





Spostrzeżenia bezpośrednie jednakowo 

dokładne 

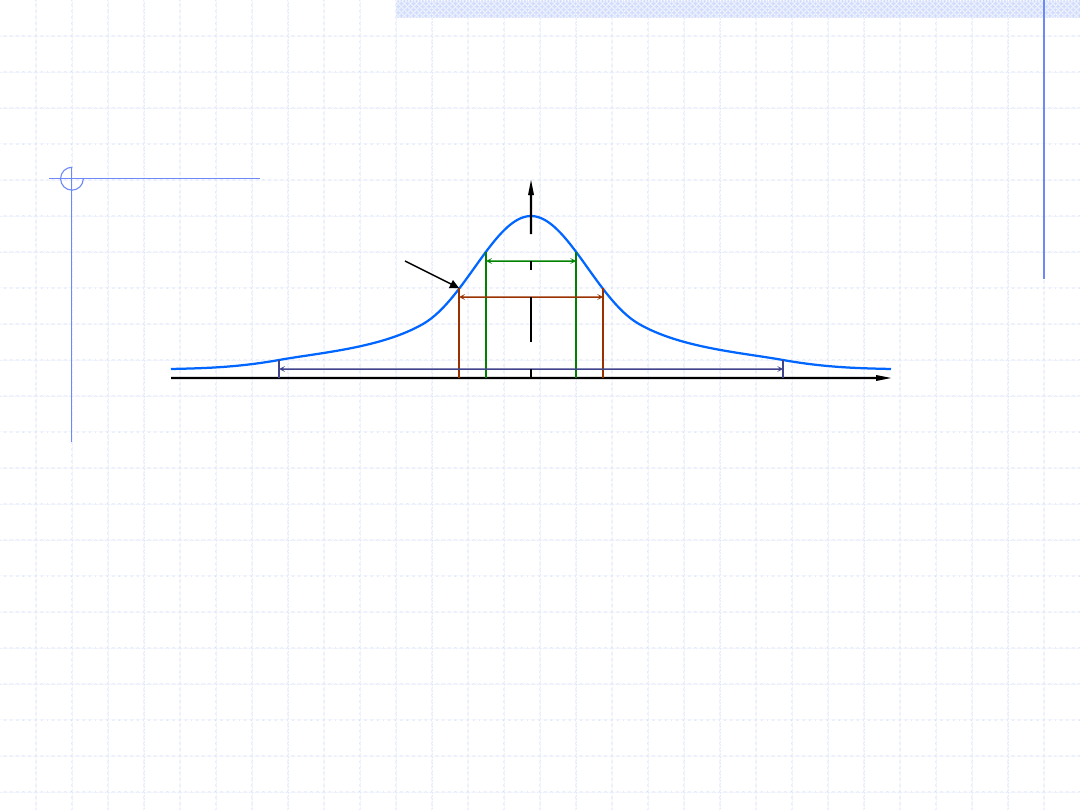
9 





997

,

0







g

g

-

P







683

,

0







m

m

-

P







5

,

0







r

r

-

P



Prawdopodobieństwa popełnienia błędu prawdziwego 

pomiaru w granicach błędów: 
• granicznego (g=3m) 
• średniego 
• prawdopodobnego 

68,3 % 

50 % 

99,7 % 

- m 

m 

- g 

g 

- r 

r 

y 

 

punkt przegięcia 

krzywej 

Krzywa błędów Gaussa 

10 

Błąd względny 

Definicja podaje, że jest to ułamek wyrażający 

stosunek absolutnej wartości błędu popełnionego 

przy pomiarze danej wielkości do wartości tej 

wielkości. 
Dla ułatwienia użycia błędu względnego, do licznika 

wprowadza się jedność: 

C

1

d

d





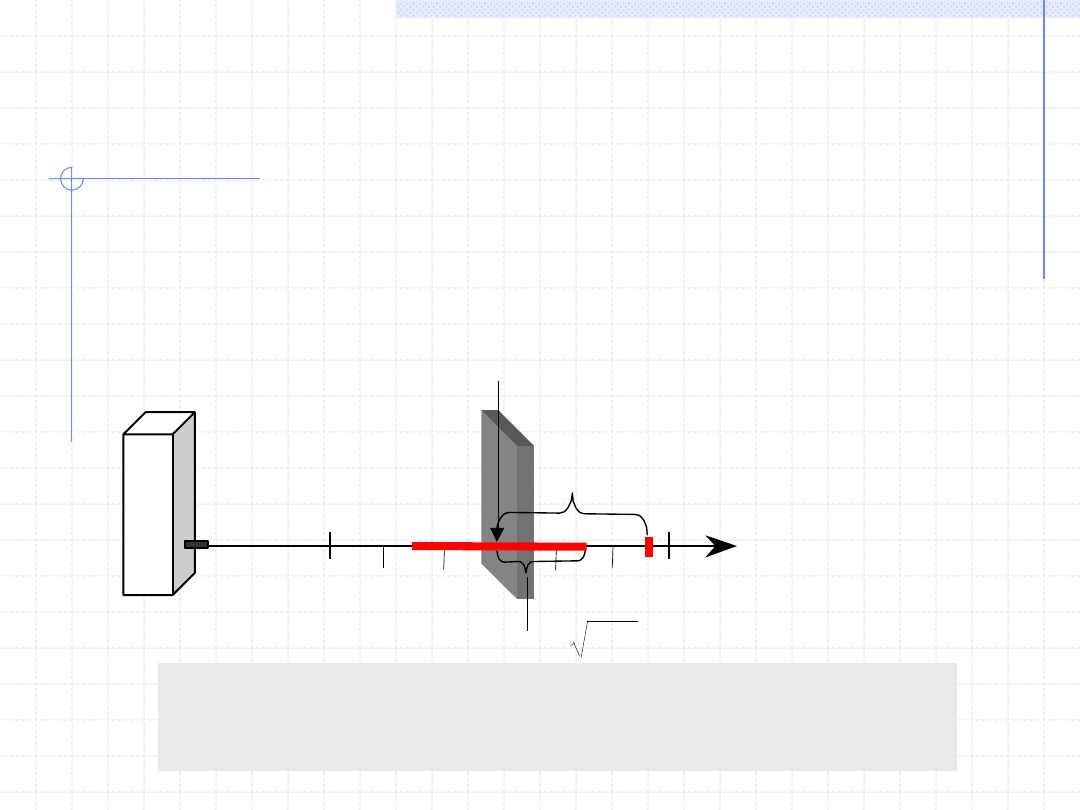
11 

 

Z doświadczenia wiadomo, że wynik pomiaru pewnej wielkości,  

np. odległości x za pomocą dalmierza DISTO, przyjmuje wartość z przedziału   

a < x < b, 

  którego wielkość zależy od dokładności użytego przyrządu pomiarowego m  

 

 
 
 

 
 
 
 

 

v = x – Ex

 - błąd pomiaru 

Ex - wartość oczekiwana wyniku pomiaru  

x 

- wynik pomiaru 

- błąd średni pomiaru 

 

2

Ev

m



 

 
 
 
 

a 

x

2

 

x

3

 

x

4

 

x

1

 

b 

DISTO 

Odchylenie wyniku pomiaru x od wartości oczekiwanej  v = x - Ex 
nazywane błędem pomiaru, ma charakter przypadkowy, zmienia się  
w czasie wykonywania pomiarów zarówno co do wielkości jak i znaku.  

Błąd średni pomiaru 

12 

Przy założeniu średniej arytmetycznej jako wartości oczekiwanej wyniku pomiaru: 

x

sr

1

n

i

x

i





n



Liczba pomiarów n = 4 

x

1

 = 4,006m 

x

2

 = 4,002m 

x

3

 = 4,008m 

x

4

 = 4,004m 

x

sr

 = 4,005m 

Błędy poszczególnych pomiarów  wynoszą:  

v

1

 = 0,001 

v

2

 = -0,003 

v

3

 = 0,003 

v

4

 = -0,001 

Odchylenie standardowe, nazywane błędem średnim pomiaru  

m

0

1

n

i

v

i

 

2





n

1





v

x

x

sr





m

0

 = 0,0026 

Błąd średni pomiaru 

13 

 

Pomiary, których odchyłki v przekraczają co do bezwzględnej wartości 

2- lub 3-krotnie ich błąd średni:  
                                        
są uznawane za odstające.  

Jeżeli  

m

0

0.0026



to wartość średnia i jej błąd: 

m

śr

2 

=

  

m

0

2

/

n

  

m

sr

m

n



m

v

m

2

m

sr

2





 

W podanym przykładzie brak pomiarów odstających, wszystkie pomiary  

spełniają kryterium |v| ≤  

 

W przypadku wystąpienia pomiarów odstających parametry rozrzutu x

sr

, m

0

 są obliczane 

iteracyjnie, odrzucając na każdym kroku pomiary odstające. W każdym kroku iteracji może się 
zmieniać zestaw usuwanych pomiarów odstających, pomiar raz usunięty może wrócić do zbioru, na 
podstawie którego oblicza się parametry rozrzutu. Postępowanie iteracyjne kontynuuje się do momentu, 
gdy parametry rozrzutu otrzymywane w kolejnych iteracjach przestaną się różnić znacząco, co oznacza, 
że zbiory w kolejnych iteracjach zawierają te same, lub prawie te same pomiary  

0 

0 

m

v

 = 0,0023 

2m

v

 = 0,0046 

m

śr

 = 0,0013 

Błąd średni pomiaru