dr Agnieszka Bobrowska

1

Ekonomia matematyczna I

Wykład 2

2. Teoria preferencji konsumenta

1

2.1. Potrzeby a preferencje konsumenta jako podstawa wyborów rynkowych

Praprzyczyn

ą

działalno

ś

ci gospodarczej człowieka jest konieczno

ść

zaspokajania jego potrzeb

konsumpcyjnych. Zatem jednym z najistotniejszych problemów ekonomii jest problem racjonalnego

zachowania si

ę

konsumenta, który wydatkuje swoje dochody na zakup towarów słu

żą

cych

konsumpcji. Za racjonalne uznaje si

ę

zachowanie, polegaj

ą

ce na wyborze, spo

ś

ród wszystkich

dost

ę

pnych na rynku towarów, takich produktów czy usług, które s

ą

u

ż

yteczne, czyli maj

ą

zdolno

ść

zaspokajania potrzeb ludzi.

Rozwa

ż

ania na temat zachowa

ń

konsumenta przeprowadzane s

ą

przy zało

ż

eniach idealizacyjnych

wła

ś

ciwych dla tak zwanego rynku doskonałego. Zatem przyjmuje si

ę

,

ż

e uczestnikami rynku jest

wielu sprzedawców i nabywców. Sprzedawcy s

ą

jednocze

ś

nie producentami towarów, które oferuj

ą

na rynku, a nabywcy pełni

ą

jednocze

ś

nie funkcj

ę

konsumentów i kupuj

ą

towary, aby zaspokoi

ć

swoje

potrzeby. Dysponuj

ą

oni pełn

ą

informacj

ą

po zerowym koszcie, co jest warunkiem podejmowania

przez nich optymalnych decyzji wyboru. Uczestnicy rynku doskonałego zachowuj

ą

si

ę

racjonalnie

(model homo economicus),

ż

aden z nich nie ma przewagi nad pozostałymi, podejmuj

ą

decyzje

niezale

ż

nie. Na rynku doskonałym nie ma barier wej

ś

cia i wyj

ś

cia (uczestnicy s

ą

mobilni). Wa

ż

n

ą

cech

ą

tego rynku jest zało

ż

enie o doskonałej podzielno

ś

ci towarów.

Pojedynczy uczestnik rynku ze wzgl

ę

du na swoja mał

ą

moc ekonomiczn

ą

, je

ż

eli tylko dostosuje si

ę

do warunków rynku (zaakceptuje cen

ę

równowagi), mo

ż

e zrealizowa

ć

swoje zamiary zakupu lub

sprzeda

ż

y.

Przyjmuje si

ę

równie

ż

,

ż

e nabywca d

ąż

y do maksymalizacji stopnia zaspokojenia swoich potrzeb

i znajduje si

ę

w sytuacji niedosytu, co skutkuje d

ąż

eniem nabywcy do wyboru i konsumpcji mo

ż

liwie

du

ż

ego koszyka towarów

2

.

2.2. Przestrze

ń

towarów jako formalne przedstawienie poda

ż

y

Zanim przejdziemy do wła

ś

ciwej tre

ś

ci wykładu wprowad

ź

my nast

ę

puj

ą

ce oznaczenia:

X- zbiór wszystkich dost

ę

pnych na rynku koszyków towarów,

R

n

+

- nieujemny orthant n-wymiarowej przestrzeni wektorowej R

n

, tj. zbiór wszystkich n-

wymiarowych

wektorów

o

nieujemnych

współrz

ę

dnych

rzeczywistych

{

}

n

i

x

R

x

x

x

i

n

n

,...,

2

,

1

,

0

:

)

,...,

,

(

2

1

=

≥

∈

+

,

x

i

(i=1,2,…,n) – ilo

ść

i-tego towaru mierzona w okre

ś

lonych jednostkach fizycznych (np.

w kilogramach, sztukach, litrach, metrach bie

żą

cych itp.) .

1

Wykład opracowany na podstawie E. Panek: Ekonomia matematyczna, Akademia Ekonomiczna w Poznaniu,

Pozna

ń

2000, rozdział 1

2

Proponujemy przypomnie

ć

sobie teori

ę

preferencji konsumenta, teori

ę

rynku doskonałego, podstawowe poj

ę

cia

dotycz

ą

ce rynku z podr

ę

czników z zakresu mikroekonomii np. B. Klimczak, Mikroekonomia, Wydawnictwo

Akademii Ekonomicznej im. Oskara Langego we Wrocławiu, Wrocław 2001, H. R. Varian, Mikroekonomia,
Wydawnictwo Naukowe PWN, Warszawa 1995 lub inne

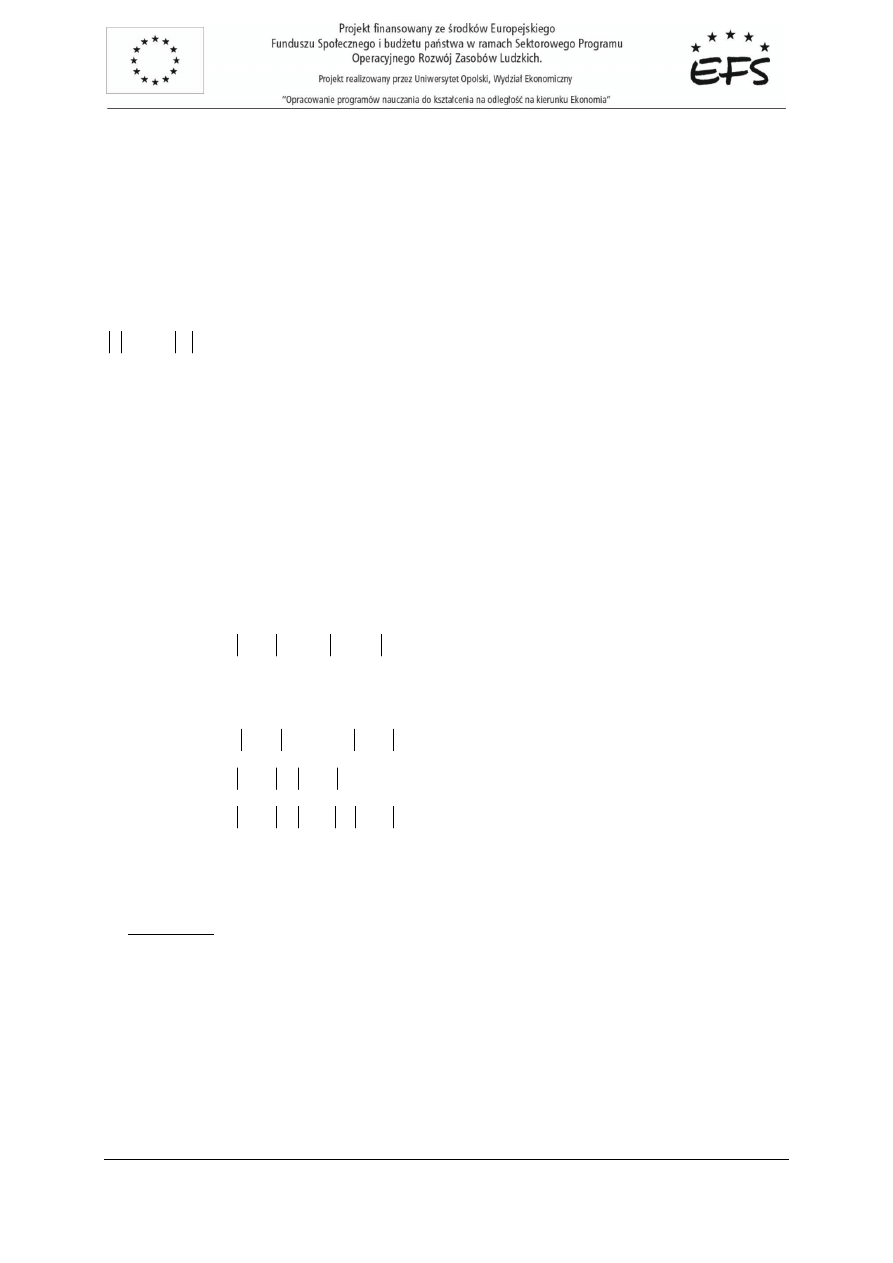
dr Agnieszka Bobrowska

2

Ekonomia matematyczna I

Zakładamy,

ż

e w danym okresie na rynek dostarczona zostaje sko

ń

czona liczba n ró

ż

nych

asortymentów towarów. Wówczas wektor postaci:

(

)

n

n

R

X

x

x

x

x

+

⊆

∈

=

,...,

,

2

1

opisuje uporz

ą

dkowany zestaw okre

ś

lonych ilo

ś

ci poszczególnych towarów wybranych przez

nabywc

ę

. Przestrze

ń

towarów stanowi sformalizowany sposób przedstawienia poda

ż

y towarów.

Zbiór

n

R

X

*

⊆

, czyli zbiór wszystkich dost

ę

pnych na rynku koszyków towarów z norm

ą

i

i

x

x

max

=

nazywamy

przestrzeni

ą

towarów

, natomiast jego elementy, czyli wektory

X

x

∈

koszykami towarów w przestrzeni X

.

Nale

ż

y podkre

ś

li

ć

, i

ż

przyj

ę

ta definicja normy, w odró

ż

nieniu od powszechnie stosowanej normy

euklidesowej pozwala unikn

ąć

m.in. popełnienia takich bł

ę

dów jak dodawanie do siebie wielko

ś

ci

o ró

ż

nych mianach, co miałoby miejsce w przypadku, gdyby współrz

ę

dne wektora towarów wyra

ż

one

były w ró

ż

nych jednostkach fizycznych.

Okre

ś

laj

ą

c norm

ę

na przestrzeni towarów w taki a nie inny sposób, skonstruowali

ś

my miar

ę

zró

ż

nicowania dwóch koszyków

(

)

n

x

x

x

x

,...,

,

2

1

=

i

(

)

n

y

y

y

y

,...,

,

2

1

=

, tj. odległo

ść

mi

ę

dzy nimi.

Co zapisujemy:

(1)

i

i

i

y

x

y

x

−

=

−

max

Poniewa

ż

norma okre

ś

lona wzorem (1) jest metryk

ą

, tj. spełnia nast

ę

puj

ą

ce warunki:

1.

X

y

x

∈

∀

,

0

≥

−

y

x

oraz

y

x

y

x

=

⇔

=

−

0

2.

X

y

x

∈

∀

,

x

y

y

x

−

=

−

3.

X

y

x

∈

∀

,

y

z

z

x

y

x

−

+

−

≤

−

,

to przestrze

ń

towarów jest przestrzeni

ą

metryczn

ą

. Ten fakt wykorzystamy przy definiowaniu wa

ż

nych

dla dalszych rozwa

ż

a

ń

poj

ęć

.

Przykład 2.1.

Załó

ż

my,

ż

e danego dnia na targu dost

ę

pne s

ą

jedynie dwa rodzaje towarów, a mianowicie kurze

jaja i jabłka, oba w ograniczonych ilo

ś

ciach, odpowiednio 300 sztuk i 120 kg. Wówczas przez

przestrze

ń

towarów dla rozwa

ż

anego rynku rozumie

ć

b

ę

dziemy zbiór:

(

)

{

}

120

,

300

;

,

:

,

2

1

2

1

2

1

≤

≤

∈

∈

=

+

x

x

R

x

N

x

x

x

X

.

dr Agnieszka Bobrowska

3

Ekonomia matematyczna I

Geometrycznie jest to zbiór odcinków prostopadłych do osi O

1

x

, co przedstawiono na rysunku 2.1.

Rys. 2.1. Przestrze

ń

towarów dla rynku z przykładu 2.1.

Przykład 2.2. (przypadek dyskretny)

Załó

ż

my,

ż

e danego dnia na rynku dost

ę

pne s

ą

jedynie dwa rodzaje towarów, a mianowicie torebki

damskie oraz portfele m

ę

skie, oba w ograniczonych ilo

ś

ciach; odpowiednio 6sztuk i 3 sztuki.

Wówczas przez przestrze

ń

towarów dla rozwa

ż

anego rynku rozumie

ć

b

ę

dziemy zbiór:

(

)

{

}

3

,

6

;

,

:

,

2

1

2

1

2

1

≤

≤

∈

=

x

x

N

x

x

x

x

X

.

Geometrycznie jest to zbiór 18 punktów, co przedstawiono na rysunku 2.2.

2

x

[kg]

1

x

[sztuki]

…

0 1 2 3 4

120

60

299 300

dr Agnieszka Bobrowska

4

Ekonomia matematyczna I

Rys. 2.2. Przestrze

ń

towarów dla rynku z przykładu 2.2.

Zadanie 2.1.:

Jak wygl

ą

da dwuwymiarowa przestrze

ń

towarów X, je

ż

eli na rynku dost

ę

pne jest 10 kg m

ą

ki oraz

20 litrów soku pomara

ń

czowego?

Rozwi

ą

zanie:

Przy zało

ż

eniu doskonałej podzielno

ś

ci towarów, przestrze

ń

towarów dla rozwa

ż

anego rynku to

zbiór postaci:

(

)

{

}

20

,

10

:

,

2

1

2

2

1

≤

≤

∈

=

+

x

x

R

x

x

X

.

Jego geometryczny obraz przedstawia rysunek 2.3.

2

x

[sztuki]

1

x

[sztuki]

0 1 2 3 4 5 6

3


2


1

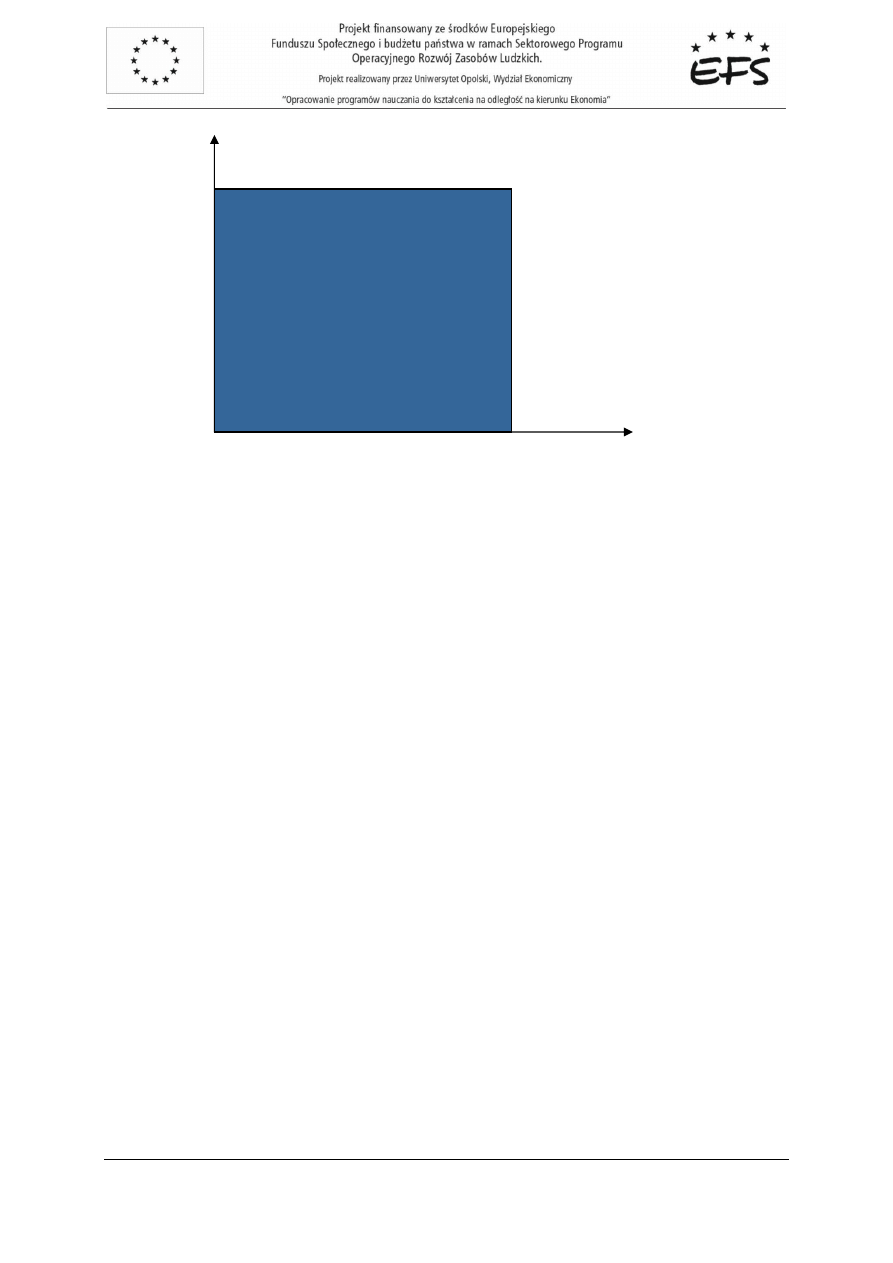
dr Agnieszka Bobrowska

5

Ekonomia matematyczna I

Rys. 2.3. Przestrze

ń

towarów z zadania 2.1.

2.3.Relacje preferencji i ich wła

ś

ciwo

ś

ci

Zachowaniem konsumenta, maj

ą

cego do dyspozycji cał

ą

przestrze

ń

towarów i staj

ą

cego przed

wyborem okre

ś

lonego koszyka towarów, kieruj

ą

pewne okre

ś

lone motywy. Przede wszystkim

konsument wybiera koszyk towarów ze wzgl

ę

du na konieczno

ść

zaspokojenia swoich potrzeb.

Ze wzgl

ę

du na przyj

ę

te zało

ż

enia o pełnej wiedzy konsumenta o rynku, mo

ż

emy przyj

ąć

,

ż

e zdaje

on sobie spraw

ę

ze swoich potrzeb, a tak

ż

e wie jakie cechy, własno

ś

ci i wła

ś

ciwo

ś

ci maj

ą

oferowane

na rynku towary. W tej sytuacji konsument jest w stanie wyrazi

ć

swoj

ą

opini

ę

o ka

ż

dym potencjalnym

koszyku towarów z punktu widzenia przydatno

ś

ci owego koszyka.

Ka

ż

dy konsument jest podmiotem, który ma swój system warto

ś

ci wynikaj

ą

cy z jego predyspozycji

psychofizycznych. Na ukształtowanie tego systemu wpływaj

ą

czynniki kulturowe, społeczne, moda itp.

Konsument zatem postawiony w sytuacji wyboru okre

ś

lonego zestawu towarów z wielu wariantów,

jest w stanie okre

ś

li

ć

, który wariant uznaje za optymalny, czy uporz

ą

dkowa

ć

zbiór dost

ę

pnych

koszyków ze wzgl

ę

du na ich subiektywnie ocenian

ą

u

ż

yteczno

ść

. W ekonomii ocenianie koszyków

traktujemy jako egzemplifikacj

ę

preferencji konsumentów, natomiast relacj

ę

porz

ą

dkuj

ą

c

ą

koszyki

nazywamy relacj

ą

preferencji konsumenta.

Dodatkowo zakładamy,

ż

e konsument jest w stanie naby

ć

ka

ż

dy koszyk dóbr lub inaczej,

ż

e na

jego decyzj

ę

nie maj

ą

wpływu (nie ograniczaj

ą

go) ani wielko

ść

osi

ą

ganych przez niego dochodów ani

ceny dóbr, a wybór konkretnego koszyka zale

ż

y jedynie od jego gustów (indywidualnych preferencji,

upodoba

ń

).

2

x

[litry]

1

x

[kg]

5 10

0

20

10

dr Agnieszka Bobrowska

6

Ekonomia matematyczna I

Dzi

ę

ki przyj

ę

tym zało

ż

eniom preferencje konsumenta mo

ż

na scharakteryzowa

ć

, jak ju

ż

wspomniano, w sposób sformalizowany za pomoc

ą

okre

ś

lonej w przestrzeni towarów X relacji słabej

preferencji

~

f

. Do opisania własno

ś

ci tej relacji zastosowano j

ę

zyk logiki matematycznej.

Poniewa

ż

teoria ekonomi zakłada doskonał

ą

podzielno

ść

towarów, to w teorii preferencji zakłada

si

ę

o relacji słabej preferencji

~

f

,

ż

e jest ci

ą

gła oraz

ż

e spełnia dwa nast

ę

puj

ą

ce aksjomaty zwane

warunkami pełnego preporz

ą

dku:

(I)













⇒

∧

∈

∀

z

x

z

y

y

x

X

y

x

~

~

~

,

f

f

f

,

(II)













∨

∈

∀

x

y

y

x

X

y

x

~

~

,

f

f

.

Uwagi:

1. Zapis „

y

x

~

f

” oznacza „koszyk towarów x jest słabo preferowany nad koszyk towarów y” albo

„koszyk x nie jest gorszy od koszyka towarów y”.

2. Aksjomat (I), zwany aksjomatem przechodnio

ś

ci (tranzytywno

ś

ci), wprowadza liniowy porz

ą

dek

w przestrzeni towarów X. Innymi słowy, je

ż

eli koszyk x jest słabo preferowany na koszyk y,

a koszyk y jest słabo preferowany nad koszyk z, to koszyk x jest te

ż

słabo preferowany nad

koszyk z.

3. Aksjomat (II), zwany aksjomatem zupełno

ś

ci, wyklucza istnienie sytuacji nieokre

ś

lonej, w której

konsument nie potrafi okre

ś

li

ć

, który z dwóch koszyków x, y

∈

X jest jego zdaniem nie gorszy

od drugiego. Nie jest to jednak sytuacja, gdy koszyki s

ą

dla niego indyferentne, jednakowo

dobre.

4. Z aksjomatu (II) wynika ponadto,

ż

e relacja słabej preferencji jest zwrotna, tj.

( )

x

x

X

x

~

,

f

∈

∀

.

Oznacza to,

ż

e ka

ż

dy koszyk jest co najmniej tak samo dobry jak on sam.

Relacja słabej preferencji „

~

f

” jest odpowiednikiem słabej nierówno

ś

ci w matematyce „

≥

”. Jest

ona zatem relacj

ą

nieostr

ą

i mo

ż

na j

ą

podzieli

ć

na dwie silne relacje, a mianowicie relacj

ę

indyferencji

„~” oraz relacj

ę

silnej preferencji „

f

”, których matematycznymi odpowiednikami s

ą

relacja równo

ś

ci

„=” i relacja ostrej nierówno

ś

ci „>”.

Je

ż

eli równocze

ś

nie

~

y

x f

oraz

x

y

~

f

, wówczas koszyki x, y nazywamy

indyferentnymi.

Je

ż

eli natomiast

( )

x

y

y

x

~

~

f

f

¬

∧

, wówczas o koszyku x mówimy,

ż

e jest on

silnie preferowany

.

Je

ż

eli koszyki s

ą

indyferentne oznacza to,

ż

e dla konsumenta s

ą

one tak samo dobre

(nierozró

ż

nialne), tzn. czerpałby z ich posiadania taka sam

ą

satysfakcj

ę

. Relacj

ę

indyferencji

oznaczamy symbolem ~.

dr Agnieszka Bobrowska

7

Ekonomia matematyczna I

Je

ż

eli natomiast koszyk x jest silnie preferowany nad koszyk y to rozumiemy przez to,

ż

e dla

konsumenta koszyk x jest lepszy od koszyka y. Relacj

ę

silnej preferencji oznaczamy symbolem

f

.

Bardzo łatwo mo

ż

na zauwa

ż

y

ć

,

ż

e relacja indyferencji jest relacj

ą

równowa

ż

no

ś

ci, tj. spełnia trzy

kolejne warunki:

(I)

(

)

x

x

X

x

~

∈

∀

(warunek zwrotno

ś

ci),

(II)

(

) (

)

(

)

x

y

y

x

X

y

x

~

~

,

⇒

∈

∀

(warunek symetryczno

ś

ci),

(III)

(

) (

)

(

) (

)

[

]

z

x

z

y

y

x

X

z

y

x

~

~

~

,

,

⇒

∧

∈

∀

(warunek przechodnio

ś

ci).

(Dowód tego faktu pomijamy. Dla zainteresowanych dowód w ksi

ąż

ce: E. Panek „Ekonomia

matematyczna”, APE, Pozna

ń

2000, str. 27-28).

Uwagi:

Ekonomiczne uzasadnienie wszystkich trzech wy

ż

ej wymienionych warunków jest intuicyjnie

bardzo oczywiste.

1. W odniesieniu do warunku zwrotno

ś

ci, wydaje si

ę

bezdyskusyjne,

ż

e dla normalnie

rozumuj

ą

cego człowieka dwa identyczne koszyki s

ą

tak samo satysfakcjonuj

ą

ce.

2. W przypadku warunku symetryczno

ś

ci stwierdzenie konsumenta, i

ż

koszyk x jest dla niego tak

samo dobry jak koszyk y i jednocze

ś

nie,

ż

e koszyk y jest jego zdaniem gorszy lub lepszy od

koszyka x, wydałoby si

ę

nielogicznie, zaprzeczałby on bowiem sam sobie.

3. Przechodnio

ść

relacji indyferencji oznacza,

ż

e nienaturalne wydaje si

ę

stwierdzenie

konsumenta, i

ż

koszyki x i y, podobnie jak koszyki y i z s

ą

dla niego parami nierozró

ż

nialne, ale

koszyk z uwa

ż

ałby za gorszy od koszyka x. W praktyce oznaczałoby to,

ż

e koszyk z jest jego

zdaniem równie

ż

gorszy od koszyka y, sk

ą

d otrzymaliby

ś

my sprzeczno

ść

.

Bazuj

ą

c na własno

ś

ciach relacji indyferencji oraz relacji słabej preferencji mo

ż

emy przyst

ą

pi

ć

do

omówienia własno

ś

ci relacji silnej preferencji, które prezentujemy w lemacie 2.1.

Lemat 2.1.

Relacja silnej preferencji ma nast

ę

puj

ą

ce własno

ś

ci:

(I)

(

)

x

x

X

x

X

x

f

∈

¬∃

∈

∀

,

(II)

x

y

y

x

X

y

x

~

,

f

f

∨

∈

∀

,

(III)

y

x

x

y

y

x

X

y

x

~

,

∨

∨

∈

∀

f

f

,

(IV)

(

)

y

x

y

x

y

x

X

y

x

~

,

~

∨

⇔

∈

∀

f

f

,

(V)

(

)

z

x

z

y

y

x

X

z

y

x

f

f

f

⇒

∧

∈

∀

~

,

,

.

dr Agnieszka Bobrowska

8

Ekonomia matematyczna I

Uwagi:

1. Pierwsza własno

ść

oznacza,

ż

e nie istnieje taki koszyk towarów, który byłby zdaniem

konsumenta lepszy od identycznego z nim koszyka. Własno

ść

ta jest zaprzeczeniem warunku

zwrotno

ś

ci relacji indyferencji.

2. Własno

ść

druga prezentuje dwie wykluczaj

ą

ce si

ę

sytuacje: albo konsument preferuje koszyk x

nad koszyk y albo koszyk y jest jego zdaniem nie gorszy od koszyka x. Własno

ść

ta opisuje

wszystkie mo

ż

liwe relacje mi

ę

dzy par

ą

koszyków. Z własno

ś

ci tej mo

ż

na wyprowadzi

ć

własno

ść

trzeci

ą

.

3. Własno

ś

ci trzecia równie

ż

prezentuje wykluczaj

ą

ce si

ę

relacje mi

ę

dzy par

ą

koszyków towarów

wyra

ż

one przy u

ż

yciu relacji silnej preferencji i indyferencji.

4. Czwarta własno

ść

, któr

ą

czytamy: koszyk x jest nie gorszy od koszyka y, wtedy i tylko wtedy,

gdy koszyk x jest lepszy od koszyka y lub koszyki x i y s

ą

indyferentne. Wskazuje na istot

ę

podziału relacji słabej preferencji na dwie wykluczaj

ą

ce si

ę

ostre relacje.

5. Pi

ą

ta własno

ść

wskazuje,

ż

e alternatywa relacji silnej preferencji i relacji słabej preferencji

koszyków (niezale

ż

nie od ich kolejno

ś

ci) jako relacje przechodnich, daj

ą

w wyniku relacj

ę

słabej preferencji.

Przykład 2.3.

Dana jest 4-elemetowa przestrze

ń

towarów

{

}

D

C

B

A

X

,

,

,

=

, gdzie A, B, C, D s

ą

koszykami

towarów. Wiedz

ą

c,

ż

e

A

D

C

B

C

A

f

f

,

~

,

, okre

ś

li

ć

zale

ż

no

ś

ci pomi

ę

dzy elementami

A

i

B

oraz

C

i

D

.

Poniewa

ż

C

B ~

, to z symetryczno

ś

ci relacji indyferencji mamy:

B

C ~

. Wiemy ponadto,

ż

e

C

A f

. Skoro

C

A f

oraz

B

C ~

równocze

ś

nie, to

B

A f

. Z kolei poniewa

ż

A

D f

oraz

C

A f

,

to z przechodnio

ś

ci relacji preferencji otrzymujemy:

C

D f

.

2.4.Definicja pola preferencji

Wychodz

ą

c z definicji przestrzeni towarów oraz relacji słabej preferencji, mo

ż

emy przyst

ą

pi

ć

do

zdefiniowania pola preferencji konsumenta:

Par

ę

(X,

~

f

), gdzie X jest przestrzeni

ą

towarów (Ø

≠

n

R

X

+

⊆

), a

~

f

relacj

ą

preferencji konsumenta

w X, nazywamy

polem preferencji konsumenta

.

Pole preferencji jest formalnym opisem mo

ż

liwo

ś

ci wyra

ż

enia przez konsumenta opinii

o wszystkich koszykach towarów, które daj

ą

si

ę

wyodr

ę

bni

ć

przy danej poda

ż

y. Obserwacje

zachowa

ń

konsumentów pozwoliły opisa

ć

na gruncie teorii ekonomii tzw. zjawisko niedosytu, które

definiujemy nast

ę

puj

ą

co:

Mówimy,

ż

e w polu preferencji

)

,

(

~

f

n

R

+

obserwujemy

zjawisko niedosytu

, je

ż

eli

dr Agnieszka Bobrowska

9

Ekonomia matematyczna I

)

(

,

y

x

y

x

y

x

R

y

x

n

f

⇒

≠

∧

≥

∈

∀

+

.

Konsument znajduj

ą

cy si

ę

w sytuacji niedosytu preferuje zatem koszyk wi

ę

kszy, tzn. zawieraj

ą

cy

wi

ę

ksze ilo

ś

ci chocia

ż

by jednego z towarów. Sytuacja niedosytu konsumenta była charakterystyczna

dla pocz

ą

tkowych faz rozwoju kapitalizmu. Wprowadzona została do teorii ekonomii jako jedna

z podstawowych cech charakteryzuj

ą

cych zachowania konsumenta na rynku doskonałym. Nale

ż

y

wspomnie

ć

,

ż

e współczesna teoria ekonomii wprowadza do swoich rozwa

ż

a

ń

analiz

ę

sytuacji

nasycenia konsumenta i skutek w postaci zmniejszenia si

ę

u

ż

yteczno

ś

ci koszyków wi

ę

kszych od

koszyka optymalnego, który maksymalizuje u

ż

yteczno

ść

konsumenta (porównaj Hal R. Varian,

„Mikroekonomia”, str. 60).

Z zało

ż

eniem niedosytu nabywcy zwi

ą

zane jest

ś

ci

ś

le zało

ż

enie wypukło

ś

ci pola preferencji.

Ograniczeniem dla tego zało

ż

enia, które szczegółowo przedyskutowane b

ę

dzie przy okazji rozwa

ż

a

ń

nad kategori

ą

popytu, jest fakt, i

ż

konsument dysponuj

ą

cy okre

ś

lon

ą

wielko

ś

ci

ą

dochodu, przy danych

cenach, nie mo

ż

e sobie pozwoli

ć

na zakup koszyka zawieraj

ą

cego wi

ę

ksz

ą

ilo

ść

dóbr.

Zało

ż

enie wypukło

ś

ci pola preferencji jest warunkiem istnienia jednego optymalnego dla

konsumenta koszyka towarów. Wypukło

ść

pola preferencji zale

ż

y od zachowa

ń

nabywców.

Mówimy,

ż

e pole preferencji jest

słabo wypukłe

, je

ż

eli koszyki dóbr s

ą

słabo rozró

ż

nialne

( )

y

x

~

f

.

Natomiast je

ż

eli mo

ż

na znale

źć

tylko jeden preferowany (optymalny) koszyk towarów, to

pole preferencji jest

silnie wypukłe

.

Słaba wypukło

ść

pola preferencji oznacza,

ż

e relacja słabej preferencji jest ci

ą

gła i istnieje

preferowany

koszyk

towarów

(mo

ż

na

wyodr

ę

bni

ć

preferowany

zbiór

koszyków

towarów:

{

}

y

x

X

x

~

: f

∈

). W tym momencie nale

ż

y podkre

ś

li

ć

,

ż

e ci

ą

gło

ść

relacji słabej preferencji

jest kolejnym, obok warunków pełnego preporz

ą

dku, fundamentalnym zało

ż

eniem teorii preferencji.

Mówimy,

ż

e

relacja słabej preferencji

~

f

jest ci

ą

gła

w przestrzeni towarów X, je

ż

eli zbiór

( )

{

}

X

y

x

y

x

y

x

G

∈

=

,

;

:

,

f

;

n

R

G

2

+

⊂

jest otwarty w przestrzeni metrycznej

X

X

×

z metryk

ą

(

) (

)

)

min

,

min

(

,

,

2

1

2

1

2

2

1

1

i

i

i

i

i

i

y

y

x

x

y

x

y

x

−

−

=

−

.

Z powy

ż

ej definicji wynika,

ż

e je

ż

eli relacja preferencji jest ci

ą

gła, to istnieje takie

−

ε

otoczenie

punktu

( )

X

X

y

x

×

∈

,

(gdzie x jest koszykiem silnie preferowanym nad y):

(

)

(

)

{

}

ε

ε

<

−

×

∈

=

)

,

(

'

,

'

:

'

,

'

)

,

(

y

x

y

x

X

X

y

x

y

x

U

ż

e dla ka

ż

dej pary

(

)

)

,

(

'

,

'

y

x

U

y

x

ε

∈

tak

ż

e koszyk x’ jest silnie preferowany nad koszyk y’.

Oznacza to tyle,

ż

e je

ż

eli zdaniem konsumenta koszyk towarów x jest silnie preferowany nad koszyk

dr Agnieszka Bobrowska

10

Ekonomia matematyczna I

y, to równie

ż

koszyk x’ (niewiele ró

ż

ni

ą

cy si

ę

od koszyka x) jest lepszy od koszyka y’ (niewiele

ró

ż

ni

ą

cy si

ę

od koszyka y).

Wniosek:

Relacja słabej i silnej preferencji jest ci

ą

gła, je

ż

eli istnieje taki zbiór, który zawiera par

ę

koszyków

( )

y

x,

, przy czym koszyk x jest silnie preferowany nad y i oba nale

żą

do n nieujemnej przestrzeni

towarów X i zbiór ten jest otwarty.

W naszych rozwa

ż

aniach zakładamy,

ż

e konsument ma nieograniczony dost

ę

p do rynku oraz

posiada o nim pełn

ą

informacj

ę

, a jego zachowanie jest racjonalne (inaczej: konsument działa

w warunkach konkurencji doskonałej). Decyzje konsumenta działaj

ą

cego w warunkach konkurencji

doskonałej zale

żą

jedynie od jego własnych odczu

ć

oraz jego ograniczenia bud

ż

etowego. Nale

ż

y

podkre

ś

li

ć

,

ż

e nie b

ę

dzie on podejmował wyborów koszyków w oparciu o cał

ą

przestrze

ń

towarów, ale

ograniczy si

ę

do takiego jej podzbioru, którego elementy b

ę

d

ą

w kr

ę

gu jego zainteresowania tzn. b

ę

d

ą

zaspokaja

ć

jego potrzeb, z uwzgl

ę

dnieniem jego gustów i wielko

ś

ci dochodów (np. konsumenta, który

nie pali papierosów, nie b

ę

d

ą

interesowały koszyki zawieraj

ą

ce papierosy).

Zakładamy zatem,

ż

e konsument dokonuje wyboru koszyka towarów ograniczaj

ą

c si

ę

do pewnego

niepustego podzbioru

X

M

⊆

, gdzie

( )

~

, f

X

- pole preferencji oraz

ż

e potrafi wskaza

ć

w podzbiorze

M koszyki optymalne, zwane M-preferowanymi.

Koszyk towarów

M

x

∈

, dla którego spełniony jest warunek:

( )

y

x

M

y

~

f

∈

∀

nazywamy

koszykiem M-preferowanym

i oznaczamy x=m.pref.M.

Inaczej mówimy równie

ż

,

ż

e koszyk x jest optymalnym koszykiem w zbiorze M, je

ż

eli jest on nie

gorszy od ka

ż

dego innego koszyka z tego zbioru. Naturalnie w zbiorze M mo

ż

e istnie

ć

wi

ę

cej ni

ż

jeden optymalnych koszyków. Załó

ż

my zatem,

ż

e w zbiorze M s

ą

dwa optymalne koszyki

M

x

x

∈

2

1

,

. Oznacza to,

ż

e

)

(

;

~

1

x

x

M

x

f

∈

∀

oraz

)

(

;

~

2

x

x

M

x

f

∈

∀

. Oba warunki implikuj

ą

,

ż

e

)

(

2

~

1

x

x f

oraz

)

(

1

~

2

x

x f

, czyli

)

~

(

2

1

x

x

. Zatem wszystkie optymalne koszyki w zbiorze M s

ą

wzgl

ę

dem siebie indyferentne. Wnioskujemy st

ą

d,

ż

e o ile w zbiorze M istnieje tylko jeden optymalny

koszyk x, to jest on najlepszy spo

ś

ród wszystkich koszyków w zbiorze M, co zapisujemy:

y

x

M

y

f

;

∈

∀

.

Wychodz

ą

c z obserwacji dotycz

ą

cych mo

ż

liwo

ś

ci zaspokojenia potrzeb nabywcy przez ró

ż

ne

koszyki towarów, a wi

ę

c z rozwa

ż

anego w teorii ekonomii zjawiska substytucji wyprowadza si

ę

poj

ę

cie

obszaru oboj

ę

tno

ś

ci, a w przypadku dwuwymiarowym (

2

+

=

R

X

) krzywej oboj

ę

tno

ś

ci.

dr Agnieszka Bobrowska

11

Ekonomia matematyczna I

Zbiór wszystkich koszyków indyferentnych z koszykiem

X

x

∈

, tj. zbiór postaci

{

}

x

y

X

y

~

;

∈

nazywamy

obszarem oboj

ę

tno

ś

ci

w przestrzeni towarów i oznaczamy

symbolem

x

K

.

Analogicznie dla przypadku dwuwymiarowego:

Zbiór wszystkich koszyków towarów, wobec których konsument pozostaje oboj

ę

tny

w porównaniu z danym koszykiem nazywamy

krzyw

ą

oboj

ę

tno

ś

ci

.

Obszar oboj

ę

tno

ś

ci (krzywa oboj

ę

tno

ś

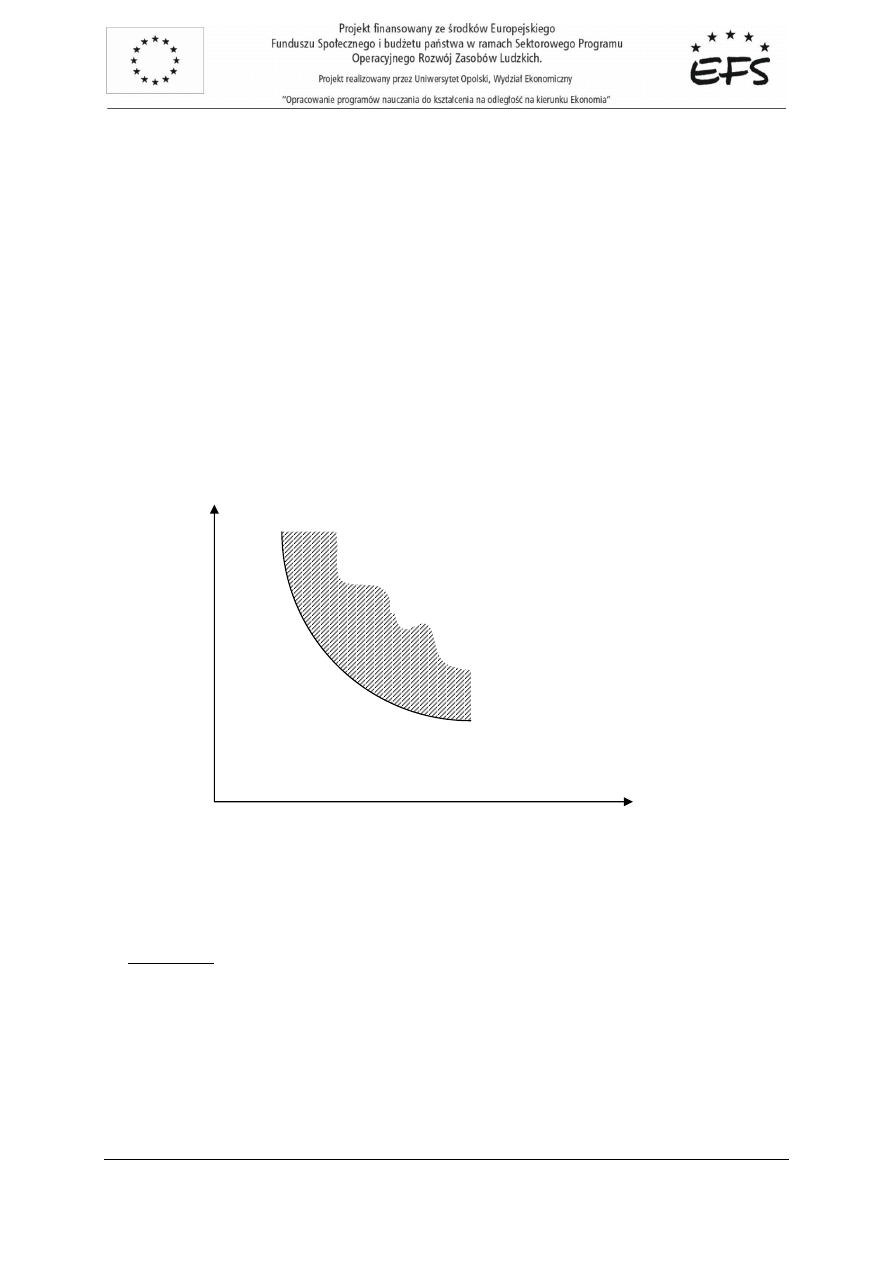
ci) jest graficznym opisem preferencji konsumenta. Przykład

krzywej oboj

ę

tno

ś

ci dla wybranych dóbr konsumpcyjnych przedstawiono na rysunku 2.4. Ilustruje on

zbiór koszyków indyferentnych wzgl

ę

dem wybranego koszyka

(

)

0

2

0

1

, x

x

. Zacieniowany obszar

prezentuje z kolei zbiór wszystkich koszyków, które s

ą

słabo preferowane wzgl

ę

dem koszyka

(

)

0

2

0

1

, x

x

.

Rys. 2.4. Przykładowa krzywa preferencji.

Przykład 2.5.

Naszym zadaniem jest znalezienie optymalnego koszyka towarów w zbiorze:

{

}

2

2

1

2

2

1

4

:

)

,

(

+

+

=

⊂

≤

+

∈

=

=

R

X

x

x

R

x

x

x

M

w przypadku, gdy relacja preferencji jest zdefiniowana nast

ę

puj

ą

co:

2

1

2

1

~

y

y

x

x

y

x

+

=

+

⇔

oraz

2

1

2

1

y

y

x

x

y

x

+

>

+

⇔

f

.

2

x

1

x

0

dr Agnieszka Bobrowska

12

Ekonomia matematyczna I

Rozwa

ż

my dwa koszyki

)

,

(

2

1

2

1

=

y

oraz

)

1

,

1

(

=

z

, dla których obszary oboj

ę

tno

ś

ci (krzywe

oboj

ę

tno

ś

ci) maj

ą

nast

ę

puj

ą

c

ą

posta

ć

:

{

}

1

:

)

,

(

2

1

2

2

1

=

+

∈

=

+

x

x

R

x

x

K

y

oraz

{

}

2

:

)

,

(

2

1

2

2

1

=

+

∈

=

+

x

x

R

x

x

K

z

.

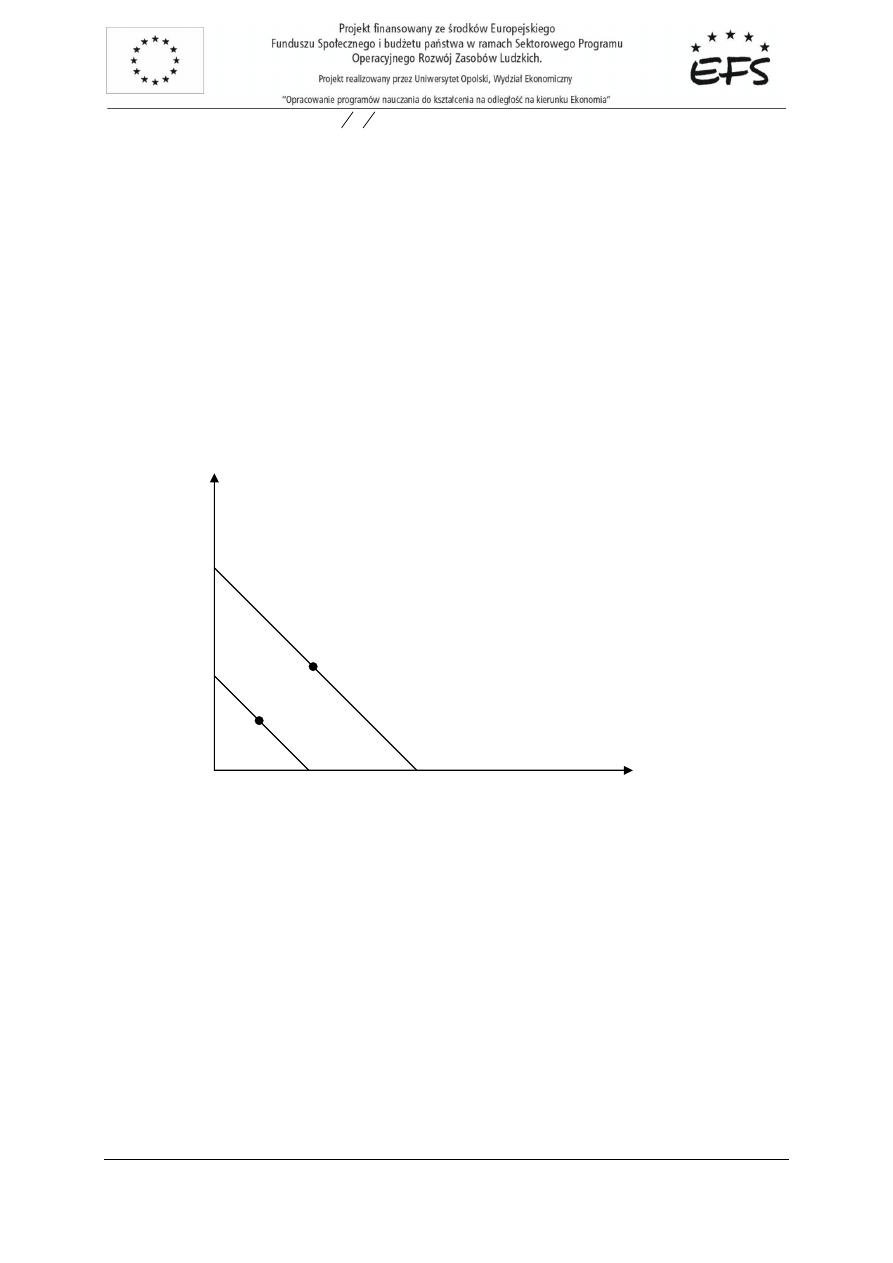
Ich przebieg ilustruje rysunek 2.5.

Krzywe

y

K

oraz

z

K

, to proste równoległe prezentuj

ą

ce ró

ż

ne poziomy u

ż

yteczno

ś

ci, przy czym

krzywa

y

K

przedstawia wszystkie koszyki, które zdaniem konsumenta s

ą

tak samo dobre jak koszyk

y, natomiast krzywa

z

K

przedstawia wszystkie koszyki indyferentne z koszykiem z. Jednocze

ś

nie

ka

ż

dy koszyk nale

żą

cy do

z

K

jest lepszy od ka

ż

dego koszyka nale

żą

cego do

y

K

, co wynika

z zało

ż

enia niedosytu konsumenta.

Rys. 2.5. Obszary oboj

ę

tno

ś

ci wzgl

ę

dem koszyków y i z dla przykładu 2.5.

Poniewa

ż

koszyki towarów s

ą

tym lepsze, im wy

ż

ej le

ż

y utworzony wzgl

ę

dem nich obszar

oboj

ę

tno

ś

ci, zatem optymalnym koszykiem towarów w zbiorze M, b

ę

dzie ten koszyk, który znajduje

si

ę

na najwy

ż

ej poło

ż

onej krzywej oboj

ę

tno

ś

ci i który nale

ż

y do zbioru M.

Przypomnijmy,

ż

e w naszym przykładzie zbiór M jest postaci:

{

}

2

2

1

2

2

1

4

:

)

,

(

+

+

=

⊂

≤

+

∈

=

=

R

X

x

x

R

x

x

x

M

.

Na rysunku 2.6. przedstawiono zbiór M, obszary oboj

ę

tno

ś

ci oraz optymalne koszyki towarów.

2

x

1

x

1 2

0

2

1

y

K

y

z

K

z

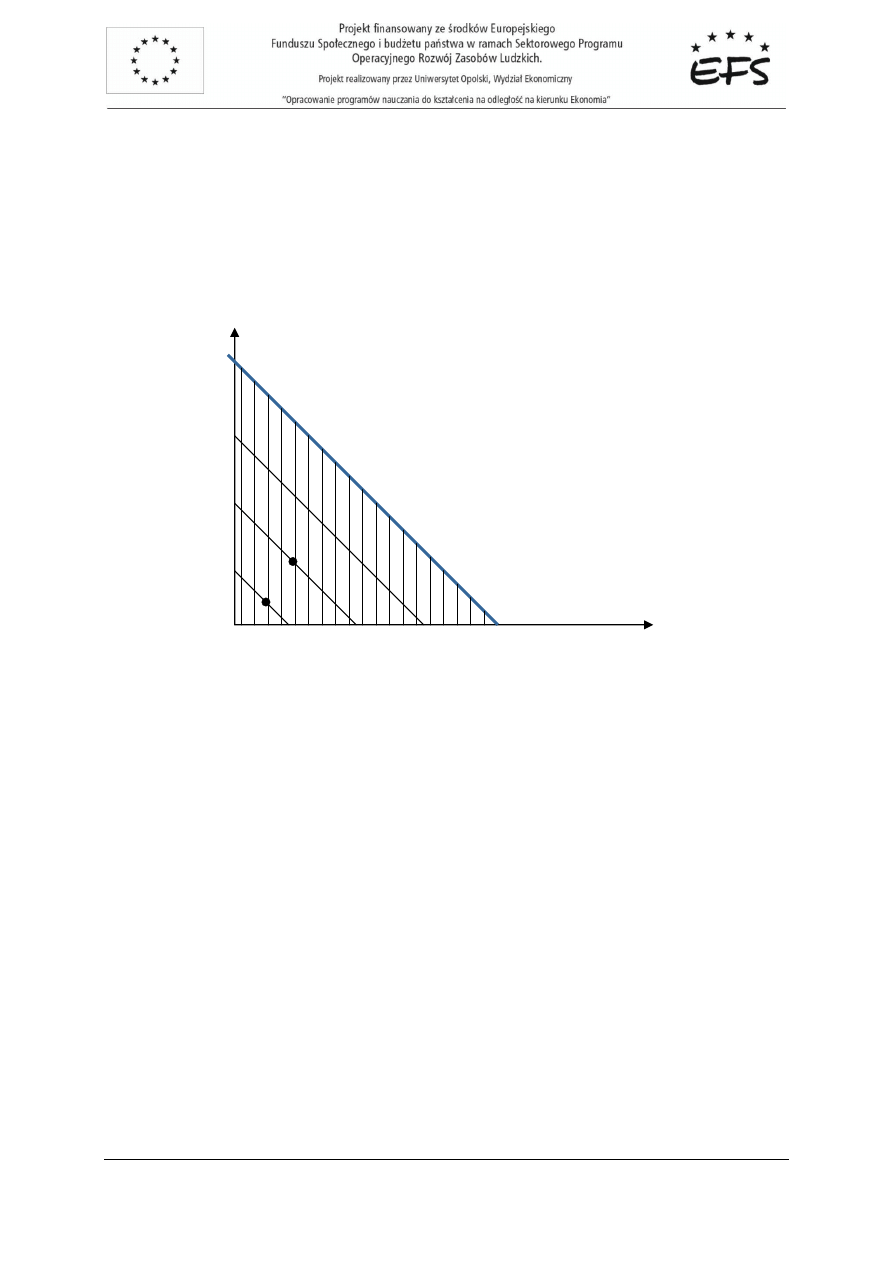
dr Agnieszka Bobrowska

13

Ekonomia matematyczna I

W naszym przypadku zbiór optymalnych koszyków towarów ma nast

ę

puj

ą

c

ą

posta

ć

:

{

}

2

2

1

2

2

1

.

4

:

)

,

(

+

+

=

⊂

=

+

∈

=

=

R

X

x

x

R

x

x

x

K

optym

Przykładem koszyka optymalnego s

ą

zatem koszyki: (4,0), (0,4) oraz ka

ż

dy koszyk postaci:

)

4

,

0

)(

1

(

)

0

,

4

(

α

α

−

+

, gdzie

]

1

;

0

[

∈

α

. Na rysunku zbiór wszystkich optymalnych koszyków

zaznaczono na niebiesko.

Rys.2.6. Zbiór optymalnych koszyków w zbiorze M wzgl

ę

dem zadanej relacji preferencji.

Przy okazji naszych rozwa

ż

a

ń

warto przypomnie

ć

podstawowe własno

ś

ci powierzchni oboj

ę

tno

ś

ci

(krzywych oboj

ę

tno

ś

ci):

1. Krzywe oboj

ę

tno

ś

ci s

ą

wypukłe wzgl

ę

dem pocz

ą

tku układu współrz

ę

dnych, co wynika

z przyj

ę

cia sytuacji niedosytu konsumenta (ka

ż

dy konsument ceni sobie bardziej koszyk

wi

ę

kszy).

2. Krzywe oboj

ę

tno

ś

ci nie przecinaj

ą

si

ę

. W przypadku przeci

ę

cia si

ę

krzywych, które zawieraj

ą

koszyki ró

ż

ni

ą

ce si

ę

u

ż

yteczno

ś

ci

ą

, koszyk le

żą

cy na przeci

ę

ciu owych krzywych

prezentowałby dwa ró

ż

ne poziomy u

ż

yteczno

ś

ci, co jest nielogiczne.

3. Im wy

ż

ej poło

ż

ona jest krzywa u

ż

yteczno

ś

ci, tym wy

ż

sz

ą

u

ż

yteczno

ść

posiadaj

ą

koszyki na

niej poło

ż

one.

Podsumowuj

ą

c, je

ż

eli poruszamy si

ę

po krzywej oboj

ę

tno

ś

ci, to znajdujemy si

ę

w zbiorze

koszyków indyferentnych, maj

ą

cych t

ą

sam

ą

u

ż

yteczno

ść

, natomiast przechodzenie z jednej krzywej

oboj

ę

tno

ś

ci na drug

ą

oznacza zmian

ę

u

ż

yteczno

ś

ci koszyków.

2

x

1

x

0 1 2 3 4

4

3

2

1

y

K

y

z

K

z

.

optym

K

M

dr Agnieszka Bobrowska

14

Ekonomia matematyczna I

Bezpo

ś

rednio z własno

ś

ci obszarów oboj

ę

tno

ś

ci oraz sytuacji niedosytu wynika monotoniczno

ść

relacji preferencji, co w rezultacie prowadzi do zało

ż

enia wypukło

ś

ci relacji preferencji.

Mówimy,

ż

e relacja preferencji okre

ś

lona na wypukłej przestrzeni towarów X jest

wypukła

,

je

ż

eli

y

y

x

y

x

X

y

x

~

~

)

1

(

,

]

1

;

0

[

f

f

α

α

α

−

+

⇒

∈

∀

∈

∀

.

Mówimy,

ż

e relacja preferencji okre

ś

lona na wypukłej przestrzeni towarów X jest

silnie

wypukła

, je

ż

eli

y

y

x

y

x

X

y

x

f

f

)

1

(

,

]

1

;

0

[

α

α

α

−

+

⇒

∈

∀

∈

∀

.

Aby ustali

ć

jednoznacznie czy dana relacja preferencji jest wypukła, posłu

ż

ymy si

ę

poni

ż

szym

twierdzeniem.

Twierdzenie 2.1.

Relacja preferencji

~

f

jest wypukła na X wtedy i tylko wtedy, gdy dla

ka

ż

dego koszyka

X

y

∈

zbiór

{

}

y

x

X

x

y

F

~

:

)

(

f

∈

=

wszystkich koszyków nie gorszych od y

jest wypukły.

Je

ż

eli relacja preferencji jest silnie wypukła, to dla ka

ż

dej pary koszyków x, y mamy nast

ę

puj

ą

ce

własno

ś

ci:

Twierdzenie 2.2.

Je

ż

eli relacja preferencji jest silnie wypukła, to spełnione s

ą

warunki:

(I)

[ ]

1

,

0

∈

∀

α

(

)

y

y

x

y

x

y

x

X

y

x

f

f

)

1

(

,

,

α

α

−

+

⇒

≠

∈

∀

(II)

)

1

;

0

(

∈

∀

α

(

)

y

y

x

y

x

y

x

X

y

x

f

)

1

(

,

~

,

α

α

−

+

⇒

≠

∈

∀

(III)

)

1

;

0

(

∈

∀

α

(

)

x

y

x

y

x

y

x

X

y

x

f

)

1

(

,

~

,

α

α

−

+

⇒

≠

∈

∀

Uwagi:

1. Warunek pierwszy, oznacza,

ż

e je

ż

eli koszyk towarów x jest silnie preferowany nad koszyk y,

to koszyk z b

ę

d

ą

cy ich kombinacj

ą

liniow

ą

postaci z=

y

x

)

1

(

α

α

−

+

(

])

1

;

0

[

(

∈

α

, czyli

zawieraj

ą

cy wi

ę

ksze ilo

ś

ci towarów ni

ż

koszyk y, ale mniejsze ni

ż

koszyk x jest silnie

preferowany nad koszyk y.

2. Warunki drugi i trzeci oznaczaj

ą

,

ż

e koszyk le

żą

cy na odcinku pomi

ę

dzy indyferentnymi

koszykami x i y, b

ę

dzie nale

ż

ał do wy

ż

ej poło

ż

onej krzywej oboj

ę

tno

ś

ci ni

ż

krzywa oboj

ę

tno

ś

ci,

na której poło

ż

one s

ą

koszyki x i y.

dr Agnieszka Bobrowska

15

Ekonomia matematyczna I

Przykład 2.6.

Dane s

ą

dwa koszyki towarów: x=(5 bułek, 1 litr mleka) oraz y=(3 bułki, 2 litry mleka). Zdaniem

konsumenta koszyk x jest silnie preferowany nad koszyk y. W przypadku wypukłej relacji preferencji

zachodzi m.in.:

y

y

x

=

=

×

+

×

=

×

+

×

)

2

,

3

(

)

1

,

5

(

)

2

,

3

(

0

)

1

,

5

(

1

0

1

f

y

y

x

=

=

×

+

×

=

×

+

×

)

2

,

3

(

)

5

,

1

,

4

(

)

2

,

3

(

5

,

0

)

1

,

5

(

5

,

0

5

,

0

5

,

0

f

y

y

x

=

=

×

+

×

=

×

+

×

)

2

,

3

(

)

2

,

3

(

)

2

,

3

(

1

)

1

,

5

(

0

1

0

f

.

Podsumowanie:

1. Zało

ż

enia (aksjomaty) stoj

ą

ce u podstaw teorii preferencji oraz sformułowane w niej

twierdzenia, pozwalaj

ą

nam na sformułowanie teorii wyboru konsumenta w kategoriach

preferencji.

2. Zało

ż

enia teorii preferencji s

ą

fundamentalne i

ż

adnego z nich nie mo

ż

na pomin

ąć

. Odrzucenie

któregokolwiek z nich doprowadziłoby m.in. do sprzeczno

ś

ci z postulowanym w teorii ekonomii

zało

ż

eniem,

ż

e konsumenci post

ę

puj

ą

racjonalnie i dokonuj

ą

„najlepszych wyborów”. W tym

przypadku odrzucenie zało

ż

enia np. o przechodnio

ś

ci relacji preferencji, oznaczałoby,

ż

e

istnieje zbiór koszyków, w obr

ę

bie którego nie ma najlepszego wyboru. Tak jednak nie jest,

poniewa

ż

zakładamy,

ż

e konsument zawsze potrafi wskaza

ć

najlepszy (jego zdaniem) lub

przynajmniej nie gorszy od pozostałych koszyków przestrzeni X koszyk towarów.

3. Wyprowadzone z relacji preferencji obszary oboj

ę

tno

ś

ci stanowi

ą

geometryczny obraz

mo

ż

liwych wyborów konsumenta na rynku doskonałym.

4. Z warunków rynku doskonałego wynika tak

ż

e,

ż

e konsument ma niesko

ń

czenie wiele

wariantów koszyków do wyboru i b

ę

dzie d

ąż

ył do wyboru jego zdaniem najlepszego koszyka.

5. Konsument pojawia si

ę

na rynku w celu dokonania wyboru koszyka, nie rozwa

ż

amy zatem

sytuacji, kiedy konsument nie jest zainteresowany udziałem w rynku.

Pytania kontrolne:

1. Podaj aksjomaty pełnego preporz

ą

dku.

2. Co oznacza,

ż

e konsument znajduje si

ę

w sytuacji niedosytu?

3. Z jakich zało

ż

e

ń

o rynku doskonałym wyprowadzana jest wypukło

ść

pola preferencji i jego

ci

ą

gło

ść

?

4. Podaj przykłady dóbr doskonale podzielnych.

5. Czym ró

ż

ni

ą

si

ę

relacje słabej i silnej preferencji?

6. Uzasadnij wyodr

ę

bnienie z przestrzeni towarów podzbioru M-preferowanych koszyków.

7. Dlaczego krzywe oboj

ę

tno

ś

ci nie mog

ą

si

ę

przecina

ć

? Zilustrowa

ć

odpowied

ź

przykładem.