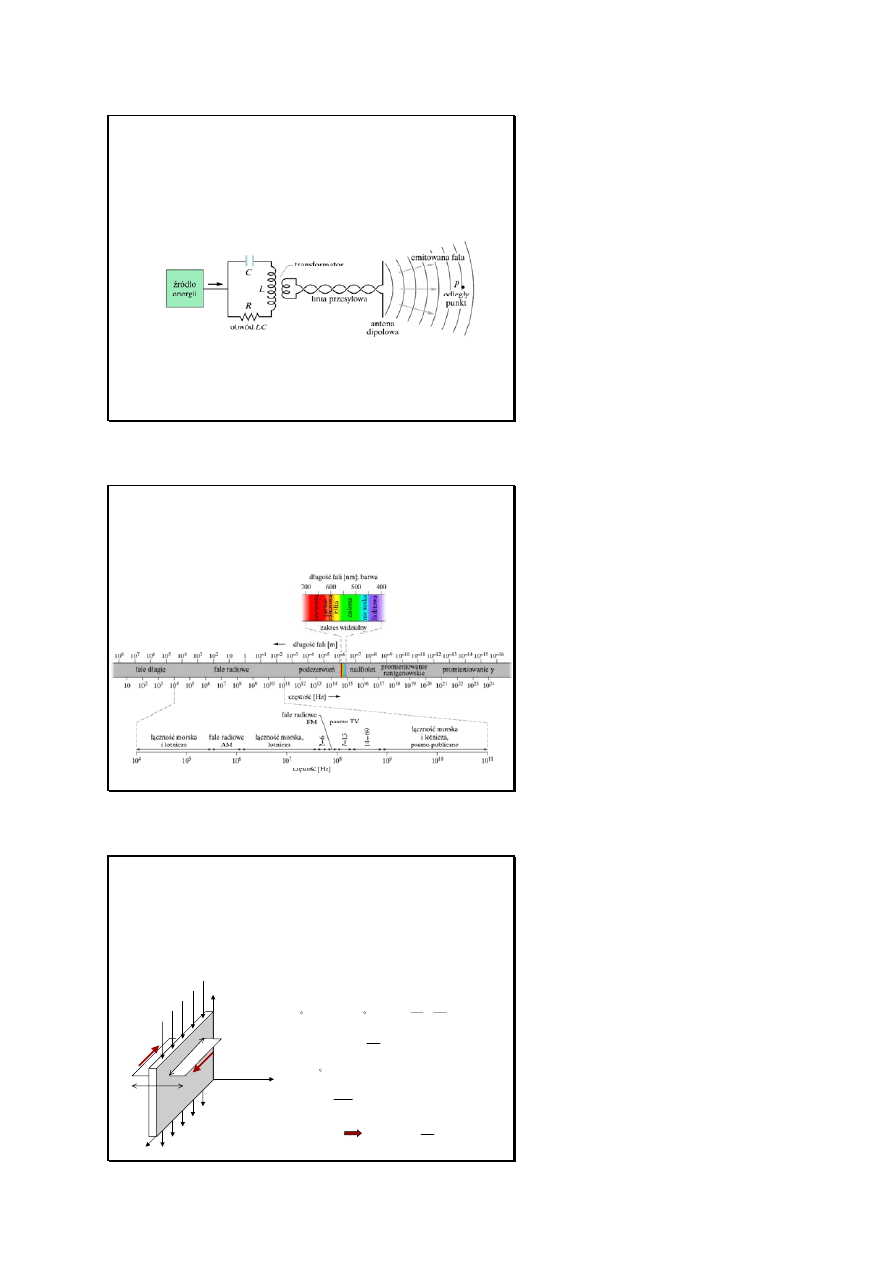
Slajd 1
Slajd 2
lajd 3
Fale elektromagnetyczne
Przyspieszony ładunek emituje pola
elektryczne i magnetyczne propagujące
się z prędkością światła c
Widmo 2
S
Równanie różniczkowe fali
elektromagnetycznej
rozpatrzmy prostokątny element nieskończonej powierzchni z prądem
powierzchniowym J [A/m]
S
d
t
E
c
S
d
j
s
d
B
S
S
C
o
r
v
r
r
r
r
⋅
∫ ∂
∂
∫
+
⋅
∫
µ
=
⋅
2
1
Jb
Bb
s
d
B
o
µ
=
=
∫ ⋅
2
r
r
2
J
B
o
µ
=
Z uogólnionego prawa Ampera dla konturu w
kształcie prostokąta o bokach a, b
wyznaczmy indukcję w pobliżu powierzchni:
0
0
→
∂
∂
⇒
→
dS
t
E
a
t
cos ω
=
o
J
J
( )
t
J
t
B
o
o
z
ω
µ
=
cos
,
2
0
J
x
z
y
0
a
b
B
r
B
r
Slajd 4
S
d
c
s
d
B
C
r
r
r
∫
∂
∂
+
=
∫ ⋅
t
E
2
1
0
(
)
(
)
bdx
c
b
B
b
dB
B
y
z
z
z
t
E
∂
∂
−
=
−
+
2
1
dx
c
dB
y
z
t
E
∂
∂
−
=
2
1
t
E
x
B
∂
∂
−
=
∂
∂
y
z
c
2
1
∫
∫
∂
∂
−
=
⋅
C
S
d
t
B
s
d
E
r
r
r
r
)
(
t
B
)
(
hdx
h
E
h
dE
E
z
y
y
y
∂
∂
−
=
−
+
Wyznaczmy pole magnetyczne w punkcie P odległym od płaszczyzny
bdx
E
dS
E
S
d
E
y
y
−
=
∫
−
=
∫ ⋅
r
r
element powierzchni (b;dx) jest
skierowany w kierunku ujemnych y
t
E
∂
∂
−
=
=
y
const
t
z
c
dx
dB
2
1
hdx
B
dS
B
S
d
B
z
z
=
∫
=
∫ ⋅
r
r
J
x
y
0
a
b
Br
Br
dx
b
P
B
r
B
d
B
r
r+
składową E
y
wyznaczymy z prawa
Faradaya dla konturu (h;dx)
Er
E
d
E
r
r+
h
dx
dE
z
y
t
B
∂
∂
−
=
t
B
x
E
∂
∂
−
=
∂
∂
z
t
B
∂
∂
−
=
=
z
const
t
y
dx
dE
y
z
Slajd 6
Slajd 5
Rozwiązując układ równań z dwiema niewiadomymi B
z
i E
y
otrzymujemy:
t
E
x
B
∂
∂
−
=
∂
∂
y
z
c
2
1
t
B
x
E
∂
∂
−
=
∂
∂
z
y
∂
∂
−
∂
∂
=
∂
∂
∂
∂
t
E
x
x
x
y
z
c
B
2
1
t
x
E
c
x
B
y
z
∂
∂
∂
−
=
∂
∂
2
2
2
2
1
2
2
2
t
t
x
t
B
t
x
E
t
∂
∂
−
=
∂
∂
∂
∂
∂
−
∂
∂
=
∂
∂
∂
∂
z
y
z
y
B
E
2
2
2
2
2
1
t
x
∂
∂
=
∂
∂
z
z
B
c
B
∂
∂
−
∂
∂
=
∂
∂
∂
∂
t
E
x
y
z
c
t
B
t
2
1
x
B
x
E
x
x
x
z
y
z
y
∂
∂
∂
−
=
∂
∂
∂
∂
−
∂
∂
=
∂
∂
∂
∂
t
t
B
E
2
2
2
2
2
2
2
1
t
E
c
x
t
B
y
z
∂
∂
−
=
∂
∂
∂
2
2
2
2
2
1
t
x
∂
∂
=
∂
∂
y
y
E
c
E
2
2
1
∂
=
∂
y
y
Porównując ze znanym
otrzymaliśmy różniczkowe
2
2
2
t
x
∂
∂
u
równaniem fali biegnącej
równania Maxwella dla E,B
Wnioski
wokół płaszczyzny z prądem zmiennym w
czasie powstają pola magnetyczne i
elektryczne, spełniające równanie falowe,
tzn. pola magnetyczne i elektryczne
rozchodzą się jak fala w kierunku osi x, z
prędkością fazową c
pola te są wzajemnie prostopadłe do
siebie i do kierunku rozchodzenia się tych
pól w przestrzeni (kierunku propagacji
fali), tzn. B
z
⊥ E
y
⊥ ñ
s
m
c
o
o
8
10
3
1
⋅
=
ε
µ
=
Br
Er
nr
B
E
B
E
n
r
r
r
r
r
×
×
=
y
x
z
Slajd 7
Slajd 8
lajd 9
Postać B
z
(x,t) i E
y
(x,t)
)
ϕ
+
−
ω
=
c
x
t
B
t
B
o
z
cos
,
2
2
2
2
2
1
t
x
∂
∂
=
∂
∂
z
z
B
c
B
(
)
−
ω
µ
=
c
x
t
J
t
x
B
o
o
z
cos
,
2
0
2
=
ϕ
µ
=
,
o
o
o
J
B
−
ω
ω
=
−
ω
∂
∂
−
=
∂
∂
−
=
∂
∂
c
x
t
c
x
t
B
t
t
B
o
o
z
y
sin
B
cos
E
const
c
x
t
cB
dx
c
x
t
E
o
o
y
+
−
ω
=
∫
−
ω
ω
=
cos
sin
B
−
ω
µ
=
=
c
x
t
J
c
cB
E
o
o
z
y
cos
2
( )
t
J
t
B
o
o
z
ω
µ
=
cos
,
2
0
Warunek brzegowy
( )
[
]
ϕ
+
ω
=
t
B
t
B
o
z
cos
,
0
Dla x=0
const=0 bo ρ=0
(
)
−
ω
=
c
x
t
E
t
x
E
o
y
cos
,
E
o
= cB
o
Korzystając ze związku:
(
x
x
Br
E
z
x
Pole elektryczne i magnetyczne wokół płaszczyzny z sinusoidalnie zmieniającym
się prądem jest falą sinusoidalną rozchodzącą się w kierunku osi x z prędkością c
nazywaną
falą elektromagnetyczną
(
)
−
ω
=
c
x
t
E
t
x
E
o
y
cos
,
(
)
−
ω
=
c
x
t
B
t
x
B
o
z
cos
,
T
k
k
c
π
ω
λ
π
ω
2
,
2
,
=
=
=
y
z
x
c
B
E
E
B
J
r
y
S
Co będzie jeżeli prąd płynący przez
płaszczyznę nie będzie sinusoidalny?
Rozważmy przypadek, kiedy prąd
powierzchniowy określony jest funkcją
piłokształtną o okresie τ=2π/ω
(
)
∑
ω
=
∞
=1
1
n
o
n
n
J
J
t
sin
−
ω
∑
µ
=
=
c
x
t
n
n
J
c
cB
E
o
o
sin
1
2
Pole w dowolnym punkcie przestrzeni ma
również piłokształtną zależność od czasu
(
)
∑
ω
=
∞
=1
1
n
n
t
F
t
n
sin
)
(
Rozkład Fouriera periodycznej funkcji F(t)
( )
(
)
(
)
+
−
=
t
sin
t
sin
t
sin
ω
ω
ω
3
3
1
2
2
1
o
J
J
n=1
n=2
n=3
n=5
t
t
t
t
J
τ
Slajd 10
Wektor Poyntinga
Jedną z ważnych własności ruchu falowego jest zdolność przenoszenia
energii od punktu do punktu. Rozpatrzmy płaską falę elektromagnetyczną
padającą na przewodzącą płytkę o grubości ∆x indukując prąd I
0
E
E
c
P
o
S
∆
µ
−
=
∆
2
x
jz
I
o
∆
=
o
Ey
V =
x
j
c
J
c
E
o
o
∆
µ
−
=
µ
−
=
∆
2
2
Indukowany prąd I promieniuje
falę elektromagnetyczną
(
)
x
∆
=
=
o
o
z
y
jE
V
I
dt
dW
Moc tracona na ciepło Joule’a
x
jE
dt
dW
z
y
P
o
o
S
∆
=
=
∆
1
Straty mocy na jednostkę powierzchni wynoszą
Całkowita moc promieniowania z jednostki powierzchni równa
jest całkowitej mocy pochłoniętej w nieskończonej liczbie płytek
r
r
r
E
∆E
∆E
B
y
o
z
o
∆ x
j
pad
pad
B
E
P
o
S
×
= 1
Wektor Poyntinga
pad
pad
o
pad
pad
o
o
S
B
E
E
E
c
EdE
P
µ
=
∫
µ
=
µ
−
=
1
1
2
2
µ
c
Slajd 12
Slajd 11
Wektor Poytinga określa moc promieniowania
na jednostkę powierzchni i pokazuje kierunek
przepływu energii. Wektory E i B są chwilowymi
wartościami pola elektromagnetycznego
dV
c
P
c
dx
A
P
dt
A
P
dW
S
S
S
=
=
=
Wyznaczmy gęstość energii pola elektromagnetycznego
padającego na powierzchnię A o grubości dx
c
P
dV
dW
w
S
=
=
µ
+
ε
=
o
o
B
E
w
2
2
2
1
o
o
o
o
o
B
c
E
B
B
B
w
µ
+
µ
=
µ
+
µ
=
µ
=
2
2
2
2
2
2
2
2
2
2
B
E
P
o
S
r
r
r
×
µ
= 1
c
dx
dt =
EB
c
w
o
µ
= 1
cB
E =
o
o
c
ε
µ
=
1
Znany wzór na gęstość energii pola elektrycznego i magnetycznego
Oddziaływanie
promieniowania z materią
słaby przewodnik absorbuje energię i pęd fali i
prawie nie odbija (grafit, zjonizowany gaz)
bardzo dobry przewodnik odbija falę całkowicie
(srebro, nadprzewodniki)
w dielektryku fala rozchodzi się z mniejszą
prędkością niż w próżni i ulega dyspersji (szkło,
gaz)
w plazmie fala rozchodzi się z prędkością
większą od prędkości światła
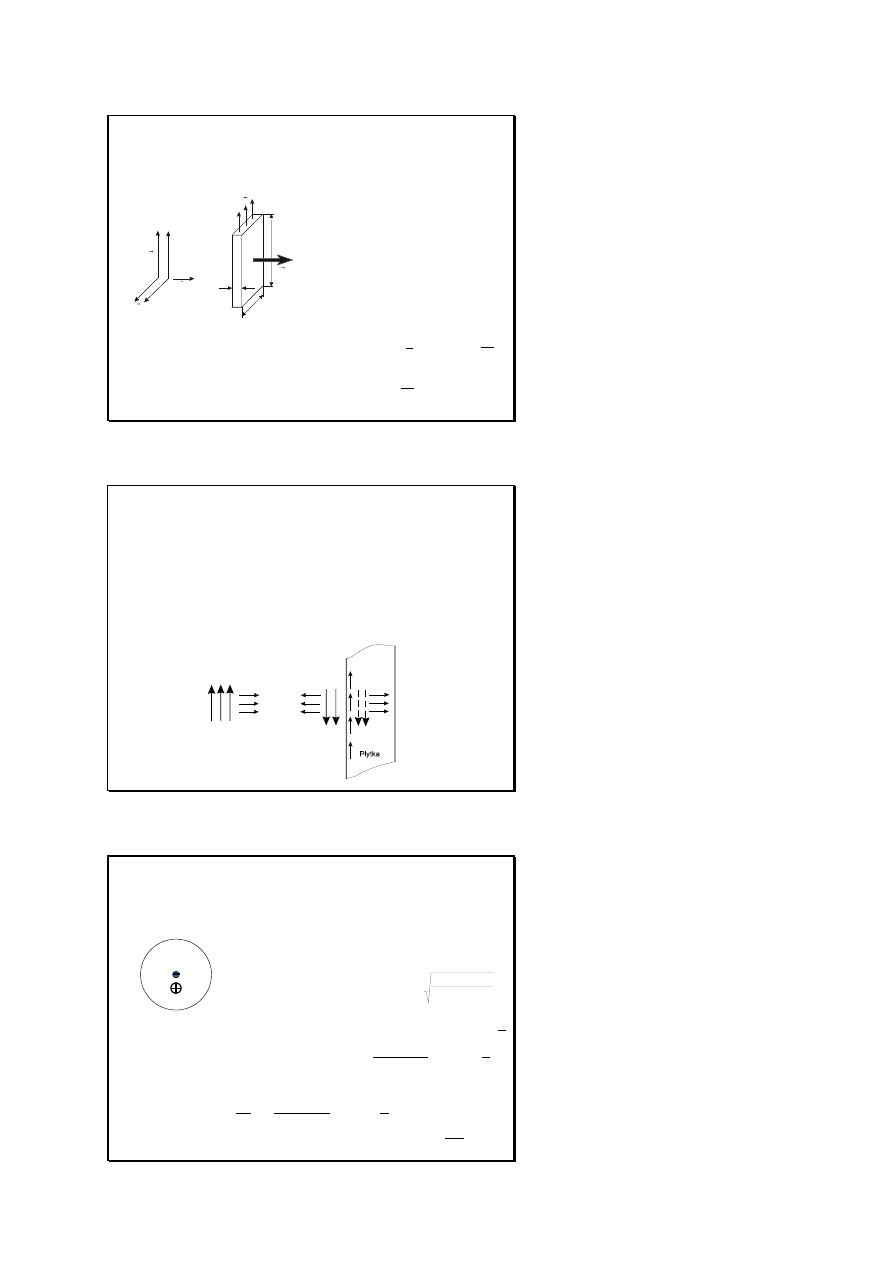
Slajd 13
lajd 15
Pęd (ciśnienie) promieniowania
∆x
B
E
F
m
J
c
y
o
z
o
(
)
x
z
j
I
o
∆
=
Bdt
cIy
dW
o
=
(
)(
)
x
z
y
jEdt
dW
o
o
∆
=
Ilość energii wydzielonej na ciepło Joule’a
w elemencie o grubości ∆x wynosi:
Bdt
y
x
cjz
dW
o
o
∆
=
cB
E =
Na indukowany prąd działa siła magnetyczna
zgodnie z kierunkiem padania fali
B
y
I
F
o
m
r
r
r
×
=
B
Iy
F
o
m
=
dV
c
P
dW
S
=
dV
c
P
p
d
S
2
r
r =
Element objętości dV cechuje wektor pędu
Pomiar pędu strumienia świetlnego jest
utrudniony bo wartość 1/c jest mała
dW
c
Bdt
Iy
dt
F
dp
o
m
1
=
=
=
Z II zas. dynamiki Newtona
Slajd 14
Odbicie promieniowania od
przewodnika
Na płytkę z idealnego przewodnika (np. nadprzewodnika) pada fala
elektromagnetyczna. Indukowany prąd powierzchniowy daje pole
promieniowania równe natężeniu fali padającej (bo nie ma strat).
pad
E
E
−
=
∆
r
E
pad
∆
r
E
∆
r
E
r
J
0
=
∆
+
=
E
E
E
pad
r
r
r
Fala stojąca
Fa
ita interferuje z padającą dając
falę stojącą. Za płytką indukowane pole
znosi się z falą padającą.
la odb
S
Oddziaływanie promieniowania z
dielektrykiem
3
2
4
r
m
e
e
r
o
o
ε
πε
=
ω
jeśli na atom pada fala elektromagnetyczna postaci
−
ω
=
c
x
t
E
E
o
pad
cos
to ustalą się drgania wymuszone
(
)
−
ω
ω
−
ω
−
=
c
x
t
m
eE
y
o
o
cos
2
2
W płytce dielektryka o N elektronach w jednostce objętości indukuje się prąd
o gęstości j
(
)
−
ω
ω
−
ω
ω
−
=
−
=
c
x
t
m
E
Ne
dt
dy
e
N
j
o
o
sin
)
(
2
2
2
Pole promieniowania emitowane przez elektrony płytki
x
j
2
c
=
E
o
∆
µ
−
∆
Elektrony w postaci chmury
elektronowej przesunięte pod wpływem
zewnętrznego pola elektrycznego
względem protonu (polaryzacja
elektronowa) zaczynają drgać z
częstością kołową drgań własnych ω
o
po usunięciu tego pola.
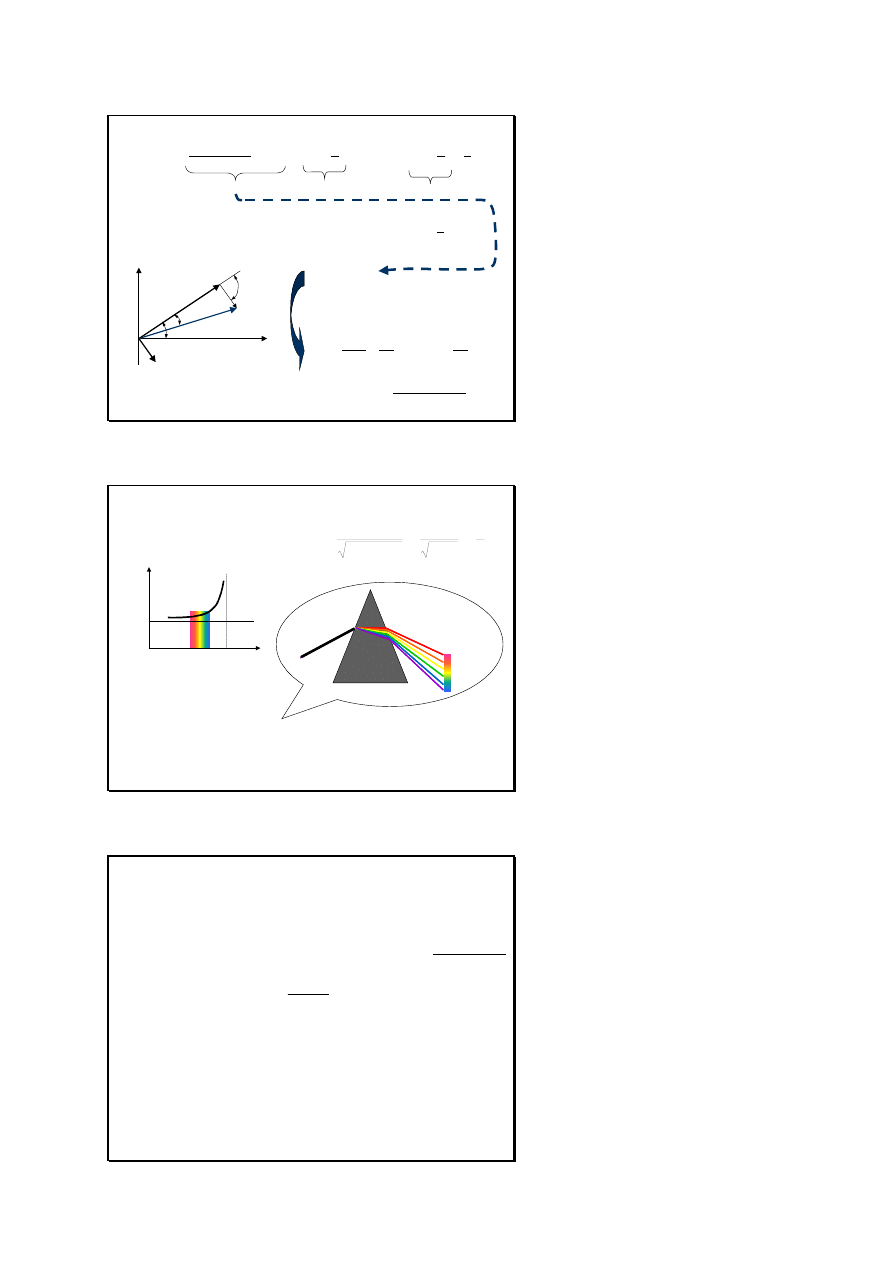
Slajd 16
Wypadkowe pole elektryczne emitowanej fali jest superpozycją E
pad
i ∆E
E
E
E
pad
∆
+
=
'
( )
2
π
−
θ
∆
+
θ
=
cos
cos
'
o
o
E
E
E
Pole to jest przesunięte w fazie względem E
pad
o kąt ϕ (dla ∆E
o
<< E
o
)
o
o
E
E
tg
/
∆
=
ϕ
≈
ϕ
Przesunięcie fazowe wynika z mniejszej
prędkości u=c/n rozchodzenia się fali EM
w płytce o współczynniku załamania n
(
)
c
x
n
c
x
n
c
x
∆
−
ω
=
∆
−
∆
ω
=
ϕ
1
/
2
Ne
y
E
o
∆E
o
E’
o
θ
ϕ
π/
2
x
∆E
o
Światło (fala EM) w ośrodku dielektrycznym
(
)
π
−
−
ω
∆
=
−
ω
∆
ω
−
ω
ω
µ
=
∆
2
2
2
2
2
c
x
t
E
c
x
t
x
E
m
Ne
c
E
O
o
o
o
cos
sin
θ
o
E
∆
θ
(
)
2
2
2
1
−
ω
ε
+
=
o
o
m
n
ulega dyspersji: większe ω czyli krótsza fala
czynnik załamania jest większy –
rsja normalna
ω
to współ
tzw. dyspe
Slajd 18
Slajd 17
pryzmat
n
1
ω
ω
o
Dla większości atomów ω
o
>ω, gdzie ω odpowiada
zakresowi widzialnemu światła. Przy przejściu od
zakresu czerwonego do fioletowego widma
n
c
c
u
r
r
r
o
r
o
=
ε
µ
=
ε
ε
µ
µ
=
1
Współczynnik załamania związany jest z
przenikalnością dielektryczną i magnetyczną ośrodka
białe
współczynnik załamania wzrasta – rośnie również
odchylenie promieni przechodzących przez pryzmat
Promieniowanie elektromagnetyczne
w ośrodku zjonizowanym
(
)
2
2
2
2
1
ω
−
ω
ε
+
=
o
o
m
Ne
n
W plazmie lub zjonizowanym gazie elektrony nie
są związane, więc ω
o
=0
2
2
2
1
ω
ε
−
=
m
Ne
n
o
W tym przypadku współczynnik załamania n<1, co
oznacza, że prędkość fali jest większa od c (u=c/n).
Zjawisko to nosi nazwę dyspersji anomalnej.
Czynnikiem fizycznym powodującym pojawienie się prędkości
większej od prędkości światła są relacje fazowe pomiędzy siła
wymuszającą a przemieszczeniem oscylującego ładunku
(siła wyprzedza przemieszczenie)
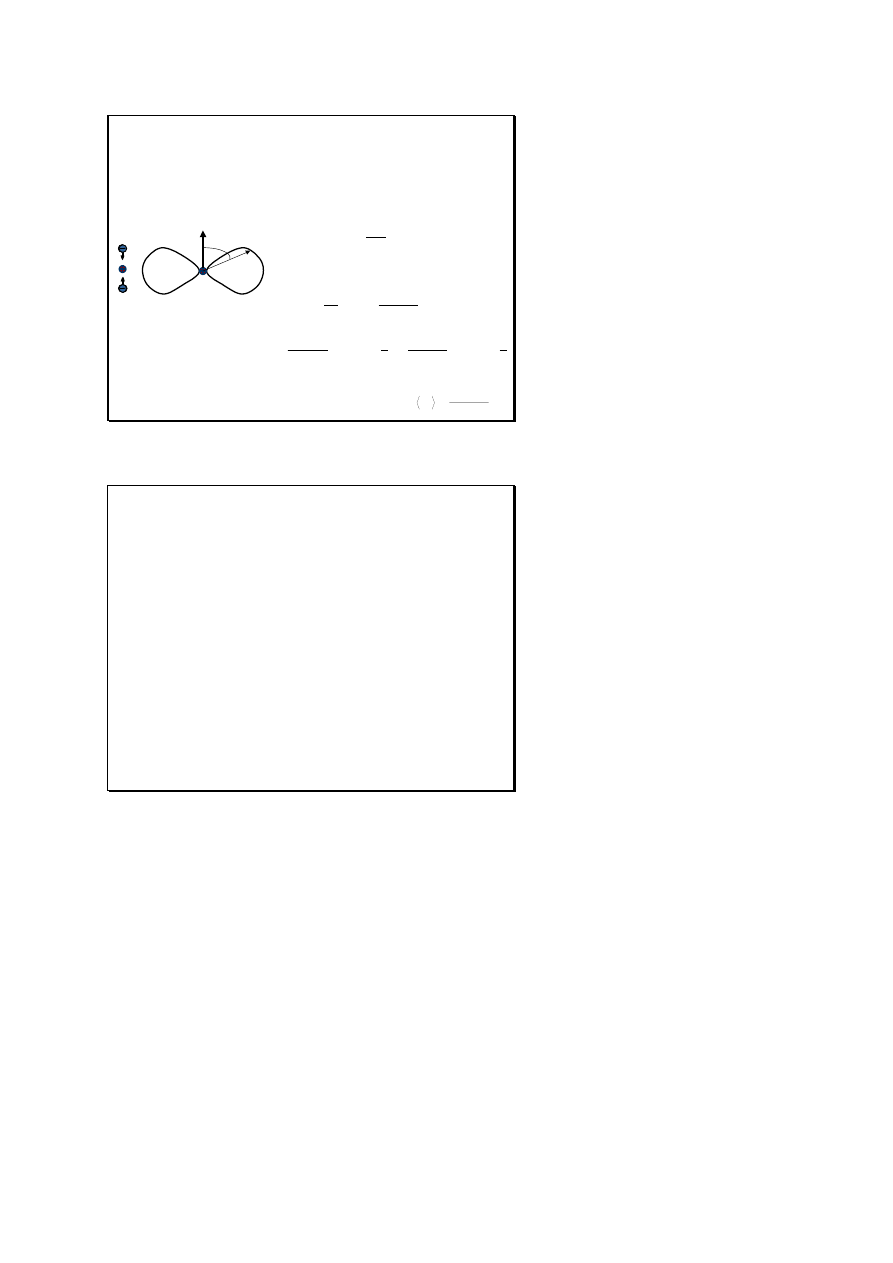
Slajd 19
Promieniowanie ładunku punktowego
(promieniowanie dipolowe)
Z równań Maxwella można pokazać, że w odległości r od ładunku punktowego q
poruszającego się z przyspieszeniem a powstaje pole promieniowania postaci
θ
π
µ
−
=
sin
a
r
q
E
o
4
Polu temu towarzyszy pole magnetyczne
B=E/c, czyli ładunek jest źródłem fali
elektromagnetycznej o wektorze Poytinga
θ
π
µ
=
⋅
µ
=
2
2
2
2
2
16
1
sin
a
c
r
q
B
E
P
o
o
s
W przypadku ruchu
harmonicznego
a=-
ω
2
Acos
ωt
w
kierunku prostopadłym do
drgań otrzymujemy pole
promieniowania oscylującego
dipolu elektrycznego o
momencie dipolowym p
o
=qA
3
4
2
12
c
p
P
o
o
s
πε
ω
=
Dla ustalonej amplitudy oscylacji całkowita średnia
moc wypromieniowania jest proporcjonalna do
ω
4
a
P
s
θ
−
ω
π
ω
µ
=
−
ω
π
ω
µ
=
c
r
t
r
p
c
r
t
r
qA
E
o
o
o
cos
cos
4
4
2
2
Wave.swf
Slajd 20
Rozpraszanie światła
fala elektromagnetyczna oddziaływują na elektrony
pobudza je do drgań, w których elektrony, zbliżając się do
jądra i oddalając od niego, tworzą oscylujące dipole
elektryczne
dipole te stają się wtórnym źródłem promieniowania fal
EM, rozchodzących się we wszystkich kierunkach z taką
samą częstością jak fala pierwotna – rozpraszanie
Rayleigha
moc promieniowania rozproszonego zależy od ω
4
– stąd
przewaga barwy niebieskiej w rozpraszanym świetle
słonecznym
oprócz rozpraszania czynnikiem osłabienia fali pierwotnej
jest absorpcja światła i dyspersja