1

BLOK 9 ZADANIA

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

ZESTAW ZADA

Ń

NA ZAJ

Ę

CIA

Uwaga: w poni

ż

szych zadaniach przyjmij,

ż

e warto

ść

przyspieszenia ziemskiego jest równa

2

s

/

m

10

|

g

|

=

r

.

MOMENT BEZWŁADNO

Ś

CI

1. Cztery kulki, ka

ż

da o masie

g

5

m

=

znajduj

ą

si

ę

w rogach kwadratu o boku

m

1

a

=

. Oblicz

moment bezwładno

ś

ci układu kulek wzgl

ę

dem osi zawieraj

ą

cej jeden z boków kwadratu oraz

wzgl

ę

dem osi zawieraj

ą

cej przek

ą

tn

ą

kwadratu. Kulki traktujemy jak punkty materialne.

2. Oblicz moment bezwładno

ś

ci kr

ąż

ka o masie M i promieniu r wzgl

ę

dem osi prostopadłej do

niego i stycznej do jego brzegu.

3. Oblicz moment bezwładno

ś

ci cienkiego jednorodnego pr

ę

ta o długo

ś

ci L i masie m, wzgl

ę

dem

osi prostopadłej do niego i przechodz

ą

cej przez:

•

punkt odległy od

ś

rodka pr

ę

ta o L/4

•

punkt le

żą

cy na ko

ń

cu pr

ę

ta

4. Układ składa si

ę

z dwóch jednorodnych kul o g

ę

sto

ś

ci

ρ

i o promieniach równych odpowiednio

r oraz R=3r. Odcinek ł

ą

cz

ą

cy

ś

rodki tych kul ma długo

ść

L=5r. Oblicz moment bezwładno

ś

ci

układu wzgl

ę

dem osi prostopadłej do odcinka ł

ą

cz

ą

cego

ś

rodki tych kul i przechodz

ą

cej przez

ś

rodek masy wi

ę

kszej kuli.

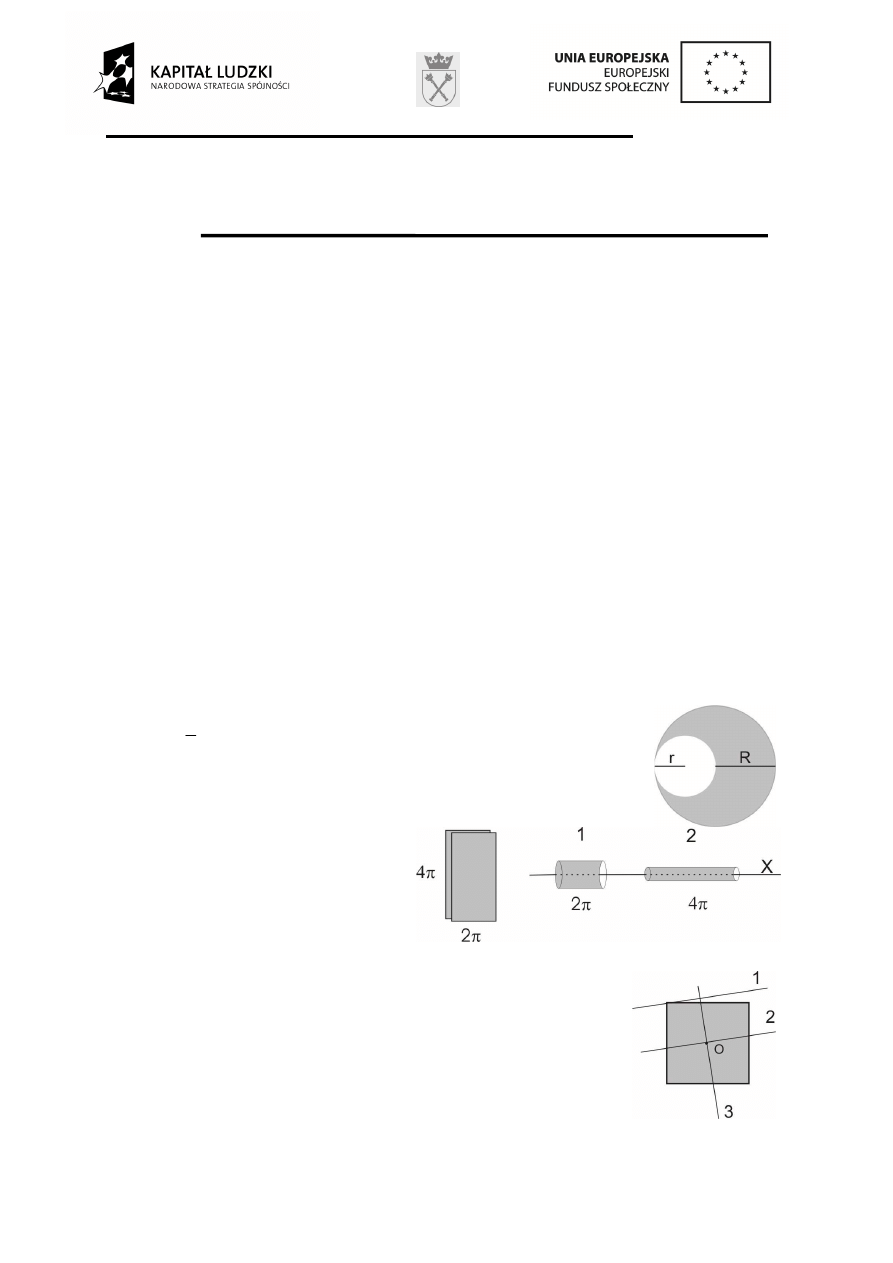
5. Z jednorodnej kuli o masie M i promieniu R wyci

ę

to kul

ę

o promieniu

2

R

r

=

, której

ś

rodek znajdował si

ę

w odległo

ś

ci r od

ś

rodka du

ż

ej kuli.

Ile wynosi moment bezwładno

ś

ci wydr

ąż

onej kuli wzgl

ę

dem osi

przechodz

ą

cej przez punkt stanowi

ą

cy

ś

rodek masy pełnej du

ż

ej kuli i

stycznej do wydr

ąż

enia?

6. Z dwóch identycznych arkuszy

cienkiej blachy wykonano dwie rurki.
Oblicz stosunek momentów
bezwładno

ś

ci

2

1

I

/

I

tych rurek

wzgl

ę

dem ich osi X.

7. Zaznaczone na rysunku osie 1, 2, 3 le

żą

w płaszczy

ź

nie

jednorodnego kwadratu o

ś

rodku w punkcie O. Momenty

bezwładno

ś

ci kwadratu wzgl

ę

dem tych osi spełniaj

ą

nierówno

ść

:

A)

3

2

1

I

I

I

>

>

B)

3

2

1

I

I

I

<

<

C)

3

2

1

I

I

I

=

>

D)

3

2

1

I

I

I

=

<

Blok 9:

Moment bezwładno

ś

ci. Moment siły.

Zasada zachowania momentu p

ę

du

2

BLOK 9 ZADANIA

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

MOMENT SIŁY

8. Stosunek warto

ś

ci sił działaj

ą

cych na brył

ę

sztywn

ą

wynosi

3

1

F

F

2

1

=

. Jaki warunek spełniaj

ą

długo

ś

ci ramion tych sił, je

ż

eli wiadomo,

ż

e bryła

obraca si

ę

ruchem jednostajnym wokół osi O

prostopadłej do płaszczyzny rysunku?

9. W spoczywaj

ą

cej windzie na wadze dwuramiennej zawieszono dwie masy:

m

i

m

2

, które

pozostawały w równowadze. Czy równowaga ta zostanie zaburzona (a je

ś

li tak, to w jaki

sposób), je

ż

eli winda porusza si

ę

w gór

ę

ruchem jednostajnie przyspieszonym z

przyspieszeniem o warto

ś

ci a<g?

ZASADA ZACHOWANIA MOMENTU P

Ę

DU

10.

Ś

redni okres wirowania gwiazdy wokół jej osi symetrii wynosi

30

T

1

=

dni ziemskich, a

gwiazda ma mas

ę

kg

10

M

30

=

i promie

ń

m

10

6

R

10

⋅

=

. Oblicz do jakich rozmiarów powinna

si

ę

skurczy

ć

ta gwiazda (bez zmiany masy), aby okres jej obrotu zmalał do

s

2

T

2

=

.

Sprawd

ź

, czy gwiazda ta byłaby wówczas stabilna, tzn. porównaj warto

ść

przyspieszenia

grawitacyjnego na równiku tej gwiazdy z warto

ś

ci

ą

przyspieszenia do

ś

rodkowego punktów

równika.

11. Dwa kr

ąż

ki obracaj

ą

si

ę

niezale

ż

nie w przeciwne strony z pr

ę

dko

ś

ciami k

ą

towymi o

warto

ś

ciach:

1

ω

i

2

ω

na jednej osi przechodz

ą

cej przez ich

ś

rodki i prostopadłej do ich

powierzchni. W pewnej chwili kr

ąż

ek górny spada na kr

ąż

ek dolny i kr

ąż

ki te „zlepiaj

ą

si

ę

”.

Oblicz pr

ę

dko

ść

k

ą

tow

ą

zł

ą

czonych kr

ąż

ków, je

ż

eli masa górnego kr

ąż

ka wynosi

1

m

, a jego

promie

ń

1

r

, natomiast masa dolnego kr

ąż

ka wynosi

2

m

, a jego promie

ń

2

r

. Oblicz zmian

ę

energii kinetycznej układu i wyja

ś

nij, dlaczego jest ona ró

ż

na od zera (tzn. dlaczego nie

obowi

ą

zuje zasada zachowania energii).

12. W

ś

rodku poziomej tarczy o masie

kg

200

M

=

i promieniu

m

2

R

=

stoi człowiek o masie

kg

50

m

=

. Tarcza obraca si

ę

z okresem

s

5

T

=

. W pewnej chwili człowiek ten przeszedł na

brzeg tarczy. Oblicz:

•

okres ruchu tarczy po przej

ś

ciu człowieka na jej brzeg

•

o ile zmieni si

ę

energia kinetyczna układu

Zakładaj

ą

c,

ż

e człowiek przemieszcza si

ę

wzdłu

ż

promienia tarczy ze stał

ą

szybko

ś

ci

ą

równ

ą

s

/

m

5

,

0

u

=

, wyprowad

ź

równanie okre

ś

laj

ą

ce zale

ż

no

ść

pr

ę

dko

ś

ci k

ą

towej tarczy od czasu.

3

BLOK 9 ZADANIA

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

ZESTAW ZADA

Ń

DO SAMODZIELNEGO ROZWI

Ą

ZANIA

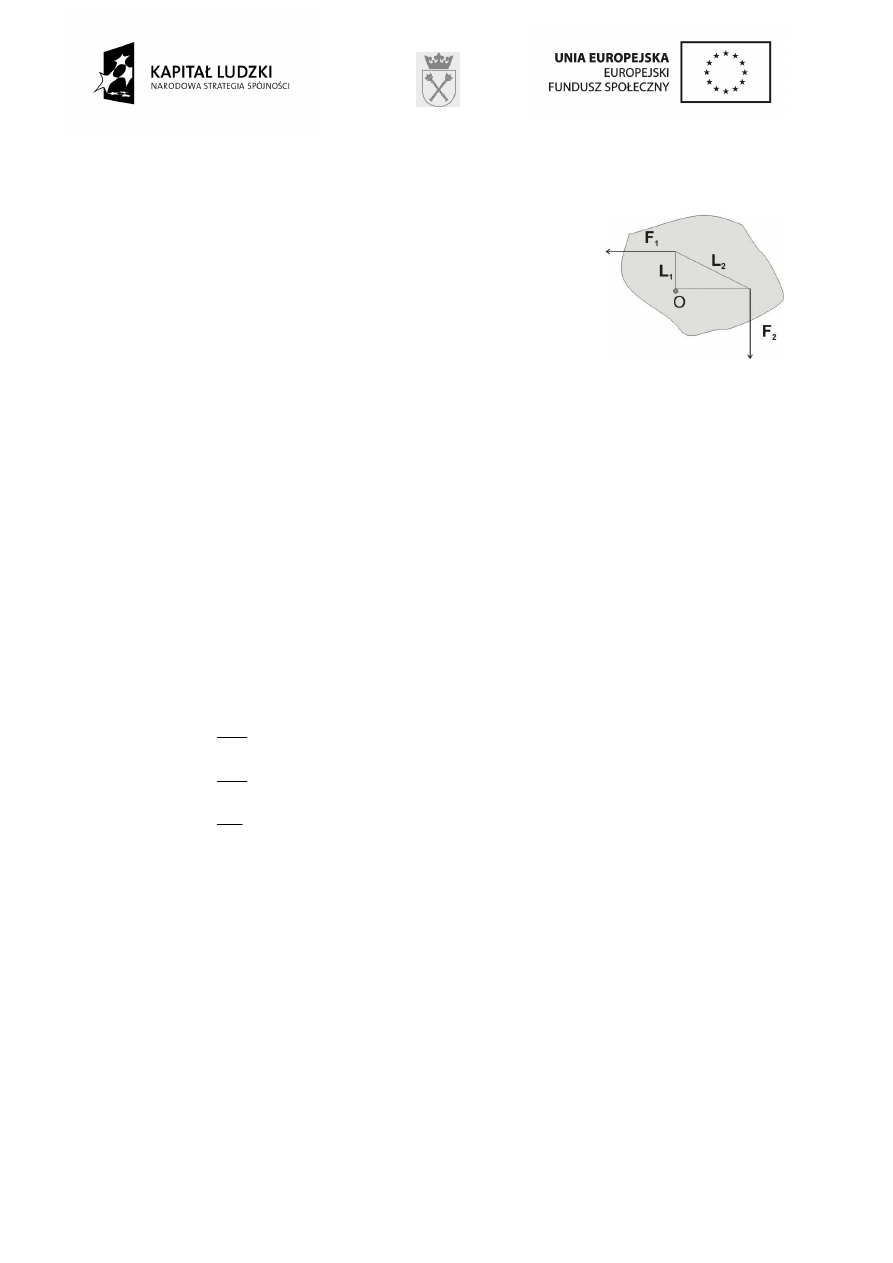
1. Na ciało działa para sił o jednakowych warto

ś

ciach. Oblicz

wypadkowy moment siły działaj

ą

cy na to ciało wzgl

ę

dem osi

prostopadłej do płaszczyzny rysunku i przechodz

ą

cej przez

punkt O. K

ą

ty pomi

ę

dzy siłami i odpowiednimi ramionami sił s

ą

k

ą

tami prostymi.

2. Je

ż

eli wypadkowy moment sił działaj

ą

cych na ciało obracaj

ą

ce

si

ę

wokół nieruchomej osi jest stały i ró

ż

ny od zera w czasie

ruchu, to moment p

ę

du tego ciała:

A)

pozostaje stały

B)

na pewno jednostajnie wzrasta z czasem

C)

na pewno jednostajnie maleje z czasem

D)

jednostajnie wzrasta lub maleje z czasem

3. Oblicz moment bezwładno

ś

ci cienko

ś

ciennego rurki o masie M i promieniu R wzgl

ę

dem osi

równoległej do jej wysoko

ś

ci i stycznej do jej pobocznicy.

4. Człowiek siedz

ą

cy na krze

ś

le obrotowym obraca si

ę

z pr

ę

dko

ś

ci

ą

k

ą

tow

ą

o warto

ś

ci

ω

(tarcie

pomijamy). W wyci

ą

gni

ę

tych na boki r

ę

kach trzyma dwa jednakowe ci

ęż

arki. Je

ś

li człowiek

opu

ś

ci r

ę

ce, to:

A)

moment p

ę

du i energia kinetyczna układu wzrosn

ą

B)

moment p

ę

du i energia kinetyczna układu zmalej

ą

C)

ani energia kinetyczna, ani moment p

ę

du układu nie ulegn

ą

zmianie

D)

moment p

ę

du układu pozostanie niezmieniony, a energia kinetyczna układu wzro

ś

nie

5. Je

ż

eli bryła sztywna wiruje wokół stałej osi i wzgl

ę

dem tej osi ma moment bezwładno

ś

ci

I

, a

wzgl

ę

dem punktu le

żą

cego na tej osi - moment p

ę

du o warto

ś

ci L, to okres obrotu bryły

wzgl

ę

dem tej osi jest równy:

A)

L

2

I

π

B)

I

L

2

π

C)

L

I

2

π

D)

IL

2

π