1

BLOK 1

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

ZESTAW ZADA

Ń

NA ZAJ

Ę

CIA

WEKTORY

1. Dany jest wektor

AB

o współrz

ę

dnych [2,3]. Oblicz k

ą

t, który tworzy ten wektor z kierunkiem

osi OX. Wyra

ź

ten k

ą

t w mierze łukowej.

2. Wiatr wieje z południowego wschodu z pr

ę

dko

ś

ci

ą

s

/

m

10

pod k

ą

tem

o

60

wzgl

ę

dem kierunku

północnego. Oblicz warto

ś

ci składowych pr

ę

dko

ś

ci: północnej i zachodniej. W układzie

współrz

ę

dnych, w którym o

ś

OX jest skierowana na wschód, a o

ś

OY – na północ, oblicz

współrz

ę

dne pr

ę

dko

ś

ci wiatru.

3. Przedstaw w układzie współrz

ę

dnych trzy wektory

]

4

,

3

[

a

=

r

,

]

1

,

2

[

b

−

=

r

i

]

5

,

1

[

c

−

−

=

r

.

•

Narysuj wektor

c

b

a

d

r

r

r

r

+

+

=

. Oblicz współrz

ę

dne tego wektora oraz jego długo

ść

.

•

Narysuj wektor

b

a

e

r

r

r

−

=

. Oblicz współrz

ę

dne tego wektora.

•

Oblicz k

ą

t, który tworz

ą

wektory

a

r

i

b

r

.

4. W układzie współrz

ę

dnych przedstaw wektory dwóch sił:

1

F

r

i

2

F

r

o warto

ś

ciach równych

odpowiednio

N

100

|

F

|

1

=

r

i

N

150

|

F

|

2

=

r

, ustawionych wzgl

ę

dem siebie pod k

ą

tem

o

105

.

Znajd

ź

wypadkow

ą

tych sił

1

F

r

i

2

F

r

. Czy istnieje tylko jedno rozwi

ą

zanie? Odpowied

ź

uzasadnij.

5. Sprawd

ź

, czy wektory:

•

]

9

,

6

[

a

=

r

oraz

]

4

,

6

[

b

−

=

r

•

]

4

,

6

[

a

=

r

oraz

]

6

,

9

[

b

−

−

=

r

s

ą

do siebie prostopadłe lub równoległe?

6. D

ź

wig podnosi pionowo w gór

ę

palet

ę

cegieł z pr

ę

dko

ś

ci

ą

o warto

ś

ci

s

/

m

5

,

0

v

=

wzgl

ę

dem

powierzchni ziemi. Pozioma pr

ę

dko

ść

d

ź

wigu wynosi

s

/

m

3

.

0

u

=

. Oblicz warto

ść

pr

ę

dko

ś

ci, z

jak

ą

przesuwa si

ę

paleta.

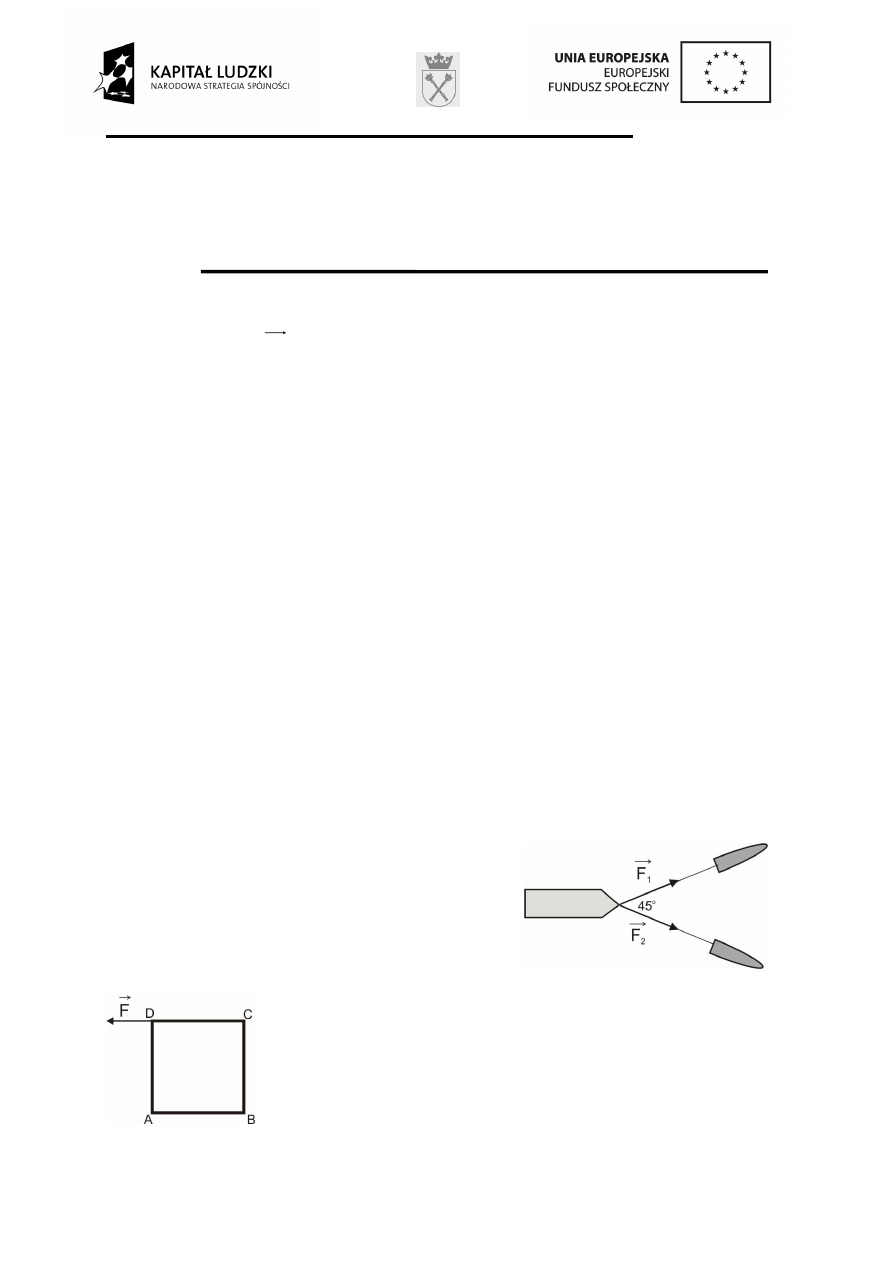
7. Dwa holowniki ci

ą

gn

ą

tankowiec jak pokazano na

rysunku. Oblicz warto

ść

|

F

|

op

r

siły oporu, je

ż

eli

wiadomo,

ż

e siły działaj

ą

ce na bark

ę

równowa

żą

si

ę

.

kN

100

|

F

|

|

F

|

2

1

=

=

r

r

.

8. Do kwadratowej ramki o boku

cm

10

a

=

przyło

ż

ono w punkcie D sił

ę

F

r

o warto

ś

ci

N

20

F

=

. Oblicz warto

ść

momentu tej siły kolejno wzgl

ę

dem

punktów A, B, C i D. Jaki jest kierunek i zwrot wektora momentu siły w
przypadkach, w których jest on ró

ż

ny od zera? Moment siły dany jest

wzorem:

F

r

M

r

r

r

×

=

, gdzie

r

r

jest wektorem ł

ą

cz

ą

cym punkt wzgl

ę

dem

którego obliczamy moment siły – z punktem przyło

ż

enia siły.

Blok 1:

Podstawowe wielko

ś

ci fizyczne w kinematyce.

Rachunek wektorowy i jego zastosowanie w fizyce. Ruch
wzgl

ę

dny.

2

BLOK 1

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

9. Na klocek działaj

ą

trzy siły w płaszczy

ź

nie XY:

]

N

5

,

0

[

F

1

−

=

r

,

]

N

2

,

N

4

[

F

2

−

=

r

i

]

N

3

,

N

1

[

F

3

=

r

.

Oblicz prac

ę

wykonan

ą

przez ka

ż

d

ą

z tych sił podczas przesuwania ciała. Wektor

przemieszczenia:

]

0

,

1

[

m

r

−

=

∆

r

. Oblicz prac

ę

siły wypadkowej działaj

ą

cej na klocek i sprawd

ź

,

czy jest ona równa sumie prac wykonanych przez poszczególne siły składowe. Praca wykonana

przez stał

ą

sił

ę

wynosi:

r

F

W

r

o

r

∆

=

.

PODSTAWOWE WIELKO

Ś

CI W KINEMATYCE

10. W pokoju na krze

ś

le siedzi człowiek. Jaki jest kształt toru tego człowieka, je

ś

li układem

odniesienia jest:

•

nie obracaj

ą

cy si

ę

wzgl

ę

dem Sło

ń

ca układ współrz

ę

dnych z pocz

ą

tkiem w

ś

rodku Ziemi

•

nie obracaj

ą

cy si

ę

wzgl

ę

dem orbity okołosłonecznej Ziemi układ współrz

ę

dnych z

pocz

ą

tkiem w

ś

rodku Sło

ń

ca?

11. Po płaszczy

ź

nie poziomej toczy si

ę

koło ze stał

ą

pr

ę

dko

ś

ci

ą

v

r

. Jaki b

ę

dzie kształt toru punktu

le

żą

cego na obrze

ż

u tego koła, je

ś

li układem odniesienia jest poziomy grunt?

12. Warto

ść

przemieszczenia w stosunku do drogi jest:

A) zawsze mniejsza
B) mniejsza lub równa
C) równa
D) zawsze wi

ę

ksza

13. Ameryka

ń

ska pływaczka Jessica Hardy ustanowiła w 2009r. rekord

ś

wiata w stylu klasycznym

ze

ś

redni

ą

szybko

ś

ci

ą

s

/

m

5625

,

1

v

=

. Warto

ść

jej

ś

redniej pr

ę

dko

ś

ci wyniosła zero dwukrotnie

podczas jej koronnego dystansu: po czasie

s

32

t

1

=

i po czasie

s

64

t

2

=

. Oblicz długo

ść

basenu.

14. Kolarz przebył pierwsze 26 km w czasie 1 godziny, a nast

ę

pne 42 km w czasie 3 godzin. Ile

wynosiła

ś

rednia szybko

ść

kolarza?

15. Rowerzysta przejechał połow

ę

drogi z szybko

ś

ci

ą

1

v

, a drug

ą

połow

ę

z szybko

ś

ci

ą

2

v

. Z jak

ą

ś

redni

ą

szybko

ś

ci

ą

przejechał cał

ą

tras

ę

?

PR

Ę

DKO

ŚĆ

WZGL

Ę

DNA

16. Pr

ę

dko

ść

łódki płyn

ą

cej z pr

ą

dem rzeki ma warto

ść

s

/

m

3

, a pod pr

ą

d:

s

/

m

5

,

0

. Pr

ę

dko

ść

tej

łódki na stoj

ą

cej wodzie miałaby warto

ść

:

A) 1,25 m/s

B) 1,75 m/s

C) 2 m/s

D) 2,5 m/s

17. Samochód i poci

ą

g poruszaj

ą

si

ę

po równoległych torach prostoliniowych w przeciwne strony.

Pr

ę

dko

ść

poci

ą

gu wzgl

ę

dem torów wynosi

p

v

r

, a pr

ę

dko

ść

samochodu wzgl

ę

dem torów

s

v

r

,

przy czym warto

ść

pr

ę

dko

ś

ci

|

|

s

s

v

v

r

=

jest wi

ę

ksza od warto

ś

ci pr

ę

dko

ś

ci

|

|

p

p

v

v

r

=

.

Pr

ę

dko

ść

samochodu wzgl

ę

dem poci

ą

gu:

A) jest sum

ą

s

p

v

v

r

r

+

, a warto

ść

tej wzgl

ę

dnej pr

ę

dko

ś

ci jest równa

s

p

v

v

+

B) jest sum

ą

s

p

v

v

r

r

+

, a warto

ść

tej wzgl

ę

dnej pr

ę

dko

ś

ci jest równa

p

s

v

v

−

C) jest ró

ż

nic

ą

p

s

v

v

r

r

−

, a warto

ść

tej wzgl

ę

dnej pr

ę

dko

ś

ci jest równa

s

p

v

v

+

D) jest ró

ż

nic

ą

p

s

v

v

r

r

−

, a warto

ść

tej wzgl

ę

dnej pr

ę

dko

ś

ci jest równa

p

s

v

v

−

3

BLOK 1

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

18. Poci

ą

g pospieszny o długo

ś

ci

m

100

jad

ą

cy z szybko

ś

ci

ą

h

/

km

108

wyprzedza poci

ą

g

osobowy o długo

ś

ci

m

200

jad

ą

cy z szybko

ś

ci

ą

h

/

km

36

po równoległym torze. Pasa

ż

er

poci

ą

gu pospiesznego widział poci

ą

g osobowy przez:

A) 10 s

B) 5 s

C) 20 s

D) 30 s

ZESTAW ZADA

Ń

DO SAMODZIELNEGO ROZWI

Ą

ZANIA

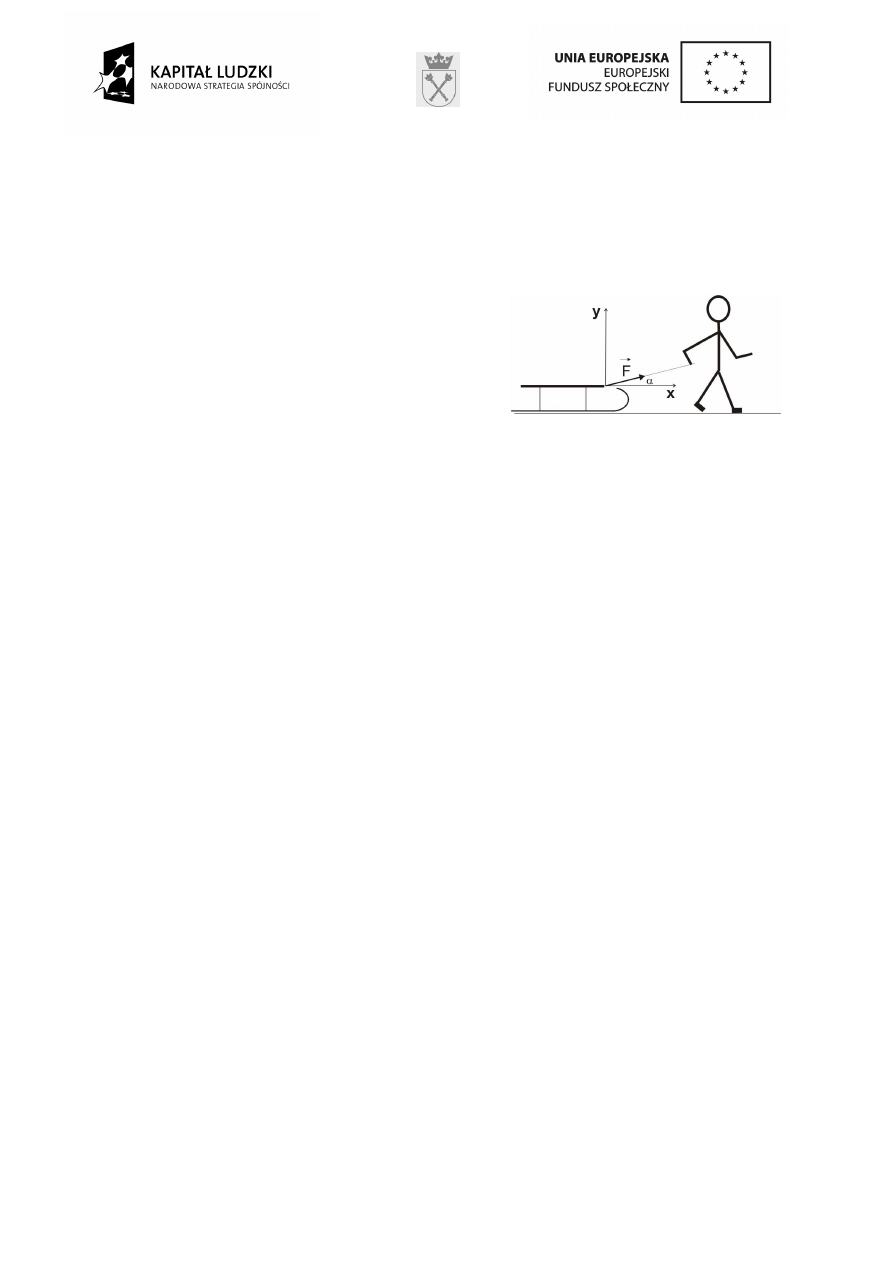
1.

Rozłó

ż

wektor siły

F

r

przyło

ż

onej do sanek na

składowe: poziom

ą

i pionow

ą

w układzie

współrz

ę

dnych przedstawionym na rysunku.

Oblicz współrz

ę

dne składowych, je

ż

eli wiadomo,

ż

e

N

0

,

50

|

F

|

=

r

i

o

30

=

α

.

2. Rozłó

ż

sił

ę

o warto

ś

ci 100 N na dwie wzajemnie prostopadłe składowe, których warto

ś

ci

pozostaj

ą

w stosunku ¾. Oblicz warto

ś

ci składowych oraz k

ą

ty, jakie te składowe tworz

ą

z

rozkładan

ą

sił

ą

.

3. Sprawd

ź

, czy wektory

]

1

,

2

[

a

=

r

oraz

]

2

,

1

[

b

=

r

s

ą

do siebie prostopadłe.

4. Po wiruj

ą

cej płycie gramofonowej idzie wzdłu

ż

promienia mrówka ze stał

ą

szybko

ś

ci

ą

wzgl

ę

dem płyty. Torem ruchu mrówki jest:

A) prosta
B) spirala
C) okr

ą

g

D) okr

ą

g lub spirala wzgl

ę

dem układu odniesienia zwi

ą

zanego ze stołem i prosta wzgl

ę

dem

układu odniesienia zwi

ą

zanego z płyt

ą

E) spirala wzgl

ę

dem układu odniesienia zwi

ą

zanego ze stołem i prosta wzgl

ę

dem układu

odniesienia zwi

ą

zanego z płyt

ą

5. W wagonie poruszaj

ą

cym si

ę

wzgl

ę

dem Ziemi zgodnie ze zwrotem osi OX, chłopiec wyrzucił

pionowo w gór

ę

piłk

ę

. Narysuj tor piłki w układzie odniesienia zwi

ą

zanym z Ziemia oraz w

układzie odniesienia zwi

ą

zanym z wagonem.

6. W ci

ą

gu pierwszej połowy czasu swego ruchu autobus jechał z szybko

ś

ci

ą

h

/

km

70

v

1

=

, a

w ci

ą

gu drugiej połowy – z szybko

ś

ci

ą

h

/

km

40

v

2

=

. Oblicz

ś

redni

ą

szybko

ść

autobusu na

całej trasie.

7. Ruchome schody w hipermarkecie poruszaj

ą

si

ę

z szybko

ś

ci

ą

h

/

km

8

,

1

wzgl

ę

dem

ś

cian

budynku. Oblicz szybko

ść

wzgl

ę

dem

ś

cian tego budynku dziecka id

ą

cego z szybko

ś

ci

ą

s

/

m

3

wzgl

ę

dem schodów, je

ż

eli:

•

dziecko idzie w stron

ę

ruchu schodów

•

dziecko idzie w stron

ę

przeciwn

ą

do ruchu schodów

8. Skutery zbli

ż

aj

ą

si

ę

do siebie ze stałymi szybko

ś

ciami

h

/

km

40

v

v

v

B

A

=

=

=

. W chwili, gdy

pojazdy znajdowały si

ę

we wzajemnej odległo

ś

ci

km

20

L

=

od siebie ze skutera A wyleciała

w kierunku skutera B pszczoła ze stał

ą

szybko

ś

ci

ą

h

/

km

60

u

=

. Gdy doleciała do skutera B,

natychmiast zawróciła i kontynuowała lot z tak

ą

sam

ą

szybko

ś

ci

ą

w kierunku skutera A itd.

Wszystkie szybko

ś

ci podano w układzie odniesienia zwi

ą

zanym z jezdni

ą

. Oblicz całkowity

czas lotu pszczoły a

ż

do chwili spotkania skuterów. Oblicz drog

ę

, jak

ą

przeb

ę

dzie w tym

czasie pszczoła.

4

BLOK 1

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego

w ramach programu operacyjnego KAPITAŁ LUDZKI

V

1

V

2

Vrz

V

3

9. Rysunek pokazuje (w skali) wektory pr

ę

dko

ś

ci: łódek L

1

, L

2

, L

3

wzgl

ę

dem wody w rzece oraz

wody wzgl

ę

dem brzegu. Która łódka przepłynie w najkrótszym czasie na drugi brzeg?

A) L

1

B) L

2

C) L

3

D) Wszystkie przepłyn

ą

w tym samym czasie

10. Z płyn

ą

cej rzek

ą

motorówki wypadło koło

ratunkowe. Po upływie 30 sekund zauwa

ż

ono jego brak. Natychmiast zawrócono motorówk

ę

i

płyn

ą

c z t

ą

sam

ą

szybko

ś

ci

ą

wzgl

ę

dem wody odnaleziono koło. Czas przebywania koła w

wodzie wynosił:
A) mniej ni

ż

60 s

B) wi

ę

cej ni

ż

60 s

C) 60 s
D) mniej ni

ż

60 s, je

ż

eli motorówka najpierw płyn

ę

ła w gór

ę

rzeki, a wi

ę

cej ni

ż

60, je

ż

eli

motorówka płyn

ę

ła najpierw w dół rzeki

E) wi

ę

cej ni

ż

60 s, je

ż

eli motorówka najpierw płyn

ę

ła w gór

ę

rzeki, a mniej ni

ż

60 s, je

ż

eli

motorówka najpierw płyn

ę

ła w dół rzeki