Spotkanie X

MODELE ARCH/GARCH - prognozowanie

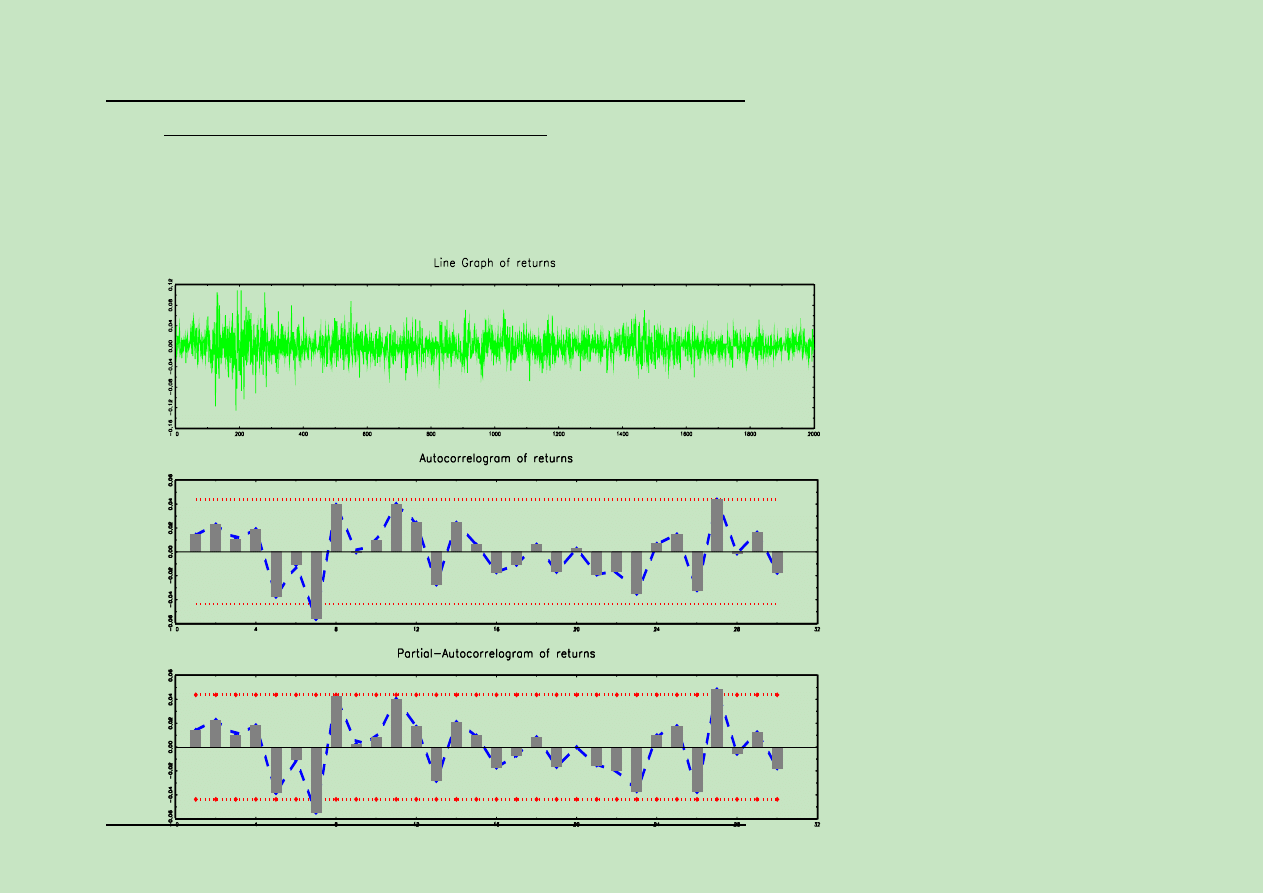
Modele GARCH:

Zacznijmy od prostego przykÃladu:
Na wykresach przedstawiono funkcj

,

e ACF i PACF zwykÃlych jednodniowych st´op

zwrotu (net returns: R

t

= (P

t

− P

t−1

)/P

t−1

) oraz ich kwadrat´ow dla sp´oÃlki

ORBIS S.A. w okresie 27.11.1997 - 16.11.2005 (2000 obserwacji):

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

2

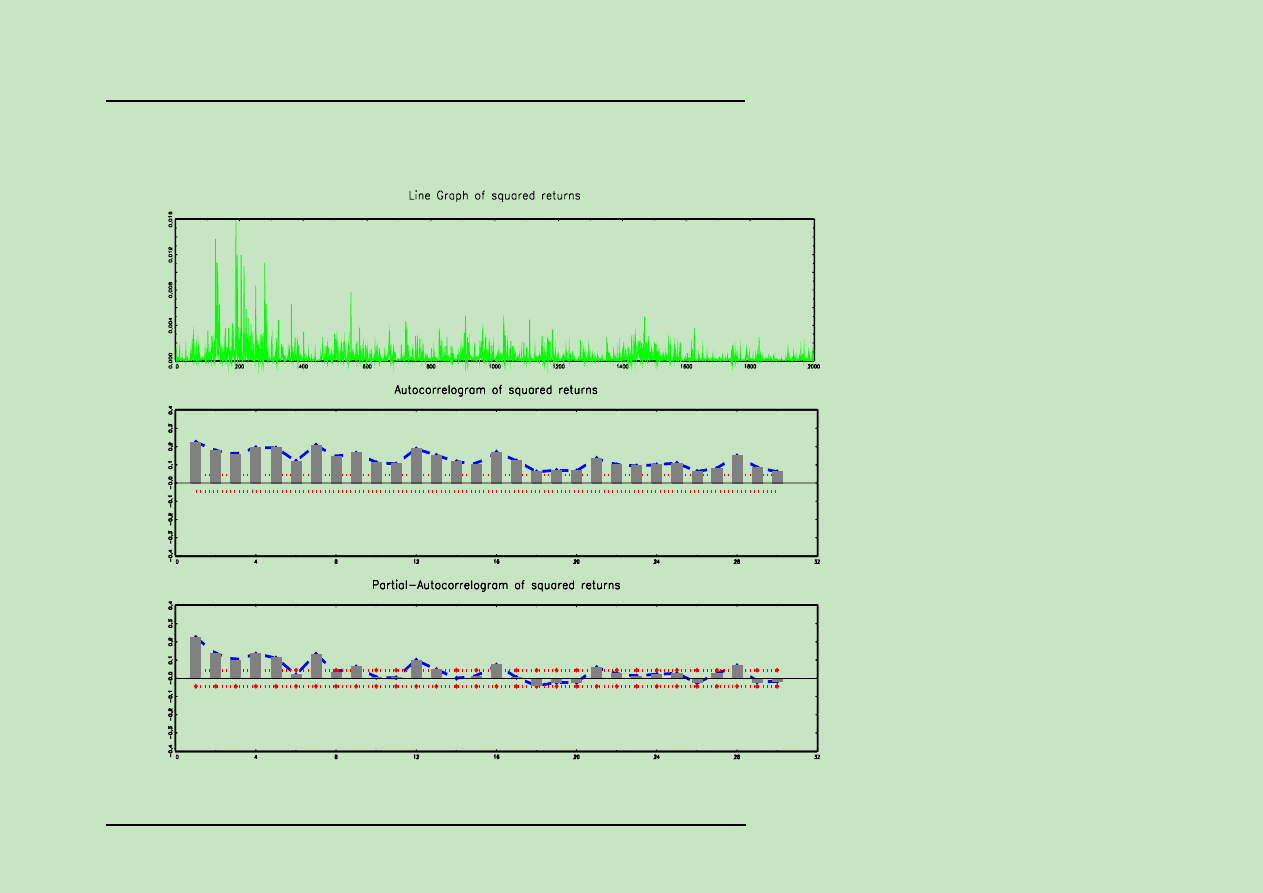
Modele GARCH:

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

3

Modele GARCH:

Ponadto:

Stopy zwrotu: LB(10)=15.07, p-value: 0.13

Kwadraty st´op zwrotu: LB(10)=600.69, p-value: 0.00

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

4

Modele GARCH:

Bazuj

,

ac na powy˙zszych statystykach, za pomoc

,

a pseudo-MNW (normalny rozkÃlad

skÃladnika losowego ε

t

) na podstawie pierwszych 1900 obserwacji oszacowano model

GARCH(1,1) o postaci:

r

t

= −0.0002 + ˆa

t

(1)

ˆa

t

=

ˆ

σ

t

ε

t

(2)

ˆ

σ

2

t

= 0.000 + 0.0955ˆa

2

t−1

+ 0.8905ˆ

σ

2

t−1

(3)

ε

t

∼ i.i.d.N (0, 1)

(4)

Uwaga: ´srednie bÃl

,

edy szacunku nale˙zy oszacowa´c wykorzystuj

,

ac formuÃl

,

e sandwich

(QML).

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

5

Modele GARCH:

Na podstawie oszacowa´

n parametr´ow uzyskano standaryzowane reszty o postaci:

˜a

t

=

ˆa

t

ˆ

σ

t

(5)

=

(r

t

+ 0.0002)

ˆ

σ

t

ˆ

σ

2

t

= 0.000 + 0.0955ˆa

2

t−1

+ 0.8905ˆ

σ

2

t−1

(6)

Nale˙zy sprawdzi´c, czy speÃlnione jest zaÃlo˙zenie:

˜a

t

∼ i.i.d.N (0, 1)

(7)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

6

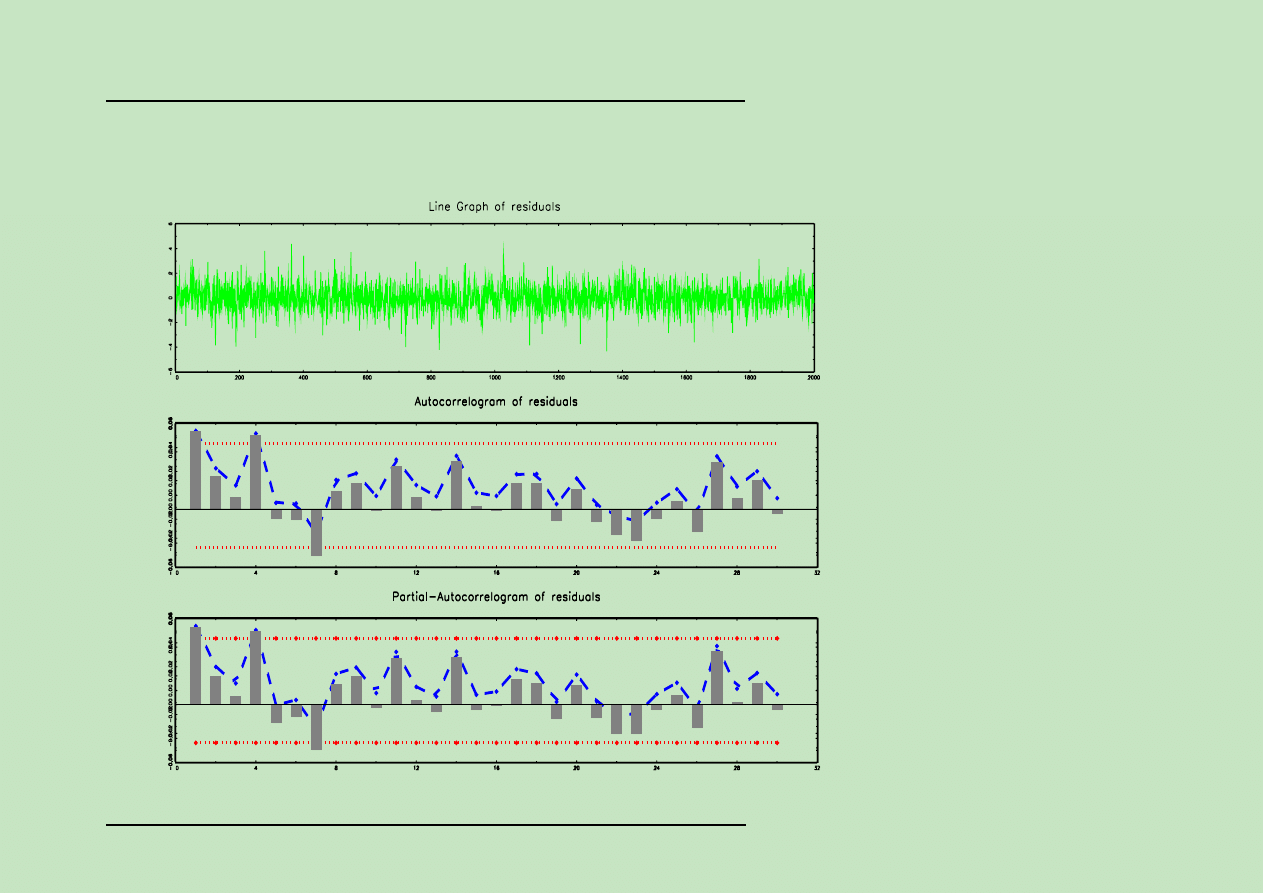
Modele GARCH:

Na wykresach przedstawiono funkcj

,

e ACF i PACF standaryzowanych reszt i reszt

do kwadratu:

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

7

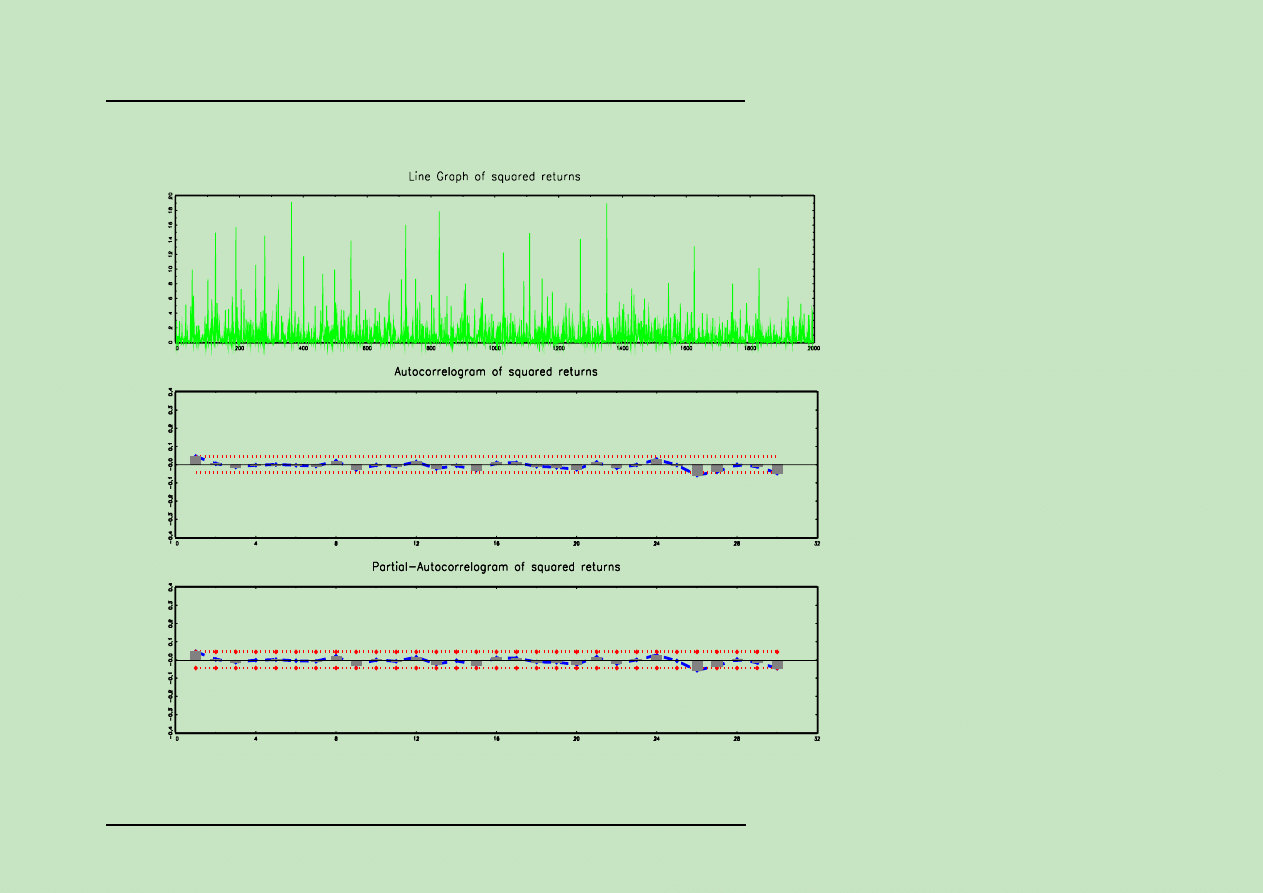
Modele GARCH:

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

8

Modele GARCH:

Ponadto:

Reszty: LB(10)=15.52, p-value: 0.11

Kwadraty reszt: LB(10)=5.14, p-value: 0.88

Jest O.K.!

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

9

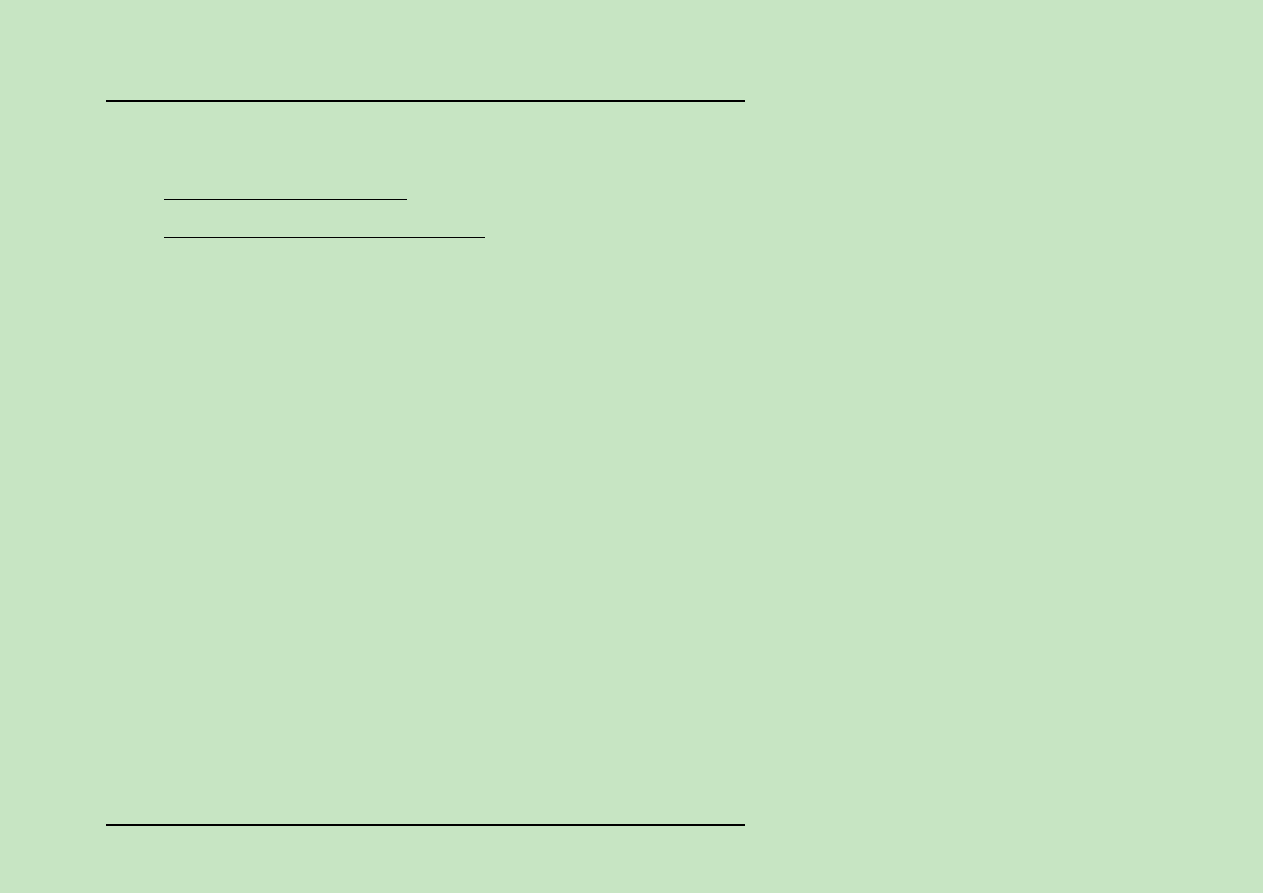
Modele GARCH:

Predykcja zmienno´sci
Na podst. Tsay R.S. (2005):
Niech r

t

= const. + a

t

. Model GARCH(1,1):

a

t

= σ

t

ε

t

(8)

ε

t

∼ i.i.d.(0, 1)

(9)

σ

2

t

= ω

0

+ α

1

a

2

t−1

+ β

1

σ

2

t−1

(10)

Zatem w momencie t = h + 1 proces σ

2

h+1

ma posta´c:

σ

2

h+1

= ω

0

+ α

1

a

2

h

+ β

1

σ

2

h

(11)

Oznaczmy przez σ

2

h

(k) prognoz

,

e zmienno´sci na k okres´ow w przyszÃlo´sci od

momentu h.
Poniewa˙z σ

2

h

(1) = E(a

2

h+1

|F

h

) = E(σ

2

h+1

|F

h

) prognoz

,

e jednookresow

,

a mo˙zemy

zapisa´c jako:

σ

2

h

(1) = ω

0

+ α

1

a

2

h

+ β

1

σ

2

h

(12)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

10

Modele GARCH:

W przypadku prognozy na jeden okres do przodu zachodzi zatem σ

2

h

(1) = σ

2

h+1

.

W momencie t = h + 2:

σ

2

h+2

= ω

0

+ α

1

a

2

h+1

+ β

1

σ

2

h+1

(13)

Mo˙zemy zatem zapisa´c:

σ

2

h

(2) = ω

0

+ α

1

E(a

2

h+1

|F

h

) + β

1

E(σ

2

h+1

|F

h

)

= ω

0

+ α

1

σ

2

h

(1) + β

1

σ

2

h

(1)

= ω

0

+ (α

1

+ β

1

)σ

2

h

(1)

(14)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

11

Modele GARCH:

Wykorzystuj

,

ac to samo rozumowanie dla k > 2:

σ

2

h

(k) = ω

0

+ α

1

E(a

2

k−1

|F

h

) + β

1

E(σ

2

k−1

|F

h

)

= ω

0

+ α

1

σ

2

h

(k − 1) + β

1

σ

2

h

(k − 1)

= ω

0

+ (α

1

+ β

1

)σ

2

h

(k − 1)

(15)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

12

Modele GARCH:

Dokonuj

,

ac kolejnych podstawie´

n, mo˙zna pokaza´c, ˙ze powy˙zszy wz´or o charakterze

rekurencyjnym mo˙zna przedstawi´c:

σ

2

h

(k) =

ω

0

[1 − (α

1

+ β

1

)

k

]

1 − α

1

− β

1

+ (α

1

+ β

1

)

k−1

σ

2

h

(1)

(16)

Zatem, je´sli α

1

+ β

1

< 1:

lim

k→∞

σ

2

h

(k) =

ω

0

1 − α

1

− β

1

(17)

Prognozowana zmienno´s´c d

,

a˙zy zatem do warto´sci wariancji bezwarunkowej a

t

w

modelu GARCH(1,1).

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

13

Modele GARCH:

PrzykÃlad - kontynuacja: W rozwa˙zanym modelu:

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

14

Modele GARCH:

Prognoza dla modelu IGARCH(1,1).
Je˙zeli warunek α

1

+ β

1

= 1 jest speÃlniony wz´or:

σ

2

h

(k) = ω

0

+ (α

1

+ β

1

)σ

2

h

(k − 1)

(18)

dla k ≥ 0 przyjmuje posta´c:

σ

2

h

(k) = σ

2

h

(1) + ω(k − 1)

(19)

Szczeg´olne wÃlasno´sci statystyczne modeli IGARCH mo˙zna znale´z´c w Nelson. D.B.
”Stationarity and persistence in the GARCH(1,1) model” Econometric Theory 6,
1990.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

15

Modele GARCH:

A je˙zeli w modelu IGARCH(1,1) ω = 0?

σ

2

h

(k) = σ

2

h

(1)

(20)

σ

2

h+1

= (1 − β

1

)a

2

h

+ β

1

σ

2

h

(21)

= (1 − β

1

)a

2

h

+ β

1

[(1 − β

1

)a

2

h−1

+ β

1

σ

2

h−1

]

= (1 − β

1

)a

2

h

+ β

1

(1 − β

1

)a

2

h−1

+ β

2

1

σ

2

h−1

= (1 − β

1

)[a

2

h

+ β

1

a

2

h−1

+ β

2

1

a

2

h−2

+ ...]

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

16

Modele GARCH:

Prognoza dla modelu EGARCH(1,1).
R´ownanie wariancji w modelu EGARCH(1,1) ma posta´c:

ln(σ

2

h+1

) = ω + α (ε

h

) + λ

"

|ε

h

| −

r

2

π

#

+ βln(σ

2

h

)

Zatem warunkowa wariancja ma posta´c:

σ

2

h+1

= σ

2β

h

exp(ω

0

)exp

"

αε

h

+ λ

"

|ε

h

| −

r

2

π

##

Zatem, tak jak w modelu GARCH(1,1), w modelu EGARCH(1,1) σ

2

h

(1) = σ

2

h+1

.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

17

Modele GARCH:

Z uwagi na nieliniowo´s´c r´ownania wariancji, sprawa komplikuje si

,

e dla k > 1.

σ

2

h+2

= σ

2β

h+1

exp(ω

0

)exp

Ã

αε

h+1

+ λ

"

|ε

h+1

| −

r

2

π

#!

Prognoza zmienno´sci ma zatem posta´c:

σ

2

h

(2) =

ˆ

σ

2β

h

(1)exp(ω

0

)E

"

exp

Ã

αε

h+1

+ λ

"

|ε

h+1

| −

r

2

π

#!#

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

18

Modele GARCH:

Jak obliczamy E

h

exp

³

αε

h+1

+ λ

h

|ε

h+1

| −

q

2

π

i´i

?

Z definicji warto´sci oczekiwanej funkcji zmiennej losowej g(ε) (poniewa˙z
f (ε

h+1

) = f (ε):

E [g(ε)] =

∞

Z

−∞

exp

Ã

αε + λ

"

|ε| −

r

2

π

#!

f (ε)dε

= exp

Ã

−λ

r

2

π

! ·

exp

µ

(α + λ)

2

2

¶

Φ(α + λ) + exp

µ

(α − λ)

2

2

¶

Φ(α − λ)

¸

Wyprowad´z powy˙zsz

,

a formuÃl

,

e samodzielnie. Rekurencyjnie otrzymujemy:

σ

2

h

(k) =

ˆ

σ

2β

h

(k − 1)exp(ω

0

)E [g(ε)]

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

19

Modele GARCH:

Ocena jako´sci prognoz zmienno´sci:
1. Minzer - Zarnowitz Regression. W odniesieniu do prognoz zmienno´sci na 1
okres do przodu konstruuje si

,

e regresj

,

e pomocnicz

,

a:

ˆa

2

h+1

= κ

1

+ κ

2

ˆ

σ

2

h

(1)

Testujemy restrykcj

,

e H

0

: (κ

1

, κ

2

) = (0, 1).

2. BÃl

,

edy ex post. Zdefiniujmy bÃl

,

ad prognozy (na 1 okres do przodu) dla

zmienno´sci jako: e

h

(1) = ˆa

2

h+1

− ˆ

σ

2

h

(1).

BÃl

,

ad ´sredniokwadratowy (Mean Squared Prediction Error, MSPE )

M SP E

=

1

m

m

X

i=1

e

h+i

(1)

2

(22)

BÃl

,

ad absolutny (Mean Absolute Prediction Error, MAPE )

M AP E

=

1

m

m

X

i=1

|e

h+i

(1)|

(23)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

20

Modele GARCH:

Je˙zeli interesuje nas wi

,

eksza kara za niedoszacowanie zmienno´sci to konstruujemy

Mean Mixed Error of Underprediction:

M M EU =

1

m

Ã

m

X

i=1

p

|e

h+i

(1)|(e

h+i

(1) > 0) +

m

X

i=1

|e

h+i

(1)|(e

h+i

(1) <= 0)

!

Je˙zeli interesuje nas wi

,

eksza kara za przeszacowanie zmienno´sci to konstruujemy

Mean Mixed Error of Overprediction

M M EO =

1

m

Ã

m

X

i=1

p

|e

h+i

(1)|(e

h+i

(1) <= 0) +

m

X

i=1

|e

h+i

(1)|(e

h+1

(1) > 0)

!

Wi

,

ecej w Brailsford, T. J., R. W. Faff, 1996. ”An evaluation of volatility

forecasting techniques”. Journal of Banking and Finance 20, 419-438.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

21

Modele GARCH:

Do por´ownania, czy prognozy generowane przez dwa konkurencyjne modele s

,

a

statystycznie r´o˙zne, a poprzez to, czy kt´ory´s z nich jest lepszy wykorzystuje si

,

e

test Diebolda i Mariano (1995). Test polega na zdefiniowaniu ”r´o˙znicy strat” (loss
differential):

d

h

= g(e

h

(1)

A

) − g(e

h

(1)

B

)

(24)

gdzie e

h

(1)

A

, e

h

(1)

A

s

,

a to bÃl

,

edy prognozy o horyzoncie jednookresowym, dla

1 <= h <= T

∗

, wynikaj

,

ace z modeli A i B odpowiednio. Funkcja g(.) to funkcja

straty, na przykÃlad g(x) = x

2

lub g(x) = |x|.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

22

Modele liniowe:

Test Diebolda i Mariano (1995) dla predykcji na 1 okres w przyszÃlo´sci.

DM =

¯

d

√

ω

(25)

gdzie ω oznacza asymptotyczn

,

a wariancj

,

e ´sredniej r´o˙znicy strat: ¯

d =

P

T

∗

h=1

d

h

,

natomiast ω:

ˆ

ω =

1

T

∗

T

∗

X

h=1

(d

h

− ¯

d)(d

h

− ¯

d)

(26)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

23

Modele GARCH:

Variance targeting:

•

Warto´s´c dÃlugookresowej zmienno´sci jest bardzo wra˙zliwa na warto´sci ocen
parametr´ow modeli GARCH (zatem na zakres wykorzystanych danych
historycznych).

•

Problem kompromisu pomi

,

edzy stabilno´sci

,

a oszacowa´

n parametr´ow a

zdolno´sci

,

a modelu do odzwierciedlania aktualnych warunk´ow rynkowych.

•

Indywidualna ocena zmienno´sci σ

2

w dÃlugim okresie albo

E(a

2

t

) = σ

2

=

1

T

Σ

T

t=1

(r − µ)

2

.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

24

Modele GARCH:

Poniewa˙z wiemy, ˙ze E(a

2

t

) = σ

2

=

ω

1−α−β

, model GARCH(1,1) mo˙zna zapisa´c jako:

σ

2

t

= σ

2

(1 − α − β) + αa

2

t−1

+ βσ

2

t−1

(27)

lub:

σ

2

t

= βσ

2

t−1

+ (1 − β)σ

2

+ α(a

2

t−1

− σ

2

)

(28)

SkÃladnik [βσ

2

t−1

+ (1 − β)σ

2

)]:

[σ

2

t−1

] − − − −[βσ

2

t−1

+ (1 − β)σ

2

)] − − − − − − − − − − − − − − − − − −[σ

2

]

czyli, je´sli σ

2

t−1

< σ

2

to σ

2

t

wzrasta.

[σ

2

] − − − − − − − − − − − − − − − − − −[βσ

2

t−1

+ (1 − β)σ

2

)] − − − −[σ

2

t−1

]

czyli, je´sli σ

2

t−1

> σ

2

to σ

2

t

maleje.

SkÃladnik α(a

2

t−1

− σ

2

):

je´sli a

2

t−1

< σ

2

to σ

2

t

maleje.

je´sli a

2

t−1

> σ

2

to σ

2

t

ro´snie.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

25

Modele GARCH:

Testowanie jako´sci modelu GARCH:
Reszty z modelu GARCH:

ˆa

t

= r

t

− µ

t

˜a

t

=

ˆa

t

ˆ

σ

t

Sprawdzamy, czy dodatnie i ujemne zaburzenia maj

,

a r´o˙zny wpÃlyw na reszty

podniesione do kwadratu.
Definiujemy zmienne zerojedynkowe:







Z

−1

t−1

= 1, je´sli ˆa

t−1

< 0

Z

−1

t−1

= 0, je´sli ˆa

t−1

> 0







Z

+1

t−1

= 1, je´sli ˆa

t−1

> 0

Z

+1

t−1

= 0, je´sli ˆa

t−1

< 0

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

26

Modele GARCH:

Rozpatrujemy r´ownanie regresji pomocniczej:

˜a

2

t

= φ

0

+ φ

1

Z

−1

t−1

+ φ

2

Z

−1

t−1

ˆa

t−1

+ φ

3

Z

+1

t−1

ˆa

t−1

+ ξ

t

(29)

Jest to test obci

,

a˙zenia znak´ow (Negative or Positive Sign Bias) lub obci

,

a˙zenia

warto´sci (Negative or Positive Size Bias).
Nast

,

epnie testujemy statystyczn

,

a istotno´s´c zmiennych za pomoc

,

a statystyki

t-studenta (dla ka˙zdej ze zmiennych pojedynczo) lub za pomoc

,

a testu LM Ãl

,

acznie

[Engle i Ng (1993)].

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

27

Modele GARCH:

Warto´s´c nara˙zona na ryzyko (Value at Risk)

Maksymalna warto´s´c straty jak

,

a mo˙zna ponie´s´c w danym okresie

z zadanym poziomem istotno´sci (w normalnych warunkach rynkowych).

Niech W

t

– warto´s´c instrumentu finansowego w momencie t,

a W

∗

t+1

– najni˙zsza warto´s´c instrumentu finansowego w momencie t + 1 z

prawdopodobie´

nstwem 0.95. Tzn. z prawdopodobie´

nstwem 0.95 warto´s´c

instrumentu finansowego b

,

edzie r´owna W

∗

t+1

lub wy˙zsza.

P (W

t+1

< W

∗

t+1

) = 0.05

W

∗

t+1

− W

t

= V aR = W

t

R

∗

t+1

(30)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

28

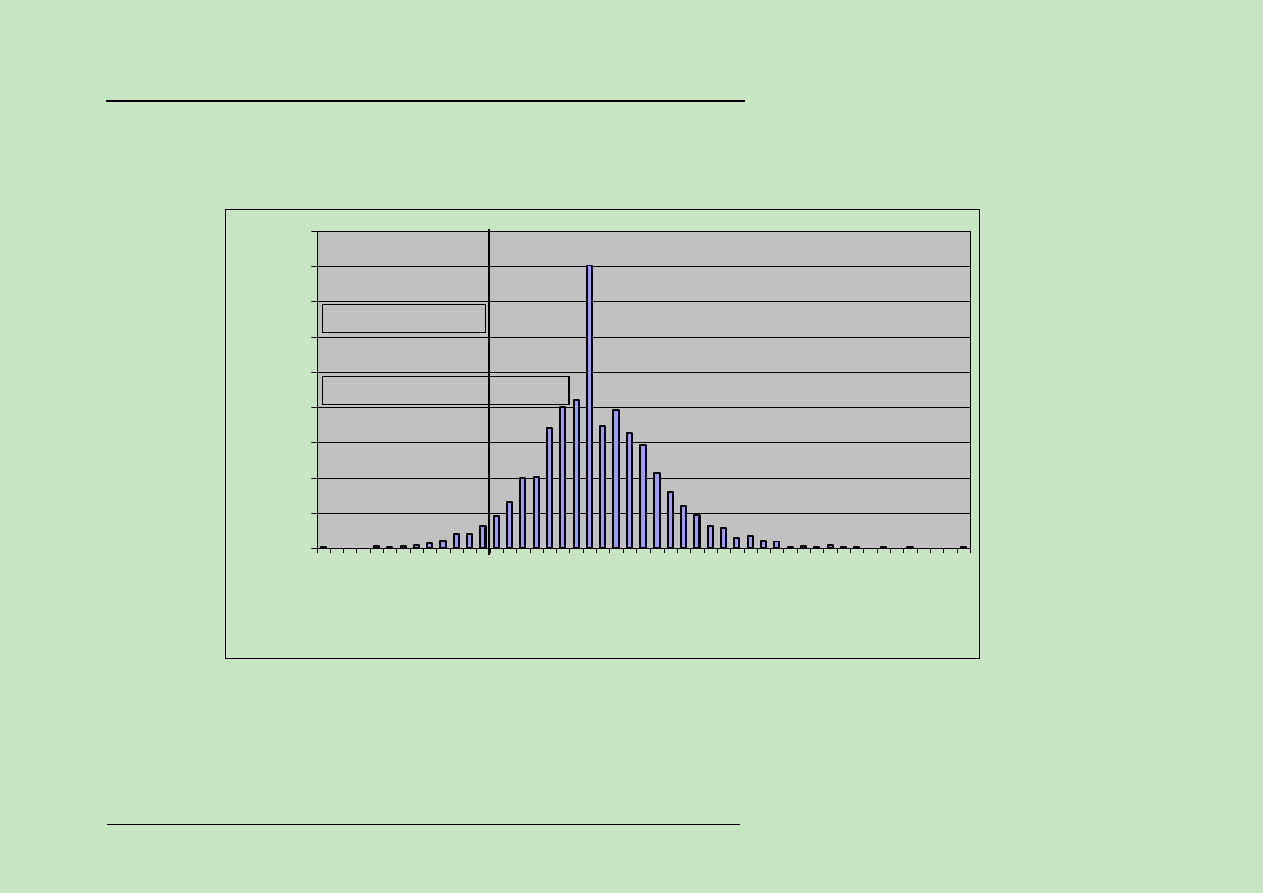
Modele GARCH:

0

0,02

0,04

0,06

0,08

0,1

0,12

0,14

0,16

0,18

-0

,0

9

6

8

-0

,0

8

7

1

-0

,0

7

7

3

-0

,0

6

7

6

-0

,0

5

7

9

-0

,0

4

8

2

-0

,0

3

8

5

-0

,0

2

8

8

-0

,0

1

9

1

-0

,0

0

9

3

0

,0

0

0

4

0

,0

1

0

1

0

,0

1

9

8

0

,0

2

9

5

0

,0

3

9

2

0

,0

4

8

9

0

,0

5

8

7

0

,0

6

8

4

0

,0

7

8

1

0

,0

8

7

8

0

,0

9

7

5

0

,1

0

7

2

0

,1

1

6

9

0

,1

2

6

6

Stopa zwrotu

C

zĊ

s

to

Ğü

Pi

ąty percentyl: R*=-0,036

VaR: W(0) · R*

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

29

Modele GARCH:

FormuÃl

,

e 30 mo˙zemy przeksztaÃlci´c:

P (W

t+1

− W

t

< W

∗

t+1

− W

t

) = 0.05

P (∆W

t+1

< V aR) = 0.05

(31)

Poniewa˙z wiemy, ˙ze:

∆W

t+1

= W

t

R

t+1

(32)

P (W

t

R

t+1

< V aR) = 0.05

(33)

oraz R

t+1

∼ N (µ

t+1

, σ

2

t+1

), widzimy, ˙ze prawdziwa jest zale˙zno´s´c:

P (W

t

R

t+1

− µ

t+1

σ

t+1

< W

t

(−1.65)) = 0.05

(34)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

30

Modele GARCH:

z czego wynika:

P (W

t

R

t+1

< W

t

(−1.65σ

t+1

+ µ

t+1

)) = 0.05

(35)

czyli:

V aR

t+1

= W

t

(−1.65σ

t+1

+ µ

t+1

)

(36)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

31

Modele GARCH:

Przy k-okresowym horyzoncie inwestycyjnym, przyjmuj

,

ac µ

t+1

= 0:

V aR(k) = V aR(1)

√

k

(37)

W odniesieniu do modelu GARCH ze skÃladnikiem losowym o rozkÃladzie t-studenta:

V aR

t+1

= W

t

(t

v

σ

t+1

/(v/(v − 2))

0.5

+ µ

t+1

)

(38)

gdzie: t

v

to odpowiedni kwantyl (dla zadanego poziomu 1-prawdopodobie´

nstwo), a

v to liczba stopni swobody rozkÃladu t-studenta.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

32

Modele GARCH:

PrzykÃlad - kontynuacja
W dniu 26.06.2005 (obserwacja nr 1900) dysponuj

,

e portfelem akcji Orbis S.A. o

warto´sci 100 000 zÃl. Ile mog

,

e maksymalnie straci´c w ci

,

agu jednego dnia z zadanym

prawdopodobie´

nstwem 0,01?

1. Na podstawie Gaussian GARCH(1,1):
Prognoza zmienno´sci stopy zwrotu na okres 1901 wynosi 0.000177, a jej poziomu
-0.0002. 1 % kwantyl standardowego rozkÃladu normalnego wynosi -2.3262, zatem
warto´s´c VaR:

V aR

1901

= 100000(−2.3262

√

0.000177 − 0.0002) = −3100.2034

(39)

2. Na podstawie t-student GARCH(1,1):
Prognoza zmienno´sci stopy zwrotu na okres 1901 wynosi 0.000166, a jej poziomu
-0.0002. 1 % kwantyl standardowego rozkÃladu T-studenta wynosi -3.3649 (dla
v = 5), zatem warto´s´c VaR:

V aR

1901

= 100000(−3.3649

√

0.000166/(5/(5 − 2))

0.5

− 0.0002) = −3283.0873

(40)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

33

Modele GARCH:

UWAGA! A jak wyprowadzimy VaR dla logarytmicznych st´op zwrotu?

P (W

t+1

− W

t

< W

∗

t+1

− W

t

) = 0.05

P (W

t+1

− W

t

< V aR) = 0.05

P

µ

W

t+1

W

t

<

V aR + W

t

W

t

¶

= 0.05

P

µ

ln

µ

W

t+1

W

t

¶

< ln

µ

V aR + W

t

W

t

¶¶

= 0.05

P

µ

r

t

< ln

µ

V aR + W

t

W

t

¶¶

= 0.05

(41)

Je˙zeli zaÃlo˙zymy r

t+1

∼ N (µ

t+1

, σ

2

t+1

), otrzymujemy:

P



 r

t+1

− µ

t+1

σ

t+1

<

ln

³

V aR+W

t

W

t

´

− µ

t+1

σ

t+1



 = 0.05

(42)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

34

Modele GARCH:

Zatem VaR wyprowadzimy z zale˙zno´sci:

ln

³

V aR+W

t

W

t

´

− µ

t+1

σ

t+1

= −1.65

(43)

Czyli:

V aR = W

t

(exp(µ

t+1

− 1.65σ

t+1

) − 1)

(44)

PrzykÃlad: p=0,01, czas trwania inwestycji: 30 dni, W

t

= 500tys., ˆ

µ

t+1

= 0.0005,

ˆ

σ

t+1

= 0.014.

V aR = 500(exp(30 ∗ 0.0005 − 2.32630.014

√

30) − 1) = −75.37

(45)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

35

Modele GARCH:

VaR w odniesieniu do portfela aktyw´ow finansowych:

Niech r - wektor zwykÃlych st´op zwrotu z n akcji, a w - wektor ich wag w portfelu o
waro´sci W. Zachodz

,

a nast

,

epuj

,

ace zale˙zno´sci:

r

p

= w

0

r

(46)

µ

p

= E[r

p

] = w

0

E[r] = w

0

µ

σ

2

p

= V ar[r

p

] = V ar[w

0

r] = w

0

V ar[r]w = w

0

Σw

Zatem je´sli r

p,t+1

∼ N (µ

p,t+1

, σ

2

p,t+1

), to:

V aR

p

= (w

0

µ

t+1

+ z

α

p

w

0

Σ

t+1

w)W

(47)

Dynamiczne modele Σ

t+1

to wielowymiarowe modele GARCH.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

36

Modele GARCH:

PrzykÃlad
Rozwa˙zamy portfel skÃladaj

,

acy si

,

e z trzech akcji: 1.) A -30 % 2.) B -30 % i 3.) C

-40 %. Oblicz warto´s´c nara˙zon

,

a na ryzyko przy poziomie ufno´sci 0,95. Wiesz

ponadto, ˙ze: µ

t,1

= 0, 0012, µ

t,2

= 0, 0025, µ

t,3

= 0, 012 oraz σ

t,1

= 0, 0196,

σ

t,2

= 0, 0411, σ

t,3

= 0, 023, ρ

t,1,2

= 0, 19, ρ

t,1,3

= 0, 55, ρ

t,2,3

= 0, 22.

ˆ

Σ

t

=









0, 0196

0

0

0

0, 0411

0

0

0

0, 023

















1

0, 19 0, 55

0, 19

1

0, 22

0, 55 0, 22

1

















0, 0196

0

0

0

0, 0411

0

0

0

0, 023









(48)

=









0, 00038 0, 00015 0, 00025

0, 00015 0, 00169 0, 00021

0, 00025 0, 00021 0, 00053









Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

37

Modele GARCH:

Przy portfelu zÃlo˙zonego z 2 instrument´ow finansowych A i B (dla µ

t+1

= 0)

uwzgl

,

edniamy stopie´

n ich skorelowania:

V aR = z

α

[w

2

A

σ

2

A,t+1

+ w

2

B

σ

2

B,t+1

+ 2w

A

w

B

σ

A,t+1

σ

B,t+1

ρ

A,B

]

0.5

W

t

(49)

= [V aR

2

A

+ V aR

2

B

+ 2ρ

A,B

V aR

A

V aR

B

]

0.5

FormuÃl

,

e mo˙zna uog´olni´c na m instrument´ow finansowych:

V aR = (

m

X

i=1

V aR

2

i

+ 2

m

X

j<i

ρ

ij

V aR

i

V aR

j

)

0.5

(50)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

38

Modele GARCH:

Szczeg´olne przypadki dla VaR:
1. ρ

A,B

= 1

V aR = [V aR

2

A

+ V aR

2

B

+ 2V aR

A

V aR

B

]

0.5

= [V aR

A

+ V aR

B

]

(51)

2. ρ

A,B

= 0

V aR = [V aR

2

A

+ V aR

2

B

]

0.5

(52)

3. ρ

A,B

= −1

V aR = [V aR

2

A

+ V aR

2

B

− 2V aR

A

V aR

B

]

0.5

= |V aR

A

− V aR

B

|

(53)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

39

Modele GARCH:

Testowanie wsteczne VaR, Backtesting:
1. Test liczby przekrocze´

n (Unconditional coverage test) – Kupiec (1995).

Dysponuj

,

ac pr´ob

,

a o liczebno´sci T, definiujemy zmienn

,

a zerojedynkow

,

a: I

t

= 1,

je˙zeli ∆W

t

< V aR oraz I

t

= 0, je˙zeli ∆W

t

> V aR. Liczba przekrocze´

n

T

1

=

P

T
t=1

I

t

powinna mie´c rozkÃlad Bernoulliego o prawdopodobie´

nstwie ”pora˙zki”

r´ownym zaÃlo˙zonemu dla VaR poziomowi istotno´sci α = π. Testujemy H

0

: π = α

vs. H

1

: π 6= α na podstawie statystyki:

LR

U C

= −2ln

(1 − π)

T

0

π

T

1

(1 − ˆ

π)

T

0

ˆ

π

T

1

(54)

gdzie: T

1

- liczba przekrocze´

n VaR, T

0

- liczba nieprzekrocze´

n VaR, ˆ

π =

T

1

T

.

Zastan´ow si

,

e, jaki b

,

edzie rozkÃlad statystyki LR

U C

.

Przegl

,

ad zaawansowanych metod testowania VaR mo˙zna znale´z´c w pracy S.D.

Campbell ”A Review of Backtesting and Backtesting Procedures” (2005).

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

40

Modele GARCH:

2. Test liczby i niezale˙zno´sci przekrocze´

n (Conditional coverage test) –

Christoffersen (1998).
Niech:
T

00

– liczba brak´ow przekrocze´

n VaR nast

,

epuj

,

acych bezpo´srednio po brakach

przekrocze´

n

T

01

– liczba przekrocze´

n VaR nast

,

epuj

,

acych bezpo´srednio po brakach przekrocze´

n

T

10

– liczba brak´ow przekrocze´

n nast

,

epuj

,

acych bezpo´srednio po przekroczeniach

T

11

– liczba przekrocze´

n VaR nast

,

epuj

,

acych bezpo´srednio po przekroczeniach

π

01

=

T

01

T

01

+T

00

– udziaÃl przekrocze´

n nast

,

epuj

,

acych po brakach przekrocze´

n

π

11

=

T

11

T

10

+T

11

– udziaÃl przekrocze´

n nast

,

epuj

,

acych po przekroczeniach

LR

cc

= −2ln

µ

π

T

1

(1 − π)

T

0

π

T

01

01

(1 − π

01

)

T

00

π

T

11

11

(1 − π

11

)

T

10

¶

(55)

LR

cc

ma asymptotyczny rozkÃlad χ

2

z DF = 2.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

41

Modele GARCH:

3. Testy zgodno´sci kwantyli (Integral Probability Transformations):

u

t

= F (r

t

) =

r

t

Z

−∞

f (z)dz

(56)

oraz z

t

= Φ

−1

(u

t

). W prawidÃlowej specyfikacji modelu u

t

∼ i.i.d.U (0, 1) oraz

z

t

∼ i.i.d.N (0, 1).

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

42

Modele GARCH:

Intuicja:
Risk (III 2007): ”Value-at-risk is defined as the loss level that will not be exceeded
with a certain confidence level during a certain period of time. For example, if a
bank’s 10-day 99% VAR is 3 million USD, there is considered to be only a 1%
chance that losses will exceed 3 million USD in 10 days. (...) One problem with
VAR is that, when used in an attempt to limit the risks taken by a trader, it can
lead to undesirable results”.

”Suppose a bank tells a trader that the one-day 99% VAR of the trader’s portfolio
must be kept at less than 10 USD million. There is a danger that the trader will
construct a portfolio where there is a 99% chance that the daily loss is less than 10
million USD and a 1% chance that it is 500 million USD. The trader is satisfying
the risk limits imposed by the bank, but is clearly taking unacceptable risks”.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

43

Modele GARCH:

Oczekiwany niedob´

or (Expected Shortfall, Conditional VaR, Expected Tail

Loss) to oczekiwana warto´s´

c straty, pod warunkiem, ˙ze strata ta jest

wi

,

eksza ni˙z VaR. Ujmuj

,

ac V aR

α

tym razem jako procentow

,

a zmian

,

e warto´sci

portfela, oczekiwany niedob´or ma posta´c:

ES

α

= E[r

t

|r

t

< V aR

α

]

(57)

PrzykÃladowo, dla α = 0.05:

ES

α

=

V aR

α

Z

−∞

f (r)

α

rdr

(58)

Je˙zeli R

t

∼ N (µ

t

, σ

2

t

), to oczekiwany niedob´or b

,

edzie miaÃl warto´s´c:

ES

α

= −α

−1

ϕ(z

α

)σ

t

+ µ

t

(59)

gdzie ϕ oznacza funkcj

,

e g

,

esto´sci standardowego rozkÃladu normalnego.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

44

Modele GARCH:

Dow´

od:

W przypadku zmiennej Z ∼ N (0, 1), ES

α

ma posta´c:

ES

z

= α

−1

z

α

Z

−∞

ϕ(z)zdz

(60)

ES

z

= (

√

2πα)

−1

z

α

Z

−∞

exp(

−1

2

z

2

)zdz

ES

z

= −α

−1

·

1

√

2π

exp(

−1

2

z

2

)

¸

z

α

−∞

= −α

−1

ϕ(z

α

)

(61)

Je˙zeli R

t

= Zσ

t

+ µ

t

, to oczekiwany niedob´or b

,

edzie miaÃl warto´s´c:

ES

= ES

z

σ

t

+ µ

t

(62)

gdzie ϕ oznacza funkcj

,

e g

,

esto´sci standardowego rozkÃladu normalnego.

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

45

Modele GARCH:

PrzykÃlad:
ZaÃl´o˙zmy ˙ze oczekiwana stopa zwrotu z portfela wynosi 0, natomiast zmienno´s´c w
uj

,

eciu rocznym 30 %. Wyznacz (w uj

,

eciu procentowym) 10-dniowy VaR oraz ES

przy poziomie ufno´sci 0,99.
Warto´s´c odchylenia standardowego dla okresu przetrzymania r´ownego 10 dniom
ma posta´c 0, 3

p

10/250 = 0, 06.

V aR

α

= z

α

σ

t

+ µ

t

= −2, 326 ∗ 0, 06 = −13, 96%

(63)

ES

α

= −α

−1

ϕ(z

α

)σ

t

+ µ

t

= −

1

0, 01

∗ ϕ(z

α

) ∗ 0, 06 = −16, 00%

(64)

Katarzyna Bie´

n

Ekonometria finansowa

Spotkanie X

46