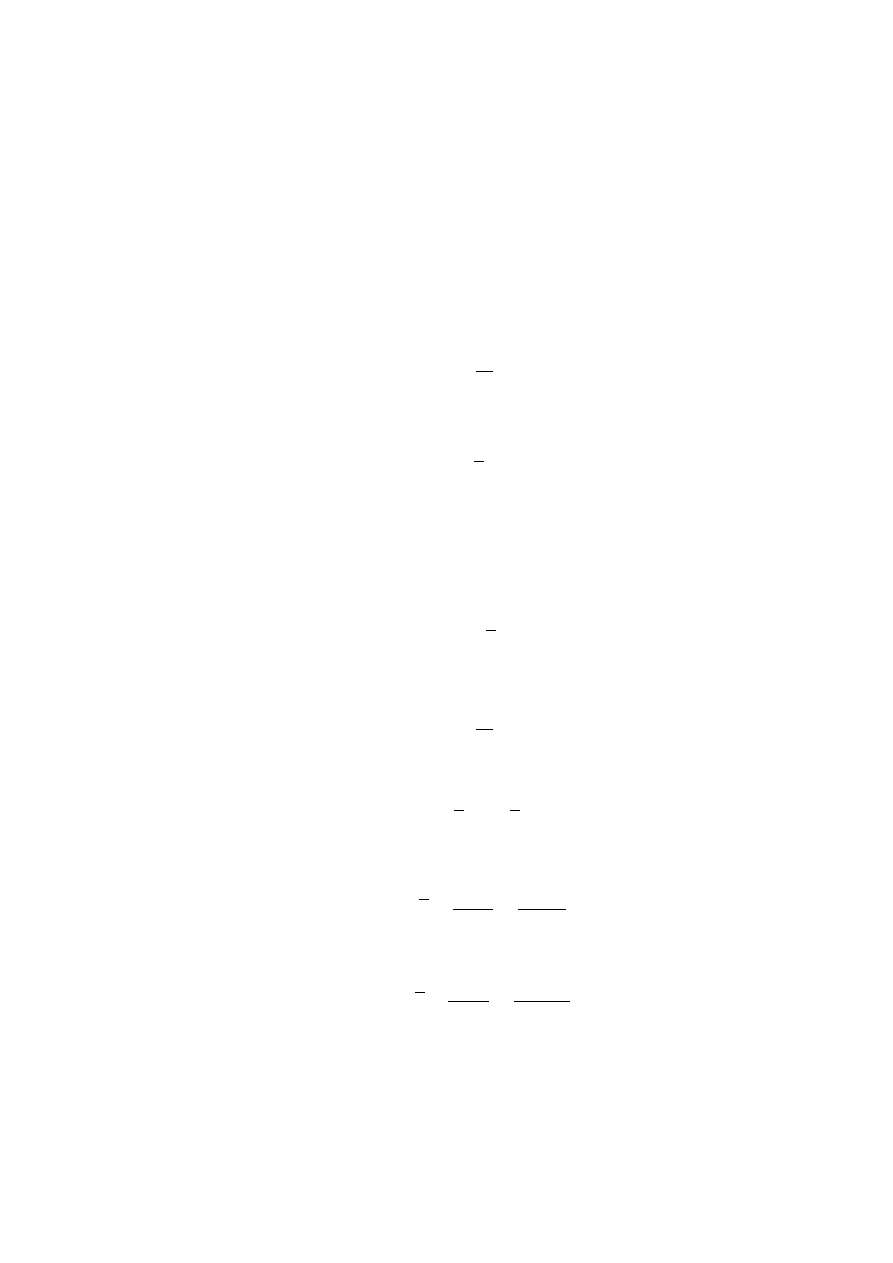
Ca lki oznaczone

1. Obliczy´

c :

a)

Z

2

−3

2x

2

dx

b)

Z

−1

−4

x

2

3

dx

c)

Z

e

1

1

x

dx

d)

Z

1

0

e

−2x

dx

e)

Z

4

1

2

√

xdx

f)

Z

−2

−5

1

x

2

dx

g)

Z

1

0

(2x −

√

x + 3

3

√

x

2

+ 1)dx

h)

Z

1

0

(2

√

x −

1

x + 1

+

x

x

2

+ 4

dx

i)

Z

1

0

(4

3

√

x +

3

x + 3

−

x

2

3x

3

+ 1

dx

1

j)

Z

1

1
2

2x − 3

x

2

− 3x + 1

dx

k)

Z

5

3

x

x

2

− 4

dx

l)

Z

π

0

(sin(x) + cos(x))dx

m)

Z

π

2

0

(2sin3x + 3cos2x)dx

n)

Z

π

3

π

6

tgxdx

o)

Z

π

3

π

6

ctgxdx

p)

Z

π

2

0

sin

2

xcosxdx

q)

Z

2

0

e

2x

1 + e

x

dx

r)

Z

2

1

lnxdx

2

s)

Z

1

0

xe

−x

dx

t)

Z

π

2

0

xcosxdx

u)

Z

e

1

xlnxdx

v)

Z

e

2

e

1

xlnx

dx

w)

Z

e

1

ln

2

x

x

dx

x)

Z

π

2

0

e

x

cosxdx

2. Obliczy´

c pole obszaru ograniczonego krzyw¸

a o r´

ownaniu y=f(x),prostymi x=a,x=b

oraz osi¸

a OX je´sli:

a) f (x) =

1

√

x

, a=1,b=4

b) f (x) = 4x − x

2

, a = 0, b = 4

c) f (x) = −x

2

+ 7x − 10, a = 0, b = 5

d) f (x) = tgx, a = 0, b =

π

3

e) f (x) = x

2

lnx, a = e, b = e

2

f) f (x) = xsin4x, a = 0, b =

π

8

g) f (x) = xe

−2x

, a = 0, b =

1
2

h) f (x) = xcos

x

3

, a =

π

2

, b = π

i) f (x) = xlog[2]x, a = 1, b = 2

3

3. Obliczy´

c pola obszar´

ow ograniczonych krzywymi o r´

ownaniach:

a)y = x

2

+ 1, y = −x + 3

b)y = x

2

, y = x + 2

c)y =

1
x

, y = −

1
3

x +

4
3

d)y = 2

√

x, y = 2x

3

e)y = x

2

, y = −x

2

+ 8

f)y = x

2

, y = 2x + 3

g)y = x

2

− x − 6, y = −x

2

+ 5x + 14

h)y =

16
x

2

, y = 17 − x

2

4. Obliczy´

c ca lki niewla´sciwe: a)

Z

1

0

lnxdx

b)

Z

1

0

x

√

1 − x

2

dx

c)

Z

1

0

xlnxdx

d)

Z

3

0

1

√

x

dx

e)

Z

1

0

1

3

√

x

dx

f)

Z

1

0

x

1 − x

dx

g)

Z

e

1

1

xlnx

dx

4

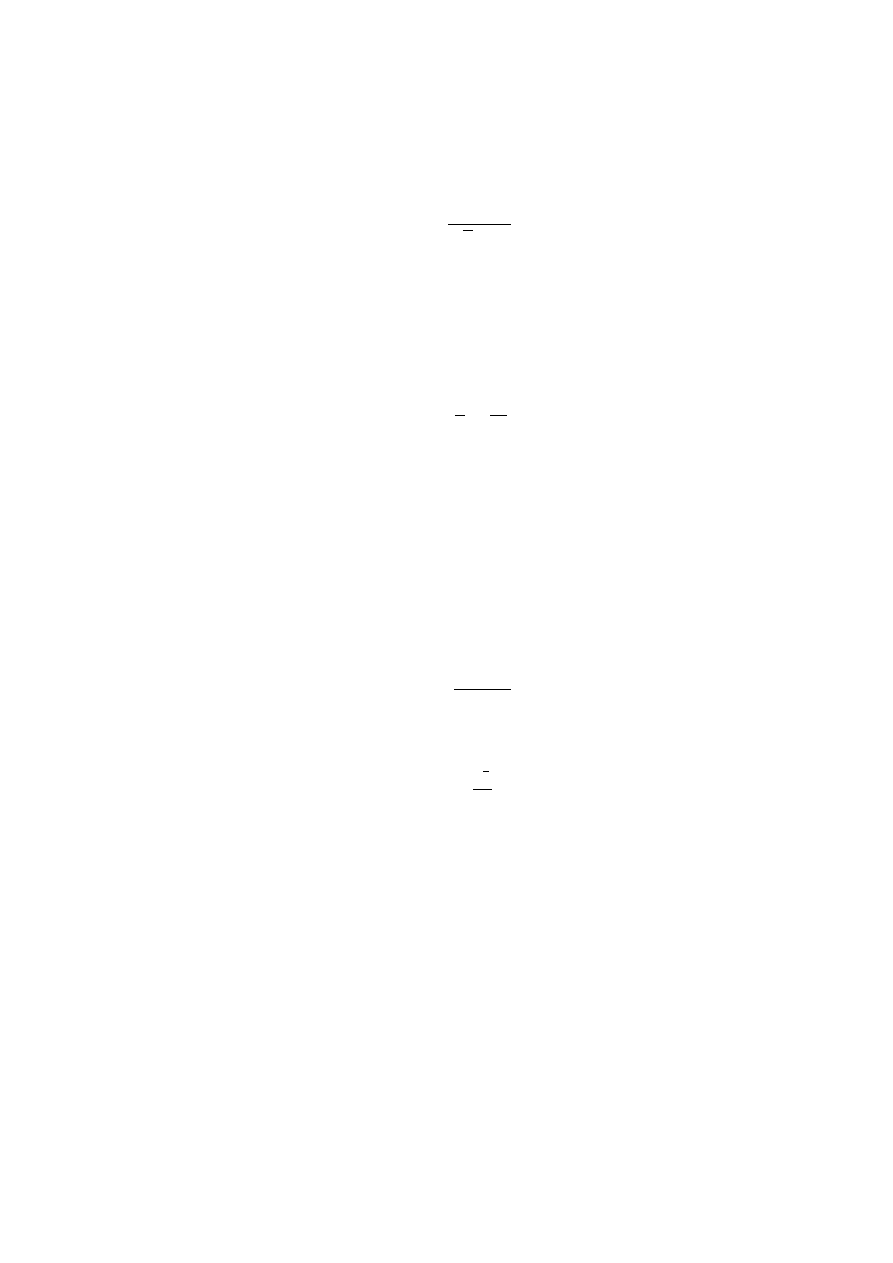
h)

Z

3

2

x

√

x

2

− 4

dx

i)

Z

∞

0

xe

−x

2

dx

j)

Z

∞

1

(

2

x

+

1

x

2

)dx

k)

Z

∞

0

e

−x

dx

l)

Z

∞

0

e

−x

sinxdx

m)

Z

∞

1

x

2x

2

+ 4

dx

n)

Z

∞

1

e

1
x

x

2

dx

5