Analiza matematyczna, całki oznaczone

1/36

Całki oznaczone

Poniższy rozdział będzie dosyć rozwarty, z dużą ilością przykładów. Temat, z którym się

dzisiaj zmierzymy, jest raczej mało ciekawy, eksperci powiedzą, że „cholernie nudnawy”. Nie ma w
nim nic „zaskakującego”, jedyne, co trzeba nowego wiedzieć do tego działu, to trudną i zdradziecką
operację odejmowania, albo czasem dodawania. Oczywiście – główną waszą zaletą, która w 90%
załatwia sprawę, ma być możliwość liczenia całek nieoznaczonych.

Pamiętacie doskonale ze szkoły średniej, że matma potrafi być tam strasznie interesująca.

Potrafiliście obliczyć deltę z funkcji kwadratowej, ale już wyzwaniem jest zadanie typu „Mam
nasiona konopi indyjskiej – tyle, ile trzeba, by spokojnie handlować i olać studia. Mam ze 10
metrów siatki. Jak zrobić taką prostokątną działeczkę, by miała ona jak największe pole?”, gdzie
zabawa również sprowadza się do funkcji kwadratowej.

Mówiąc inaczej, pierdolimy się z jebanymi deltami, wzorami, funkcjami

trygonometrycznymi (patrz pan, robotnicy zbudowali częstochowską Galerię Jurajską, a wątpię, by
któryś z nich korzystał z jakichś sinusów) czy wzorami redukcyjnymi. Ale ni chuja nie potrafimy
tego przenieść do rzeczywistości, do dupy, a nie do życia jest ta matma.

Całki oznaczone są takim fajnym bajerem, który może i mało się analizuje w matmie. Ale

akurat zastosowanie ma ogromne, niemal we wszystkich dziedzinach techniki. Mogę się założyć o
swoje zęby (wypadną mi niebawem z powodu nadużywania coca-coli), że pierwszy lepszy
wykładowca z elektroniki czy fizyki już pieprzy całkami, mimo że kompletnie nie wie, że tego się
w szkołach (już) nie uczy.

Ale my się nauczymy... no, chociaż spróbujemy. Poniżej minimalny spis treści:
Przypomnienie o całkach, co to całka oznaczona

2

Całki oznaczone – obliczanie przed podstawienie

11

Dzielenie obszarów całkowania

16

Zamiana zmiennych niezależnych

20

Przykłady z kolokwiów i egzaminów

25

I umawiamy się tak – przy logarytmie nie piszę wartości bezwzględnych. Pisze zamiennie

oś y, oś Oy, oś OY itp. Nie jestem matematykiem, tylko kiepskim studentem, z niepełną na pewno
wiedzą, więc błędów w zapisie jest więcej niż w ustawie o wychowaniu w trzeźwości. I ogólnie –
nie traktować tego jako podręcznik, tylko ewentualną, ostateczną pomoc, jak nic inne nie pomoże.

Autor: vbx

(c) 2010

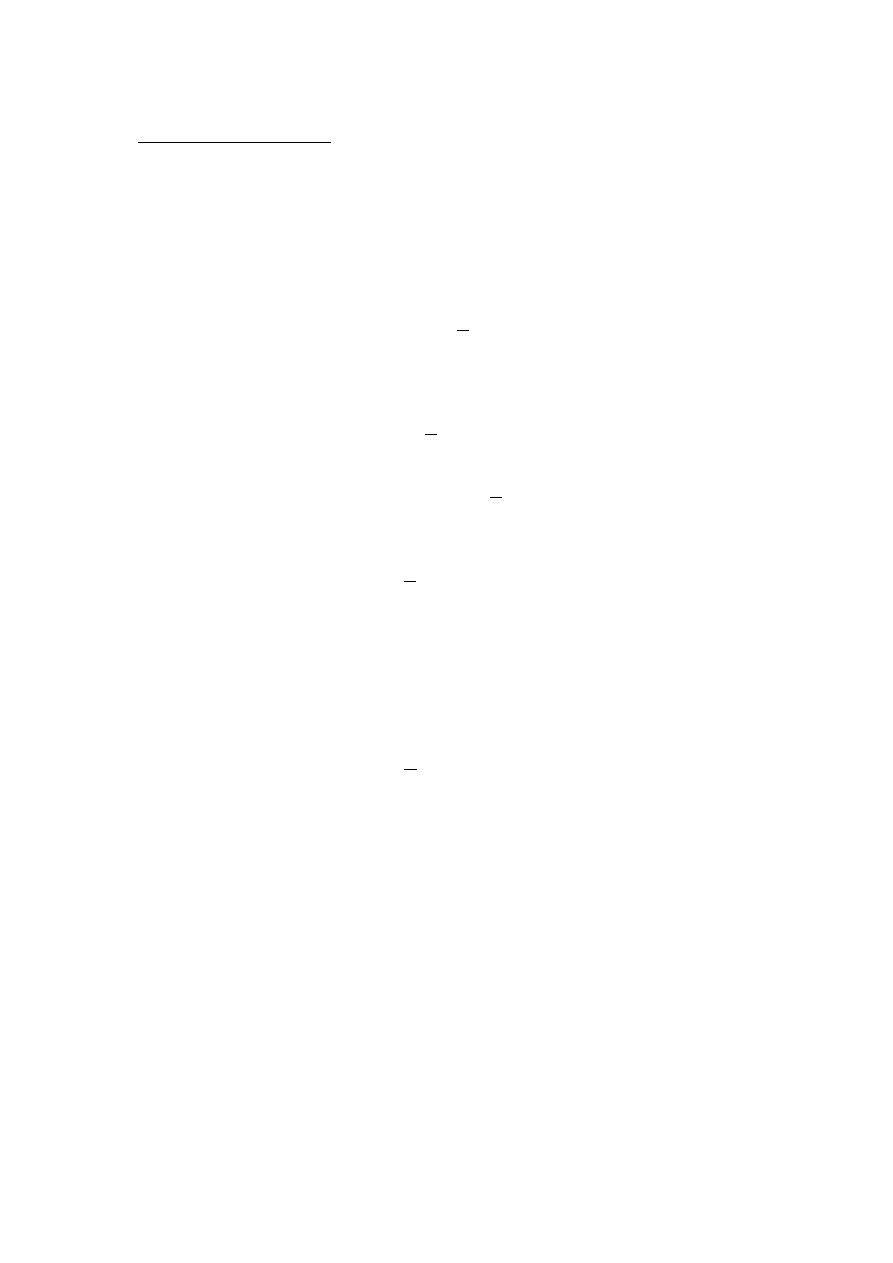
Analiza matematyczna, całki oznaczone

2/36

Przypomnienie, co to jest

Przypominania nigdy za wiele, więc przypomnijmy, co w ogóle nazwaliśmy tak dziwnie

„całką nieoznaczoną”.

Jak mamy sobie ulubiony przeze mnie logarytm:

y=ln  x 

to ja se z niego walnę pochodną (choćby z tablic):

y ' =

1

x

Odwrotną operacją od „walnę pochodną” jest „walnę całkę”, bądź bardziej sztywniarsko – obliczę

całkę nieoznaczoną:

∫

1

x

dx =...

Przypomnijmy – ten „wężyk” to symbol całki, potem

1

x

, czyli to, co rąbiemy, a na końcu

dx

,

co oznacza „x jest se zmienną, po której ja se tutaj całkuję” i właściwie, służy ino do dekoracji.

No dobra, obliczamy:

∫

1

x

dx=ln x...

(przypominam – w tablicach wynikiem jest wprawdzie ln∣x∣ , ale ja ten moduł pomijam dla

czystości zapisu, więc jak kogoś to razi – niech sobie domaluje długopisem czy mazakiem na

monitorze)

Pamiętamy, że do tego dodajemy liczbę (pochodną z takiej czystej i niewinnej liczby jest zero),

którą zwiemy „stałą całkowania” i oznaczamy jako C:

∫

1

x

dx=ln xC

I już, po krzyku. Ale typowy student już zakrzyknie „kurwa, chcę się napić, a nie uczyć się

jakiś beznadziejnych całek, po chuja mi to?”

Wynik może i jest ładny, ale właściwie, nie wiadomo, co on oznacza (dlatego pewno „całka

nieoznaczona”). Obliczyliśmy jakąś funkcję, z którą ładnie można se pochodne liczyć, ale przyda
nam się to po coś?

Popatrzmy na rysunek, stworzony za pomocą specjalistycznego, komputerowego programu

do obliczeń, takiego, jakiego używają w NASA:

Autor: vbx

(c) 2010

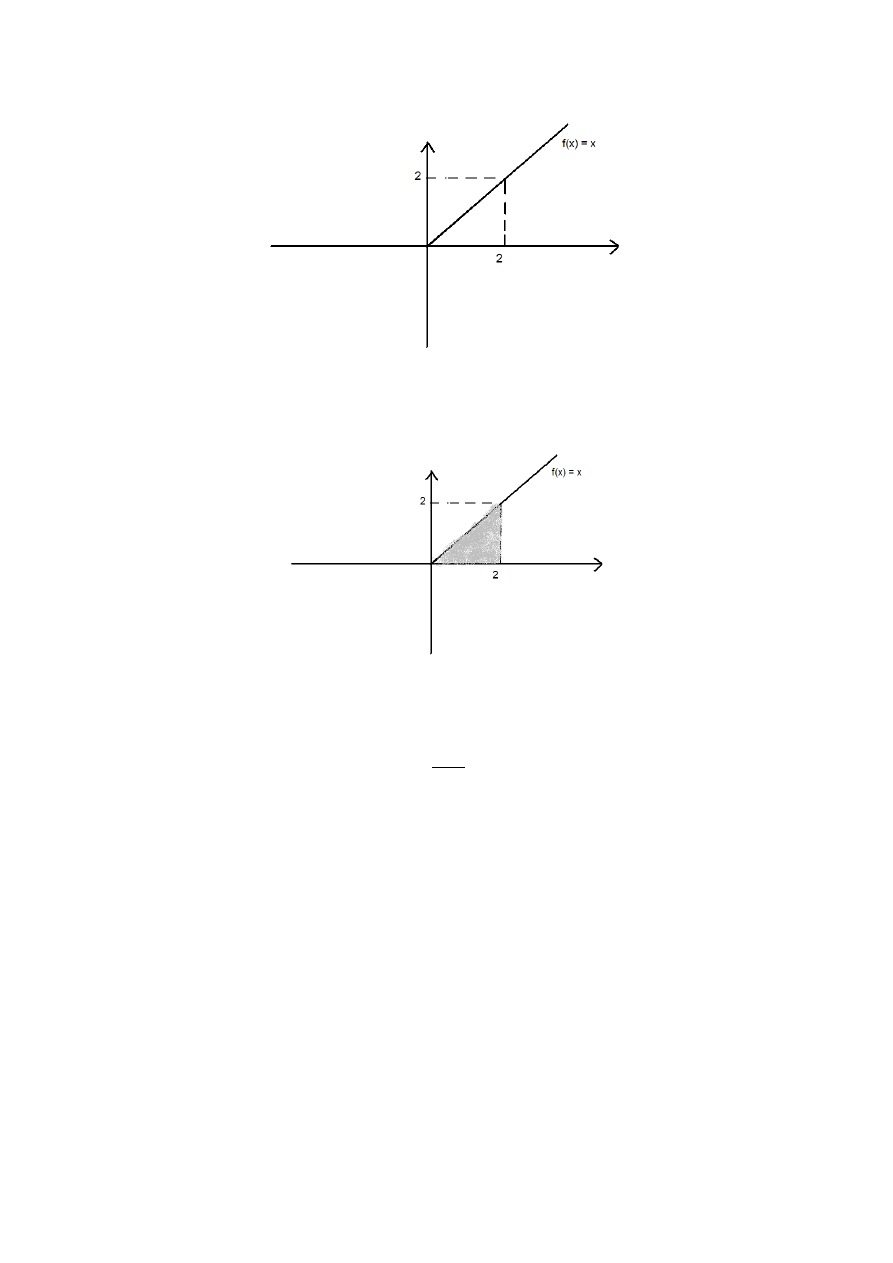
Analiza matematyczna, całki oznaczone

3/36

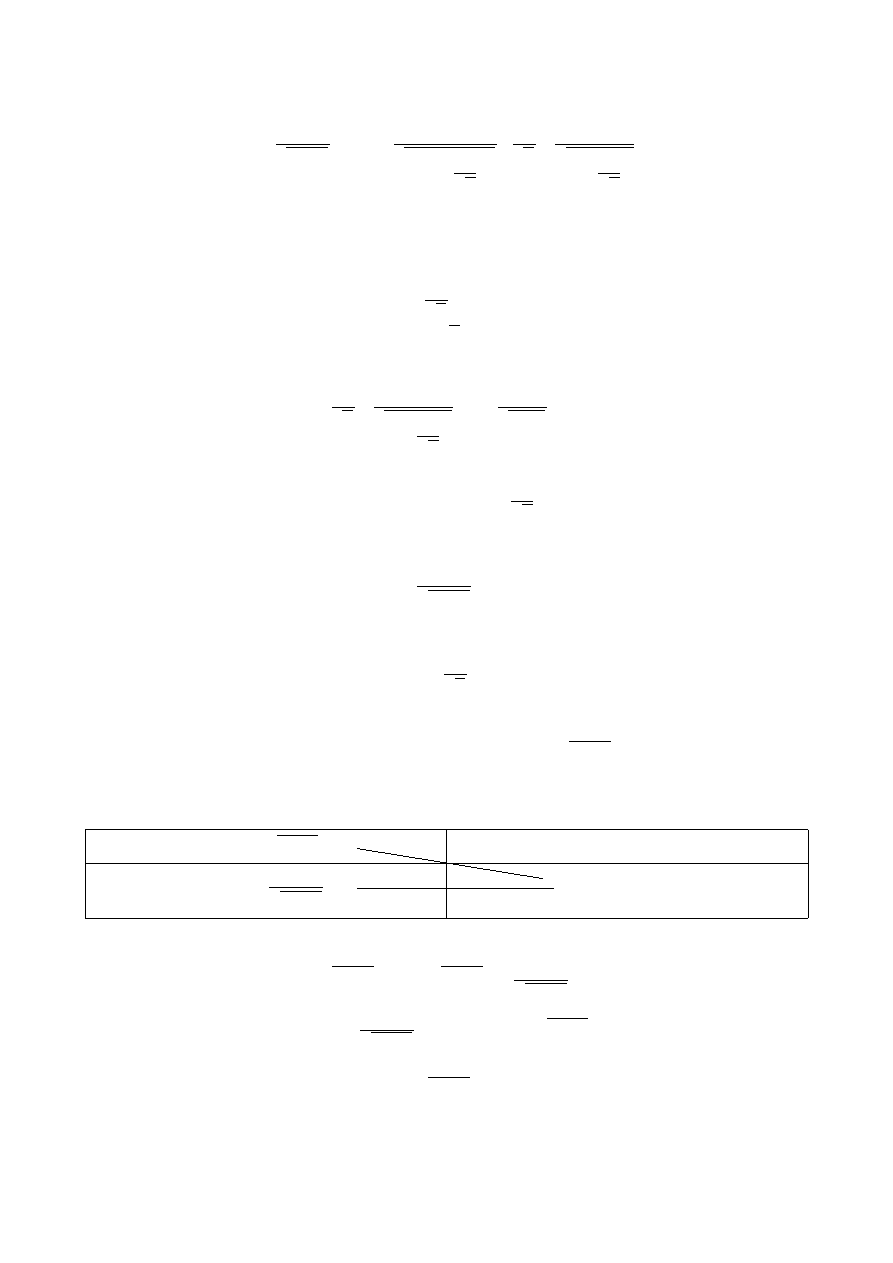
Mamy se układ współrzędnych, mamy se jakiś kawałek funkcji liniowej (ta taka kreska na

ukos), zaznaczyłem jakieś tam dwie liczby, no i wzorek tej funkcji.

Ja się teraz pytam „kurturalnie” - ile wynosi o to, szare pole:

Rewelacyjny rysunek, musicie sami przyznać, a obliczycie bardzo, bardzo prosto. Otóż

możemy sobie zauważyć, że będzie se to trójkąt, o jednym boku równym 2, o drugim równym a i
też 2. Ponieważ jest to trójkąt prostokątny, więc już krzyczymy „Yes, yes, yes”:

P=

2∗2

2

=

2

Prosto, do cholery. Ale ja zrobię ulubioną rzecz przez wykładowców, czyli „zagmatwam

sposób rozwiązania”.

Ktoś se kiedyś, pewno jakiś Newton czy Reimann, odkrył, że:

pole pod wykresem funkcji=...=F  b−F  a *

Ale nam to wyjaśniło, normalnie, kurwa, brawo, i jeszcze jakieś kropki (zaraz się nimi zajmiemy).

Najpierw, czym jest b i a: są to skrajne argumenty, b – prawy, a – lewy. Pojedźcie stronę wyżej. W

tym przykładzie b będzie się równać 2 (bo pole ogranicza x = 2 z prawej strony), zaś a = 0 (z lewej

ogranicza go x = 0).

Wiemy, że:

∫

f  x  dx=F  xC

mówiąc inaczej – całka „wypluwa” nam jakąś funkcję razem z C.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

4/36

Więc to nasze F b będzie równe:

∫

f  x =F  x C=(podstawiamy za x - b) F b

Podobnie F a  . Cały problem, całe działanie F b−F a  możemy zapisać w ładnej i

eleganckiej formie, którą zwiemy całką oznaczoną:

∫

a

b

f  x  dx

Jezu, ale namotałem. Postaram się odmotać przez rozwiązanie przykładu (a potem

prosiłbym o przeczytanie raz jeszcze tego, co napisałem).

Linia, która ogranicza to szare pole z góry, to wykres takiej funkcji:

f  x =x

Widzimy dodatkowo, że z lewej strony to pole jest ograniczone przez:

x=0

Zaś z prawej:

x=2

Skoro znamy „namiary” na linie, które ograniczają nam ten szary obszar, to obliczymy se teraz

całkę:

∫

f  x  dx=

∫

x dx=

x

2

2



C

To

x

2

2

to jest nasze F  x  („scałkowana” funkcja, która ogranicza nasze pole od góry; brak

stałej C zara wyjaśnimy).

Po raz kolejny – z lewej strony ogranicza

x=0

, zaś z prawej:

x=2

, więc:

pole pod wykresem funkcji=...=F  to, co ogranicza z prawej−F to, co ogranicza z lewej

więc obliczmy:

F 2−F 0=[

x

2

2

]

2
0

=

2

2

2

−

0

2

2

= 4

2

=

2

Właściwie, są to zapisy równoważne – te dwie liczby po prawej stronie

nawiasu kwadratowego oznaczają „podstaw to, co siedzi na górze, wylicz, podstaw to, co na dole,
wylicz, odejmij”.

Autor: vbx

(c) 2010

F (x) to jest po prostu jakiś

wzorek, funkcja, gdzieś tam

będzie gołe x, za które po

prostu podstawimy b.

Analiza matematyczna, całki oznaczone

5/36

Czy wynik, liczba 2 czegoś nie przypomina? Obliczyliśmy po raz pierwszy całkę

oznaczoną. Jeżeli zbyt zamotałem i nic już nie wiecie, to obliczymy raz jeszcze, korzystając z
zapisu:

∫

a

b

f  x  dx

Korzystając z danych w zadaniu:

∫

0

2

x dx

(nad wężykiem zawsze powinna być liczba większa od tej pod wężykiem)

Całkując:

∫

0

2

x dx=[

x

2

2

]

2
0

Idziemy dalej:

[

x

2

2

]

2
0

=

2−0=2

co już wcześniej wyliczyliśmy i co jest polem zakreślonego obszaru.

Zauważmy, że tutaj nie ma sensu mieszać w to stałej całkowania C, bo nawet jak, to:

∫

0

2

x dx=[

x

2

2



C ]

2
0

=

2C −0C =2C−C =2

Żadnych korzyści, a pomylić się jest łatwiej, o wiele łatwiej.

Autor: vbx

(c) 2010

całkujemy

Analiza matematyczna, całki oznaczone

6/36

Dla wprawy – kolejny przykładzik:

Naszym zadaniem jest obliczenie pola, gdzie z lewej strony pilnuje nas 1, z prawej – 3.

Wzorek na funkcję, która ogranicza nas z góry:

f  x =x

2

Wiedząc, że pole (w tak prostym przypadku):

∫

a

b

f  x  dx ->

∫

1

3

x

2

dx

obliczymy se:

∫

1

3

x

2

dx =[

x

3

3

]

3
1

=

3

3

3

−

1

3

3

=

27

3

−

1
3

= 26

3

=

8

2
3

Patrz Pan, w szkole średniej nie do pomyślenia, by wyliczyć takie pole, a my chwila, moment,

znaleźliśmy haki i zrobione.

Autor: vbx

(c) 2010

całkujemy

Analiza matematyczna, całki oznaczone

7/36

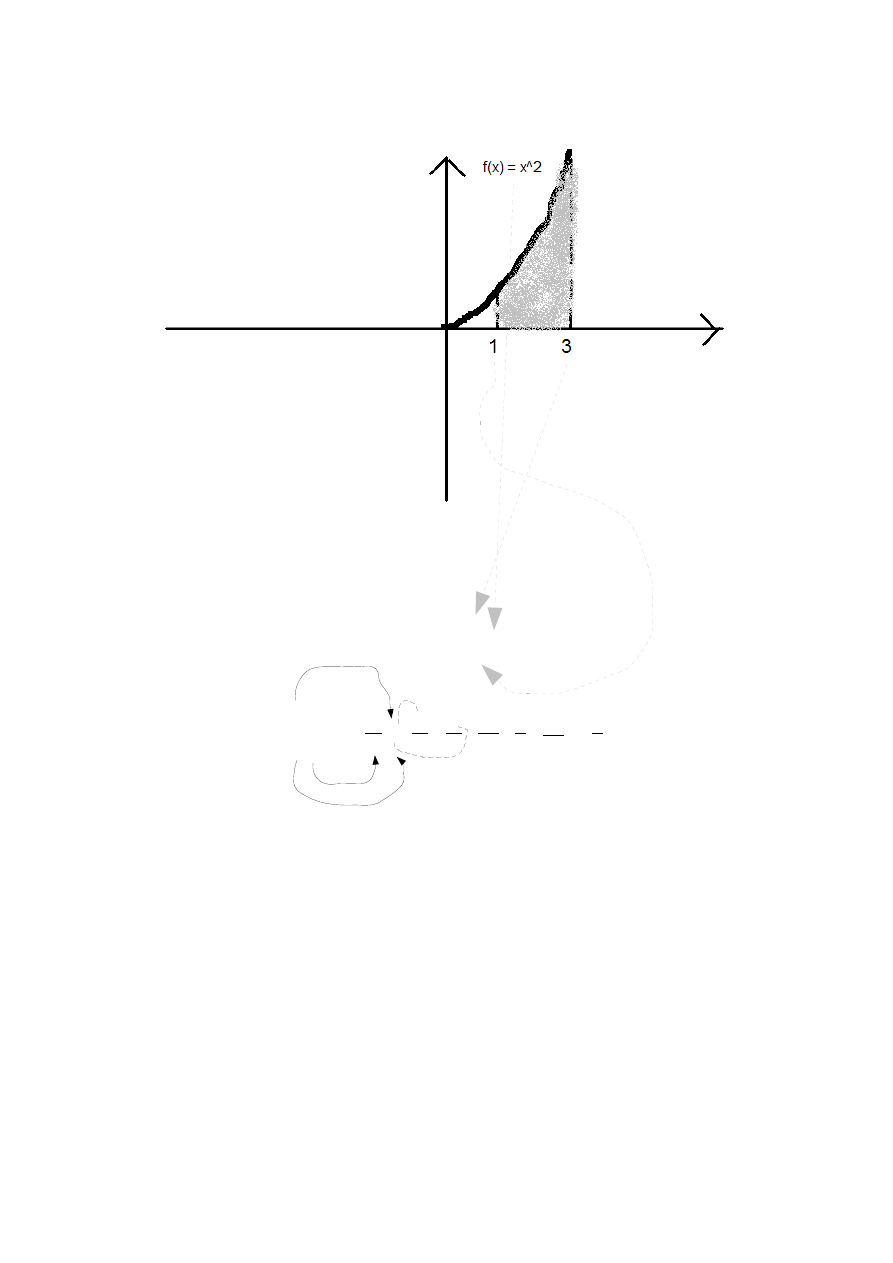
W ramach eksperymentu, policzmy sobie pole takiego zwierzątka:

Najlepiej, abyście sami policzyli, ile takie coś jest równe, a potem sprawdzili.

Otóż, jak widzimy, mamy sobie takie ładne hiperbole. Obliczymy pole tego szarego obszaru.

Na dole ogranicza nas funkcja f  x =

−

1

x

. Z prawej strony straszy dwójka, z lewej – jedynka.

Więc rozwiążmy:

∫

1

2

f  x  dx=

∫

1

2

−

1

x

dx

W całce oznaczonej możemy robić prawie te same numery (prócz całkowania przez

podstawianie, o czym za kilka ładnych momentów), co przy „normalnych” całkach, czyli np. Stałe
wyrzucać przed nawias. Ot, tak jak tutaj:

∫

1

2

−

1

x

dx=−

∫

1

2

1

x

dx

z tablic wiemy, ile wynosi całka z

1

x

- jest to logarytm naturalny, a ponieważ i 2, i 1 to liczby z

pewnością dodatnie, to my możemy zapisać logarytma bez modułu:

∫

1

x

dx=ln x

obliczając:

−

∫

1

2

1
x

dx=−[ln x ]

2
1

=−

ln 2−ln 1=−ln 2≈−0,6931...

Hmm... normalnie, fajnie, koniec przykładu i fajrant.

Jedna rzecz mnie jednak dziwi. Tak, jak rzadko pociągi u nas rozpędzają się do 300 km/h,

tak rzadko kiedy znajdujemy ujemne pola. Aczkolwiek, w tym przypadku, jest ono uzasadnione.

Otóż, jeżeli mamy za zadanie „obliczyć pole pod wykresem funkcji”, to to, co jest „nad”

osią OX, jest dodawane, a to, co pod – odejmowane.

Autor: vbx

(c) 2010

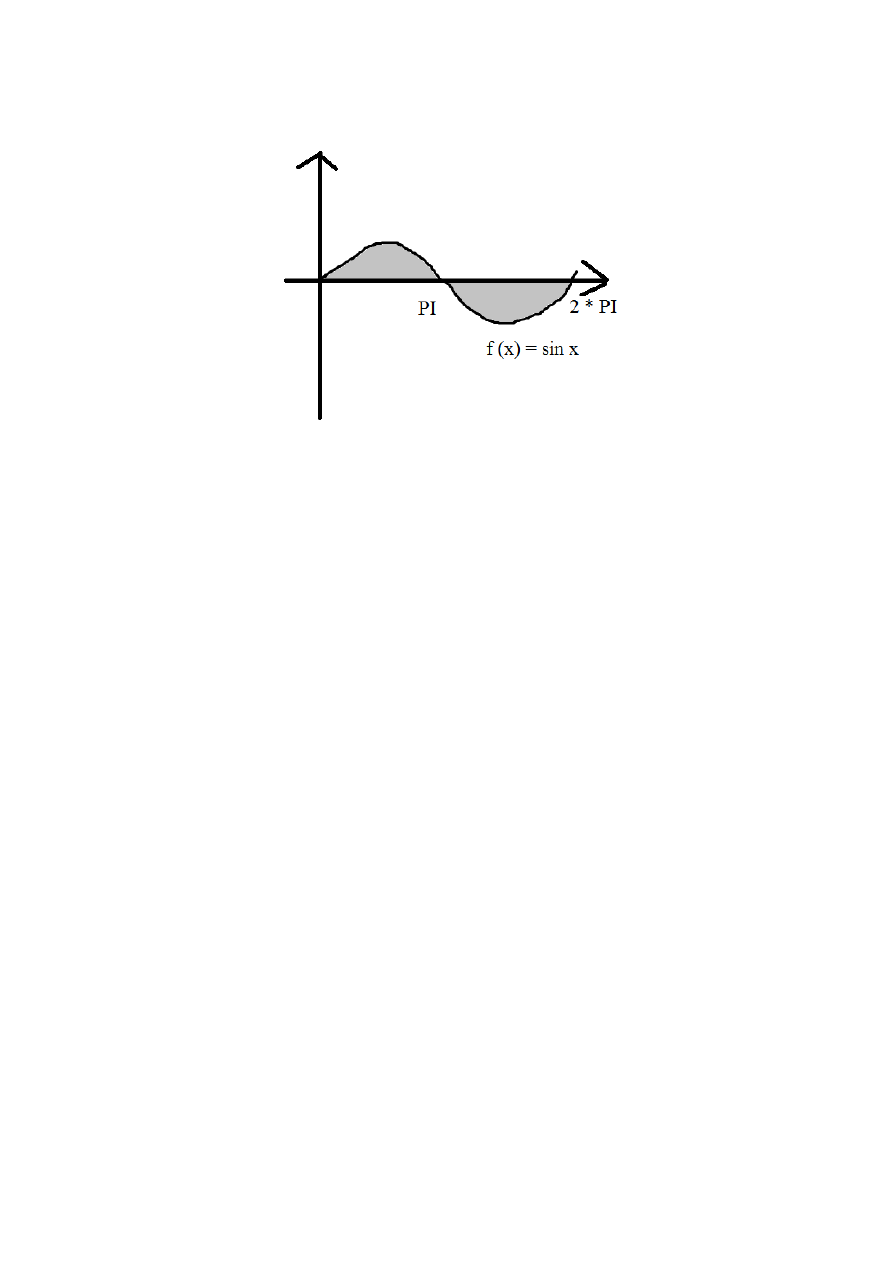
Analiza matematyczna, całki oznaczone

8/36

Nie wierzycie? To obliczymy kolejne „pole pod wykresem”.

Ten profesjonalny wykres przedstawia wykres funkcji sin x. Jeżeli dobrze pogłówkujemy,

widzimy mniej więcej, że ten garb nad osią iksów jest taki sam, jak pod (jak nie wierzycie, bo
rysunek jest do dupy – to spójrzcie w Google). W związku z tym, pole pod wykresem tej funkcji od
0 do 2π powinno wynieść 0 (no bo pole nad osią jest takie samo, jak pod osią). Sprawdźmy.

Liczymy całkę w granicach (tak się mówi profesjonalnie) od 0 do 2π, co wygląda

następująco.

∫

0

2π

sin x dx

Tablice już podpowiedziały, co jest całką sinusa, więc:

∫

0

2π

sin x dx=[−cos x ]

2π

0

=−

cos2π −−cos 0=−1−−1=−11=0

No cóż, zgadza się. Ale czy to oznacza, że licząc coś, co jest pod iksami, musimy sobie

wiecznie „zamieniać” minusy na plusy, by uzyskać interesujący nas efekt?

Nie, bo teraz zobaczymy drugą twarz całek oznaczonych, pewien trik, który umożliwia

liczenie pól dowolnych kształtów.

Autor: vbx

(c) 2010

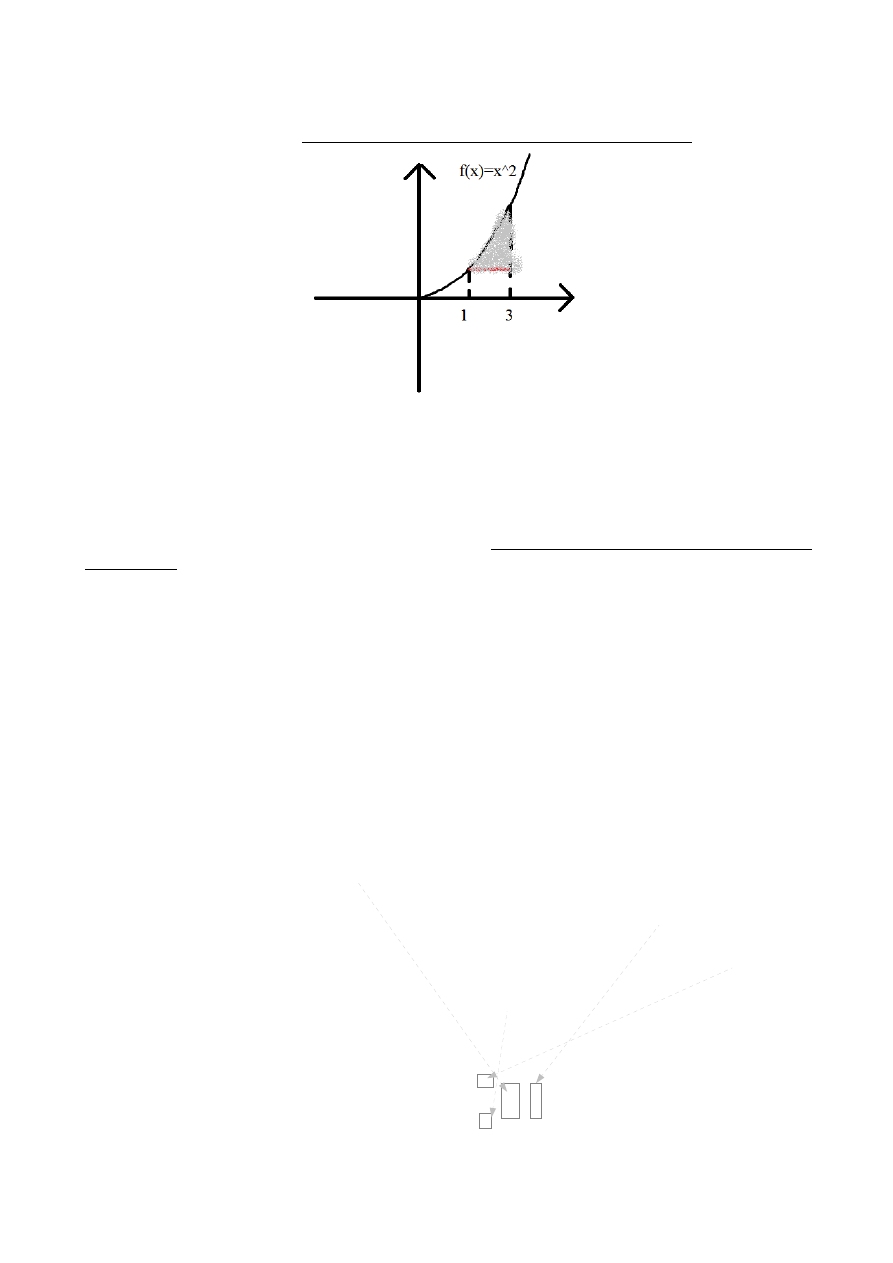
Analiza matematyczna, całki oznaczone

9/36

Gdyż teraz policzymy pole obszaru, ograniczonego jakimiś tam równaniami.

Takie pole, z góry ograniczone wykresem funkcji f  x=x

2

, z prawej x=3 , z lewej

x=1 . „Doszedło” dodatkowe ograniczenie – mianowicie, y=1 z dołu (równe jeden, bo

f 1=1 , a uznajmy, że tak kreska czerwona jest równoległa do iksów)... Rany boskie, co z tym

zrobić.

Przedstawmy sobie taki już porządny wzorek na pole obszaru, ograniczonego funkcjami (vel

równaniami):

∫

to, co po lewej ogranicza

to, co po prawej ogranicza



funkcja, która pilnuje nas z góry−ta funkcja, która ogranicza rysunek z dołu dx

co też w podręcznikach jest opisane jako:

∫

a

b



f  x −g  x  dx

Wcześniej (tzn. bez przykładów, w których pole wychodziło ujemne) nie było potrzeby

„uznawania” g (x) – zauważmy, że od dołu „pilnowała” nas oś OY (o równaniu y=0 ). W
związku z tym, odejmowalibyśmy zero, co jest równie sensowne, jak te wszystkie „pomoce
dydaktyczne”...

Wróćmy do przykładu, rozpiszmy i wyliczmy wszystko:

•

z góry ogranicza nas f  x =x

2

•

zaś z dołu

y=1

, właściwie – jest to funkcja stała o wyglądzie g  x=1

•

po prawej gorylem, stojącym na bramce do dyski jest pionowa kreska w trójce: x=3

•

zaś po lewej ubezpiecza go kreska w jedynce:

x=1

No i jadąc dalej:

∫

a

b



f  x −g  x  dx=

∫

1

3



x

2

−

1 dx

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

10/36

Obliczmy se na spokojnie całkę nieoznaczoną, która siedzi w środku. Krótko mówiąc,

zrobię se tak:

Całka – liniowe zwierzątko, więc ja sobie zrobię o tak:

∫



x

2

−

1 dx=

∫

x

2

dx−

∫

1 dx

Korzystając z tablic, obliczam całkę (dosyć nieładnie, bo zapominam o stałej C, ale co mi tam):

∫

x

2

dx −

∫

1 dx=

x

3

3

−

x

Wrzucając to w całkę oznaczoną, mogę se ją bez problemu policzyć:

∫

1

3



x

2

−

1 dx=[

x

3

3

−

x ]

3
1

=

3

3

3

−

3−

1
3

−

1=6

1
3

=19

3

(chyba)

Obliczyliśmy pole pod wykresem funkcji pole obszaru, które jest ograniczone jakimiś tam

równaniami.

Radzę się nie przejmować – póki co i tylko w tym dziale – tym, co zaznaczyłem „kułkami”:

∫

to, co po lewej ogranicza

to, co po prawej ogranicza



funkcja bla bla bla dx

obecnie możemy uznać, że będą to liczby. Jednakże, nastaną dni sądne, w których

„wężyków” (symboli całek) będzie odrobinę więcej, a wtedy to już będzie przesrane.

Więc widzimy – żeby obliczyć pole pod wykresem jakiejś funkcji, trzeba sobie scałkować tą

funkcję – wyskoczy nam nowy „przepis, co zrobić z iksem” (po prostu jakaś nowa funkcja).
Następnie, bierzemy liczbę, która nas ogranicza z prawej strony i wrzucamy w nową funkcję,
skrzętnie notujemy wartość. Teraz – liczbę z lewej strony, wrzucamy, notujemy – i to odejmujemy
od pierwszej zanotowanej wartości. I po robocie.

Żeby obliczyć jakiś obszar, od tego, co jest pod całką, odejmujemy wzorek

funkcji/równania/wykresu/byle czego (ostatnie nie gwarantuje sukcesu na kolokwium) tego, co nas
ogranicza z dołu. Resztę robimy analogicznie – całkujemy, podstawiamy, odejmujemy i mamy
wynik.

Pod koniec zajmiemy się obliczaniem bardziej zaawansowanych obszarów. Natomiast teraz

przejdziemy do pewnej różnicy w obliczaniu całek oznaczonych.

Jak pamiętacie, możemy całkować przez części oraz przez podstawienie. Całkowanie przez

części w przypadku całek oznaczonych jest nudne i takie samo, jak w nieoznaczonych – tylko na
końcu tradycyjnie – podstawiamy i odejmujemy. W przypadku jednak całkowania przez
podstawienie – mamy problem.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

11/36

Całki oznaczone – obliczanie przez podstawienie

Załóżmy, że mamy do policzenia taką ambitną całkę oznaczoną:

∫

0

π
2

sin 2x dx

Na początek – zrobimy klasycznie, czyli najpierw obliczymy całkę nieoznaczoną, następnie

– podstawimy i odejmiemy.

I SPOSÓB

Całkę postaci

∫

sin 2x dx

obliczymy sobie przed podstawienie. Podstawimy sobie tak:

2 x =t

Musimy się pozbyć dx, więc obustronnie różniczkujemy:

2 dx=dt

Dzięki czemu wiemy, co podstawić za dx:

dx=

dt

2

Już ładnie wykonamy sobie podstawienie:

∫

sin 2x dx=

∫

sin t

dt

2

I już dalej rozwiążemy tego zawodnika (pomijając stałą całkowania C):

∫

sin t

dt

2

=

1
2

∫

sin t dt=

1
2

∗−

cos t=

−

cost

2

„Przywracając” zmienną x wiemy, że:

∫

sin 2x dx=

−

cos 2 x

2

Wykorzystamy tą wiedzę do obliczenia całki oznaczonej (wszelkie stałe wyrzuciłem przed całkę):

∫

0

π
2

sin 2x dx=−

1
2

[ cos2 x ]

π

2
0

=−

1
2



cos

2∗π

2

−

cos 2∗0=

=−

1

2



cos π −cos0=−

1
2

−

1−1=−

−

2

2

=

1

Wyliczona przez nas całka równa się 1. Sprawdzimy to drugim, takim bardziej eleganckim

sposobem, w którym niejako jednocześnie się podstawia i całkuje.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

12/36

II SPOSÓB

My już na tym etapie dokonamy podstawienia. Widzimy, że można se ładnie w tej całce:

∫

0

π
2

sin 2x dx

podstawić:

2 x =t

i zróżniczkować:

2 dx=dt => dx=

dt

2

zupełnie jak poprzednio.

Już wstawiliśmy – to obliczmy:

∫

0

π
2

sin 2x dx=

1
2

∫

0

π
2

sin t dt=−

1
2

[cost ]

π
2
0

=−

1
2



cos

π
2

−

cos0=

1

2

Hmm... jak pewno zauważyliście, jest pewien problem. Wynik uzyskany powyżej jest inny od tego,

co nam wyszedł z I sposobu. Wniosek taki – albo się rąbnęliśmy stronę temu, albo teraz.

Odpowiem, że teraz – i to w tych miejscach:

=

1
2

∫

0

π
2

sin t dt=−

1

2

[cost ]

π

2

0

=

W chwili, gdy podstawiamy i mamy zamiar od razu obliczać całkę oznaczoną, dochodzi do

czegoś takiego, jak zmiany granic całkowania. Zmienia się de facto funkcja, zmieniają się również
granice całkowania.

To trochę tak, jakby z jakiegoś powodu powołano nowego selekcjonera piłkarskiej

reprezentacji. Nawet jak trenerem by został i Mourihno, to i tak zmieni se skład, godziny treningów.
Nowy trener mówi „Nie, Panowie, nie będziemy trenować od 10 do 10:10, a potem czas wolny,
tylko my zmienimy granicę treningów od 9 do 16”.

Więc – skoro nowa funkcja, to i nowe granice całkowania. Proste.

A czemu tak? Nie mam pojęcia, ale ma to związek z tym, że my właściwie podstawiamy

nową funkcję i niejako całkujemy zupełnie co innego. A żeby to miało ręce, nogi i zgadzało się z
przykładem, to wymyślamy nowe granice.

Należy obliczyć „nowe” granice całkowania, a jest to proste. Wracamy do podstawienia:

2 x =t

Za iksa wstawimy górną granicę całkowania – wyliczymy nową:

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

13/36

2∗

π

2

=

π

Tak samo z dolną:

2∗0=0

Wróćmy i naprawmy błąd:

=

∫

0

π
2

sin 2x dx=

1
2

∫

0

π

sin t dt=−

1
2

[ cos t ]

π
0

=−

1
2



cos π−cos 0=1

Jak najbardziej – bardzo ładnie.

Dla wprawy – obliczymy sobie przykład z nieocenionej książeczki tandemu Gewert i

Skoczylas.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

14/36

Zadanie 1

Obliczyć podaną całkę oznaczoną (dokonując wskazanych podstawień):

∫

0

1

x



1x dx ,



1 x=t

Wybrałem taki przykład, bo nie chciało mi się kombinować z podstawianiem. Mam

nadzieję, że z „technicznego” punktu widzenia co nieco wyjaśniłem w pomocy dotyczącej całek
nieoznaczonych (gdzie masa przykładów polegała na podstawianiu).

Okej, najpierw (dla pewności) sprawdźmy, czy wskazane podstawienie ma sens.
Mamy



1 x=t (*)

więc różniczkując:

1

2



1x

dx=dt

i stąd dx jest równe:

dx=2



1x dt

a wiedząc (*), ostatecznie:

dx=2∗t dt (**)

Obliczmy jeszcze, ile w tym podstawieniu jest równe x (obustronnie podnosząc do kwadratu):

| 1x |=t

2

Moduł możemy pominąć, bo w tych granicach nic się złego nie stanie:

x=t

2

−

1

(***)

Wrzucając w odpowiednie miejsca (*), (**) i (***), mamy:

∫

0

1

x



1x dx =

∫

...

...



t

2

−

1∗t∗2∗t dt=2∗

∫

...

...



t

4

−

t

2



dt

Musimy pamiętać o zamianie granic całkowania.

Górna granica będzie równa:



11=



2

Zaś dolna:



10=1

Ostatecznie, nasze zwierzątko do wyliczenia, lampiąc się na nas swoimi dużymi oczkami, będzie

tak się prezentować:

2∗

∫

1



2



t

4

−

t

2



dt

a musicie sami przyznać, że całkowanie takiego zawodnika jest dużo prostsze i w czasach, gdy

nauka często koliduje z czasem wolnym – widzimy, że lepiej sprowadzić sobie całkę do prostej

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

15/36

postaci, którą możemy rozwalić razem z tablicami.

Nie owijając dalej w bawełnę, skończmy ten przykład. Po scałkowaniu:

2∗

∫

1



2



t

4

−

t

2



dt=2∗[

t

5

5

−

t

3

3

]



2

1

=

sobie kurturalnie policzymy:

=

2∗[



2

5

5

−



2

3

3

−

1

5

5

−

1

3

3

]=

=

2∗[

2

5
2

5

−

2

3
2

3

−

1

5

5

−

1

3

3

]=

=

2∗[

4



2

5

−

2



2

3

−

3

15

−

5

15

]=

=

2∗[

2



2

15



2

15

]=

=

4∗



21

15

Ostatecznie, wyliczyliśmy, że

∫

0

1

x



1x dx =

4∗



21

15

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

16/36

Dzielenie obszarów całkowania

Na końcu (tej strony, oczywiście), zgodnie z obietnicą, zajmiemy się obliczaniem

ciekawszych obszarów całkowania, które „składają” się nie z jednej czy dwóch funkcji, ale np. z
trzech czy czterech.

Jak widzicie, jeżeli umie się obliczać całki nieoznaczone – to prawie umie się liczyć całki

oznaczone. Różnica polega tylko na podstawieniu tych „granicznych” wartości na końcu i
odpowiednim odjęciu.

Jednym z zastosowań, które tutaj sobie pokazaliśmy – to liczenie pól. O ile liczenie pola pod

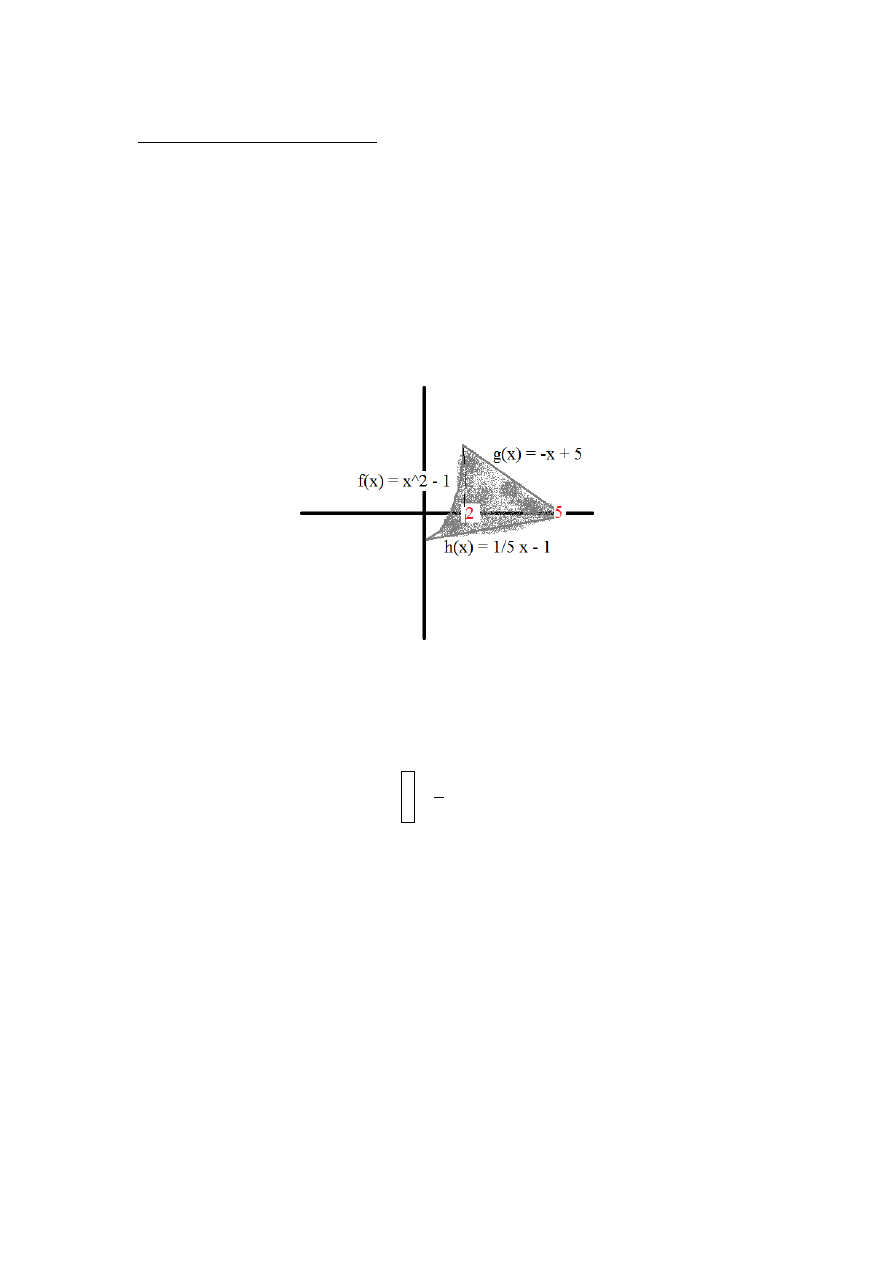
zwykłą funkcją kwadratową, to zaczyna się problem przy, załóżmy, takim zawodniku:

I mamy za zadanie obliczenie pola takiego Pudziana. Jednak problem pojawia się od razu –

zauważmy, że z „góry” ograniczają nas dwie funkcje – najpierw działa funkcja kwadratowa f, a
następnie funkcja liniowa g. Z dołu działa jedna i ta sama funkcja h.

Gdybyśmy chcieli już walnąć wzorka i liczyć całkę, to mamy problem:

∫

0

5

?−

1
5

x −1 dx

bo mamy dwie funkcje, które ograniczają nam obszar z góry.

Ale jest pewien trik, który się zwie – dzielenie obszaru całkowania.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

17/36

Otóż:
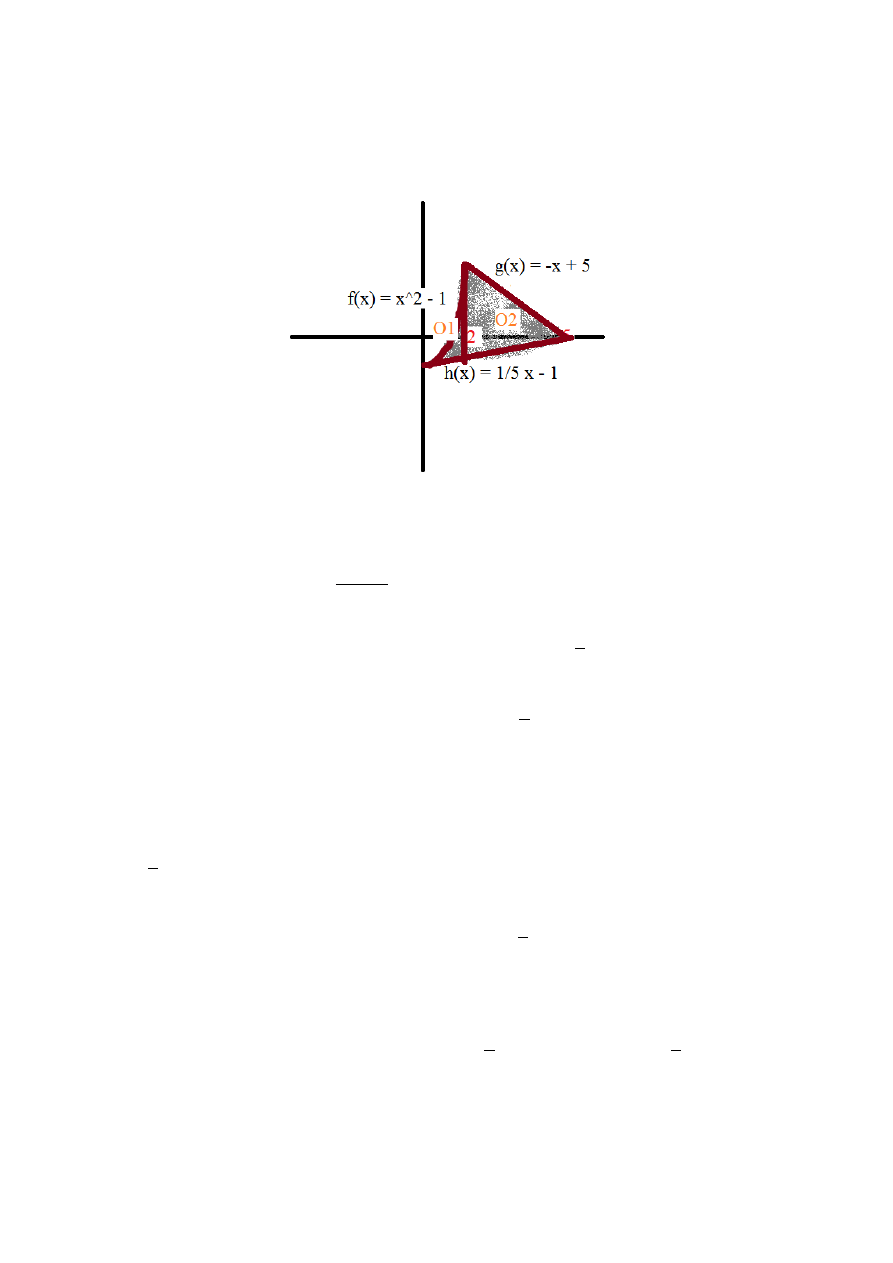
Po pierwsze – dzielimy obszar tak, by była jedna funkcja ograniczająca z góry i jedna z

dołu. W tym przykładzie – możemy to zrobić tak:

Po prostu podzieliłem sobie nasze „pole” na dwa – po to, by było łatwiej sobie policzyć

pole. Obszar, który z góry jest ograniczony przez f  x =x

2

−

1 , oznaczyłem sobie O1. Zaś ten,

który z góry ogranicza tam g  x=−x5 , oznaczyłem se jako O2.

Po drugie – liczymy sobie osobno dane pola, a następnie – dodajemy je i finito:

Nasz pierwszy obszar trzymają w ryzach – po lewej bramkarz numer 0 ( x=0 ), po prawej

bramkarz numer 2 ( x=2 ). Z dołu ogranicza nas funkcja h  x =

1
5

x−1 , zaś z góry – funkcja

kwadratowa f  x =x

2

−

1 . W związku z tym, obliczając pole O1, zakurwiamy taką całką:

∫

0

2

[

f  x−h x ]dx=

∫

0

2

[

x

2

−

1−

1
5

x−1] dx *

i ją sobie zostawimy, obliczając później.

By obliczyć pole O2, musimy wiedzieć, co nam ten obszar ogranicza z lewej strony (tym

razem

x=2

, bo cały ten obszar „zaczyna” się dopiero tutaj), z prawej (

x=5

), z dołu (nadal

h  x =

1
5

x−1 ), a z góry tym razem g  x=−x5 . Obliczymy to wszystko, obliczając takie

zwierzątko:

∫

2

5

[

g  x −h  x]dx=

∫

2

5

[−

x5−

1
5

x−1] dx **

Ostatecznie, korzystając z powyższych zapisów – pole całego obszaru (a, nazwę go O) będzie się

równać:

pole obszaru= poleO1 pole O2=

∫

0

2

[

x

2

−

1−

1
5

x−1]dx 

∫

2

5

[−

x5−

1
5

x−1]dx

Najlepiej byłoby dodać te dwie całki i zapisać pod jedną. Problemem są granice całkowania – są

one różne i kompletnie się nie nadają do spółkowania.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

18/36

Powolutku obliczymy obydwie całki. Najpierw zaczniemy od (*), czyli:

∫

0

2

[

x

2

−

1−

1
5

x−1]dx

zrobimy porządek pod nawiasem kwadratowym:

∫

0

2



x

2

−

1
5

x  dx

następnie kulturalnie scałkujemy:

∫

0

2



x

2

−

1
5

x  dx=[

x

3

3

−

x

2

10

]

2
0

i wyliczymy:

[

x

3

3

−

x

2

10

]

2
0

=

2

3

3

−

2

2

10

−

0
3

−

0

10

=

8
3

−

4

10

= 34

15

Nie mam najmniejszego pojęcia, czy taki faktycznie jest wynik, ale jestem takim leniem, że i nawet

tego nie chce mi się dokładnie sprawdzać.

Weźmy się za obliczanie pola O2 (**). Jeżeli ktoś bardzo mądrze zauważy – to O2 jest

trójkątem, którego pole jest dziecinnie proste do obliczenia (jak się wyliczy współrzędne
wierzchołków). Ja jednak jestem ludziem, który, kupując bułki w delikatesach, 50 metrów ode
mnie, używa samochodu, więc całe to pole obliczymy, przyjebując se całkę.

∫

2

5

[−

x5−

1
5

x−1]dx

Trochę posprzątamy po imprezie:

∫

2

5

−

6
5

x6 dx

obliczymy całkę:

∫

2

5

−

6
5

x6 dx=[−

6 x

2

10



6 x ]

5
2

Zobaczmy, jaka będzie wartość tego zwierzątka w nawiasie, gdy za iksa wstawimy 5:

−

6∗5

2

10



6∗5=−1530=15

i dwójeczkę:

−

6∗2

2

10



6∗2=−2,412=9,6

Wiadomo, co od czego odjąć (wartość nawiasa od 5 – wartość nawiasa od 2):

Autor: vbx

(c) 2010

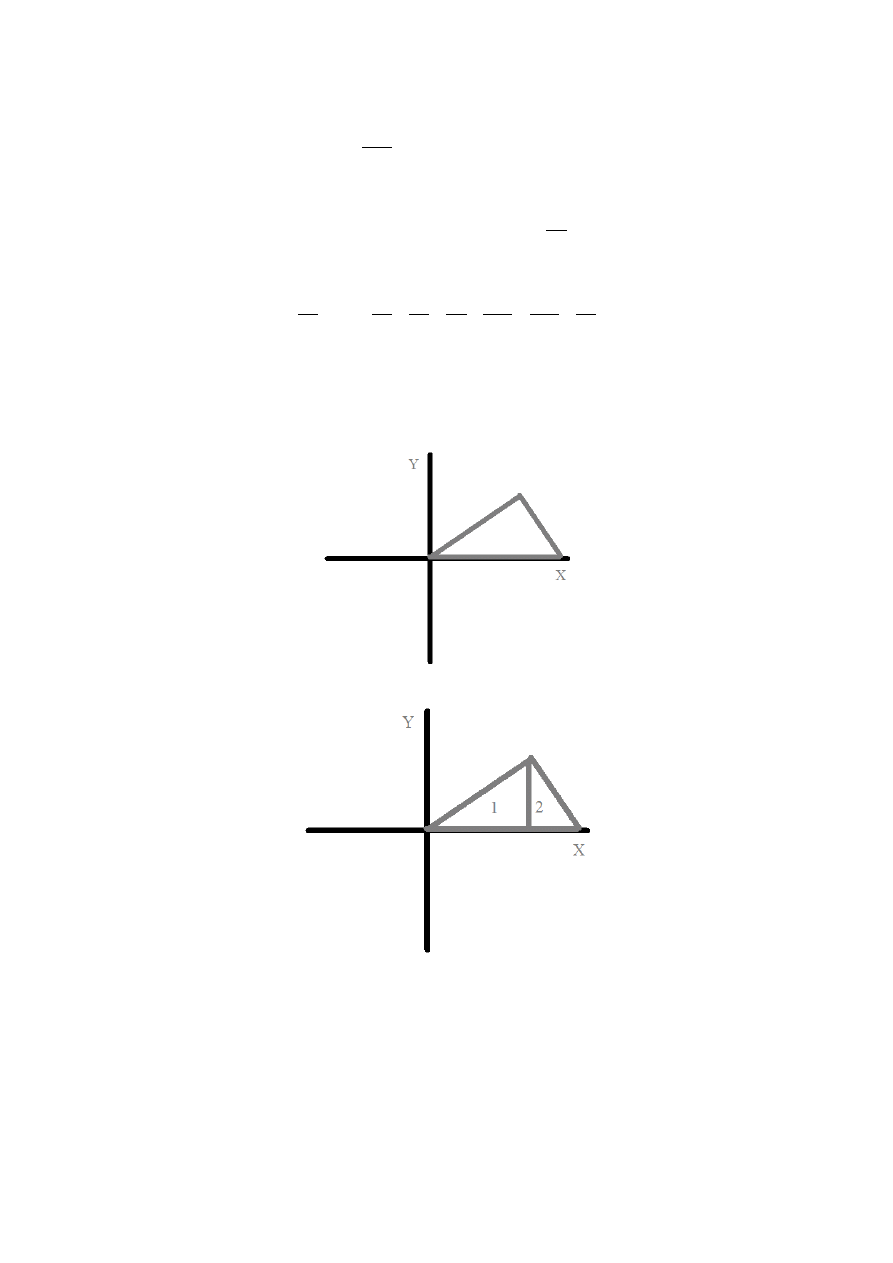
Analiza matematyczna, całki oznaczone

19/36

[−

6 x

2

10



6 x ]

5
2

=

15−9,6=5,4

Dlatego my już możemy wyliczyć pole całego obszaru:

pole obszaru= poleO1 pole O2=

34
15



5,4

Ostatecznie:

34
15



5,4=

34
15



54
10

=

68
30



162

30

=

230

30

=

23

3

I koniec mocowania się z tym przykładem. Obliczyliśmy pole danego obszaru, który był taki trochę

„nieregularny” - po prostu dany „bok” ograniczały nam dwie różne funkcje.

Przy obliczaniu obszarów stosuje się pewien numer. Załóżmy, że mamy taki obszar:

Pomijając fakt, że to tylko trójkąt, możemy go podzielić na dwa obszary całkowania:

i sobie wyliczyć całkę.

Jest jednak pewien numer, który stosujemy, by w ogóle nie dzielić tego obszaru.

Autor: vbx

(c) 2010

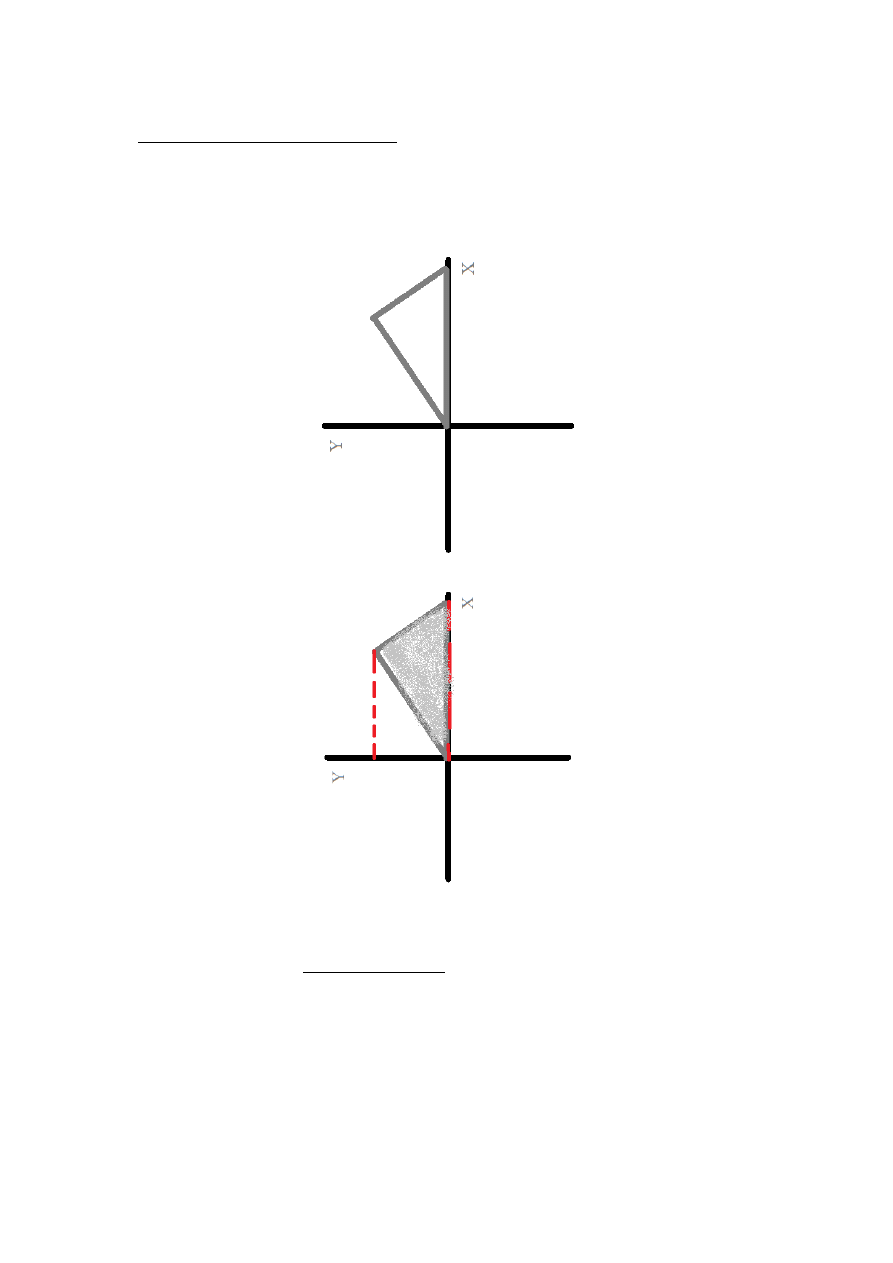
Analiza matematyczna, całki oznaczone

20/36

Zamiana zmiennych niezależnych

Jak widać na przykładzie – musimy stosować dwa obszary całkowania, bo „górę”

przykrywają nam dwie różne funkcje.

Ale spróbujmy przechylić łeb w prawo:

Jeżeli tak na to spojrzymy, to wywnioskujemy, że

czerwone linie wyznaczają nam lewą i prawą granicę całkowania, zaś z góry i z dołu mamy

jakieś dwie funkcje, które ograniczają nam tą szarą plamę oleju.

Gdybyśmy uznali y za zmienną niezależną (tak to się mądrze pisze), to oszczędzamy sobie

w tej chwili dzielenia na dwa obszary, dodawania itd.

Mówiąc obrazowo – możemy sobie „obrócić” obraz o 90 stopni. Może się wtedy okazać, że

tylko jedna „linia” ogranicza nas z góry i jedna z dołu.

Problem polega na tym, że to „obrócenie”, to nie do końca „obrócenie” i że mimo wszystko

– nie warto obracać kartki i rysować wykresu od nowa. Będziemy musieli jakoś matematycznie

Autor: vbx

(c) 2010

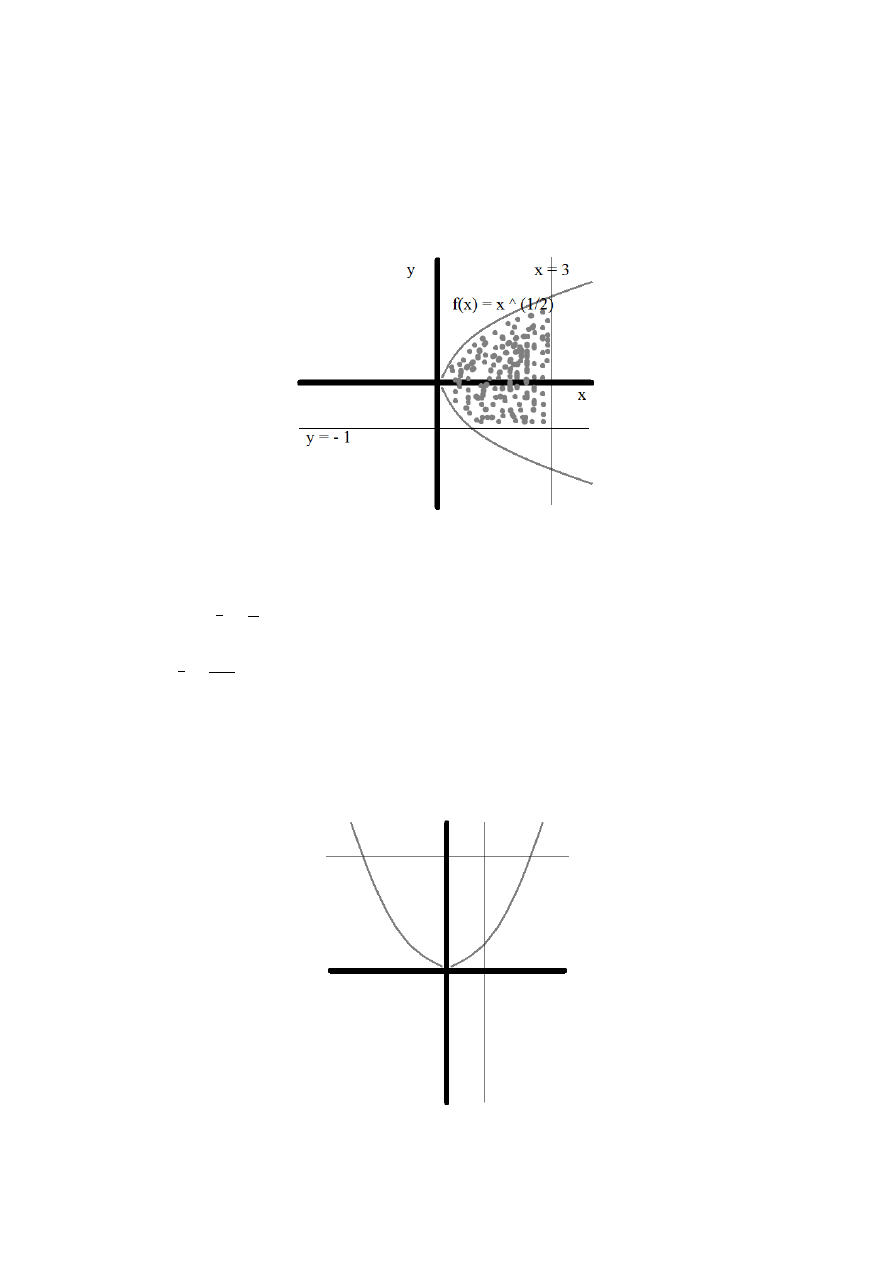
Analiza matematyczna, całki oznaczone

21/36

„obrócić” te linie.

By takie coś zastosować... zastosujemy przykład.
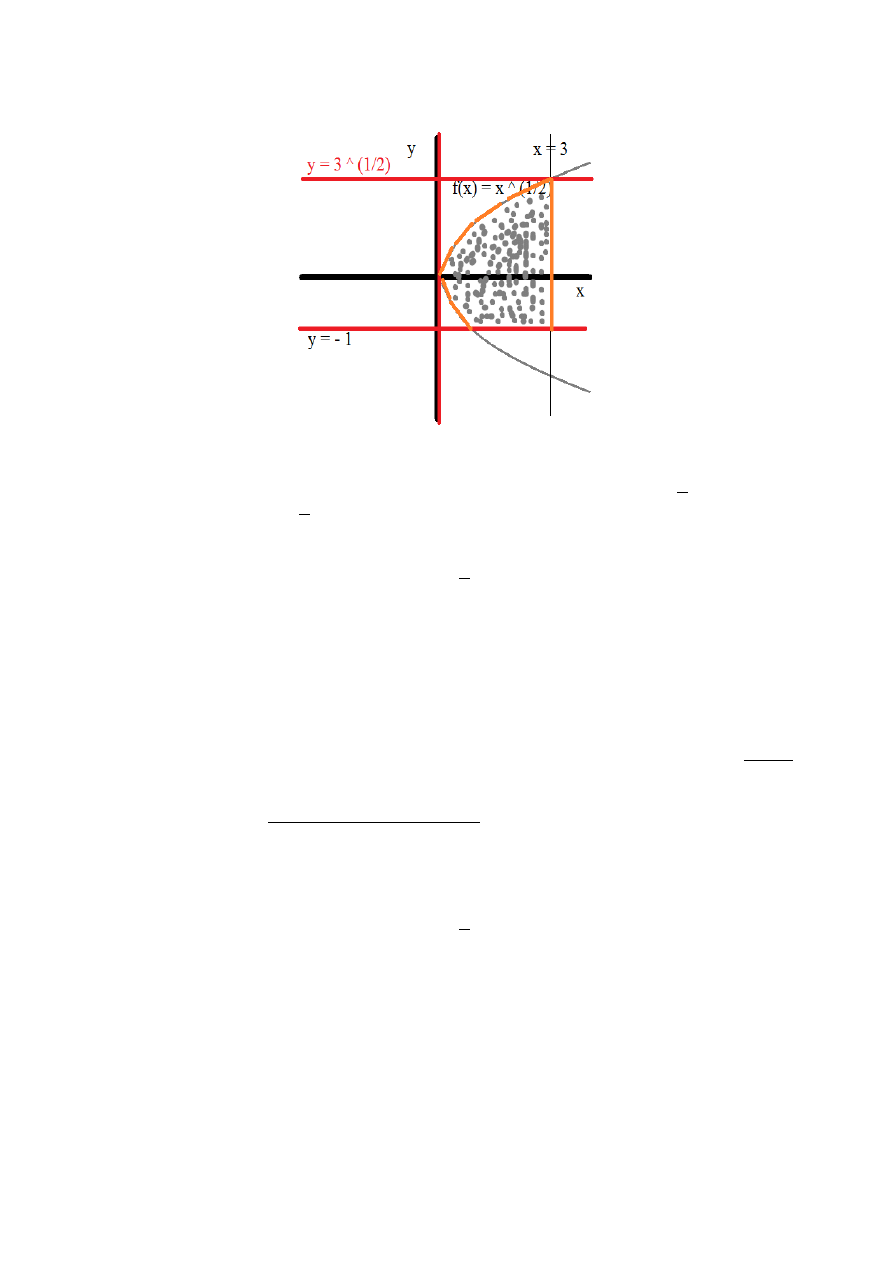
Zadanie (chyba) 2

Obliczyć pole obszaru, ograniczonego prostymi bądź równaniami:

•

y=−1

•

x=3

oraz

•

f  x =x

1
2

=



x (zapisałem tak, bo w Pain... Bardzo Drogim Programie do malowania

wykresów nie da się wstawić symbolu pierwiastka. Wiemy jednak, że

coś

1
2

=



coś

Ilustracja tego przedsięwzięcia jest przedstawiona powyżej.

Oczywiście, możemy podzielić obszar całkowania na dwa i iść podanym kilka stron

wcześniej tropem. My jednak zmienimy zmienną niezależną. Zauważcie, że gdyby „w myślach”
obrócić ten rysunek w lewo:

Autor: vbx

(c) 2010

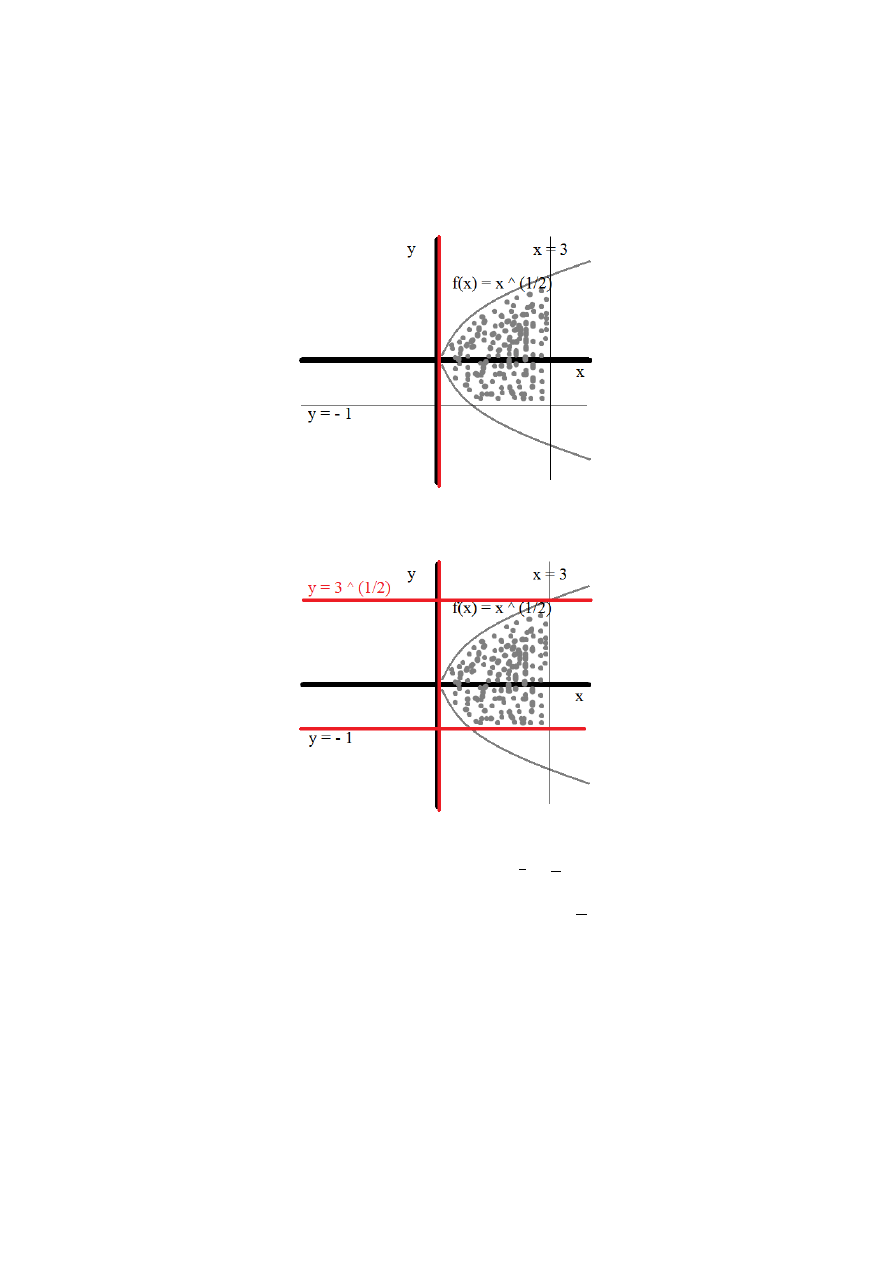
Analiza matematyczna, całki oznaczone

22/36

to wtedy mamy jedną funkcję „ograniczającą” nas z góry oraz jedną – z dołu. Jak już jednak

napisałem – będziemy majstrować na oryginalnym rysunku.

Na początku – dotychczas, całkowaliśmy po x. Teraz, nowość, będziemy całkować po y,

więc zaznaczmy to.

Zmieniamy zmienną niezależną – przynajmniej w teorii.

Następnie, spróbujemy znaleźć linie, które w poziomie ograniczają nasz obszar.

Linie ograniczające obszar w poziomie

Myślę, że wiecie, jak doszedłem do tej kreski y=3

1
2

=



3 , a dokładniej – do jej wzorku.

Widzimy, że siedzi tam, gdzie przecinają się x=3 i y=



x .

W tym momencie... niestety, nie mogę prosić, byście się napili czegoś procentowego, bo

jeszcze przeczytają to nieletni, a ja będę siedzieć. Dlatego, proszę włączyć wyobraźnie.
Przypomnieć sobie, co wspominałem o liniach czy funkcjach ograniczających obszar do tej pory.
Bo będziemy niejako odwracać nasze myślenie o granicach.

Dobra, teraz musimy znać funkcje, które ograniczają nasz obszar w pionie. I uwaga, muszą

mieć postać

x=cośtam

! Jedno znamy: x=3 . Zaś drugą funkcję będziemy musieli poznać.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

23/36

Na pomarańczowo – funkcje, ograniczające nasz obszar z lewej i prawej.

O ile znajdziemy bez problemu wzorek prawej, pomarańczowej linii – toż to x=3 , to

schody zaczynają się przy fragmencie paraboli (tak się mądrze nazywa funkcję



x ). Owszem,

mamy wzorek: f  x = y=



x (y jest zmienną zależną, więc można spokojnie i wymiennie

wypisywać f (x) i y = coś tam... no chyba, że zaczynamy robić cuda, wtedy trzeba uważać). No, ale
właśnie:

y=



x

a my potrzebujemy czegoś postaci:

x=cośtam

a nawet dokładniej to powinien być nawet taki zapis:

g  x=cośtam

gdzie g to jakaś funkcja, zależna od x. Jeszcze prościej – po lewej stronie równania siedzi tylko

x .

Zaś po prawej – jakieś równanie z y.

Szukamy wzorku (równania) funkcji odwrotnej funkcji f. Dokładniejsze zabawy, związane z

funkcjami odwrotnymi, robi się przy okazji granic i pochodnych.

Jak szukamy równania odwrotnego? Prosto.

Szukamy tego odwrotnego pojebańca z takiego czegoś:

y=



x

Wyznaczamy x, obustronnie podnosząc do kwadratu:

y

2

=

x

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

24/36

I po robocie. Znamy teraz wzorek tej lewej, pomarańczowej funkcji, z perspektywy y. Podsumujmy:

•

na górze i na dole (bądź z lewej i prawej, patrząc z perspektywy osi

Y

) ograniczają

nas odpowiednio y=



3 oraz

y=−1

Znamy już granice. Wiemy także, że na wszystko patrzymy z perspektywy osi Y i to po niej

będziemy całkować.

∫

−

1



3



3− y

2



dy

Znamy również funkcje, rządzące tym obszarem.

•

z prawej i lewej (bądź z góry i z dołu, patrząc z perspektywy osi

Y

) ograniczają nas

odpowiednio x=3 i

x= y

2

.

Skoro mamy całkę – to całkujmy:

∫

−

1



3



3− y

2



dy=[3 y−

y

3

3

]



3

−

1

=

3



3−



3−[−3−−

1
3

]=

2



3−

−

8

3

=

2



3

8
3

=

6



38

3

Dla treningu – jak ktoś chce – może sobie bez problemu podzielić obszar całkowania.

Jak zauważyliśmy, zmieniliśmy nieco przykład. Klasycznie, to y zależy od x, to znaczy – w

zależności, jak się zmienia x, zmienia się wartość y. Im więcej węgla i żelaza władujemy w hutę,
tym więcej powstanie stali. Jeżeli nadmuchamy balonik (i pisząc „balonik”, mam na myśli gumowy
balonik, nic innego, z czego również dałoby się to zrobić) większa ilością powietrza, to tym
większe ciśnienie jest w środku.

Jednakże, nieco wygodniej jest nieco zamotać. Popatrzeć nie z perspektywy zmian na osi x,

a na osi y. Być może łatwiejsze do analizy jest jednak takie zdanie – im więcej powstanie stali, tym
więcej trzeba było zużyć węgla i żelaza. Im większe ciśnienie jest w baloniku, tym więcej se
podmuchaliśmy (aczkolwiek, nie musi to tylko zależeć od napompowania, jednakże to nie fizyka).

Zamieniliśmy niemalże miejscami x z y, by ułatwić se przykład, wręcz takie zmutowane

całkowanie przed podstawienie. Podstawiliśmy nową funkcję – i wszystko się poprzestawiało. Ten
trik jest często stosowany w dalszych zastosowaniach całek, ale o tym – kiedy indziej. Czas na
garść tylko i wyłącznie przykładów.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

25/36

Zadania z kolokwiów i egzaminów

Zadania pochodzą ze zbioru „Analiza matematyczna 1 – kolokwia i egzaminy”

nieocenionego duetu Gewert&Skoczylas. Rozwiązania się pojawią – jak będę potrafił je rozwiązać.

Zadanie (poważne) 1

Obliczyć całkę oznaczoną

∫

0

e

ln  x1 dx .

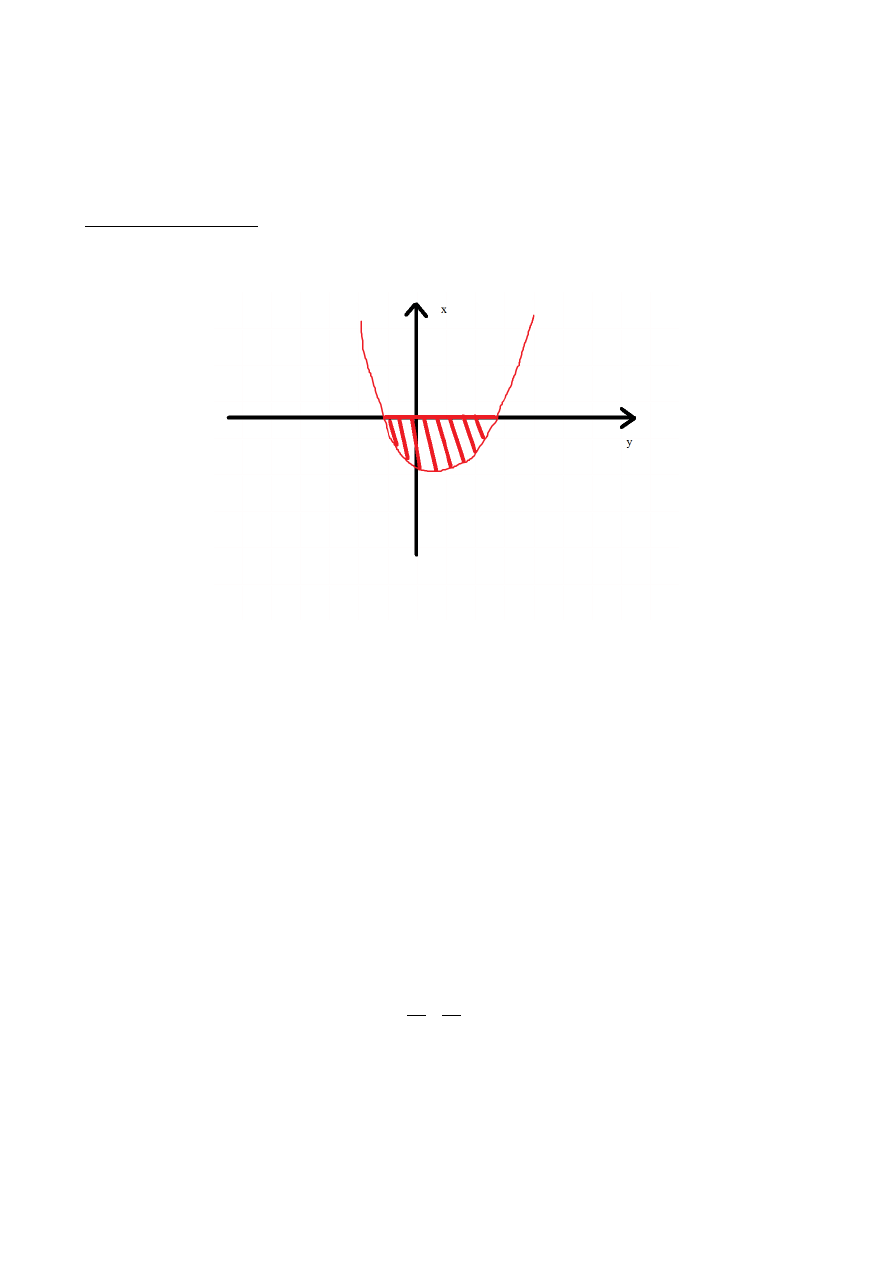
Zadanie 2

Obliczyć pole obszaru D ograniczonego krzywą

x y = y

2

−

2

i osią Oy.

Zadanie 3

Obliczyć pole obszaru D ograniczonego wykresami funkcji: y=



2−x

2

, y=x

2

.

Zadanie 4

Obliczyć pole obszaru D ograniczonego krzywymi:

y=x e

−

x

, x=1 , y=0 .

No i walczymy:

Rozwiązanie zadania 1

∫

0

e

ln  x1 dx

Do obliczenia takiej całki nie trzeba będzie (zbyt) wiele kombinować. Jak już pewno

zauważycie, idealnie nadaje się tutaj całkowania przez podstawienie.

W takim razie, podstawienia typu:

x1=t

dx=dt

oraz nowe granice całkowania:

e1=...e1

01=1

wrzucamy na pełnej kurwie w przykład:

∫

0

e

ln  x1 dx=

∫

1

e1

ln t dt (*)

Liczyliśmy kiedyś całkę nieoznaczoną z logarytmu naturalnego i pozwólcie, że zrobimy to

raz jeszcze, całkując przez części. Potem to, co nam wyjdzie, wykorzystamy przy obliczaniu całki
oznaczonej.

Nic się nie stanie, jeżeli napiszemy taką bzdurę:

∫

ln t dt=

∫



ln t∗1 dt

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

26/36

Robimy na szybko coś w stylu tabelki:

f t=ln t

g ' t=1

f ' t=

1

t

g t =t

Mnożymy to, co jest na krzyż (z lewej do prawej):

ln t∗t ...

I odejmujemy całkę z pomnożenia dolnego wiersza:

ln t∗t−

∫



1

t

∗

t  dt

I to jest całka z logarytmu naturalnego:

∫

ln t dt=ln t∗t−

∫



1

t

∗

t dt=ln t∗t−

∫

dt=ln t∗t−t=t ln t−1

Wracamy se do miejsca oznaczonego (*):

∫

1

e1

ln t dt=[t ln t−1]

e1

1

Najpierw obliczymy wartość dla e + 1:



e1∗lne1−1=e1ln e1−e−1

i nic więcej tutaj nie zakombinujemy, zaś dla jedynki:

1ln 1−1=−1

w związku z tym zwierzątko się wyliczy takie:

[

t ln t−1]

e1

1

=

e1 lne1−e−11=e1ln e1−e

Rozpieprzyliśmy ten przykład. A więc odpowiedzią będzie:

∫

0

e

ln  x1 dx=e1ln e1−e

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

27/36

Rozwiązanie zadania 2

Musimy znaleźć pole obszaru, ograniczonego równaniem

x y = y

2

−

2

i ośką Oy.

Wygodnie będzie tutaj operować y jako zmienną niezależną (albo, jak nadal nie wiecie, o co biega –
zamieniamy rolami

x i

y , nie zaprzątamy sobie głowy innymi pierdołami):

x= y

2

−

y−2

Będzie to parabola w stylu:

Znamy wzór funkcji, która ogranicza nas z góry ( y=0 ), z dołu (

x= y

2

−

y−2

).

Potrzebujemy bramkarzy z lewej i prawej, ale wystarczy obliczyć miejsca zerowe tej funkcji
kwadratowej. Nic trudnego, poziom na pewno maturalny – wiecie, delta i te sprawy. Ja jednak
pozgaduję, korzystając z twierdzenia o pierwiastkach całkowitych wielomianu (o co biega?
Polecam jakikolwiek podręcznik do matematyki z liceum):

x  2=4−2−2=0

x −1=11−2=0

No i mamy granice całkowania. Obliczmy taką całkę:

∫

−

1

2

[

0− y

2

−

y −2]dy=

Wyrzućmy minus przed całkę:

=−

∫

−

1

2



y

2

−

y−2 dy=

Scałkowanie tego nie jest specjalnie trudne:

=−[

y

3

3

−

y

2

2

−

2 y ]

2

−

1

Proponuję tym minusem zająć się na samym końcu (po prostu dołożymy go przed rozwiązanie).

Obliczmy wartość tego zawodnika dla y = 2:

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

28/36

8
3

−

4
2

−

4=

16

6

−

12

6

−

24

6

=

−

20

6

A teraz dla y = - 1:

−

1

3

−

1
2



2=

−

2

6

−

3
6



12

6

=

7
6

Pierwsze minus drugie:

−

20

6

−

7

6

=

−

27

6

=

−

9

2

A ponieważ mieliśmy tam jeszcze minusa przed całką, to:

∫

−

1

2

[

0− y

2

−

y −2]dy=−

−

9

2

=

9
2

Znów rozwaliliśmy kolejnego Pudziana.

Następny przykład tak naprawdę powinien się pojawić w pomocy o całkach

nieoznaczonych. A to dlatego, że do obliczenia zwierzątka, które się tam pojawi, potrzeba odprawić
szamańskie rytuały. Ale i z tym sobie poradzimy... chyba.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

29/36

Rozwiązanie zadania 3

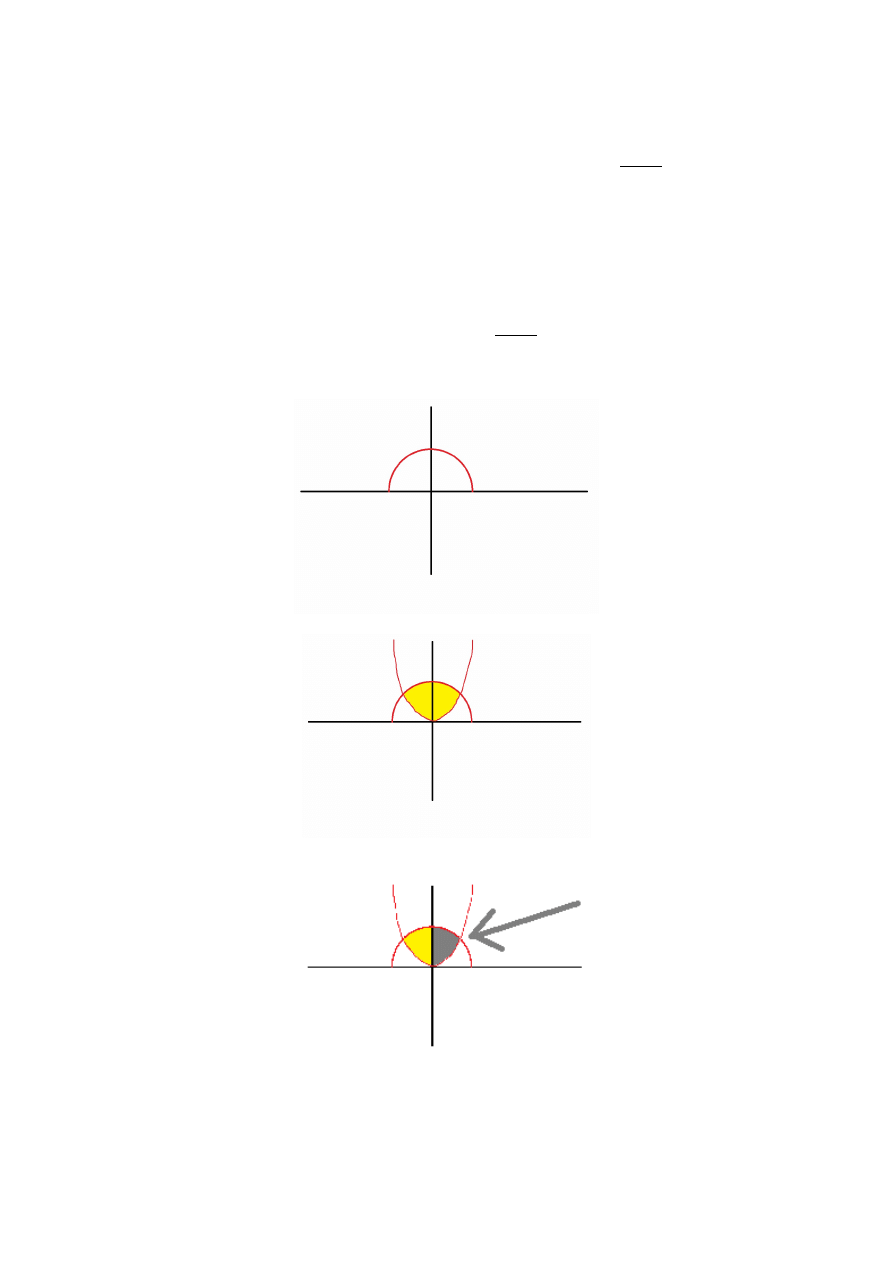
Obliczyć pole obszaru D ograniczonego wykresami funkcji:

y=



2−x

2

,

y=x

2

.

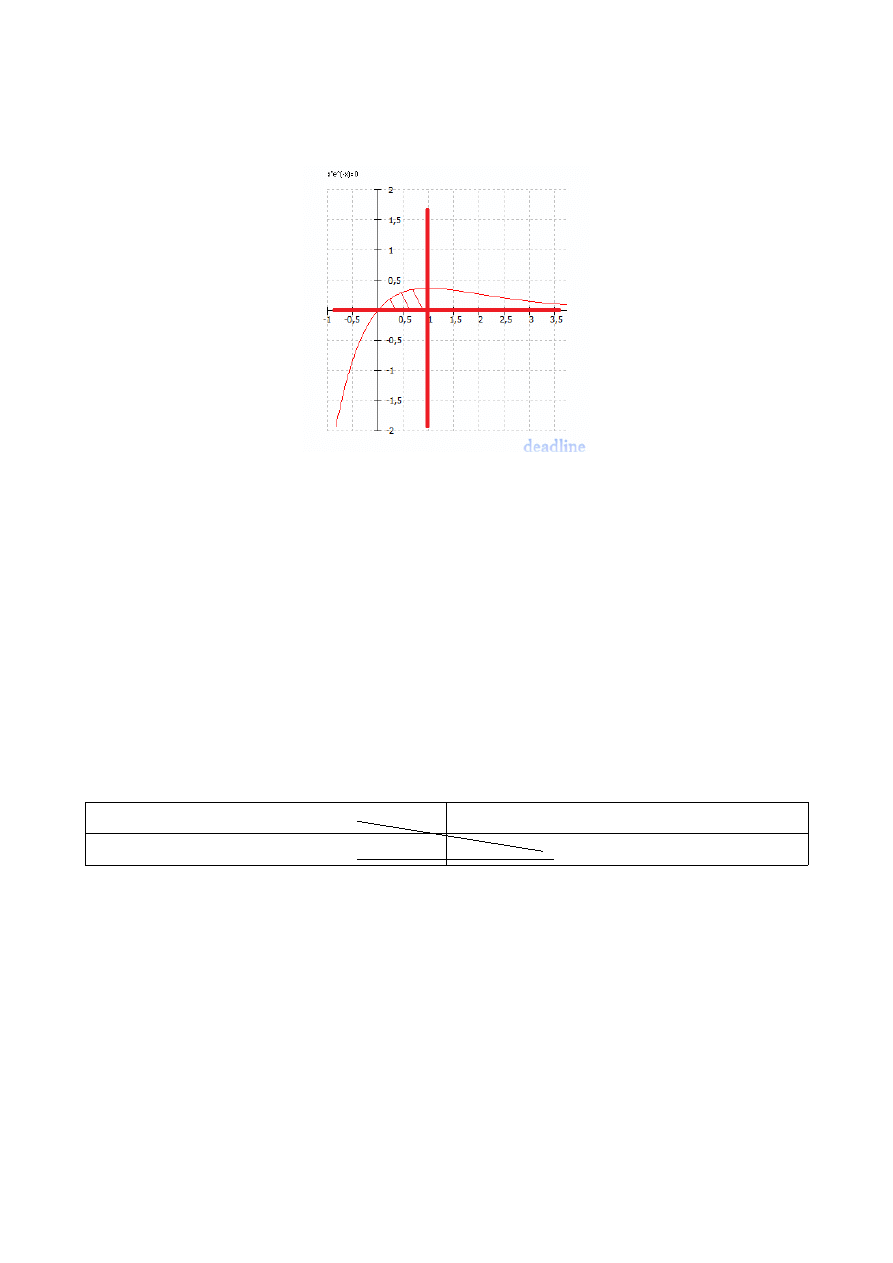
Póki co – wygląda niewinnie... Błąd, kurwa – wygląda na taki przykład, któremu

spuściłbym wpierdol, gdybym tylko miał jakąś siłę czy doświadczenie na siłowni (dres już mam).

Problem zaczyna się z narysowaniem tego na wykresie. Jeżeli pojawi się tu jakiś obszar, to

na pewno jakby „zamknięty” z czterech stron – ja się pytam „Gdzie jest obszar”?

Okej, narysujemy najpierw wykres funkcji y=



2−x

2

(jak ktoś uważał w liceum czy

technikum, to wie od razu, co namaluję):

jest to pół jebanego kółka. A parabolę już łatwo namalujemy:

Możemy zauważyć, że – ponieważ obydwie funkcje są symetryczne – to dzielą się na dwie

równe połówki. W związku z tym – wystarczy, że obliczymy pole tego zaznaczonego na szaro:

pomnożymy razy 2 – i po robocie, przykład rozwalony.

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

30/36

Poszukajmy równań, które ograniczają nam ten obszar. Z góry niewątpliwie będzie to

y=



2−x

2

, z dołu

y=x

2

. Z lewej ogranicza nas, co widać, x=0 . Prawą stronę musimy se

wyliczyć, albo zgadnąć.

Wiemy, że przecinają się tam te dwa gópie równania, w związku z tym:



2−x

2

=

x

2

Ponieważ bawimy się w tej części układu współrzędnych, gdzie wartości funkcji są dodatnie, a

słońce nigdy nie zachodzi, to bez problemu podniesiemy to wszystko do kwadratu:

2−x

2

=

x

4

A wszystko – na lewą stronę:

−

x

4

−

x

2



2=0

Trzeba obliczyć iksa – takie coś robi się na pewno w zakresie rozszerzonym w liceum. Przypomnę:

za iksa do kwadratu coś podstawiamy:

x

2

=

t

(*)

Wracamy do równania:

−

t

2

−

t2=0

Wyliczmy deltę:

Δ=18=9

Oraz możliwe wartości t:

t

1

=

1−3

−

2

=

1

t

2

=

13

−

2

=−

2

Od razu odrzucamy t

2

, bo zapis

x

2

=−

2

wygląda bezsensownie, a wierzcie mi – nie ma najmniejszej potrzeby mieszać w to liczb urojonych.

W związku z tym, wróćmy do (*) i zobaczmy, czego się dowiedzieliśmy:

x

2

=

1

No więc, tak zacznę zdanie,

x=1 ˅ x=−1

Wiemy, że poruszamy się w obszarze, gdzie wszystko jest na plusie, więc granica całkowania z

prawej strony będzie równa x=1 , co można było o wiele szybciej zgadnąć albo odczytać z

rysunku.

Całka do wyliczenia będzie miała w takim razie postać:

2

∫

0

1





2− x

2

−

x

2



dx

(razy dwa, ponieważ tak naprawdę policzymy połówkę obszaru, mnożąc przez 2 – cały obszar)

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

31/36

Pomińmy, póki co, tą dwójkę stojącą z przodu i rozpieprzmy całkę na dwie:

∫

0

1





2− x

2

−

x

2



dx=

∫

0

1



2−x

2

dx−

∫

0

1

x

2

dx (*)

Wyliczymy wszystko z tej drugiej, bo jest trochę łatwiejsza:

∫

0

1

x

2

dx =[

x

3

3

]

1
0

=1

3

By obliczyć tą:

∫

0

1



2−x

2

dx

obliczymy se najpierw całkę nieoznaczoną:

∫



2−x

2

dx

i tutaj, proszę Państwa, zaczniemy najbardziej powalony przykład z tej pomocy.

Ni chuja tego nie ruszymy przez podstawienie (gdzieś się będzie pałętać niezamienione x, albo

sobie skomplikujemy przykład), a przez części – zapewne będziemy liczyć pochodną z tego

pierwiastka i cały przykład pójdzie w pizdu. Dlatego – dziękując Panu Włodarskiemu i

Krysickiemu za napisanie „Analizy matematycznej w zadaniach” - zaczniemy powoli. Radzę

bardzo powoli, notując sobie niektóre rzeczy na kartce, przejrzeć ten przykład bez pośpiechu.

Ostatnią deską ratunku będzie zadziałanie z tym pierwiastkiem. Otóż, zróbmy takiego myka:



2−x

2

=



2−x

2

∗



2−x

2



2− x

2

=

2− x

2



2− x

2

Wrzućmy to do całki – i od razu rozjebmy na dwie

∫



2−x

2

dx=

∫

2−x

2



2−x

2

dx=

=

∫

2



2− x

2

dx −

∫

x

2



2−x

2

dx

Jeżeli oznaczymy sobie całkę

∫



2−x

2

dx jako I

1

, zaś całkę

∫

x

2



2− x

2

dx= I

2

, otrzymamy

dosyć osobliwe równanie:

I

1

=

∫

2



2−x

2

dx−I

2

(**)

Została nam tutaj jedna całka, którą wyliczymy. Kiedyś liczyliśmy coś podobnego, a byłoby fajnie,

gdyby trafić na wzorek:

∫

1



1−x

2

dx=arcsin x

W związku z tym, zrobimy kolejnego myka:

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

32/36

∫

2



2−x

2

dx=2

∫

dx



2[1−

x



2



2

]

=

2



2

∫

dx



1−

x



2



2

Dwójka poszła przed całkę, zaś w pierwiastku wyłączyliśmy 2 przed nawias. Potem, wiedząc, co w

pierwiastku wolno, pierwiastek z dwóch również wyrzuciliśmy przed całkę.

Zrobimy se podstawienie:

x



2

=

t

dx=



2∗dt

Wrzucając to w całkę:

2



2

∫

dx



1−

x



2



2

=

2

∫

dt



1−t

2

=

otrzymamy:

=

2 arcsin t=2 arcsin 

x



2



Pokręćmy trochę rolką w górę, do tego miejsca (**):

I

1

=

∫

2



2−x

2

dx−I

2

i wrzućmy to w koszta:

I

1

=

2 arcsin 

x



2

−

I

2

(***)

Pisałem coś o obliczaniu całki przez części – my jednak zaryzykujemy i przekornie, wbrew temu,

co napisałem, obliczymy całkę I

1

(przypomnę:

I

1

=

∫



2− x

2

dx ) przez części.

Znów – prowizoryczna tabelka:

f  x =



2−x

2

g '  x =1

f '  x=

−

x



2−x

2

g  x= x

Skąd sobie wypiszemy, że:

∫



2−x

2

dx= x∗



2−x

2



∫

x



2− x

2

dx

Wróćmy do (**). Ponieważ I

2

=

∫

x

2



2− x

2

dx , zaś I

1

=

∫



2− x

2

dx , to powyższe równanie

mogę zapisać w postaci:

I

1

=

x∗



2− x

2



I

2

(iv)

Autor: vbx

(c) 2010

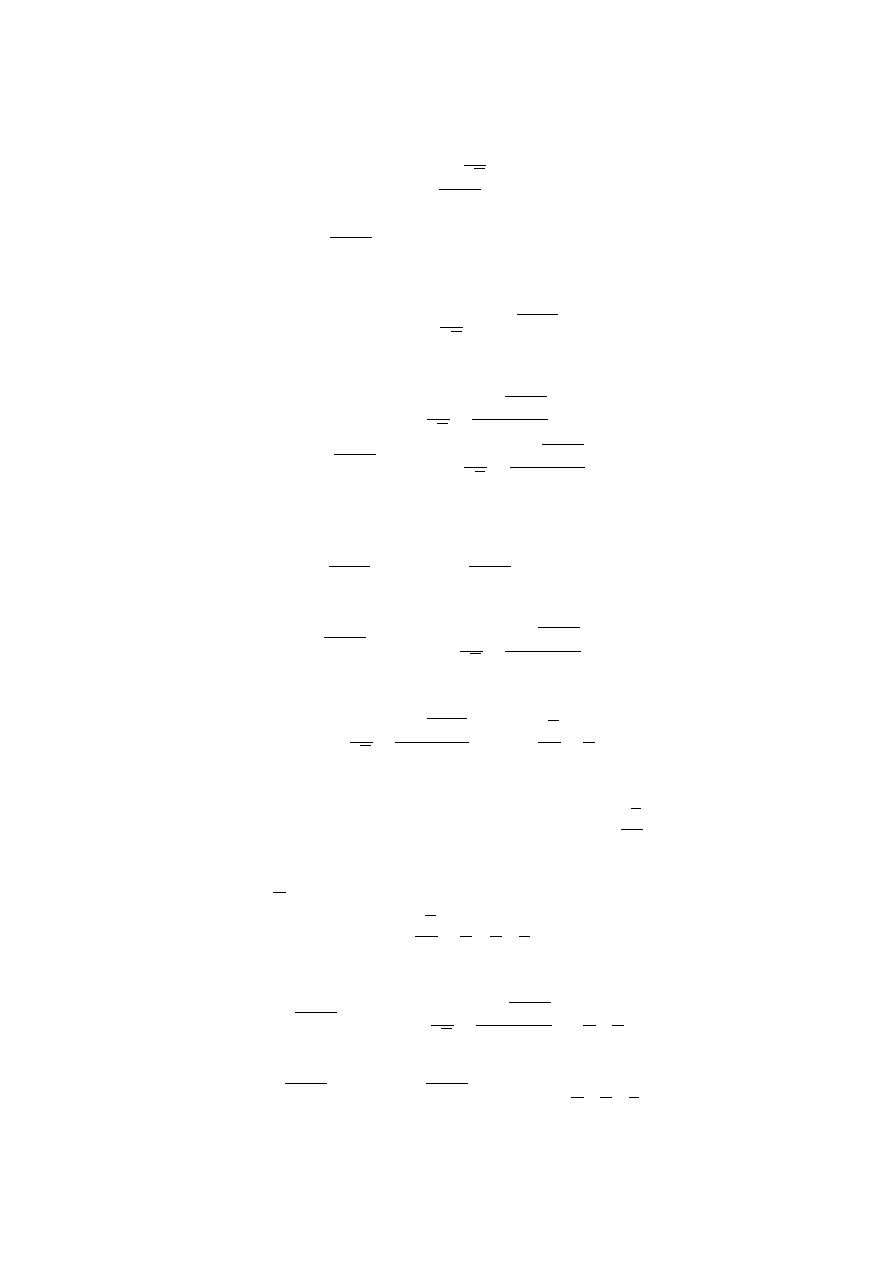
Analiza matematyczna, całki oznaczone

33/36

Przepiszmy równania (***) i (iv):

I

1

=

2 arcsin 

x



2

−

I

2

I

1

=

x∗



2− x

2



I

2

,

z czego I

1

=

∫



2− x

2

dx (przypomnę – to nasza szukana całka!)

Gdy powyższe dwa równania dodamy stronami, wyjdzie nam ( I

2

się zredukuje):

2 I

1

=

2 arcsin 

x



2



x∗



2− x

2

Dzieląc przez dwa, wyliczamy I

1

, czyli szukaną całkę... Uff!

I

1

=

arcsin 

x



2



x∗



2− x

2

2

∫



2−x

2

dx=arcsin 

x



2



x∗



2− x

2

2

Ło Jezu, ile mordęgi! Na szczęście, jesteśmy blisko wyliczenia wszystkiego. Otóż, wróćmy aż do

(*):

∫

0

1





2− x

2

−

x

2



dx=

∫

0

1



2−x

2

dx−

∫

0

1

x

2

dx

Tą drugą całkę po prawej stronie wyliczyliśmy, wyliczmy pierwszą:

∫

0

1



2−x

2

dx=[arcsin 

x



2



x∗



2−x

2

2

]

1
0

Wyliczmy wartość tego, co w nawiasie kwadratowym, dla jedynki:

arcsin 

1



2



1∗



2−1

2

2

=

arcsin 



2

2



1
2

Trochę problemów może być z arcus sinusem. Korzystając z tabelki z wartościami funkcji

trygonometrycznych, zapytajmy się: „Dla jakiego kąta sinus ma wartość



2

2

„? Szybko

odpowiemy sobie – dla 45 stopni, co w radianach (w takiej jednostce wyrażamy zwykle kąty w

matematyce) daje jakieś

π
4

. W związku z tym,

arcsin 



2

2



1
2

=

π
4



1
2

Okej, obliczyliśmy wartość dla 1. Dla 0 nie warto marnować papieru – arcus sinus da równe 0, zaś

odejmiemy też zero. W związku z tym,

∫

0

1



2−x

2

dx=[arcsin 

x



2



x∗



2−x

2

2

]

1
0

=

π

4



1

2

co za tym idzie:

∫

0

1





2− x

2

−

x

2



dx=

∫

0

1



2−x

2

dx−

∫

0

1

x

2

dx=

π
4



1
2

−

1
3

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

34/36

Może już zapomnieliście, a może i nie – jest to pole tego obszaru:

A że cały obszar, o którym wspomina zadanie, to też jego identyczna (pod względem

powierzchni) lewa połówka, więc cały wynik pomnożymy razy dwa (wspomniałem o tym na
początku zabawy):

2∗

π

4



1
2

−

1
3

=

π

2

−

1
3

O kurwa, to koniec!

2

∫

0

1





2− x

2

−

x

2



dx=

π

2

−

1
3

Miejmy nadzieję, że następny przykład będzie mniej zacięty w walce...

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

35/36

Rozwiązanie zadania 4
Ten jeden, jedyny raz posłużymy się prawie gotowym wykresem:

Ta cieńsza czerwona linia – to wykres y=x e

−

x

, zaś czerwonymi oznaczyłem

x=1

oraz

y=0

.

Na koniec – raczej prosta całka do obliczenia, proponuję, byście wy najpierw ją obliczyli, a

potem bluzgali mnie za moje błędy w rozwiązaniu.

Granice znamy – z góry

y=x e

−

x

, z dołu y=0 , z lewej x=0 (to odczytujemy z

wykresu) oraz z prawej x=1 . Obliczymy takiego zwierzaczka

∫

0

1

x e

−

x

dx

ja tam najpierw obliczę całkę nieoznaczoną (by potem ją wykorzystać).

Aby obliczyć to:

∫

x e

−

x

dx

trochę pocałkujemy przez części:

f  x =x

g '  x =e

−

x

f '  x=1

g  x=−e

−

x

(*)

(*) - obliczenie tego to tylko scałkowanie tej górnej funkcji, przez banalne podstawienie –

pozwolicie, że pominę tą część.

I uzyskamy:

∫

x e

−

x

dx=−x∗e

−

x



∫

e

−

x

dx

Drugą całkę przed chwilą zgadywaliśmy, tak więc:

∫

x e

−

x

dx=−x∗e

−

x

−

e

−

x

=

e

−

x

−

x−1

Autor: vbx

(c) 2010

Analiza matematyczna, całki oznaczone

36/36

Nie będzie problemem wstawienie tego do całki oznaczonej:

∫

0

1

x e

−

x

dx=[e

−

x

−

x−1]

1
0

Wartość dla jedynki będzie równa:

e

−

1

−

1−1=

−

2

e

Zaś dla 0:

e

−

0



0−1=1∗−1=−1

Kończąc ten przykład i tego bryka:

∫

0

1

x e

−

x

dx=[e

−

x

−

x−1]

1
0

=

−

2

e

−−

1=1−

2
e

No, to by było na tyle. Jeżeli chodzi o całki oznaczone, to mają zastosowania typu

„Wyliczyć długość łuku” albo „objętość walca, powstałego przez obrót wokół osi OY”. Jednak i
one sprowadzają się do całek oznaczonych, bo są na to gotowe wzory.

Moim celem było pokazanie, jak walczyć z całkami oznaczonymi, a przy okazji – trochę

jeszcze poćwiczyliśmy z nieoznaczonych. Bo sami chyba przyznacie, że jak umiecie liczyć „te
spierdolone całki”, to wszystko umiecie.

A jak nie udało mi się wszystkiego wyjaśnić, to trudno. Co napisałem, co zjadłem i co

wypiłem (za Wasze powodzenie, oczywiście) podczas pisania tej pomocy, to moje.

pj
poap[at]interia.pl

Bryki, do których się tutaj często odnoszę, są dostępne na stronie:

http://www.poap.yoyo.pl/matd/

Autor: vbx

(c) 2010