1

Elementy cyfrowe i układy

logiczne

Wykład 1

2

2

2

2

Literatura

• M. Morris Mano, Charles R. Kime – Podstawy projektowania

układów logicznych i komputerów, Wydawnictwa Naukowo-
Techniczne

• Giovanni De Micheli - Synteza i optymalizacja układów

cyfrowych, Wydawnictwa Naukowo-Techniczne,

• Majewski

Władysław

-

Układy

logiczne,

Podręczniki

akademickie EiT,

• Jan Pieńkos, Janusz Turczyński - Układy scalone TTL w

systemach cyfrowych, Wydawnictwa Komunikacji i Łączności,

• Łuba Tadeusz - Synteza układów cyfrowych, Wydawnictwa

Komunikacji i Łączności,

• Wilkinson Barry - Układy cyfrowe,

• Grocki Wojciech - Układy cyfrowe.

2

3

3

3

3

Legenda:

Rodzaje bramek

Sposoby zapisu funkcji logicznych

Algebra Boole’a

4

4

4

4

Bramki logiczne

• Bramki logiczne

– układy elektroniczne, które

wykonują operacje na jednym lub więcej sygnałach
wejściowych i wytwarzają sygnał wyjściowy.

• Sygnały elektryczne

– przyjmują jedną z dwóch

rozpoznawalnych wartości: {0, 1}

5,0

4,0

3,0

2,0

1,0

0,0

Stan wysoki

Stan wysoki

Stan niski

Stan niski

wyjście

wejście

Dlaczego

system

dwójkowy a

nie np.

dziesiętny?

3

5

5

5

5

Rodzaje bramek

AND

OR

NOT

NAND

NOR

ExOR

ExNOR

Inne …

Wyjścia bramek są

połączone z wejściami

innych bramek, tworząc

układ cyfrowy

6

6

6

6

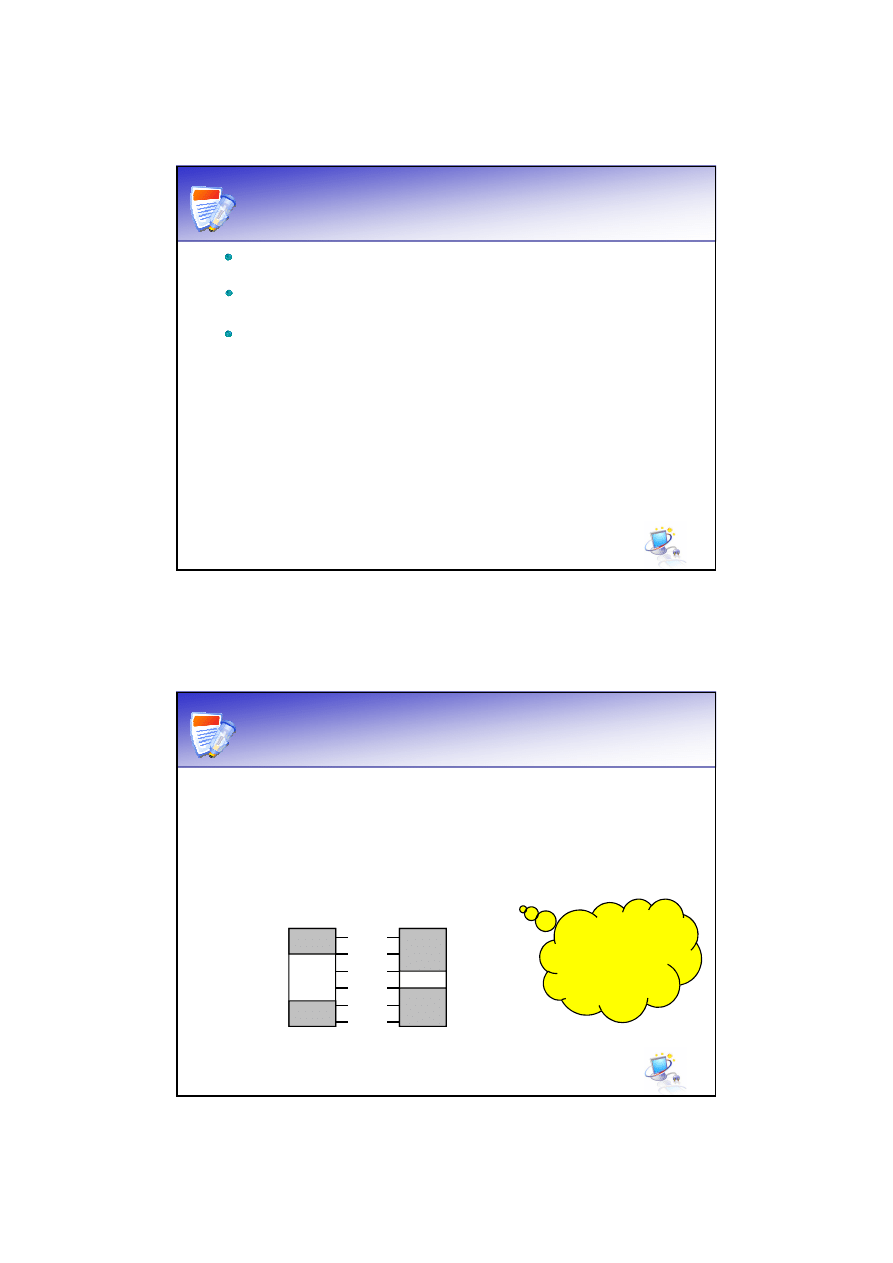
Bramka AND

Wejście

Wyjście

x

1

x

2

y

0

0

0

0

1

0

1

0

0

1

1

1

x

2

Tablica prawdy:

Bramka

AND

(koniunkcja)

realizuje funkcję:

Wyjście bramki AND jest w stanie
wysokim

tylko

wtedy,

gdy

oba

wejścia są w stanie wysokim.

x

1

y

2

1

2

1

2

1

x

x

x

x

x

x

y

=

⋅

=

∧

=

4

7

7

7

7

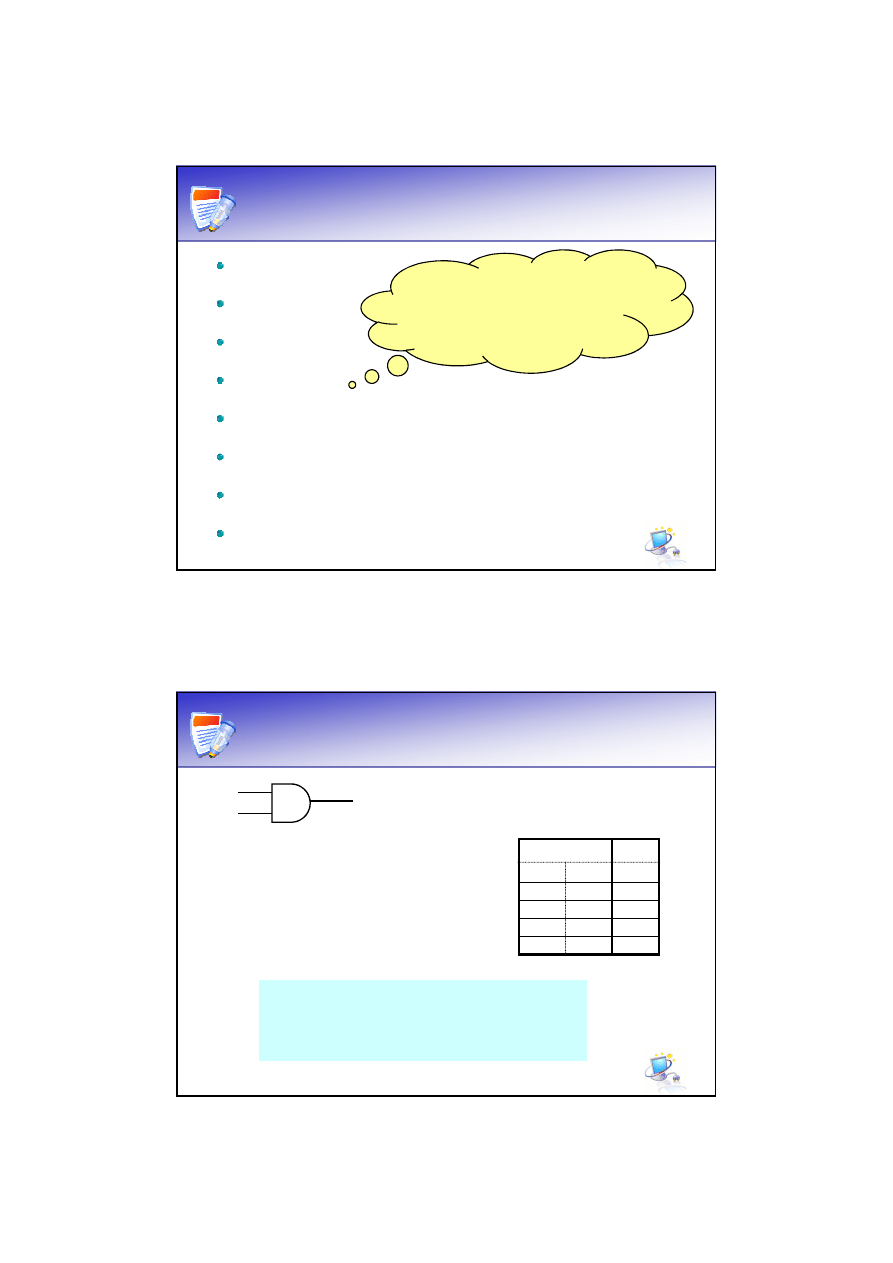
Bramka

OR

Wejście

Wyjście

x

1

x

2

y

0

0

0

0

1

1

1

0

1

1

1

1

Tablica prawdy:

Bramka

OR

(alternatywa)

realizuje funkcję:

Wyjście

bramki

OR

jest

w

stanie

wysokim, jeżeli któreś z wejść (lub oba)
są w stanie wysokim.

x

2

2

1

x

x

y

∨

=

x

1

y

8

8

8

8

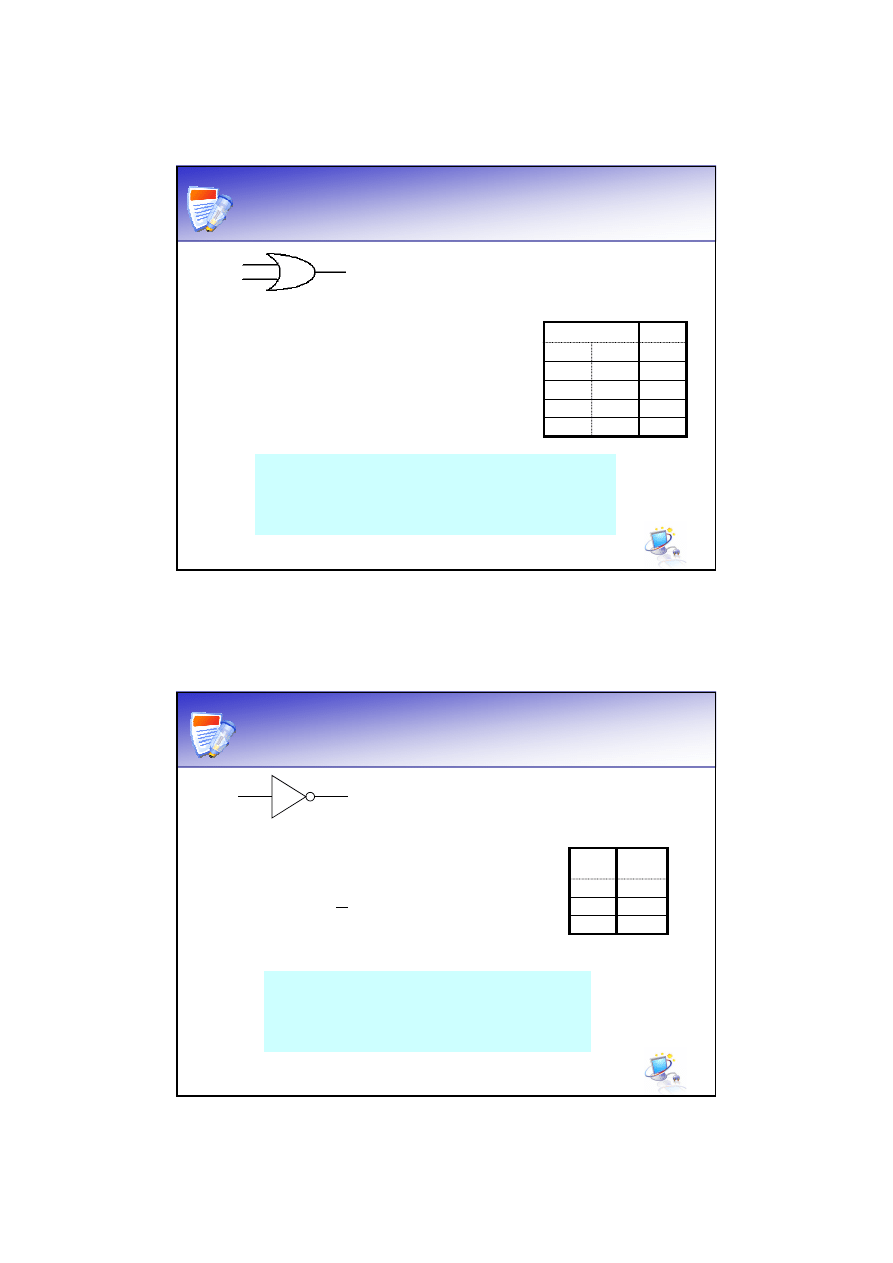
Bramka NOT

x

Tablica prawdy:

Wejście

Wyjście

x

y

0

1

1

0

Bramka NOT (inwerter) realizuje
funkcję:

y= x

Bramka NOT pozwala nam zmienić
stan logiczny na przeciwny (tzw.
negowanie stanu logicznego).

y

5

9

9

9

9

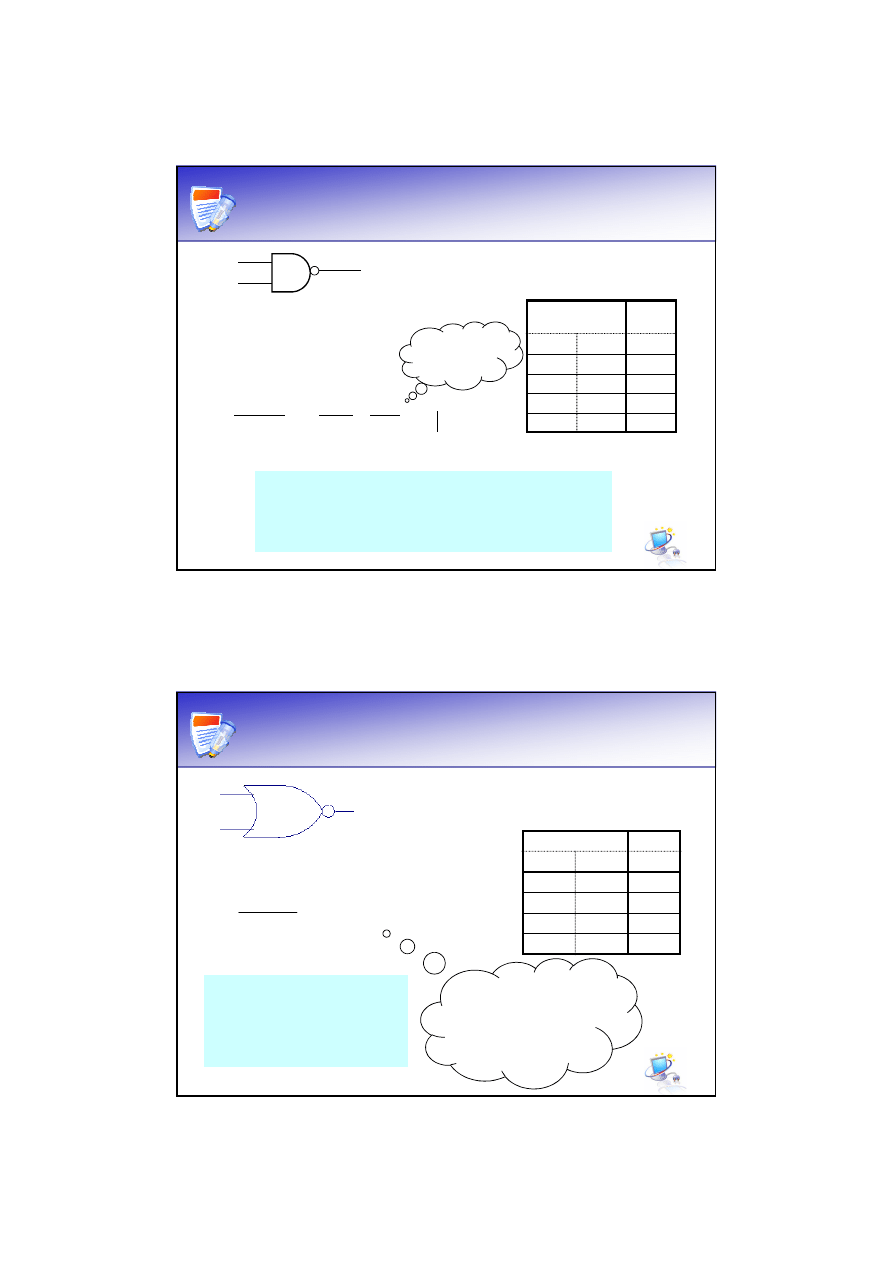
Bramka NAND

x

2

Bramka NAND realizuje funkcję:

y=x

1

= x

1

· x

2

= x

1

x

2

x

2

∧

= x

1

x

2

Wyjście bramki NAND jest w stanie
wysokim, jeżeli któreś z wejść (lub oba)
są w stanie niskim.

Tablica prawdy:

Wejście

Wyjście

x

1

x

2

y

0

0

1

0

1

1

1

0

1

1

1

0

Funkcja

Scheffera

x

1

y

10

10

10

10

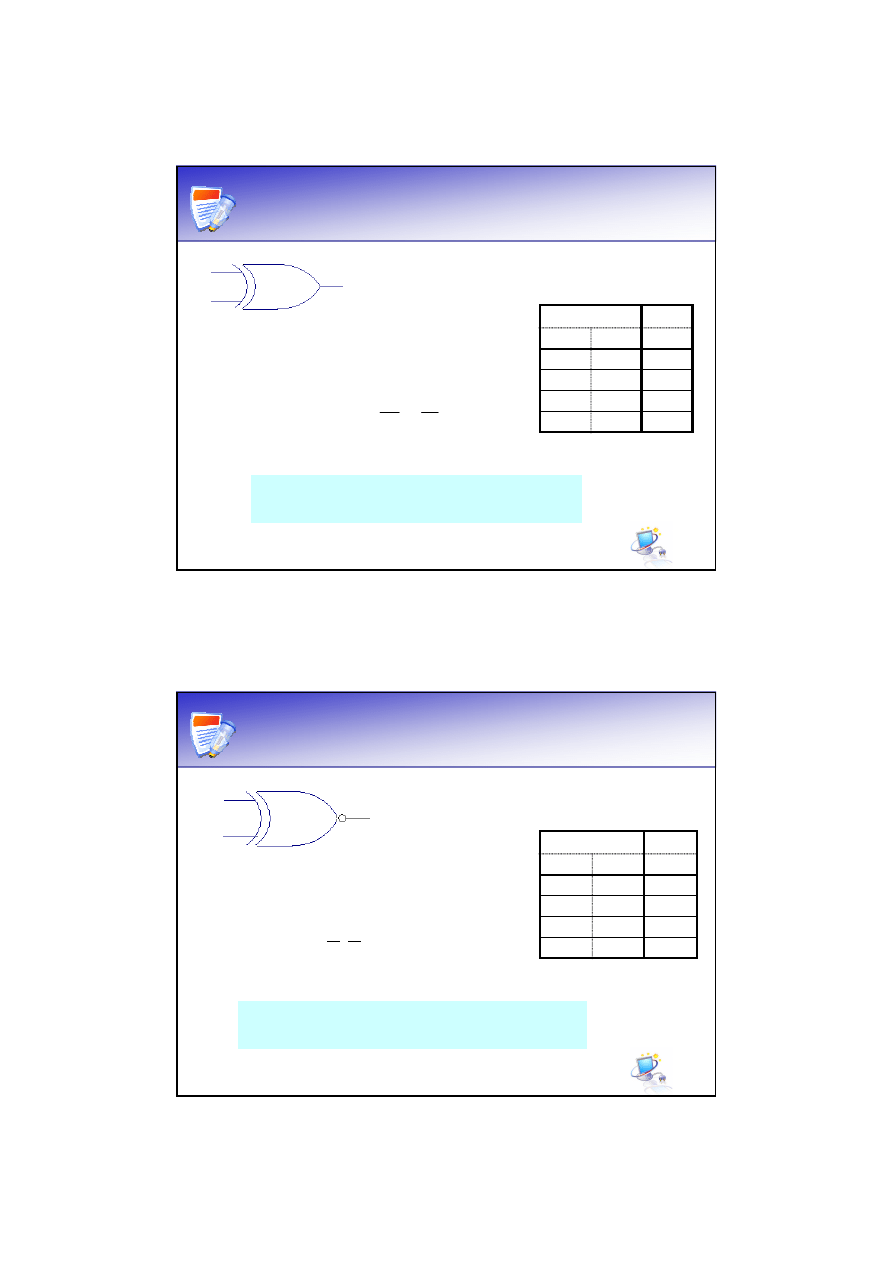
Bramka NOR

Bramka NOR realizuje funkcję:

Tablica prawdy:

Funkcja Webba

(strzałka Pierce’a)

x

1

x

2

y

Wejście

Wyjście

x

1

x

2

y

0

0

1

0

1

0

1

0

0

1

1

0

2

1

2

1

x

x

x

x

y

↓

=

∨

=

Wyjście bramki NOR jest
w stanie wysokim, jeżeli
oba wejścia są w stanie
niskim.

6

11

11

11

11

Bramka XOR (ExOR, Albo)

Wejście

Wyjście

x

1

x

2

y

0

0

0

0

1

1

1

0

1

1

1

0

Tablica prawdy:

Bramka

XOR

(suma

modulo)

realizuje funkcję:

y

x

1

x

2

y

2

1

2

1

2

1

x

x

x

x

x

x

y

∨

=

⊕

=

Wyjście bramki Exclusive-OR jest w stanie
wysokim, jeżeli stany wejść są różne.

12

12

12

12

Bramka ExNOR

Wejście

Wyjście

x

1

x

2

y

0

0

1

0

1

0

1

0

0

1

1

1

Tablica prawdy:

Bramka ExNOR (ekwiwalencja,
równoważność) realizuje funkcję:

y

∨

y= x

1

~ x

2

= x

1

x

2

x

1

x

2

x

1

x

2

y

Wyjście bramki Exclusive-NOR jest w stanie
wysokim, jeżeli stany wejść są takie same.

7

13

13

13

13

Algebra Boole’a

Prawa przemienności

Prawa łączności

Prawa rozdzielności

Prawa de Morgana

Prawa idempotentności

Prawo podwójnej negacji

Prawa pochłaniania

14

14

14

14

Prawa przemienności

x

y

y

x

x

y

y

x

∧

=

∧

∨

=

∨

Prawa łączności

z

y

x

z

y

x

z

y

x

z

y

x

∧

∧

=

∧

∧

∨

∨

=

∨

∨

)

(

)

(

)

(

)

(

8

15

15

15

15

Prawa rozdzielności

Prawa de Morgana

)

(

)

(

)

(

)

(

)

(

)

(

z

x

y

x

z

y

x

z

x

y

x

z

y

x

∨

∧

∨

=

∧

∨

∧

∨

∧

=

∨

∧

...

...

...

...

z

y

x

z

y

x

z

y

x

z

y

x

∨

∨

=

∧

∧

∧

∧

=

∨

∨

16

16

16

16

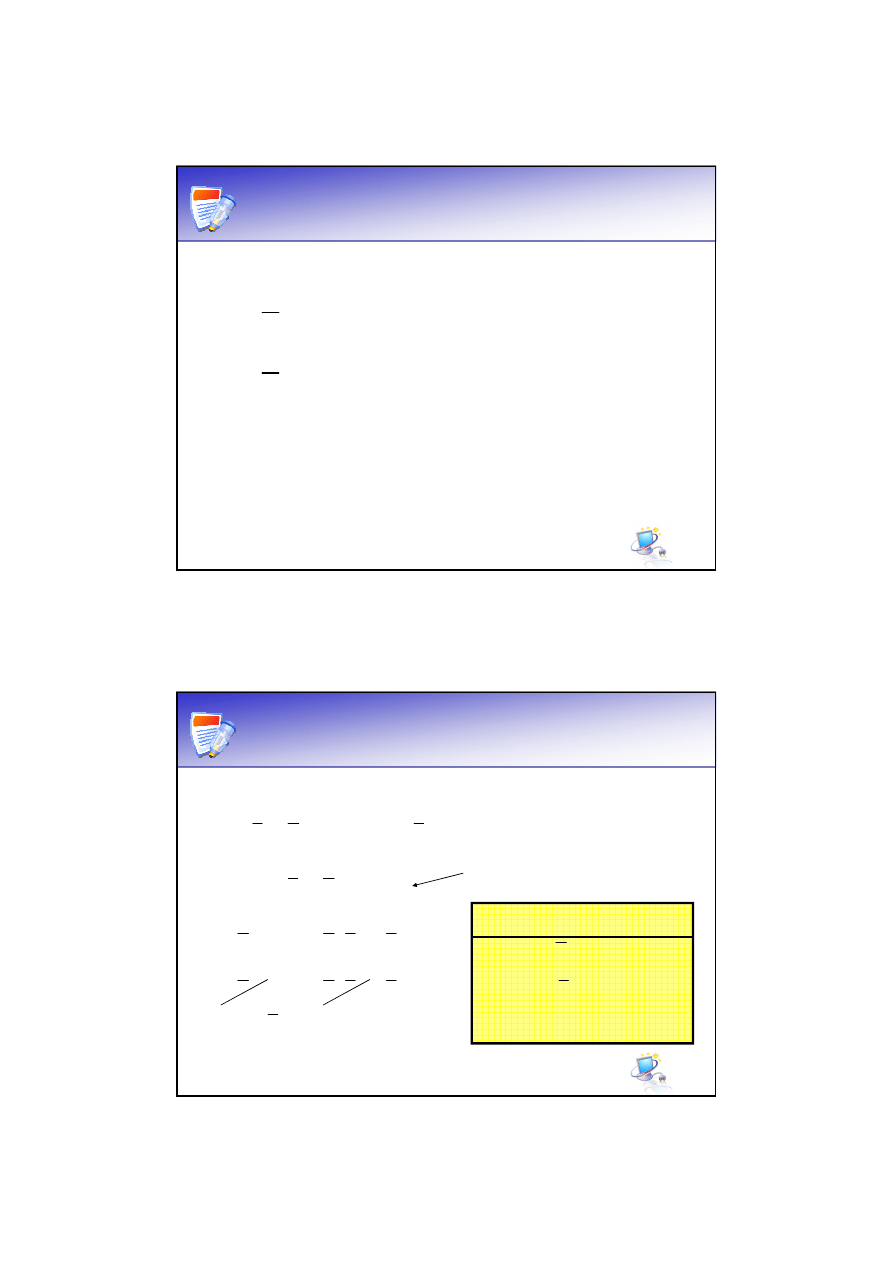
Prawa idempotentności

Prawo podwójnej negacji

x

x

x

x

x

x

=

∧

=

∨

x

x =

9

17

17

17

17

Prawa pochłaniania

1

0

=

∨

=

∧

x

x

x

x

1

1

1

=

∨

=

∧

x

x

x

x

x

x

=

∨

=

∧

0

0

0

18

18

18

18

Pamiętaj:

Zastosowanie algebry Boole’a

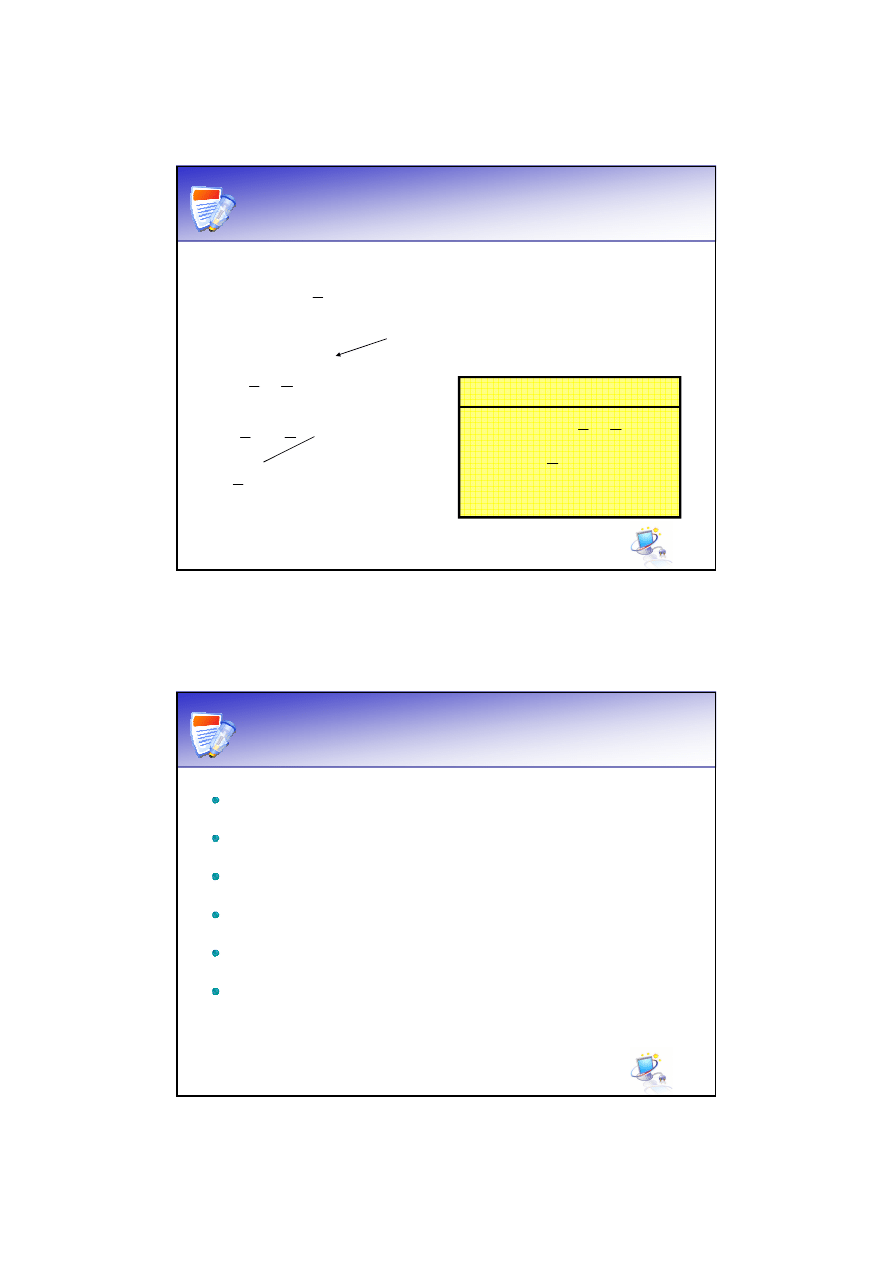
Udowodnij, że lewa strona jest równa prawej:

c

b

ac

c

b

a

c

b

a

∨

=

∨

∨

)

)(

(

=

∨

∨

=

)

)(

(

c

b

a

c

b

a

L

mnożymy nawiasy przez siebie

=

∨

∨

∨

=

cc

b

c

b

b

a

ac

b

a

a

c

b

ac ∨

=

L=P

0

=

a

a

0

=

b

b

c

cc =

=

∨

∨

∨

=

cc

b

c

b

b

a

ac

b

a

a

10

19

19

19

19

Zastosowanie algebry Boole’a

Udowodnij, że lewa strona jest równa prawej:

b

a

b

a

a

=

⊕ )

(

=

⊕

=

)

(

b

a

a

L

wykonujemy działanie w nawiasie

=

∨

=

)

(

b

a

b

a

a

b

a

=

L=P

0

=

a

a

a

aa =

=

∨

=

b

a

a

b

aa

b

a

b

a

b

a

∨

=

⊕

Pamiętaj:

20

20

20

20

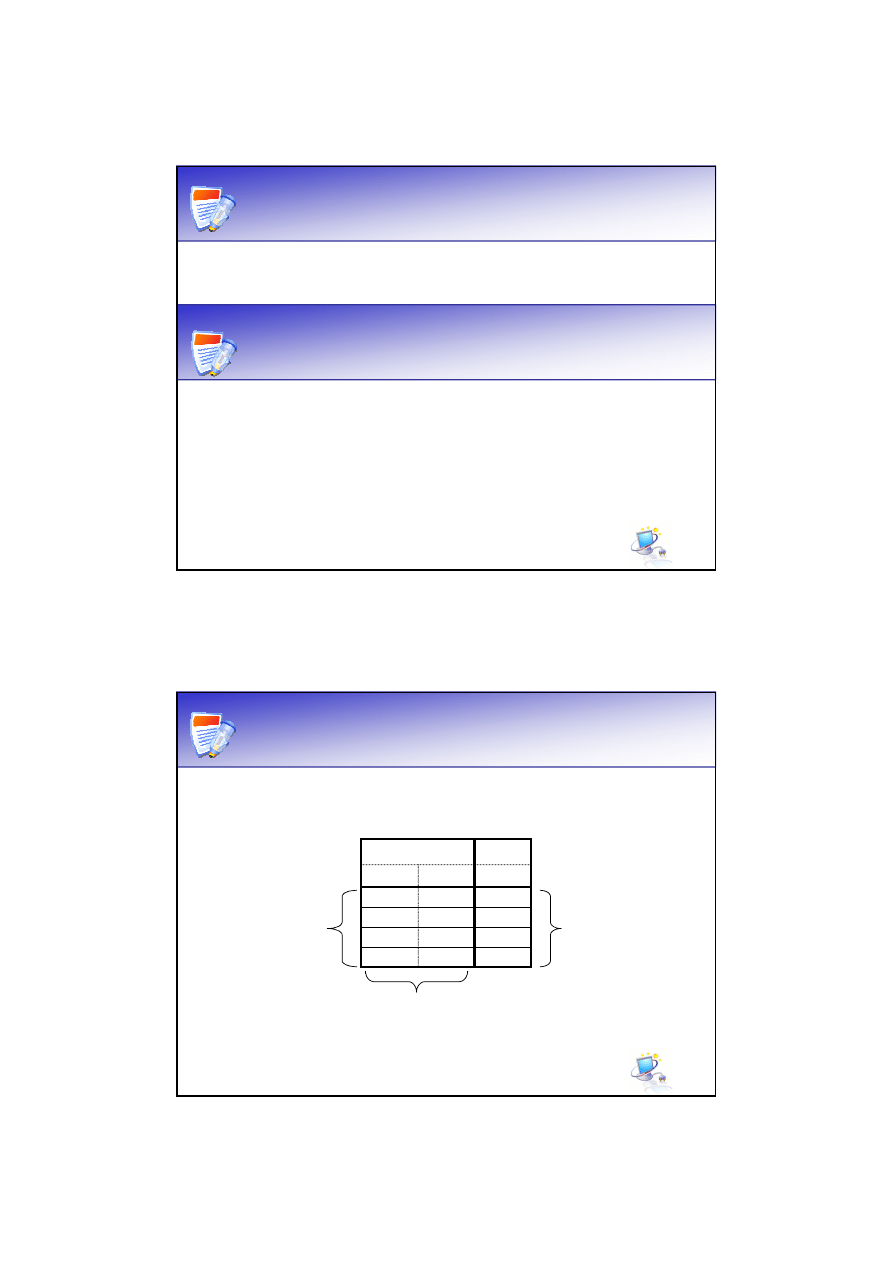
Sposoby zapisu funkcji

zapis algebraiczny

tablica prawdy

wektor prawdy

postać FDCF

postać FCCF

i inne…

11

21

21

21

21

Zapis algebraiczny

Tablica prawdy

2

1

)

(

x

x

x

f

∨

=

Tablica prawdy (ang. Truth Table - nazywana inaczej
tablicą

wartości),

to

zestawienie

w

kolejnych

wierszach

wszystkich

możliwych

kombinacji

wartości i odpowiadających im wartości funkcji.
Kombinacje te muszą być uporządkowane tak, aby
tworzyły

kolejne

liczby

naturalne

zapisane

w

systemie dwójkowym.

22

22

22

22

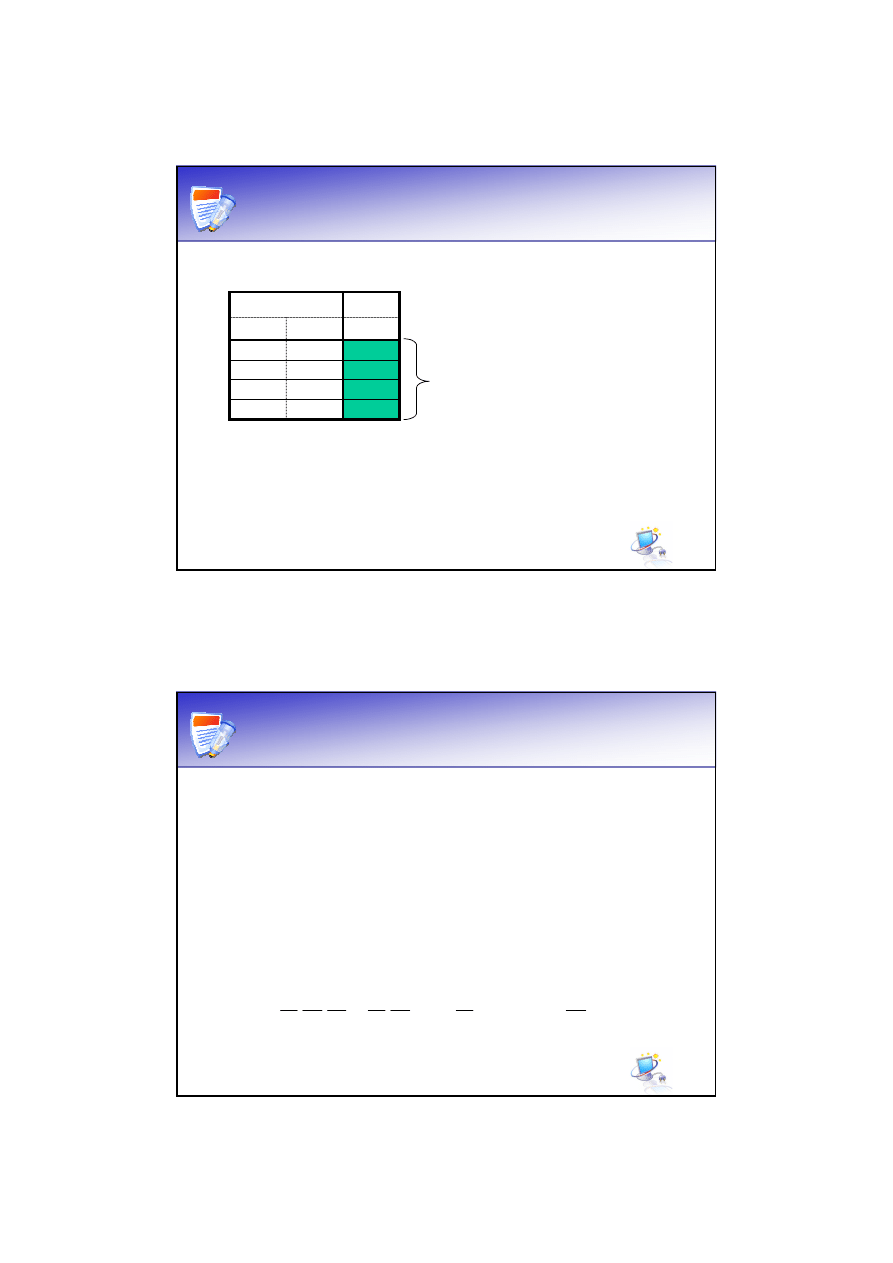
Tablica prawdy c.d.

Wejście

Wyjście

x

1

x

2

y

0

0

0

0

1

0

1

0

0

1

1

1

Zestawienie
wszystkich
możliwych
kombinacji:
2

n

, gdzie n to

liczba wejść.

Wartości
funkcji
odpowiadające
wejściom.

Tablica prawdy bramki AND:

Kombinacje

muszą

być

uporządkowane.

00

2

=0

10

, 01

2

=1

10

, 10

2

=2

10

, 11

2

=3

10

…

12

23

23

23

23

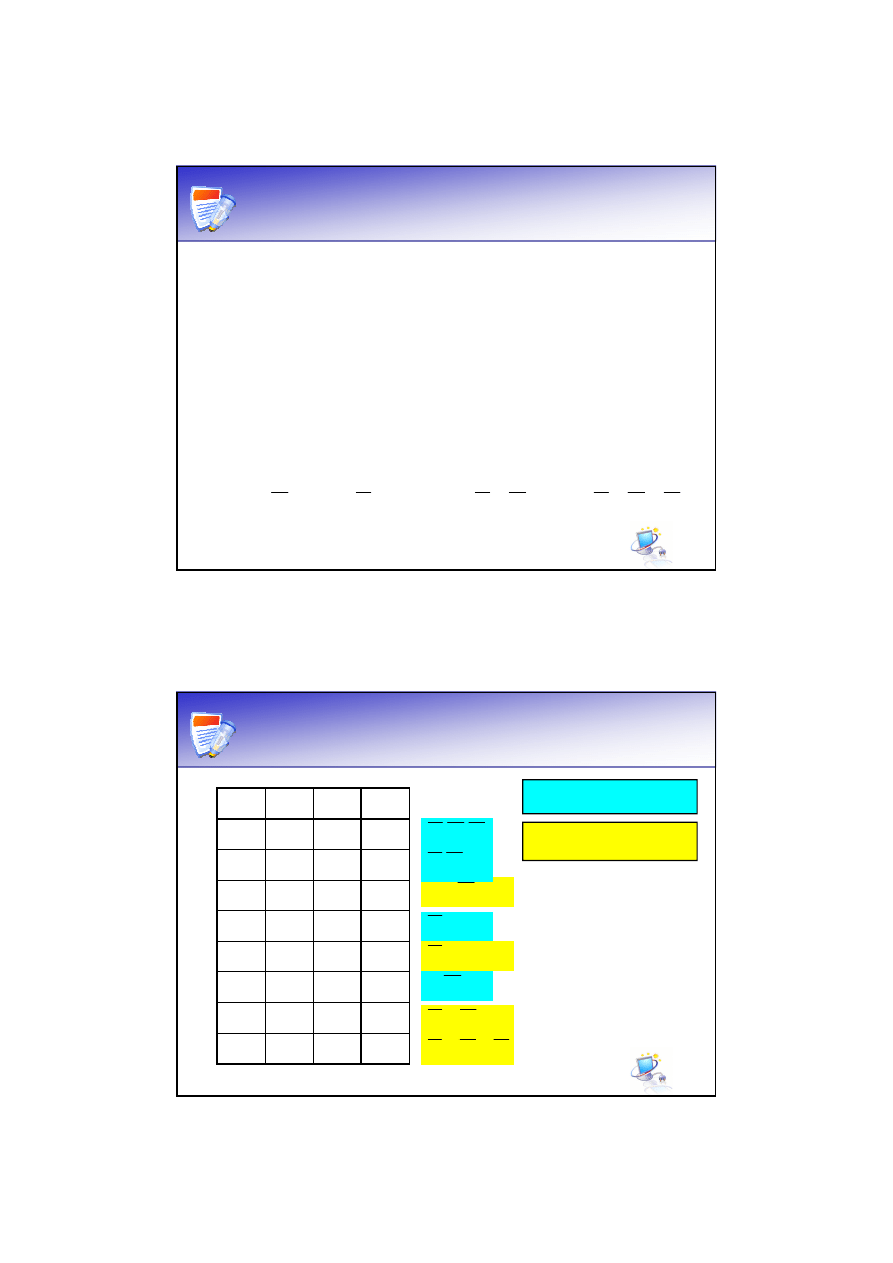
Wektor prawdy

Wejście

Wyjście

x

1

x

2

y

0

0

0

0

1

0

1

0

0

1

1

1

Tablica prawdy bramki AND:

Wektor prawdy funkcji to
wartości funkcji.

X=[0 0 0 1]

T

- wektor prawdy dla bramki AND

24

24

24

24

Postać FDCF (SOP)

To postać dyzjunkcyjna, której składnikami są
zupełne iloczyny elementarne (ang.

minterm

- to

iloczyn wszystkich zmiennych danej funkcji, przy
czym zmienne te mogą występować jako proste lub
zanegowane) - jest to tzw. konstytuenta „1”.

=

=

=

∑

∑

2

10

)

101

,

011

,

001

,

000

(

)

5

,

3

,

1

,

0

(

)

(x

f

3

2

1

3

2

1

3

2

1

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

∨

∨

∨

=

Full Disjunctive Canonical Form, Sum of Products

13

25

25

25

25

Postać FCCF (POS)

To postać koniunkcyjna, której czynnikami są
zupełne sumy elementarne (ang.

maxterm

- to suma

wszystkich zmiennych danej funkcji, przy czym
zmienne te mogą występować jako proste lub
zanegowane) - jest to tzw. konstytuenta „0”.

∏

∏

=

=

2

10

)

111

,

110

,

100

,

010

(

)

7

,

6

,

4

,

2

(

)

(x

f

)

(

)

(

)

(

)

(

3

2

1

3

2

1

3

2

1

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

∨

∨

∧

∨

∨

∧

∨

∨

∧

∨

∨

=

Full Conjunctive Canonical Form, Product of Sum

26

26

26

26

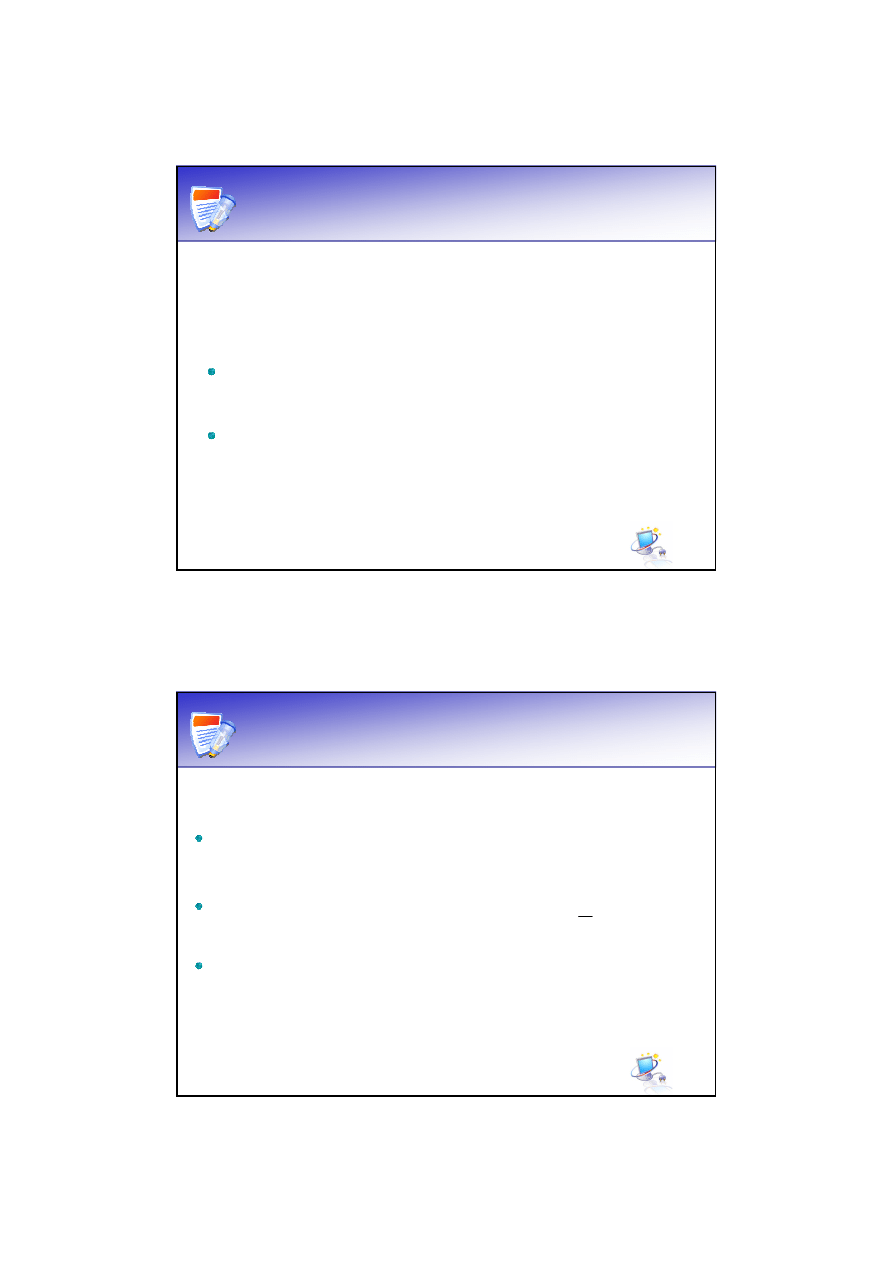
Tablica prawdy

x

1

x

2

x

3

f

(x)

0

0

0

1

0

0

1

1

0

1

0

0

0

1

1

1

1

0

0

0

1

0

1

1

1

1

0

0

1

1

1

0

3

2

1

x

x

x

3

2

1

x

x

x

3

2

1

x

x

x

3

2

1

x

x

x

3

2

1

x

x

x

∨

∨

3

2

1

x

x

x

∨

∨

3

2

1

x

x

x

∨

∨

3

2

1

x

x

x

∨

∨

∑

=

10

)

5

,

3

,

1

,

0

(

)

(x

f

10

)

7

,

6

,

4

,

2

(

)

(

∏

=

x

f

14

27

27

27

27

Uzyskiwanie postaci FDCF i FCCF

Każdą z funkcji logicznych da się zapisać w postaci
FDCF i FCCF.

Wyróżniamy następujące metody:

drogą

przekształceń

opartych

na

prawach

algebry logiki

przy pomocy tablicy prawdy lub wektora
prawdy [X] lub tablicy Karnaugha

28

28

28

28

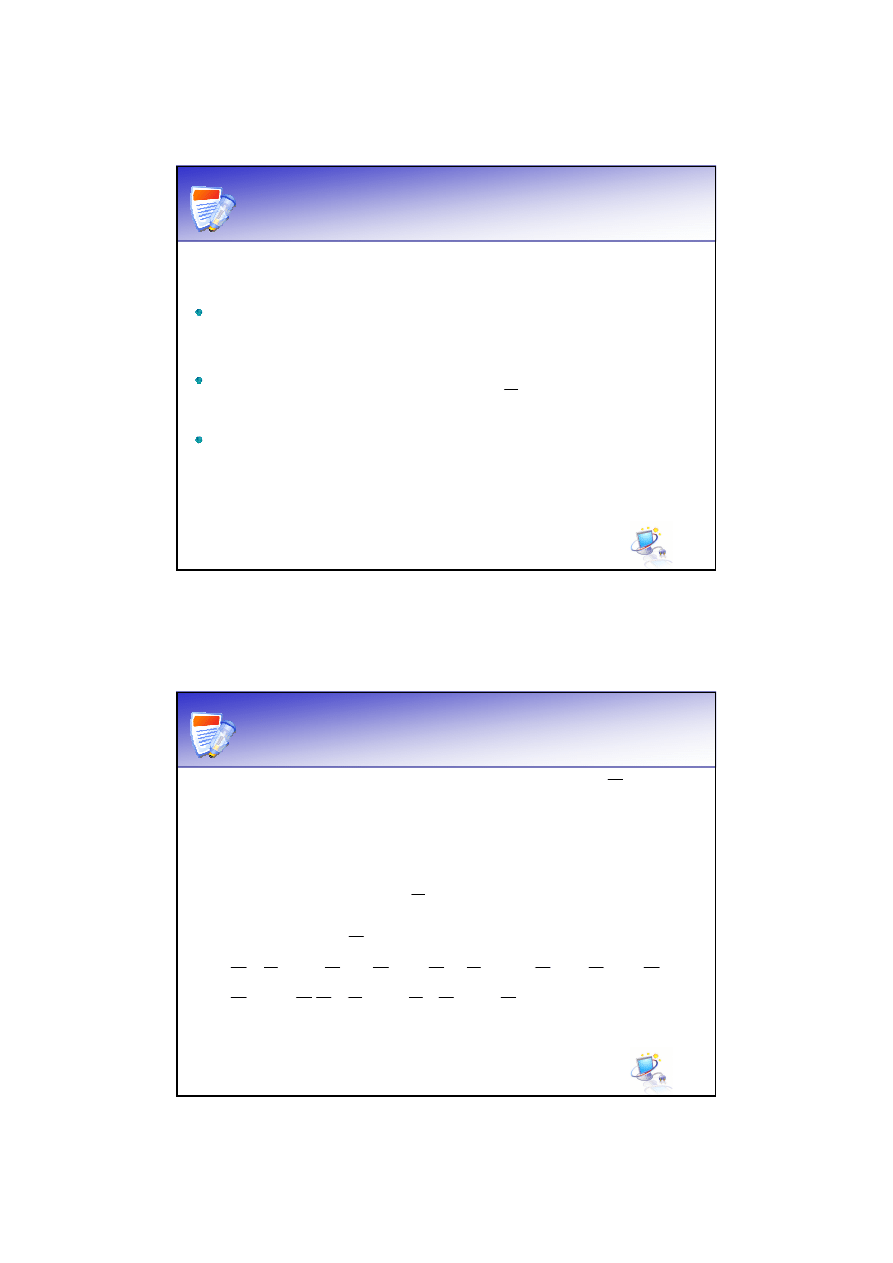
funkcję logiczną doprowadzić do postaci suma
iloczynów

te iloczyny, które nie są zupełnymi iloczynami
elementarnymi pomnożyć przez sumy:

skorzystać

z

prawa

rozdzielności

mnożenia

względem dodawania

Przekształcenia algebraiczne

Dla otrzymania FDCF należy:

)

1

(

=

∨

i

i

x

x

15

29

29

29

29

należy funkcję logiczną doprowadzić do postaci
iloczyn sum

do tych sum, które nie są zupełnymi sumami
elementarnymi dodać iloczyny:

skorzystać

z

prawa

rozdzielności

dodawania

względem mnożenia

Przekształcenia algebraiczne

Dla otrzymania FCCF należy:

)

0

(

=

i

i

x

x

30

30

30

30

Przekształcenia algebraiczne

Daną mamy funkcję logiczną:

3

1

2

1

)

(

)

(

x

x

x

x

x

f

∨

⊕

=

Szukamy FDCF metodą przekształceń analitycznych
(stosujemy prawo rozdzielności mnożenia względem
dodawania, a potem wprowadzamy brakujące zmienne
mnożąc przez sumę:

1

=

∨

i

i

x

x

).

3

2

1

3

2

1

3

2

1

3

2

1

3

2

1

2

2

3

1

3

3

2

1

3

3

2

1

3

1

2

1

2

1

3

1

2

1

)

(

)

(

)

(

)

(

)

(

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

f

∨

∨

∨

∨

=

=

∨

∨

∨

∨

∨

=

∨

∨

=

=

∨

⊕

=

16

31

31

31

31

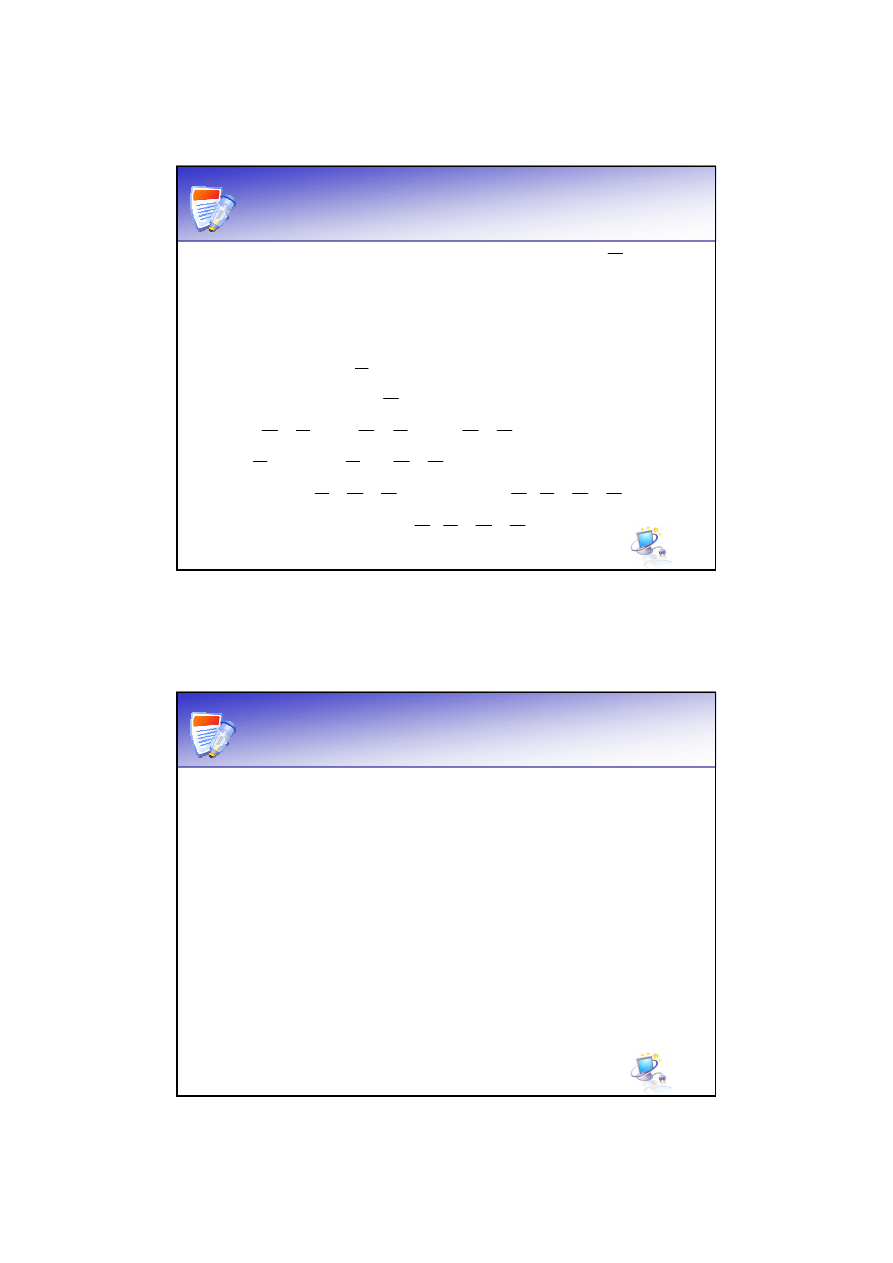
Przekształcenia algebraiczne

Daną mamy funkcję logiczną:

3

1

2

1

)

(

)

(

x

x

x

x

x

f

∨

⊕

=

Szukamy FCCF metodą przekształceń analitycznych
(stosujemy prawo rozdzielności dodawania względem
mnożenia, a potem wprowadzamy brakujące zmienne
przez dodanie:

0

=

i

i

x

x

).

)

)(

)(

(

)

)(

(

)

)(

(

)

(

)

(

)

(

)

(

)

(

3

2

1

3

2

1

3

2

1

3

2

1

3

3

2

1

3

2

1

1

2

3

2

2

1

1

2

1

3

2

1

2

1

3

1

2

1

2

1

3

1

2

1

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

f

∨

∨

∨

∨

∨

∨

=

=

∨

∨

∨

∨

=

∨

∨

∨

=

=

∨

∨

∨

∨

=

=

∨

∨

=

∨

∨

=

=

∨

⊕

=

32

32

32

32

Koniec

Dziękuję za uwagę