1

Elementy cyfrowe i układy

logiczne

Wykład 3

2

2

2

2

Legenda

System funkcjonalnie pełny

Optymalizacja wielopoziomowa

Inne typy bramek logicznych

2

3

3

3

3

Optymalizacja układów

wielopoziomowych

Układy wielopoziomowe

– układy zawierające

więcej niż dwa poziomy logiczne.

Istnieją dodatkowe możliwości uzyskania

oszczędności kosztów związane z

zastosowaniem układów wielopoziomowych.

4

4

4

4

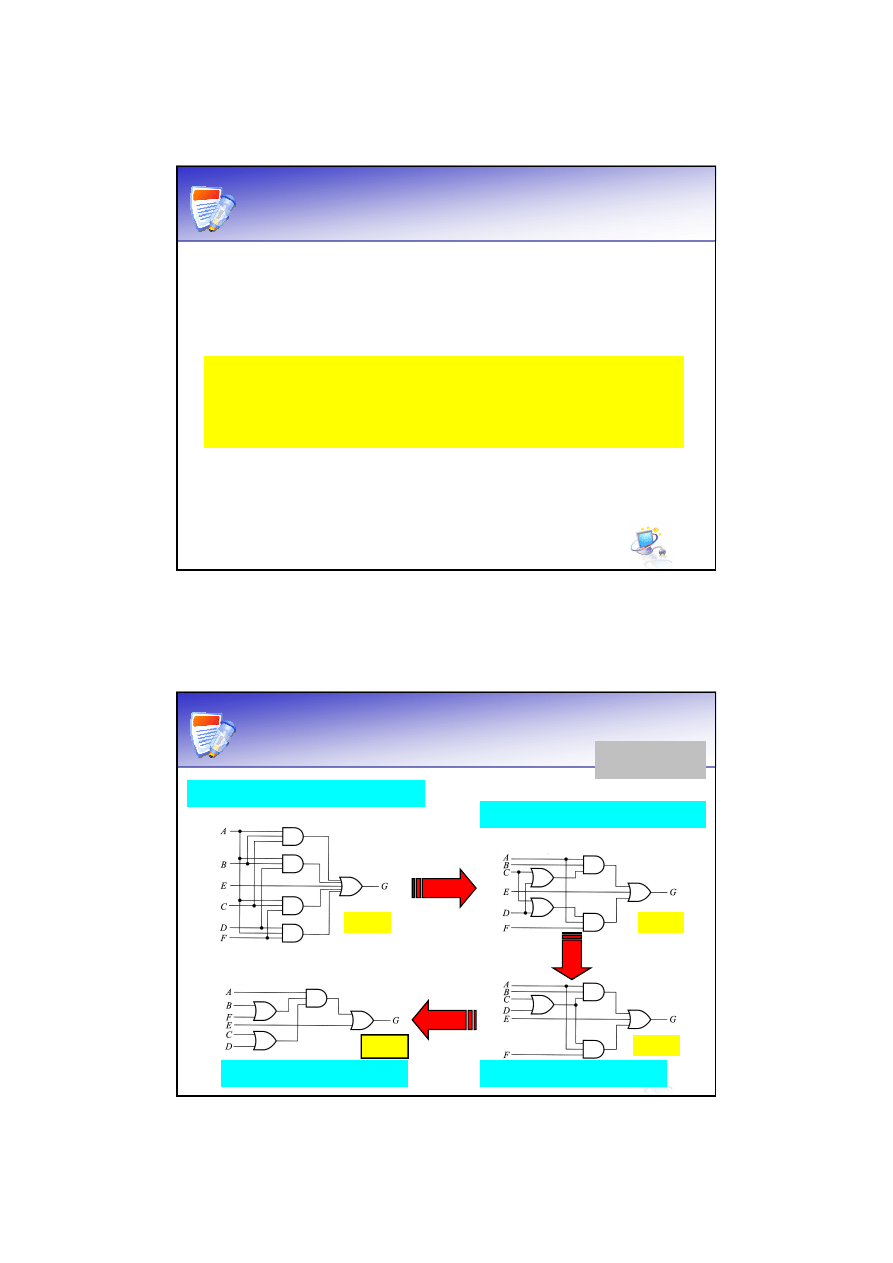
Optymalizacja układów

wielopoziomowych

G

= ABC+ABD+E+ACF+ADF

Koszt wejść

bramkowych - K

b

K

b

=17

Prawo rozdzielności

G

= AB(C+D)+E+A(C+D)F

K

b

=13

Pojedyncza

implementacja CD

K

b

=11

G

= (AB+AF)(C+D)+E

G

= A(B+F)(C+D)+E

A przed (

K

b

=9

3

5

5

5

5

Optymalizacja układów

wielopoziomowych

Optymalizacja

wielopoziomowa

bazuje

na

zastosowaniu ciągu przekształceń, które są
wykonywane w powiązaniu z obliczeniami
kosztów w celu znalezienia dobrego, choć
nieoptymalnego, rozwiązania.

6

6

6

6

Optymalizacja układów

wielopoziomowych

Możliwe transformacje:

Faktoryzacja (ang. factoring)

–

to znalezienie postaci iloczynowej na

podstawie zarówno wyrażenia funkcji w postaci sumy iloczynów, jak i
wyrażenia w postaci iloczynu sum.

Dekompozycja (ang. decomposition)

–

to wyrażenie funkcji za pomocą

zbioru nowych funkcji.

Ekstrakcja (ang.extraction)

–

wyrażenie wielu funkcji za pomocą zbioru

nowych funkcji.

Zastępowanie (ang. substitution) funkcji G w funkcji F

–

to

wyrażanie funkcji F jako funkcji G oraz niektórych lub wszystkich
pierwotnych zmiennych funkcji F.

Eliminacja (ang. elimination)

–

to operacja odwrotna do zastępowania,

podczas której funkcja G występująca w wyrażeniu funkcji F jest
zastępowana wyrażeniem opisującym G. Eliminacja nazywana jest również

spłaszczaniem (ang. flattening)

lub

składaniem (ang. collapsing)

4

7

7

7

7

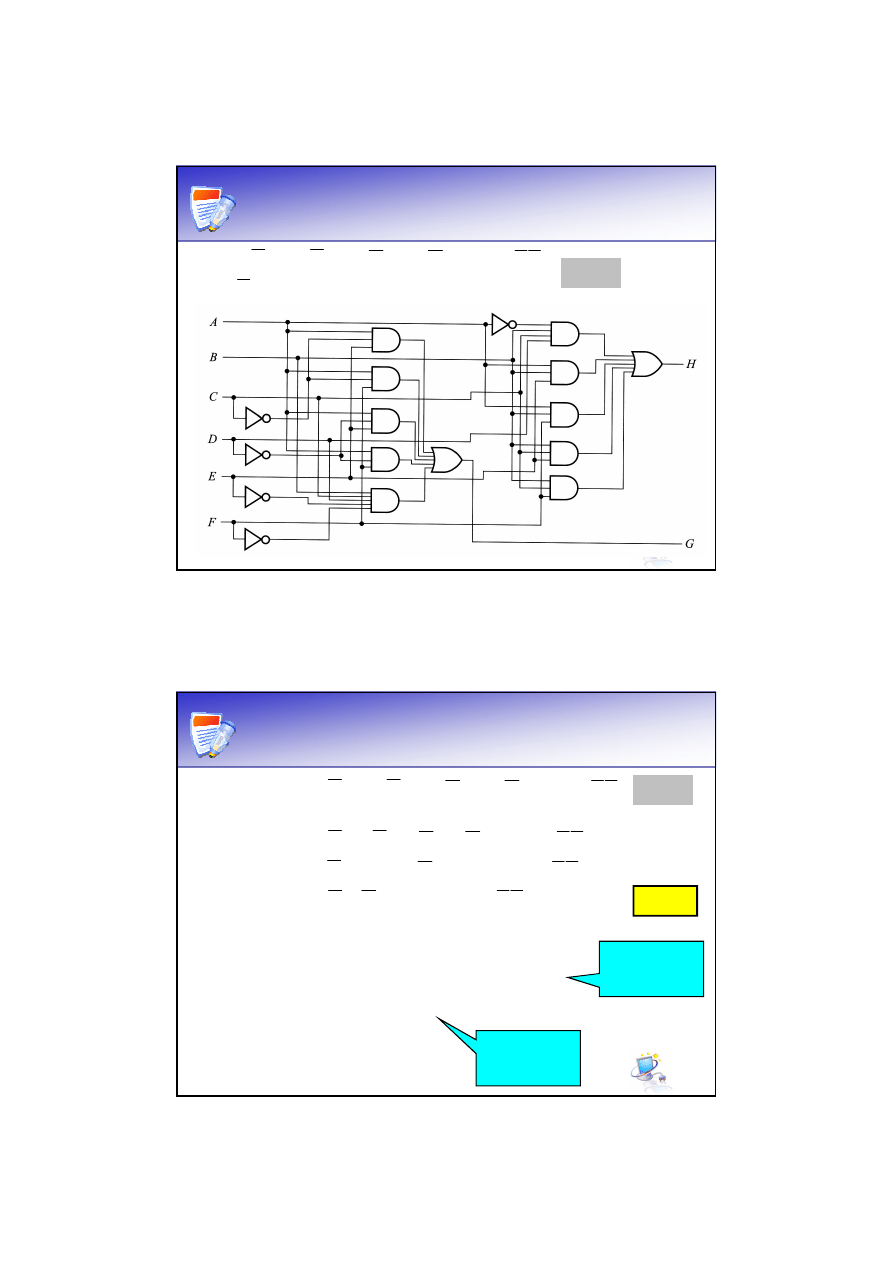
Przykład

F

E

BCD

F

D

A

E

D

A

F

C

A

E

C

A

G

+

+

+

+

=

BCF

BCE

ABF

ABE

BCD

A

H

+

+

+

+

=

K

b

=48

Bez

wspólnych

iloczynów i

inwerterów

8

8

8

8

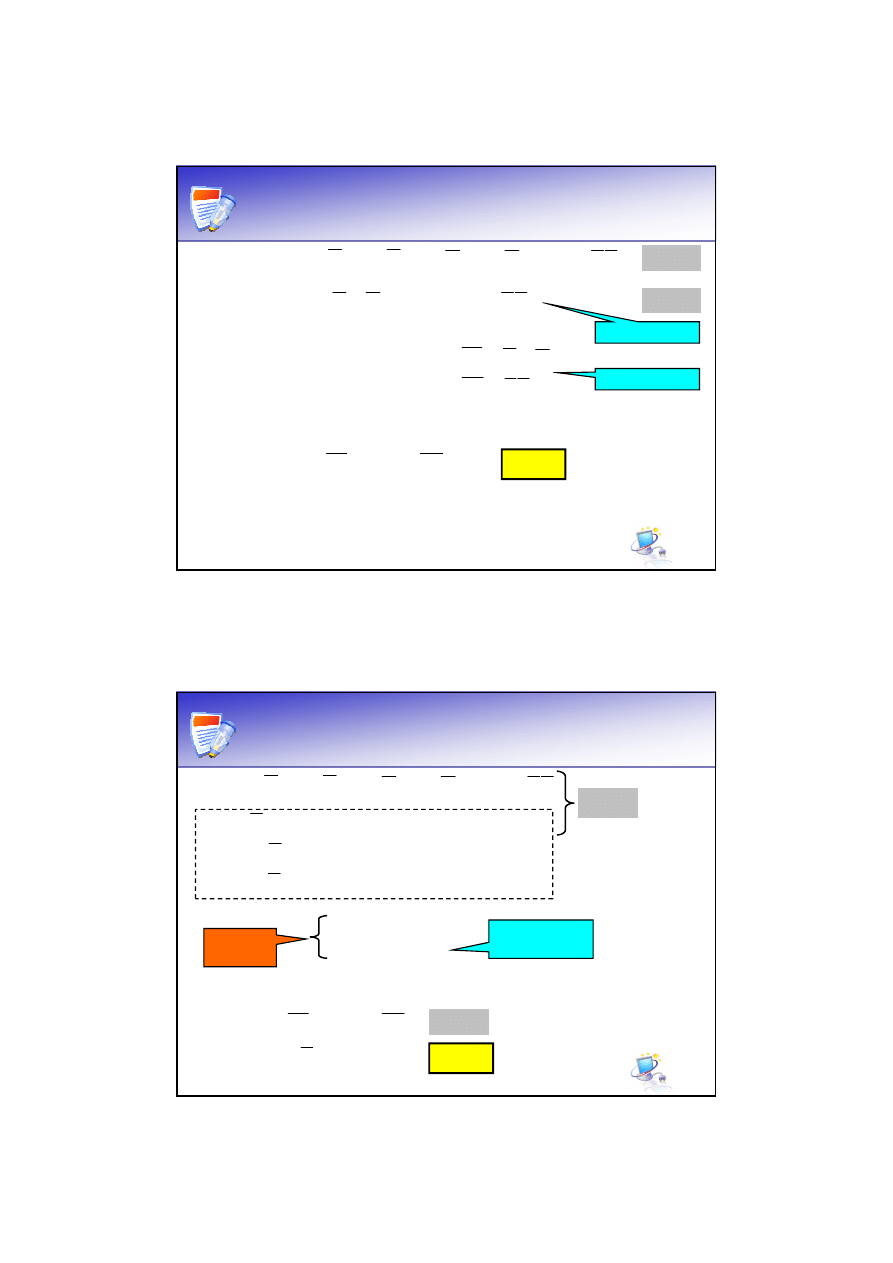
Faktoryzacja – przykład

K

b

=26

F

E

BCD

F

D

A

E

D

A

F

C

A

E

C

A

G

+

+

+

+

=

(

)

F

E

BCD

F

D

E

D

F

C

E

C

A

G

+

+

+

+

=

(

)

(

)

[

]

F

E

BCD

F

E

D

F

E

C

A

G

+

+

+

+

=

(

)

(

)

F

E

BCD

F

E

D

C

A

G

+

+

+

=

K

b

=18

• zwiększenie liczby poziomów (z 3 do 4)

• układ może charakteryzować się dużym

opóźnieniem

Więcej bramek

połączonych

szeregowo

W zależności

od technologii
implementacji

5

9

9

9

9

Dekompozycja – przykład

K

b

=26

F

E

BCD

F

D

A

E

D

A

F

C

A

E

C

A

G

+

+

+

+

=

(

)

(

)

F

E

BCD

F

E

D

C

A

G

+

+

+

=

K

b

=18

CD

X =

1

F

E

X

+

=

2

D

C

X

+

=

1

F

E

X =

2

2

1

2

1

X

BX

X

X

A

G

+

=

K

b

=12

Po faktoryzacji

Dopełnienie

10

10

10

10

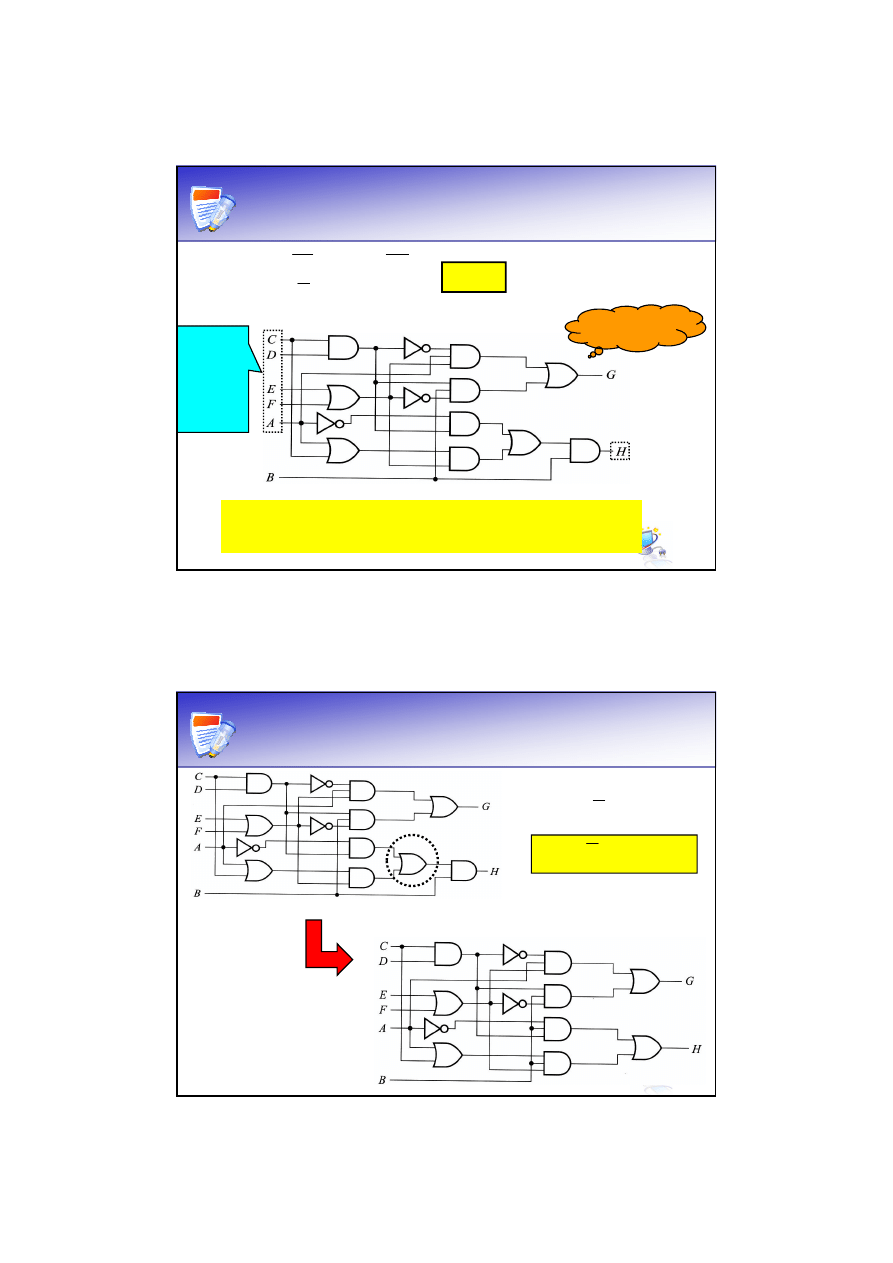
Ekstrakcja – przykład

K

b

=48

F

E

BCD

F

D

A

E

D

A

F

C

A

E

C

A

G

+

+

+

+

=

K

b

=31

2

1

2

1

X

BX

X

X

A

G

+

=

K

b

=25

Ekstrahowanie

czynników

(

)

2

3

1

X

X

X

A

B

H

+

=

BCF

BCE

ABF

ABE

BCD

A

H

+

+

+

+

=

(

)

CF

CE

AF

AE

CD

A

B

H

+

+

+

+

=

(

) (

)(

)

[

]

F

E

C

A

CD

A

B

H

+

+

+

=

Wspólne

dla G i H

CD

X =

1

F

E

X

+

=

2

C

A

X

+

=

3

Bez

wspólnych

iloczynów i

inwerterów

Po dekompozycji, bez

wspólnych iloczynów

Z uwzględnieniem

wspólnych iloczynów

6

11

11

11

11

2

1

2

1

X

BX

X

X

A

G

+

=

K

b

=25

(

)

2

3

1

X

X

X

A

B

H

+

=

Z uwzględnieniem

wspólnych iloczynów

Sygnały

przechodzą

ce przez 4

2-

wejściowe

bramki

opóźnienie

Skracanie ścieżek powinno być dokonane przy

minimalnym wzroście liczby wejść bramkowych

12

12

12

12

Eliminacja – przykład

(

)

2

3

1

X

X

X

A

B

H

+

=

2

3

1

X

BX

X

A

B

H

+

=

Eliminacja

czynnika B

7

13

13

13

13

Inne typy bramek

14

14

14

14

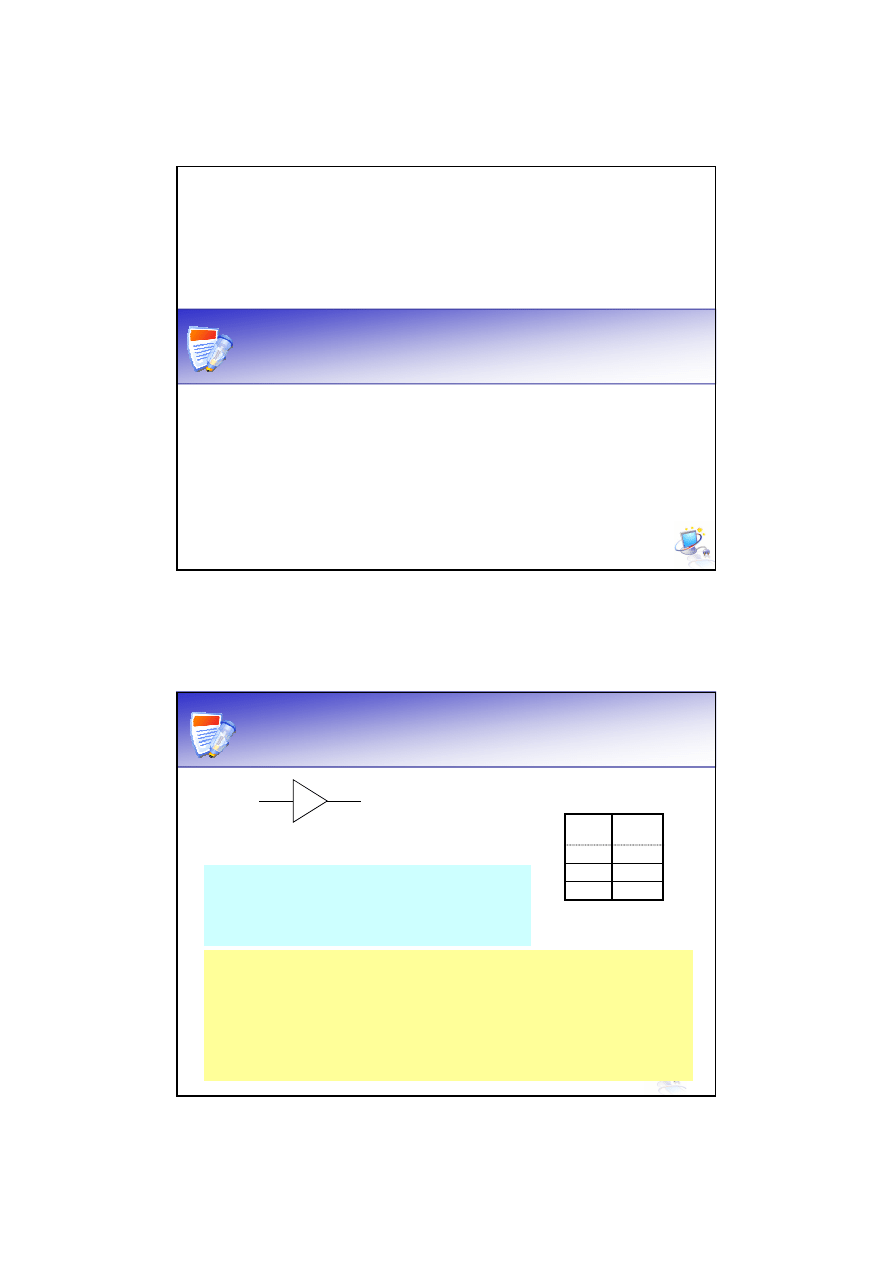
Bufor

Tablica prawdy

Wejście

Wyjście

X

F

0

0

1

1

Bufor realizuje funkcję:

F

= X

Wyjściowa wartość binarna równa
jest wartości binarnej podanej na
wejście.

X

F

Zastosowanie:

• wzmacnianie sygnału elektrycznego, aby umożliwić
większe obciążenie wyjścia (wejściami innych bramek)

• skracanie czasu propagacji sygnałów przez układ

8

15

15

15

15

Bufor 3-stanowy

Wejście

Wyjście

E

X

F

0

0

Hi-Z

0

1

Hi-Z

1

0

0

1

1

1

Tablica prawdy

X

F

E

Stan wysokiej

impedancji

(rozwarcie,

przerwa w

obwodzie).

Bramki z wyjściami przyjmującymi wartości Hi-Z
można łączyć ze sobą wyjściami, pod warunkiem, że

ż

adne dwie bramki w tym samym czasie nie przyjmą

na wyjściach przeciwnych wartości 0 i 1

Bufor 3-stanowy
realizuje funkcję: F=X

16

16

16

16

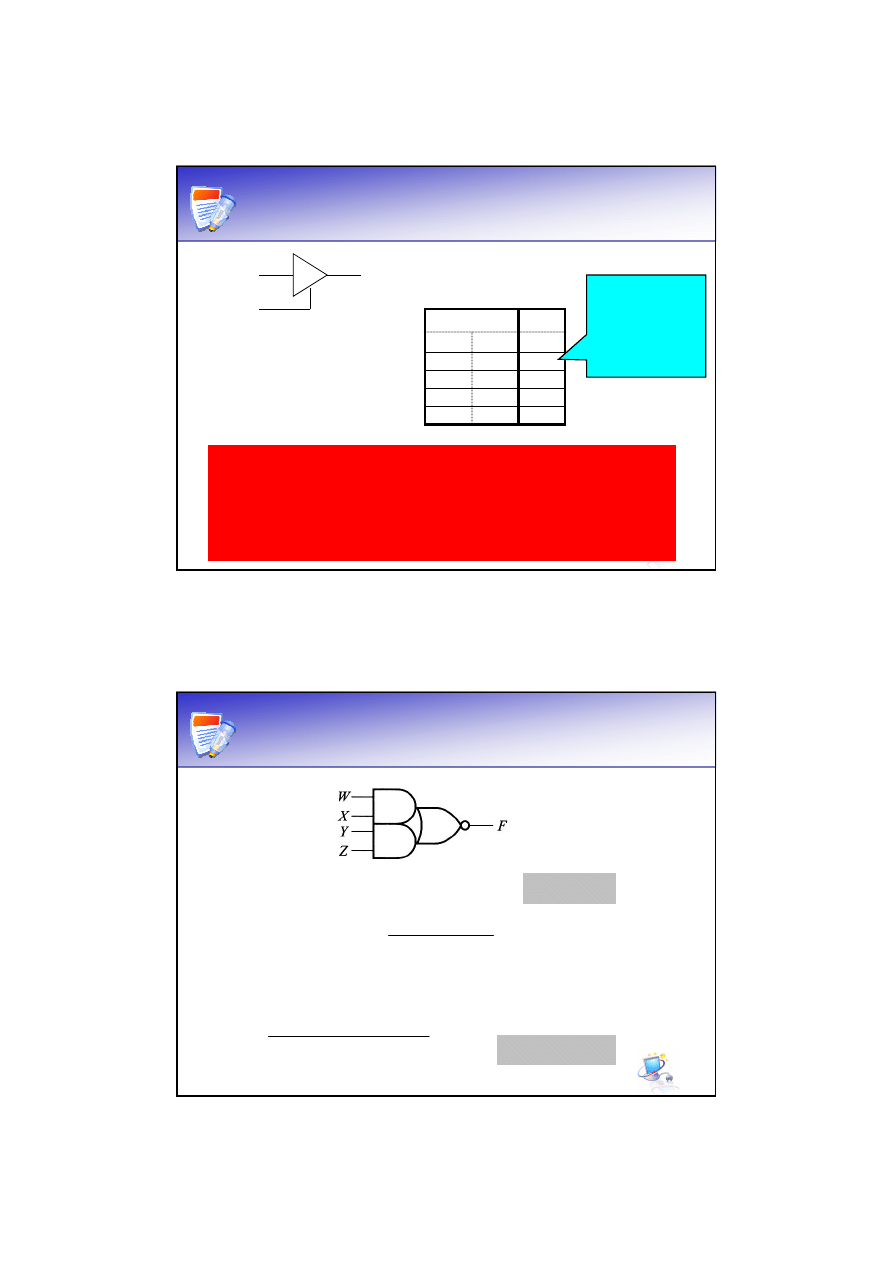
AND-OR-INVERTER (AOI)

AOI realizuje funkcję:

YZ

WX

F

+

=

2-2 AOI

YZ

WX

ABC

F

+

+

=

3-2-2 AOI

9

17

17

17

17

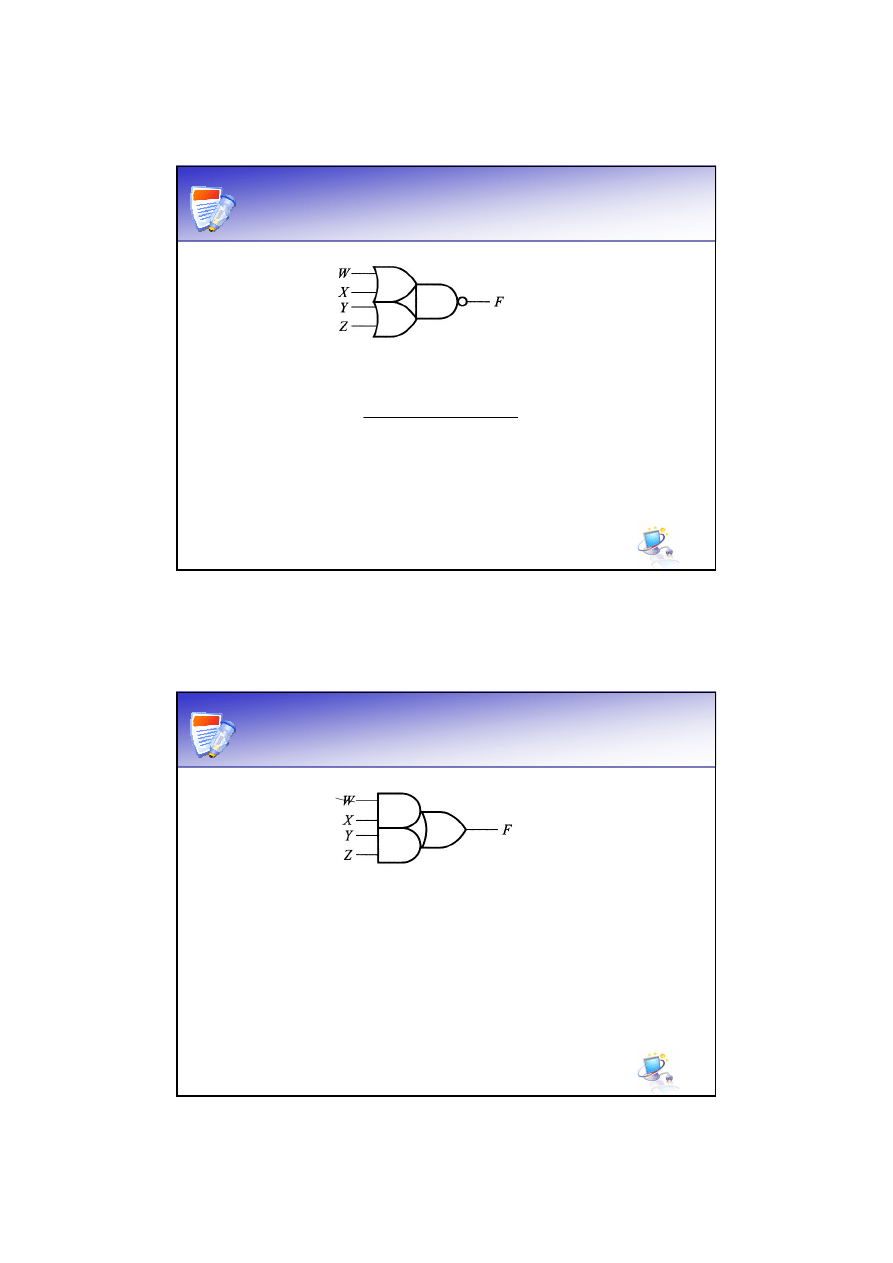
OR-AND-INVERTER (OAI)

OAI realizuje funkcję:

(

)(

)

Z

Y

X

W

F

+

+

=

18

18

18

18

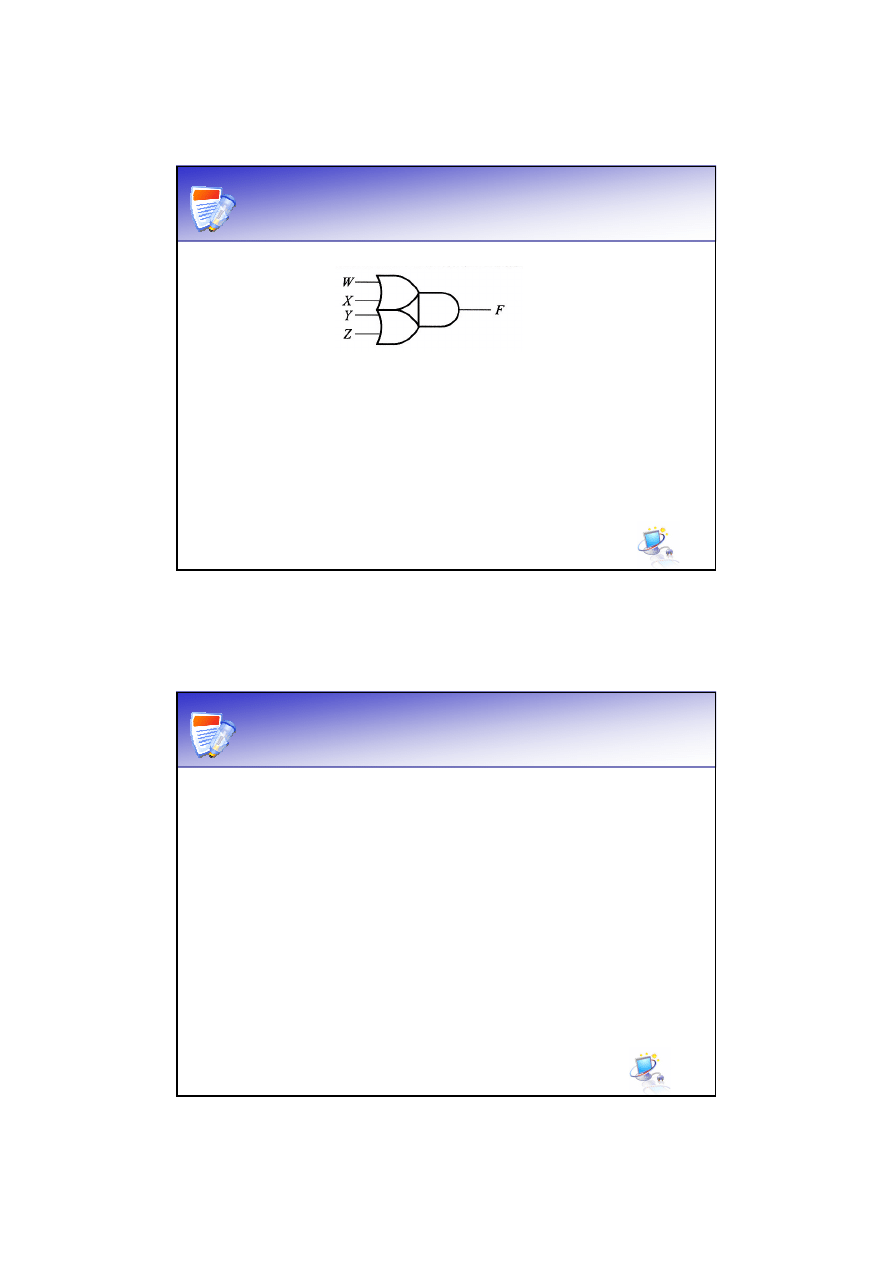
AND-OR (AO)

AO realizuje funkcję:

YZ

WX

F

+

=

10

19

19

19

19

OR-AND (OA)

OA realizuje funkcję:

(

)(

)

Z

Y

X

W

F

+

+

=

20

20

20

20

Definicje podstawowe

Funkcjonalnie pełnym zestawem bramek

logicznych

nazywamy

zestaw

bramek

realizujących wszystkie działania, tworzący

funkcjonalnie pełny zestaw operatorów.

11

21

21

21

21

System funkcjonalnie pełny

System operatorów złożony z operatorów binarnych,

unitarnych oraz stałych 0 i 1 nazywamy

systemem

funkcjonalnie

pełnym

,

jeżeli

każda

funkcja

zmiennych x

1

…x

n

może być przedstawiona za pomocą

formuły zbudowanej z tych zmiennych, z użyciem

operatorów wchodzących do tego systemu.

22

22

22

22

System funkcjonalnie pełny c.d.

Rodzaje systemów funkcjonalnie pełnych:

AND, OR, NOT
NAND

NOR

AND, NOT
OR, NOT
implikacja, stała 0

i z zakazem, NOT
implikacja, NOT
i z zakazem, stała 1
równoważność, AND, stała 0
równoważność, OR, stała 1

12

23

23

23

23

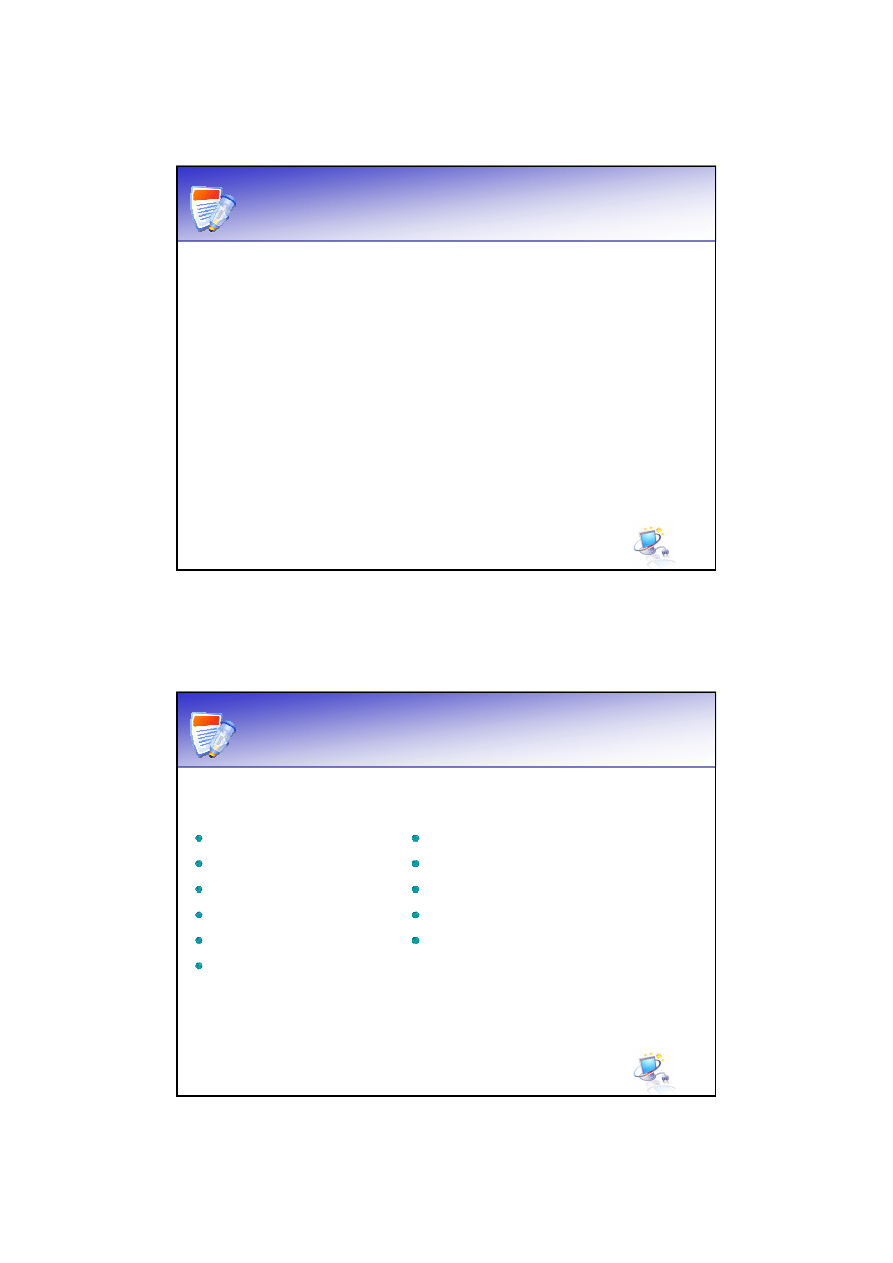
System funkcjonalnie pełny

2

0

1

0

3

2

1

)

(

x

x

x

x

x

x

x

x

f

∨

∨

=

Daną mamy następującą funkcję zapisaną w formie DCF:

Schemat funkcji:

x

0

x

1

x

2

x

3

3

2

1

x

x

x

1

0

x

x

2

0

x

x

f(x)

1

x

0

x

2

x

24

24

24

24

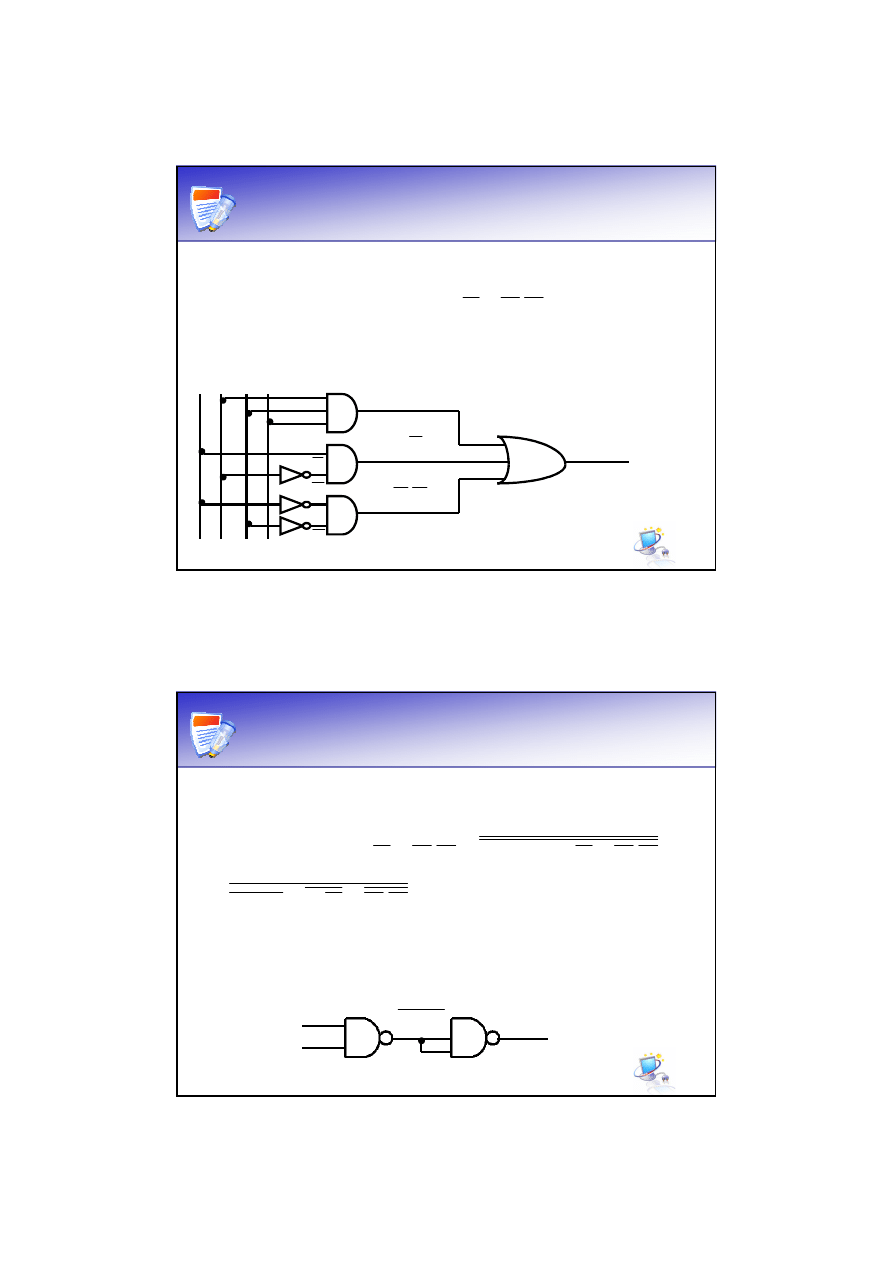
Zapis funkcji przy pomocy

bramek NAND

Przy

pomocy

dwóch

bramek

NAND

możemy

zrealizować funkcję AND.

Funkcję musimy doprowadzić do postaci składającej się z
zaprzeczeń koniunkcji.

2

0

1

0

3

2

1

2

0

1

0

3

2

1

2

0

1

0

3

2

1

)

(

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

f

∧

∧

=

=

∨

∨

=

∨

∨

=

x

1

x

2

2

1

x

x ∧

2

1

x

x ∧

13

25

25

25

25

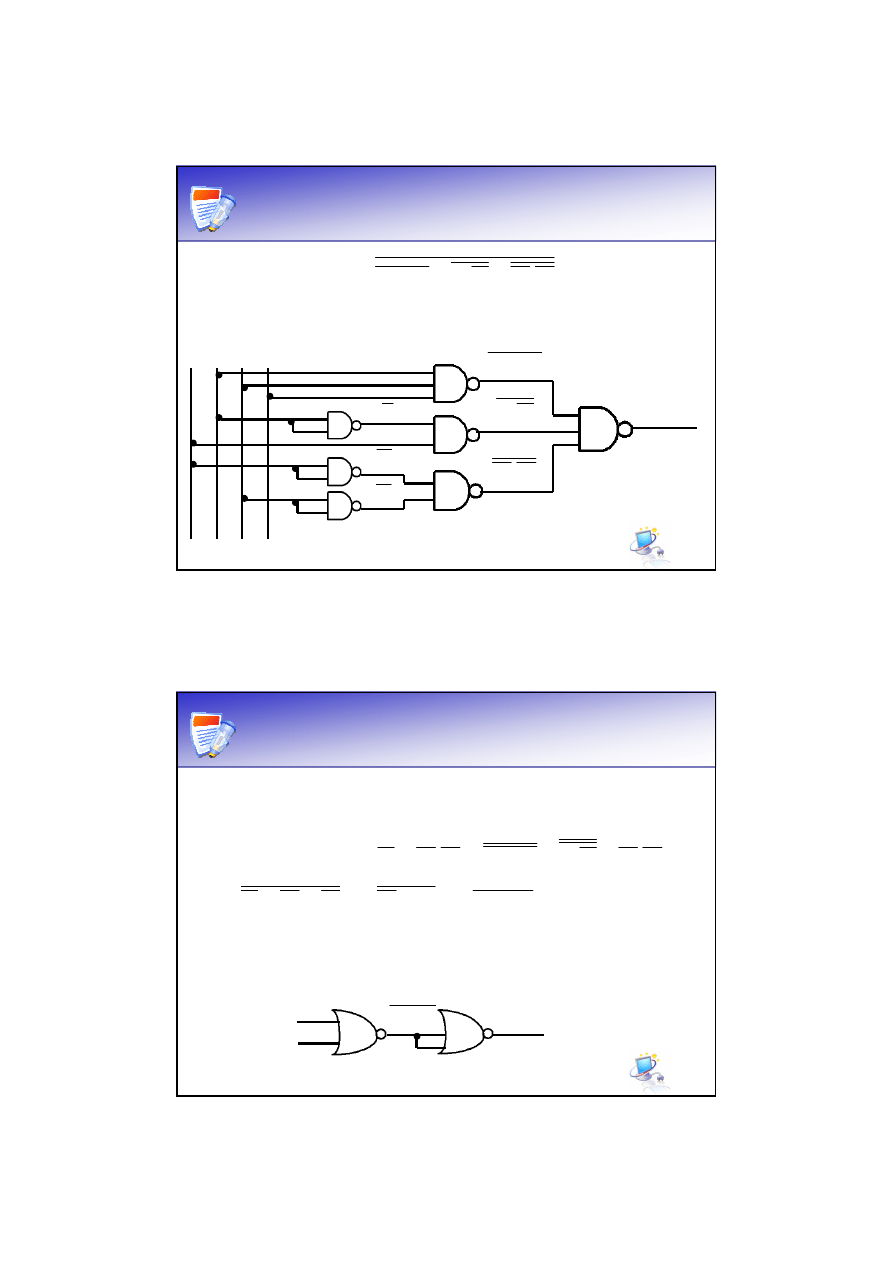
Zapis funkcji przy pomocy

bramek NAND c.d.

2

0

1

0

3

2

1

)

(

x

x

x

x

x

x

x

x

f

∧

∧

=

x

0

x

1

x

2

x

3

3

2

1

x

x

x

1

0

x

x

2

0

x

x

0

x

1

x

2

x

f(x)

26

26

26

26

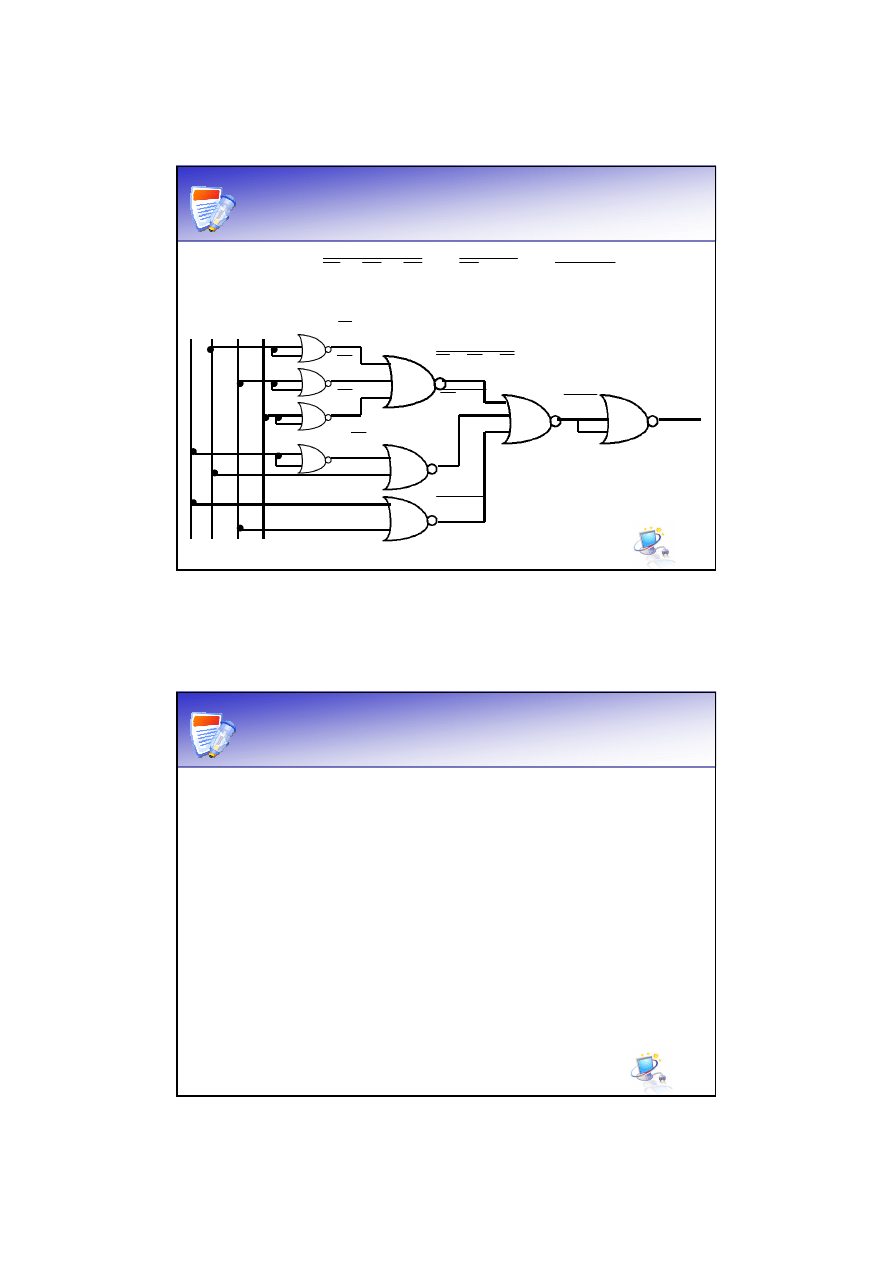
Zapis funkcji przy pomocy

bramek NOR

2

1

x

x ∨

Przy pomocy dwóch bramek NOR możemy zrealizować
funkcję OR.

x

1

x

2

2

1

x

x ∨

Funkcję musimy doprowadzić do postaci składającej się z
zaprzeczeń alternatywy.

)

(

)

(

)

(

)

(

2

0

1

0

3

2

1

2

0

1

0

3

2

1

2

0

1

0

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

f

∨

∨

∨

∨

∨

∨

=

=

∨

∨

=

∨

∨

=

14

27

27

27

27

Zapis funkcji przy pomocy

bramek NOR

)

(

)

(

)

(

)

(

2

0

1

0

3

2

1

x

x

x

x

x

x

x

x

f

∨

∨

∨

∨

∨

∨

=

x

0

x

1

x

2

x

3

1

x

3

x

2

x

0

x

3

2

1

x

x

x

∨

∨

2

0

x

x ∨

1

0

x

x ∨

)

(x

f

)

(x

f

28

28

28

28

Koniec

Dziękuję za uwagę