1

Dyfuzja

Wstęp

Generalnie o dyfuzji. Skupiałem się na stronie obliczeniowej, bo do kolosa to

dla was najważniejsze jest.

Otoczką dla całego wywodu są gotowe rozwiązania kolosa. Przy zadaniach

postaram się opisać, dlaczego jest tak, a nie inaczej

1

.

Wyjaśnienia potrzebnych fenomenów są, dla kontrastu, niezbyt dogłębnie

- nie będzie tu dokładnych opisów typów dyfuzji w ciele stałym.

2

Ponadto,

ponieważ zadania wyraźnie ograniczają się do jednego wymiaru

3

, definicje przy

wyjaśnieniach zwykle będą korzystały z pochodnej po jednej zmiennej, zamiast
z adekwatnego tam operatora gradientu.

Podstawy dyfuzji - pierwsze prawo Ficka

Dyfuzja ma różne powody działania w różnych substancjach, stanach sku-

pienia; zależą one też od tego, co dyfunduje

4

. Szczęśliwie, większość z nich ma

taką samą interpretację, która zawiera się w prawach Ficka.

Pierwsze z nich w ogólnej postaci to

J = −Dgradφ

(1)

gdzie J to strumień

5

dyfuzji, D to współczynnik dyfuzji, a φ to koncentracja.

Operator gradientu φ to miara rozkładu substancji w ośrodku - pozwala nam
zidentyfikować obszary, gdzie koncentracja jest duża, a gdzie mała

6

. Ponieważ

dyfuzja działa tak, że z obszarów o dużej koncentracji przechodzimy do obszarów
o małej koncentracji, to strumień działa przeciwnie do gradientu. Dlatego we
wzorze jest minus.

Forma pierwszego prawa dla jednego wymiaru x:

J = −D

∂φ

∂x

(2)

Jak widać, dla jednego wymiaru używamy po prostu pochodnej po x.

Przydatne mogą być jednostki, w jakich są te rzeczy wyrażone. x jest jed-

nostkach odległości, np. cm. φ to jednostka ilości substancji przez odległość do
trzeciej, np.

mol

m

3

. Gradient φ jest typu

mol

m

4

. D to odległość do kwadratu przez

1

Powinno wam pozwolić rozwiązać zadanie w ogólnym przypadku - zmienione dane, wa-

runki brzegowe...

2

Chwała niebiosom.

3

Nawet drugie, które wyprowadzałem z przekonaniem dla dwóch wymiarów i wychodził mi

wynik

√

2 razy za duży...

4

Np. wolne elektrony w przewodnikach; temperatura może być opisana poprzez dyfuzję.

5

Jak pamiętacie, strumień to miara ilości substancji przechodzącej przez daną powierzchnię.

6

Jest to taka pochodna dla dowolnej ilości wymiarów - pozwala nam widzieć, w którą stronę

funkcja rośnie i w jakim tempie.

1

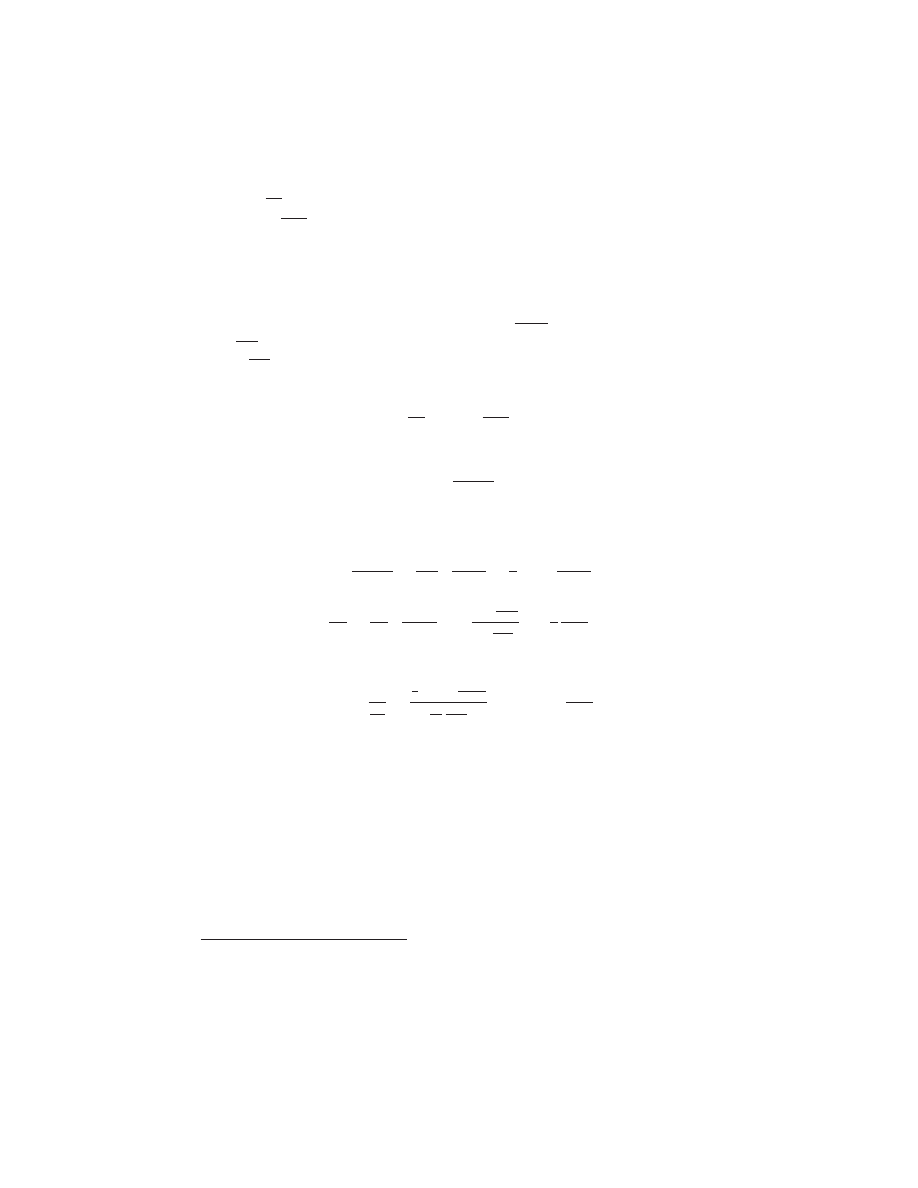
czas, np.

m

2

s

. Wreszcie, strumień to (jak łatwo wywnioskować z definicji stru-

mienia) typ

mol

m

2

·s

. Jednostki “ilość substancji” będą różniły się pomiędzy typami

dyfuzji - nie ma czegoś takiego jak mol temperatury.

To prawo wystarczy do przerobienia zadania pierwszego...

1.1

Zad 1

Treść: Strumień dyfuzji składnika wynosi

10

13

at

cm

2

s

przy gradiencie gęstości

−100

g

cm

4

. Oblicz współczynnik dyfuzji składnika, wiedząc, że masa molowa wy-

nosi 12

g

mol

.

Zaczynamy od wyciągnięcia z treści danych - gradient gęstości:

∂ρ

∂x

= −100

g

cm

4

(3)

Strumień dyfuzji:

J =

10

13

at

cm

2

s

(4)

Jak widzimy, są w różnych jednostkach ilości substancji. Najłatwiej sobie przy
tych danych przeliczyć na mole substancji:

J =

10

13

at

cm

2

s

=

1

N

A

·

10

13

cm

2

s

≈

1

6

10

−10

mol

cm

2

s

.

(5)

∂φ

∂x

=

∂φ

∂x

·

1

m

mol

= −

100

g

cm

4

12

g

mol

= 8

1

3

mol

cm

2

(6)

Wystarczy przekształcić pierwsze prawo Ficka na odpowiednią postać:

D = −

J

∂φ
∂x

=

1
6

10

−10 mol

cm

2

s

25

3

mol

cm

2

= 2 · 10

−12

cm

2

s

(7)

co daje nam rozwiązanie zadania.

Dyfuzja - głębokość dyfuzji

Żeby wiedzieć, jak głęboko będzie zachodziła dyfuzja, musimy znaleźć jakiś

wzór łączący głębokość ze współczynnikiem dyfuzji. Tutaj wyprowadzam go
najłatwiejszym sposobem, jaki znalazłem - nie musicie czytać wyprowadzenia,
jeżeli nie chcecie; możecie od razu przejść do zadania

7

. Wzór będzie użyty w

zadaniu. A ja dla sportu rozpiszę rozumowanie.

Wyprowadzę tutaj całe prawo Ficka dla jednego wymiaru

9

- przez przypadek

wyjdzie nam definicja D.

7

Ale pozwoli to lepiej zrozumieć mechanizm dyfuzji, więc polecam!

8

8

A ponadto mnie by to ucieszyło.

9

To znaczy, przyjmujemy, że ruch zachodzi tylko wzdłuż jednego wymiaru, nawet, jeżeli

pręt ma grubość

2

Mamy długi pręt. Wzdłuż niego definiuję sobie wymiar x. W pręcie znaj-

dują się cząstki substancji dyfundującej, które wykonują losowe ruchy w miarę
upływu czasu t. Niech N (x, t) to ilość cząstek w punkcie x o czasie t. Przyjmu-
jemy, że badamy ruch cząstek w prawą stronę pręta.

Przy każdym kroku czasowym, średnio połowa cząstek pójdzie w lewo, a

połowa w prawo. Zbadajmy sobie, ile w ogólności cząstek przejdzie z punktu x
do następnego po prawej punktu x + ∆x: będzie to połowa cząstek z punktu
x (te, które pójdą w prawo) minus połowa cząstek z punktu x + ∆x (te, które
pójdą w lewo), czyli:

1

2

· [N (x, t) − N (x + ∆x, t)]

(8)

Strumień J to będzie ten ruch przez jakiś przekrój o polu a, w trakcie wyko-
nywanego kroku czasowego ∆t. Zatem ogólny ruch cząstek możemy podzielić
przez a∆t, by otrzymać strumień (od razu wyciągam minus przed nawias):

J = −

1

2∆t

· [

N (x + ∆x, t)

a

−

N (x, t)

a

]

(9)

Teraz zauważmy, że gęstość cząstek jest zdefiniowana jako ilość cząstek przez
objętość badanego obszaru - w naszym przypadku to objętość “przedzialiku” o
długości ∆x i przekroju a

φ(x, t) =

N (x, t)

a∆x

(10)

I w tym momencie stosujemy brudną sztuczkę matematyczną: mnożymy prawą

stronę równania strumienia przez

(∆x)

2

(∆x)

2

:

J = −

(∆x)

2

2∆t

· [

N (x + ∆x, t)

a(∆x)

2

−

N (x, t)

a(∆x)

2

] = −

(∆x)

2

2∆t

· [

φ(x + ∆x, t)

∆x

−

φ(x, t)

∆x

]

(11)

Jeżeli pamiętacie definicję pochodnej, to widzicie, że w nawiasie kwadratowym
mamy definicję pochodnej

∂φ
∂x

, a zatem:

J = −

(∆x)

2

2∆t

∂φ

∂x

= −D

∂φ

∂x

(12)

Czyli współczynnik dyfuzji to:

D =

(∆x)

2

2∆t

(13)

z czego głębokość wnikania to:

∆x =

√

2D∆t

(14)

a czas wnikania na głębokość to:

∆t =

(∆x)

2

2D

(15)

Tak, to naprawdę najłatwiejszy sposób, jaki znam.

3

1.2

Zad 2

Podstawić do wzoru:

∆t =

(∆x)

2

2D

(16)

i tyle.

Dyfuzja - drugie prawo Ficka

Drugie prawo Ficka przewiduje, jak będzie zachowywała się gęstość substan-

cji dyfundującej wraz z czasem:

∂φ

∂t

= −

∂J

∂x

= D

∂

2

φ

∂x

2

(17)

1.3

Zad 3

Z drugiego prawa Ficka:

∂T

∂t

= −

∂J

∂x

(18)

Ponieważ stan stacjonarny, to rozkład temperatury nie zmienia się w czasie:

∂T

∂t

= 0

(19)

Z dwóch ostatnich wynika, że

∂J

∂x

= 0

(20)

zatem

J = const

(21)

Nie wiem dokładnie o co chodzi z warunkami brzegowymi Neumanna. Zwykle
oznaczają, że mamy podaną wartość pochodnej temperatury na krańcach ob-
szaru. Tutaj jest tylko powiedziane, że mają być warunki brzegowe Neumanna,
więc przyjąłem, że w takim razie są równe 0 (w sumie inaczej ciężko cokolwiek
policzyć ręcznie bez przybliżeń, więc ma to sens). Oznacza to, że strumień będzie
równy 0, z czego wynika, że:

0 = J = −D

∂T

∂x

(22)

z czego wynika, że

∂T

∂x

= 0, a z tego T = const. Do tego wiemy, że żadna ener-

gia nam nie ucieknie, więc wystarczy zsumować energię będącą na początku w
pręcie, a następnie podzielić ją przez długość pręta, by otrzymać ogólną tempe-
raturę.

A jak podliczyć energię? Trza zrobić To-Czego-Nazwy-Nie-Wolno-Wymawiać.

Resztę rozwiązania macie w tym gotowcu, nie sprawdzałem, czy wynik się zga-
dza, ale punkcik jest, więc jest okejka.

4

1.4

Zad 4

Tak jak wcześniej, tylko że mamy warunki brzegowe Dirichleta. Warunek

brzegowy ten mówi, że wartości na granicach mierzonego obszaru są podane i
ustalone. Ponieważ nie są podane w zadaniu, przyjmujemy, że będą takie, jakie
wychodzą według podanego wzoru na temperaturę. Skoro

J = const

(23)

to

∂T

∂x

= const

(24)

czyli rozkład temperatury będzie funkcją liniową.

Zatem musimy zrobić interpolację liniową, czyli znaleźć odpowiednią funkcję

liniową łączącą punkty (0, T (0)) i (d, T (d)) według wzoru:

T

2

(x) = T (0) + x ·

T (d) − T (0)

d

(25)

Ogólny wzór interpolacji punktów (x

1

, y

1

), (x

2

, y

2

) to

y = y

1

+ (x − x

1

)

y

2

− y

1

x

2

− x

1

(26)

1.5

Zad 5

1.5.1

a)

Ponownie zadanie z wnikania. Najpierw korzystamy z wzoru, by otrzymać

D

1000

:

x

2

= 2D

1000

t ⇒ D

1000

=

x

2

2t

(27)

A potem wstawiamy do wzoru na głębokość wnikania w czasie 2t, zastępując
D

1050

przez 2D

1000

:

x

2

=

p

2D

1050

· 2t =

p

8D

1000

t =

√

4x

2

= 2x

(28)

1.5.2

b)

Tutaj wystarczy skorzystać z równania Arrheniusa. Wiecie, że D(1050K)

jest dwa razy większe od D(1000K), więc wystarczy po lewej stronie podzielić
jedno przez drugie, a po prawej podzielić odpowiadające równania Arrheniusa:

D

1050

D

1000

=

D

0

exp(−

E

1050K·R

)

D

0

exp(−

E

1000K·R

)

(29)

2D

1000

D

1000

=

exp(−

E

1050K·R

)

exp(−

E

1000K·R

)

(30)

5

2 = exp(−

E

1050K · R

+

E

1000K · R

)

(31)

ln 2 =

−E · 1000K + E · 1050K

1000K · 1050K · R

(32)

ln 2 =

E · 5K

105000 · R

(33)

Czyli

E = 21000K · ln 2 · R

(34)

6