Akademia Górniczo-Hutnicza im. Stanisława Staszica

w Krakowie

 

 

 

Wydział Inżynierii Mechanicznej i Robotyki 

Podstawy Konstrukcji Maszyn 2

Projekt nr 2 – Łożysko Ślizgowe

Wykonał:
Tomasz Siudak
Grupa 5

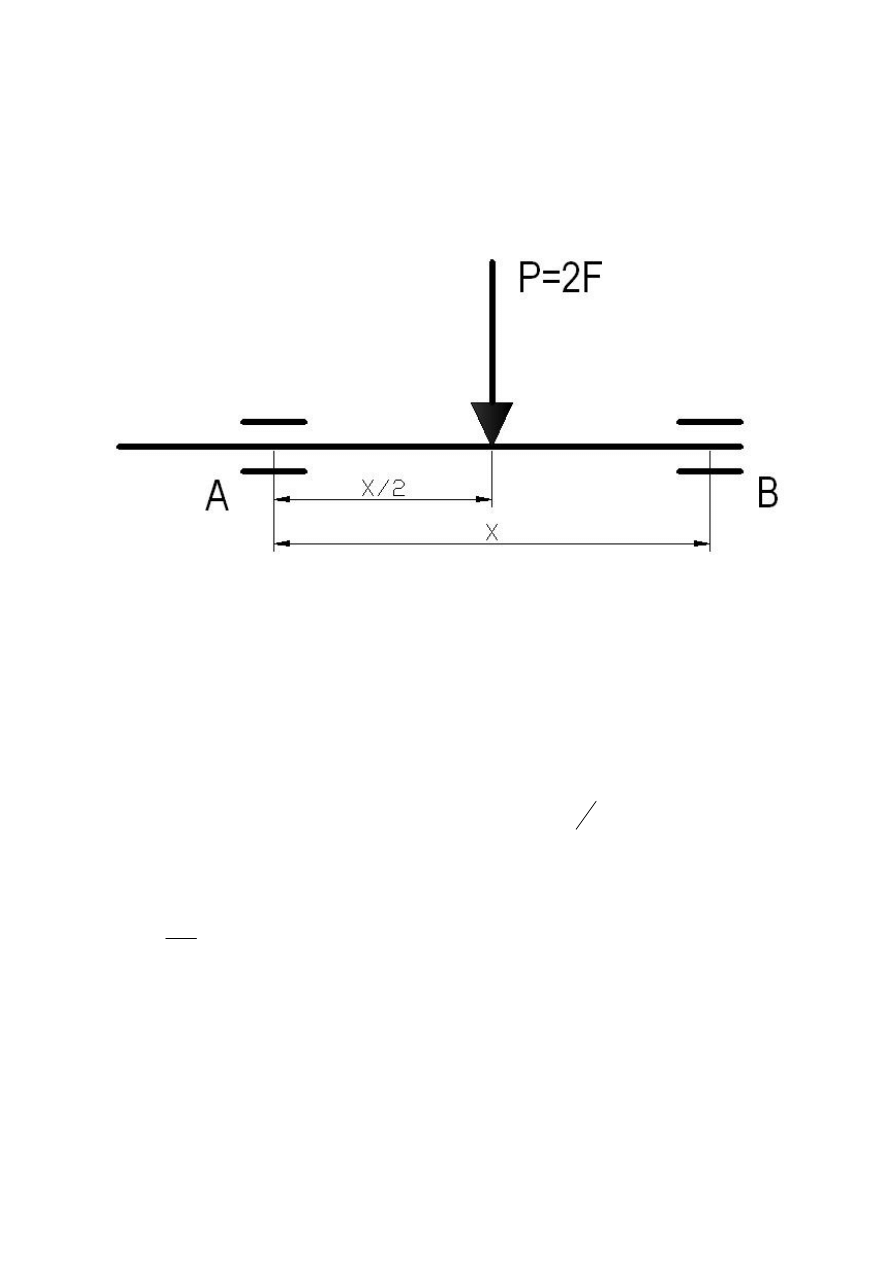
Temat:

Zaprojektować poprzeczne łożysko ślizgowe, pracujące w

warunkach tarcia płynnego dla przyjętego stosunku

1

l

d

λ

=

=

, kąta opasania

β π

=

. Technologia wykonania pozwala na uzyskanie wysokości nierówności

1,6

zc

R

m

μ

=

i

3, 2

zp

R

m

μ

=

. Olej przyjąć wg klasyfikacji ISO. Obciążenie, prędkość

obrotową oraz średnice czopa należy przyjąć następujące:

125

F

kN

=

,

250

min

obr

n

=

,

.

320

d

m

=

m

1

Dane Obliczenia Wynik

1

l

d

λ

=

=

β π

=

1,6

zc

R

m

μ

=

3, 2

zp

R

m

μ

=

125

F

k

=

N

250

min

obr

n

=

320

d

m

=

m

1. Obliczenia wstępne

Prędkość kątowa jest równa:

2

250

26,18

60

30

30

n

n

π

π

π

ω

⋅

=

=

=

=

1

s

−

Prędkość ślizgowa (obwodowa)

1

0,32

26,18

4,19

2

m

m

V

r

V

s

s

ω

−

= ⋅ ⇒ =

⋅

=

Nacisk średni

sr

p (ponieważ

1

l

d

=

)

(

)

3

2

2

3

125 10

125000

1,22

0,1024

320 10

sr

F

F

N

N

p

MPa

l d

d

m

−

⋅

=

=

=

=

=

⋅

⋅

2. Dobór materiału
Dobieram materiał panewki stop PbSb14Sn9CuAs do wylewania na
taśmy stalowe, dla którego

10

dop

p

MPa

=

i t

, wał – stal 45

130

dop

C

<

D

3. Obliczenia luzu względnego

Obliczam luz względny w zależności od prędkości obwodowej dla

łożysk metalowych.

4

0,8

V 30%

ψ

≈

⋅

±

3

1,15 10

ψ

−

=

⋅

min

0,7

ψ

ψ

≈

⋅

max

1,3

ψ

ψ

≈

⋅

3.1 Wyznaczam luz minimalny i maksymalny

3

3

min

min

min

0,7 1,15 10

320

257,6 10

L

d

L

mm

mm

ψ

−

−

=

⋅ ⇒

=

⋅

⋅

⋅

=

⋅

min

257,6

L

m

μ

=

3

3

max

max

max

1,3 1,15 10

320

478, 4 10

L

d

L

mm

mm

ψ

−

−

=

⋅ ⇒

=

⋅

⋅

⋅

=

⋅

max

478,4

L

m

μ

=

3.2 Dobór pasowania

Dla średnicy d = 320mm sprawdzam odchyłki graniczne zalecanych

pasowań (

min

L

EI

es

−

max

L

ES

ei

;

=

=

− ).

H7/e8

57

0

125

214

ES

EI

es

ei

= +

=

= −

= −

min

max

0 125 125

57 214 271

L

m

L

m

μ

μ

= +

=

=

+

=

H8/d9

89

0

210

350

ES

EI

es

ei

=

=

= −

= −

min

max

0 210 210

89 350 439

L

m

L

m

μ

μ

= +

=

=

+

=

H11/d11

360

0

210

570

ES

EI

es

ei

=

=

= −

= −

min

max

0 210 210

360 570 930

L

m

L

m

μ

μ

= +

=

=

+

=

1

26,18s

ω

−

=

4,19

m

V

s

=

1,22

sr

p

MPa

=

3

1,15 10

ψ

−

=

⋅

min

257,6

L

m

μ

=

max

478,4

L

m

μ

=

2

3

C

60

sr zal

t

−

=

D

0,048Pa s

η

≈

⋅

360

0

360

720

ES

EI

es

ei

=

=

= −

= −

min

max

0 360 360

360 720 1080

L

m

L

m

Sprawdzam odchyłki graniczne dla pasowań z poza szeregu zalecanego

H11/c11

μ

μ

= +

=

=

+

=

Na podstawie obliczeń luzów minimalnych i maksymalnych

stwierdzam, że najbardziej optymalnym pasowaniem (najbardziej

zbliżonym do szacunkowego) będzie H8/d9, w związku z powyższym,

takie też pasowanie przyjmuję.

(

)

min

max

1

324,5

2

sr

L

L

L

m

μ

=

+

=

3

324,5

1,014 10

320

sr

sr

L

d

ψ

−

=

=

=

⋅

3.3 Zmiana luzu wywołana temperaturą

(

) (

)

p

w

p

ot

t

t

ψ

α

α

Δ =

−

⋅

−

p

gdzie:

α - współczynnik rozszerzalności liniowej panewki

w

α

- współczynnik rozszerzalności liniowej czopa wału

p

t

ot

t

rz

sr

- średnia temperatura pracy łożyska (średnia temperatura środka

smarnego w łożysku podczas pracy)

- temperatura otoczenia

3.4 Luz względny rzeczywisty

ψ

ψ

ψ

=

+ Δ

0

Ponieważ obliczenia mają charakter szacunkowy, pomijam wpływ

temperatury na geometrię pasowania a co za tym idzie i luzu

względnego (

ψ

Δ =

rz

sr

)

Zatem:

ψ

ψ

=

czyli:

3

1,014 10

rz

ψ

−

=

⋅

60

sr zal

−

=

D

0,05Pa s

4. Dobór środka smarnego
4.1 Założenia wstępne

Zakładam wstępnie średnią temperaturę pracy oleju

t

C

dla

zadanej prędkości obwodowej czopa, oszacować można wstępnie

wymaganą lepkość oleju

η

≈

⋅

60

t

C

=

D

48

0,048

mPa s

Pa s

(dane zaczerpnięte z literatury).

Na podstawie w/w założeń dobieram wstępnie olej maszynowym,

którego lepkość dynamiczna w założonej temp. pracy jest najbardziej

zbliżona do zalecanej. Dobieram olej ISO VG 150, którego lepkość

dynamiczna dla temp.

jest równa:

η

≈

⋅ =

⋅

4.2 Obliczenia liczby Sommerfelda

(

)

2

2

6

3

''

0,048 4,16

0,19968

0,16

1, 25439912

1, 22 10

1,014 10

sr

rz

n

S

S

p

η

ψ

−

⋅

⋅

=

⇒ =

=

≈

⋅

⋅

⋅

⋅

gdzie:

η - lepkość dynamiczna oleju

[

]

Pa s

⋅

''

n

- prędkość obrotowa czopa

obr

s

⎡

⎤

⎢

⎥

⎣

⎦

sr

p - średni docisk powierzchniowy

[ ]

Pa

324,5

sr

L

m

=

μ

3

1,014 10

sr

−

ψ

=

⋅

3

1,014 10

rz

−

ψ

=

⋅

0,16

S

=

1,9

kJ

c

kg K

≈

⋅

3

950

kg

m

ρ

=

14

sr

c

T

p

ρ

⋅ ⋅ Δ

≈

(

)

1

328,15

55

T

K

=

D

4

C

(

)

343

358

70

85

dop

T

K

K

=

÷

÷

D

D

rz

ψ

- względny luz rzeczywisty [wartość bezwymiarowa]

4.3 Obliczenia przyrostu temperatury oleju w łożysku

Dla

:

60

t

C

=

D

1,9

kJ

kg K

≈

c

⋅

;

3

950

kg

m

ρ

=

0,16

S

=

Z wykresu dla obliczonej wcześniej liczby Sommerfelda (

)

odczytuje wskaźnik przyrostu temp. oleju

14

sr

c

T

p

ρ

⋅ ⋅ Δ

≈

Zatem przyrost temperatury oleju wyniesie:

6

3

14

14 1,22 10

17080000

9,46

950 1,9 10

1805000

sr

p

T

T

K

c

ρ

⋅

⋅

⋅

Δ =

⇒ Δ =

=

=

⋅

⋅

⋅

Przyjmuję, że temp. oleju wpływającego do szczeliny smarnej łożyska

(

)

1

328,15

55

T

K

C

=

D

Dla tych warunków temp. średnia filmu olejowego wyniesie:

(

)

'

1

'

9, 46

328,15

332,88

59,73

2

2

sr

sr

T

T

T

T

K

C

Δ

= +

⇒

=

+

=

D

Ponieważ obliczona temp.

sr

60

sr zal

C

−

=

D

T nieznacznie się różni od założonej

wcześniej (

t

), wobec tego nie ma potrzeby ponownego jej

zakładania i przeprowadzania obliczeń. Różnica w stosunku do przyjętej

wartości wynosi zaledwie:

332,88

1

100% 0,08%

333,15

K

K

⎛

⎞

−

⋅

=

⎜

⎟

⎝

⎠

co w zupełności wystarczy.

Temperatura oleju na wypływie ze szczeliny smarnej wynosi:

(

)

2

1

2

328,15 9, 46 337,61

64, 46

T

T

T

T

K

C

= + Δ ⇒

=

+

=

D

Temp. ta jest niższa od wartości dopuszczalnej dla oleju smarnego

(

)

343

358

70

85

dop

T

K

K

=

÷

÷

D

D

5. Wstępny bilans cieplny łożyska
5.1 Współczynnik tarcia płynnego

Z wykresu dla obliczonej wcześniej liczby Sommerfelda odczytuje

2,5

μ

ψ

=

3

2,5

2,5 1,014 10

0,002535

sr

μ

ψ

μ

−

=

⋅

⇒ =

⋅

⋅

=

T

N

F V

5.2 Moc tarcia

μ

= ⋅ ⋅

3

3

2,535 10 125 10

4,19

1327,71

T

m

N

N

W

s

−

=

⋅

⋅

⋅

⋅

=

k

A

(

)

2

2

25 30

27,5 0,32

2,816

k

k

5.3 Obliczenia powierzchni wymiany ciepła
5.3.1 Powierzchnia wymiany ciepła korpusu

A

D L

A

m

=

÷

⋅ ⋅ ⇒

=

⋅

=

w

A

0

0,5

w

A

D L

5.3.2 Powierzchnia wymiany ciepła wału

π

=

⋅ ⋅ ⋅

0

L

320

gdzie:

- jest to obliczeniowa długość wału przez którą zostanie

odprowadzone ciepło.

Dla D

mm

=

;

0

0

3, 425

3, 425

L

L

D

D

≈

⇒

≈ ⋅

9, 46

T

K

Δ =

(

)

'

332,88

59,73

sr

T

K

C

=

D

(

)

2

337,61

64,46

T

K

C

=

D

μ

2,5

ψ

=

0,002535

μ

=

1327,71

T

N

W

=

2

2,816

k

A

m

=

2

15

W

m

K

α

=

⋅

(

)

293,15

20

ot

T

K

=

D

(

)

333,15 60

sr zal

T

−

=

D

C

C

0

0,32 3,425 1,096

L

m

≈

⋅

≈

2

0,5 0,32 1,096

0,551

w

A

m

π

=

⋅

⋅

⋅ =

2

2,816 0,551 3,367

k

w

5.3.3 Całkowita powierzchnia wymiany ciepła

A

A

A

A

m

=

+

⇒ =

+

=

5.4 Sprawdzenie temperatury łożyska (na możliwość przegrzania)

W ogólnym przypadku bilans cieplny łożyska jest następujący:

5

(

)

(

)

2

1

T

T

ot

c

N

M

F V

A T

T

c

Q T

T

ω μ

α

ρ

=

⋅ = ⋅ ⋅ = ⋅ ⋅

−

+ ⋅ ⋅

−

ot

T

1

T

2

T

c

Q

gdzie:

T

- temp. łożyska

- temp. otoczenia

- temp. środka smarnego przed łożyskiem

- temp. środka smarnego za łożyskiem

- natężenie przepływu smaru w obiegowym układzie chłodzenia

ρ - gęstość właściwa

c - przewodność cieplna

Przy czym człon:

(

)

2

1

c

c

Q T

T

ρ

⋅ ⋅

−

odnosi się do łożysk, w których

odprowadzanie ciepła realizowane jest również poprzez ciecz chłodząco

– smarującą, która za pośrednictwem wymuszonego obiegu, po

przejściu przez szczelinę smarna zostaje schłodzona to temp.

początkowej. Zakładam, że łożysko będzie chłodzone naturalnie, bez

zastosowania dodatkowego układu chłodzącego środek smarny, zatem

nie uwzględniam w/w członu.

5.4.1 Obliczania współczynnika

α

7 12

p

V

α

= +

p

gdzie:

V

- prędkość opływającego powietrza

Na etapie wstępnego projektowania łożyska z wystarczającą

dokładnością można przyjąć

1

p

m

s

≥

V

, zatem

2

19

W

m

K

α

=

⋅

, jednak dla

zapewnienia zwiększonego bezpieczeństwa termicznego i możliwości

zabrudzenia łożyska (zapylenie, osiadanie kurzu) przyjmuję

2

15

W

m

K

α

=

⋅

5.4.2 Temperatura łożyska

Przy założeniu, że łożysko będzie chłodzone naturalnie przez

przepływające powietrze, w warunkach o temperaturze otoczenia

średnia temp. łożyska (obliczeniowa - wynikła z

bilansu cieplnego a nie z założenia), wyniesie:

(

)

293,15

20

ot

T

K

C

=

D

(

)

1327,71

293,15 319,44

46,29

15 3,367

T

sr obl

ot

sr obl

N

T

T

T

K

C

A

α

−

−

=

+

⇒

=

+

=

⋅

⋅

D

(

)

333,15 60

sr zal

T

C

−

=

D

Temperatura ta, znacznie różni się od wstępnie założonej

, wobec czego niezbędne jest przeprowadzenie

ponownych obliczeń (poprawkowych) dla średniej temp, pracy łożyska:

(

)

/

/

333,15 319, 44

326,3

53

2

2

sr zal

sr obl

sr

sr

T

T

K

C

−

−

+

+

=

⇒

=

=

D

(

)

/

326,3

53

sr

K

C

=

D

2

0,551

w

T

T

6. Obliczenia poprawkowe

Dla

T

lepkość dynamiczna wcześniej wybranego

A

m

=

2

3,367

A

m

=

(

)

319, 44

46, 29

sr obl

T

K

C

−

=

D

6

' 70mPa s

η

≈

⋅

3

' 950

kg

m

ρ

≈

' 1,87

kJ

c

kg K

≈

⋅

' '

'

15

sr

c

T

p

ρ

⋅ ⋅ Δ

≈

(

)

/

1

318,15

45

T

K

=

D

C

' 70mPa s

oleju wynosi:

η

≈

⋅

, oraz pozostałe parametry:

3

' 950

kg

m

ρ

≈

,

' 1,87

kJ

c

kg K

≈

⋅

6.1 Liczba Sommerfelda

(

)

2

2

6

3

' ''

0,07 4,16

0, 2912

'

'

0, 23

1, 25439912

1, 22 10

1,014 10

sr

rz

n

S

S

p

η

ψ

−

⋅

⋅

=

⇒

=

=

=

⋅

⋅

⋅

⋅

rz

przy czym należy zaznaczyć że luz względny rzeczywisty (

ψ

) nie

zmienia się, gdyż jak już wcześniej zaznaczyłem (pkt 3.3), nie

uwzględniam wpływu temp. na zmianę wymiarów panwi i czopu wału

wynikłej z rozszerzalności cieplnej materiałów z których są zrobione.

6.2 Przyrost temp. oleju

' '

'

15

sr

c

T

p

ρ

⋅ ⋅ Δ

≈

6

3

1,22 10 15

'

10,46

950 1,87 10

T

K

⋅

⋅

Δ =

=

⋅

⋅

Przyjmuję temp oleju wpływającego do szczeliny smarnej łożyska:

(

)

/

1

318,15

45

T

K

C

=

D

Średnia temp. oleju w szczelinie:

(

)

/

/

/

'

1

'

10,46

318,15

323,38

50, 23

2

2

sr

sr

T

T

T

T

K

C

Δ

=

+

⇒

=

+

=

D

Temperatura oleju na wypływie ze szczeliny:

(

)

/

/

/

2

1

2

328,61

55, 46

T

T

T

T

K

C

=

+ Δ ⇒

=

D

6.3 Współczynnik tarcia płynnego

'

3,2

μ

ψ

≈

3

' 3,2 1,014 10

0,0032448

μ

−

≈

⋅

⋅

=

/

3

0,0032448 125 10 4,19 1699, 464

T

N

W

=

⋅

⋅

⋅

=

6.4 Moc tarcia

6.5 Sprawdzenie temp. łożyska

(

)

/

1699,464

293,15 326,8

53,65

15 3,367

sr obl

T

K

C

−

=

+

=

⋅

D

/

/

Ponieważ

sr obl

sr

T

−

≈

T

nie ma potrzeby przeprowadzania kolejnych

obliczeń iteracyjnych, przyjmuje, zatem ostatecznie:

(

)

326,8

53,65

sr

T

K

C

=

D

7. Sprawdzenie geometrycznego warunku tarcia płynnego
7.1 Luz promieniowy

3

3

320

1,014

10

162, 24 10

2

2

D

mm

δ ψ

δ

−

−

= ⋅

⇒ =

⋅

⋅

=

⋅

7.2 Minimalna szczelina smarownicza

Z wykresu dla obliczonego luzu promieniowego (

δ

) odczytuje

współczynnik:

3

0

0

0,55

162, 24 10

0,55 89, 232

h

h

m

μ

δ

−

=

⇒

=

⋅

⋅

=

Ponieważ

może to powodować niestabilność ruchu czopa w

(

)

/

326,3

53

sr

T

K

C

=

D

' 0, 23

S

=

' 10, 46

T

K

Δ =

(

)

/

'

323,38

50,23

sr

T

K

C

=

D

(

)

/

2

328,61

55, 46

T

K

C

=

D

0

0,35

h

δ

≥

'

3,2

μ

ψ

≈

0,0032448

μ

=

/

1699, 464

T

N

W

=

(

)

/

326,8

53,65

sr obl

T

K

C

−

=

D

(

)

326,8

53,65

sr

T

K

C

=

D

3

162, 24 10 mm

δ

−

=

⋅

0

0,55

h

δ

=

3, 4

''

Q

R

n L

δ

≈

⋅ ⋅ ⋅

panwi oraz powstawanie w wyniku tego drgań łożyskowanego wału. W

związku z powyższym należy zadbać o odpowiednio dokładne

wyrównoważenie wału i mas wirujących.

7.3 Warunek geometryczny tarcia płynnego

0

1

2

h

h

h

h

≥ + +

3

gdzie:

1

h - średnia wysokość nierówności powierzchni czopa

zc

R i panwi

zp

R

2

h - ukośne położenie czopa w otworze panwi wskutek ugięcia wału

3

h - zakrzywienie czopa pod obciążeniem

1

2

4

2

3

4

2

zc

zp

R

R

h

b

h

d

b

h

d

α

γ

+

=

=

=

gdzie

α

,

γ - odpowiednie współczynniki zależne od obciążenia.

Ponieważ nie znam dokładnych wymiarów wału, oraz przebiegu

obciążenia na jego długości nie mogę obliczyć ugięcia wału oraz

stwierdzić czy może dojść do skoszenia czopa w panwi, w związku z

tym zakładam, że wał nie odkształci się sprężyście w wyniku działania

na niego obciążenia lub ciężaru własnego, oraz że jego oś pozostanie

równoległa do osi panwi, wtedy to warunek geometryczny uzyskania

tarcia hydrodynamicznego przyjmie postać:

0

0

0

1,6

3, 2

89, 2

4,8

zc

zp

h

R

R

h

m

m

h

m

μ

μ

m

μ

μ

≥

+

≥

+

=

≥

Warunek, zatem jest spełniony

Ponadto łożysko będzie samonastawne, a jego panewka będzie podparta

na przegubie kulistym, dzięki czemu nawet jeśli wał się odkształci do

pewnego stopnia, to nie spowoduje to zmniejszenia szczeliny

smarowniczej na tyle, aby mogło nastąpić zatarcie łożyska.

8. Obliczenia strumienia oleju przepływającego przez szczelinę
łożyskową
8.1 Strumień oleju przepływającego przez szczelinę w wyniku ruchu
obrotowego czopa

Dla obliczonego wcześniej

odczytuje z wykresu współczynnik:

'

S

3

3, 4

3, 4 160

162, 24 10

4,16

320

''

Q

obr

Q

mm

mm

R

n L

s

δ

−

≈

⇒ ≈

⋅

⋅

⋅

⋅

⋅

⋅

⋅ ⋅ ⋅

mm

3

3

117489,7951

7,05

min

mm

dm

Q

Q

s

=

⇒ =

8.2 Strumień wypływów bocznych oleju

Z wykresu dla ' odczytuje:

S

0,49

s

Q

Q

≈

więc:

3

0,49

3,45

min

s

s

dm

Q

Q

Q

=

⋅ ⇒

=

Zatem taka ilość oleju powinna być dostarczona do łożyska jeśli ma ono

pracować w obliczeniowych warunkach tarcia płynnego.

Taką ilość oleju może zapewnić poprzez smarowanie za pomocą

jednego „luźnego” pierścienia. (Jeden pierścień „luźny” jest w stanie

0

89,232

h

m

μ

=

3

7,05

min

dm

Q

=

7

0,49

s

Q

Q

≈

max

0,44

sr

p

p

≈

max

11 30'

p

θ

=

D

54

φ

=

D

75

po

θ

=

D

dostarczyć do „górnej” części wału olej w ilości

3

1 4

min

dm

⎡

⎤

÷ ⎢

⎥

⎣

⎦

)

Z polskiej normy dobieram pierścień smarujący luźny o parametrach:

Średnica

475

D

mm

=

, szerokość

40

b

mm

=

, t

m

60 m

=

9. Obliczenia pozostałych parametrów (na podstawie
współczynników odczytanych z wykresów w funkcji liczby
Smmerfelda)
9.1 Maksymalne ciśnienie w filmie olejowym

max

max

1, 22

0,44

2,77

0, 44

0, 44

sr

sr

p

p

MPa

p

M

p

≈

⇒

=

=

=

Pa

9.2 Kąt określający miejsce maksymalnego ciśnienia

max

11 30'

p

θ

=

D

9.3 Kąt określający miejsce minimalnej grubości filmu olejowego

54

φ

=

D

9.4 Kąt określający koniec klina smarnego

75

po

θ

=

D

10. Obliczenie prędkości granicznej

2

2

32 32 25735,93

4

4

obl

obl

V

D

L

V

c

3

m

π

π

= ⋅

⋅ ⇒

= ⋅

⋅

=

Minimalna prędkość obrotowa, przy której w łożysku może występować

jeszcze tarcie płynne:

12500,0

6,94 7

0,070 25735,93

min

kr

kr

obl

p

obr

n

n

V

η

=

⇒

=

=

≈

⋅

⋅

Z obliczeń można wywnioskować, że w warunkach nominalnych (przy

luzie nominalnym i przy smarowaniu olejem o lepkości

0,07Pa s

η

=

⋅

w

temp. średniej

(

)

326,8

54

sr

T

K

=

D

C

łożysko przechodzi w stan tarcia

mieszanego, jeśli liczba obrotów spadnie poniżej

7

min

obr

, z tych

względów, szczególnie przy powolnym rozruchu i wybiegu oraz przy

obciążonym łożysku zachodzi obawa przyspieszonego zużywania się

łożyska. Aby temu zaradzić zaleca się stosowanie możliwie krótkiego

czasu rozruchu i wybiegu, a także zmniejszenie obciążenia.

3

3,45

min

s

dm

Q

=

max

2,77

p

MPa

=

3

25735,93

obl

V

c

=

m

7

min

kr

obr

n

=

Literatura

:

1. Osiński Z., Bajon W., Szucki T.: Podstawy Konstrukcji Maszyn, PWN, Warszawa 1986
2. Orlik Z., Surowiak W., Rutkowski A.: Części maszyn cz. I i II, WSiP, Warszawa 1985
3. Skoć A., Spałek J.: Podstawy Konstrukcji Maszyn: Tom I, WNT, Warszawa 2006
4. Skoć A., Spałek J., Markusik S.: Podstawy Konstrukcji Maszyn: Tom II, WNT, Warszawa 2008
5. Neyman A.: Wykład z Podstaw Konstrukcji Maszyn z ćwiczeniami rachunkowymi: Łożyska

Ślizgowe, Wydawnictwo Politechniki Gdańskiej, Gdańsk 2000

6. Korewa W., Zygmunt K.: Podstawy Konstrukcji Maszyn - cz. II, WNT, Warszawa 1965
7. Przykłady obliczeń z Podstaw Konstrukcji Maszyn, pod redakcją Eugeniusza Mazanka, WNT,

Warszawa 2005

8