1

PRZESTRZENIE SYGNAŁÓW

Spis treści

1. Przestrzenie metryczne –

odległość miedzy sygnałami

2. Przestrzenie unormowane –

moc sygnału

3. Przestrzenie unitarne –

iloczyn skalarny

4. Związki pomiędzy przestrzeniami

0 .2 1

0 .2 1 5

0 .2 2

0 .2 2 5

0 .2 3

-0 .2

-0 .1

0

0 .1

0 .2

2

Definicja przestrzeni metrycznej

Zbiór S nazywamy

przestrzenią metryczną

, jeżeli każdej parze

elementów przyporządkowana jest liczba nieujemna

w taki sposób, że spełnione są następujące warunki zwane

aksjomatami metryki:

s s

S

1

2

,





( , )

s s

1

2



( , )

s s

s

s

1

2

1

2

0

  





( , )

( , )

s s

s s

1

2

2

1









( , )

( , )

( , )

s s

s s

s s

1

2

2

3

1

3





1.

2.

3.

3

Przykłady przestrzeni metrycznych

sygnałów analogowych 1-D

L

T

2

0

( , )



L

T

s s

s t

s t

dt

2

1

2

1

2

0

2

( , )

( )

( )







L

2

( )

R



L

s s

s t

s t

dt

2

1

2

1

2

2

( , )

( )

( )













C

t T

s s

s t

s t

( , ) max ( )

( )

1

2

0

1

2





 

)

,

0

( T

C

)

,

(

1





L

dt

t

s

t

s

s

s

L













)

(

)

(

)

,

(

2

1

2

1

1



L

T

p

( , )

0

s t

dt

p

T

( )

0



 

1

  

p



L

p

T

p

p

s s

s t

s t

dt

( , )

( )

( )

1

2

1

2

0

1



















4

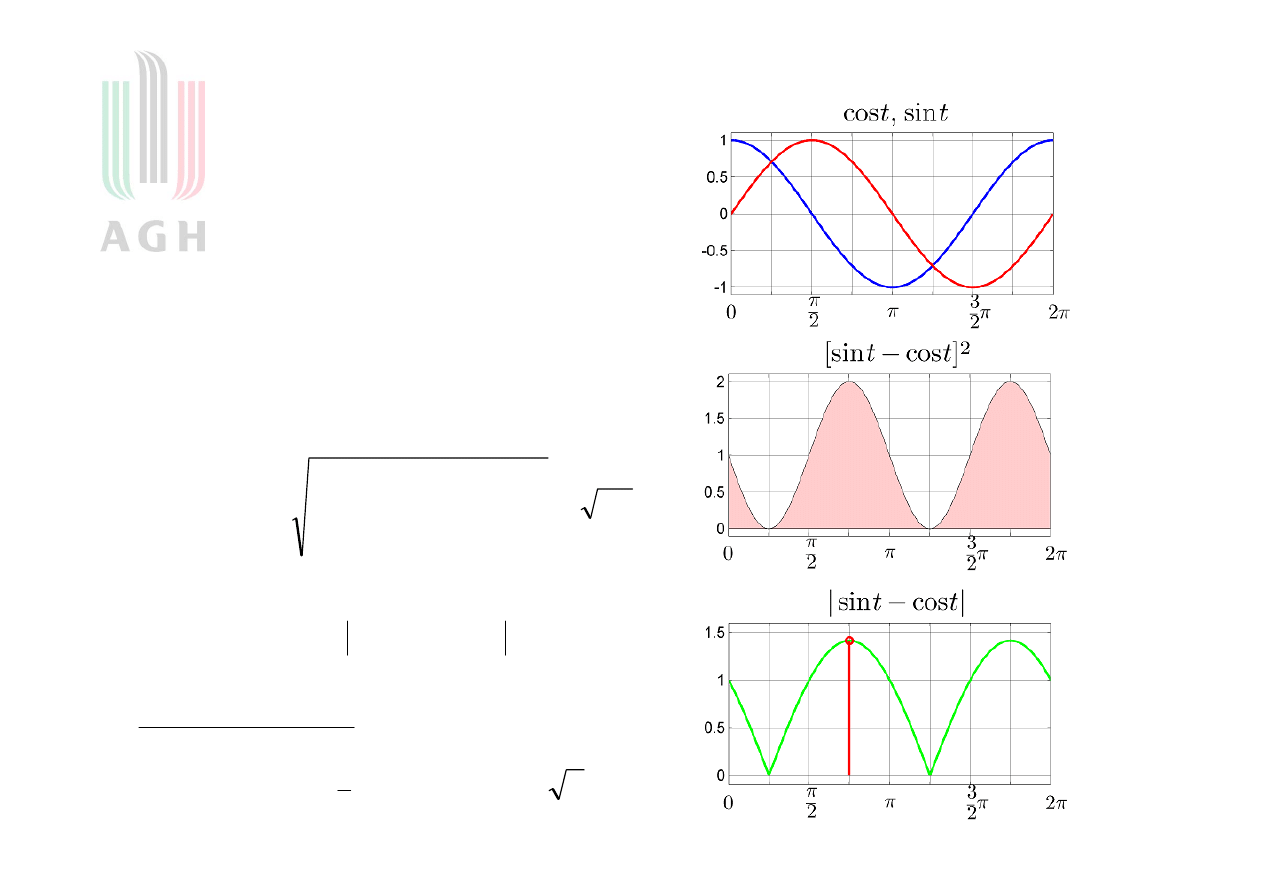
Przykład odległości między sygnałami

Dane są dwa sygnały :

s t

t

1

( )

sin( )



s t

t

2

( )

cos( )



Jaka jest między nimi odległość

w przestrzeniach i C(0, 2



) ?

L

2

0 2

( ,

)













L

s s

t

t

dt

2

1

2

2

0

2

2

( , )

sin( ) cos( )













C

t

s s

t

t

( , )

max sin( ) cos( )

1

2

0

2





 





d

t

t

dt

t

t

sin( ) cos( )

cos( ) sin( )







2

)

,

(

1

)

(

2

1

4

3













s

s

t

t

tg

C





oraz

5

Przykłady przestrzeni metrycznych

obrazów analogowych





]

,

0

[

]

,

0

[

2

Y

X



L



L

X

Y

s s

s x y

s x y

dx dy

2

1

2

1

2

0

0

2

( , )

( , )

( , )









 

L

2

2

R



L

s s

s x y

s

x y

dx dy

2

1

2

1

2

2

( , )

( , )

( , )



















C

x X

y Y

s s

s x y

s x y

( , )

max

( , )

( , )

1

2

0

0

1

2





 

 





]

,

0

[

]

,

0

[

Y

X

C



6

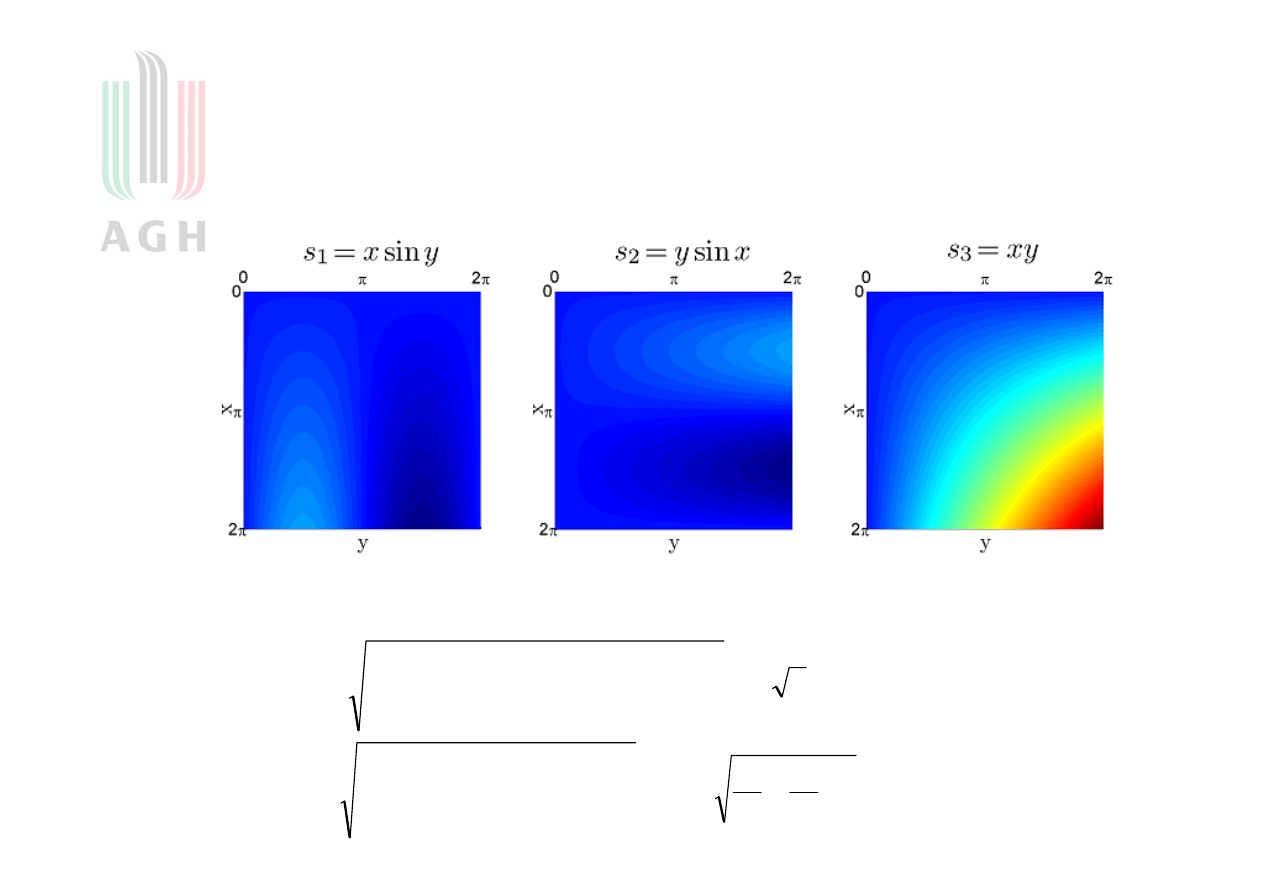
Przykład odległości między obrazami













L

s s

x

y

y

x

dx dy

2

1

2

2

0

2

0

2

2 2

( , )

sin( )

sin( )

























L

s s

x

y

xy dx dy

2

1

3

2

0

2

0

2

2

2

2

10

3

16

9

( , )

sin( )













)

,

(

)

,

(

3

1

2

1

2

2

s

s

s

s

L

L







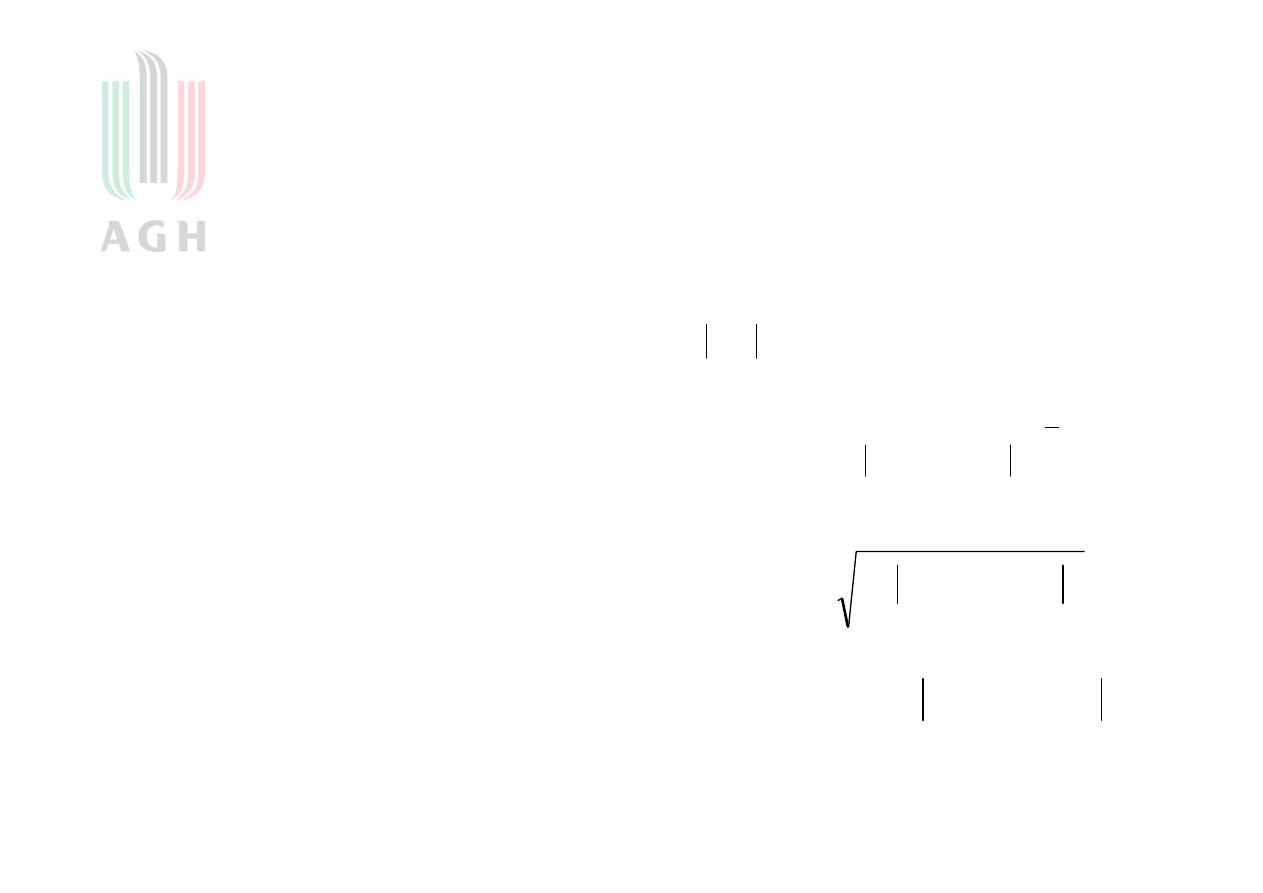
Czy obraz

)

sin(

)

,

(

1

y

x

y

x

s



jest bliższy obrazowi

s x y

xy

3

( , )



w przestrzeni

?

)

sin(

)

,

(

2

x

y

y

x

s



czy obrazowi





L

x

2

0 2

0 2

[ ,

] [ ,

]





Obraz z lewej jest bliższy obrazowi centralnemu niż obrazowi z prawej strony

7

Przykłady przestrzeni metrycznych

sygnałów dyskretnych 1-D

s

s

s

 [ ( ), ( ),...]

0

1

s n

p

n

( )



 

l

p

1

  

p



l

p

n

p

p

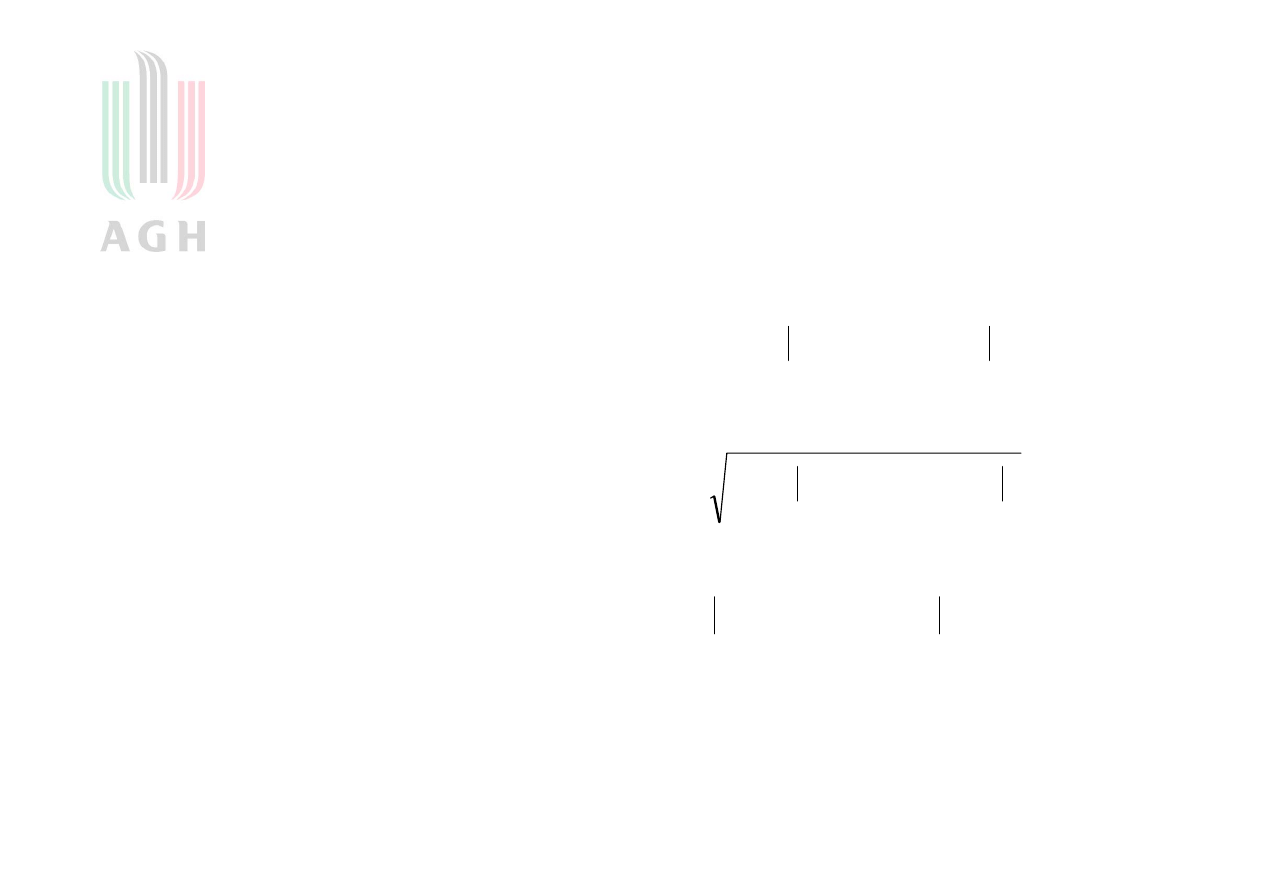
s s

s n

s

n

( , )

( )

( )

1

2

1

2

1

















s s

l

1

2

2

,





l

n

s s

s n

s n

2

1

2

1

2

2

( , )

( )

( )







l





l

n

s s

s n

s n







( , )

max

( )

( )

1

2

1

2

2

l

8

Przykłady przestrzeni metrycznych

sygnałów dyskretnych 2-D



l

n

m

s s

s m n

s m n

2

1

2

1

2

2

( , )

( , )

( , )











l



l

m n

s m n

s m n







max

( , )

( , )

,

1

2

1

l

2

l











N

n

M

m

l

n

m

s

n

m

s

s

s

0

0

2

1

2

1

)

,

(

)

,

(

)

,

(

1



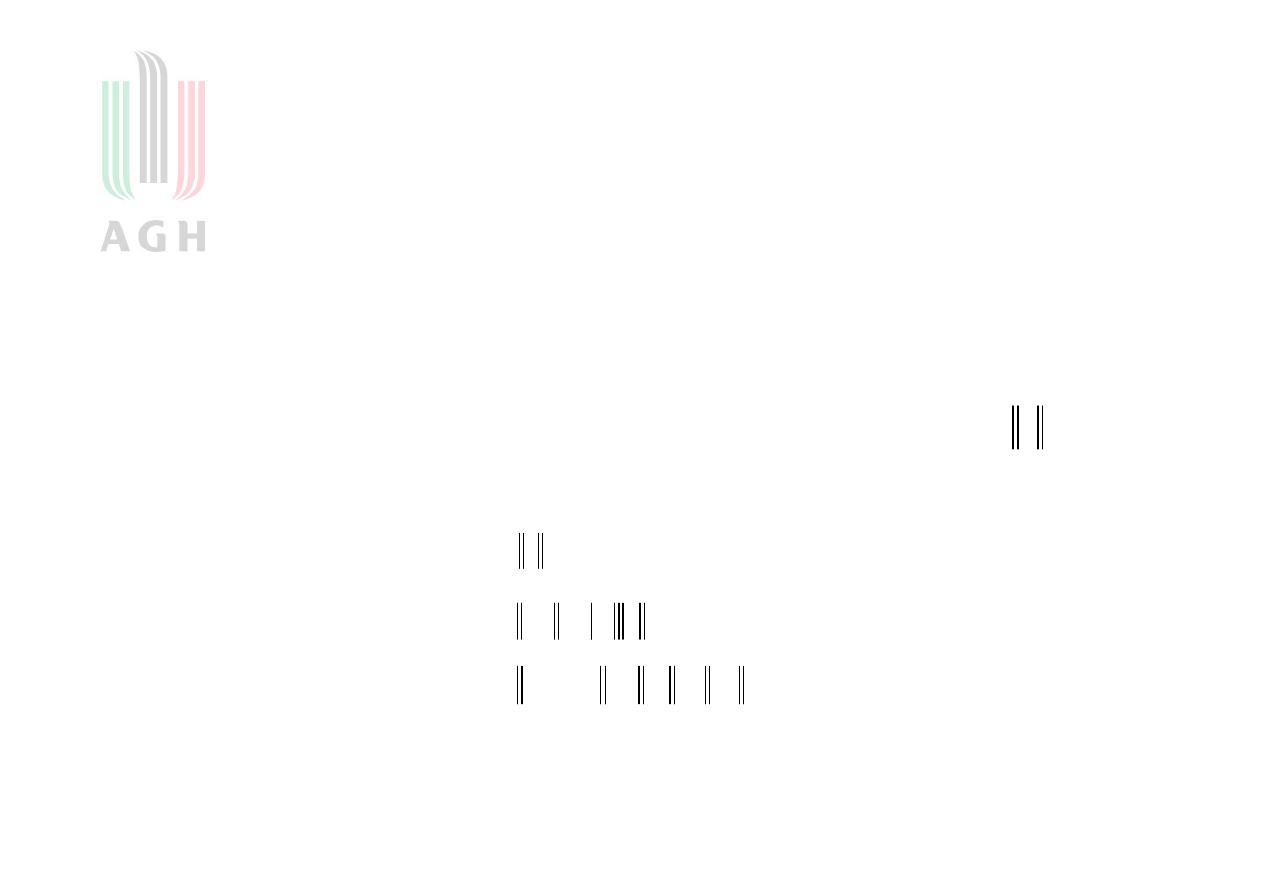
9

1.

2.

gdzie

3.

Definicja przestrzeni unormowanej

Zbiór S nazywamy

przestrzenią unormowaną

jeżeli każdemu jej

elementowi ,

przyporządkujemy liczbę nieujemną

w taki

sposób, że spełnione są następujące warunki:

s

S



s

s

s

   

0





s

s





R

s

s

s

s

1

2

1

2







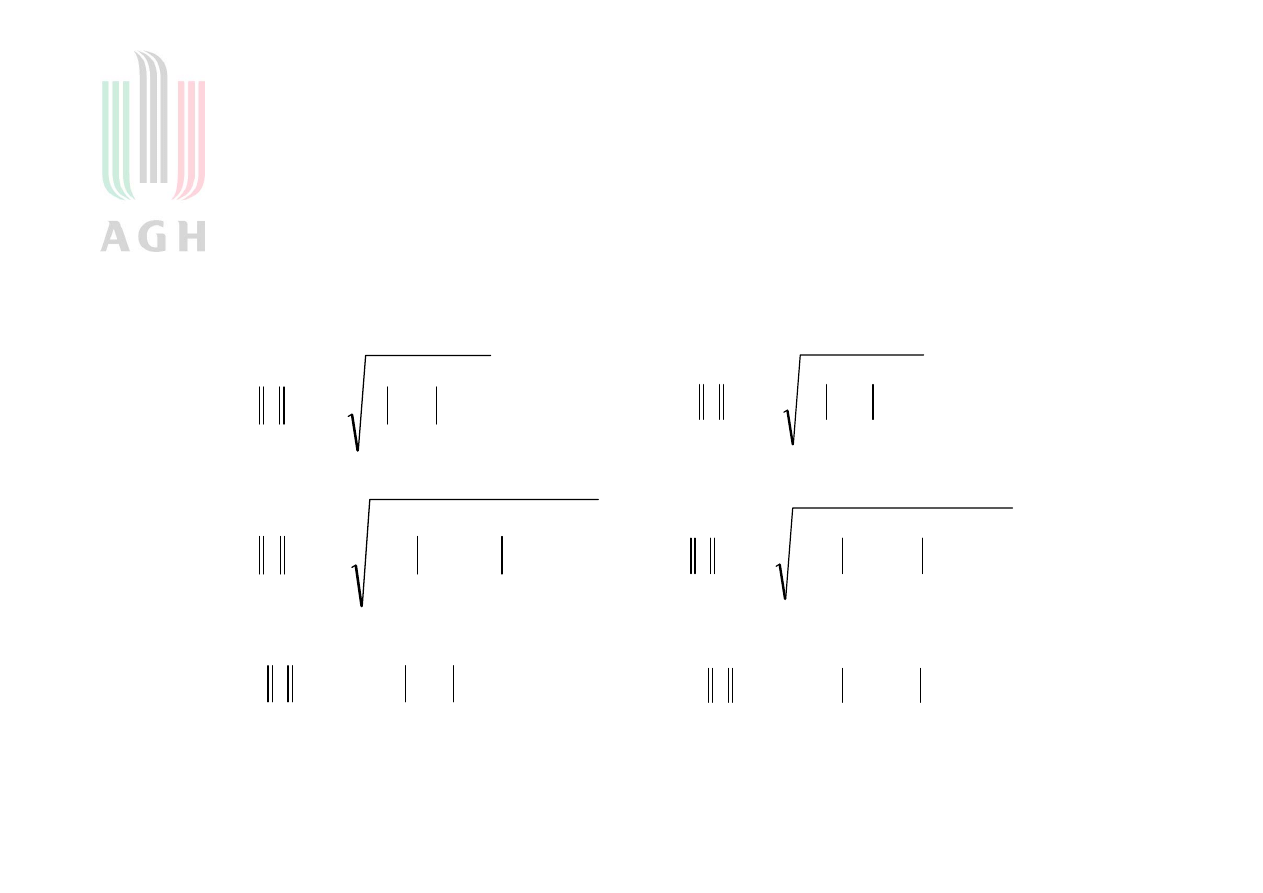
10

Przykłady przestrzeni unormowanych

sygnałów analogowych

s

s t

dt

L

T

2

2

0





( )

s

s t

dt

L

2

2









( )

s

s x y

dx dy

L

X

Y

2

2

0

0







( , )

s

s x y

dx dy

L

2

2















( , )

s

s t

C

t

 max ( )

s

s x y

C

x y

 max ( , )

,

11

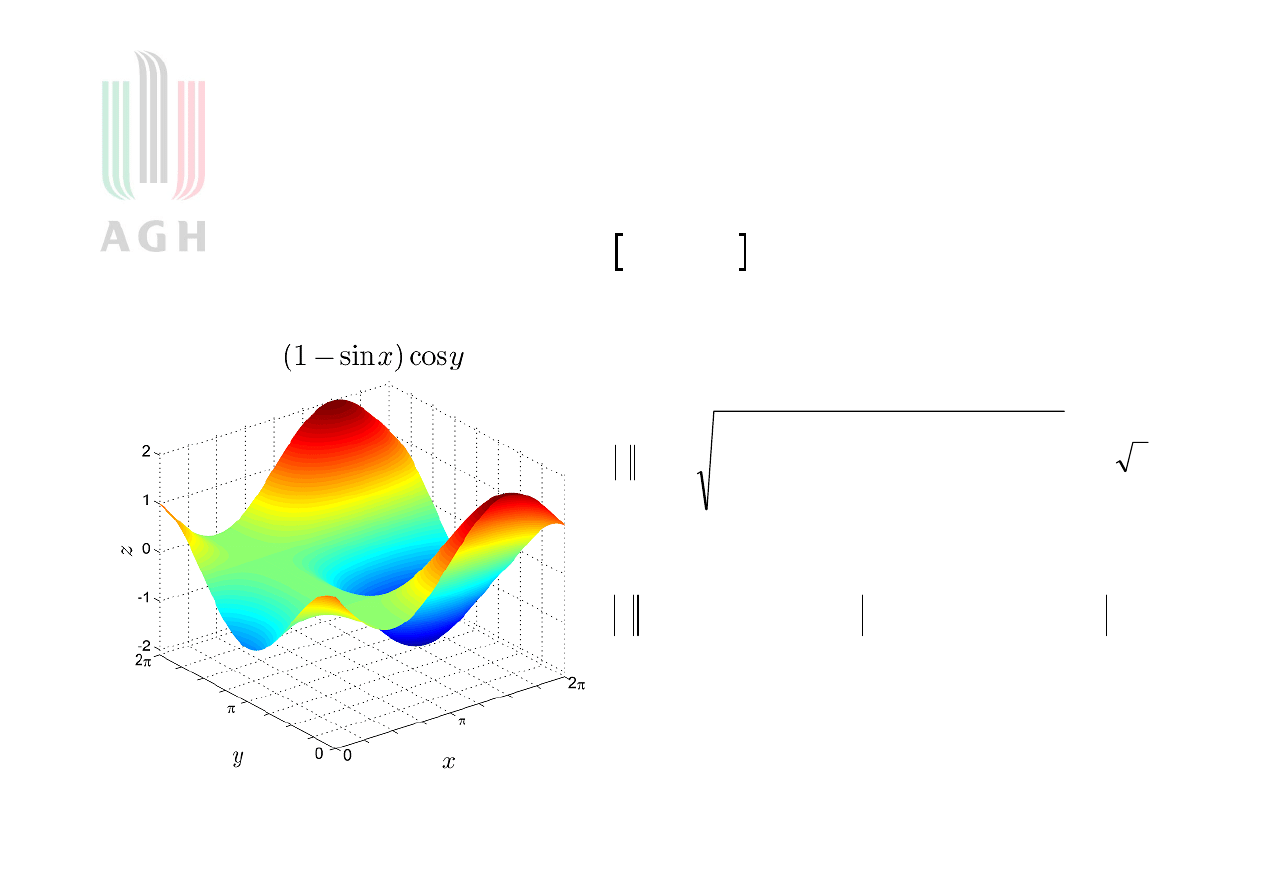
Norma sygnału sinusoidalnego

Jakie są normy sygnału w

przestrzeniach

i

?

L

2

0 2

( ,

)



C( ,

)

0 2



s

t dt

t

t

L2

2

0

2

0

2

2

2

4

















sin ( )

sin( )







s

t

C

t





 

max sin( )

0

2

1



)

sin(

)

(

t

t

s



12

Norma sygnału analogowego 2-D

Czy norma sygnału

w przestrzeni

jest taka sama jak w przestrzeni

?

s x y

x

y

( , )

sin( ) cos( )

 

1





L

x

2

0 2

0 2

[ , ] [ , ]









C

x

[ ,

] [ ,

]

0 2

0 2









s

x

y dx dy

L2

2

2

0

2

0

2

1

3











sin( ) cos ( )







s

x

y

C

x y

x









max

[

sin( )]cos( )

( , ) [ ,

] [ ,

]

0 2

0 2

1

2





13

Przykłady unormowanych przestrzeni

sygnałów dyskretnych

s

s

s

s N

 [ ( ), ( ),..., ( )]

0

1

2

l

s

s n

l

n

N

2

2

0







( )

l



s

s n

l

n



 max ( )

s

s m n

l

n

N

m

M

2

2

0

0











( , )

s

s m n

l

m n



 sup ( , )

,

14

Definicja iloczynu skalarnego

Iloczynem skalarnym

pary elementów należących do S nazywamy

operację, która tej parze przyporządkowuje liczbę

w taki

sposób, że spełnione są następujące aksjomaty :

s s

1

2

,

1.

2.

3.

4.

s s

,

 0

dla

i

dla

s

 

s s

,

 0

s

 





s s

s s

1

2

1

2

,

,





C

s

s s

s s

s s

1

2

3

1

3

2

3







,

,

,

*

1

2

2

1

,

,

s

s

s

s



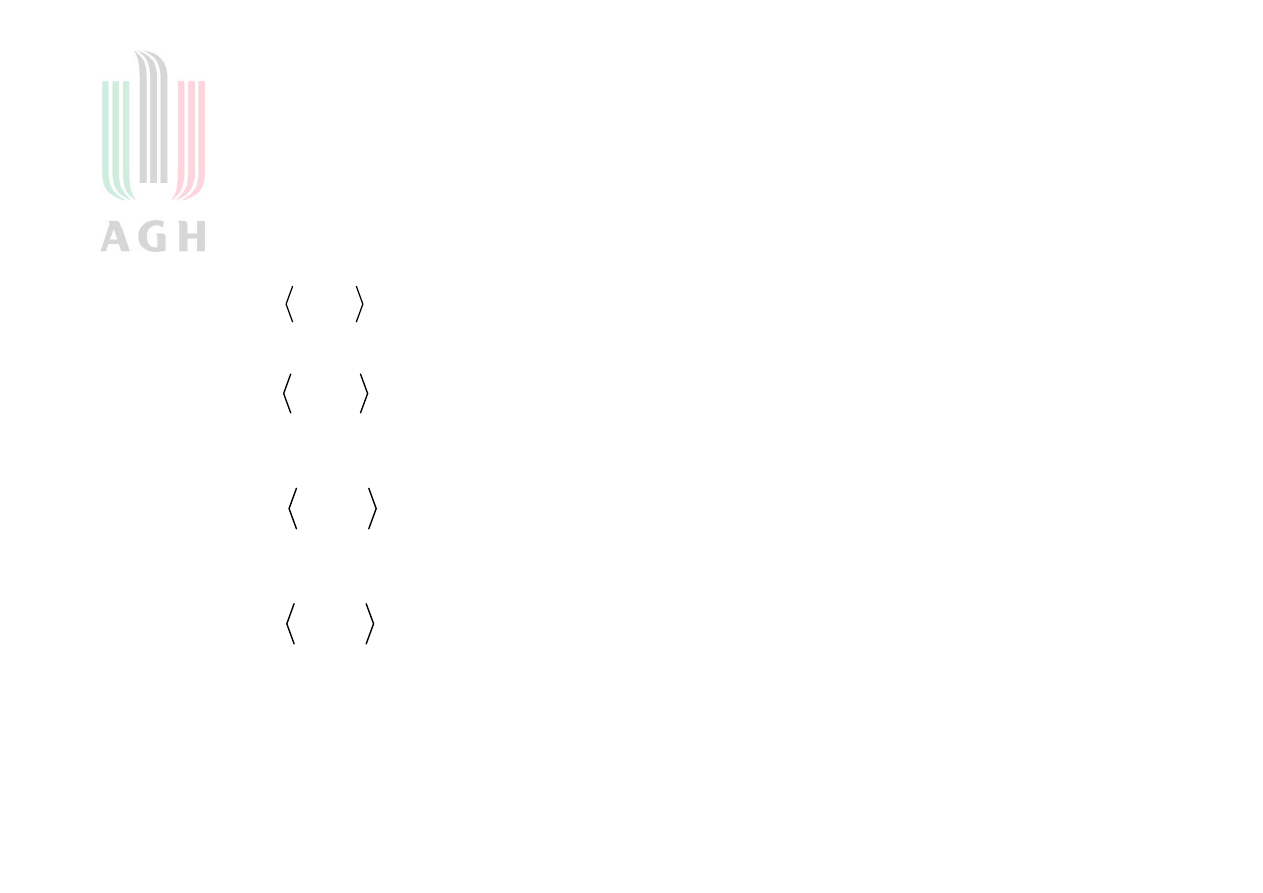
15

Przykłady przestrzeni unitarnych





T

L

dt

t

s

t

s

s

s

0

*

2

1

2

1

)

(

)

(

,

2







n

T

n

s

n

s

s

s

s

s

)

(

)

(

,

*

2

1

*

2

1

2

1

 



Y X

dy

dx

y

x

s

y

x

s

s

s

0 0

*

2

1

2

1

)

,

(

)

,

(

,





m

n

n

m

s

n

m

s

s

s

)

,

(

)

,

(

,

*

2

1

2

1

16

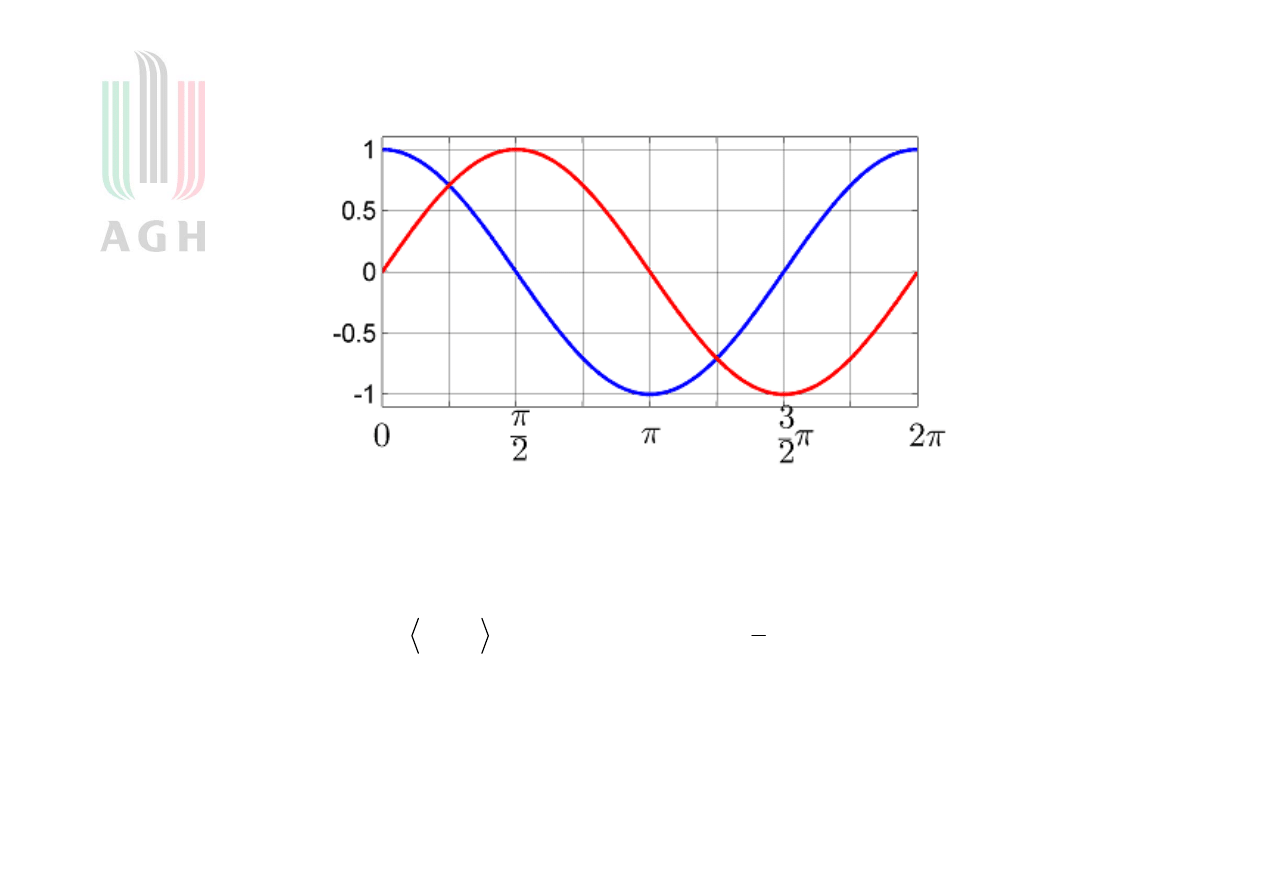
Przykład sygnałów ortogonalnych

Czy sygnały

oraz

są sygnałami ortogonalnymi

w przestrzeni

?

Zerowa wartość oznacza, że sygnały s

1

i s

2

są ortogonalne w

)

sin(

)

(

1

t

t

s



L

2

0 2

( ,

)



s s

t

t dt

t dt

1

2

1

2

0

2

0

2

2

0

,

sin( ) cos( )

sin( )















L

2

0 2

( ,

)



)

cos(

)

(

t

t

s

s



17

Odległość między sygnałami ortogonalnymi

Czy sygnały

i

są ortogonalne?

1

)

(

1



t

s









s s

t

dt

t

t

1

2

2

0

1

0

1

2

1

0

,

|













Zerowanie iloczynu skalarnego oznacza, że sygnały są względem
siebie prostopadłe. Odległość między nimi wynosi







( , )

s s

t

dt

1

2

2

0

1

2

2

2

3









)

1

,

0

(

2

L

1

2

)

(

2



 t

t

s

Jaka jest między nimi odległość w przestrzeni

?

18

Związek między przestrzenią

unitarną i unormowaną

Funkcjonał zdefiniowany wzorem

dla

jest normą w przestrzeni unitarnej S.

s

s s



,

s

S



Twierdzenie 1.

19

Związek między przestrzenią

unormowaną i metryczną

Twierdzenie 2.

Funkcjonał zdefiniowany wzorem

dla

jest metryką w unormowanej przestrzeni S.



( , )

s s

s

s

1

2

1

2





s s

S

1

2

,



20

Definicja metryki przesuwalnej

i bezwzględnie jednorodnej

Mówimy, że

metryka

w przestrzeni S jest

przesuwalna

jeśli

spełniony jest warunek





(

,

)

( , )

s

s s

s

s s

1

3

2

3

1

2







dla dowolnych

s s s

S

1

2

3

, ,



Metryka

jest

bezwzględnie jednorodna

jeśli zachodzi

  

 

(

,

)

( , )

s

s

s s

1

2

1

2



dla dowolnych

oraz dla każdego

s s

S

1

2

,







21

Związek między przestrzenią

metryczną i unormowaną

Twierdzenie 3.

Jeżeli metryka w przestrzeni S jest przesuwalna i bezwzględnie
jednorodna to wtedy i tylko wtedy przestrzeń S jest unormowana.
Norma dana jest wzorem

s

s







( , )