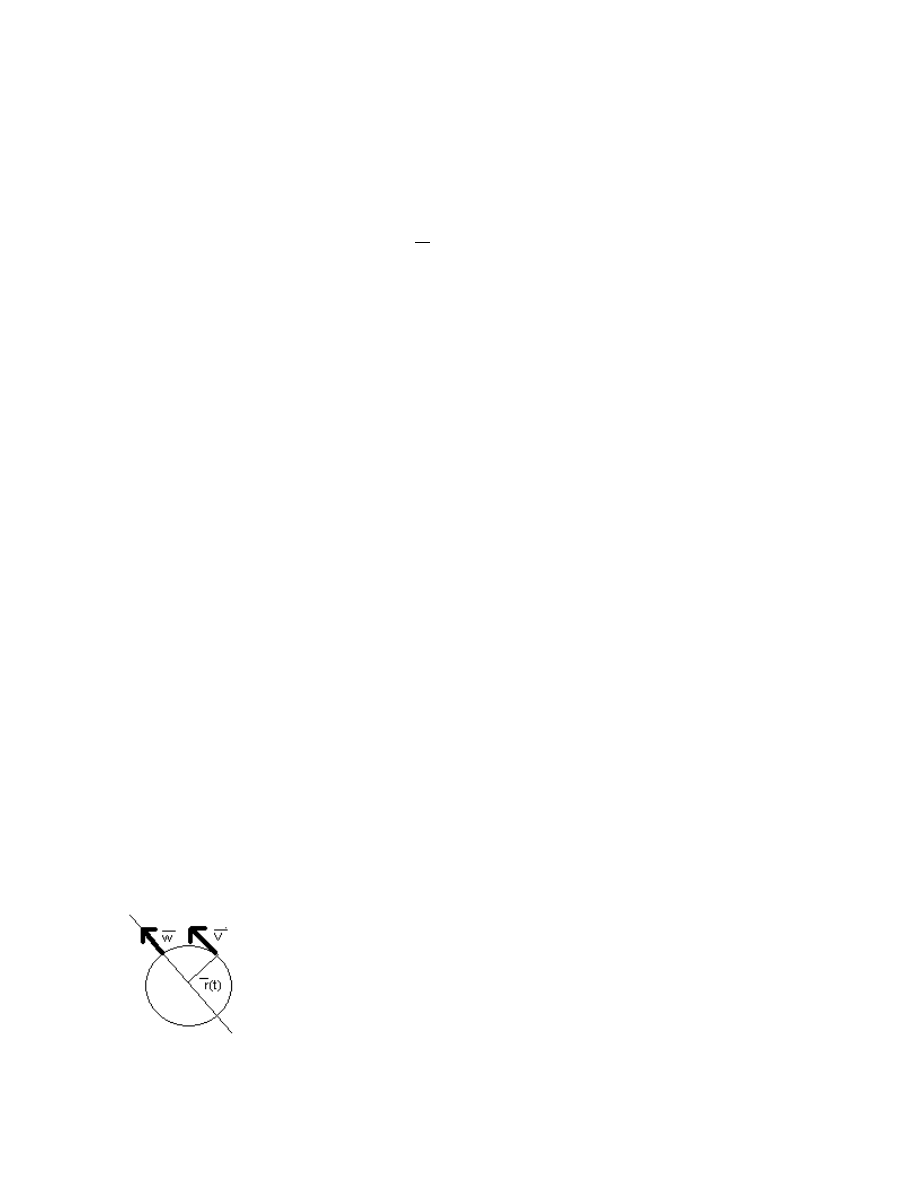
‘-‘ w indeksie gornym oznacza wektor, ‘*’ mnożenie skalarne, ‘x’ mnożenie wektorowe

1. Do czego redukuje się uklad wektorow którego momenty względem 3 niewspolliniowych pktow sa rowne?
ODP: Jeżeli tak jest to suma układu wynosi zero (S=0) wiec układ redukuje się do pary wektorow (S=0, M=/0) lub do układu zerowego (S=0,
M=0).
2. Jakie 2 uklady sil nazywamy ukladami równoważącymi się? Podac przykład takich układów w mechanice.
ODP: 2 uklady wekt nazywamy równoważnymi jeśli maja rowne sumy i momenty względem każdego pktu (o) rowne. [S(A)=S(B),
Mo(A)=Mo(B)]. Przykłady: I. dwa układy wektorow, które maja momenty wzgl 3 niewspolliniowych pktow rowne. II. Dwa układy wektorow,
które maja momenty wzgl 2 pktow rowne i rzuty sum na prosta nieprostopadla do prostej łączącej te 2 pkty, tez rowne.
3.Podac def układu statycznie wyznaczalnego.
ODP: Układ statycznie wyznaczalny to układ pretowy, dla którego niewiadome reakcje podporowe można wyznaczyc z równań równowagi w
sposób jednoznaczny.
4. Jakie własności ma srodek masy sztywnego układu materialnego?
ODP: Srodek masy O* ma współrzędne: xo=Syz/m, yo=Sxz/m, zo=Sxy/m. Moment statyczny układu materialnego, liczony wzgl dowolnej
płaszczyzny ∏ jest rowny momentowi statycznemu srodka masy wzgl laszczyzny ∏. Jeżeli plaszczyzna przechodzi przez srodek masy układu, to
moment statyczny układu materialnego jest rowny 0, bo miara odległości srodka masy od tej płaszczyzny jest rowna 0.
5. Podac def wypadkowej i warunki jakie musi spełniać układ wektorow aby redukowal się do wypadkowej?
ODP: Wypadkowa nazywamy układ równoważny danemu, złożony z jednego niezerowego wektora o scisle określonej prostej dzialania.
Wypadkowa nie jest wektorem swobodnym! WKW aby układ redukowal się do wypadkowej jest by S=/0 i k=0 (k=S*M[skalarnie]).

6. Kiedy moment wektora a- wzgl prostej l jest rowny 0?

ODP: wtw gdy prosta l i wektor a- leza w jednej płaszczyźnie ∏. Ogolne przypadki: a-=0, a-||l, A(pkt zaczepienia wektora a) €l, a-€∏ i l€∏.
7. Podac zasade kretu. Do czego wykorzystujemy te zasade w mechanice?

ODP: Ogolna postac: KB

- = MB-(F)+p-xVB- Pochodna kretu wzgl danego pktu po czasie w danej chwili ruchu jest rowna sumie momentu sil

działających na ten układ wzgl tego pktu i iloczynu wektorowego pedu całego układu oraz prędkości tego pktu. Potrzebna w obliczaniu
chwilowego ruchu obrotowego ciala sztywnego.
8. Def i twierdz o momencie wektora a-> wzgl prostej l.
ODP: momentem wektora wzgl prostej nazywamy moment rzutu tego wektora na dowolna płaszczyznę prostopadla do tej prostej wzgl pktu

przebicia z ta plaszczyzna. M-l(a

-)=a-∏ x A’0. Tw. o momencie wektora wzgl prostej: M-l(a-)=[M-o(a-)]l Moment wekt wzgl prostej jest rowny

rzutowi momentu tego wektora wzgl dowolnego pktu tej prostej na ta prosta.
9. Twierdz o zmianie bieguna i wnioski.

ODP: M-o’(A)=M

-

o(A) + S

-(A) x OO’-. Wnioski: 1. S(A)-=0 moment tego ukl jest staly tzn nie zalezy od bieguna wzgl którego liczymy [

M-o(A)=const ]. 2. Moment ukl wzgl pktow lezacych na jednej prostej równoległej do S

-(A) jest taki sam. 3. Jeżeli momenty ukl wekt wzgl 3

niewspolliniowych pktow sa rowne to S-=0. 4. Parametr ukl k=S-(A)*M-(A) jest dla danego ukl staly.
10. Przypadki redukcji ukl do najprostszej postaci.

ODP: 1. ukl zerowy (S-=0, M-=0). 2. para wektorow – nie zalezy od bieguna reakcji (S-=0, M-=/0). 3. dwa wekt skosne(S-=/0, M-=/0 i S- nie

jest prostopadla do M-, wtedy k=/0). 4. wypadkowa (wekt glowny ukl wektorow) (k=0 wtw S-=/0 i M-=0, lub S-=/0 i M-=/0 i M- nie jest

prostopadly do S-). 5. skretnik (os srodkowa, jest to najprostszy ukl zredukow złożony z 3 wektorow – 1 suma zaczepiona w pkcie osi srodkowej

a 2 pozostale para o M- || do sumy) (k=/0 wtw S-(A)=/0, M-=/0 S- || M-).
11. Na czym polegaja przekształcenia elementarne układu wektorow?
ODP: 1. przekszt elementarne I rodz polega na dolaczeniu lub odlaczeniu z danego układu dwoch wektorow przeciwnych lezacych na jednej

prostej. 2. przekszt elem II rodz polega na dolaczeniu albo odlaczeniu układu zbieżnego o S-=0.
12. Które układy maja os srodkowa (WKW)?

ODP: WKW by ukl posiadal os srodkowa jest by S-=/0. r(Λ)= (S-xM-o)/S

2 + Λ*S – rown osi srodkowej ukl. r(Λ)=OO’- + Λ*S – rown

parametryczne w postaci wektorowej. Osia srodkowa nazywamy miejsce geometryczne pktow wzgl których moment ukl jest rowny zero lub jest
|| do sumy.
13. Def wektora predk katowej ω.

ODP: ω-(t)= { ω-||l , |ω-|=|α|, ω-, r-, V- trojka prawoskretna } V-(t)=ω- x r-(t), |V-|=|ω-|*|r-|*sin(ω-,r-), |ω-|*R=|α|*R

14. Ile wynosi an w ruchu po prostej?

ODP: an

-=ac—as- , as-=(ac- * V-/|V-|)*(V-/|V-|)

15. Podaj wzory na predk i przaysp w ruchu wzglednym.

ODP: V-(t)=lim∆t->0(∆r

-/∆t)=dr/dt=ro-(t) a-= lim∆t->0(∆V-/∆t)

16. Twierdz o rozkladzie predk w bryle sztywnej.
ODP: 1. Twierdz o rzutach wektorow prędkości pktow ciala sztywnego lezacych na jednej prostej: Jeżeli pkty ciala sztywnego leza na jednej
prostej to rzuty wektorow predk tych pktow na ta prosta sa sobie rowne w każdej chwili ruchu. 2. Twierdz o położeniu końców wekt predk pktow
ciala sztywn lezacych na jednej pr: Jeżeli pkty ciala sztywnego leza na jednej pr to konce wekt predk tych pktow w danej chwili ruchu tez leza na
pr.
17. Def ruchu płaskiego, kulistego, obrotowego.
ODP: KULISTY- ruch w którym wystepuje jeden pkt nazlezacy do ciala lub nie, który w trakcie ruchu jest nieruchomy. Trajektoria – krzywa
lezaca na pow. kuli o r=OA (lss=3). OBROTOWY- ruch w którym istnieja 2 pkty należące do ciala lub nie, które w trakcie ruchu sa nieruchome.

Trajektoria – okrag, V- styczna do okregu, Va= ωxOA- (lss=1). PŁASKI- ruch w którym istnieje pewna plaszcz. ∏ (kierujaca) od której odlegl
pktow ciala w czasie ruchu sa stale. Trajektorie pktow w ruchu i wektory predk leza w jednej płaszczyźnie (lss=3).
18. Aksjomaty mechaniki klasycznej:

-aksjomat bezwładności: istnieja układy odniesienia w których jeśli na pkt materialny nie dziala żadna sila to ped pktu jest staly ( p-=MV-=po

-).

-aksjomat ruchu: istnieja ukl odniesienia w których jeśli na pkt materialny dziala sila to zmienia się jego ped wedlug prawa: dp-/dt=F- jeśli

założymy ze m=const to prawo to ma postac m*r-o-o-=F-
-aksjomat wzajemnego oddziaływania: (prawo akcji i reakcji) 2 pkty materialne dzialaja na siebie zawsze wzajemnie z silami rownymi,

przeciwnie skierowanymi i lezacymi na jednej prostej: FAB

- + FBA- = O-.

19. Pojecie równowagi ciala i rownowagi sil (relacje miedzy nimi):
ODP: Mowimy ze cialo jest w spoczynku/równowadze jeżeli wszystkie pkty tego ciala nie zmieniaja swego położenia względem przyjętego
układu odniesienia. Mowimy ze ukl sil działających na cialo swobodne jest w równowadze jeżeli suma wszystkich sil tego ukl jest wektorem
zerowym oraz moment ukl wzgl każdego pktu jest rowny 0. Rownowaga sil jest WKW równowagi ciala zas rownowaga sil ze spoczynkiem ciala
jest WKW równowagi ciala.
20. ZPW (czego dotyczy? Równowagi ciala czy równowagi sil działających na cialo?)
ODP: WKW równowagi sil działających na ukl materialny swobodny lub nieswobodny o wiezach geometryczn, stacjonarnych, gładkich,

dwustronnych, jest by suma wszystkich sil czynnych i biernych działających na ten ukl była rowna 0. δL=Σni=1Fi

-*δsi-=0 (dla kazd δsi).

21. Więzy – wszelkiego rodzaju ograniczenia nałożone na ruch ciala. Więzy sa: geometryczne (ograniczenia na pkty ciala sztywnego),
kinematyczne (ogran na szybkość i przysp ciala sztywnego), stacjonarne i niestacjonarne (zalezne i niezależne od czasu), jednostronne i
dwustronne, gładkie (praca reakcji rowna 0), szorstkie.
22. Postulat o wiezach – ruch pktu materialnego lub ciala sztywnego nie ulegnie zmianie jeśli wiezy myślowo usuniemy a ich dzialanie
zastapimy odpowiednimi silami zwanymi silami reakcji więzów.
23. Przesuniecia – możliwe – wektor łączący dwa możliwe położenia pktu, zalezy od więzów; rzeczywiste – wekt łączący dwa rzeczywiste
położenia pktu. Kazde polaczenie rzeczywiste jest tez możliwym; wirtualne – każdy wekt współliniowy z wektorem prędkości możliwej.
24. Def powierzchni ekwipotencjalnej – to taka powierzchnia na której potencjal ma stala wartość; linie ekwipotencjalne – krzywe przecięcia

pow. ekwipotencjalnych plaszczyzna; w każdym pkcie potencj pola sil linie pola sil sa prostopadle do linii ekwipotencj gdyz F-=grad-V.
25. Podaj związek miedzy praca sily F i Ek pktu swobodnego na który dziala ta sila.
ODP: Prace sil pola po zadanej krzywej C od pktu A do B definiowac będziemy jako calke krzywoliniowa skierowana z iloczynu skalarnego sil

pola i elementu liniowego ds- krzywej. C – krzywa (postac parametryczna C:{x=x(Λ), y=y(Λ), z=z(Λ), Λ€R} Licząc prace po torze C w którym

parametrem jest czas mamy ∫tkto = F

-*V-dt. Wyrażenie Ek=mV2/2 nazywamy energia kinetyczna pktu materialnego. Równość Ek(tk)-

Ek(to)=Lto,tk stanowi zasade równoważności pracy i Ek. Przyrost Ek miedzy chwilami to, tk jest rowny pracy wykonanej przez sily pola w tym
samym przedziale czasu.
26. Zasada zachowania energii w polu potencjalnym
ODP: zasade ta stanowi równość Ek(tk)+(-VB)=Ek(to)+(-VA)=const gdzie –V=U – energia potencjalna.
27. Jak liczymy pęd i kręt dla układu pktow materialnych, a jak dla bryly sztywnej?

ODP: Kręt dla pktu materialnego: KB

-o-=MB-. Kręt dla bryly sztywnej: r-(t)={x=x(t), y=y(t), z=z(t)} KB-=∫∫∫vφ(x,y,z) * V-(x,y,z) x

AB-dxdydz. Pręt dla pktu materialnego:p-(t)=Σni=1miVi

-. Pęd dla bryly sztywnej: p-(t)= ∫∫∫ΩpAUA-dΩ (Ω-obszar).

28. Moment bezwładności Ix=∫∫Dρ*y

2dxdy Iy=∫∫Dρ*x2dxdy.

29. Moment dewiacji D=Ixy=∫∫Dρ*xydxdy
30. Twierdzenie Steinera dla momentow bezwładności Moment bezwładności względem dowolnej prostej sztywnego ukl materialnego jest
rowny sumie momentow bezwładności wzgl prostej do niej || i przechodzącej przez srodek masy oraz iloczynowi masy całego ukl i kwadratowi

odległości miedzy tymi prostymi. Il=Ilo+M*a

2 Ix=Ix*+M*y2o* Iy=Iy*+M*x2o*

31. Twierdzenie Steinera dla momentu dewiacji Moment dewiacji figury plaskiej wzgl osi || przesuniętych jest rowny momentowi
dewiacyjnemu wzgl osi centralnych powiekszonemu o iloczyn powierzchni i obu składowych || przesuniecia. Ixy=Ixoyo+M*xo**yo*
32. WKW równowagi bryly sztywnej. WKW rownowagi ukl sil działającego na sztywny ukl materialny swobodny lub nieswobodny o wiezach
stacjonarnych, gładkich, dwustronnych jest by suma prac wirtualnych od wszystkich czynnych sil uogólnionych na każdym uogólnionym
przesunieciu wirtualnym była rowna 0.

33. Zasada pędu: Pochodna po czasie pedu ukl materialnego jest rowna sumie sil działających na dany układ. p-o-= Σni=1mi*Vi

-=

Σni=1Fi

-=S-(F). Zasada zachowania pedu: jeżeli układ sil rowna się 0 to ped jest staly (S-=0 => p-(t)=po-=const).

34. Zasada krętu: Pochodna kretu wzgl danego pktu po czasie w danej chwili ruchu jest rowna sumie momentu sil działających na ten układ

wzgl tego pktu i iloczynu wektorowego pedu całego układu oraz prędkości tego pktu. KB

- = MB-(F)+p-xVB-. Zasada zachowania krętu: Jeżeli

moment układu sil wzgl stalego pktu lub srodka masy jest rowny 0 to kret ukl materialnego jest staly (KB

-=const.).

35. Co można powiedziec o sumie S ukladu jeżeli MA=MB?
ODP: S-=0.

36. Twierdzenie o wekt wlasnych i wart wlasnych: 1) Λ1=/Λ2=/Λ3 Λ1=>w1

- Λ2=>w2- Λ3=>w3- jeżeli tensor symetryczny II rzedu ma 3

wart wlasne rozne od siebie to odpowiadajace im wektory wlasne sa do siebie prostopadle. 2) Λ1=Λ2=/Λ3 jeżeli tensor symetryczny II rzedu
posiada 2 wartosci wlasne rowne to istnieje wtedy niesk wiele wektorow wlasnych lezacych w plaszcz prostopadlej do wektora wlasnego. 3)
Λ1=Λ2=Λ3=Λ jeżeli tensor symetryczny II rzedu posiada 3 wart wlasne rowne to każdy wektor jest wektorem wlasnym tego tensora.
37. Twierdzenie o postaci diagonalnej tensora symetrycznego II rzedu. Jeżeli tensor II rzedu jest ten sam to w ukl osi wyznaczonych przez

wektory wlasne przyjmuje on postac diagonalna przy czym na przekatnej głównej leza wartości wlasne tego wektora. Równanie wiekowe: Λ3-

I1Λ

2+I2Λ-I3=0.

38. Podaj def Lagunowa stanu równowagi trwalej układu materialnego.

ODP: q-=(q1,q2,…,qs) – opisuje położenie układu materialnego q

-=(q1*,q2*,…,qs*) – opisuje polozenie rownow statecznej. Trwaly stan

równowagi ukl materialnego to taki stan w którym dla każdej dowolnie malej liczby ε>0 można dobrac η1(ε), η2(ε), takie ze sa spełnione
nierówności: {|q(to)-q

*|< η1(ε) |qo(to)-q*-|< η2(ε)} to zachodzi taki związek: |q(t)-q*|<ε |qo(to)-q*-|<ε.

39. Stany równowagi: - w stanie rownow trwalej w potencj polu sil En potencj przyjmuje wart minimalne; - w stanie rownow niestatecznej w
potencjalnym polu sil En potencj przyjmuje wart maksymalne; - w stanie rownow obojętnej w potencj polu sil En potencj przyjmuje wart stala.
40. Zasada d’Alamberta: Jeżeli ukl materialny poddany wiezom geometr, stacjonarn, gładkich, dwustronnych jest w ruchu rzeczywistym to

suma prac wirtualnych od wszystkich sil czynnych i sil bezwładności na każdym przesunieciu wirtualnym rowna jest 0. δL=Σni=1(Bi

-+Fi-+Ri-)

δSi

-=0 dla każdego δSi.

41. Równania Lagrange’a równanie II rodzaju dla dowolnego pola sil (d/dt)(∂Ek/∂qi)-(∂Ek/∂qi)=Qj j=1,2,…,j. równanie I rodzaju m*r

-o-

o-(t)=F-+Λgrad-f f(x,y,z)=0 warunki początkowe: +t=t0 r-(to)=ro- r-o-(to)=Vo-