FIZYKA 2 – luty 2013

1. Zasada zachowania ładunku.

Jedną z konsekwencji zasady zachowania ładunku jest pierwsze prawo Kirchhoffa.
Zasada ta stwierdza, że w izolowanym układzie ciał całkowity ładunek elektryczny,
czyli suma algebraiczna ładunków dodatnich i ujemnych, nie ulega zmianie. Co za
tym idzie, zmiana ładunku układu może zachodzić tylko na drodze przepływu
ładunku.

2. Pole elektryczne ładunku punktowego i układu ładunków punktowych.

Pole elektryczne to własność przestrzeni w otoczeniu ładunków elektrycznych,

jest to pole

wektorowe.

a) Prawo Coulomba:

Jeśli dwie naładowane cząstki (zwane także ładunkami punktowymi) o

ładunkach

i

znajdują się w odległości r, to siła elektrostatyczna

przyciągania lub odpychania między nimi ma wartość:

|

||

|

gdzie k jest stałą = 1/4πε

0

.

b) Linie siły pola:

Linie pola elektrycznego nie istnieją w rzeczywistości, są jedynie formą

zobrazowania zagadnienia pola elektrycznego. Linie te wychodzą od ładunku
dodatniego i są skierowane ku ujemnemu. Ładunki jednoimienne się odpychają,
różnoimienne przyciągają.

⃗⃗

gdzie: E – natężenie pola elektrycznego, F – siła działająca na dodatni ładunek
próbny,

q

0

– ładunek próbny.

c) natężenie pola elektrycznego wytwarzanego przez ładunek punktowy:

Wartość natężenia pola elektrycznego E wytworzonego przez ładunek

punktowy q w odległości r wynosi:

| |

gdzie ε

0

– przenikalność elektryczna próżni.

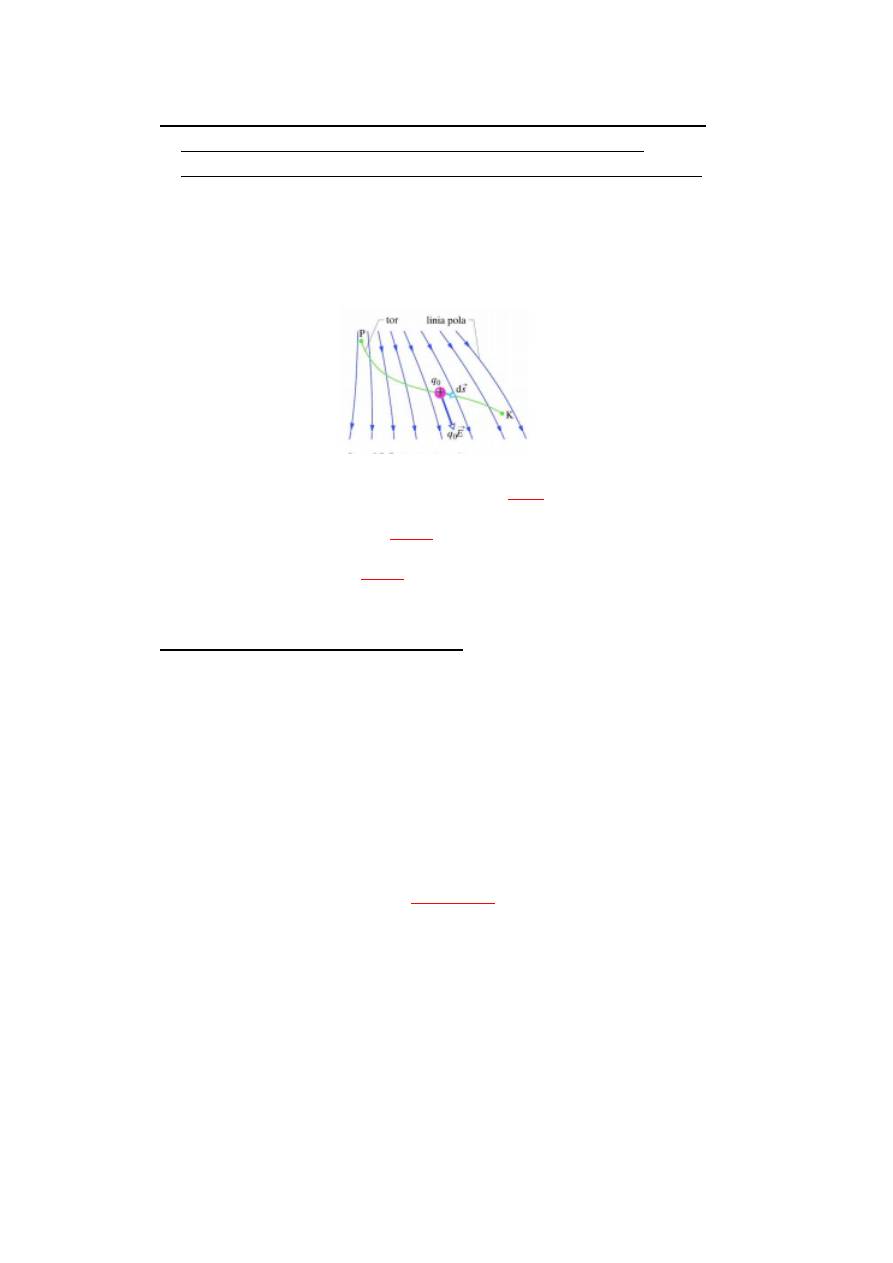
3. Ruch ładunku w jednorodnym polu elektrycznym: wyprowadź wzór na

równanie toru elektronu w przypadku gdy wpada on w obszar
jednorodnego pola elektrycznego z prędkością prostopadłą do linii sił.

Pod wpływem jednorodnego pola, gdzie prędkość elektronu jest prostopadła

do wektora natężenia pola, kierunek zostanie zakrzywiony w stronę dodatnią.
Jeżeli porusza się z prędkością v

x,

to w polu będzie to stała prędkość, zaś v

y

będzie

ruchem przyspieszonym.

( ) ( )

4. Prawo Gaussa dla pola elektrycznego.

a) Definicja strumienia elektrycznego:

Strumień elektryczny φ przenikający przez powierzchnię Gaussa jest

proporcjonalny do całkowitej liczby linii pola elektrycznego, przechodzących przez
tę powierzchnię.

∮

⃗⃗ ⃗⃗

b) Sformułuj prawo Gaussa i podaj jego interpretację:

gdzie ε to konkretna przenikalność elektryczna.

Prawo Gaussa określa związek między natężeniem pola elektrycznego w

punktach na zamkniętej powierzchni Gaussa i całkowitym ładunkiem objętym tą
powierzchnią. Opisuje ono związek między strumieniem i całowitym ładunkiem
znajdującym się wewnątrz danej powierzchni. Aby spełniać poniższy wzór ładunek
musi znajdować się w próżni lub, z pewnym przybliżeniem, w powietrzu.

∮

⃗⃗ ⃗⃗

c) Korzystając z prawa Gaussa wyprowadź wzór na zależność wartości natężenia
pola elektrycznego od odległości dla ładunku punktowego:

∮

⃗⃗ ⃗⃗ ∮ ∮

d) Wyprowadzić wzór na natężenie pola elektrycznego wytwarzanego przez
jednorodnie naładowaną nieskończoną powierzchnię przewodnika:

5. Potencjał pola.

a) Potencjał pola elektrycznego, linie ekwipotencjalne:

Potencjał elektryczny pojedynczego ładunku punktowego w odległości r od tego
ładunku wynosi:

Potencjał pola, wytworzonego przez układ ładunków punktowych wynosi:

∑

Linie ekwipotencjalne oznaczają ten sam potencjał w miejscach, przez które
przebiegają.

b) Praca sił pola elektrycznego:

Praca wykonana przez siłę elektrostatyczną przy przesunięciu
jednostkowego

ładunku

z punktu A do punktu B:

⃗ ⃗⃗

∫ ⃗ ∫

∫

(

) (

)

c) Wyprowadź zależność potencjału pola elektrycznego wytwarzanego przez
ładunek punktowy od odległości od tego ładunku:

Potencjał pola w punkcie A jest stosunkiem pracy przesunięcia jednostkowego
ładunku

z punktu A do miejsca, w którym pole zanika, do tego ładunku. Potencjał jest
wielkością addytywną.

∫ ∫ ⃗

∫

d) Potencjał i natężenie pola elektrycznego wytwarzanego przez układ ładunków
punktowych – zasada superpozycji pól:

Zasada superpozycji pól wywodzi się z prawa Coulomba. Stwierdza ona, że siłę
wypadkową działającą na ładunek w polu elektrycznym można obliczyć sumując
siły pochozdące od pozostałych ładunków.

⃗⃗

⃗⃗⃗⃗⃗⃗⃗

⃗⃗⃗⃗⃗⃗⃗

∑

⃗⃗⃗

e) Zależność pomiędzy potencjałem a natężeniem pola elektrycznego:

f) Wyprowadzić wzór na wartość potencjału elektrycznego wytwarzanego przez
ładunek rozmieszczony na metalowej obręczy:

∫

√

√

|

√

(

)

6. Dipol elektryczny w jednorodnym polu elektrycznym.

a) Moment dipolowy dipola elektrycznego – definicja:

Dipol – układ dwóch ładunków o jednakowych wartościach, ale przeciwnych
znakach.

Elektryczny moment dipolowy p dipola elektrycznego definiuje się jako wektor
skierowany od ujemnego do dodatniego ładunku dipola.

b) Moment sił działających na dipol w jednorodnym polu elektrycznym:

p – moment dipolowy

c) Energia potencjalna dipola elektrycznego:

Energia potencjalna jest określona tak, że przyjmuje wartość równą zeru, gdy
moment p jest prostopadły do natężenia E.

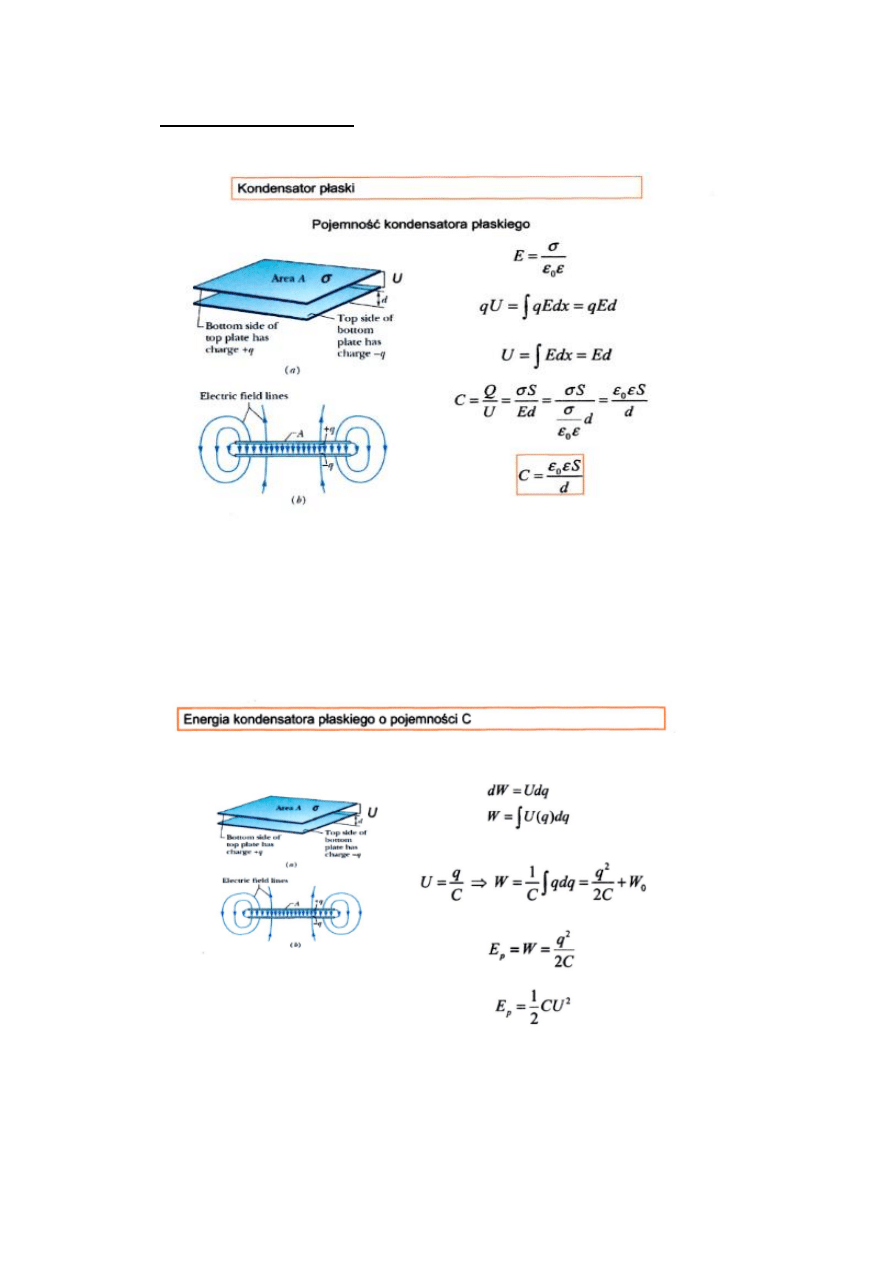
7. Pojemność elektryczna.

a) Wyprowadzić wzór na pojemność kondensatora płaskiego

E – natężenie pola elektrycznego, σ – ładunek na jednostkę powierzchni, ϵ -
przenikalność elektryczna, U – napięcie, d – odległość między okładkami, S – pole
powierzchni okładki, Q – ładunek w kondensatorze

b) Wyprowadzić wzór na energię zgromadzoną w kondensatorze płaskim:

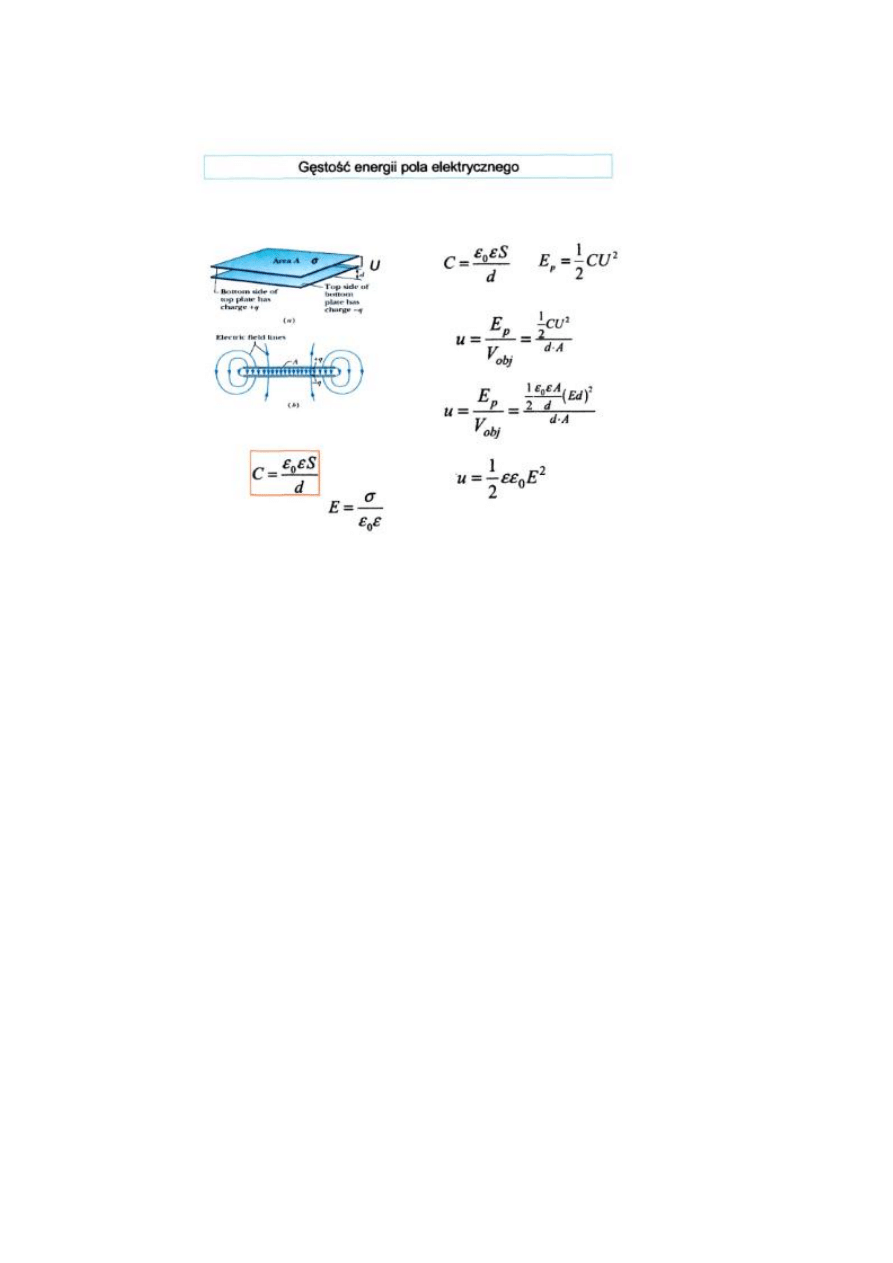
c) Wyprowadź wzór na gęstość energii pola elektrycznego:

d) Wyjaśnij zmianę natężenia pola elektrycznego wewnątrz kondensatora po
wprowadzeniu dielektryka pomiędzy okładki kondensatora:

Zarówno w dielektrykach polarnych, jak i niepolarnych natężenie dowolnego
przyłożonego do nich pola ulega osłabieniu. Jeśli przestrzeń między okładkami
kondensatora jest wypełniona materiałem dielektrycznym, to pojemność
kondensatora jest większa o ε

R

, czyli przenikalność elektryczną względną. ε

0

zostaje pomnożone przez ε

R

.

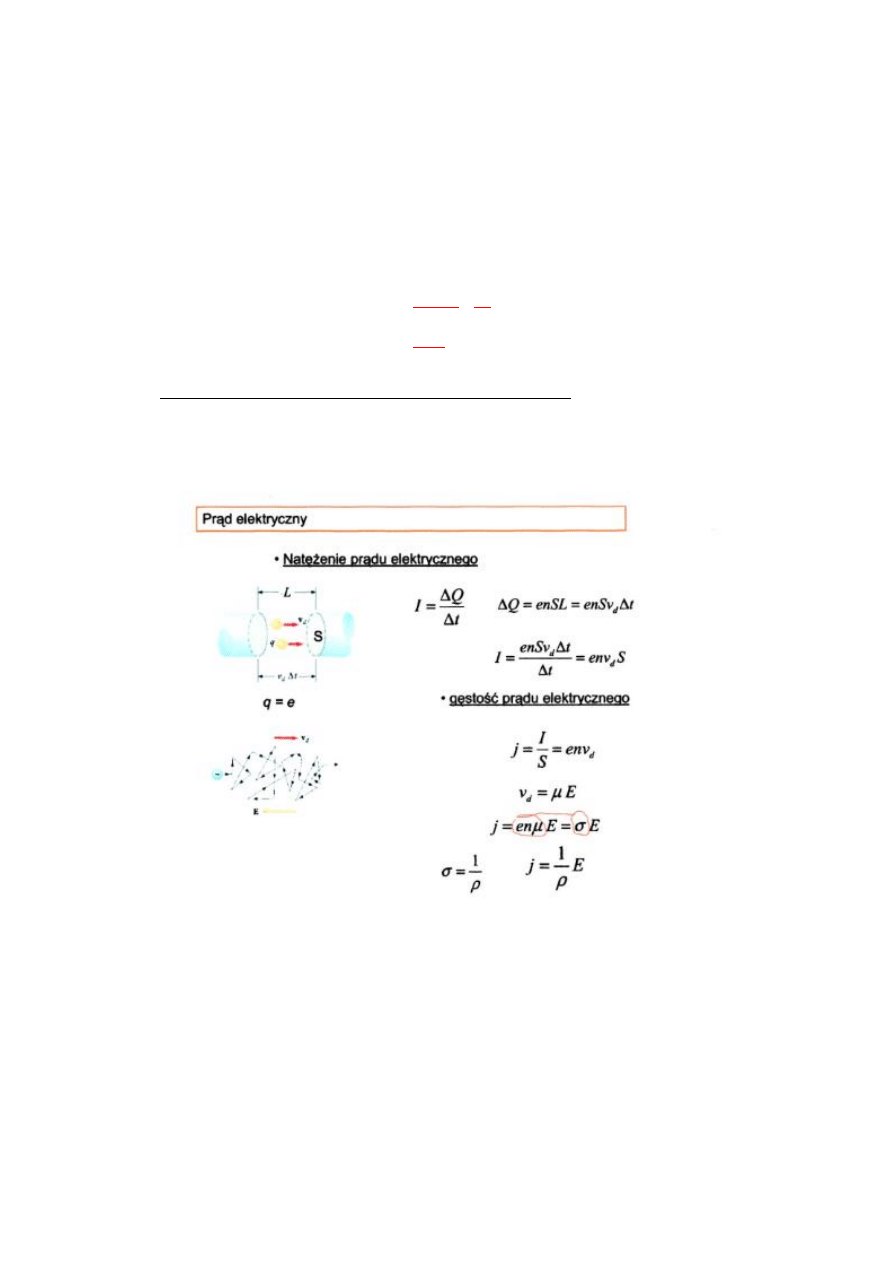
8. Prąd elektryczny w metalach – model mikroskopowy

a) Na podstawie mikroskopowej teorii przewodnictwa w metalach wyprowadzić
wzór na zależność gęstości prądu elektrycznego płynącego w metalu od
natężenia pola elektrycznego:

ρ – gęstość ładunku, v

d

– prędkość dryfu, n – koncentracja elektronów, j –

gęstość prądu, σ – konduktywność, E – natężenie pola, I – natężenie prądu, e =
q, μ – ruchliwość nośników

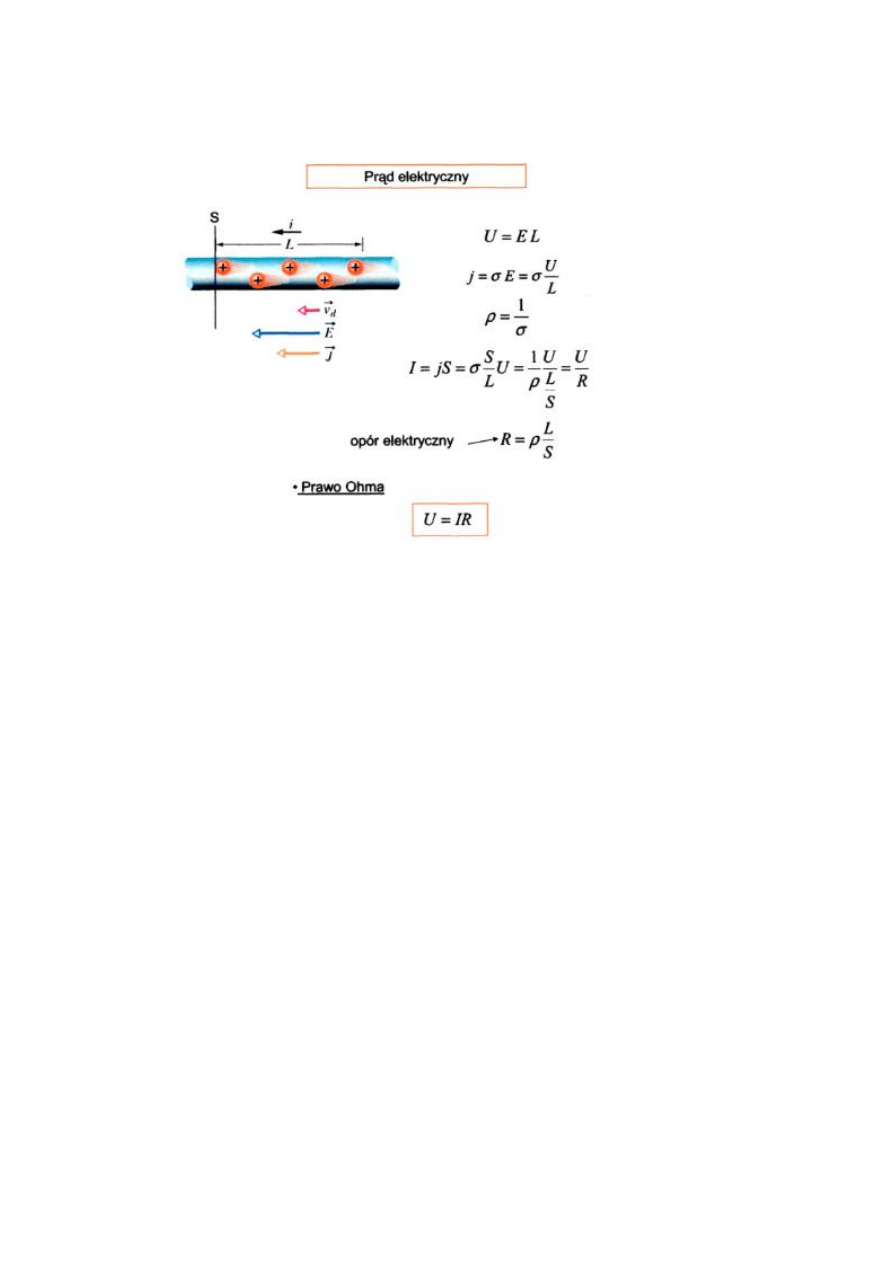
b) Wyprowadź wzór na prawo Ohma:

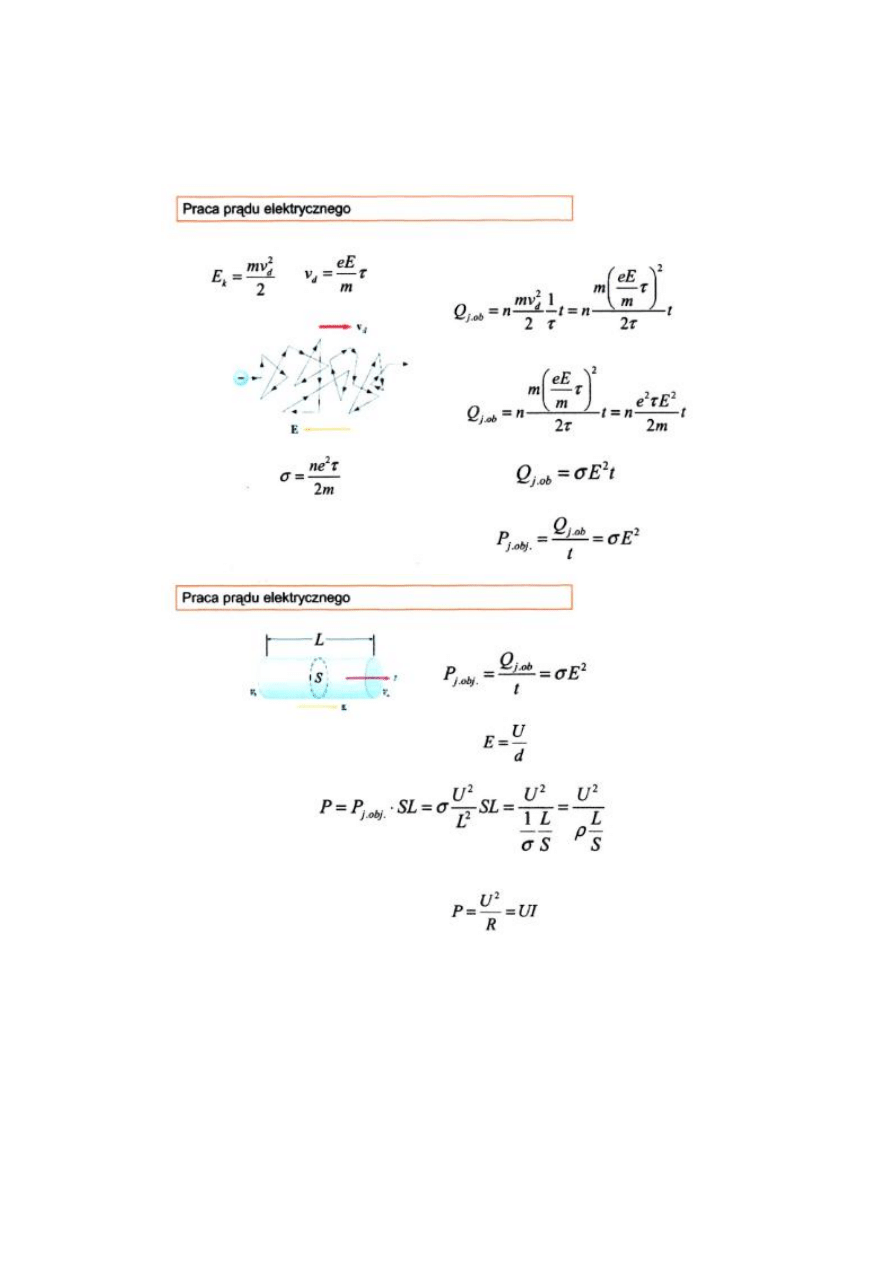
c) Na podstawie mikroskopowej teorii przewodnictwa w metalach wyprowadzić
wzór na moc wydzielaną w jednostce objętości metalu, przez który płynie prąd
elektryczny oraz wzór na pracę prądu:

d) Przedstaw I i II prawo Kirchhoffa:

I – Suma natężeń prądów wpływających i wypływającyh w dowolnym węźle jest
taka sama.

II – Algebraiczna suma zmian potencjału w napotykanych przy pełnym obejściu
dowolnego oczka musi być równa zeru.

– SEM źródła napięcia

9. Pole magnetyczne.

a) Podstawowe wielkości charakteryzujące pole magnetyczne:



Wektor indukcji – jest to wielkość wektorowa skierowana wzdłuż
wyróżnionej osi, na której siła działająca na cząstkę jest równa zeru.

| |

Gdzie Fb – siła działająca na ładunek w polu, B – indukcja magnetyczna, v
– prędkość ładunku. Fb jest proporcjonalna Usinφ, gdzie φ to kąt między
wektorem v a wyróżnioną osią, wzdłuż której Fb=0. Fb jest zawsze
prostopadła do wektorów v i B.



Linie sił pola magnetycznego



Strumień pola

∫



Dipolowy moment magnetyczny

Gdzie N – liczba zwojów cewki, I- natężenie prądu płynącego przez cewkę,
S – pole powierzchni

Jest to pseudowektor skierowany do powierzchni pętli. Kierunek
dipolowego momentu magnetycznego określony jest przez kierunek
natężenia I oraz regułę prawej dłoni.

b) Przedstaw właściwości siły działającej na ładunek elektryczny poruszający się
w polu magnetycznym:

Jest to iloczyn wektorowy prędkości i wektora indukcji B. Siła działająca na
ładunek jest prostopadła do płaszczyzn v i B. Siła Fb nigdy nie ma składowej
równoległej do wektora v. Oznacza to, że siła Fb nie może zmienić wartości
prędkości v cząstki, a zatem także jej energii kinetycznej.

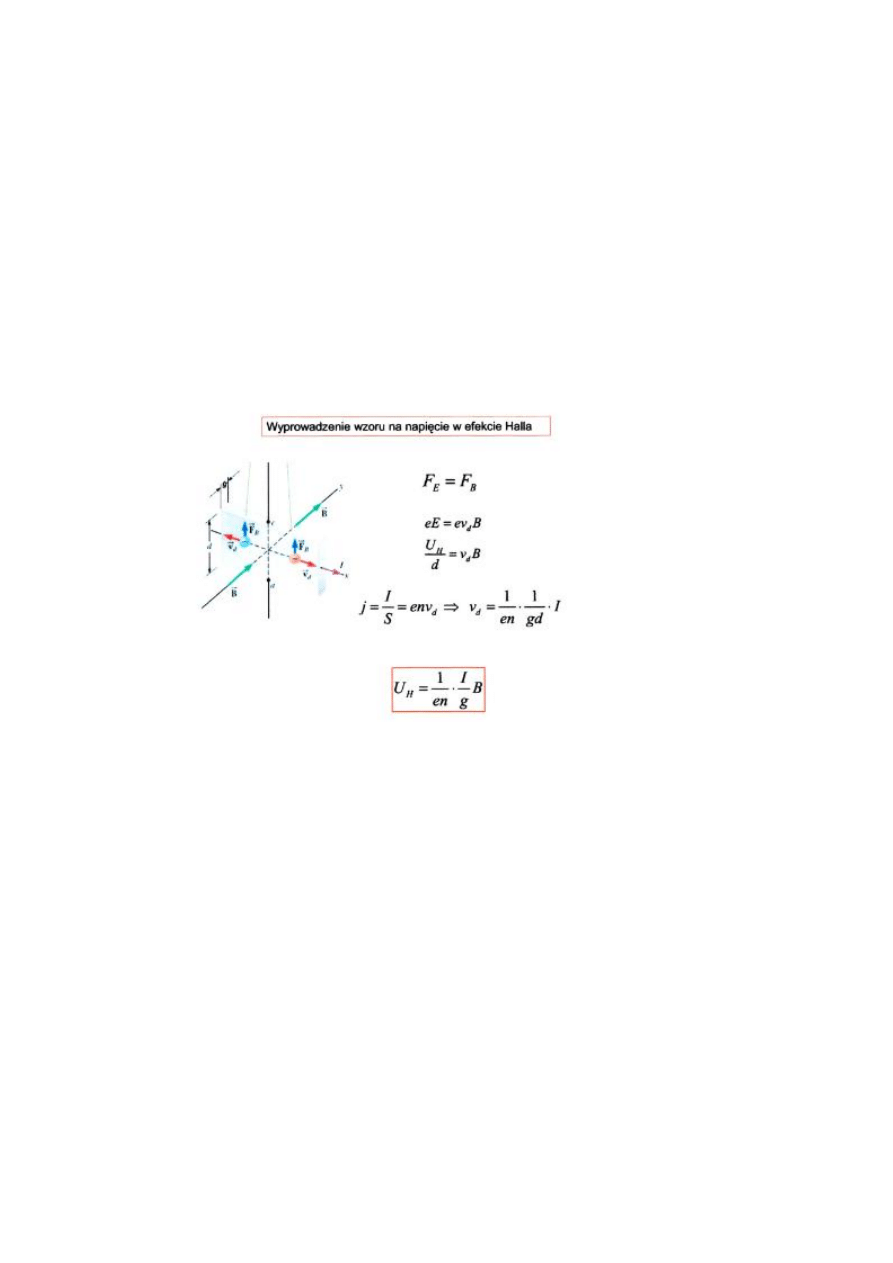
c) Wyjaśnił dlaczego prąd elektryczny płynący w metalowej płytce umieszczonej
prostopadle do linii sił jednorodnego pola magnetycznego powoduje pojawienie
się różnicy potencjałów między jej bokami (efekt Halla). Wyprowadź wzór na
wartość tej różnicy potencjałów:

Zjawisko Halla polega na tym, że pole magnetyczne odchyla elektrony
przewodnictwa, np. w drucie miedzianym.

Kiedy przewodzący pasek o grubości l, w którym płynie prąd o natężeniu I,
zostanie umieszczony w jednorodnym polu magnetycznym o indukcji B, to nośnik
ładunku e zaczyna się gromadzić na brzegu paska, wytwarzając poprzeczne
napięcie U.

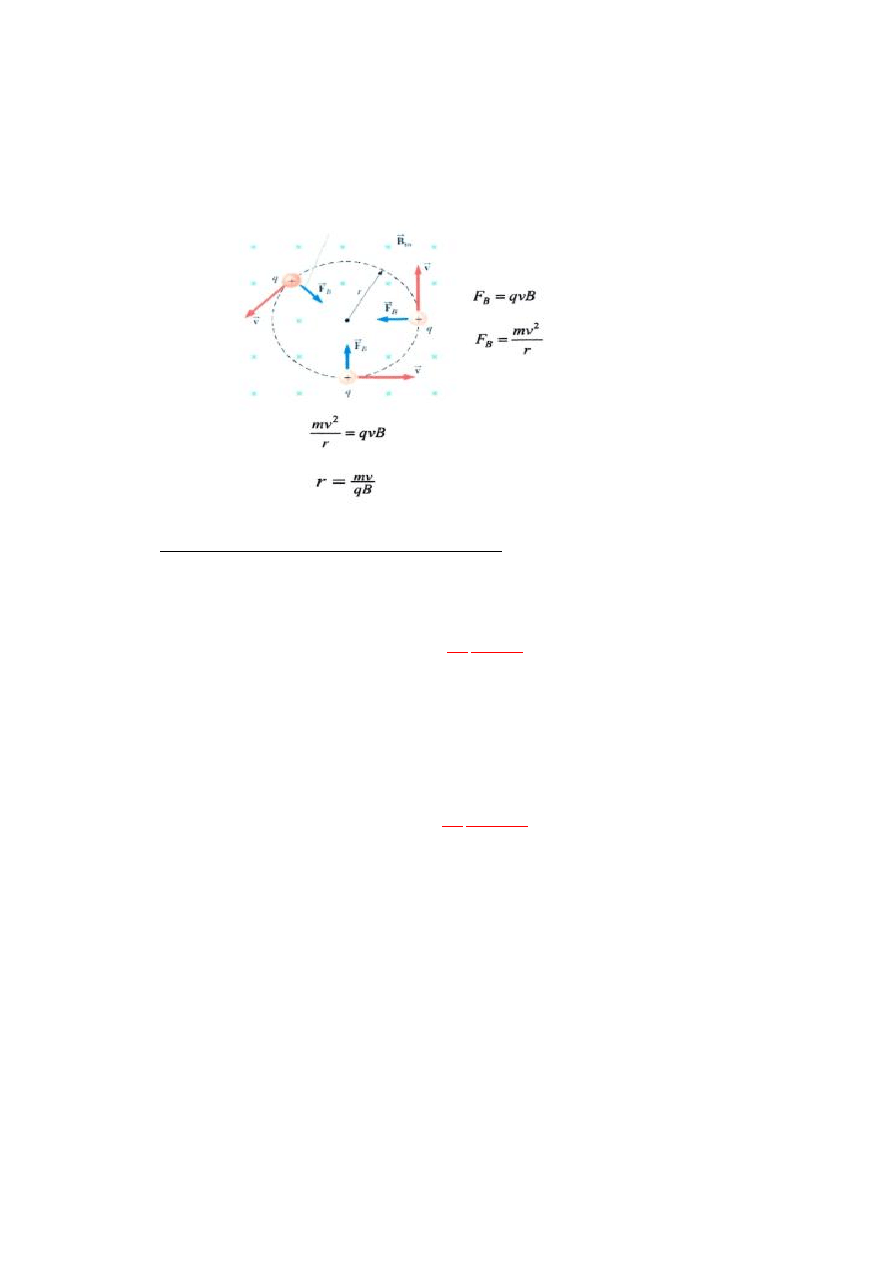
d) Ruch naładowanej cząstki w polu magnetycznym. Wyprowadź wzór na
promień okręgu po jakim porusza się cząstka wpadająca w obszar pola
magnetycznego z prędkością prostopadłą do wektora indukcji pola
magnetycznego:

10. Pole magnetyczne przewodnika z prądem.

a) Prawo Biota – Savarta:



Sformułuj prawo Biota – Savarta:

To prawo opisuje odwrotną proporcjonalność indukcj magnetycznej i
kwadratu promienia (w postaci skalarnej, w wektorowej jest to sześcian
promienia). Jest stosowane do obliczenia wypadkowej indukcji B pola
wytworzonego w punkcie P przez prądu o różnych rozkładach. Postać
skalarna:

Pozwala określić w dowolnym punkcie przestrzeni indukcję pola magnetycznego.



Wyprowadź zależność na wartość indukcji pola magnetycznego
wytwarzanego przez stały prąd elektryczny płynący przez przewodnik
kołowy:

11. Oddziaływanie dwu przewodników prostoliniowych przez które płynie
stały prąd elektryczny. Definicja jednostki natężenia prądu elektrycznego.

Jednostką natężenia prądu w układzie SI jest amper, który jest równy kulombowi
na sekundę:

Dwa równoległe przewody, w których płyną prądy w tym samym kierunku
wzajemnie się przyciągają. B

a

jest wektorem indukcji magnetycznej. F

BA

jest siłą,

która działa na przwód B, na skutek prądu znajdującego się w polu indukcji B

A

.

Przewody, w których płyną prądy równoległe przyciągają się, a antyrównoległe
odpychają.

12. Prawo Ampere’a dla pola magnetycznego.

∮

Gdzie μ

0

– przenikalność magnetyczna próżni, Ip – całkowite natężenie prądu

przecinającego powierzchnię całkowania

Prawo to wiąże indukcję magnetyczną wokół przewodnika z natężeniem prądu w
tym przewodniku zgodnie z powyższym wzorem. Całka krzywoliniowa obliczana
jest wzdłuż zamkniętego konturu.

13. Na podstawie prawa Ampere’a wyprowadzić zależność wartośći pola
magnetycznego wewnątrz solenoidu.

n – liczba zwojów na jednostkę długości, N – liczba zwojów

14. Indukcja elektromagnetyczna.

a) Definicja strumienia indukcji pola magnetycznego:

∫

gdzie kąt alfa, to kąt między B i S. Jednostką strumienia magnetycznego jest weber
(1Wb=1T*m^2)

Jest to strumień przepływający przez powierzchnię S jest zdefiniowany jako iloczyn
skalarny wektora indukcji magnetycznej i wektora powierzchni S.

b) Prawo Gaussa dla pola magnetycznego:

Zgodnie z prawem Gaussa najprostszą strukturą magnetyczną jest dipol
magnetyczny, nie istnieją zaś monopole magnetyczne. Zgodnie z tym prawem
wypadkowy strumień magnetyczny φ

B

przez dowolną zamkniętą powierzchnię jest

równy zeru:

∮

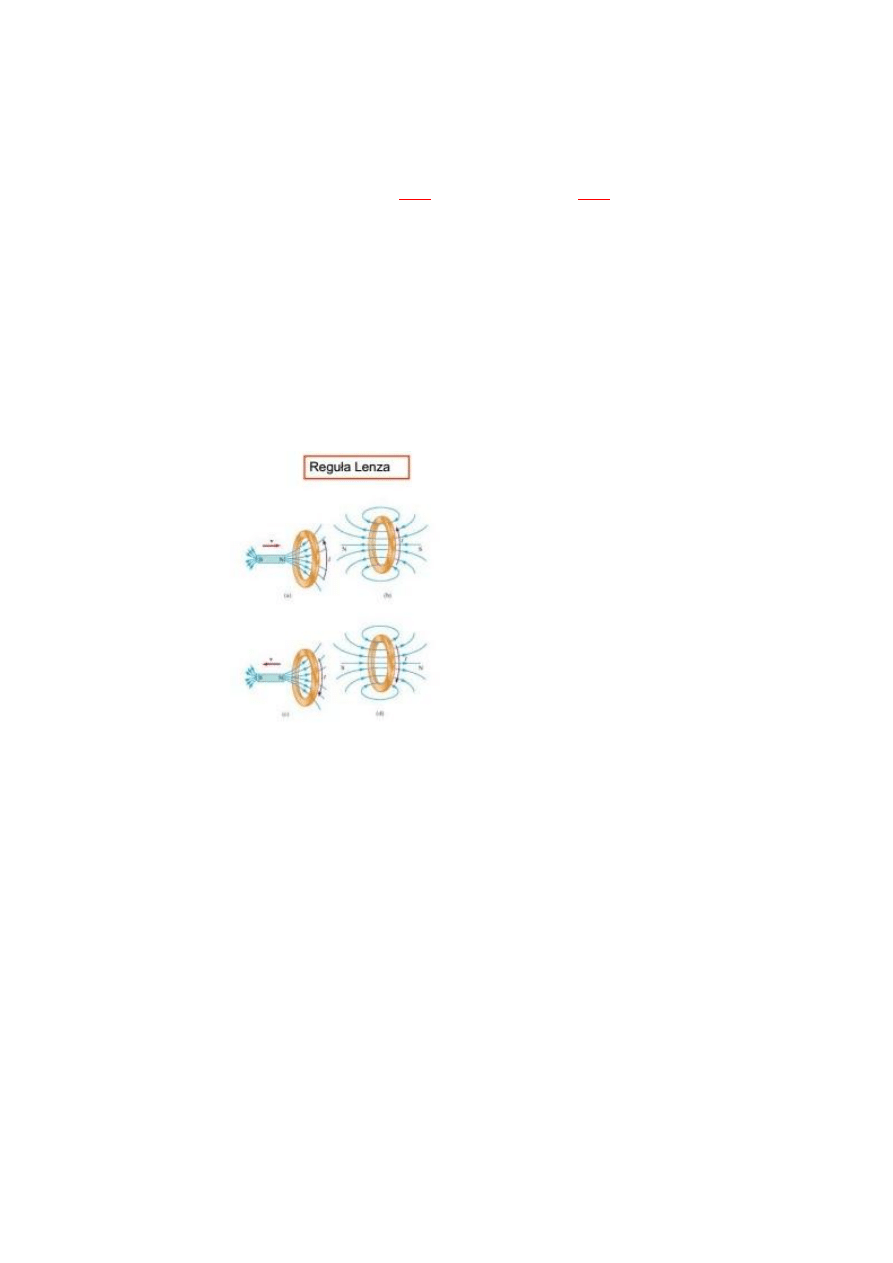
c) Zjawisko indukcji elektromagnetycznej i prawa nim rządzące:



Prawo Faradaya:

∮

∮

∮ ( ), N – liczba zwojów w przypadku cewki

W zamkniętym obwodzie znajdującym się w zmiennym polu magnetycznym
pojawia się siła elektromotoryczna indukcji równa szybkości zmian strumienia
indukcji pola magnetycznego.



Reguła przekory Lenza:

Prąd indukowany płynie w takim kierunku, że pole magnetyczne
wytworzone przez ten prąd przeciwdziała zmianie strumienia pola
magnetycznego, który ten prąd produkuje

dipolowy moment magnetyczny

zorientowany na

przeciwdziałanie ruchowi magnesu

Pole magnetyczne powoduje indukowanie prądu, który wytwarza pole
magnetyczne wtórne, która przeciwdziała przyczynie oryginalnego pola
magnetycznego.



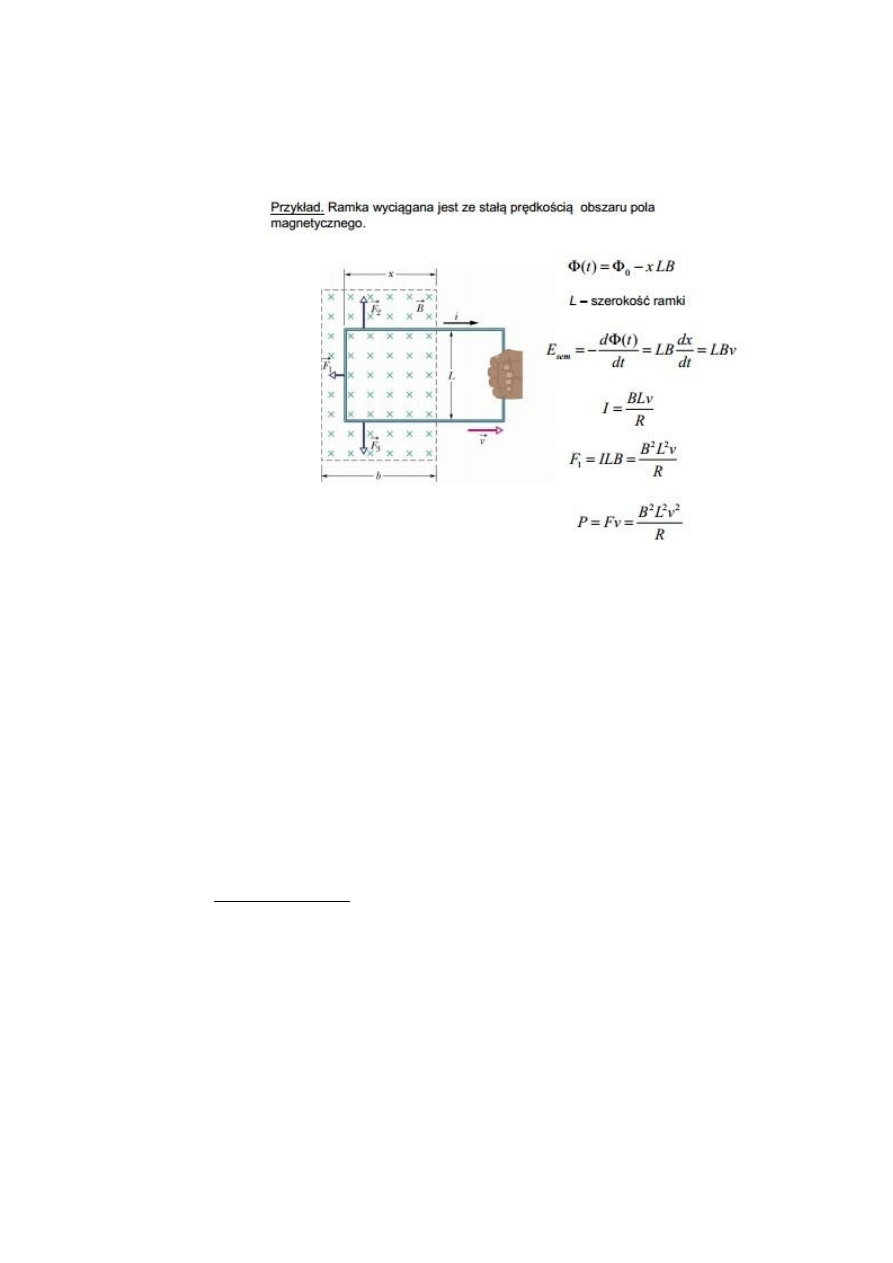
Przykład – ramka wyciągana jest ze stałą prędkością z obszaru pola
magnetycznego:

Podczas ruchu ramki indukuje się w niej prąd o natężeniu I, płynący w
kierunku zgodnym z ruchem wskazówek zegara. Na odcinki ramki
znajdujące się w polu magnetycznym działają siły F

1

, F

2

i F

3

.

d) Wyjaśnić w jakich warunkach powstają prądy wirowe i jaka jest tego
przyczyna:

Prądy wirowe indukują się w przewodzącej (np. litowej) płycie, gdy usuwa
się ją z pola magnetycznego (tak jak na schemacie z poprzedniego punktu
dla ramki). Dzieje się tak, ponieważ elektrony przewodnictwa w płycie,
które tworzą w niej prąd indukowany nie muszą się poruszać wzdłuż
jednego toru (tak jak w ramce). Elektrony krążą za to w płycie tak jakby
wpadły w wir wodny.

15. Samoindukcja.

Jeżeli dwie cewki znajdują się blisko siebie, to prąd o natężeniu I, płynący
w jednej z nich wytwarza strumień magnetyczny φ

B

, przechodzący

również przez drugą cewkę. Jeżeli ten strumień zostanie zmieniony, przez
zmianę natężenia prądu, to w drugiej cewce pojawi się indukowana SEM
(prawo Faradaya). Jednak indukowana SEM pojawi się też w pierwszej
cewce.

Indukowane SEM ε

L

występuje w każdej cewce, w której prąd się zmienia.

a) Indukcyjność solenoidu:

W dowolnej cewce lub solenoidzie pojawia się SEM samoindukcji, o ile
natężenie prądu zmienia się w czasie. Indukcyjność solenoidu zależy od
liczby jego zwojów, jego długości, pola przekroju i przenikalności
magnetycznej rdzenia solenoidu.

b) Energia pola magnetycznego i jej gęstość:

E

B

– energia magnetyczna, L – cewka, I – natężenie prądu

Energia zmagazynowana w jednostce objętości:

l – długość odcinka solenoidu, S – pole przekroju, B – indukcja
magnetyczna

16. Fale elektromagnetyczne.

a) Podstawowe własności fali elektromagnetycznej:

Fala elektromagnetyczna składa się z drgających (oscylujących) pól elektrycznych i
magnetycznych. Różne możliwe częstości fal elektromagnetycznych tworzą
widmo, którego małą częścią jest światło widzialne. Wartość natężenia pola
elektrycznego E i indukcji pola magnetycznego B fali elektromagnetycznej
rozchodzącej się wzdłuż osi x zależą od x i od t:

( )

( )

E

m

, B

m

– amplitudy E i B

Prędkość rozchodzenia się fali elektromagnetycznej w próżni:

√

b) Szybkość przepływu energii przenoszonej przez falę elektromagnetyczną:

Szybkość ta, na jednostkową powierzchnię, dana jest przez wektor Poyntinga S:

Kierunek S jest prostopadły do kierunku wektorów E i B. Uśredniona szybkość
przepływu energii S

śr

nazywa się natężeniem fali:

(

√

)

Punktowe źródło fal elektromagnetycznych emituje fale izotropowo. Natężenie
fali w odległości r od źródła mocy P

źr

jest równe:

c) Ciśnienie fali elektromagnetycznej:

Fale elektromagnetyczne mają energię oraz pęd, zatem oświetlając jakieś ciało
wywieramy na nie ciśnienie, choć jest ono na tyle małe, że pomija się je w skali
makroskopowej. Ciśnienie promieniowania wyraża się dwoma wzorami:

Przykład: pył uwalniany z komety nie porusza się za nią po orbicie, ponieważ
ciśnienie światła słonecznego odpycha go radialnie od Słońca.

17. Interferencja fali elektromagnetycznej. Prążki interferencyjne.

Interferencja to zjawisko powstania nowego, przestrzennego rozkładu amplitudy
fali (wzmocnienia i wygaszenia) w wyniku nakładania się (superpozycji) fal.
Warunkami trwałej interferencji fal jest ich spójność, czyli korelacja faz i
częstotliwości.

Zasada Huygensa:

„Wszystkie punkty czoła fali zachowują się jak punktowe źródła elementarnych
kulistych fal wtórnych. Po czasie t nowe położenie czoła fali jest wyznaczone przez
powierzchnię styczną do powierzchni fal wtórnych”.

Prążki interferencyjne powstają w wyniku umieszczania na drodze światła (np.
dwóch interferencyjnych fal) ekranu, na który to światło będzie padało. Na
ekranie można wtedy zaobserwować szereg jasnych kresek (prążków
interferencyjnych). Odpowiadają one maksimom interferencji. Całość nazywa się
obrazem interferencyjnym. Eksperyment, który udowodnił istnienie interferencji
nazywa się „doświadczeniem interferencyjnym Younga”.

Oświetlenie w każdym punkcie ekranu w doświadczeniu interferencyjnym Younga
z dwiema szczelinami jest określone przez różnicę dróg ∆l, jakie przebywają
promienie świetlne docierające do tego punktu.

18. Dyfrakcja promieniowania X na materiach krystalicznych. Warunek
wystąpienia maksimów interferencyjnych (prawo Bragga).

Regularnie uszeregowane atomy w krysztale stanowią trójwymiarową siatkę
dyfrakcyjną dla promieniowania o małych długościach fal (np. promieniowanie
rentgenowskie). W celu analizy dyfrakcji atomy kryształu można opisywać jako
uporządkowane w płaszczyznach o odległości międzypłaszczyznowej d. Choć jest
to skomplikowane zjawisko, to maksima natężenia powstają w takich kierunkach,
jak gdyby promieniowanie rentgenowskie było odbijane od rodziny równoległych
płaszczyzn odbijających (płaszczyzn sieciowych), w których leżą regularnie
uporządkowane atomy kryształu. Maksima dyfrakcyjne (wytworzone jako wynik
konstruktywnej interferencji) pojawiają się gdy spełniony zostanie warunek
Bragga:

m (= 1,2,3...) – rząd maksimum natężenia, λ – długość fali promieniowania,
odległość międzypłaszczyznowa

Inaczej niż w optyce, kąty na rysunku nie są zdefiniowane jako kąty między
promieniami a normalną do płaszczyzny, lecz jako ąty między promieniami a
płaszczyzną odbijającą.

19. Szczególna teoria względności.

a) Postulaty szczególnej teorii względności:



Postulat Względności:

Dla wszystkich obserwatorów w inercjalnych układach odniesienia prawa
fizyki są takie same.



Postulat Stałej Prędkości Światła:

We wszystkich inercjalnych układach odniesienia i we wszystkich
kierunkach światło rozchodzi się z tą samą prędkością c.

b) Przedstaw wnioski wynikające z transformacji Lorentza dotyczące:



Równoczesności zdarzeń:

Jeżeli dwa zdarzenia zachodzą w różnych miejscach w układzie odniesienia
S’, to wartość ∆x’ jest różna od zera. Wynika z tego, że nawet jeżeli
zdarzenia są jednoczesne w układzie S’, to nie będą jednoczesne w
układzie S. Odstęp czasu między nimi wynosi:

√

(

)



Skrócenia czasu i odległości:

Dylatacja czasu wynika ze wzoru:

Skrócenie odległości wynika ze wzoru:

( )



Czasu pomiędzy zdarzeniami:

Jeżeli dwa zdarzenia zachodzą w inercjalnym układzie odniesienia w tym
samym miejscu, to dzielący je czas t

0

zmierzony w miejscu zdarzenia

nazywa się czasem własnym. Obserwatorzy poruszający się względem
tego układu zmierzą większy odstęp czasu.

20. Transformacja prędkości.

Relatywistyczna transformacja prędkości:

u – prędkość zmierzona w jednym układzie odniesienia, u’ – prędkość zmierzona
w innym układzie,
v – prędkość układów względem siebie

Dla prędkości dużo mniejszych od c prawdziwa jest także transformacja Galileusza
(w przybliżeniu):

Wynika to z tego, że dwaj obserwatorzy w dwóch układach inercjalnych zmierzą
czas i odległość przestrzenną między zdarzeniami.

21. Dynamika relatywistyczna.

a) II zasada dynamika w mechanice relatywistycznej:

II zasada dynamiki mówi, że zmiana pędu ciała jest proporcjonalna do działającej
siły wypadkowej. Pęd nierelatywistyczny definiowany jest wzorem:

W dynamice relatywistycznej prawdziwy jest wzór:

ϒ – współczynnik Lorentza

b) Związek między masą spoczynkową, pędem i energią całkowitą:

( )

(

)

Wzór ten powstał z zależności relatywistycznej między pędem a energią
kinetyczną, po usunięciu z obu stron równania v.

Energia spoczynkowa a masa:

c) Energia kinetyczna w dynamice relatywistycznej i jej przybliżenie dla małych
prędkości:

Dla małych prędkości można posłużyć się nierelatywistyczną formą:

Jednak w dynamice relatywistycznej będzie to:

( )

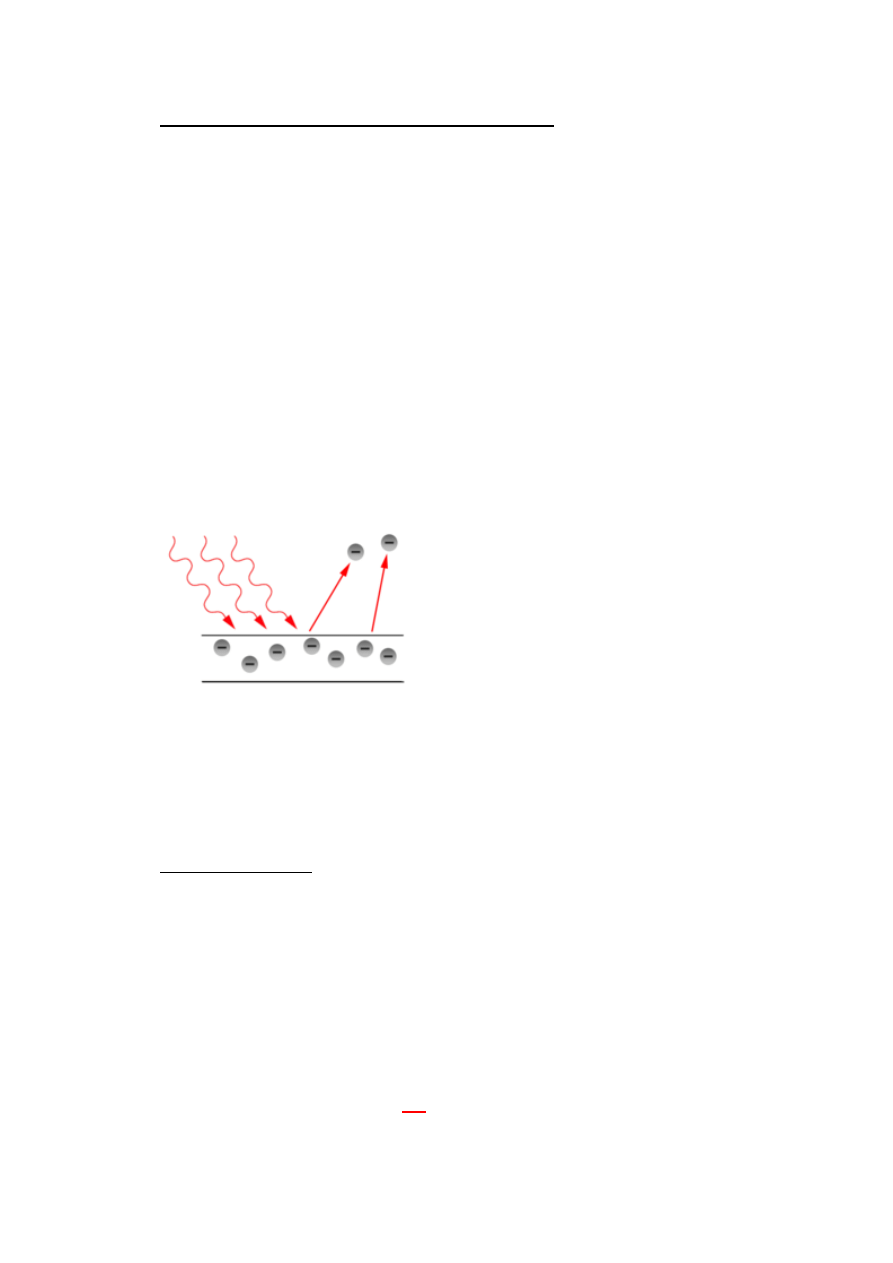
22. Własności efektu fotoelektrycznego (fotoefektu).

a) Przedstaw własności efektu fotoelektrycznego, których wyjaśnienie wymaga
założenia korpuskularnej natury fali elektromagnetycznej:

Zjawisko fotoelektryczne polegające na wybijaniu elektronów z pewnej
powierzchni jest niemożliwe do wyjaśnienia przy klasycznym założeniu, że światło
jest falą. Wynika z tego doświadczenia, że dla światła o danej częstotliwości
energia Ek

max

nie zależy od natężenia światła. Bowiem zwiększając natężenie

zwiększamy ilość fotonów w wiązce, ale energia jednego fotonu pozostanie taka
sama. Zmieni się ona wraz z częstotliwością fali.

Zjawisko fotoelektryczne zachodzi gdy energia hv jest większa od energii pracy
wyjścia φ, powyżej której elektrony są uwalniane. Częstotliwość fali musi być
większa niż częstotliwość progowa. Praca wyjścia dla większości metali wynosi ok.
4eV.

gdzie: φ – praca wyjścia, hv – energia fotonu, v – częstość, h – stała Plancka

b) Wyjaśnij powstanie fotoprądu w fotokomórce po oświetleniu katody:

Po oświetleniu katody falą elektromagnetyczną o częstości większej od progowej
następuje przekazanie elektronom przez fotony energii wystarczającej (większej
od pracy wyjścia) do opuszczenia powierzchni katody i rozpoczyna się przepływ
fotoprądu. Fala musi być krótsza niż długość progowa, by generować fotoprąd.

23. Efekt Comptona.

a) Opisz efekt Comptona:

Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku
jej rozpraszania na swobodnych elektronach. Zgodnie z fizyką klasyczną elektron
pod wpływem sinusoidalnej fali elektromagnetycznej powinien drgać z tą samą
częstością co ta fala, a zatem emitować falę o tej samej długości. Jednak, jak
zaobserwował Arthur Compton dla promieniowania rentgenowskiego długość fali
λ’ różni się od λ o ∆λ. Ta ostatnia wielkość nazywana jest przesunięciem
comptonowskim:

( )

gdzie h/mc to stała comptonowska długość fali.

Wartość przesunięcia zależy od kąta pod jakim obserwuje się rozproszone
promieniowanie.

b) Wyjaśnij dlaczego długość fali ugiętej (rozproszonej) musi być większa od
długości padającej:

W wyniku zderzenia fotonów ze poczywającymi elektronami wzrasta pęd
elektronów a maleje pęd fotonów, w wyniku czego zmienia się długość fali oraz
kierunek propagacji fali.

24. Opisz mechanizm powstawania promieniowania X. Wyjaśnij dlaczego
świadczy on o kwantowej naturze promieniowania
elektromagnetycznego.

Promieniowanie X, to rodzaj promieniowania elektromagnetycznego o długości
fali zawartej w przedziale od 0,1pm do ok. 50nm. Promieniowanie to powstaje w
wyniku hamowania elektronu w polu jąder atomów materiału anody w lampie
rentgenowskiej (jest to bańka próżniowa posiadająca zatopione elektrody: anodę i
katodę w postaci wolframowej spirali).

Roentgen zauważył, że jedną z cech promieniowania X jest to, że nie ulega ono
odchyleniu w polu magnetycznym lub elektrycznym, co dowodzi, że nie jest ono
strumieniem naładowanych cząstek. Jedną z cech widma rentgenowskiego jest
występowanie bardzo ostrej krótkofalowej granicy promieniowania λ

min

, poniżej

której natężenie promieni X jest równe zeru. Wartość λ

min

zależy od napięcia U na

lampie rentgenowskiej. Wyjaśnienie tej prawidłowości daje kwantowa teoria
promieniowania. Podczas hamowania elektronu w ośrodku materialnym jego
energia zostaje całkowicie lub częściowo wyemitowana w postaci fotonów.

25. Fale materii.

a) Przedstaw hipotezę de Broglie’a i doświadczenie C.J. Davissona oraz L.G.
Germera ją potwierdzające:

Louis de Broglie przypisał cząstkom o masie większej od zera takie same
właściwości jakie ma światło, tzn. strukturę korpuskularno-falową, gdzie pęd i
energia są przekazywane punktowo, ale np. elektrony mają też właściwości
falowe. Długość fali materii wyraża się wzorem:

gdzie: p – pęd, h – stała plancka. Doświadczenie Davissona i Germera polegało na
bombardowaniu strumieniem elektronów spoczywającego krształu niklu. Jako
pierwsi zaobserwowali na skutek tego doświadczenia, dyfrakcję elektronów w
krysztale niklu.

b) Czym jest funkcja falowa. Przedstaw jej podstawowe własności:

Fala materii opisywana jest przez funkcję falową Ψ (x, y, z, t), którą można również
zapisywać jako
ψ (x, y, z)e

-iωt

, gdzie e jest funkcją czasu, a ω = 2πv jest częstością kołową materii.

W przypadku cząstki o masie m poruszającej się w kierunku x ze stałą energią
całkowitą E w obszarze, gdzie jej energia potencjalna jest równa U(x),
odpowiednią funkcję falową można znaleźć, rozwiązując równanie Schroedingera
bez czasu.

Opisuje ona własności falowe cząstki w mechanice kwantowej, jest rozwiązaniem
równania Schroedingera.|Ψ|

2

– gęstość prawdopodobieństwa znalezienia cząstki

w danej chwili w pewnym punkcie przestrzeni.

26. Napisz równanie Schroedingera dla cząstki swobodnej i wyznacz wzór
na jej energię.

gdzie k – liczba falowa 2π/λ

,

ℏ to stała Plancka h/2π

27. Omów zasadę nieoznaczoności.

Zasada nieoznaczoności została zaproponowana w 1927 roku przez Wernera
Heisenberga. Stwierdza ona, że położeniu r i pędowi p cząstki nie można
równocześnie przypisać wartości pomiarowych z nieograniczoną dokładnością.

Zasada nieoznaczoności Heisenberga dla składowych położenia i pędu:

ℏ

ℏ

ℏ

Nie oznacza to, że metoda pomiaru jest wadliwa, ale że gdy określimy jedną z tych
wartości, np. pęd, to położenie cząstki może być z jednakowym
prawdopodobieństwem wszędzie na danej osi.

Przykład:

Jeżeli pęd zmierzono z dokładnością 0,01%, to ∆p=0,01, a dokładność wyznaczenia
położenia określa wzór:

ℏ

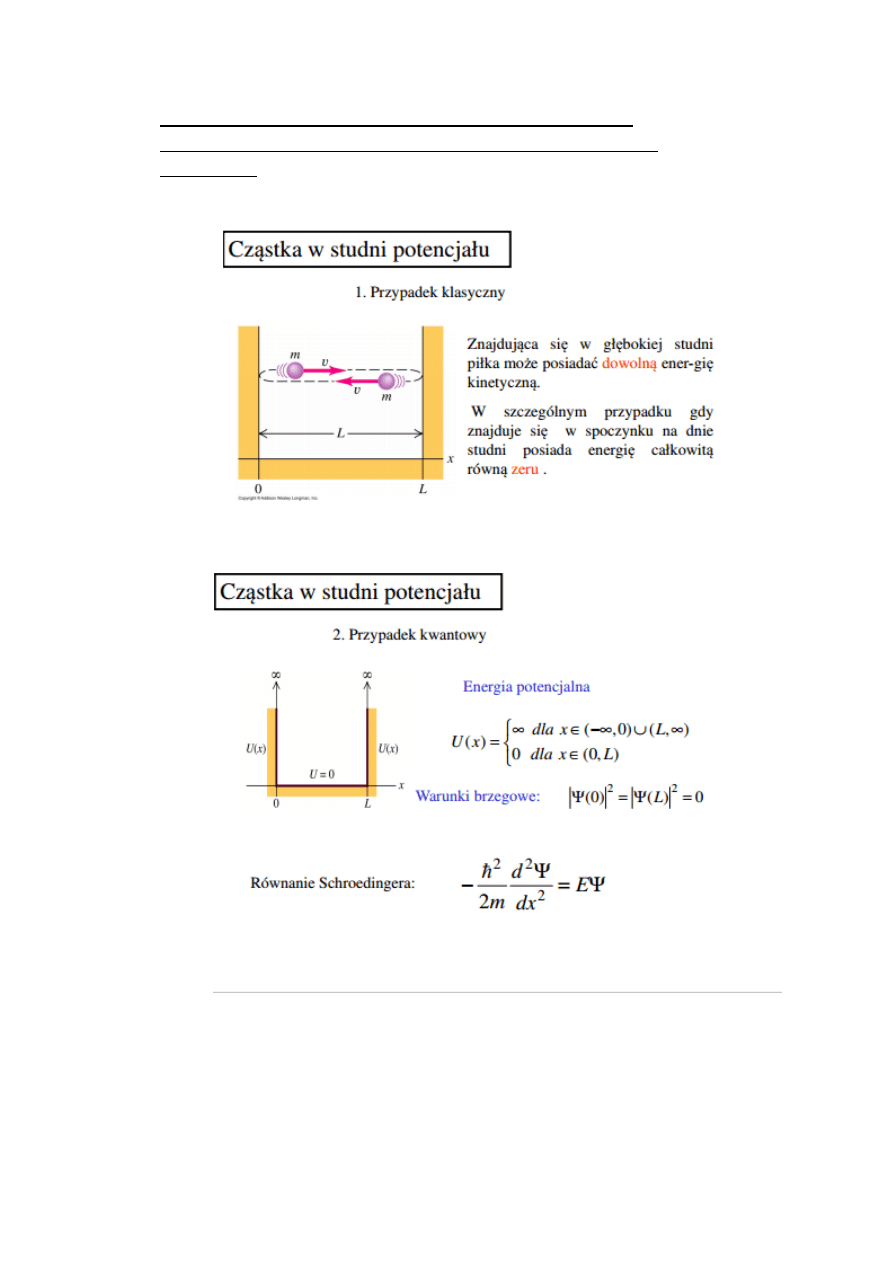
28. Wyprowadź wzór na energię cząstki w nieskończonej studni
potencjału i wyjaśnij różnicę pomiędzy rozwiązaniem klasycznym a
kwantowym.



Przypadek klasyczny:



Przypadek kwantowy:

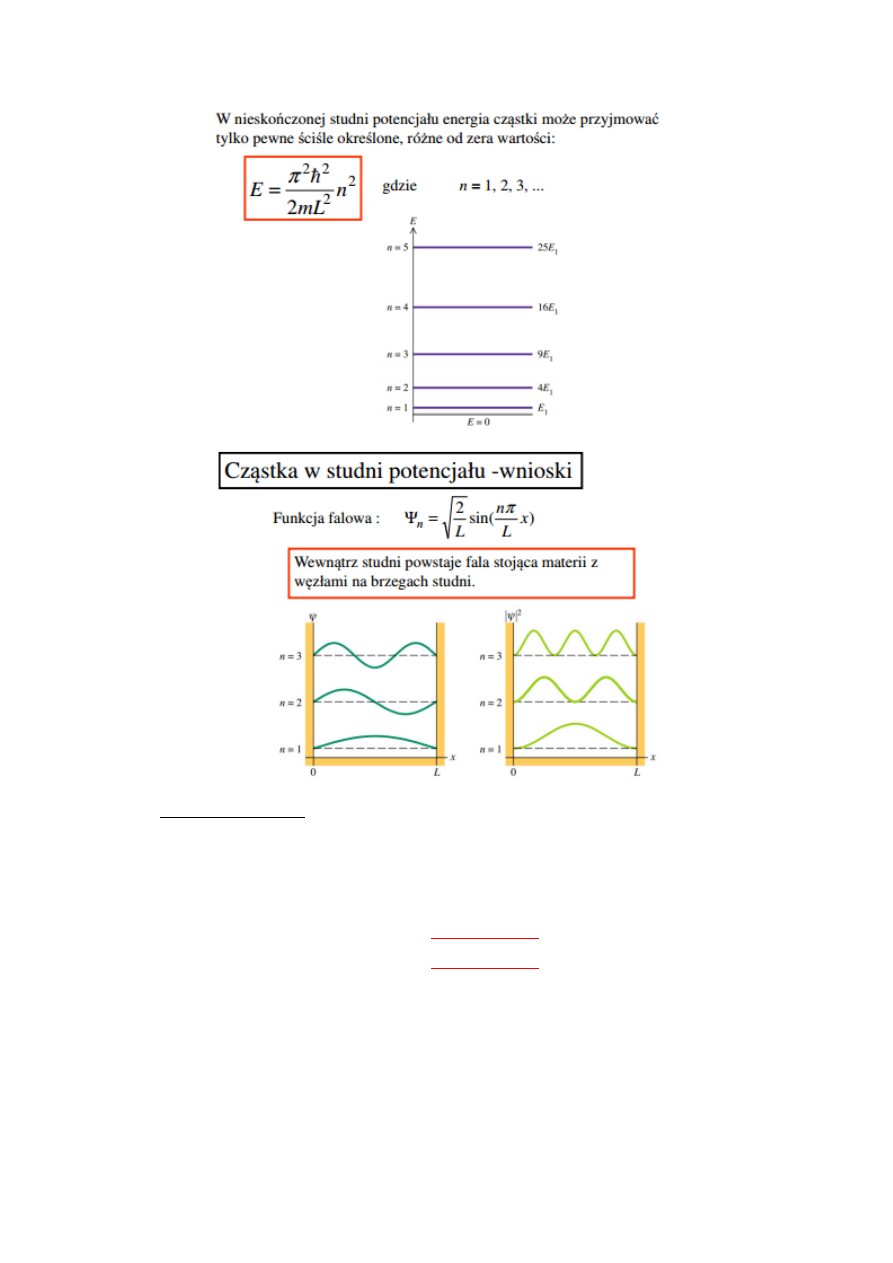
29. Efekt tunelowy.

a) Wyjaśnij czy cząstka o energii całkowitej E może się znaleźć w obszarze o
energii potencjalnej U>E. Odpowiedź uzasadnij wyznaczając
prawdopodobieństwo takiego zdarzenia:

√

(

)

Elektron o energii całkowitej E poruszający się wzdłuż osi x napotyka barierę
potencjału, czyli obszar, w którym jego energia potencjalna na skutek działania sił
ma stałą wartość U. Ponieważ U>E, to w fizyce klasycznej elektron odbiłby się od
tej bariery. Jednak zgodnie z prawami fizyki kwantowej elektron ten może ze
skończonym prawdopodobieństwem znaleźć się po drugiej stronie bariery.
Prawdopodobieństwo tego zdarzenia wyrażone jest przez wartość T –

współczynnika przejścia. Zjawisko tunelowe nie zachodzi jeżeli bariera potencjału
ma nieskończoną szerokość.

b) Przedstaw zjawisko tunelowania oraz zasadę działania mikroskopu
tunelowego:

Skaningowy mikroskop tunelowy, którego działanie oparte jest na zjawisku
tunelowym, umożliwia otrzymywanie szczegółowych map powierzchni z
ujawnionymi na nich szczegółami w skali atomowej z dokładnością znacznie
większą niż możliwa do uzyskania w mikroskopii optycznej lub elektronowej.

30. Fizyka jądra atomowego.

a) Budowa jądra, defekt masy, izotopy:

Jądro atomowe zbudowane jest z jednego lub więcej protnów i neutronów,
nazywanych ogólnie nukleonami. Znajduje się w centrum atomu i zawiera prawie
całą jego masę.

b) Własności sił jądrowych, model oddziaływania:

Siły jądrowe - siły, które wiążą ze sobą protony i neutrony w jądrze atomowym. Są
szczególnym przypadkiem oddziaływań silnych.

Ich właściwości:



krótki zasięg (rzędu femtometrów)



są siłami przyciągającymi, dla bardzo małych odległości między nukleonami
stają się siłami odpychającymi



w przybliżeniu siły p-p, n-p i n-n są równe



występują tylko w jądrach atomowych, bo są krótkozasięgowe



siła tych oddziaływań jest ok. stokrotnie większa od sił elektrostatycznych



wykazują niezależność od ładunku elektrycznego



występują tylko pomiędzy nukleonami



mają charakter dwuciałowy, tzn. obecność innych nukleonów ma niewielki
wpływ na oddziaływanie pary nukleonów



wykazują tzw. wysycenie: za pomocą sił jądrowych oddziałują na siebie tylko
najbliżej leżące nukleony

c) Proces rozpadu uranu po pochłonięciu terminczego neutronu:

d) Synteza termojądrowa na Słońcu:

Synteza termojądrowa polega na połączeniu dwóch mniejszych jąder w jedno
jądro o średniej masie. Deficyt masy, jaki wynika z różnicy między sumaryczną
masą składników reakcji syntezy i masą jądra powstałego w wyniku ich
połączenia, jest źródłem wyzwolonej w takiej reakcji olbrzymiej energii (E = mc2).
Reakcje syntezy termojądrowej zachodzą w Słońcu, gdzie jądra helu powstają z
dwóch jąder wodoru (deuteru).

W Słońcu i innych gwiazdach reakcje syntezy termojądrowej zachodzą
spontanicznie. Aby na Ziemi konstruktywnie wykorzystać energię, jaka wyzwala
się w reakcjach syntezy termojądrowej, należy nauczyć się przeprowadzać je w
sposób kontrolowany. Podczas reakcji syntezy termojądrowej nie powstaje
szkodliwe promieniowanie jądrowe, dlatego ten sposób otrzymywania energii jest
bezpieczniejszy dla naszego środowiska niż rozszczepienie jąder uranu
wykorzystywane w istniejących na świecieelektrowniach jądrowych.

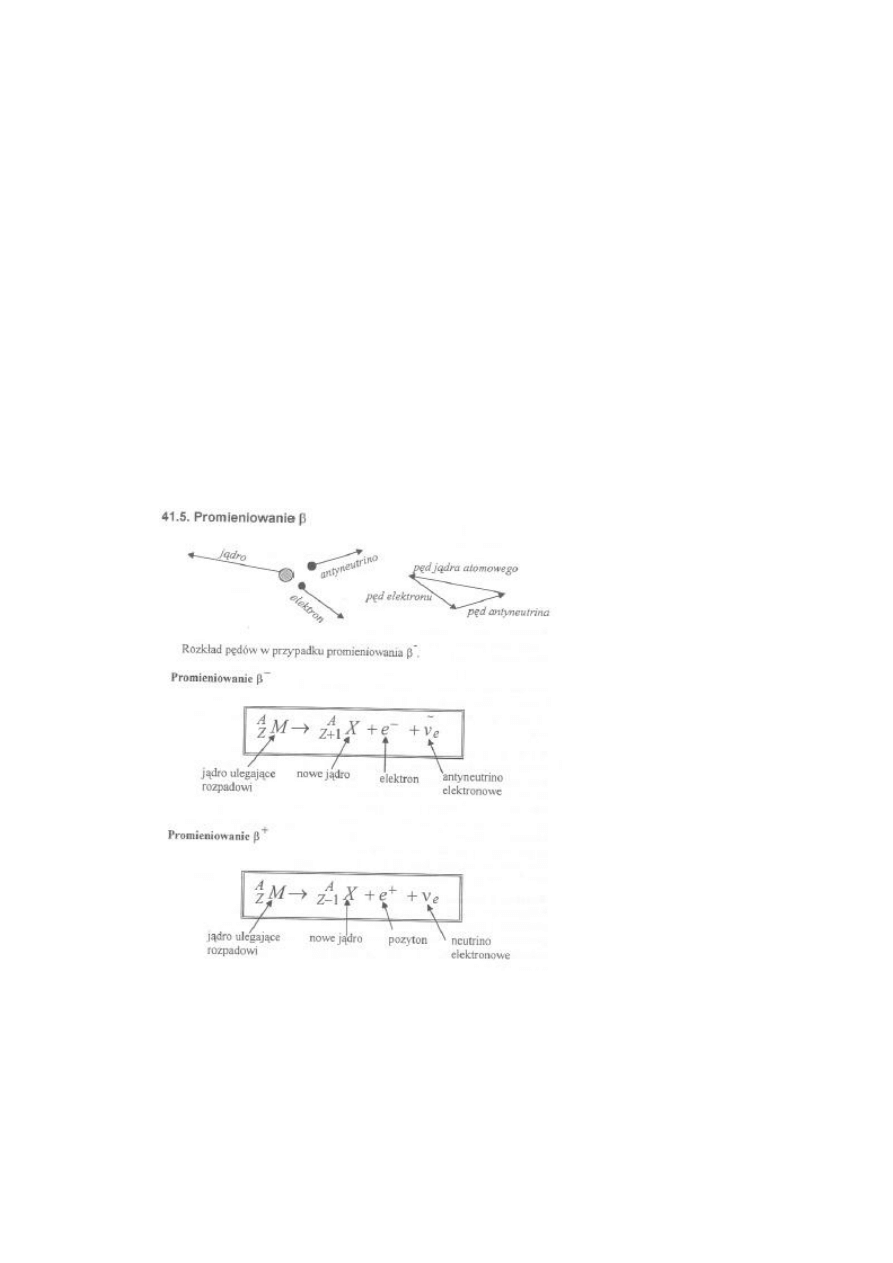
31. Promieniowanie Beta:

Promieniowanie beta

-

polega na emisji elektronów z jąder atomowych. W wyniku

rozpadu jednego z neutronów znajdujących się w jądrze atomowym z jądra
emitowany jest elektron oraz antyneutrino elektronowe. W jego wyniku liczba
porządkowa jądra zwięszka się o jeden.

Promieniowanie beta

+

polega na emisji pozytonów z jąder atomowych poddanych

sztucznym przemianom jądrowym (np. bombardowanych protonami, neutronami

lub cząstkami alfa). W wyniku rozpadu protonu emitowany jest pozyton oraz
neutrino elektronowe. W wyniku tego procesu liczba porządkowa jądra zmniejsza
się o jeden.

I TERMIN:

Efekt fotoelektryczny:

O zjawisku fotoelektrycznym mówimy, gdy wiązka światła o wystarczająco krótkiej
fali skierowana na czystą powierzchnię metalu powoduje uwolnienie elektronów z
tej powierzchni, tzn. że światło wybija elektrony z powierzchni. Zjawisko to jest
wykorzystywane w wielu urządzeniach, takich jak kamery telewizyjne, kamery
wideo, noktowizory itd. Jest to zjawisko, którego nie da się zrozumieć jedynie na
podstawie fizyki klasycznej, potrzebna jest tu fizyka kwantowa.

Aby elektron mógł opuścić powierzchnię metalu należy dostarczyć mu „pracę
wyjścia”, czyli minimalną wartość energii potrzebną do uwolnienia elektronu.
Można ją uzyskać np. przez absorpcję energii fali elektromagnetycznej. Aby tak się
stało światło padające na czystą powierzchnię metalu musi mieć odpowiednią
częstość. W klasycznym rozumieniu elektrony byłyby wyzwalane przez światło
niezależnie od częstotliwości fali elektromagnetycznej, a jedynie dzięki
wystarczająco dużemu natężeniu źródła światła. Zaobserwowano jednak, że nic
takiego nie zachodzi i że poniżej pewnej częstości progowej zjawisko
fotoelektryczne nie zachodzi, bez względu na to jak intensywne jest źródło
światła.

Istnienie częstości progowej można się spodziewać, jeżeli energia przekazywana
jest punktowo, w postaci fotonów. Elektrony urzymywane są wewnątrz tarczy
siłami elektrycznymi (w przeciwnym wypadku pod wpływem grawitacji by z niej
wypadły). Do uwolnienia się z jej powierzchni potrzebna jest minimalna energia,
czyli wspomniana wcześniej praca wyjścia.

Albert Einstein podsumował wyniki powyższych doświadczeń fotoelektrycznych w
równaniu:

Wyraża ono zasadę zachowania energii w przypadku pochłonięcia pojedynczego
fotonu przez tarczę o pracy wyjścia φ. Aby elektron mógł wyrwać się z tarczy
potrzebuje energi φ, cała dodatkowa energia (hv- φ), jaką elektron otrzymuje od
fotonu, pojawi się jako jego energia kinetyczna E

k

.

Efekt Halla, wzór na napięcie:

Jeżeli w przewodzącym pasku o grubości I, w którym płynie prąd o natężeniu I,
zostanie umieszczony w jednorodnym polu magnetycznym o indukcji B, to nośniki
o ładunku e zaczną się gromadzić na brzegu tego paska, wytwarzając poprzeczne
napięcie U. Znak napięcia między brzegami paska wskazuje na znak nośników
ładunku. Koncentracja n nośników ladunku może być obliczona z równania:

W 1879 roku Edwin Hall wykazał, że zachodzi zjawisko odchylania przez pole
magnetyczne elektronów przewodnictwa w drucie miedzianym. Zjawisko nazwane
od jego nazwiska pozwala sprawdzić czy nośniki w przewodniku są naładowane
dodatnio czy ujemnie. Można także zmierzyć liczbę takich nośników na jednostkę
objętości przewodnika, czyli koncentrację nośników.

Jeżeli prąd w pasku miedzianym płynie od góry ku dołowi, to elektrony, będące
nośnikami ładunku, będą poruszały się w przeciwnym kierunku, czyli do góry. Po
włączeniu pola magnetycznego siła magnetyczna F

b

będzie odchylała strumień

elektronów w prawą stronę. Wraz z upływem czasu elektrony przemieszczają się
w prawo i gromadzą głównie przy prawym brzegu paska i pozostawiają
nieskompensowane ładunki dodatnie w ustalonych położeniach przy lewym
brzegu. Rozdzielenie dodatnich i ujemnych ładunków powoduje powstanie
wewnątrz paska pola elektrycznego o natężeniu E, skierowanego od lewej do
prawej. Pole to będzie działało siłą elektryczną F

e

na każdy elektron i dążyć do

przemieszczenia go w lewo, zatem układ wraca do stanu równowagi, a siła
elektryczna rośnie dopóki nie zrówna się z magnetyczną. W momencie gdy te siły
się równoważą elektrony poruszają się z prędkością v

d

w górę rysunku. Z tym

polem elektrycznym związana jest różnica potencjałów, czyli napięcie, nazywane
napięciem Halla.

Wzór na napięcie Halla:

gdzie: n – koncentracja nośników, e – ładunek nośnika prądu, g – grubość płytki, I
– natężenie prądu, B – wartość indukcji magnetycznej, v

d

– prędkość nośnika

ładunku

Siły jądrowe. Przedstaw model oddziaływań jądrowych.

Siły, które działają pomiędzy cząsteczkami na poziomie atomowym nazywamy
oddziaływaniami elementarnymi. Są to oddziaływania, których nie da się
sprowadzić do innych działań. W ich skład wchodzą: oddziaływanie
elektromagnetyczne, oddziaływanie grawitacyjne, oddziaływanie słabe i
oddziaływanie silne. Oddziaływania elektromagnetyczne i słabe są różnymi
aspektami ogólniejszego oddziaływania elektrosłabego. Między leptonami oraz
między leptonami i kwarkami występuje oddziaływanie słabe odpowiedzialne za
promieniowanie beta i rozpad promieniotwórczy z wymianą ciężkich cząstek
pośredniczących W i Z. Oddziaływania silne wiążą ze sobą kwarki we wnętrzu
hadronów. Cząstki pośredniczące w tym procesie nazywane są gluonami,
przewiduje się, że podobnie jak fotony nie mają one masy. Za wtórny przejaw
oddziaływań silnych między kwarkami, z których zbudowane są nukleony, uważa
siły jądrowe. Jądra istnieją jako całość dzięki siłom przyciągania między
nukleonami. Charakteryzują się one:



Krótkim zasięgiem (rzędu 10

-15

m)



Niezależnością od ładunku elektrycznego



Własnością wysycenia, tzn. każdy nukleon oddziaływuje tylko z
ograniczoną liczbą innych nukleonów (protonów i neutronów)



Dla bardzo małych odległości między nukleonami są siłami odpychającymi



Występują tylko w jądrach atomowych

Istotą oddziaływania jądrowego polega na wymianie mezonów π

+

, π

-

oraz π

0

pomiędzy nukleonami.

Efekt Comptona:

Efekt Comptona lub tzw. przesunięcie comptonowskie zachodzi gdy
prmomieniowanie rentgentowskie ulega rozproszeniu na słabo związanych
elektronach tarczy i część promieniowania rozproszonego ma większą długość fali
niż promieniowanie padające. Przesunięcie, czyli zmianę długości fali, można
wyrazić wzorem:

( )

Gdzie φ jest kątem, pod jakim rozprasza się promieniowanie rentgenowskie.

Doświadczenie, które przeprowadził Arthur Compton potwierdziło pogląd, że przy
udziale fotonów przekazywane są zarówno pęd, jak i energia. W jego
eksperymencie wiązka promieniowania X była kierowana na grafitową tarczę.
Zaobserwował on co powyżej. W klasycznym podejściu promieniowanie X
padające na grafitową tarczę jest sinusoidalną falą elektromagnetyczną. Pod
wpływem drgającego pola elektrycznego tej fali elektron w tarczy powinien także
drgać sinusoidalnie z taką samą częstością jak padająca fala, a także powinien
wysyłać falę o takiej samej częstości, tak jakby był małą anteną. Zatem
promieniowanie rentgenowskie rozproszone przez ten elektron powinno mieć
taką samą częstość i tę samą długość fali co promieniowanie padające. Tak jednak
nie jest. Jest tak ponieważ energia i pęd są przekazywane przez fotony, co za tym
idzie odrzucony elektron, który otrzyma pewną energię kinetyczną, a ponieważ w
tym izolowany oddziaływaniu energia zostanie zachowana, zmniejszy się ona dla
fotonu. Zatem rozproszone promieniowanie rentgenowskie musi mieć niższą
częstość i większą długość fali.

Wzór na gęstość prądu:

Gdzie: Q – ładunek całkowity, t – czas, S – pole przekroju, L – długość odcinka, v

d

–

prędkość elektronu, σ – ładunek na jednostkę powierzchni, e = q

Opisać strukturę wewnętrzną protonów, elektronów i neutronów oraz
właściwości cząstek, z których się składają:

Według Modelu Standardowego proton jest cząsteczką wchodzą w skład grupy
hadronów, a konkretnie barionów i jest zbudowany z trzech kwarków (dwóch
górnych „u” o ładunku elektrycznym +2/3e i jednego dolnego „d” o ładunku
elektrycznym -1/3e, czyli tworzy układ uud). Jest to cząstka elementarna o
ładunku +1 i masie spoczynkowej ok. 1u. Razem z neutronami protony tworzą
nukleony, które wchodzą w skład jądra atomowego. Liczba protonów w danym
atomie jest równa jego liczbie atomowej w układzie pierwiastków.

Neutron ma podobną do protonu masę, z tym że składa się z dwóch kwarków
dolnych i jednego górnego (udd) związanych ze sobą oddziaływaniem silnym.
Neutrony w jądrze są trwałe, ale swobodny neutron rozpada się po około 900
sekundach.

Elektron jest cząstką wchodzą w skład leptonów i ferminów, a także jedną z rzech,
które wchodzą w skład atomu, choć nie znajduje się jądrze, tak jak proton i
neutron. Masa elektronu to ok. 5,5*10

-4

u. Ze względu na ujemny ładunek

elektryczny elementarny nazywany jest też negatonem. Ładunek elektronu = -1.

Kwarki, które tworzą protony i neutrony dzielą się na trzy pary: górny i dolny,
powabny i dziwny oraz prawdziwy i piękny. Ich niezwykłą właściwością jest to, że
mają ułamkowy ładunek elektryczny, równy 2/3 lub -1/3. Kwarki mają także inny
niż elektryczny rodzaj ładunku, zwany kolorowym. Siły między cząstkami
naładowanymi kolorowo są bardzo duże i od nich wywodzi się tzw. oddziaływanie
silne, jedna z elementarnych sił wszechświata. Oddziaływanie to zespala kwarki
tworząc hadrony. Całkowity ładunek kolorowy cząstek złożonych z kwarków = 0,
dlatego oddziaływanie to występuje tylko na bardzo małych odległościach
pomiędzy kwarkami.

W rozpadzie beta neutron rozpada się na proton, elektron i antyneutrino.