Przestrzenie metryczne
1/6
•
•
1
•
1
1
•
•
•
•
•
•
X
480 Przestrzenie metryczne
Definicja
Niech
X
b
ę
dzie dowolnym niepustym zbiorem. Odwzorowanie
)
,
0
:
+∞
<
→
×
X
X
d
nazywamy
metryk
ą
na zbiorze
X
, gdy
0
)
,
(
≥
y
x
d
,
y
x
y
x
d
=
⇔
=
0
)
,
(
,
jednoznaczno
ść
)
,
(
)
,
(
x
y
d
y
x
d
=
symetria
)
,
(
)
,
(
)
,
(
y
z
d
z
x
d
y
x
d
+
≤
warunek trójk
ą
ta.
System
)
,
(
d
X
nazywamy
przestrzeni
ą
metryczn
ą
. Warto
ść
)
,
(
y
x
d
nazywamy
odległo
ś
ci
ą
mi
ę
dzy punktami
x
i
y
.
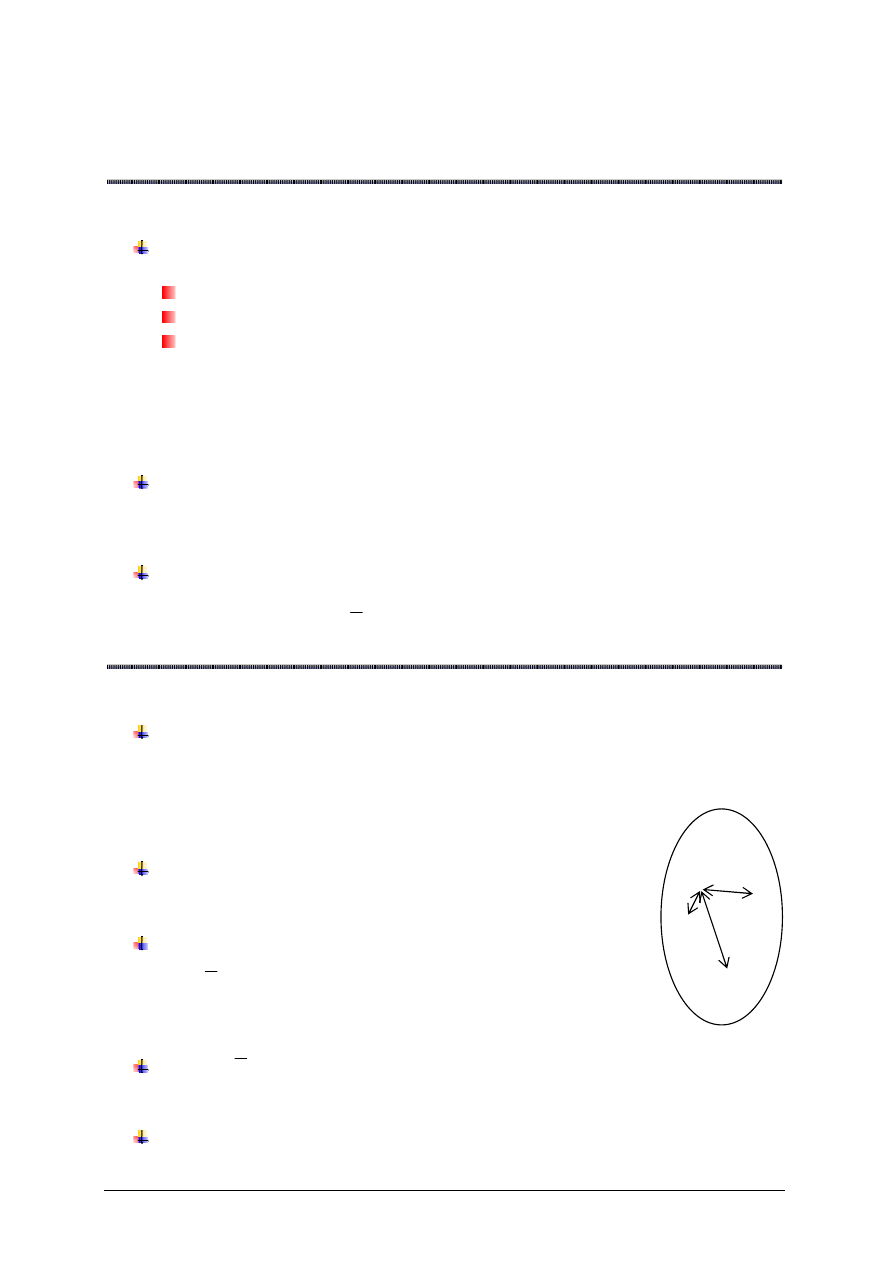
Definicja
Kul
ą
otwart
ą
o
ś
rodku w punkcie
X
x
∈
i promieniu
0
>
r
w przestrzeni
metrycznej
)
,
(
d
X
nazywamy zbiór
}
)
,
(
:
{
)
,
(
r
y
x
d
X
y
r
x
K
<
∈
=
.
Kul
ą
domkni
ę
t
ą
o
ś
rodku w punkcie
X
x
∈
i promieniu
0
>
r
w przestrzeni
metrycznej
)
,
(
d
X
nazywamy zbiór
}
)
,
(
:
{
)
,
(
r
y
x
d
X
y
r
x
K
≤
∈
=
.
Definicja
Niech
X
b
ę
dzie dowolnym niepustym zbiorem. Odwzorowanie
)
,
0
:
+∞
<
→
×
X
X
d
,
≠
=
=
y
x
y
x
y
x
d
gdy
,
1
,
gdy
,
0
)
,
(
nazywamy
metryk
ą
dyskretn
ą
na zbiorze
X
.
Kula otwarta w metryce dyskretnej
>
≤
<
=
<
∈
=
.
1
r
gdy
,
1
0
gdy
},
{
}
)
,
(
:
{
)
,
(
X
r
x
r
y
x
d
X
y
r
x
K
Kula domkni
ę
ta w metryce dyskretnej
≥
<
<
=
≤
∈
=
.
1
r
gdy
,
1
0
gdy
},
{
}
)
,
(
:
{
)
,
(
X
r
x
r
y
x
d
X
y
r
x
K
Wniosek
)
,
(
)
,
(
r
x
K
r
x
K
=
dla wszystkich
1
≠
r
.
Twierdzenie
W ka
ż
dym niepustym zbiorze
X
mo
ż
emy wprowadzi
ć
metryk
ę
.
Przestrzenie metryczne
2/6
)
,
(
b
a
)
,
( d
c
Definicja
Metryk
ą
naturaln
ą
na prostej nazywamy odwzorowanie
)
,
0
:
+∞
<
→
×
R
R
d
nat
,
|
|
)
,
(
x
y
y
x
d
−
=
.
Kula otwarta w metryce naturalnej
)
,
(
}
:
{
}
|
|
:
{
)
,
(
r
a
r
a
r
a
x
r
a
R
x
r
a
x
R
x
r
a
K
+
−
=
+
<
<
−
∈
=
<
−
∈
=
Kula domkni
ę
ta w metryce naturalnej
>
+
−
=<
+
≤
≤
−
∈
=
≤
−
∈
=
r
a
r
a
r
a
x
r
a
R
x
r
a
x
R
x
r
a
K
,
}
:
{
}
|
|
:
{
)
,
(
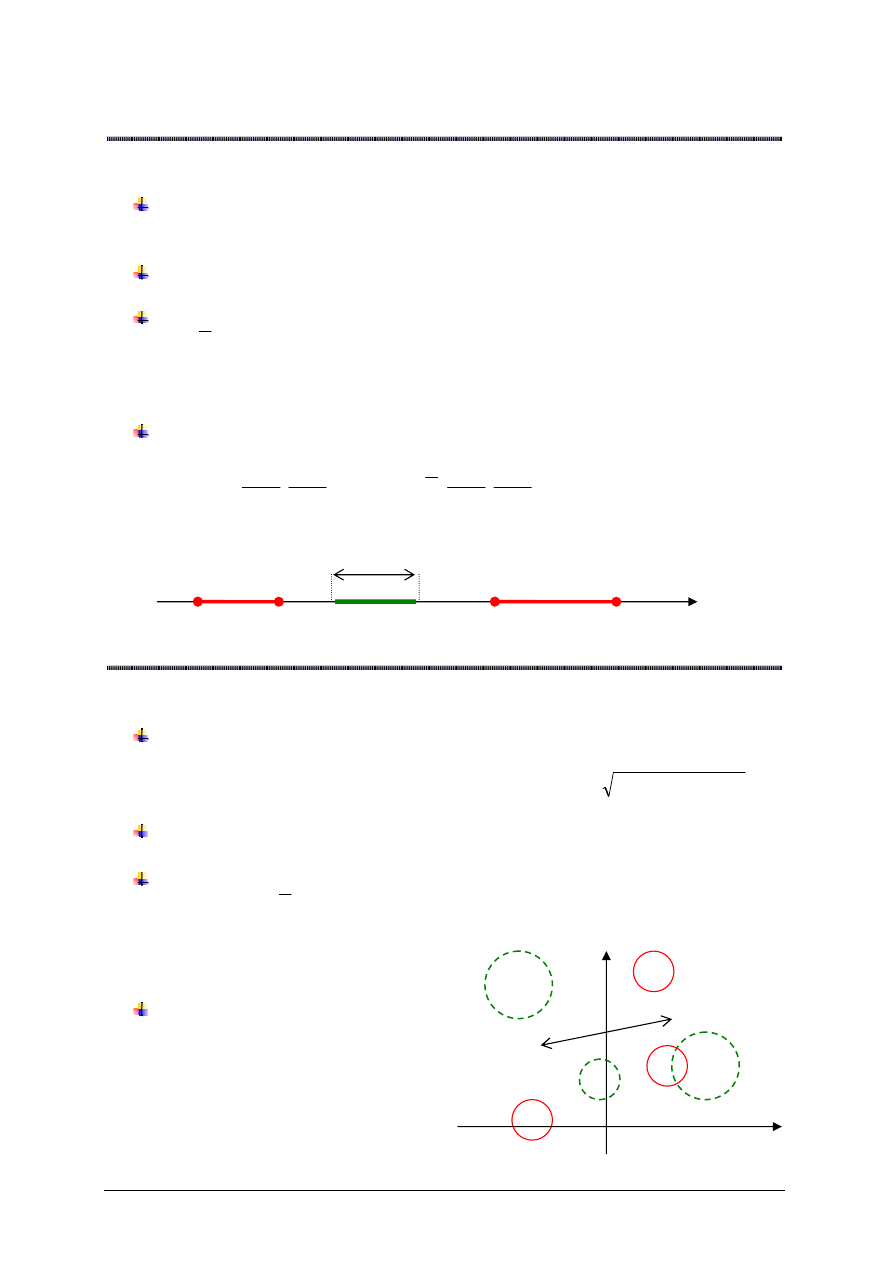
Wniosek
Kule otwarte w metryce naturalnej to przedziały otwarte, a kule domkni
ę
te to
przedziały domkni
ę
te
−
+
=
2
,
2
)
,
(
a
b
b
a
K
b
a
,
−
+
>=
<
2
,
2
,
a
b
b
a
K
b
a
Definicja
Metryk
ą
euklidesow
ą
na płaszczy
ź
nie
2
R
(a wi
ę
c i na zbiorze liczb
zespolonych
C
) nazywamy odwzorowanie
)
,
0
:
2
2
+∞
<
→
×
R
R
d
E
,
2
2
)
(
)
(
|
)
,
(
)
,
(
|
))
,
(
),
,
((
b
d
a
c
b
a
d
c
d
c
b
a
d
E
−
+
−
=
−
=
.
Kula otwarta w metryce euklidesowej
}
)
(
)
(
:
)
,
{(
)
),
,
((
2
2
2
2
r
b
y
a
x
R
y
x
r
b
a
K
<
−
+
−
∈
=
Kula domkni
ę
ta w metryce euklidesowej
}
)
(
)
(
:
)
,
{(
)
),
,
((
2
2
2
2
r
b
y
a
x
R
y
x
r
b
a
K
≤
−
+
−
∈
=
Wniosek
Kule otwarte w metryce
euklidesowej to koła bez
brzegu, a kule domkni
ę
te to
koła z brzegiem.
a
a
b
b
a
d
−
=
)
,
(
b
o
o
R
Przestrzenie metryczne
3/6
)
,
( b
a
)
,
( d
c
r
2
)
,
( b
a
)
,
( d
c
r
2
Definicja
Metryk
ą
maksimum
na płaszczy
ź
nie
2
R
(a wi
ę
c i na zbiorze liczb zespolonych
C
) nazywamy odwzorowanie
)
,
0
:
2
2
max
+∞
<
→
×
R
R
d
,
|}
|
|,
|
max{
))
,
(
),
,
((
max
b
d
a
c
d
c
b
a
d
−
−
=
.
Kula otwarta w metryce maksimum
}
|}
|
|,
max{|
:
)
,
{(
)
),
,
((
2
r
b
y
a
x
R
y
x
r
b
a
K
<
−
−
∈
=
Kula domkni
ę
ta w metryce maksimum
}
|}
|
|,
max{|
:
)
,
{(
)
),
,
((
2
r
b
y
a
x
R
y
x
r
b
a
K
≤
−
−
∈
=
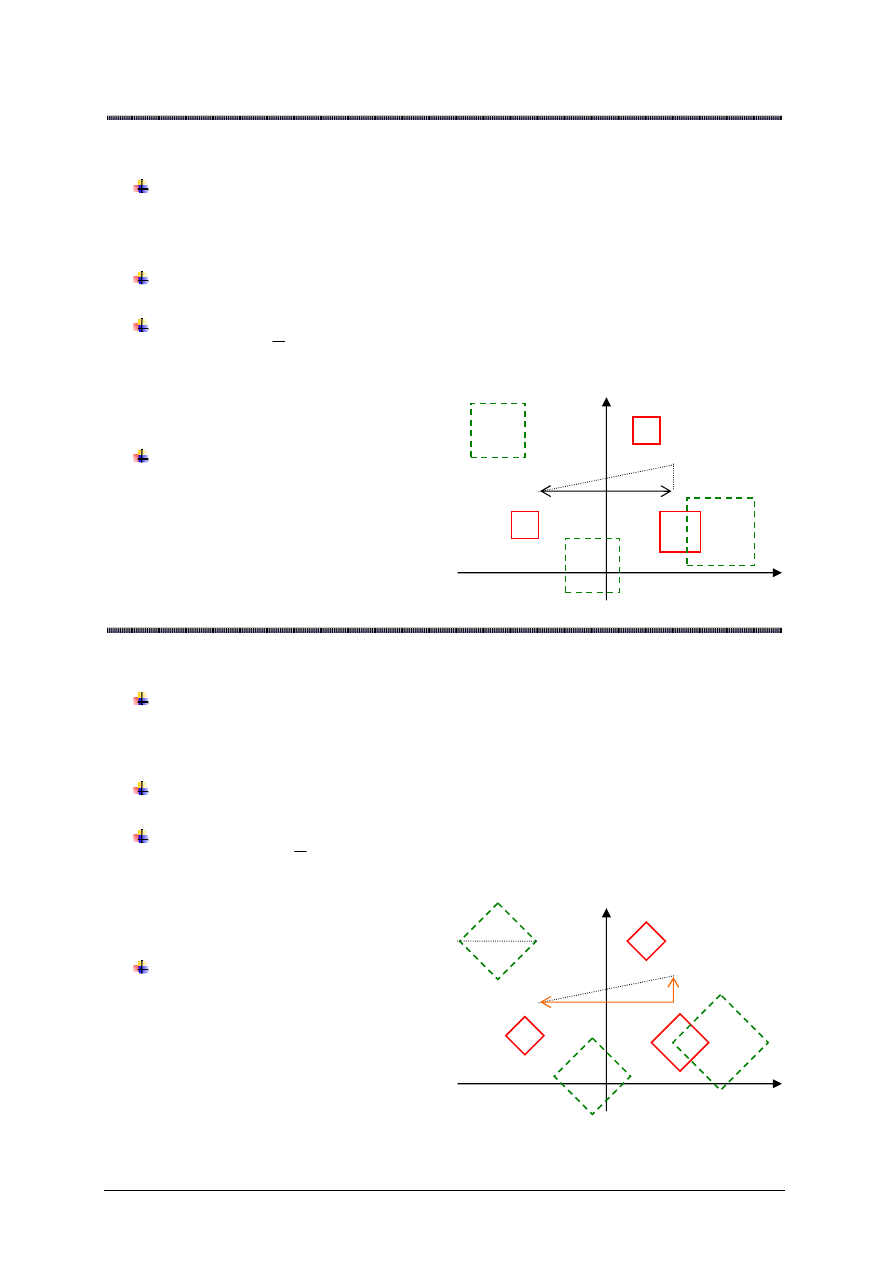
Wniosek
Kula otwarta o
ś
rodku w
punkcie
)
,
( b
a
i promieniu
0
>
r
w metryce maksimum to
kwadrat bez brzegu o
ś
rodku w
punkcie
)
,
( b
a
i boku
r
2
, a kula
domkni
ę
ta to kwadrat z
brzegiem.
Definicja
Metryk
ą
taksówkow
ą
na płaszczy
ź
nie
2
R
(a wi
ę
c i na zbiorze liczb
zespolonych
C
) nazywamy odwzorowanie
)
,
0
:
2
2
1
+∞
<
→
×
R
R
d
,
|
|
|
|
))
,
(
),
,
((
1
b
d
a
c
d
c
b
a
d
−
+
−
=
.
Kula otwarta w metryce taksówkowej
}
|
|
|
|
:
)
,
{(
)
),
,
((
2
r
b
y
a
x
R
y
x
r
b
a
K
<
−
+
−
∈
=
Kula domkni
ę
ta w metryce taksówkowej
}
|
|
|
|
:
)
,
{(
)
),
,
((
2
r
b
y
a
x
R
y
x
r
b
a
K
≤
−
+
−
∈
=
Wniosek
Kula otwarta o
ś
rodku w
punkcie
)
,
( b
a
i promieniu
0
>
r
w metryce taksówkowej to
romb bez brzegu o
ś
rodku w
punkcie
)
,
( b
a
i
ś
rednicy
r
2
, a
kula domkni
ę
ta to romb z
brzegiem.
Przestrzenie metryczne
4/6
)
,
( b
a
)
,
(
v
b
u
a
+
+
)
,
( v
u
)
),
,
((
)
,
(
)
),
,
((
r
v
b
u
a
K
v
u
r
b
a
K
+
+
=
+
Definicja
Je
ż
eli na zbiorze
X
jest zdefiniowane działanie dodawania spełniaj
ą
ce
aksjomaty A1-A4, to
metryk
ą
inwariantn
ą
wzgl
ę
dem translacji (niezmiennicz
ą
wzgl
ę
dem przesuni
ęć
)
nazywamy metryk
ę
spełniaj
ą
c
ą
poni
ż
szy warunek
dla dowolnych
,
,
,
X
w
y
x
∈
)
,
(
)
,
(
y
x
d
w
y
w
x
d
=
+
+
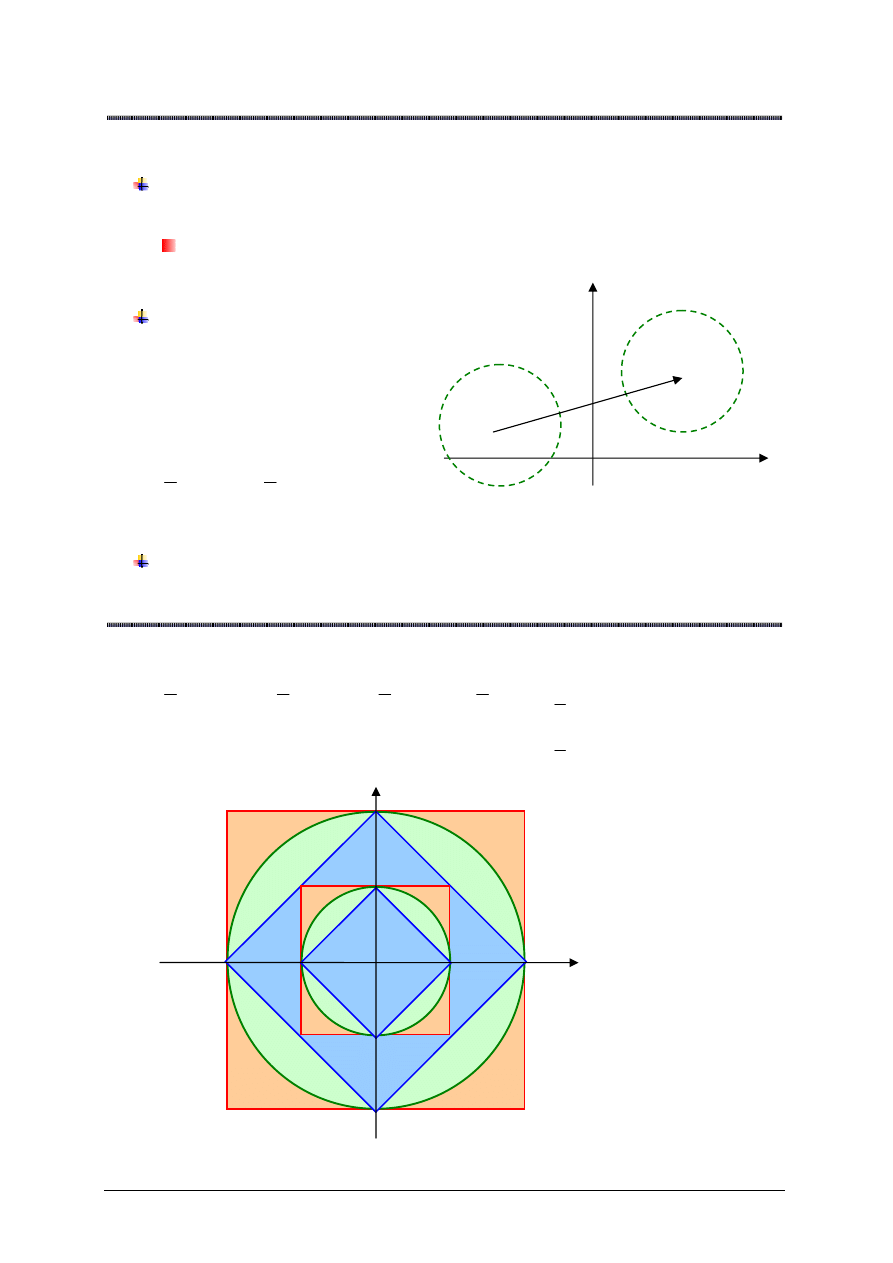
Wniosek
Je
ś
li
d
jest metryk
ą
inwariantn
ą
wzgl
ę
dem
translacji, to translacja ka
ż
dej
kuli o
ś
rodku w
x
o element
(wektor)
w
jest nadal kul
ą
(o
ś
rodku w
w
x
+
) i tym samym
promieniu, tzn.
)
,
(
)
,
(
r
w
x
K
w
r
x
K
+
=
+
,
)
,
(
)
,
(
r
w
x
K
w
r
x
K
+
=
+
Przykład
Metryka dyskretna (na zbiorze
X
z dodawaniem), naturalna na prostej,
metryka euklidesowa, metryka maksimum i metryka taksówkowa s
ą
inwariantne wzgl
ę
dem translacji.
Uwaga
...
)
2
1
),
0
,
0
((
)
1
),
0
,
0
((
)
1
),
0
,
0
((
)
1
),
0
,
0
((
max
1
max
⊃
⊃
⊃
⊃
K
K
K
K
E
...
)
2
1
),
0
,
0
((
)
1
),
0
,
0
((
)
1
),
0
,
0
((
)
1
),
0
,
0
((
max
1
max
⊃
⊃
⊃
⊃
K
K
K
K
E
Przestrzenie metryczne
5/6
)
,
( b
a
)
,
( d
c
rzeka
r
2
Definicja
Metryk
ą
rzeki
na płaszczy
ź
nie
2
R
(a wi
ę
c i na zbiorze liczb zespolonych
C
)
nazywamy odwzorowanie
)
,
0
:
2
2
+∞
<
→
×
R
R
d
r
,
≠
+
−
+
=
−
=
.
gdy
|,
|
|
|
|
|
,
gdy
|,
|
))
,
(
),
,
((
c
a
b
a
c
d
c
a
b
d
d
c
b
a
d
r
.
Kula otwarta w metryce rzeki
>
−
<
+
−
∈
∪
<
−
∈
≤
<
−
∈
=
.
|
|
r
gdy
},
|
|
|
|
:
)
,
{(
}
|
|
:
)
,
{(
|,
|
r
gdy
},
|
|
:
)
,
{(
)
),
,
((
2
2
2
b
b
r
y
a
x
R
y
x
r
b
y
R
y
a
b
r
b
y
R
y
a
r
b
a
K
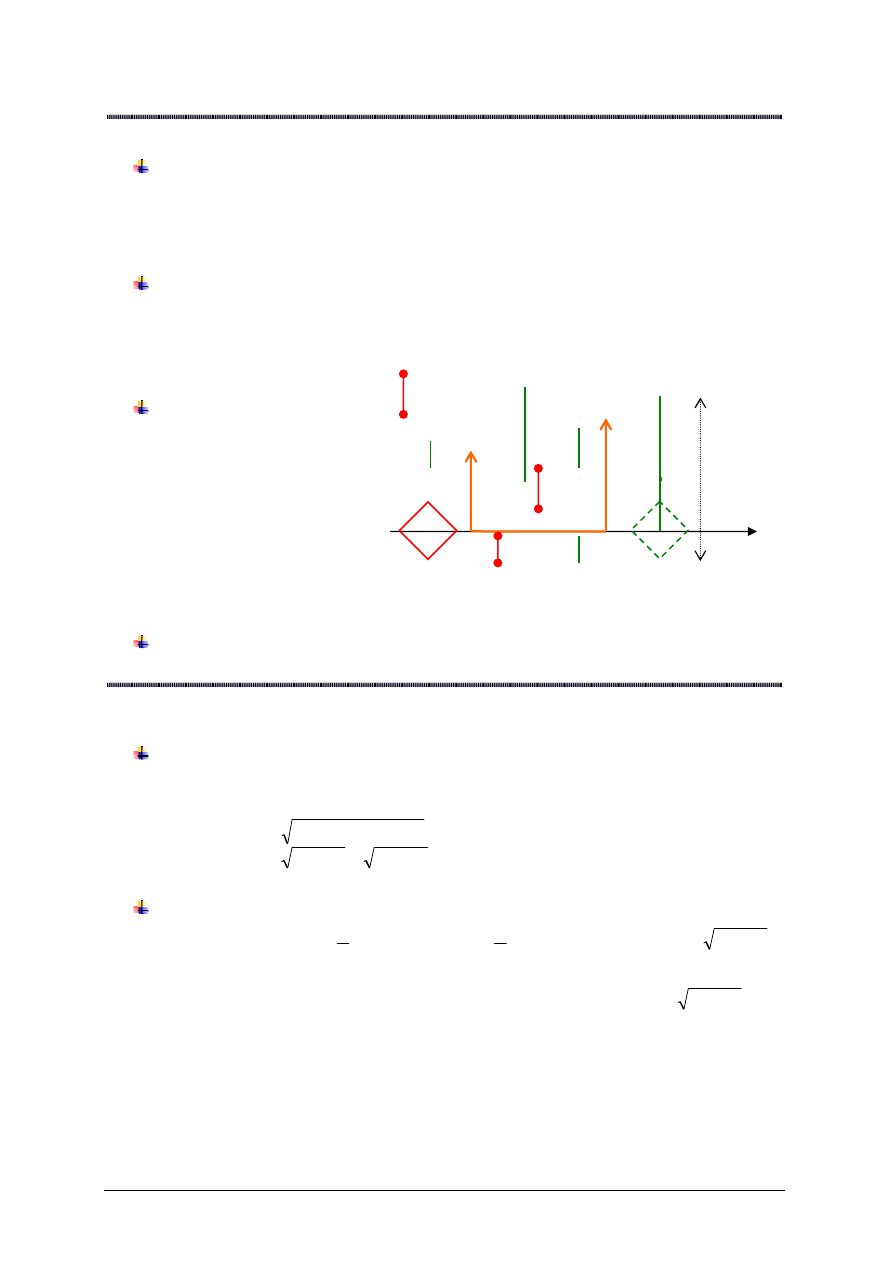
Wniosek
Kula otwarta o
ś
rodku
w punkcie
)
,
( b
a
i
promieniu
0
>
r
w
metryce rzeki to albo
odcinek otwarty
prostopadły do osi
rzeki (gdy
b
r
≤
<
0
),
albo romb bez brzegu
o
ś
rednicy
r
2
(gdy
0
=
b
), albo suma tych
dwóch zbiorów (gdy
0
>
>
b
r
).
Metryka rzeki
nie
jest inwarianta wzgl
ę
dem translacji.
Definicja
Metryk
ą
kolei paryskiej
na płaszczy
ź
nie
2
R
(a wi
ę
c i na zbiorze liczb
zespolonych
C
) nazywamy odwzorowanie
)
,
0
:
2
2
+∞
<
→
×
R
R
d
k
,
+
+
+
−
+
−
=
przypadku.
przeciwnym
w
,
|
są
)
,
(
),
,
(
punkty
gdy
,
)
(
)
(
|
))
,
(
),
,
((
2
2
2
2
2
2
d
c
b
a
d
c
b
a
b
d
a
c
d
c
b
a
d
k
e
wspóliniow
Kula otwarta w metryce kolei paryskiej
>
+
>
∪
=
<
=
=
<
+
∈
=
=
+
≤
<
<
−
+
−
∈
=
=
=
.
0
gdy
,
,
r
0
b
a
gdy
},
:
)
,
{(
,
r
0
gdy
},
)
(
)
(
:
)
,
{(
)
),
,
((
2
2
2
2
2
2
2
2
2
2
2
2
b
a
r
B
A
r
y
x
R
y
x
B
b
a
r
b
x
a
b
a
x
R
x
a
b
x
A
r
b
a
K
Przestrzenie metryczne
6/6
)
,
( b
a
)
,
( d
c
)
0
,
0
(
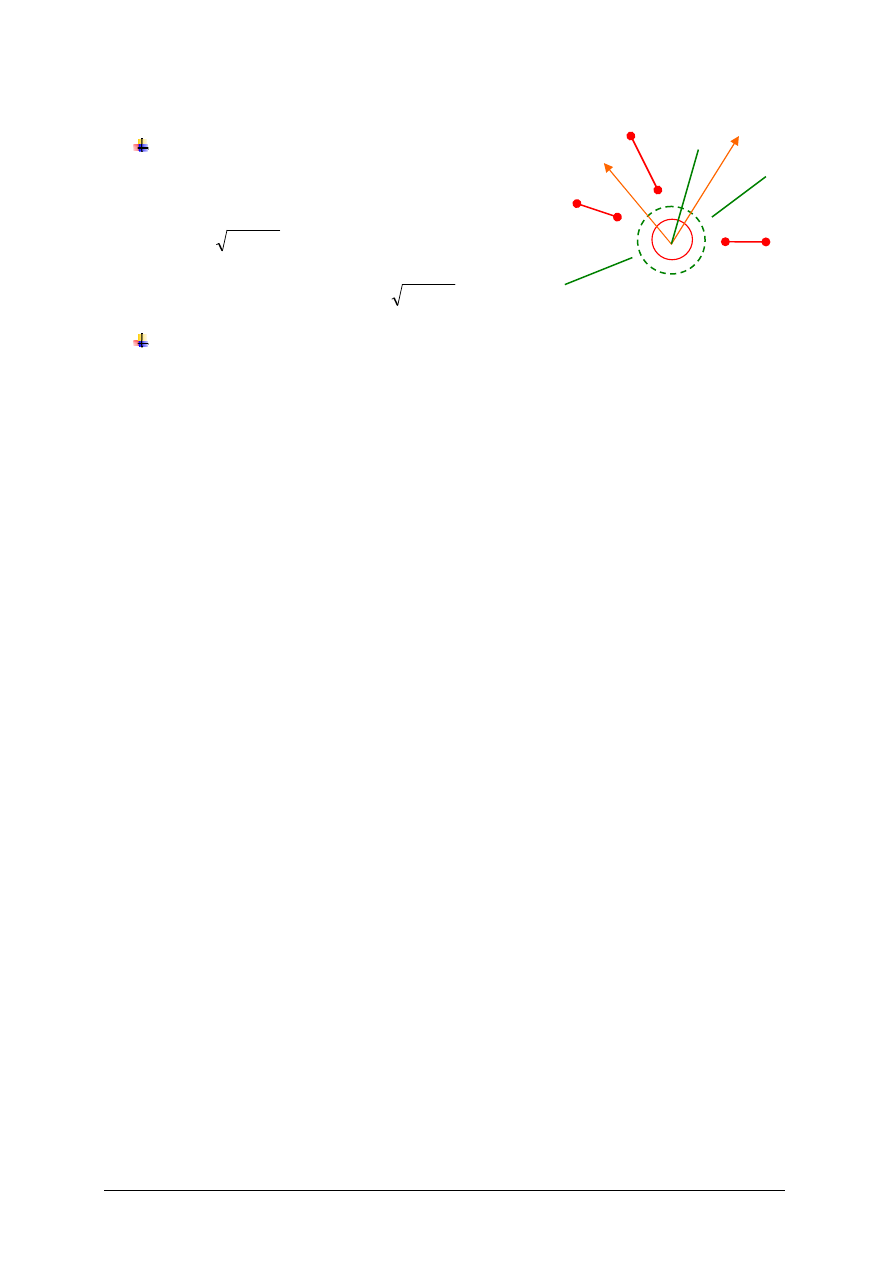
Wniosek
Kula otwarta o
ś
rodku w punkcie
)
,
( b
a
i
promieniu
0
>
r
w metryce kolei paryskiej
to albo odcinek otwarty le
żą
cy na prostej
przechodz
ą
cej przez punkt
)
0
,
0
(
(gdy
2
2
0
b
a
r
+
≤
<
), albo koło bez brzegu o
ś
rednicy
r
(gdy
)
0
,
0
(
)
,
(
=
b
a
), albo suma
tych dwóch zbiorów (gdy
0
2
2
>
+
>
b
a
r
).
Metryka kolei paryskiej
nie
jest inwarianta wzgl
ę
dem translacji.
Wyszukiwarka
Podobne podstrony:
1 Przestrzenie metryczneid 8656
Definicja przestrzeni metrycznej Zbieżność ciągów w przestrzeni metrycznej
zagadnienia, punkt 2, II Przestrzenie metryczne zupełne
2 Przestrzenie metryczneid 19646
2. Przestrzenie metryczne
Algebra liniowa Przestrzenie metryczne
przestrzenie metryczne 08
lista analiza 2008 4 przestrzenie metryczne
3 Przestrzenie metryczne
przestrzenie metryczne 08
źwyklad przestrzenie metryczne
9 - Przestrzenie metryczne cd, Analiza matematyczna
26.Definicja przestrzeni metrycznej. Zbieznosc ciagow w przestrzeni metrycznej, Studia, Semestr VI,
8 - Przestrzeń metryczna, Analiza matematyczna
3. Przestrzenie metryczne
1. Przestrzenie metryczne
Przestrzenie metryczne
więcej podobnych podstron