
Przestrzenie metryczne.

1. Definicja metryki i przestrzeni
metrycznej.
Rozważmy niepusty zbiór X.
Definicja:
Jeżeli dowolnym elementom (punktom) x,y
X można
przyporządkować liczbę rzeczywistą nieujemną
(x,y) spełniającą następujące warunki:
1.
2.
(warunek symetrii)
3.
(warunek trójkąta)
to przyporządkowanie to nazywamy
metryką
.
y
x
y
x
0
)
,
(
)
,
(
)
,
(
,
x
y
y
x
X
y
x
)
,
(
)
,
(
)
,
(
,
,
y
z
z
x
y
x
X
z
y
x
)
,
0
:
na
X
X
Definicja:
Parę (X,
) nazywamy
przestrzenią metryczną
.
- odległością x
i y
2. Przykłady przestrzeni metrycznych.
1. X –dowolny niepusty zbiór, przyjmujemy,że:
Łatwo sprawdzić, że jest to metryka (tzw.metryka
dyskretna).
Taką parę (X,
) nazywamy
przestrzenią dyskretną
.
y
x
y
x
y
x
X
y
x
dla
1
dla
0
)
,
(
,
y
x
y
x
0
)
,
(
1.
)
,
(
)
,
(
2.
,
x
y
y
x
X
y
x
)
,
(
)
,
(
)
,
(
3.
,
,
y
z
z
x
y
x
X
z
y
x
2. X=R
- metryka
Euklidesowa
Taką parę (R,
) nazywamy
jednowymiarową
przestrzenią kartezjańską.
x
y
y
x
R
y
x
)
,
(
,
3. X=R
2
- metryka naturalna
Taką parę (R
2
,
) nazywamy
dwuwymiarową przestrzenią
kartezjańską.
2
2
2
2
1
1
2
1
2
1
)
(
)
(
)
(
)
,
(
)
,
(
2
x
y
x
y
y
y
x
x
R
y
x,
y
x
y
x,
4. X=R
k
- metryka
euklidesowa
Taką parę (R
2
,
) nazywamy
k-wymiarową przestrzenią
kartezjańską.
)
,...,
,
(
)
,...,
,
(
2
1
2
1
k
k
y
y
y
x
x
x
y
x
2
2
2
2
2
1
1
1
2
)
(
...
)
(
)
(
)
(
)
(
2
k
k
k
i
i
i
R
x
y
x
y
x
y
x
y
y
x,
y
x,

UWAGA:
Czasami sam zbiór X nazywamy przestrzenią
metryczną, gdy jest dokładnie wiadomo jak jest
zdefiniowana metryka w tym zbiorze –
najczęściej metryka Euklidesowa.
5. X=R
2
- metryka miasto
)
,
(
)
,
(
2
1
2
1
y
y
x
x
y
x
odległość wg metryki
euklidesowej =
odległość wg metryki
miasto=
j
2
6
j
12
2
2
1
1
)
(
2
y
x
y
x
R
y
x,
y
x,

3. Ważne podzbiory przestrzeni
metrycznych.
Definicja:
Otoczeniem
punktu x
0
X o promieniu r>0 w
przestrzeni (X,
)
nazywamy zbiór
U(x
0
,r)
wszystkich
punktów x tej przestrzeni, spełniających warunek
(x
0
,x)<r (czyli takich których odległość od x
0
jest
mniejsza od r).
U(x
0
,r)={x : x
X
(x
0
, x) < r }
Definicja:
Sąsiedztwem
punktu x
0
X o promieniu r>0 w
przestrzeni (X,
)
nazywamy otoczenie U(x
0
,r)
punktu x
0
bez tego punktu.
S(x
0
,r)=U(x
0
, r) \ {x
0
}
Przykłady:
1. (R
1
,
) - jednowymiarowa przestrzeń
kartezjańska
x
0
R
U(x
0
, r) - przedział (x
0
-r, x
0
+r)
Np. U(0,2)=(-2,2);
U(1,3)=(-2, 4)
S(x
0
, r) – suma przedziałów (x
0
-r, x
0
)
(x
0
, x
0
+r)
Np. S(0,2)=(-2,0)
(0,2); S(1,3)=(-2,1)
(1,4)
r
x
x
x
x
0
0
)
,
(
x
0
r
r
x
0
+r
x
0
-r
2. (R
2
,
) - dwuwymiarowa przestrzeń kartezjańska
U(x
0
, r) - wnętrze koła o środku w punkcie x
0
i
promieniu r.
S(x
0
, r) – wnętrze koła o środku w punkcie x
0
i
promieniu r bez środka.
)
,
(
)
,
(
0
0
y
x
y
x
x
x
0
r
y
y
x
x
r
y
y
x
x
2
0
2
0
2
0
2
0
)
(
)
(
)
(
)
(
)
(
x
,
x
0
3. (R
3
,
) trójwymiarowa przestrzeń kartezjańska
U(x
0
, r) - wnętrze kuli o środku w punkcie x
0
i
promieniu r.
S(x
0
, r) – wnętrze kuli o środku w punkcie x
0
i
promieniu r bez środka.
)
,
,
(
)
,
,
(
0
0
0
z
y
x
z
y
x
x
x
0
r
z
z
y
y
x
x
r
z
z
y
y
x
x
2
0
2
0
2
0
2
0
2
0
2
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
x
,
x
0
4. Ciąg punktów w przestrzeni
metrycznej.
Odwzorowanie a:N
X , określone na zbiorze N o
wartościach w przestrzeni metrycznej (X,
)
nazywamy
nieskończonym ciągiem punktów
w
przestrzeni (X,
).
Wartości tego odwzorowania zapisujemy:
a(1)=a
1
, a(2)=a
2
, ..., a(n)=a
n
.
Przykłady:
1. X=R - (R,
) - jednowymiarowa przestrzeń
kartezjańska , (a
n
) – ciąg liczbowy
Np.
a
n
=3n-1
2. X=R
2
(R
2
,
) - dwuwymiarowa przestrzeń
kartezjańska, (a
n
) – ciąg punktów na
płaszczyźnie
Np.
a
n
=(n+1,3n-1)

Mówimy, że ciąg liczbowy
(a
n
)
n
N
jest:
1. rosnący
2. malejący
3. stały
4. ograniczony z góry
5. ograniczony z dołu
1
n
n
n
a
a
1
n
n
n
a
a
a
a
n
n
R
a
g
a
n
n
g
d
a
n
n
d
Np.
(a
n
)
n
N
jest malejący i ograniczony z
góry.
2
1
1
n
n
a
n
Własności ciągów liczbowych:

5. Granica ciągu punktów w przestrzeni
metrycznej.
Niech będzie dana przestrzeń metryczna (X,
),
ciąg (a
n
)
n
N
oraz g
X.
Definicja (granicy ciągu punktów w przestrzeni
metrycznej)
:
Mówimy, że ciąg
(a
n
)
n
N
ma
granicę
g
(jest zbieżny do g lub dąży do g) jeżeli dla każdej
liczby >0 istnieje taka liczba n
0
, że wszystkie wyrazy
ciągu o wskaźnikach większych od n
0
spełniają
warunek:
(a
n,
g)<
Zapisujemy to symbolicznie:
g
a
g
a
n
n
n
n
n
n
,
lim
0
0
0
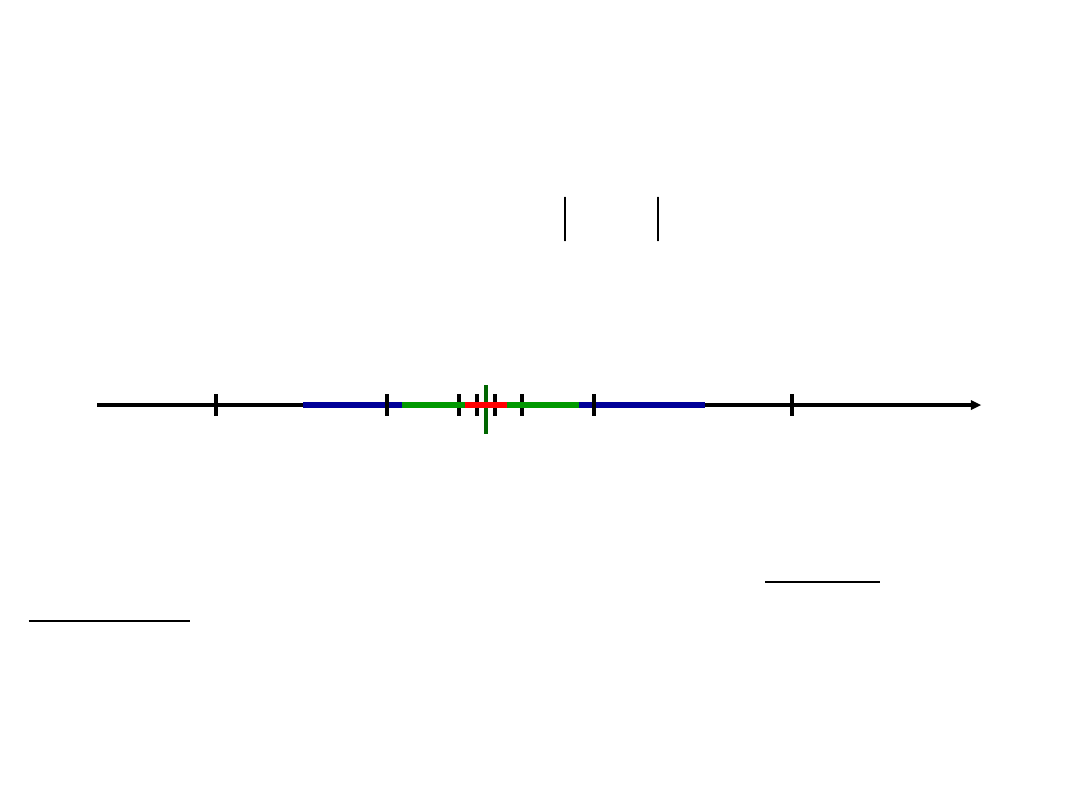
g
a
g
a
n
n
n
n
n
n
0
0
0
lim
a
1
a
2
a
3
a
4
a
5
a
6
W dowolnie małym otoczeniu punktu g leżą prawie
wszystkie wyrazy ciągu, poza tym otoczeniem pozostaje
tylko skończona liczba wyrazów.
g
W jednowymiarowej przestrzeni kartezjańskiej
definicja granicy ciągu liczbowego przyjmuje
postać:
Ciągi mające granicę nazywamy
zbieżnymi
, a
pozostałe
rozbieżnymi
.
Przykład:
1)
Pokażemy, że :
,...
1
,
,...
5
1
,
4
1
,
3
1
,
2
1
,
1
1
n
n
N
n
0
1
lim
n
n
g
a
g
a
n
n
n
n
n
n
0
0
0
lim
0
1
0
1
lim
0
0
0
n
n
n
n
n
n
Czyli dla:
10000
0001
,
0
;
100
01
,
0
10
1
,
0
;
2
5
,
0
0
0
0
0
n
n
n
n
1
:
0
n
1
n
n
1
n
1
2
1
1
2
lim
n
n
n
2)
3)
2
1
lim
?
n
n
Dowód:
prawda dla
każdego n.
Twierdzenie 1:
Ciąg stały
(a
n
)
n
N
:
jest zbieżny i
.
a
a
n
n
a
a
n
n
lim
a
a
a
a
n
n
n
n
n
n
0
0
0
lim
0
a
a
Twierdzenie 2:
Jeżeli ciąg
(a
n
)
n
N
jest zbieżny, to ma tylko jedną
granicę.
2. Twierdzenia o ciągach
liczbowych.

Określenie podciągu:
Jeżeli z ciągu (a
n
)
n
N
wybierzemy „co któryś” wyraz, to
otrzymamy nowy ciąg zwany
podciągiem
ciągu (a
n
)
n
N.
Np. a
n
=n 1,2,3,...
b
n
=2n 2,4,6,... podciąg ciągu (a
n
)
n
N
c
n
=2n+1
3,5,7,... podciąg ciągu (a
n
)
n
N
Twierdzenie 3:
Każdy podciąg ciągu
zbieżnego do liczby g jest zbieżny
do tej liczby.

Wniosek:
Jeżeli ciąg (a
n
)
n
N
ma dwa podciągi zbieżne do
różnych granic, to ciąg (a
n
)
n
N
jest rozbieżny.
Np.
n
n
a
1
n
n
b
2
1
1
n
n
b
1
1
lim
lim
n
n
n
b
1
2
1
n
n
c
1
n
n
c
1
1
lim
lim
n
n
n
c
Ciąg (a
n
)
n
N
, a
n
=(-1)
n
jest
rozbieżny.
Podciągi (b
n
)
n
N
i (c
n
)
n
N
są zbieżne do różnych
granic
Tw.3
Twierdzenie 4:
Jeżeli ciąg (a
n
)
n
N
jest zbieżny, to jest ograniczony.
UWAGA:
ciąg zbieżny
ograniczony
Twierdzenie odwrotne nie jest prawdziwe. Może być
ciąg ograniczony, a mimo to rozbieżny – np. (-1)
n
.
Twierdzenie 5 (kryterium zbieżności ciągu):
Jeżeli ciąg (a
n
)
n
N
jest monotoniczny i ograniczony, to
jest zbieżny.
Twierdzenie 6 (o działaniach na ciągach zbieżnych):
Jeżeli ciągi (a
n
)
n
N
i (b
n
)
n
N
są zbieżne i
,
to:
1.
2.
3.
4.
a
a
n
n
lim
b
b
n
n
lim
b
a
b
a
b
a
n
n
n
n
n
n
n
lim
lim
lim
b
a
b
a
b
a
n
n
n
n
n
n
n
lim
lim
lim
b
a
b
a
b
a
n
n
n
n
n
n
n
lim
lim
lim
b
a
b
a
b
a
b
b
n
n
n
n
n
n
n
n
n
lim
lim
lim
0
0
Np.
n
n
n
n
n
2
1
3
2
lim
2
2
n
n
n
n
n
n
n
2
2
2
3
2
3
5
2
3
lim
Twierdzenie 7:
Jeżeli
i ciąg (b
n
)
n
N
jest ograniczony, to
0
lim
n
n
a
0
lim
n
n
n
b
a
Np.
0
)
!
cos(
1
lim
2
n
n
n
0
)
1
2
sin(
lim
3
2
n
n
n
n
Twierdzenie 8 (o trzech ciągach):
Jeżeli dane są trzy ciągi (a
n
)
n
N
, (b
n
)
n
N
, (c
n
)
n
N
oraz:
•
•
(od pewnego miejsca zachodzą
nierówności)
to ciąg (c
n
)
n
N
jest zbieżny i
g
b
a
n
n
n
n
lim
lim
n
n
n
n
n
n
b
c
a
0
0
g
c
n
n
lim
Np.
2
3
)
1
(
2
lim
n
n
n
n
n
n
n
n
n
4
3
2
lim

Twierdzenie 9 :
1. Dla każdej liczby a>0
2. Jeżeli to
3.
4. Dla a>0
5.
6.
1
lim
n
n
a
0
0
lim
n
n
n
n
a
a
a
1
lim
n
n
n
a
1
lim
n
n
n
0
!
lim
n
a
n
n
0
!
lim
n
n
n
n
1
gdy
1
gdy
istnieje
nie
1
gdy
1
)
1
;
1
(
gdy
0
lim
a
a
a
a
a
n
n

3. Granice niewłaściwe.
Jeżeli granicą ciągu (a
n
)
n
N
jest pewna liczba
rzeczywista g to mówimy, że ma on granicę
właściwą
.
Wśród ciągów rozbieżnych możemy wyróżnić ciągi
mające tzw. granice niewłaściwe: .
Definicja :
Mówimy, że ciąg liczbowy
(a
n
)
n
N
ma
granicę
niewłaściwą + (-)
jeżeli prawie wszystkie wyrazy
ciągu są większe od dowolnie wybranej liczby
rzeczywistej.
M
a
a
n
n
n
n
R
M
n
n
0
0
lim
A
a
a
n
n
n
n
R
A
n
n
0
0
lim
Twierdzenie 10:
Jeżeli
, to:
1.
2.
3.
4.
5.
a
a
n
n
lim
n
n
b
lim
a
b
a
n
n
n
lim
a
b
a
n
n
n
lim
0
gdy
0
gdy
lim
a
a
a
b
a
n
n
n
0
lim
a
b
a
n
n
n
0
gdy
0
gdy
lim
0
0
a
a
a
a
b
a
a
n
n
n
n
n
Np.
7
2
3
3
5
2
lim
2
2
4
n
n
n
n
n
n
n
n
2
3
lim
n
n
n
2
1
3
lim
2
Twierdzenie 11:
Jeżeli
, to:
1.
2.
n
n
a
lim
n
n
b
lim
n
n
n
b
a
lim
n
n
n
b
a
lim
?
lim
n
n
n
b
a
?
lim
n
n
n
b
a
Np.
7
2
3
1
2
3
lim
2
2
n
n
n
n
n
n
n
n
5
3
lim
3
2
1
2
lim
2
2
n
n
n
10
3
5
3
lim
n
n
n
4. Symbole nieoznaczone.
1. gdy i to
0
lim
n
n
a
0
lim
n
n
b
?
0
0
lim
n
n
n
b
a
0
0
1
1
lim
Np.
2
n
n
n
0
0
1
1
lim
Np.
2
n
n
n
0
0
2
3
1
2
lim
Np.
2
2
n
n
n
n
2. gdy i to
3.
4.
5.
6.
7.
n
n
a
lim
n
n
b
lim
?
lim
n
n
n
b
a
S.N.
0
0
S.N.
S.N.
S.N.
0
0
S.N.
0
S.N.
0
S.N.
1
gdy i to
ale, gdy
1
lim
n
n
a
n
n
b
lim
S.N.
1
lim
n
b
n
n
a
1
1
lim
lim
1
n
n
b
n
b
n
n
n
n
a
a
5. Liczba Eulera.
Rozważmy ciąg o wyrazie ogólnym:
Można udowodnić, że ten ciąg jest monotoniczny
(rosnący) i ograniczony, czyli (Tw.5) jest zbieżny do
granicy właściwej. Istnieje liczba rzeczywista, która
jest granicą tego ciągu.
Przyjęto oznaczać tą liczbę „e” – liczba Eulera.
Jest to liczba niewymierna.
n
n
n
a
1
1
...
,48
2
5
6
,44;
2
4
5
2,36;
3
4
2,25;
2
3
;
2
5
5
4
4
3
3
2
2
1
a
a
a
a
a
e
n
a
df
n
n
n
n
1
1
lim
lim
59045235
7182818284
,
2
e

Twierdzenie 11:
Jeżeli
to
n
n
a
lim
.
1
1
lim
e
a
n
a
n
n
Twierdzenie 12:
Jeżeli
to
0
lim
n
n
b
.
1
lim
1
e
b
n
b
n
n
UWAGA:
Jeżeli wyznaczając granicę ciągu natrafimy na
symbol nieoznaczony [1
] to szukamy powiązania
z liczbą e.
Np.
n
n
n
a
5
3
1
n
n
n
a
1
1
2
3
2
1
4
2
n
n
n
n
n
a
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
Wyszukiwarka
Podobne podstrony:
1 Przestrzenie metryczneid 8656
Definicja przestrzeni metrycznej Zbieżność ciągów w przestrzeni metrycznej
zagadnienia, punkt 2, II Przestrzenie metryczne zupełne
2 Przestrzenie metryczneid 19646
2. Przestrzenie metryczne
Algebra liniowa Przestrzenie metryczne
przestrzenie metryczne 08
lista analiza 2008 4 przestrzenie metryczne
3 Przestrzenie metryczne
przestrzenie metryczne 08
9 - Przestrzenie metryczne cd, Analiza matematyczna
26.Definicja przestrzeni metrycznej. Zbieznosc ciagow w przestrzeni metrycznej, Studia, Semestr VI,
8 - Przestrzeń metryczna, Analiza matematyczna
3. Przestrzenie metryczne
1. Przestrzenie metryczne
Przestrzenie metryczne
000480 Przestrzenie metryczne
wyklad09, Przestrzenie metryczne
więcej podobnych podstron