Konspekt lekcji matematyki

Autor:

Klasa: I liceum (matematyczna)

Dział tematyczny: Funkcje trygonometryczne

Temat: Wartości funkcji trygonometrycznych szczególnych kątów.

Budowanie kąta o danej wartości funkcji trygonometrycznej.

Program: Oficyna Edukacyjna*Krzysztof Pazdro

Baza:
- Uczeń zna pojęcie dowolnego kąta;
- Uczeń zna pojęcie sinusa, cosinusa, tangensa i cotangensa (kąta ostrego i dowolnego kąta);
- Uczeń zna pojęcie łukowej miary kąta;
- Uczeń zna wartości funkcji trygonometrycznych kątów 30

◦

, 45

◦

, 60

◦

;

- Uczeń wie, jakie znaki mają funkcje trygonometryczne w poszczególnych ćwiartkach układu
współrzędnych.

Cele:
- Poznanie przez uczniów wartości funkcji trygonometrycznych dla kątów, których ramiona koń-
cowe pokrywają się z osiami układu;
- Poznanie przez uczniów algorytmu rysowania kątów w układzie współrzędnych, gdy dana jest
wartość jednej z funkcji trygonometrycznych i opcjonalnie warunek na inną funkcję tego kąta.

Metody:
- Podająca (wytłumaczenie algorytmu rysowania kąta o podanej wartości funkcji trygonome-
trycznej);
- Poszukująca (wspólne uzupełnianie tabelki z wartościami funkcji trygonometrycznych szczegól-
nych kątów; niektóre etapy wprowadzania algorytmu rysowania kąta o danej wartości funkcji try-
gonometrycznej; pytania pojawiające się w czasie rozwiązywania zadań);
- Praktyczna (rozwiązywanie zadań).

Zasady:
- Trwałości wiedzy (zadanie pracy domowej; powtórzenie materiału na początku lekcji);
- Świadomego i aktywnego udziału ucznia w procesie nauczania i uczenia się (samodzielne rozwiązy-
wanie zadań; próby rozwiązania pojawiających się problemów);
- Przystępności (dobór zadań według możliwości uczniów; stopniowanie trudności zadań);
- Systematyczności (wykorzystanie znajomości definicji funkcji trygonometrycznych dowolnego kąta
do uzupełnienia tabeli; użycie umiejętności określenia znaku wartości funkcji trygonometrycznych
w poszczególnych ćwiartkach do wykluczania nieprawidłowych rozwiązań zadania);
- Poglądowości (pomoc w postaci rysowania kątów w układzie współrzędnych do obliczenia wartości
funkcji trygonometrycznych szczególnych kątów).

1

Szczegółowy przebieg lekcji:

Czynności wstępne:

Witam się z uczniami i sprawdzam obecność. Podaję temat lekcji: Wartości funkcji trygonom-

etrycznych szczególnych kątów. Budowanie kąta o danej wartości funkcji trygonometrycznej.

Część przypominająca:

Przypominam z uczniami wiadomości, które poznali na poprzednich lekcjach.

Przykładowe pytania:
– Czym jest sinus dowolnego kąta?
– Jaki znak ma wartość funkcji sinus w III ćwiartce układu współrzędnych?
– Czym jest cotangens dowolnego kąta?
– Jaki znak ma cosinus w IV ćwiartce układu współrzędnych?
– Wierszyk o znakach funkcji trygonometrycznych w poszczególnych ćwiartkach.
– Ile wynosi tg

π

4

, sin

π

6

, cos 45

◦

, ctg 60

◦

?

Część wprowadzająca:

Pierwsza część tematu ma na celu zwrócenie uwagi uczniów na kąty o szczególnym położeniu w

układzie współrzędnych. Dokładniej na kąty, których ruchome ramię pokrywa się z osiami układu
współrzędnych.

Mówię uczniom, że wykorzystamy poznane dotąd wiadomości do stworzenia tabeli, która zbierze

nam wartości funkcji trygonometrycznych takich szczególnych kątów. Pytam uczniów o miary tych
kątów i rysuję tabelę na tablicy:

1
2

2

α

0(0

◦

)

π

2

(90

◦

)

π(180

◦

)

3
2

π(270

◦

)

1
2

sin α

1
2

cos α

1
2

tg α

1
2

ctg α

Następnie rysuję układ współrzędnych i zaznaczam pierwszy kąt, czyli ten o mierze 0:

X

Y

0

0

◦

Pytam uczniów, co należy dalej zrobić, żeby policzyć funkcje trygonometryczne tego kąta, jako

kąta dowolnego. W rezultacie rysujemy pewien punkt P na końcowym ramieniu kąta, na przykład:

2

X

Y

0

0

◦

P (10, 0)

Wypisujemy wartości potrzebne do dalszych obliczeń:

x = 10

y = 0

r =

p

10

2

+ 0

2

= 10

I liczymy wartości funkcji trygonometrycznych tego kąta:

sin 0

◦

=

y

r

=

0

10

= 0

cos 0

◦

=

x

r

=

10

10

= 1

tg 0

◦

=

y

x

=

0

10

= 0

ctg 0

◦

=

x

y

=

10

0

→ nie istnieje

I na bieżąco uzupełniamy tabelkę:

1
2

2

α

0(0

◦

)

π

2

(90

◦

)

π(180

◦

)

3
2

π(270

◦

)

1
2

sin α

0

1
2

cos α

1

1
2

tg α

0

1
2

ctg α

—

Analogicznie postępujemy dla kolejnych kątów:

X

Y

0

P (10, 0)

90

◦

R(0, 10)

x = 0

y = 10

r =

p

0

2

+ 10

2

= 10

sin 90

◦

=

y

r

=

10

10

= 1

3

cos 90

◦

=

x

r

=

0

10

= 0

tg 90

◦

=

y

x

=

10

0

→ nie istnieje

ctg 90

◦

=

x

y

=

0

10

= 0

X

Y

0

P (10, 0)

R(0, 10)

S(−10, 0)

180

◦

x = −10

y = 0

r =

p

(−10)

2

+ 0

2

= 10

sin 180

◦

=

y

r

=

0

10

= 0

cos 180

◦

=

x

r

=

−10

10

= −1

tg 180

◦

=

y

x

=

0

−10

= 0

ctg 180

◦

=

x

y

=

−10

0

→ nie istnieje

X

Y

0

P (10, 0)

R(0, 10)

S(−10, 0)

270

◦

T (0, −10)

x = 0

y = −10

r =

p

0

2

+ (−10)

2

= 10

sin 270

◦

=

y

r

=

−10

10

= −1

cos 270

◦

=

x

r

=

0

10

= 0

tg 270

◦

=

y

x

=

−10

0

→ nie istnieje

4

ctg 270

◦

=

x

y

=

0

−10

= 0

Cały czas na bieżąco wypełniając tabelkę:

1
2

2

α

0(0

◦

)

π

2

(90

◦

)

π(180

◦

)

3
2

π(270

◦

)

1
2

sin α

0

1

0

−1

1
2

cos α

1

0

−1

0

1
2

tg α

0

—

0

—

1
2

ctg α

—

0

—

0

(Jeśli rachunki będą całkowicie zrozumiałe dla uczniów, to do funkcji cosinus, tangens i cotangens
nie będziemy wykonywać wszystkich obliczeń.)

Następnie pytam uczniów, co otrzymamy dla kątów 360

◦

, 450

◦

, 540

◦

, 630

◦

, 720

◦

, .... Po krótkiej

dyskusji dochodzimy do wniosku, że tabelkę można „przesuwać” o 360

◦

.

Po tych rozważaniach przechodzimy do drugiej części tematu, czyli zadań:

Zadanie 8.48
Zbuduj kąt o mierze α takiej, że:
a) sin α =

3
5

Na początku rysujemy układ współrzędnych i zapisujemy wzór na sinus dowolnego kąta:

sin α =

y

r

Tłumaczę, że zadanie to polega na znalezieniu ramienia ruchomego kąta, który mamy narysować.
Pytam, co wystarczy znaleźć, aby otrzymać to ramię. Wspólnie dohodzimy do wniosku, że musimy
odszukać dowolny punkt należący do tego ramienia.

Mówię uczniom, że zaczniemy od ustalenia dowolnych y i r spełniających warunek:

sin α =

3

5

Zapisujemy kilka propozycji. Mówię uczniom, że dla każdego wypisanego zestawu otrzymane kąty
będą takie same.

Rozwiązujemy dalej dla:

(

y = 3

r = 5

.

Pytam uczniów, gdzie znajdują się punkty spełniające warunek y = 3. Dochodzimy do wniosku,
że na prostej równoległej do osi OX. Rysujemy ją w układzie współrzędnych.

Następnie proszę uczniów, żeby zastanowili się, gdzie znajdują się punkty odległe o 5 od

początku układu współrzędnych. Po krótkiej dyskusji wiemy, że leżą one na okręgu o środku
w punkcie (0, 0) i promieniu równym 5. Rysujemy także ten okrąg w układzie współrzędnych.

Przypominam uczniom, że punkty, których szukamy muszą spełniać obydwa omówione warunki.

Pytam, gdzie one się znajdują. Oczekuję odpowiedzi, że w punktach przecięcia narysowanych
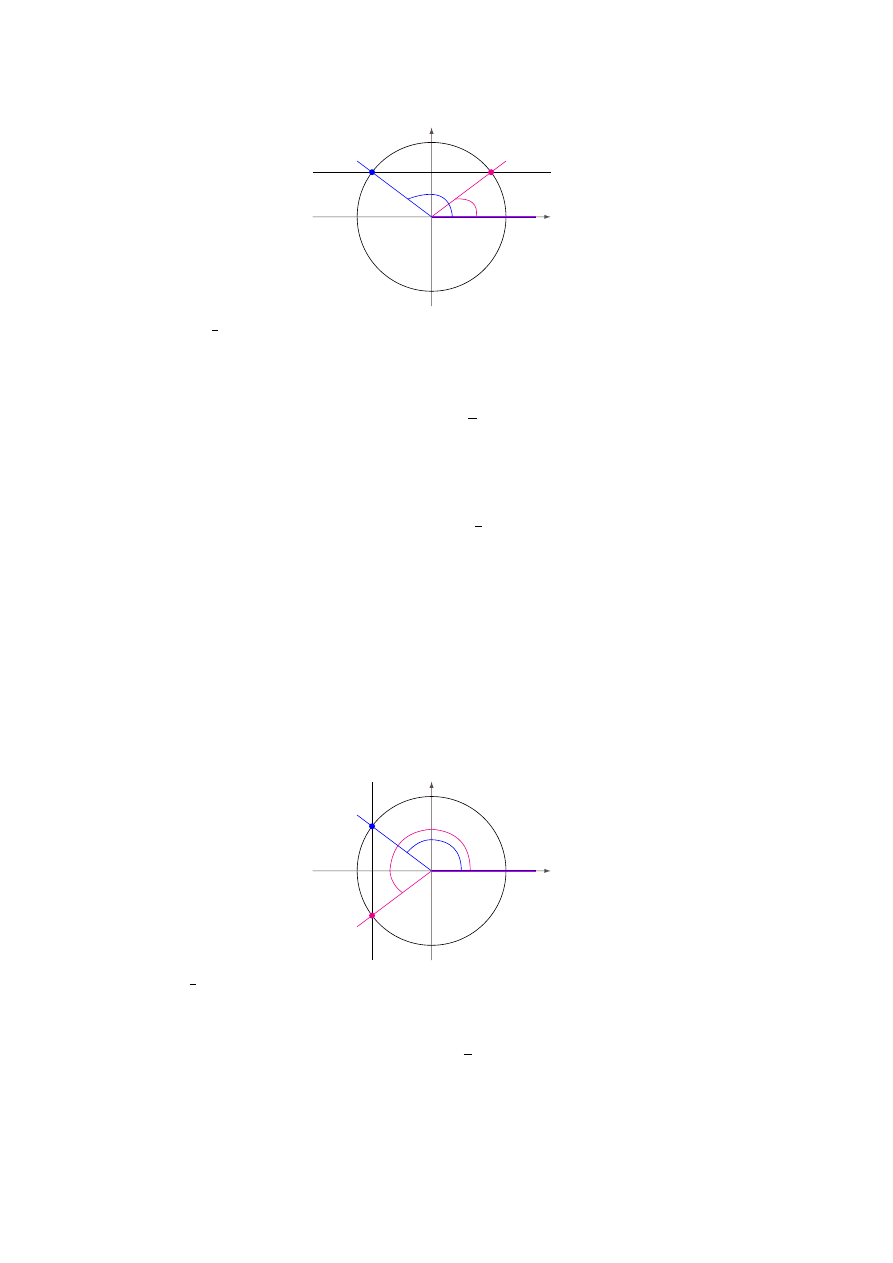
prostej i okręgu. Zaznaczamy te punkty i rysujemy szukane kąty. Nasze rozwiązanie wygląda
zatem następująco:

5

X

Y

0

y = 3

5

α

1

α

2

b) cos α = −

4
5

Ten przykład rozwiązujemy bardzo podobnie do poprzedniego:
Rysujemy układ współrzędnych i zapisujemy wzór na cosinus dowolnego kąta:

cos α =

x

r

Musimy znaleźć ruchome ramię kąta, który mamy narysować. Szukamy zatem punktu należącego
do tego ramienia.

Ustalamy dowolne x i r spełniających warunek:

cos α = −

4

5

Zapisujemy kilka propozycji. Zwracamy uwagę, że tutaj x musi być ujemne, ponieważ r musi być
dodatnie. Przypominam, że dla każdego wypisanego zestawu otrzymane kąty będą takie same.

Rozwiązujemy dalej dla:

(

x = −4

r = 5

.

Pytam uczniów, gdzie znajdują się punkty spełniające warunek x = −4. Dochodzimy do wniosku,
że na prostej równoległej do osi OY . Rysujemy ją w układzie współrzędnych.

Następnie przypominamy, że punkty odległe o 5 od początku układu współrzędnych leżą na

okręgu o środku w punkcie (0, 0) i promieniu równym 5. Rysujemy także ten okrąg w układzie
współrzędnych.

Przypominamy że punkty, których szukamy to punkty przecięcia narysowanych prostej i okręgu.

Zaznaczamy te punkty i rysujemy szukane kąty. Nasze rozwiązanie wygląda zatem następująco:

X

Y

0

x = −4

5

α

2

α

1

c) tgα =

1
2

Rozwiązanie tego przykładu różni się trochę od poprzednich rozwiązań. Na początku rysujemy
układ współrzędnych i zapisujemy wzór na tangens dowolnego kąta:

tgα =

y

x

Zadanie to również polega na znalezieniu ruchomego ramienia kąta, który mamy narysować.
Szukamy zatem dowolnego punktu należącego do tego ramienia.

6

Zaczynamy od ustalenia dowolnych y i x spełniających warunek:

tg α =

1

2

Zapisujemy kilka propozycji.

Rozwiązujemy dalej na przykład dla:

(

y = 1

x = 2

.

Rysujemy proste y = 1 i x = 2, znajdujemy punkt przecięcia jak poprzednio i rysujemy jeden z
kątów:

X

Y

0

x = 2

y = 1

α

1

Następnie pytam uczniów, czy istnieje para (x, y), spełniająca powyższy warunek i która da

nam w rezultacie inne ramię końcowe kąta (inny kąt). Dyskutując, dochodzimy do wniosku, że
dwa ujemne punkty dadzą nam inne ramię. Rysujemy również ten przypadek dla wybranej pary

punktów, na przykład:

(

x = −2

y = −1

:

X

Y

0

x = 2

y = 1

α

1

x = −2

y = −1

α

2

Przy tym przykładzie i każdym następnym, w którym podana jest wartość tangensa lub cotan-

gensa, zwracam uwagę uczniów, aby zaznaczać proste z oddzielnych przypadków różnymi kolorami.
Zapobiegnie, to wybieraniu niepoprawnych punktów przecięcia.

Następnie przechodzimy do kolejnego zadania:
Zadanie 8.49
Zbuduj kąt o mierze α takiej, że:
b) cos α = −

2
7

i ctgα > 0

Do tablicy proszę ucznia. Mówię, że zadanie to jest prawie takie samo jak poprzednie. Proszę, aby
uczniowie rozwiązywali je, znajdując najpierw punkty spełniające warunek:

cos α = −

2

7

Rozwiązujemy zatem analogicznie do przykładu b) z zadania poprzedniego: rysujemy układ

współrzędnych, szukamy x i r spełniających warunek:

x

r

= −

2

7

7

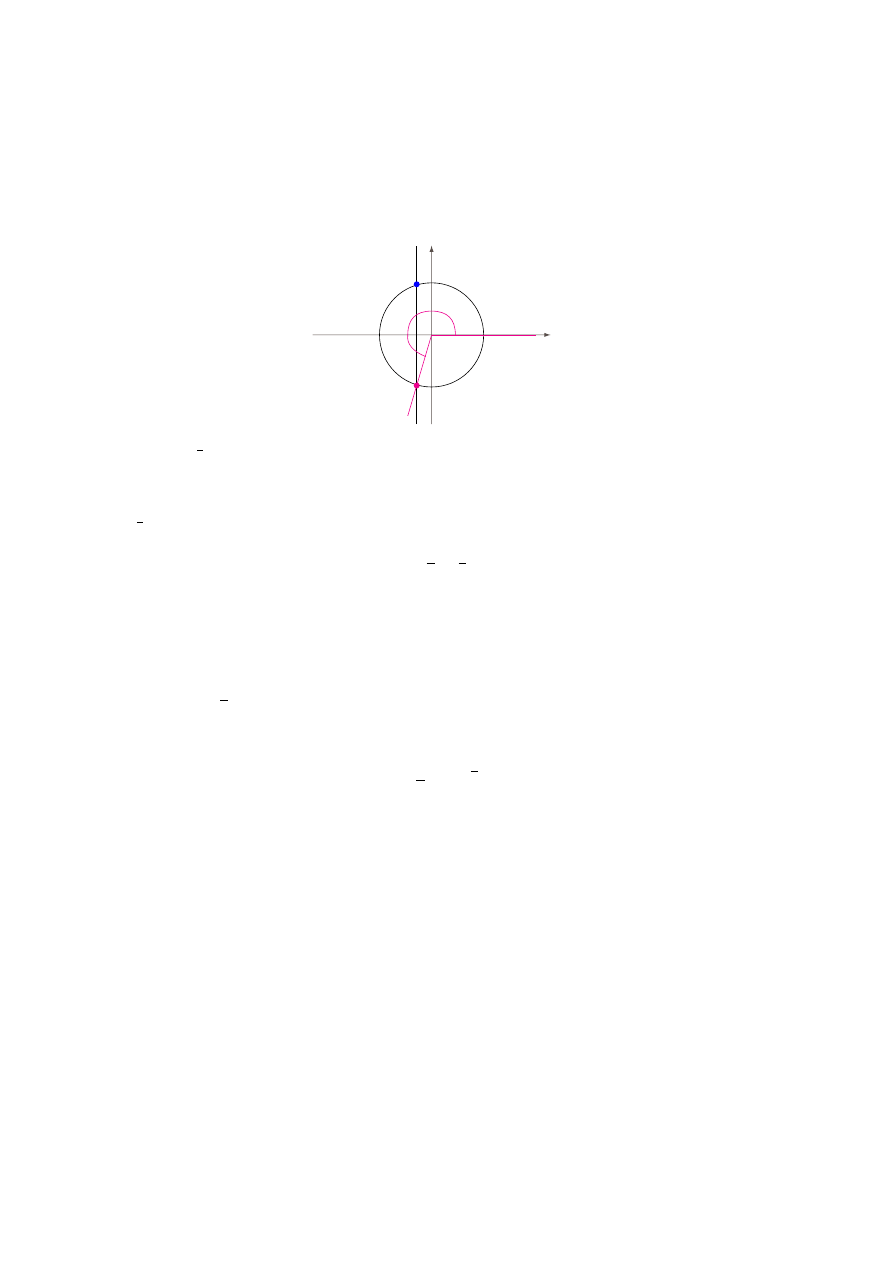
Wybieramy jedną taką parę i rysujemy odpowiednią prostą równoległą do osi OY i odpowiedni
okrąg, otrzymując dwa punkty – jeden w II i jeden w III ćwiartce.

Na tym etapie proszę uczniów o zwrócenie uwagi na drugi z podanych warunków. Pytam, dla

kątów w której ćwiartce cotangens jest dodatni. Po krótkiej dyskusji odrzucamy kąt z II ćwiartki
i jako rozwiązanie rysujemy tylko kąt w ćwiartce III:

X

Y

0

x = −2

7

α

c) tgα = 2

1
3

i sin α < 0

Również proszę ucznia do tablicy i proponuję rozwiązanie podobne do tego, które przedstawiłam w
poprzednim przykładzie. Zajmujemy się najpierw pierwszym warunkiem, przy czym zamieniamy
2

1
3

na ułamek niewłaściwy, otrzymując równość:

y

x

=

7

3

Podobnie jak w przykładzie c) z poprzedniego zadania, wybieramy odpowiednie pary punktów

(x, y), które spełniają powyższą zależność otrzymując dwa punkty wyznaczające końcowe ramiona
kątów – jedno w I i jedno w III ćwiartce.

Na tym etapie także wracamy do warunku sin α < 0 i odrzucamy rozwiązanie z pierwszej

ćwiartki, rysując kąt wyznaczony w III ćwiartce jako rozwiązanie.

d) ctgα = −

√

2 i cos α > 0

Ten przykład rozwiązujemy również analogicznie do poprzednich. Z otrzymanego warunku:

x

y

= −

√

2

uzyskujemy wiele par punktów, z których wybieramy dwie prowadzące do różnych rozwiązań –
jednego w II i drugiego i IV ćwiartce. Zaznaczamy otrzymane punkty w układzie współrzędnych i
biorąc pod uwagę nierówność sin α < 0 wykluczamy punkt z IV ćwiartki. Jako rozwiązanie rysu-
jemy kąt w II ćwiartce.

Podsumowanie

Jeśli rozwiązanie powyższych przykładów nie zajmie mi całej lekcji, to na koniec podsumuję z

uczniami wiadomości wprowadzone na tej lekcji. Przypomnimy sobie wówczas, w jaki sposób uzu-
pełniliśmy tabelkę z wartościami trygonometrycznymi szczególnych kątów, a także jak rysowaliśmy
kąty – krok po kroku.

8

Zadanie domowe

Zadanie domowe będzie zależało od momentu, w którym skończy się lekcja. Oprócz przykładów,

które przedstawiam poniżej i które celowo ominę podczas lekcji poproszę także uczniów o dokończe-
nie bieżącego zadania, na którym zakończy się lekcja.

Zadanie 8.48
d) ctgα = −2

Przykład ten należy rozwiązać analogicznie do przykładu c) z tego zadania. Trzeba zapisać wzór
na cotangens dowolnego kąta:

ctg α =

x

y

I znaleźć dowolne punkty należące do ramion końcowych kątów spełniających powyższy warunek,
na przykład:

(

x = −2

y = 1

∨

(

x = 2

y = −1

Następnie należy narysować odpowiednie proste i zaznaczyć poprawnie punkty przecięcia, narysować
końcowe ramiona kątów oraz oznaczyć te kąty.

Zadanie 8.49
a) sin α =

5
6

i tg α < 0

Przykład ten uczniowie mogą rozwiązać także bardzo podobnie do przykładu przedstawionego
na lekcji (b) z tego zadania), czyli pamiętając o definicji sinusa:

sin α =

y

r

znaleźć y i r, które spełniają warunek:

y

r

=

5

6

Taką parą liczb jest na przykład:

(

y = 5

r = 6

.

Następnie wystarczy narysować prostą y = 5 oraz okrąg o środku w początku układu współrzęd-

nych i promieniu równym 6 oraz zaznaczyć ich punkty przecięcia. Jeden z punktów będzie należał
do I ćwiartki i należy go wykluczyć, ponieważ tangens szukanego kąta ma być mniejszy od 0.
Rozwiązaniem okaże się więc kąt w IV ćwiartce układu współrzędnych.

9