Analiza Dyskryminacyjna

wprowadzenie

Idea



Wykorzystywana do przewidywania

przynależności do kategorii/grup na

podstawie jednego bądź więcej

predyktorów



Predyktor: zmienna ciągła



Zmienna zależna: kategorialna



Odwrotność analizy wariancji

Analiza wariancji



Interesujemy się tym, czy grupy różnią się

od siebie istotnie pod względem



zmiennej zależnej (ANOVA)



liniowo powiązanych ze sobą zmiennych

zależnych (MANOVA)



Jeśli jest to prawdą to w drugą stronę też

można przewidywać:



Te same zmienne zależne można

wykorzystać do przewidywania

przynależności do poszczególnych grup

Co nas nurtuje?



Jaki jest najlepszy predyktor
zaklasyfikowania osoby do danej
grupy.



Jak jest najlepsza kombinacja
predyktorów pozwalająca przewidzieć
znalezienie się uczestnika badania w
danej grupie?

Co nas nurtuje?



Pedagogów może zastanawiać, jakie czynniki
sprawiają, że niektórzy studenci psychologii
decydują się kontynuować naukę na studiach
doktoranckich, inni znajdują pracę w biznesie, a inni
znajdują pracę w terapii.



Badając szereg zmiennych przed ukończeniem
studiów możemy dzięki analizie dyskryminacyjnej
odpowiedzieć na pytanie, która z tych zmiennych
lub jaka kombinacja predyktorów najlepiej
przewiduje wybór drogi życiowej po studiach.

Co się kryje za grupami?



Z matematycznego punktu widzenia analiza wariancji i

analiza dyskryminacyjna są podobne, ale na co innego kładą

nacisk



Jeżeli grupy różnią się istotnie statystycznie pod względem

jakiejś zmiennej to oznacza, że zmienna to dobrze rozdziela

(discriminate) badanych.



w AD skupiamy się na pokategoryzowaniu ludzi do grup i

sprawdzamy jak dobrze/źle udało się nam dokonać

klasyfikacji

•

interesujemy się tym,

jak można rozróżnić grupy

między sobą

– Jacy ludzie trafiają do jednej a jacy do drugiej

kategorii

•

a nie czy te różnice są istotne statystycznie

Co się kryje za grupami?



Mierzymy samoocenę w grupie 20 mężczyzn i 20 kobiet.



Mężczyźni posiadają zazwyczaj wyższą samoocenę niż
kobiety, więc uzyskamy istotną statystycznie różnicę między
średnimi w poprównywanych grupach.



Oznacza to, że z prawdopodobieństwem większym niż
przypadkowe możemy wnioskować, że osoba posiadająca
wysoki wynik w skali samooceny należy do grupy mężczyzn,
a osoba posiadająca wynik niski należy do grupy kobiet.

PRZYKŁAD

so far, so good...



Podstawowa idea analizy dyskryminacyjnej to
sprawdzenie czy grupy różnią się pod
względem wyróżnionych zmiennych/zmiennej,



a następnie wykorzystaniu tej
zmiennej/zmiennych do przewidywania
przynależności do grup, np. w przypadku
nowych uczestników badania.

Więcej niż jeden predyktor



Najczęściej analizę dyskryminacyjną
stosujemy wtedy, kiedy chcemy
sprawdzić, która z wielu zbadanych
zmiennych najlepiej przewiduje
przynależność do różnych grup.



W tym wypadku AD podobna jest do
MANOVy

Więcej niż jeden predyktor



Jeżeli mamy większą liczbę
predyktorów to chcemy zbudować
model na podstawie, którego
będziemy mogli w najlepszy sposób
przewidzieć przynależność
poszczególnych przypadków do grup.

Cel



Głównym celem jest:



znalezienie wymiarów na których grupy różnią

się między sobą



stworzenie funkcji klasyfikacyjnych



Czy przynależność do grup może być

trafnie przewidziana na podstawie

zestawu predyktorów?



Czy to w której grupie jest dana osóbka

może być wyjaśnione na postawie np.

tego co myśli o …

Analiza dyskryminacyjna dla dwóch grup



Nazywana liniową analizą
dyskryminacyjną Fishera.



Podobna do wielokrotnej analizy regresji.
Jeżeli zakodujemy wartości zmiennej
grupującej jako 1 i 2, a następnie
potraktujemy tą zmienną jako zależną w
wielokrotnej analizie regresji to uzyskany
wynik będzie podobny do wyniku AD.

Analiza dyskryminacyjna dla dwóch grup



Model jaki jest dopasowywany w tej analizie
jest prostym równaniem liniowym

gdzie, a to stała, b

1

do b

n

wartości współczynników regresji.

Interpretując wyniki porównujemy współczynniki

β. Te zmienne, które mają największe te
współczynniki wyjaśniają najbardziej rozdział
uczestników do grup.

Grupa=a+b

1

x

1

+b

2

x

2



. . .+b

n

x

n

FUNKCJA DYSKRYMINACYJNA

Analiza dyskryminacyjna dla większej liczby

grup



Możemy oszacować i przetestować
więcej niż jedna funkcję
dyskryminacyjną.



wybieramy między którymi grupami
chcemy rozróżniać uczestników badania

• np. jeżeli mamy 3 grupy to możemy

oszacować funkcje dyskryminacyjne 1)
pomiędzy grupą 2 i 3 oraz 2) pomiędzy
grupami 1 vs łącznie 2 i 3.

Wymiary/ funkcje dyskryminacyjne



Na ilu wymiarach grupy różnią się od siebie?

Ile sensownych funkcji możemy wyodrębnić –

liniowych kombinacji predyktorów



Testujemy istotność każdej z nich

•

Zwykle udaje się wyodrębnić jedną, dwie sensowne
funkcje, reszta nie jest warta zachodu



Funkcje są ortogonalne (niezależne) – ich wkład w

rozróżnienie między grupami nie nachodzi na siebie.



Liczba wymiarów (funkcji dyskryminacyjnych) jest

równa liczbie grup-1 lub liczbie predyktorów w

zależności, która z wartości jest mniejsza

Analiza dyskryminacyjna dla większej liczby

grup



Funkcje dyskryminacyjne dla różnych kombinacji
grup, w popularnych pakietach statystycznych, są
wyliczane automatycznie.



pierwsza funkcja oznacza największe
rozróżnienie między grupami, kolejna mniejsze,
itd.



Obliczeniowo oszacowanie funkcji odbywa się za
pomocą kanonicznej analizy korelacji, która
oszacowuje funkcje dyskryminacyjne oraz ich
wartości własne.

Korelacja kanoniczna



Pozwala sprawdzić związek pomiędzy
dwoma zestawami zmiennych.



np. zestaw czynników ryzyka vs zestaw
objawów chorobowych

Wartości własne funkcji



Każdej funkcji przypisane są wartości

własne (eigenvalues)



Wskazują jak dobrze dana funkcja różnicuje

między grupami



Im większa wartość własna tym lepiej/trafniej

jesteśmy w stanie przypisać osoby do grup



Wartość własna

• proporcja sumy kwadratów międzygrupowej do

wewnątrzgrupowej (ANOVA), gdzie funkcja

dyskryminacyjna jest zmienną zależną a niezależną

grupy jako poziomy czynnika

Trzeba się zastanowić …



Czy wyodrębnione funkcje

dyskryminacyjne są

interpretowalne i sensowne



Jakie są korelacje pomiędzy

funkcjami dyskryminacyjnymi a

każdym z predyktorów?

pytania



Czy na podstawie tych funkcji moglibyśmy

zaklasyfikować nowe osóbki do grup?



Jak dokładni jesteśmy w klasyfikowaniu



Jeśli się mylimy, to czy jest jakaś

tendencyjność w pomyłkach?



Jak silny jest związek między

przynależnością do grup a predyktorami?

Przykład

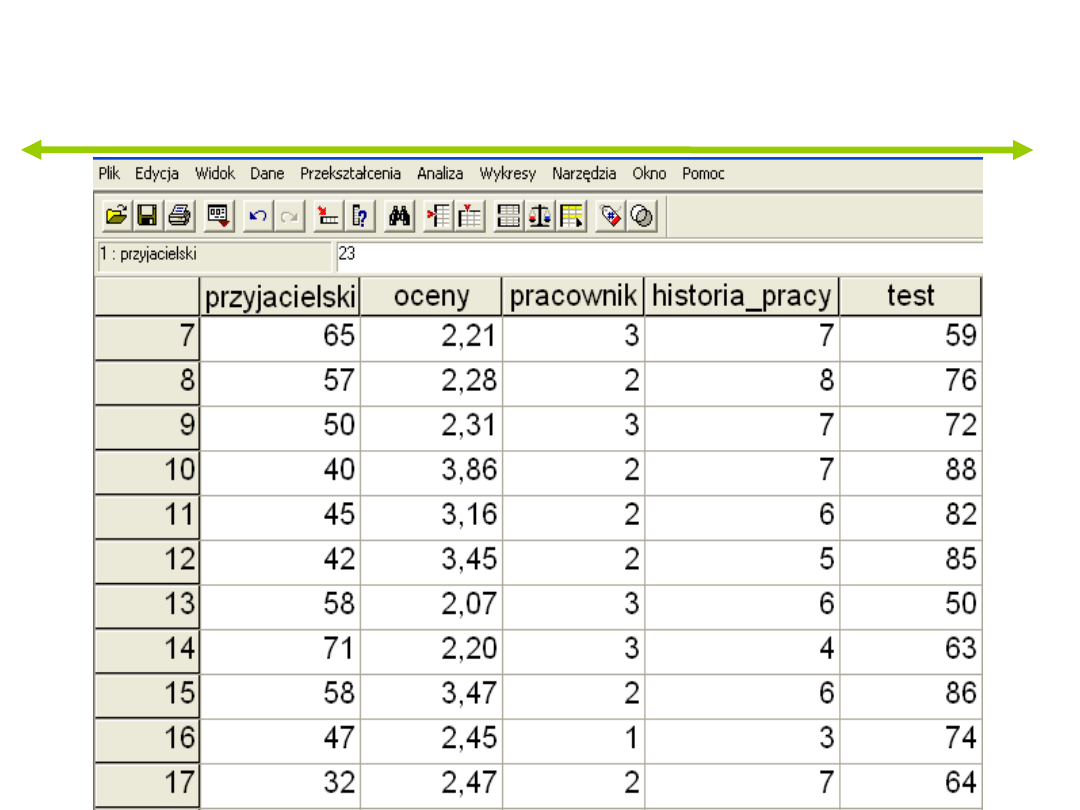
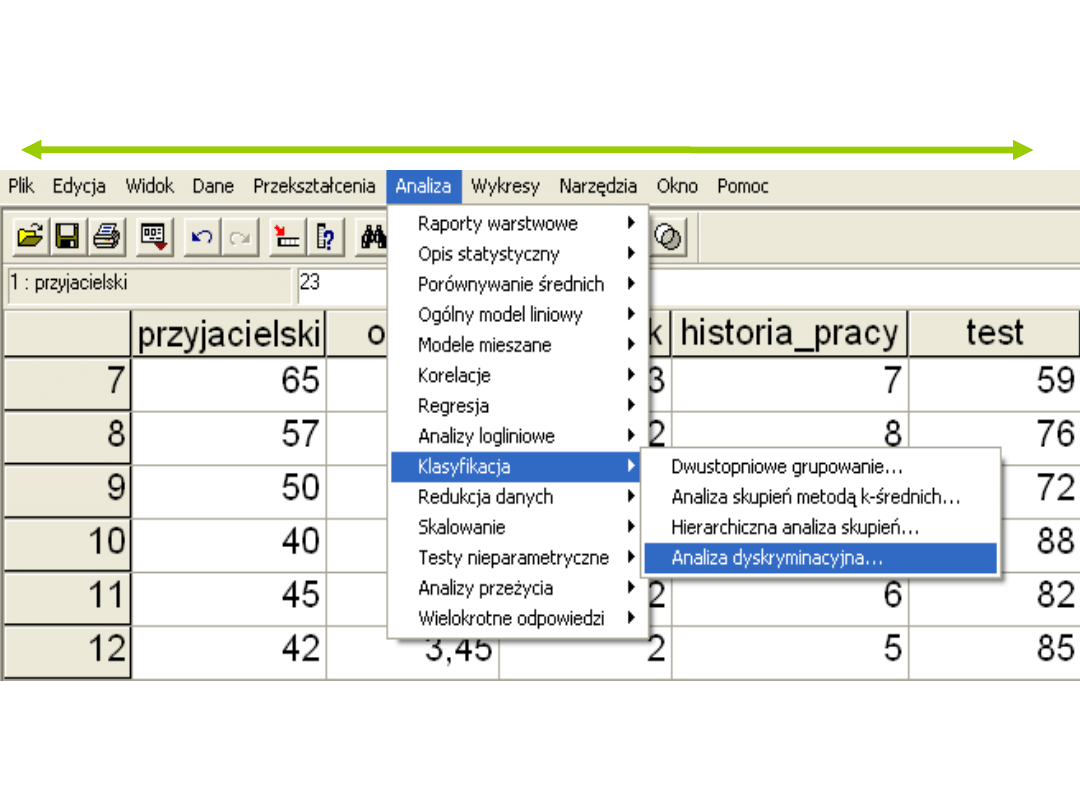
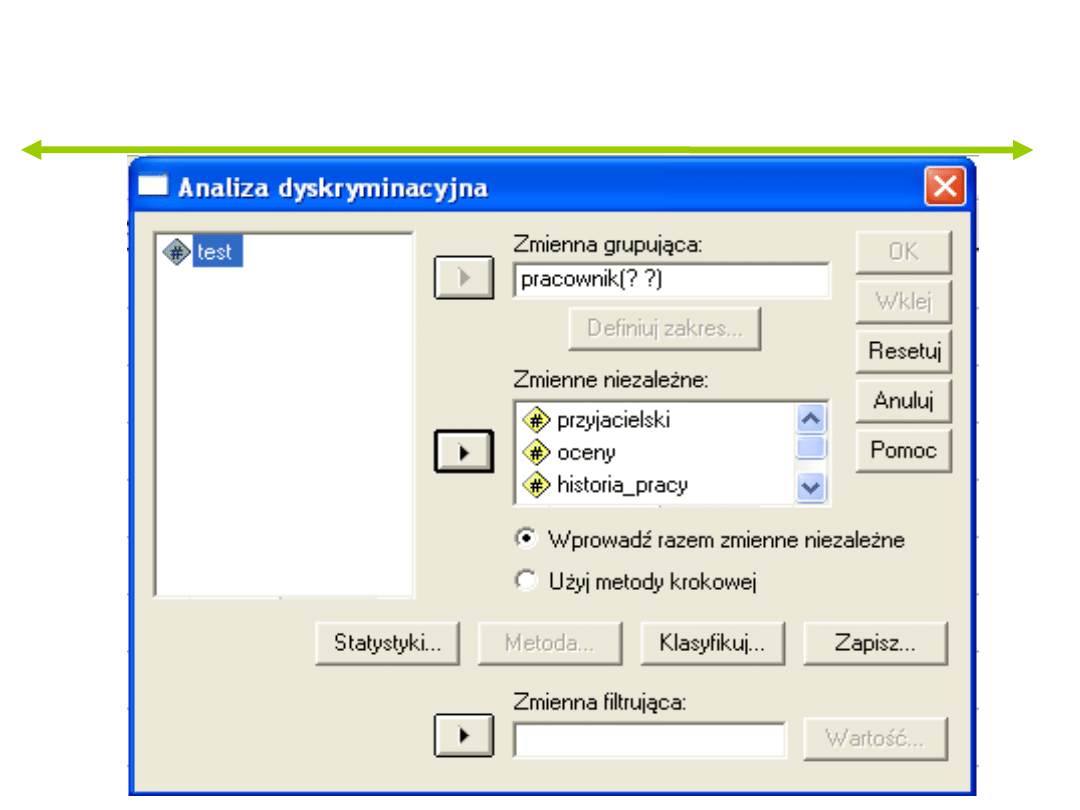
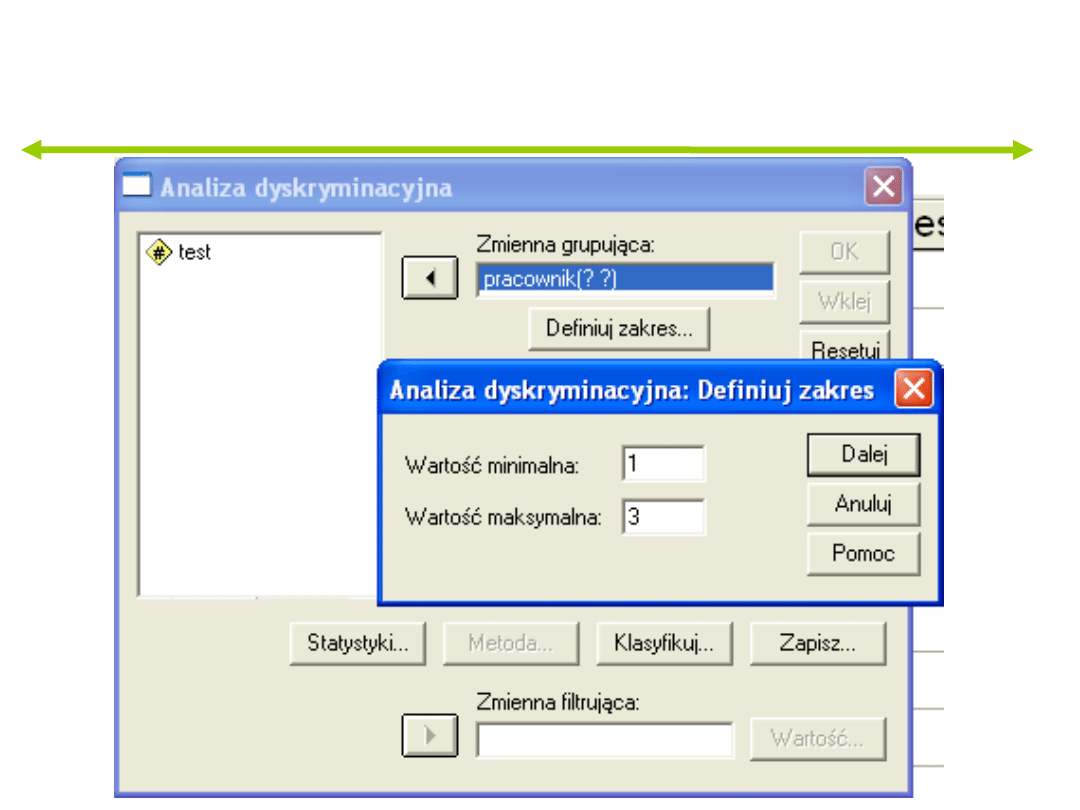
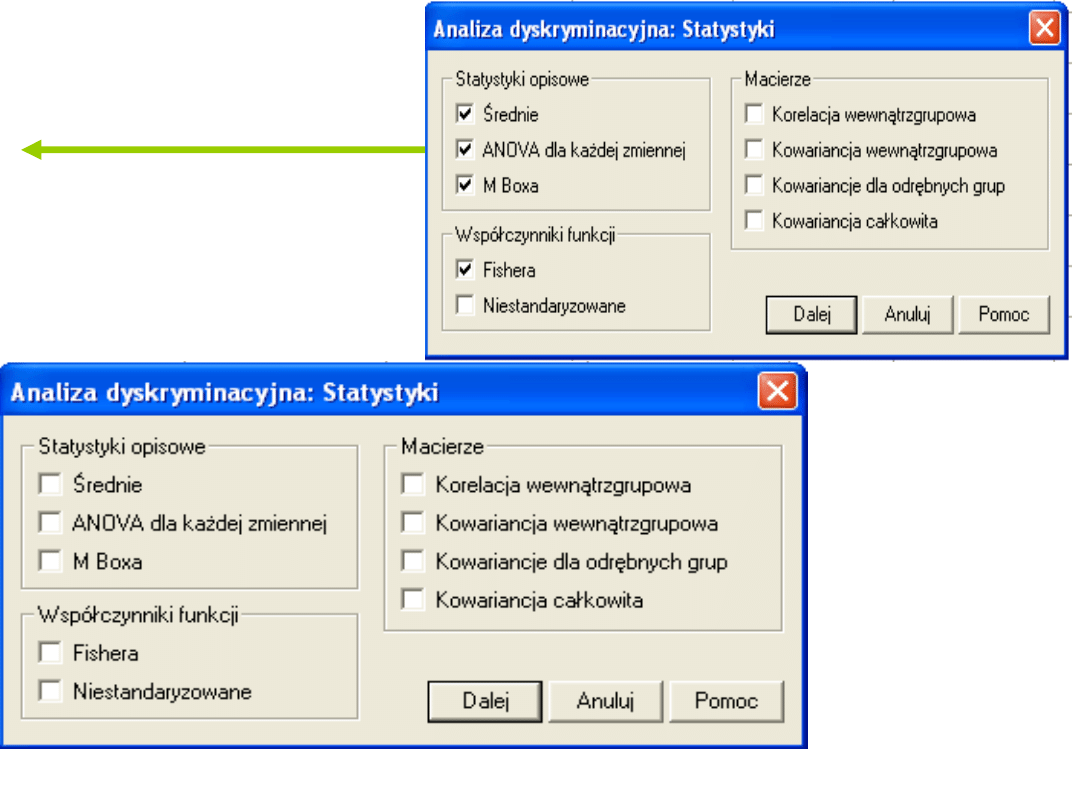
Statystyki dla grup

44,296

9,87933

27 27,000

2,9517

,64832

27 27,000

5,5556

1,78311

27 27,000

68,259

9,02387

27 27,000

51,837 12,15756

43 43,000

3,1318

,55756

43 43,000

6,4419

1,63740

43 43,000

79,860

9,97039

43 43,000

55,111

8,64317

54 54,000

2,7612

,47821

54 54,000

5,5741

1,65520

54 54,000

69,204

9,23770

54 54,000

51,621 10,97417

124 124,00

2,9312

,56603

124 124,00

5,8710

1,71539

124 124,00

72,694 10,74931

124 124,00

przyjacielski

oceny

historia_pracy

test

przyjacielski

oceny

historia_pracy

test

przyjacielski

oceny

historia_pracy

test

przyjacielski

oceny

historia_pracy

test

pracownik
słaby pracownik

indywidualna gwiazda

zespołowiec

Ogółem

Średnia

Odchylenie

standardowe

Nieważone

Ważone

N Ważnych (usuwanie

obserwacjami)

Testy równości średnich grupowych

,858 10,040

2

121

,000

,916

5,533

2

121

,005

,941

3,813

2

121

,025

,761 19,004

2

121

,000

przyjacielski

oceny

historia_pracy

test

Lambda

Wilksa

F

df1

df2

Istotność

Wyniki testu

26,716

1,265

20

28454

,190

M Boxa

Przybliżenie

df1

df2

Istotność

F

Testuje hipotezę zerową o równości
macierzy kowariancji w populacji.

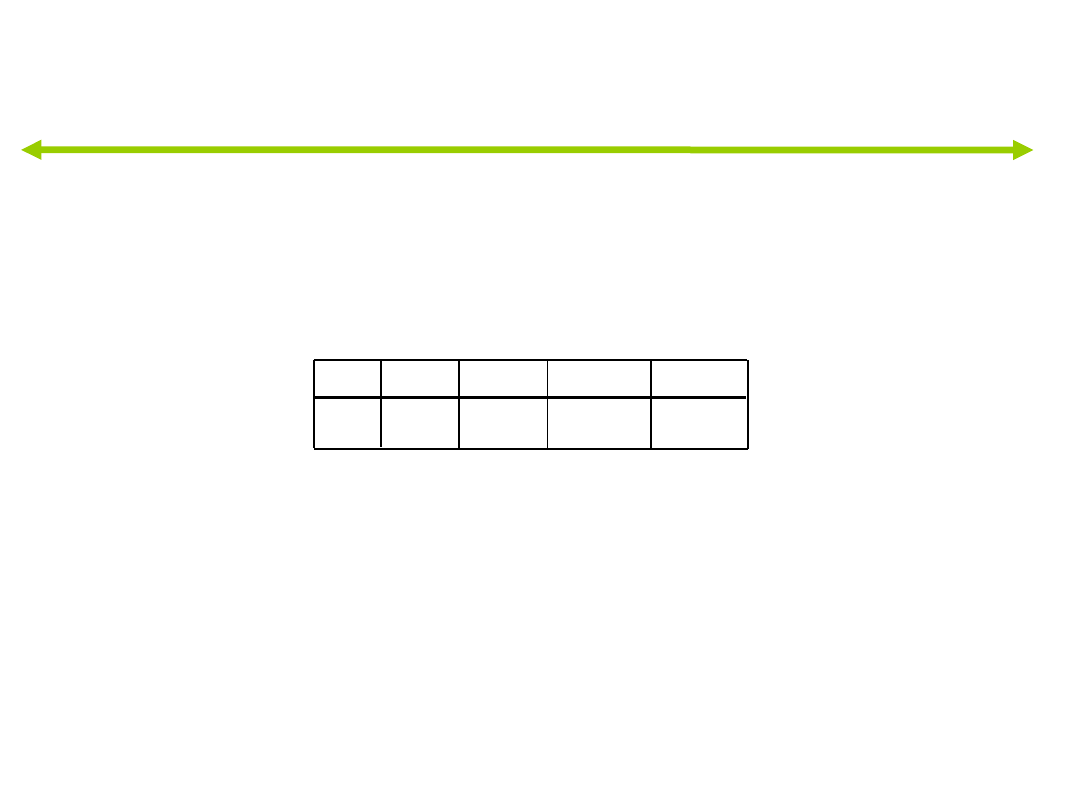
Wartości własne

,343

a

60,4

60,4

,506

,225

a

39,6

100,0

,429

Funkcja
1

2

Wartość

własna

% wariancji

%

skumulowany

Korelacja

kanoniczna

W analizie użyto pierwszych 2 funkcji dyskryminacyjnych.

a.

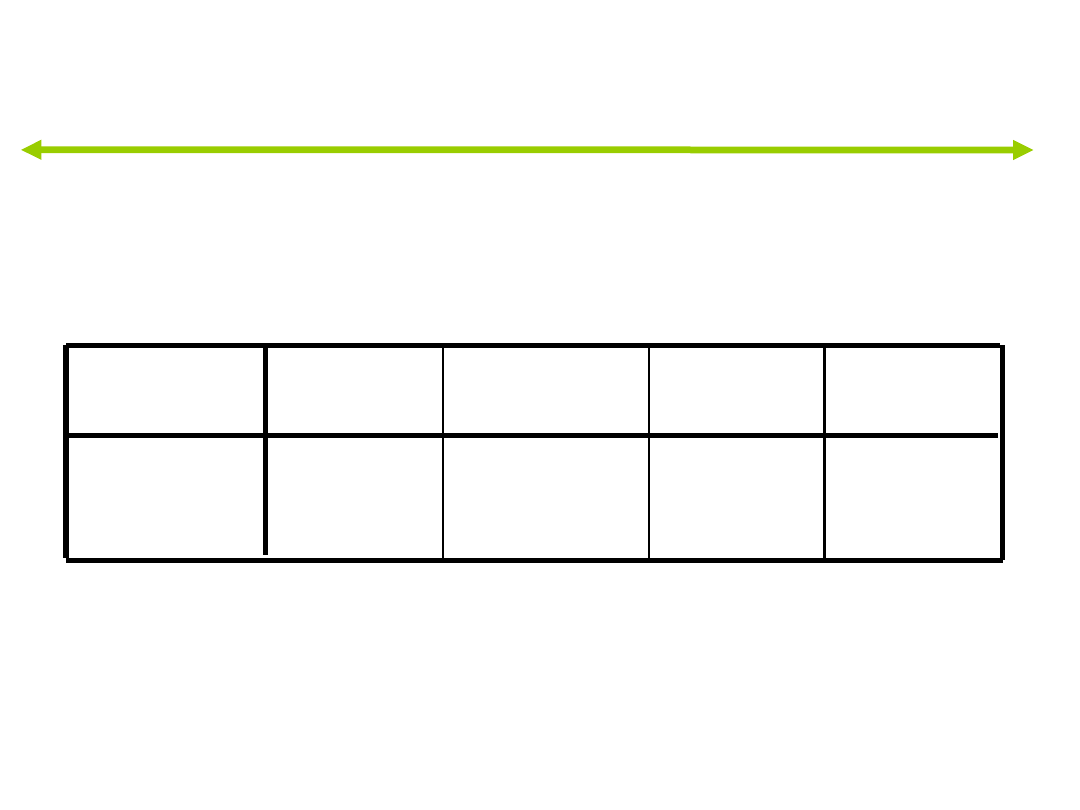
Lambda Wilksa

,608

59,527

8

,000

,816

24,243

3

,000

Test funkcji
1 przez 2

2

Lambda

Wilksa

Chi-kwadrat

df

Istotność

Analiza dyskryminacyjna dla większej liczby

grup.

Interpretacja funkcji kanonicznych.



Uzyskaliśmy dwie funkcje istotne
statystycznie.



Jednak nie wiemy między, którymi
grupami funkcje te dokonują
rozróżnień.

Analiza dyskryminacyjna dla większej liczby

grup.

Interpretacja funkcji kanonicznych.



W wynikach uzyskamy wartości b i β
dla każdej zmiennej w każdej funkcji
dyskryminacyjnej.



Im wartość standaryzowana
współczynnik kanonicznej funkcji
dyskryminacyjnej jest większa tym
większy wkład w rozróżnienie między
grupami w danej funkcji.

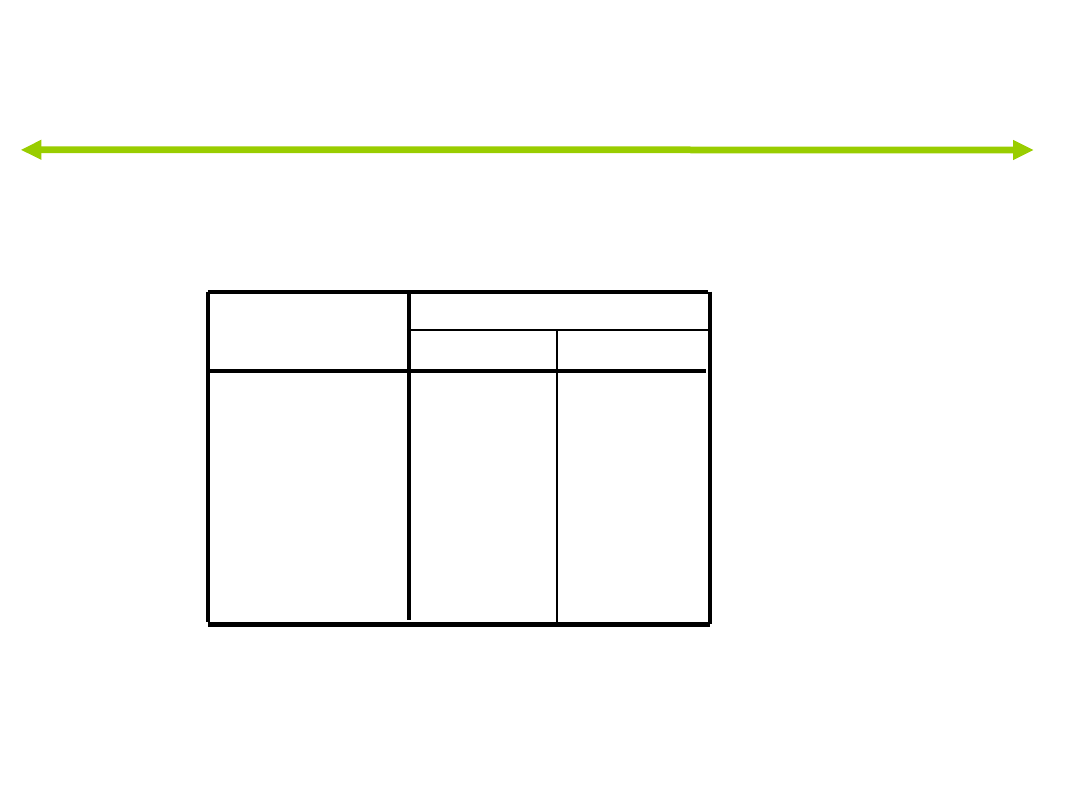
Współczynniki niewystandaryzowane (b)

funkcji dyskryminacyjnych

Współczynniki kanonicznych funkcji dyskryminacyjnych

-,008

,093

,162 -1,031
,164

,024

,094

,026

-7,798 -3,816

przyjacielski

oceny

historia_pracy

test

(Stała)

1

2

Funkcja

Współczynniki niestandaryzowane.

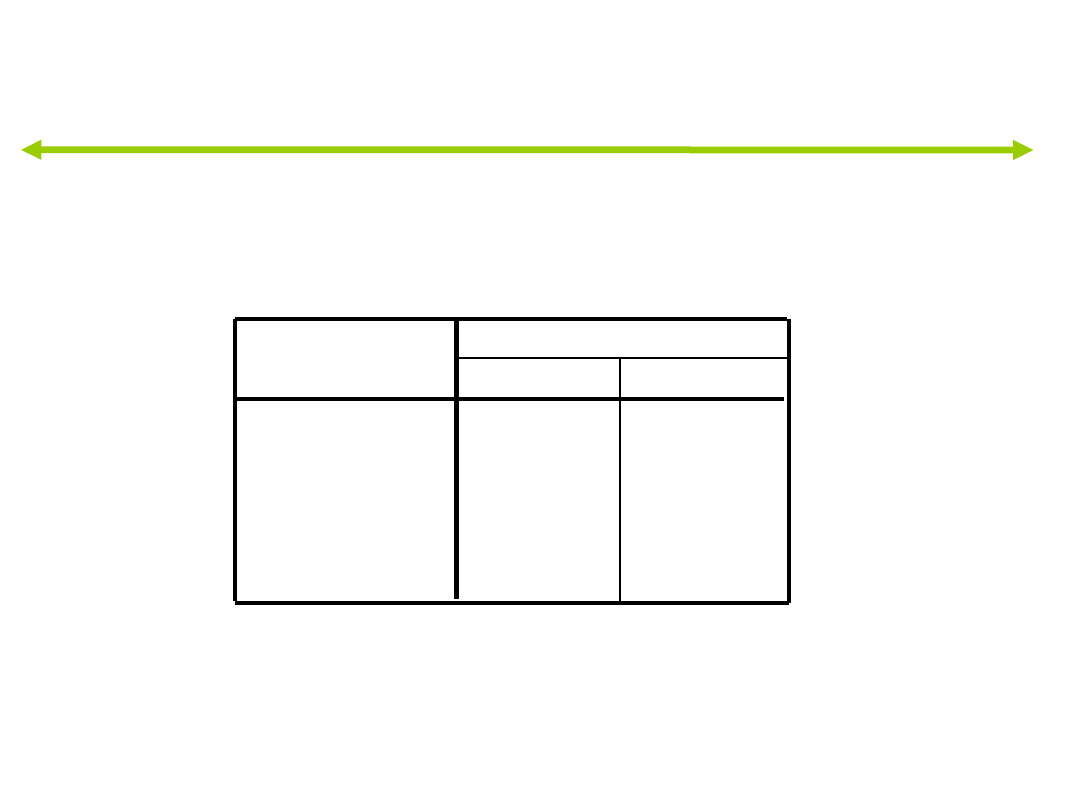
Standaryzowane współczynniki (β)

funkcji kanonicznych

Standaryzowane współczynniki

kanonicznych funkcji dyskryminacyjnych

-,087

,955

,088

-,563

,275

,040

,884

,245

przyjacielski

oceny

historia_pracy

test

1

2

Funkcja

Macierz struktury czynników



Innym sposobem interpretacji, która zmienna
jest istotna w danej funkcji jest interpretacja
macierzy czynników.



jest to macierz pokazująca współczynniki
korelacji pomiędzy poszczególnymi
predyktorami a wyodrębnionymi funkcjami.



analogiczna do macierzy ładunków w
analizie czynnikowej.

Macierz struktury czynników

Macierz struktury

,953*

,105

,467*

-,272

,428*

,020

,012

,859*

test

oceny

historia_pracy

przyjacielski

1

2

Funkcja

Połączone korelacje wewnątrzgrupowe pomiędzy zmiennymi
dyskryminującymi i standaryzowanymi kanonicznymi
funkcjami dyskryminacyjnymi. Zmienne są uporządkowane
według wartości bezwzględnej korelacji w obrębie funkcji.

Największa wartość bezwzględna korelacji pomiędzy
każdą zmienną i dowolną funkcją dyskryminacyjną.

*.

Standaryzowane współczynniki czy

ładunki czynnikowe?



Najważniejsza różnica:



standaryzowane współczynniki –
wskazują na unikalny wkład każdego
predyktora do funkcji (podobne do
korelacji cząstkowych)



ładunki czynnikowe – proste korelacje
pomiędzy predyktorami i funkcją
(funkcjami).



Wykorzystujemy je do różnych celów.

Kolejne kroki w analizie dyskryminacyjnej



Sprawdź, które funkcje są istotne statystycznie



rozważaj w dalszych analizach wyłącznie te istotne



Następnie patrzymy na standaryzowane
współczynniki funkcji



im wyższe współczynniki tym większy unikalny wkład
predyktora w rozróżnienie między grupami



W celu znalezienia znaczenia istotnych funkcji
patrzymy na macierz ładunków czynnikowych



predyktory najbardziej skorelowane z funkcją nadają jej
znaczenie



Patrzymy na średnie dla poszczególnych funkcji w
grupach



pozwala to wykryć między którymi grupami rozróżniają
poszczególne funkcje.

Średnie dla poszczególnych funkcji w

grupach

Funkcje w środkach ciężkości grup

-,401

-,826

,794

,013

-,432

,403

pracownik
słaby pracownik

indywidualna gwiazda

zespołowiec

1

2

Funkcja

Niestandaryzowane kanoniczne funkcje
dyskryminacyjne ocenione w średnich dla grup.

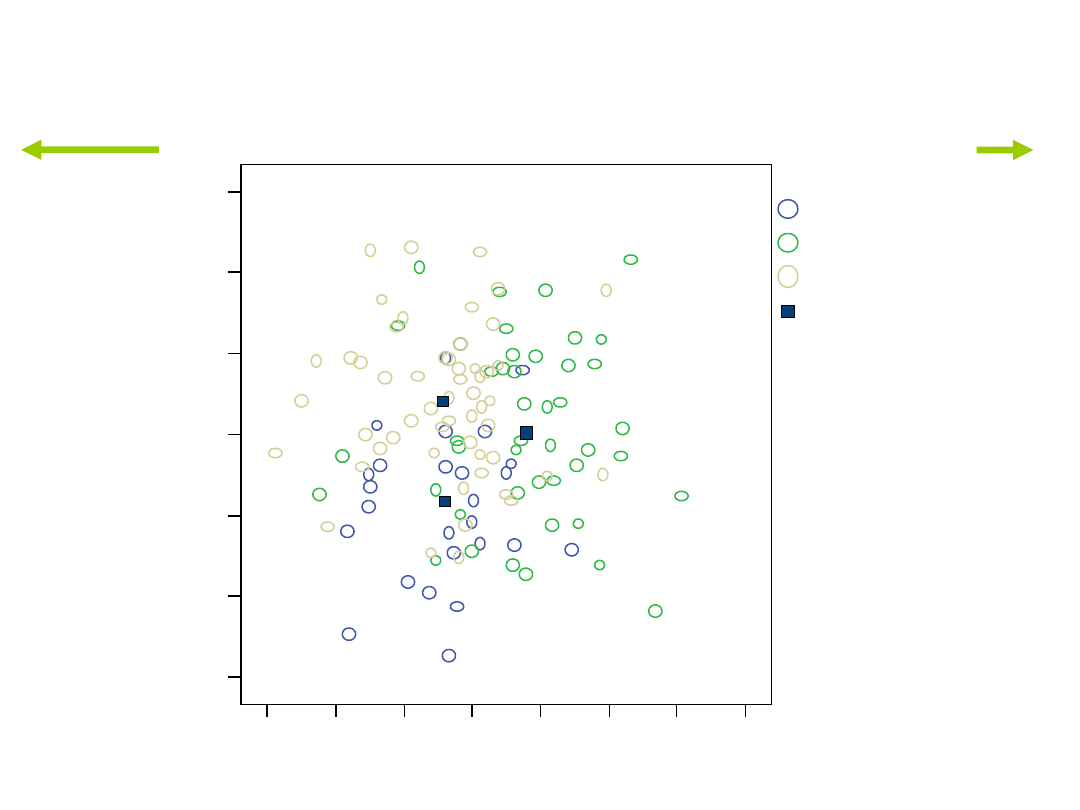
-3

-2

-1

0

1

2

3

4

Funkcja 1

-3

-2

-1

0

1

2

3

F

u

n

k

c

ja

2

słaby pracownik

indywidualna gwiazda

zespołowiec

pracownik

słaby pracownik
indywidualna

gwiazda

zespołowiec

Środek ciężkości
grupy

Kanoniczne funkcje dyskryminacyjne

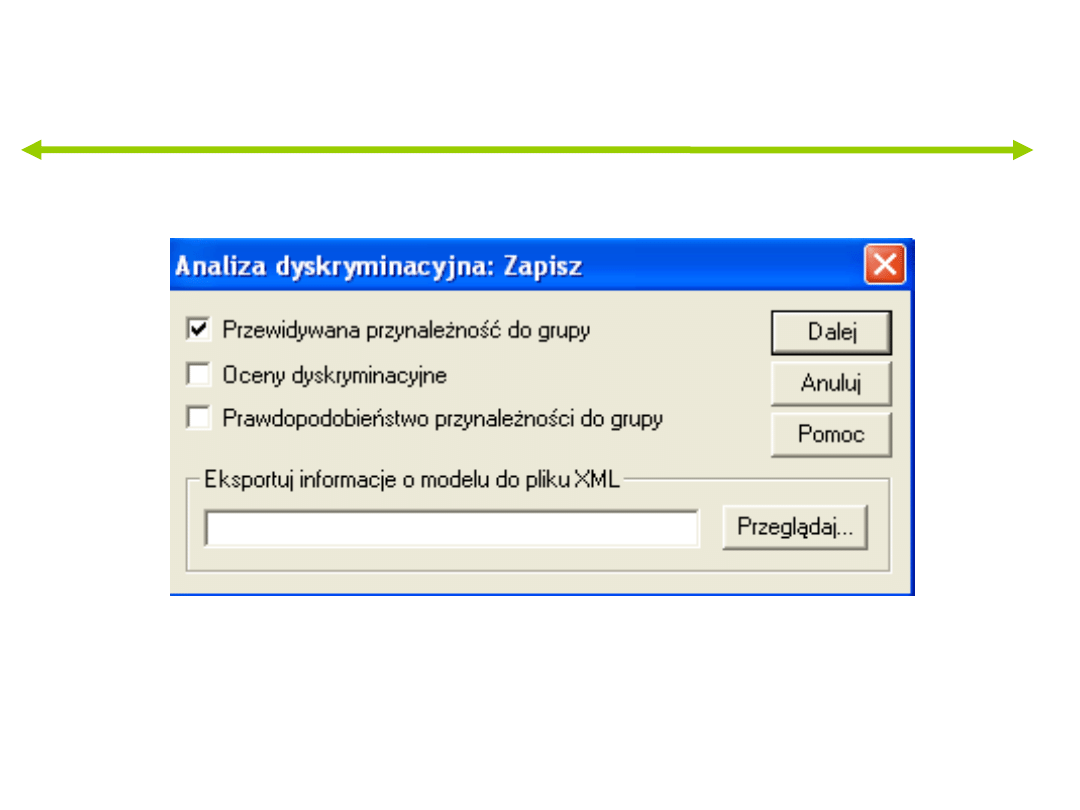
Wyniki klasyfikacji

b,c

12

5

10

27

4

27

12

43

4

7

43

54

44,4

18,5

37,0

100,0

9,3

62,8

27,9

100,0

7,4

13,0

79,6

100,0

10

5

12

27

5

25

13

43

5

7

42

54

37,0

18,5

44,4

100,0

11,6

58,1

30,2

100,0

9,3

13,0

77,8

100,0

pracownik
słaby pracownik

indywidualna gwiazda

zespołowiec

słaby pracownik

indywidualna gwiazda

zespołowiec

słaby pracownik

indywidualna gwiazda

zespołowiec

słaby pracownik

indywidualna gwiazda

zespołowiec

Liczebność

%

Liczebność

%

Oryginalne

Sprawdzane krzyżowo

a

słaby

pracownik

indywidualna

gwiazda

zespołowiec

Przewidywana przynależność do grupy

Ogółem

Sprawdzanie krzyżowe jest wykonywane jedynie dla analizowanych obserwacji. W procesie sprawdzania, każda
obserwacja jest klasyfikowana przez funkcję wykorzystującą wszystkie obserwacje, za wyjątkiem danej obserwacji.

a.

66,1% pierwotnie pogrupowanych obserwacji zostało prawidłowo sklasyfikowanych.

b.

62,1% obserwacji sprawdzanych krzyżowo zostało prawidłowo sklasyfikowanych.

c.

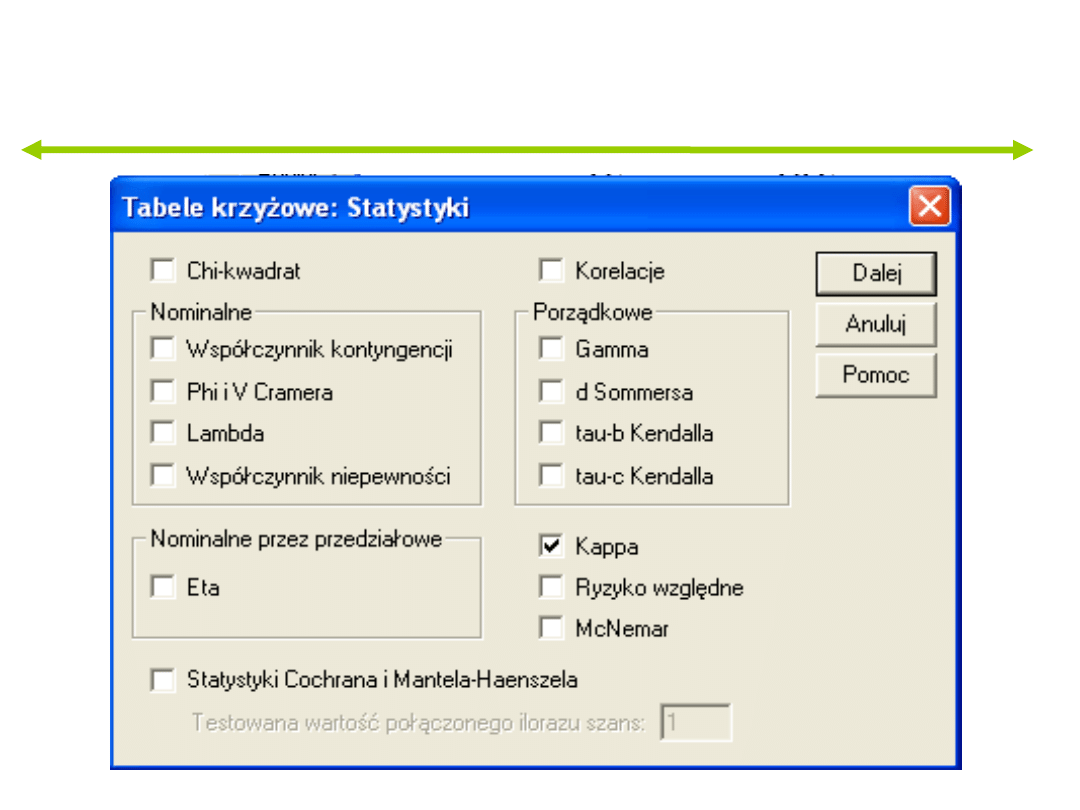
Miary symetryczne

,460

,066

7,074

,000

124

Kappa

Miara zgodności

N Ważnych obserwacji

Wartość

Asymptotyczny

błąd

standardowy

a

Przybliżone T

b

Istotność

przybliżona

Nie zakładając hipotezy zerowej.

a.

Użyto asymptotycznego błądu standardowego, przy założeniu hipotezy zerowej.

b.

Standardy prezentacji wyników



Podajemy dla wszystkich istotnych funkcji wartość λ, χ

2

i jej

istotność statystyczną



λ = 0,61; χ

2

(8, N=124) = 59,53; p<0,01



Wyniki wskazują, że predyktory różnicowały przynależność
do trzech grup.



Ponadto wyodrębniono druga funkcję, która niezależnie od
pierwszej pozwalała różnicować istotnie między grupami

• λ = 0,82; χ

2

(3, N=124) = 24,24; p<0,01



Prezentujemy tabele z korelacjami pomiędzy predyktorami i
funkcjami oraz wystandaryzowane współczynniki.



Prezentujemy i interpretujemy średnie wartości dla
poszczególnych funkcji w grupach.



Podajemy procent poprawnie zaklasyfikowanych uczestników
badania.

założenia



Rozkład normalny



rozkłady poszczególnych zmiennych są zbliżone do rozkładu
normalnego



Homogeniczność wariancji/kowariancji



macierze wariancji/kowariancji są homogeniczne w poszczególnych
grupach



najlepiej sprawdzić to za pomocą wykresów rozrzutu



Korelacje pomiędzy średnimi i wariancjami



średnie zmiennych w grupach nie mogą być skorelowane
wariancjami



pojawia się najczęściej jeżeli w jednej z grup istnieje kilka wyników
skrajnych, które zmieniają średni i wariancję.



Zmienne nie mogą być zupełnie redundantne



taka sytuacja może wystąpić jeżeli jedna ze zmiennych jest np.
wskaźnikiem sumarycznym wyciągniętym z trzech innych zmiennych
branych pod uwagę w analizie.

Podsumowanie



Analizę dyskryminacyjną używamy
jeżeli jeżeli chcemy:



znaleźć zmienne, które wyróżniają
„naturalnie” pojawiające się grupy,



klasyfikować przypadki do różnych grup z
trafnością lepszą niż przypadkowa.

koniec