Układy napędowe i ich sterowanie
Przekładnie planetarne
1
0
2
0
1
0
2
0
1
0
12
ω
ω
ω
ω
ω
ω
−
−
=
=
i
3. Przekładnie planetarne
3.1. Idea przekładni planetarnych .Wzór Willisa. Kinematyka przekładni.
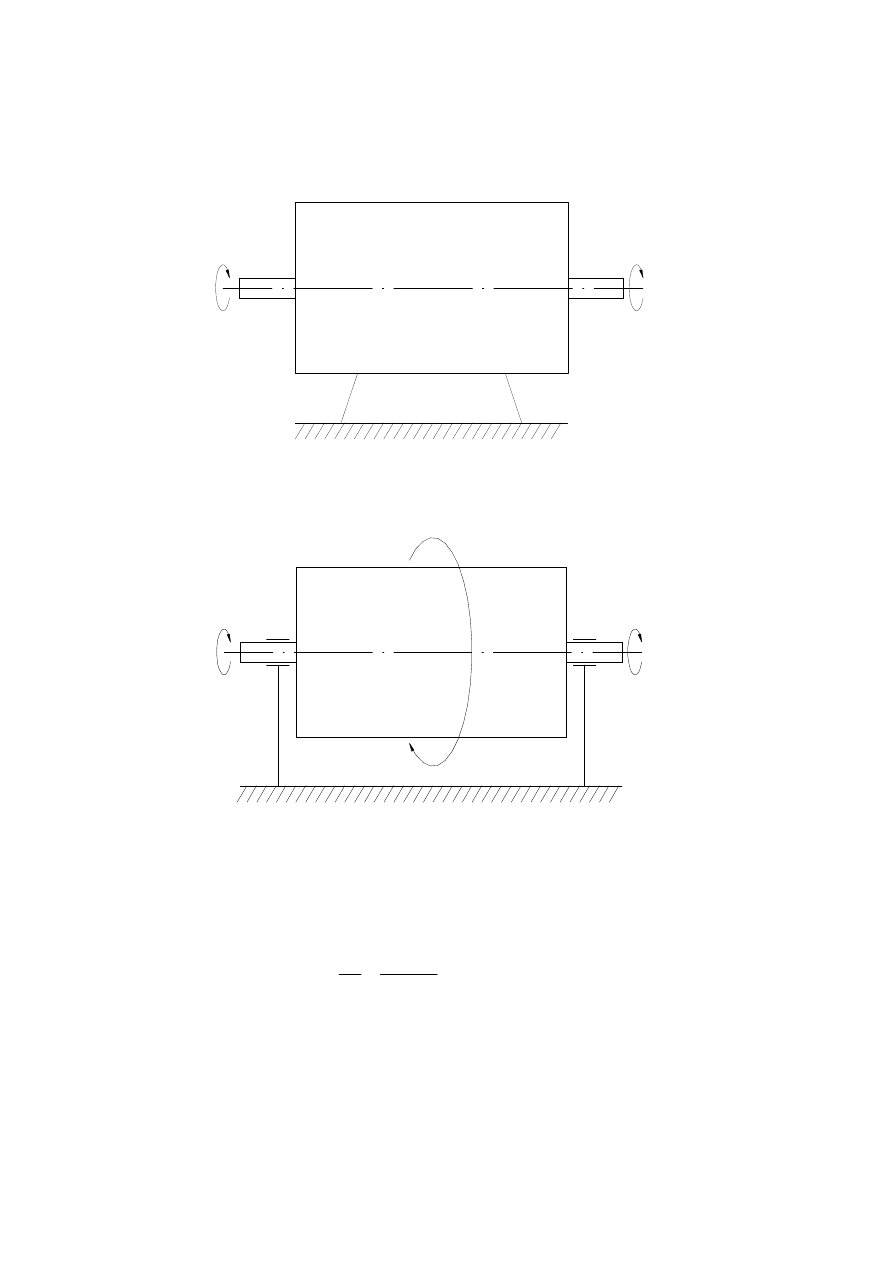
Przekładnia o osiach stałych (
ω
0
= 0):
Gdy prędkości kątowe
ω
1
,
ω
2
mają ten sam zwrot, to i > 0. W przeciwnym razie: i < 0.
Przekładnia o osiach wirujących (
ω
0
≠
0) – przekładnia planetarna:
ω
1
,
ω
2
,
ω
3
– prędkości kątowe względem nieruchomego układu odniesienia.
Prędkości względem ruchomego korpusu:
Zależność na przełożenie wewnętrzne przekładni (przy zatrzymanym korpusie):
- równanie Willisa.
Możliwe są trzy warianty uzyskania przekładni:
ω
0
= 0 przekładnia o osiach stałych;
ω
1
= 0 przekładnia planetarna;
ω
2
= 0 przekładnia planetarna.
Mechanizm opisany równaniem Willisa – mechanizm różnicowy (wszystkie 3 elementy są w
ruchu, i
12
0
może być i
12
0
< 0 ; i
12
0
>0).
0
2
0
2
0
1
0
1
ω
ω
ω
ω
ω
ω
−
=
−
=
ω
1
ω
2
ω
0
= 0
ω
2
ω
1
ω
0
Układy napędowe i ich sterowanie
Przekładnie planetarne
2
0
1
2
Przykłady szeregów planetarnych
0
0
1
2
2
1
0
12
=
−
=
=
ω
ω
ω
z
z
i
0
1
0
0
12
1
2
0
21
=
=
=
ω
ω
ω
i
i
0
12
1
0
2
01
2
1
1
0
i
i
−
=
=
=
ω
ω
ω
0
1
2
2
1
0

Układy napędowe i ich sterowanie
Przekładnie planetarne
3
0
12
2
10
0
1
0
0
1
0
2
0
1
0
12
0
1
2
10
2
1
1
0
i
i
i
i
−
=
−
=
−
−
=
−
−
=
=
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
(
)
0
12
0
12
0
12
1
02
0
12
0
12
1
02
0
12
1
02
0
12
1
02
2
0
2
0
0
2
0
0
2
0
1
0
12
2
0
1
02
1
1
1
1
1
1
1
0
i
i
i
i
i
i
i
i
i
i
i
i
i
−
=
−
=
=
−
⋅
−
=
−
−
−
=
−
−
=
−
−
=
=
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
0
12
0
2
1
20
1
1
1
0
i
i
−
=
=
=
ω
ω
ω
0
2
1
1
2
0
0
1
2
Układy napędowe i ich sterowanie
Przekładnie planetarne
4
Ogólnie:
L
KM
M
KL
M
LK
M
KL
i
i
i
i
−
=
=
1
1
1
2
0
12
1
2
0
12
z
z
i
z
z
i
−
=
=
0
12
0
21
0
12
1
02
0
12
2
01
0
12
1
20
0
12
2
10
1
1
1
1
1
1
1
1
1
i
i
i
i
i
i
i
i
i
i
=
−
=
−
=
−
=
−
=
1
2
0
z
1
z
2
1
2
0
z
1
z
2
Układy napędowe i ich sterowanie
Przekładnie planetarne
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
)
(
0
12
2
10
i
f
i
=
)
(
0
12
1
20
i
f
i
=
)
(
0
12
2
01
i
f
i
=
)
(
0
12
1
02
i
f
i
=
)
(
0
12
0
21
i
f
i
=
0
12
i
i
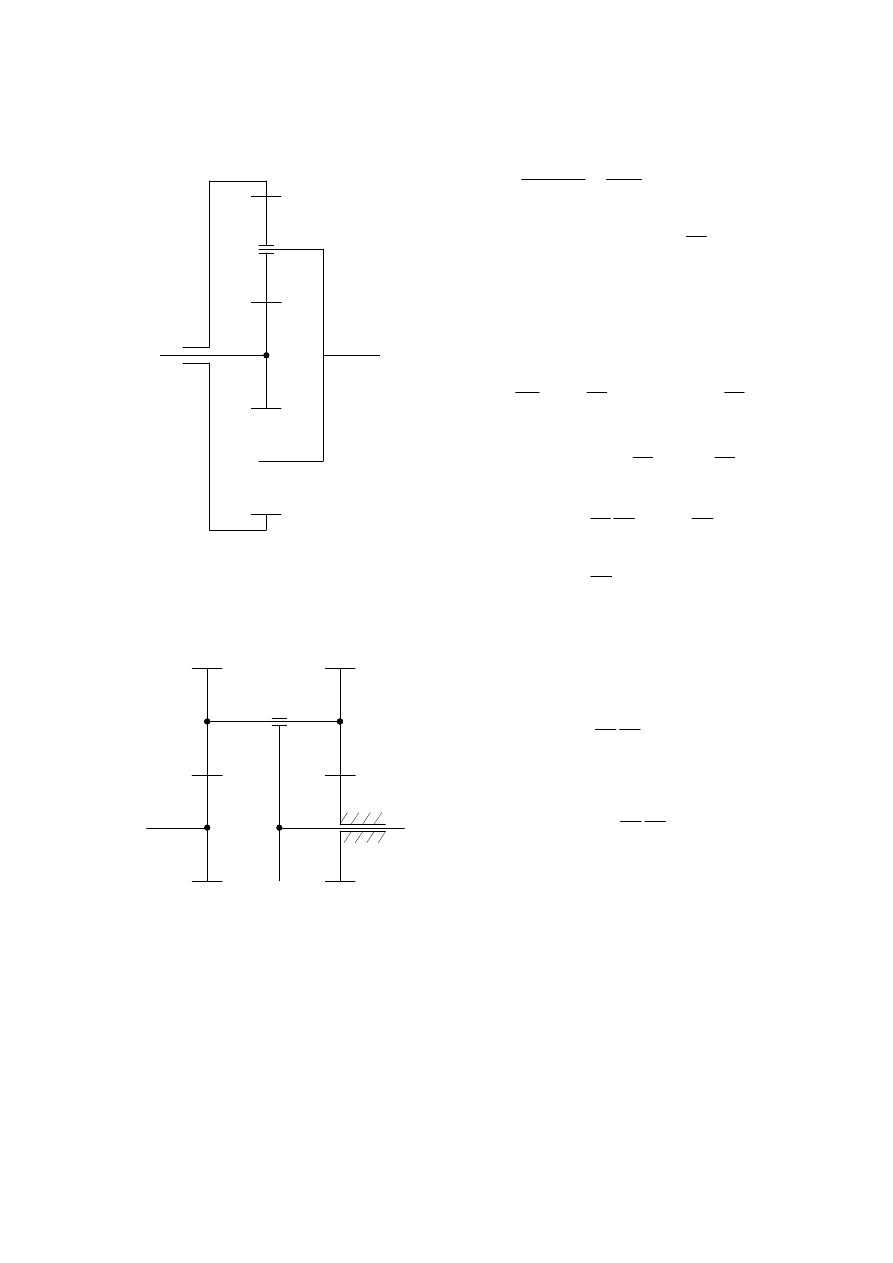
Układy napędowe i ich sterowanie
Przekładnie planetarne
6
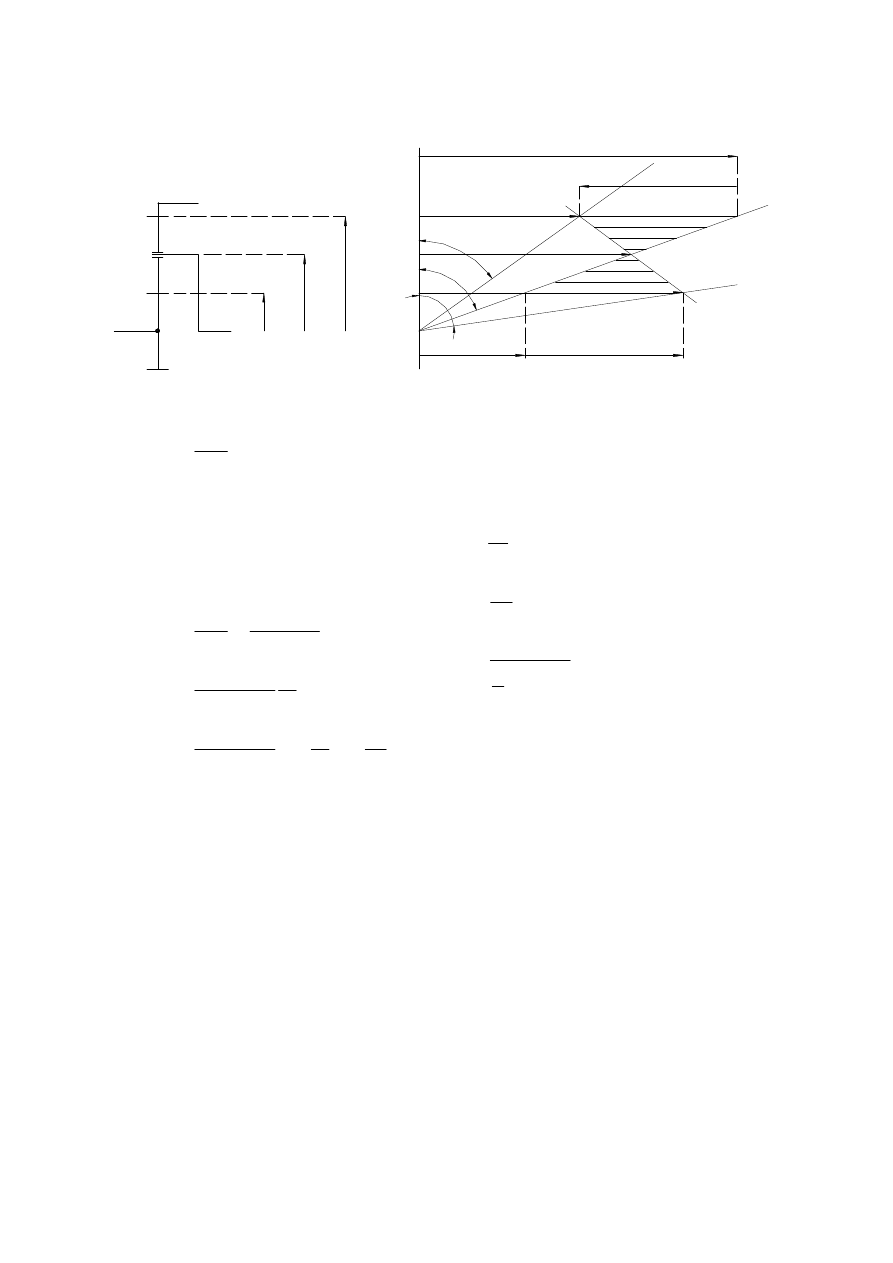
Prędkość względna satelity względem jego osi:
z
S
- liczba zębów satelity
ω
0
jest znane gdyż znamy:
Przekładnia o zazębieniu zewnętrznym:
(
)
0
.
2
1
0
1
0
1
0
0
1
=
−
−
=
−
−
=
−
−
ω
ω
ω
ω
ω
ω
ω
ω
ω
np
z
z
z
z
S
S
S
S
S
S
S
S
S
S
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
i
2
0
0
2
0
1
1
2
0
0
1
2
0
1
2
0
0
1
2
0
1
1
2
0
1
2
10
1
1
1
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−
=
−
−
=
−
=
−
−
+
−
=
−
+
=
+
=
=
1
2
4
3
3
10
0
13
3
10
1
2
4
3
0
13
1
1
z
z
z
z
i
i
i
z
z
z
z
i
−
=
−
=
=
ω
1
ω
0
ω
2
z
1
z
2
z
S
z
2
z
1
ω
1
ω
0
z
3
z
4
Układy napędowe i ich sterowanie
Przekładnie planetarne
7
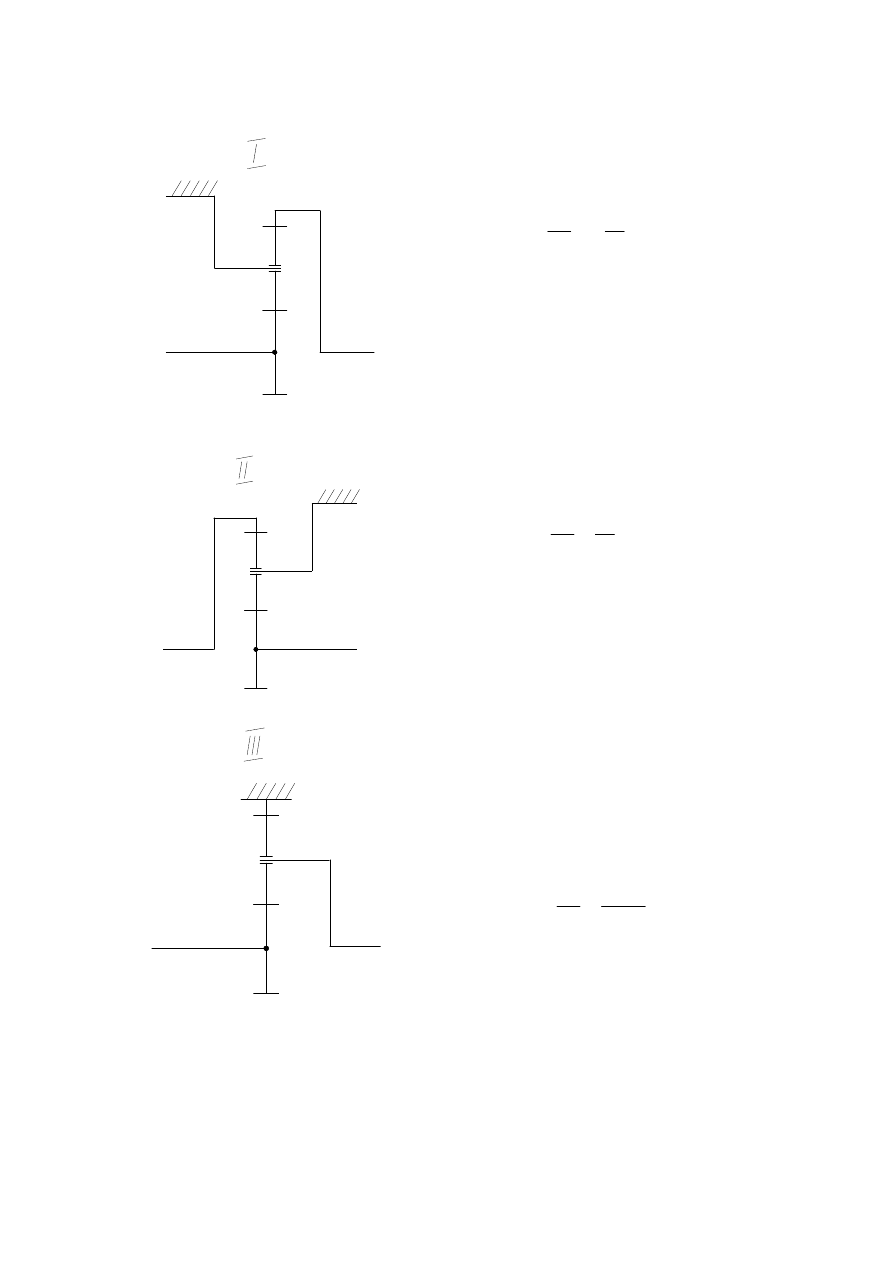
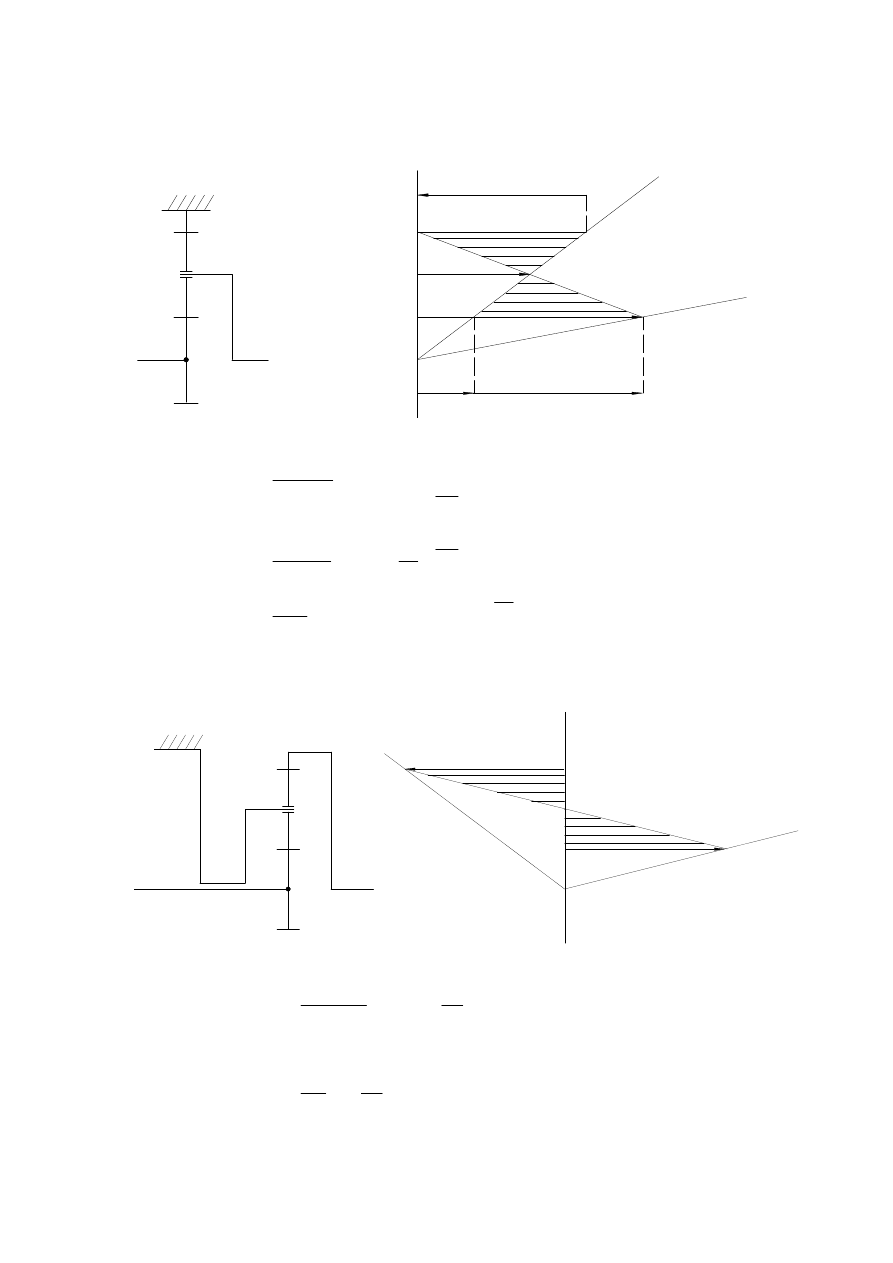
3.2. Metoda wykreślna rozwiązywania przekładni planetarnych. Plan prędkości.
0
2
1
0
0
2
2
2
2
1
1
1
1
0
12
1
2
2
1
0
2
0
1
2
1
0
2
0
1
2
2
1
1
2
1
2
0
2
1
0
1
2
2
2
1
1
1
1
2
tg
)
(
2
1
tg
tg
)
(
)
(
1
)
(
)
(
1
1
α
ω
α
ω
α
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
=
+
=
=
=
=
=
=
−
=
−
=
−
−
−
=
−
−
−
=
−
−
=
=
=
−
=
−
=
−
=
r
r
V
r
V
r
V
i
z
z
r
r
r
r
V
V
V
V
V
V
r
V
r
V
V
V
V
V
V
V
V
V
U
U
W
W
U
U
U
W
U
W
W
W
2
z
2
1
z
1
0
r
1
r
0
r
2
v
u1
v
w1
v
u2
v
u
v
2
v
1
v
w2
ω
2
ω
1
ω
0
α
1
α
0
α
2
Układy napędowe i ich sterowanie
Przekładnie planetarne
8
Elementarne przykłady szeregów planetarnych stosowanych
w układach napędowych maszyn roboczych
---------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------
1
2
2
10
2
10
0
1
0
12
0
1
0
12
0
1
1
2
0
12
0
0
1
2
0
12
0
2
0
1
1
1
1
0
z
z
i
i
i
i
z
z
i
i
+
=
=
−
=
=
+
−
−
=
=
−
−
=
=
−
−
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
0
0
0
2
0
2
1
0
1
1
2
2
1
0
1
2
0
12
0
2
0
1
=
=
=
=
−
=
=
−
=
=
−
−
r
V
r
V
z
z
z
z
i
U
U
ω
ω
ω
ω
ω
ω
ω
ω
ω
1
z
1
0
z
2
ω
0
ω
1
ω
2
= 0
v
2
= 0
v
w2
v
u
v
1
v
u1
v
w1
1
z
1
2
0
z
2
v
2
= v
w2
v
1
= v
w1
v
u
= 0
ω
0
= 0
ω
1
ω
2
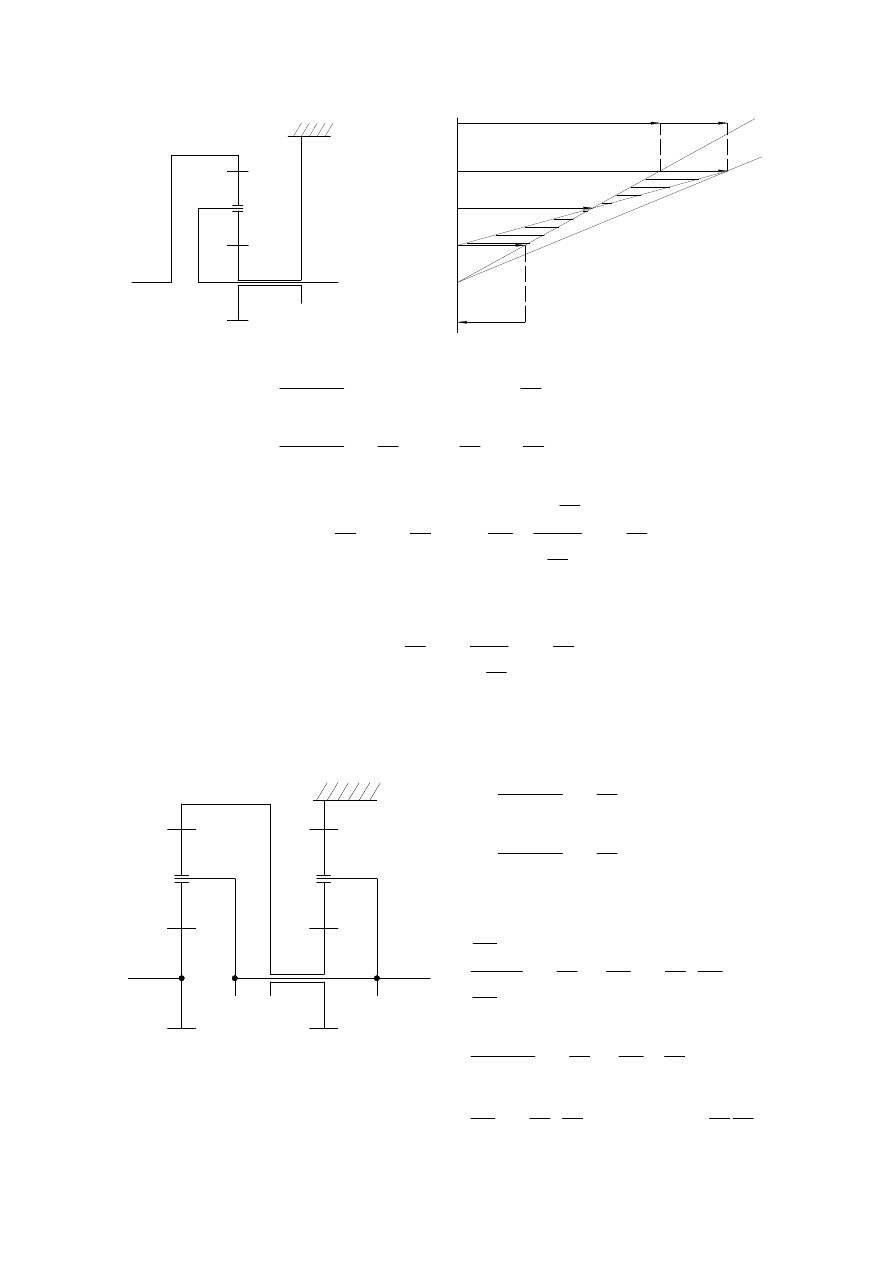
Układy napędowe i ich sterowanie
Przekładnie planetarne
9
---------------------------------------------------------------------------------------------------------------------
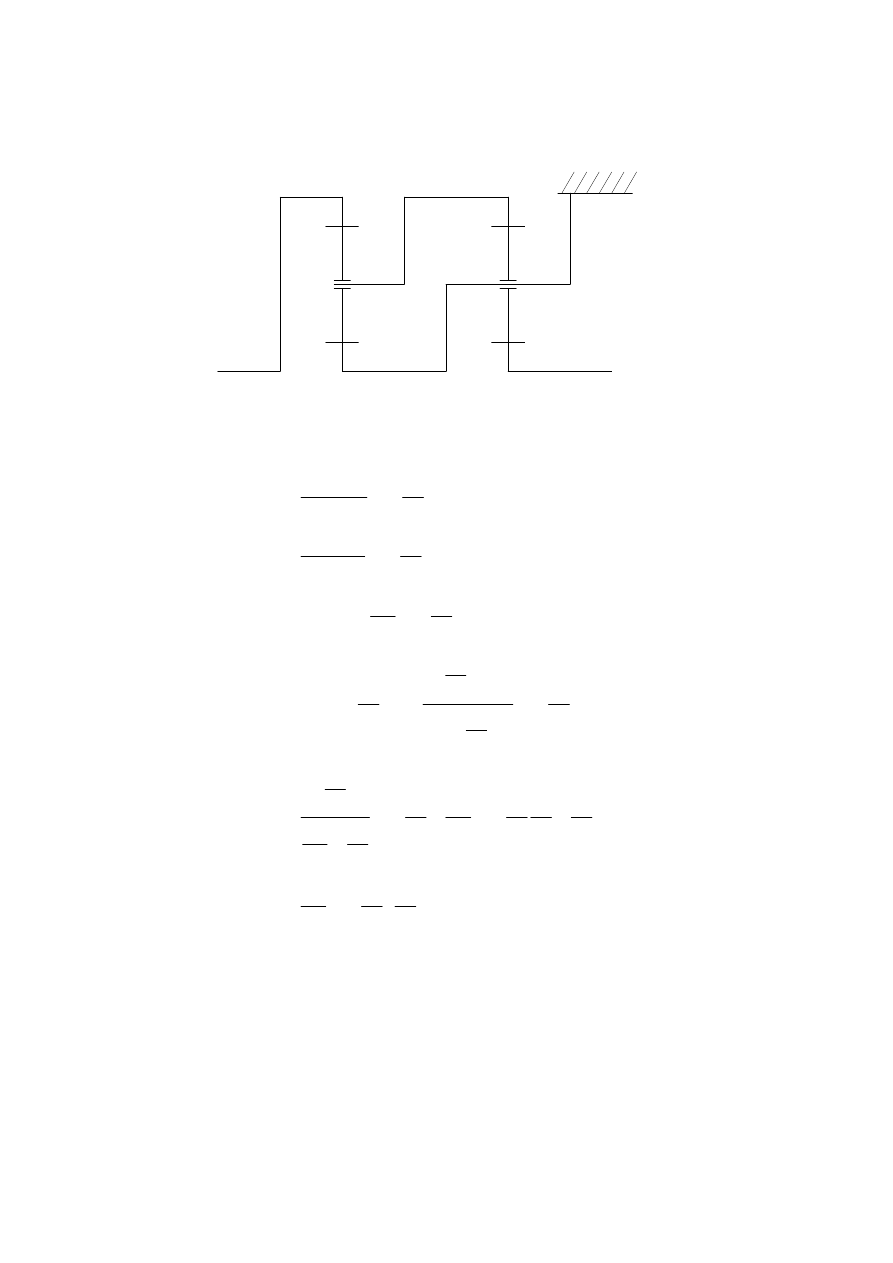
Przykład I
3
4
1
2
3
4
1
2
0
1
3
4
0
2
3
4
0
0
2
0
2
1
2
0
1
1
2
0
2
0
1
4
3
2
10
3
4
0
4
0
3
1
2
0
2
0
1
1
1
1
1
1
1
1
1
1
0
?
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
i
z
z
z
z
−
=
+
−
+
−
=
+
=
⇒
−
=
−
−
+
−
−
=
⇒
−
=
−
−
=
=
=
−
=
−
−
−
=
−
−
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
1
ω
0
z
2
z
1
z
4
z
3
z
1
z
2
1
2
0
ω
1
= 0
ω
1
= 0
ω
2
ω
0
v
1
= 0
v
u
v
u2
v
w2
v
w1
v
u1
v
2
2
1
1
2
0
12
0
21
1
20
2
1
1
2
1
2
0
2
0
12
1
2
2
1
2
0
0
1
2
2
1
2
0
1
2
0
2
0
1
2
0
12
1
0
12
0
2
0
1
1
1
1
1
1
1
lub
1
1
1
0
z
z
z
z
i
i
i
z
z
z
z
z
z
i
z
z
z
z
z
z
z
z
z
z
z
z
i
i
+
=
−
−
=
−
=
−
=
+
=
+
=
=
=
+
−
=
−
=
−
−
−
=
=
=
−
−
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
Układy napędowe i ich sterowanie
Przekładnie planetarne
10
Przykład II
+
−
=
−
−
=
−
=
+
−
=
+
−
=
−
=
=
−
=
−
−
−
=
−
−
1
0
2
1
4
3
3
2
4
3
4
3
2
1
3
2
1
2
4
3
3
2
4
3
1
2
3
4
3
2
3
4
3
3
4
3
4
3
4
4
3
1
3
4
1
4
1
3
1
2
4
2
4
1
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
z
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
z
1
z
2
z
4
z
3
ω
2
ω
3
Układy napędowe i ich sterowanie
Przekładnie planetarne
11
3.3. Dynamika szeregu planetarnego
3.3.1. Wprowadzenie
N
A
– moc wejściowa
N
B
– moc wyjściowa
3.3.2. Przekładnie o osiach stałych
a)
B
B
N
A
A
A
B
A
B
A
B
A
M
N
M
N
M
M
M
M
ω
ω
ω
ω
=
=
−
=
⇒
=
+
=
0
N
A
N
B
ω
Α
(+)
M
A
(+)
ω
Β
(+)
(
−
)
M
B
P
2
P
1
ω
1
(+)
(−)
ω
2
M
1
(+)
M
2
(+)
N
1
N
2
N
1
(+)
N
2
(
−
)
η
Ζ
r
2
r
1

Układy napędowe i ich sterowanie
Przekładnie planetarne
12
b)
(
)
−
−
=
−
−
=
−
=
+
−
=
=
+
+
⇒
=
−
=
−
=
−
=
−
=
−
=
=
=
−
=
=
∑
12
2
0
1
12
1
0
2
12
2
0
1
12
1
0
0
2
1
1
12
2
12
2
1
12
1
2
1
1
2
2
1
2
2
2
2
1
1
1
2
1
2
1
12
1
1
1
0
0
1
1
i
M
M
i
M
M
M
i
M
M
M
i
M
M
M
M
M
M
M
i
M
i
M
M
i
M
M
M
M
N
N
M
N
M
N
z
z
i
Z
Z
Z
Z
Z
Z
Z
η
η
η
η
η
η
ω
ω
η
ω
ω
ω
ω
ω
1
(+)
N
1
N
1
(
−
)
N
2
(+)
N
2
(−)
ω
2
(
−)
M
1
r
1
η
Ζ
P
2
r
2
P
1
(
−
)
M
2
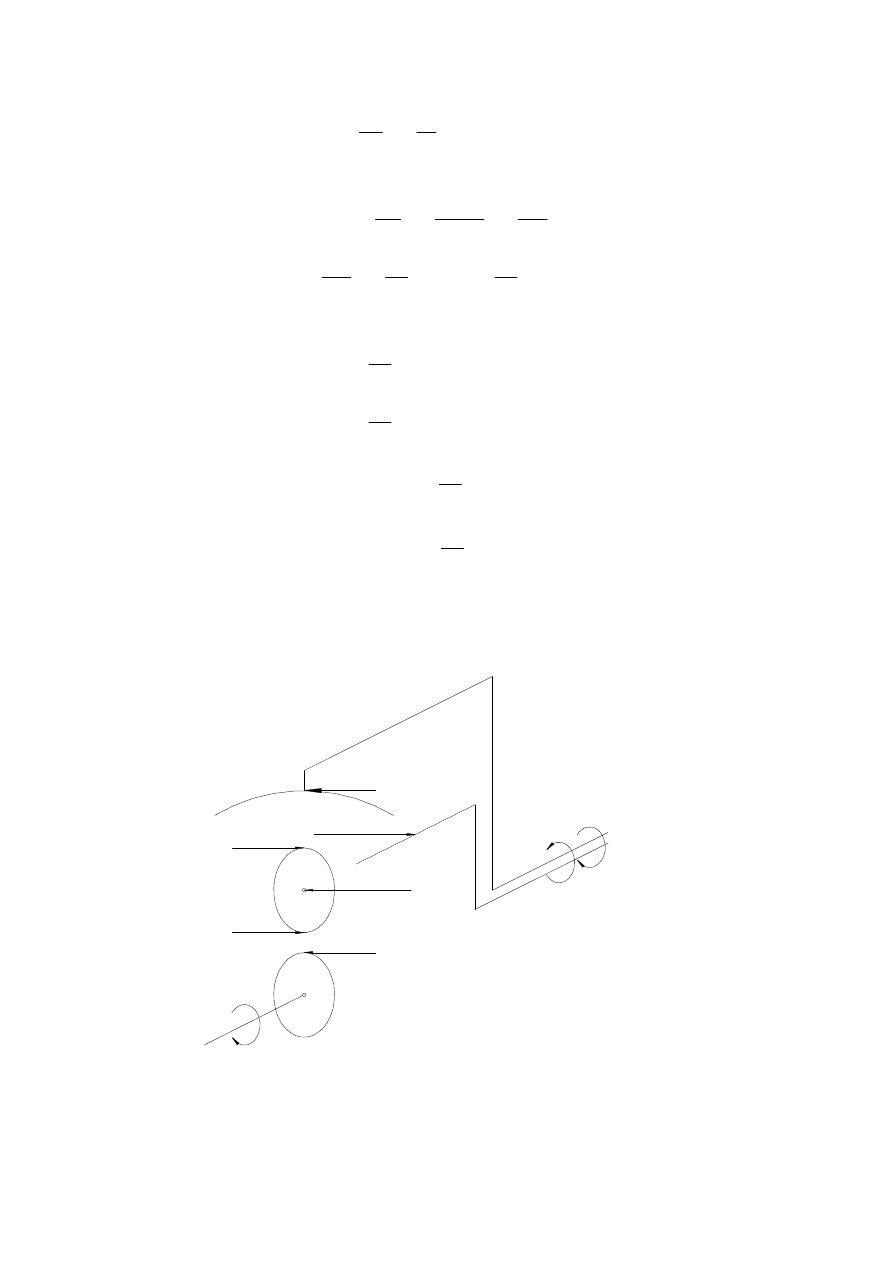
Układy napędowe i ich sterowanie
Przekładnie planetarne
13
3.3.3. Równowaga elementów szeregu planetarnego
Założenie:
η
=1
−
−
=
−
−
=
−
=
−
=
−
−
=
−
=
⇒
−
=
−
=
−
=
−
=
=
=
−
=
=
12
2
0
12
1
0
1
1
12
0
2
2
12
0
2
1
0
2
12
1
12
2
1
12
2
1
2
2
1
1
2
1
2
2
2
1
1
1
2
1
2
1
12
1
1
i
M
M
i
M
M
M
M
i
M
M
M
i
M
M
M
M
M
i
M
i
M
M
i
M
M
M
M
N
N
M
N
M
N
z
z
i
Z
Z
Z
Z
Z
Z
Z
η
η
η
η
η
η
ω
ω
η
ω
ω
ω
ω
P
S1
P
1
M
1
P
S0
P
S2
P
2
M
0
M
2
P
0

Układy napędowe i ich sterowanie
Przekładnie planetarne
14
Warunki równowagi:
lub:
(
)
0
12
1
0
2
1
1
0
1
1
1
2
1
0
1
0
0
0
0
0
12
1
2
0
12
1
2
1
2
1
2
1
2
1
1
1
1
2
2
2
0
0
2
1
2
1
0
0
0
2
2
2
1
1
1
1
2
2
2
2
1
2
1
0
0
0
i
M
M
r
r
M
M
r
M
P
r
r
r
P
P
r
P
M
i
M
M
i
z
z
r
r
r
r
M
M
r
M
P
P
P
r
P
M
P
P
P
P
P
P
r
P
M
r
P
M
r
P
M
S
S
S
−
=
+
=
−
=
+
=
−
=
−
=
−
=
−
=
=
=
−
=
=
−
=
=
−
=
−
=
−
=
=
=
+
=
+
=
+
( )
0
12
1
0
1
0
12
1
0
1
0
12
2
2
1
0
0
2
1
1
0
i
M
M
M
i
M
M
M
i
M
M
M
M
M
M
M
−
−
=
+
−
=
−
=
−
−
=
=
+
+
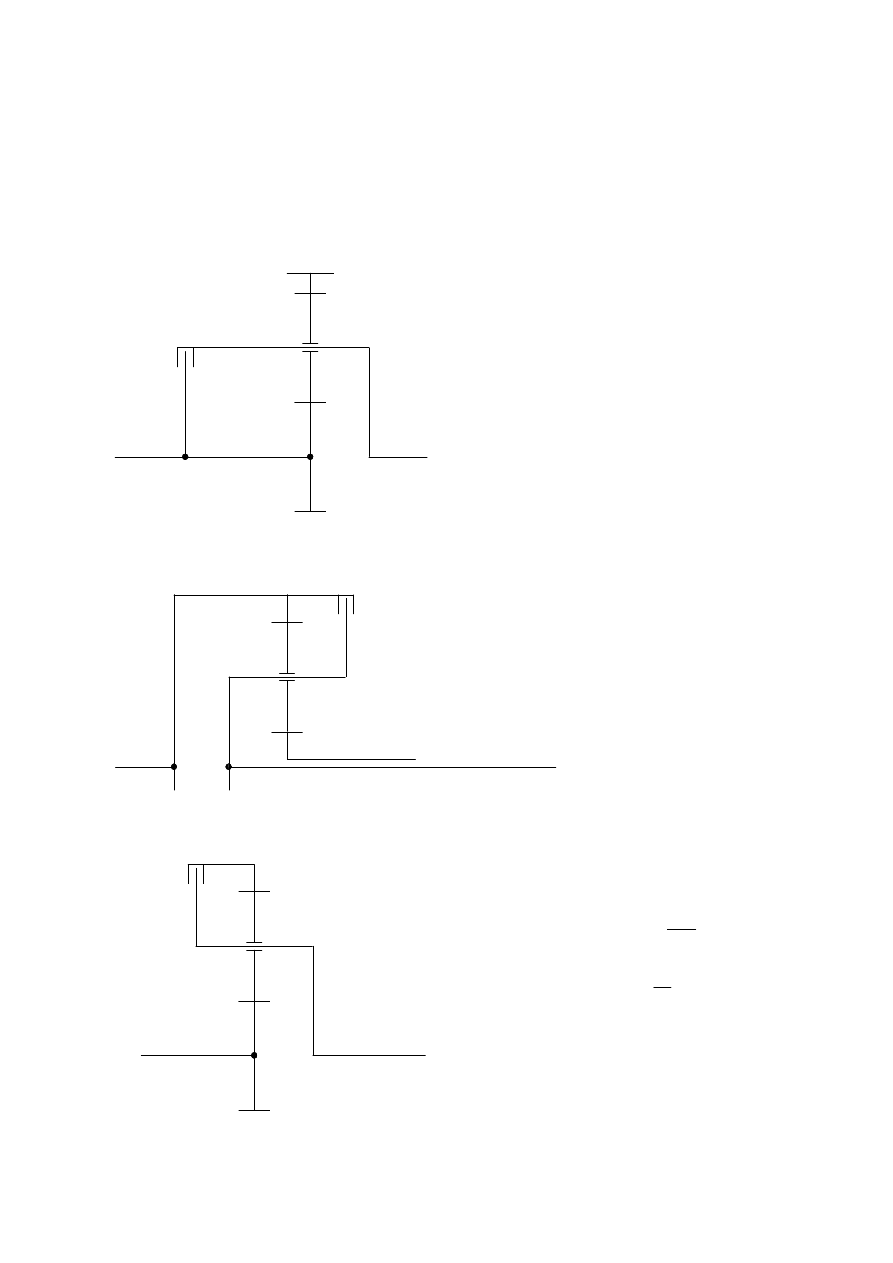
Układy napędowe i ich sterowanie
Przekładnie planetarne
15
3.3.4. Momenty na hamulcach
3.3.5. Momenty na sprzęgłach
a)
b)
c)
( )
0
12
1
0
0
1
0
12
2
2
1
1
1
0
0
0
i
M
M
M
M
i
M
M
M
M
H
H
H
−
=
−
=
⇒
=
=
−
=
⇒
=
−
=
⇒
=
ω
ω
ω
s
B
A
M
M
M
M
M
=
=
=
=
0
0
2
1
s
B
A
M
M
M
=
=
1
0
12
1
0
12
1
2
1
1
1
1
2
2
2
2
M
i
M
M
i
r
r
M
M
r
M
P
P
r
P
M
M
S
s
s
−
=
−
=
=
−
=
=
−
=
=
z
2
z
1
M
B
M
A
M
S
1
M
S
z
1
z
2
M
1
= 0
M
0
= M
B
M
A
z
2
z
1
M
0
= M
B
M
A
= M
1
M
S
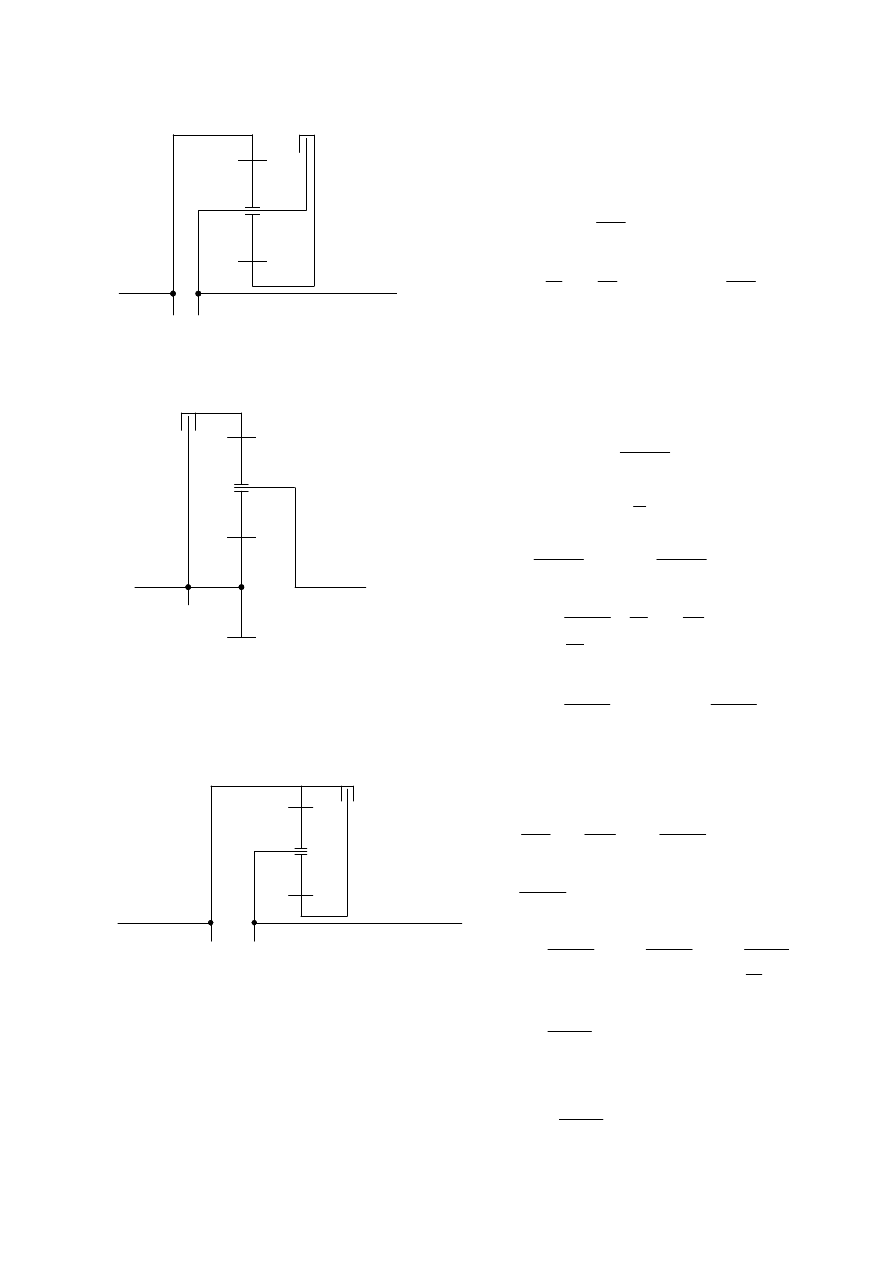
Układy napędowe i ich sterowanie
Przekładnie planetarne
16
d)
e)
f)
0
12
2
2
0
12
2
1
2
1
2
2
2
1
2
2
2
2
1
1
1
1
2
1
i
M
M
M
i
r
r
M
M
r
M
P
P
P
r
P
M
r
P
M
M
M
M
M
M
M
s
s
s
B
A
−
=
−
=
=
−
=
=
−
=
−
=
=
=
=
1
1
1
1
1
2
2
1
2
2
0
12
0
12
0
12
0
12
2
0
12
2
1
2
1
2
2
1
2
2
1
0
0
2
2
0
2
1
0
0
0
2
2
2
2
−
=
−
−
=
−
=
+
−
=
+
−
=
+
−
=
−
=
⇒
−
=
+
−
=
−
=
−
=
−
=
=
i
i
M
M
i
i
M
M
i
r
r
r
r
M
M
r
r
M
P
r
r
M
P
P
P
P
P
r
r
P
r
P
M
r
P
M
M
M
M
M
A
s
B
B
B
B
B
B
A
s
M
A
M
B
M
S
z
1
0
12
0
12
2
1
2
1
1
2
1
1
2
1
1
2
1
0
0
0
0
1
0
1
1
1
1
1
1
1
1
1
1
2
2
i
M
M
M
M
i
M
M
r
r
M
r
r
r
M
r
r
r
M
M
r
r
M
P
r
r
M
r
M
r
M
P
P
P
r
P
M
M
M
A
s
A
B
B
s
B
B
B
s
B
B
B
s
−
−
=
−
=
−
=
+
=
+
=
+
=
+
−
=
+
−
=
−
=
−
=
−
=
−
=
=
M
A
z
2
z
1
M
B
M
S
M
A
= M
2
z
1
z
2
M
S
M
B
= M
0
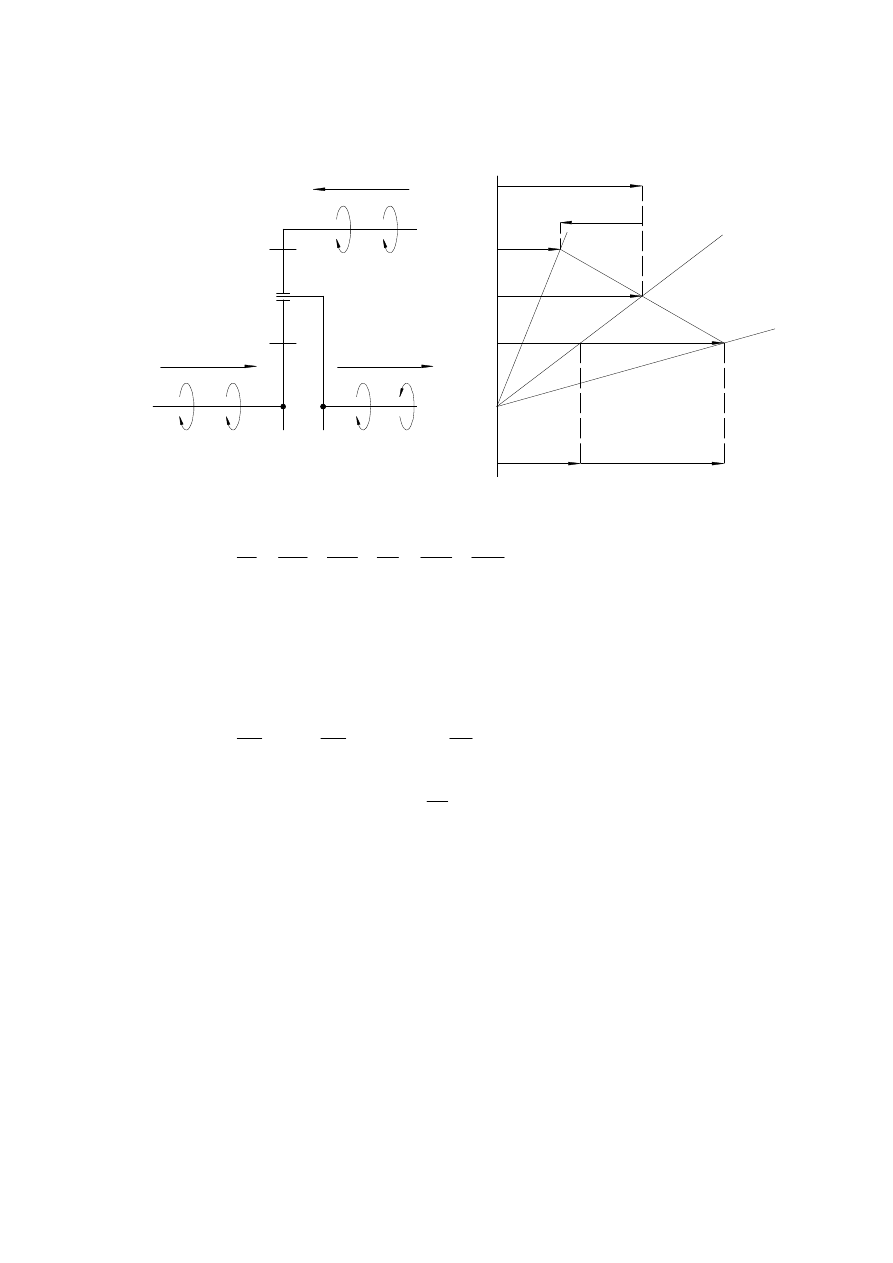
Układy napędowe i ich sterowanie
Przekładnie planetarne
17
3.4. Przepływ mocy przez przekładnię planetarną. Sprawność przekładni.
3.4.1. Przepływ mocy przez szereg planetarny
(
)
(
)
−
=
−
=
=
=
=
+
=
+
=
=
−
−
=
−
=
=
+
+
+
=
+
=
+
=
+
=
+
=
+
=
10
1
0
1
1
10
1
0
20
0
2
10
0
1
1
1
1
0
1
1
1
1
0
12
1
0
1
0
12
2
0
2
1
2
0
2
1
0
1
2
2
2
2
2
2
1
1
1
1
1
1
2
2
2
1
1
1
1
1
1
0
i
i
i
i
N
N
M
M
N
i
M
M
M
i
M
M
M
M
r
V
r
V
r
V
r
V
r
V
r
V
V
V
V
V
V
V
W
W
U
W
W
W
W
U
W
U
W
U
W
U
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
(
)
(
)
−
=
−
=
=
=
=
+
=
+
=
=
−
−
=
−
=
=
+
+
+
=
+
=
+
=
+
=
+
=
+
=
10
1
0
1
1
10
1
0
20
0
2
10
0
1
1
1
1
0
1
1
1
1
0
12
1
0
1
0
12
2
0
2
1
2
0
2
1
0
1
2
2
2
2
2
2
1
1
1
1
1
1
2
2
2
1
1
1
1
1
1
0
i
i
i
i
N
N
M
M
N
i
M
M
M
i
M
M
M
M
r
V
r
V
r
V
r
V
r
V
r
V
V
V
V
V
V
V
W
W
U
W
W
W
W
U
W
U
W
U
W
U
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
N
1
M
1
ω
1
N
0
N
2
ω
2
M
2
ω
0
M
0
v
u1
v
w1
v
u2
v
w2
ω
2
ω
0
ω
1
v
1
v
2
v
0

Układy napędowe i ich sterowanie
Przekładnie planetarne
18
Ogólnie:
(
)
−
=
−
=
=
=
=
=
−
=
−
=
−
=
=
+
=
=
−
=
−
=
=
=
=
=
20
2
20
12
2
2
2
2
20
2
20
2
2
0
2
2
20
2
20
2
2
0
2
2
20
2
0
2
0
2
2
2
2
10
1
10
1
1
1
1
1
10
1
10
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
i
N
i
M
M
N
i
N
i
M
M
N
i
i
i
M
M
N
i
N
i
M
M
N
i
N
i
M
M
N
W
W
U
W
W
W
W
U
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−
=
=
0
0
1
1
1
X
X
WX
X
X
UX
i
N
N
i
N
N
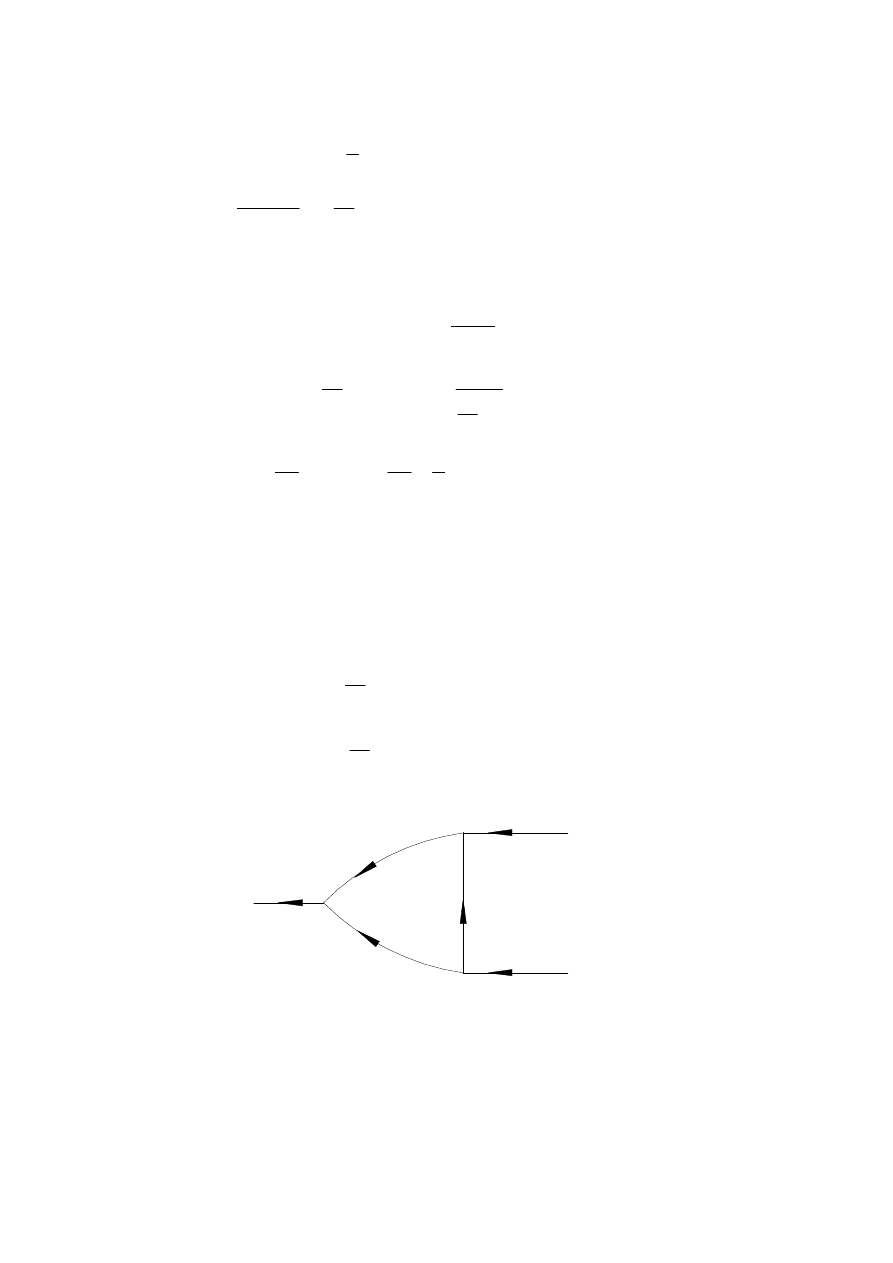
Układy napędowe i ich sterowanie
Przekładnie planetarne
19
Przykład 1
( )
25
,
0
1
1
25
,
0
1
1
75
,
0
25
,
0
1
5
,
0
5
,
0
3
2
2
75
,
0
1
1
1
1
25
,
0
1
1
75
,
0
25
,
0
1
3
3
1
3
2
2
0
12
2
2
0
12
1
1
0
2
2
0
1
1
0
0
0
2
2
2
1
1
1
0
2
20
0
1
10
0
12
0
2
0
12
2
0
0
12
0
1
0
12
1
0
2
1
0
1
2
0
2
0
1
0
12
0
2
1
−
=
−
=
=
−
=
=
=
=
=
−
=
=
=
=
=
=
=
=
=
=
=
−
−
=
−
=
=
−
−
=
−
−
=
=
=
−
=
−
=
−
=
−
−
−
=
⇒
=
=
=
i
N
N
i
N
N
M
N
M
N
M
N
M
N
M
N
i
i
i
M
M
i
M
M
i
M
M
i
M
M
M
M
M
gdy
z
z
i
W
W
U
U
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
N
2
=0,5
N
W1
= -N
W2
=0,25
N
1
=0,5
N
o
= -1
N
U1
=0,25
N
U2
=0,75

Układy napędowe i ich sterowanie
Przekładnie planetarne
20
Przykład 2
1
10
0
12
1
0
2
2
2
2
1
10
0
12
1
10
1
1
0
12
0
2
2
2
1
10
1
1
1
10
1
1
0
12
0
2
20
0
12
0
1
10
1
2
1
0
12
2
2
2
2
0
12
2
4
3
4
3
0
4
3
1
1
4
1
3
4
1
1
4
1
3
0
3
0
N
i
i
N
M
M
N
N
i
i
N
i
M
i
M
N
N
N
i
N
N
N
i
N
N
i
i
i
i
M
M
M
i
M
M
N
i
W
W
U
W
U
−
=
=
=
=
=
−
=
=
=
=
=
−
=
=
=
=
−
=
=
=
−
=
=
=
−
=
=
=
−
=
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
1
0
z
2
z
1

Układy napędowe i ich sterowanie
Przekładnie planetarne
21
Przykład 3
1
10
0
12
1
0
2
2
2
2
1
10
0
12
1
10
1
1
0
12
0
2
2
1
10
1
1
1
10
1
1
0
12
10
0
12
2
2
3
2
3
2
3
1
1
2
1
2
1
3
0
N
i
i
N
M
M
N
N
i
i
N
i
M
i
M
N
N
i
N
N
N
i
N
N
i
i
i
W
W
U
W
U
−
=
=
=
=
=
−
=
=
=
=
−
=
−
=
=
−
=
−
=
=
=
ω
ω
ω
ω
ω
N
2
=0
N
W1
=0,75N
1
= -N
W2
N
o
= -N
1
N
1
N
U1
=0,25N
1
N
U2
=0,75N
1
z
1
N
1
z
2
z
S2
z
S1
N
0
=
−
N
1
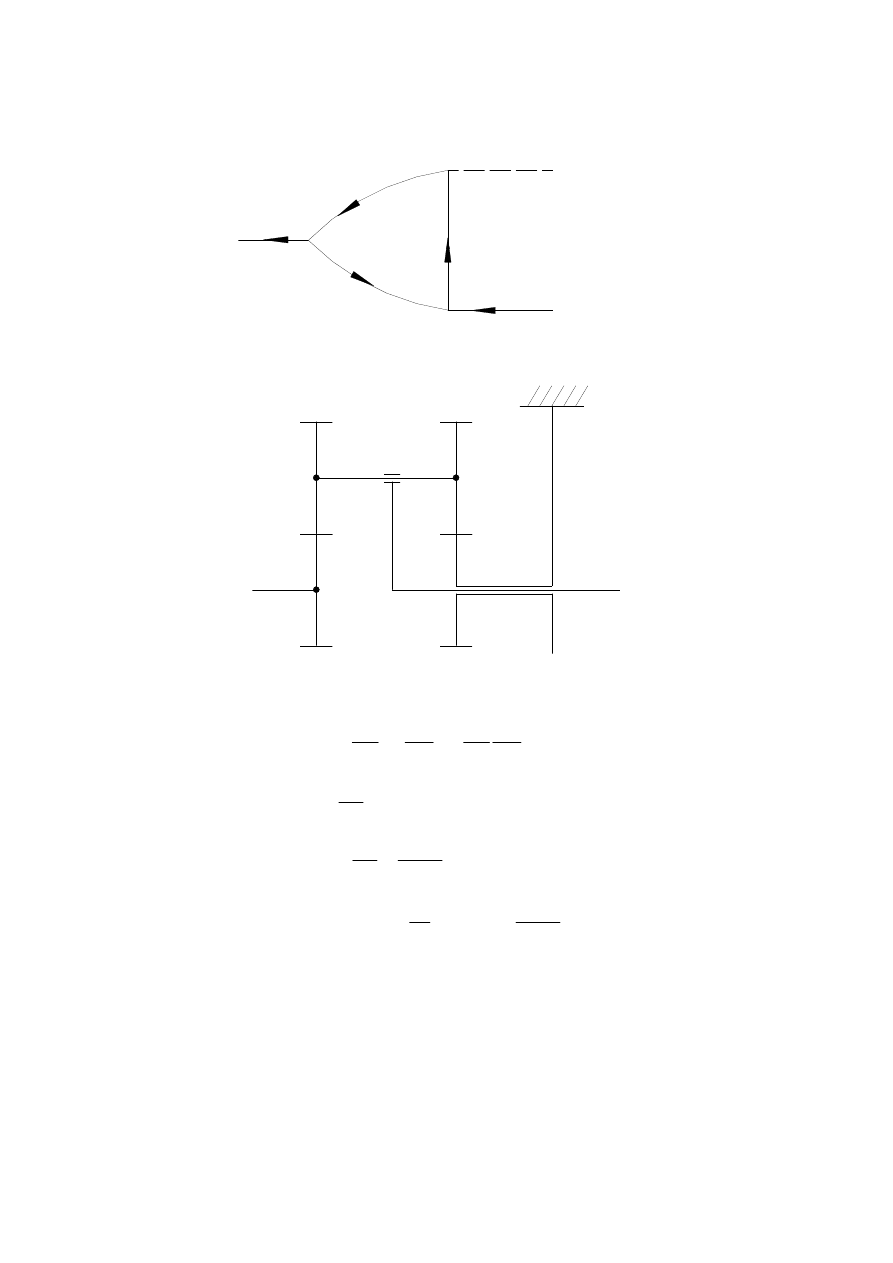
Układy napędowe i ich sterowanie
Przekładnie planetarne
22
Można też i
12
0
> 0 uzyskać w inny sposób, np.:
∞
≤
≤
≤
≤
∞
−
∞
≤
≤
−∞
≤
≤
∞
≤
≤
≤
≤
−
−
=
−
=
−
=
=
−
=
=
=
−
−
=
=
1
1
1
0
12
1
1
1
0
12
0
12
1
10
1
1
1
0
12
10
1
1
0
12
0
1
10
2
2
1
1
2
2
1
1
0
12
2
0
10
0
1
0
1
1
1
1
1
1
1
1
0
W
U
W
U
W
U
S
S
S
S
N
N
N
i
N
N
N
i
gdy
i
N
i
N
N
N
i
i
N
N
i
i
z
z
z
z
z
z
z
z
i
ω
ω
ω
N
2
=0
N
W1
=1,5N
1
= -N
W2
N
o
= -N
1
N
1
N
U1
= -0,5N
1
N
U2
= 1,5N
1
z
1
z
S1
ω
1
z
2
ω
0
z
S2
ω
2
= 0
Układy napędowe i ich sterowanie
Przekładnie planetarne
23
0
12
i
1
W
N
1
W
N
0
N
1
U
N
1
U
N
1
N
1
Układy napędowe i ich sterowanie
Przekładnie planetarne
24
Przykład 4
(
)
(
)
2
20
2
0
12
2
0
1
1
1
2
20
12
0
12
2
0
1
1
2
20
2
2
0
2
2
2
2
20
2
2
0
12
20
0
12
10
2
0
12
2
1
1
0
12
2
1
1
1
0
12
1
4
1
0
4
1
4
1
1
1
4
3
3
4
1
1
4
1
3
1
0
3
0
N
i
i
M
M
N
N
i
i
M
M
N
N
i
M
M
N
N
i
N
N
i
i
i
i
M
i
M
M
M
i
M
M
N
i
W
U
W
U
−
=
−
−
=
−
=
=
−
=
=
=
−
=
−
=
=
=
=
−
=
=
−
=
=
−
−
=
⇒
−
=
=
=
−
=
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
N
W2
= -N
W1
=0,25N
2
N
o
= -N
2
N
1
=0
N
2
N
U1
= 0,25N
2
N
U2
= 0,75N
2
z
1
z
2
ω
1
= 0
0
2
Układy napędowe i ich sterowanie
Przekładnie planetarne
25
Przykład 5
(
)
(
)
1
1
1
0
12
1
1
0
12
0
2
2
2
1
1
1
0
1
1
1
0
2
2
0
1
1
0
12
0
0
0
3
0
N
M
i
M
i
M
N
N
M
M
N
M
N
M
N
i
W
W
U
U
−
=
−
=
−
=
−
=
=
−
=
−
=
=
=
=
=
−
=
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
1
0
2
z
1
z
2
N
2
=-N
1
N
W1
=-N
W2
=N
1
N
1
N
o
=0
N
U1
= 0
N
U2
= 0
Układy napędowe i ich sterowanie
Przekładnie planetarne
26
4.4.2. Sprawność szeregu planetarnego
Ogólnie:
Sprawność odniesiona do mocy wejściowej:
Sprawność odniesiona do mocy wyjściowej:
gdzie:
N
U
– moc unoszenia (sprzężenia),
N
W
– moc względna (zazębienia)
η
0
– sprawność bazowa.
Mocy względnej towarzyszą straty mocy wyrażone przez sprawność wewnętrzną (bazową)
η
0
,
którą oblicza się jak dla przekładni o osiach stałych (iloczyn sprawności poszczególnych par
zazębień).
Do wstępnych obliczeń przyjmuje się:
η
Z
= 0,985 – sprawność zazębienia zewnętrznego,
η
w = 0,995 – sprawność zazębienia wewnętrznego.
Dla prostego szeregu planetarnego o dwóch stopniach swobody istnieje sześć możliwości
przepływu mocy.
I Różnicowanie mocy
∑
∑
∑
−
=
−
=
=
WE
WE
WY
WY
WE
WY
M
M
N
N
N
ω
ω
η
0
W
U
W
U
WE
WY
N
N
N
N
N
N
+
+
=
−
=
0
η
η
0
η
η
W
U
W
U
WE
WY
N
N
N
N
N
N
+
+
=
−
=
1
0
2
0
2
1
N
N
N
+
−
=
<
η
N
1
N
o
N
2
I a
N
o
N
1
N
2
I b
0
2
1
2
1
0
N
N
N
+
−
=
<
η
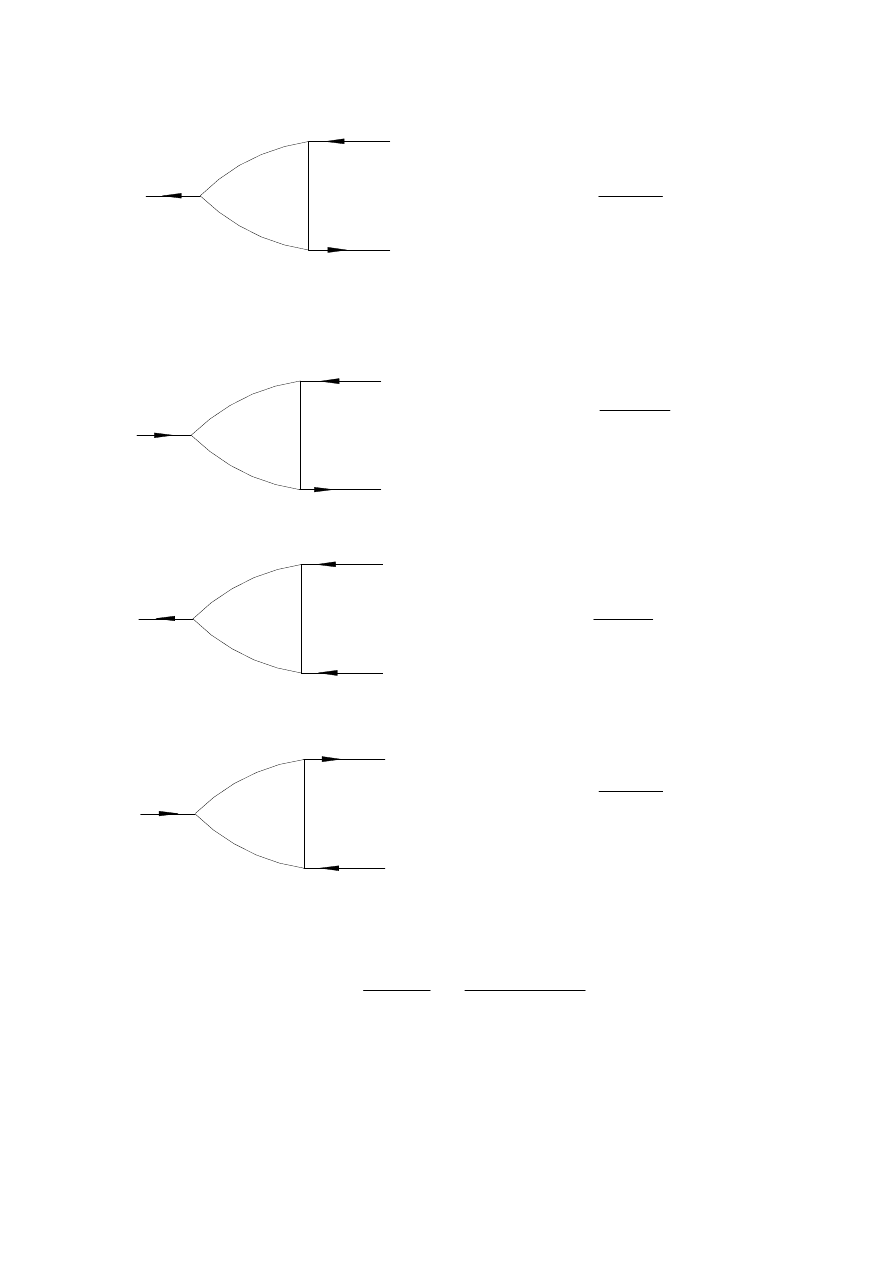
Układy napędowe i ich sterowanie
Przekładnie planetarne
27
II Sumowanie mocy
Sposób postępowania przy określaniu sprawności dla mechanizmu planetarnego o 2 stopniach
swobody na przykładzie I a:
Podstawiając:
(
)
1
0
0
12
1
0
0
0
12
1
2
+
−
−
=
−
=
η
η
i
M
M
i
M
M
otrzymuje się:
2
1
0
1
0
2
N
N
N
+
−
=
<
η
0
2
1
1
0
2
N
N
N
+
−
=
>
η
1
2
0
0
2
1
N
N
N
+
−
=
>
η
0
1
2
2
0
1
N
N
N
+
−
=
>
η
1
1
0
0
2
2
1
0
2
0
2
1
ω
ω
ω
η
M
M
M
N
N
N
+
−
=
+
−
=
<
N
1
N
o
N
2
I c
N
o
N
1
N
2
II a
N
1
N
o
N
2
II b
N
o
N
1
N
2
II c
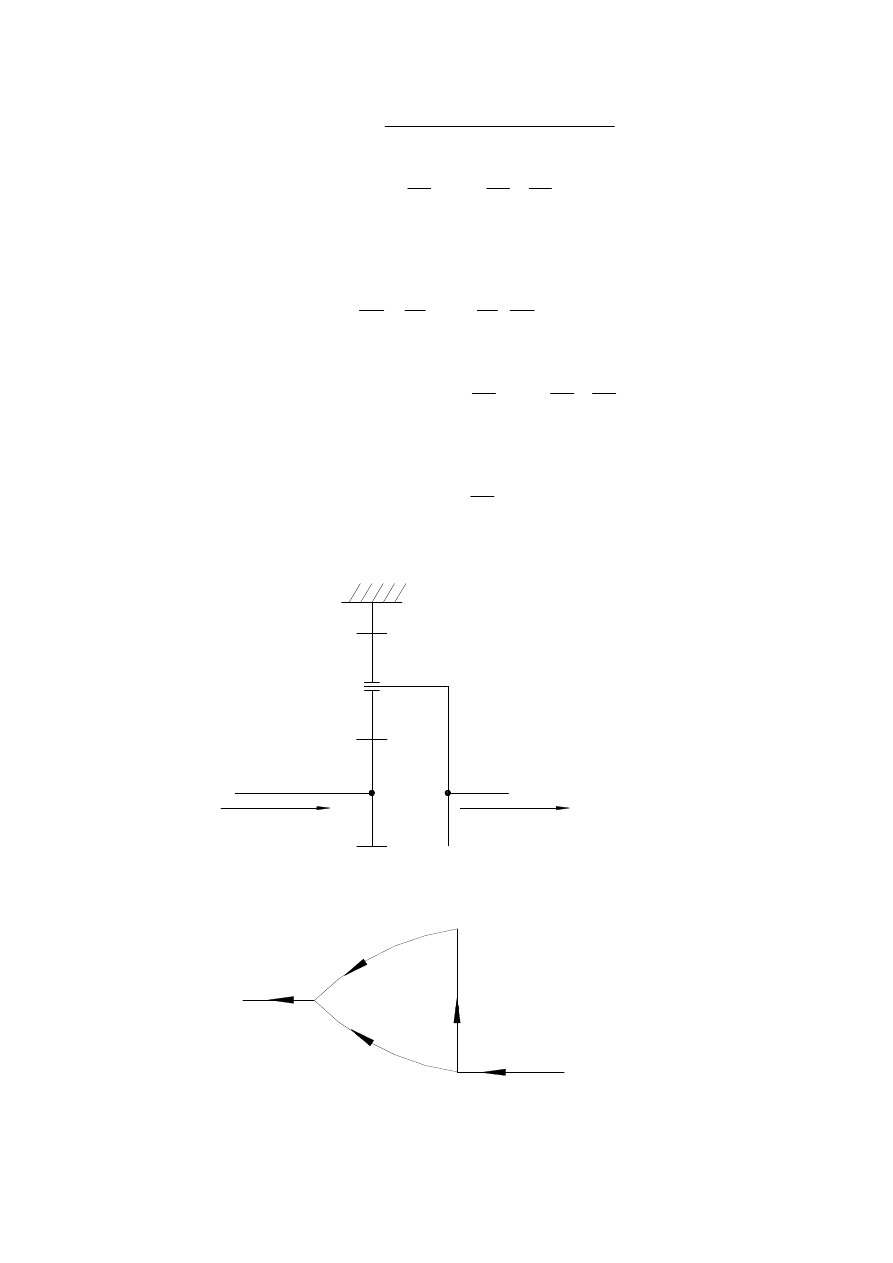
Układy napędowe i ich sterowanie
Przekładnie planetarne
28
Uwzględniając z równania Willisa, że:
otrzyma się:
i ostatecznie:
Obliczanie sprawności dla przekładni planetarnych o jednym stopniu swobody (zablokowany
element „1” lub „2” ). Wyprowadzenie zależności na przykładzie
η
10
:
(
)
1
0
1
0
0
0
12
1
2
0
0
12
0
2
1
1
1
0
0
0
12
1
2
0
0
12
1
0
2
1
1
ω
ω
ω
ω
η
ω
ω
η
η
ω
ω
η
ω
η
η
+
−
=
−
+
−
−
=
<
<
i
i
M
i
M
i
M
1
0
0
12
0
12
1
2
1
1
1
ω
ω
ω
ω
−
+
=
i
i
(
)
1
0
1
0
0
0
12
1
0
0
0
0
12
0
0
2
1
ω
ω
ω
ω
η
ω
ω
η
η
η
η
+
−
−
+
=
<
i
i
(
)
1
0
0
0
0
2
1
1
ω
ω
η
η
η
−
+
=
<
N
U1
N
o
N
U2
N
1
a
N
W1
b
1
0
z
2
z
1
N
1
N
0

Układy napędowe i ich sterowanie
Przekładnie planetarne
29
Zestawienie sprawności dla szeregu planetarnego o 1 stopniu swobody:
gdzie: indeks „A” dla i
12
0
< 0
indeks „B” dla i
12
0
> 0
(
)
(
)
(
)
( )
(
)
(
)
(
)
0
12
0
12
0
10
0
12
0
12
0
1
0
1
0
12
0
1
10
0
12
1
0
0
12
0
1
0
0
12
0
1
0
12
0
2
0
1
0
12
0
1
2
1
0
0
2
1
0
12
0
1
2
0
12
1
2
0
1
1
0
2
2
0
0
1
1
0
2
2
1
1
2
2
1
1
0
1
1
0
0
1
0
10
1
1
1
1
1
1
1
1
1
0
i
i
i
i
M
i
M
i
i
i
i
i
M
M
M
M
M
M
M
i
M
M
i
M
M
M
M
M
M
N
N
M
M
N
N
W
W
W
W
A
W
B
W
−
−
=
−
−
=
−
−
=
−
=
−
=
−
=
−
=
−
−
−
−
=
−
−
=
=
+
+
−
=
⇒
−
=
−
−
−
=
−
=
−
=
−
=
−
=
−
=
−
=
η
η
η
ω
ω
η
η
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
η
η
ω
ω
ω
ω
η
ω
ω
ω
ω
ω
ω
ω
ω
η
ω
ω
η
(
)
( )
( )
0
12
0
0
12
0
20
02
0
12
0
12
0
02
20
0
12
0
0
12
0
01
01
0
12
0
12
0
10
10
1
1
1
1
1
1
1
1
i
i
i
i
i
i
i
i
B
A
B
A
B
A
B
A
η
η
η
η
η
η
η
η
η
η
η
η
η
η
−
−
=
=
−
−
=
=
−
−
=
=
−
−
=
=
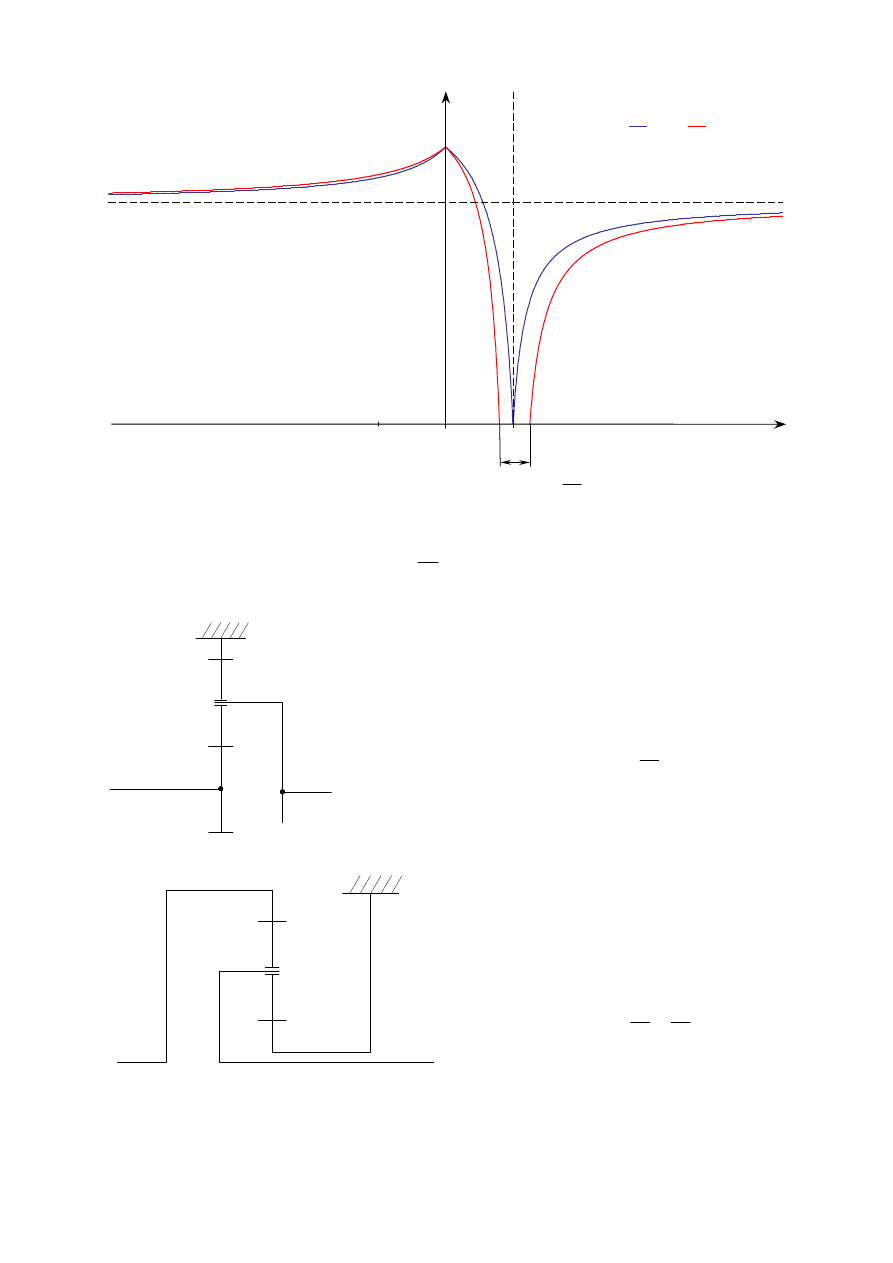
Układy napędowe i ich sterowanie
Przekładnie planetarne
30
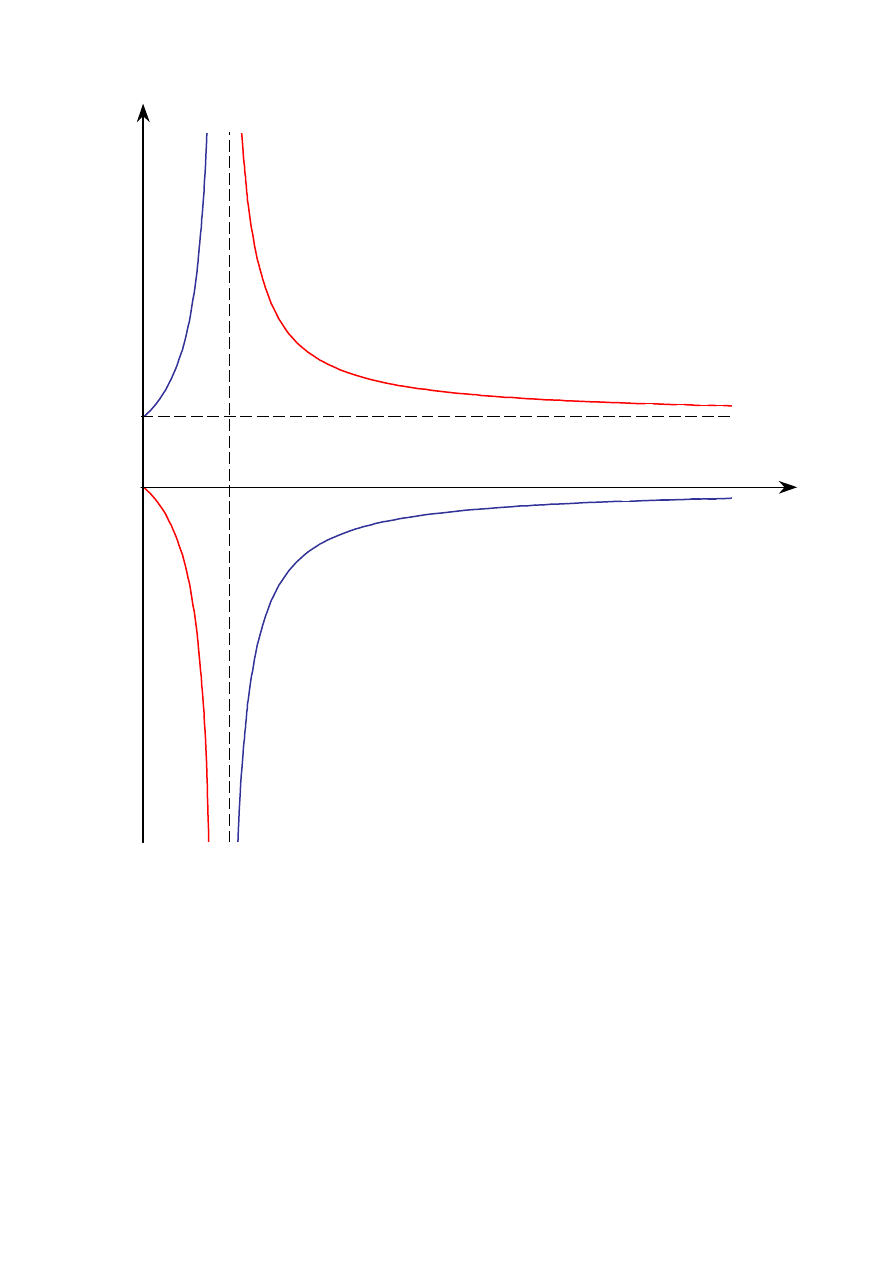
∗
- obszar samohamowności:
---------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------
0
0
1
η
η
<
<
W
i
2
1
0
12
0
21
2
20
1
0
1
z
z
i
i
i
i
W
W
A
A
=
=
=
≤
≤
−
η
η
z
2
z
1
2
1
0
12
01
10
1
z
z
i
i
i
W
W
A
A
−
=
=
−
≤
<
∞
−
η
η
η
0
η
X
0
η
0
X
η
0
1
1
W
i
0
η
=
W
i
∗
0
1
η
=
W
i
1
−
z
2
z
1
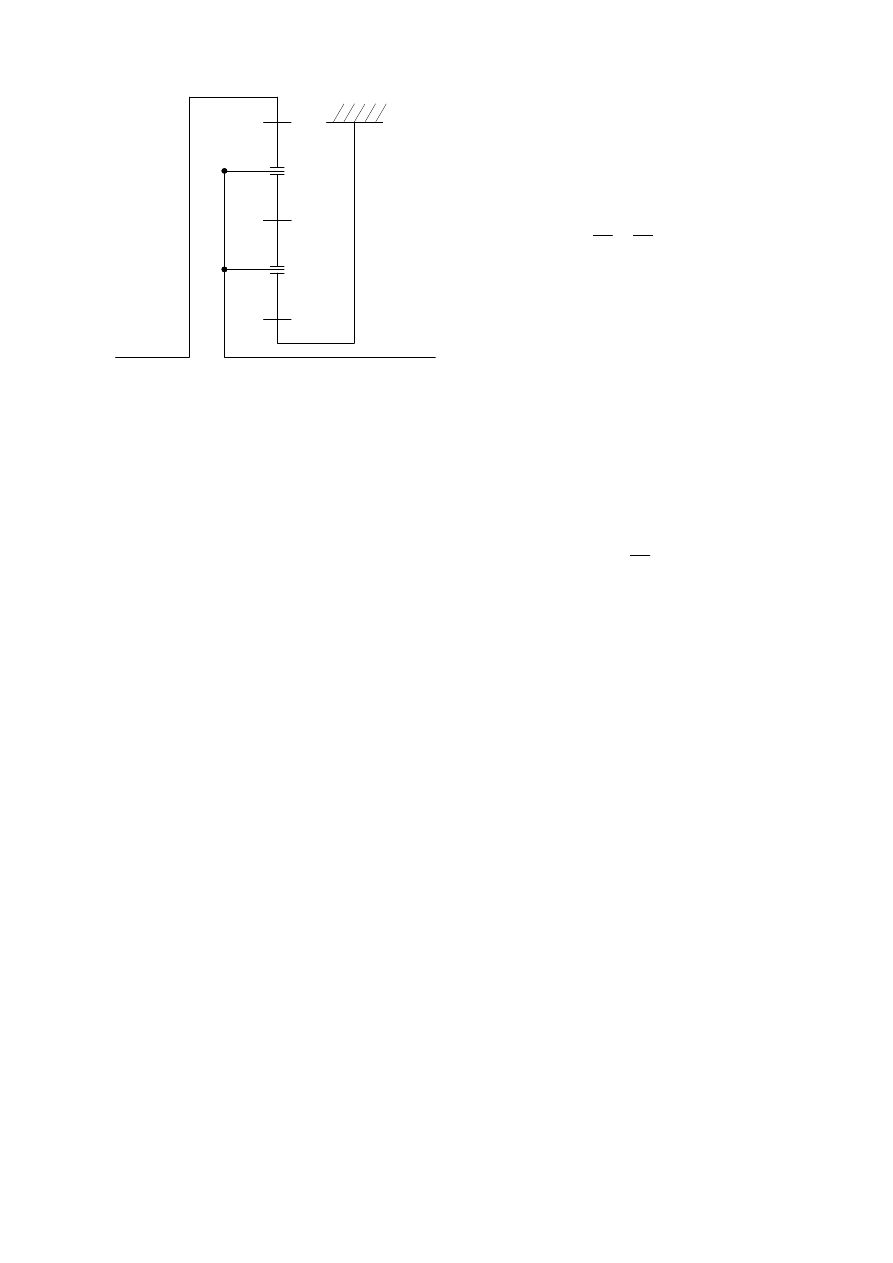
Układy napędowe i ich sterowanie
Przekładnie planetarne
31
---------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------
2
1
0
12
02
20
1
1
0
z
z
i
i
i
W
W
B
B
=
=
≤
≤
η
η
1
2
0
12
01
10
1
z
z
i
i
i
W
W
B
B
=
=
∞
≤
≤
η
η
1
2
0
12
01
10
1
z
z
i
i
i
W
W
B
B
=
=
∞
≤
≤
η
η
z
1
z
2
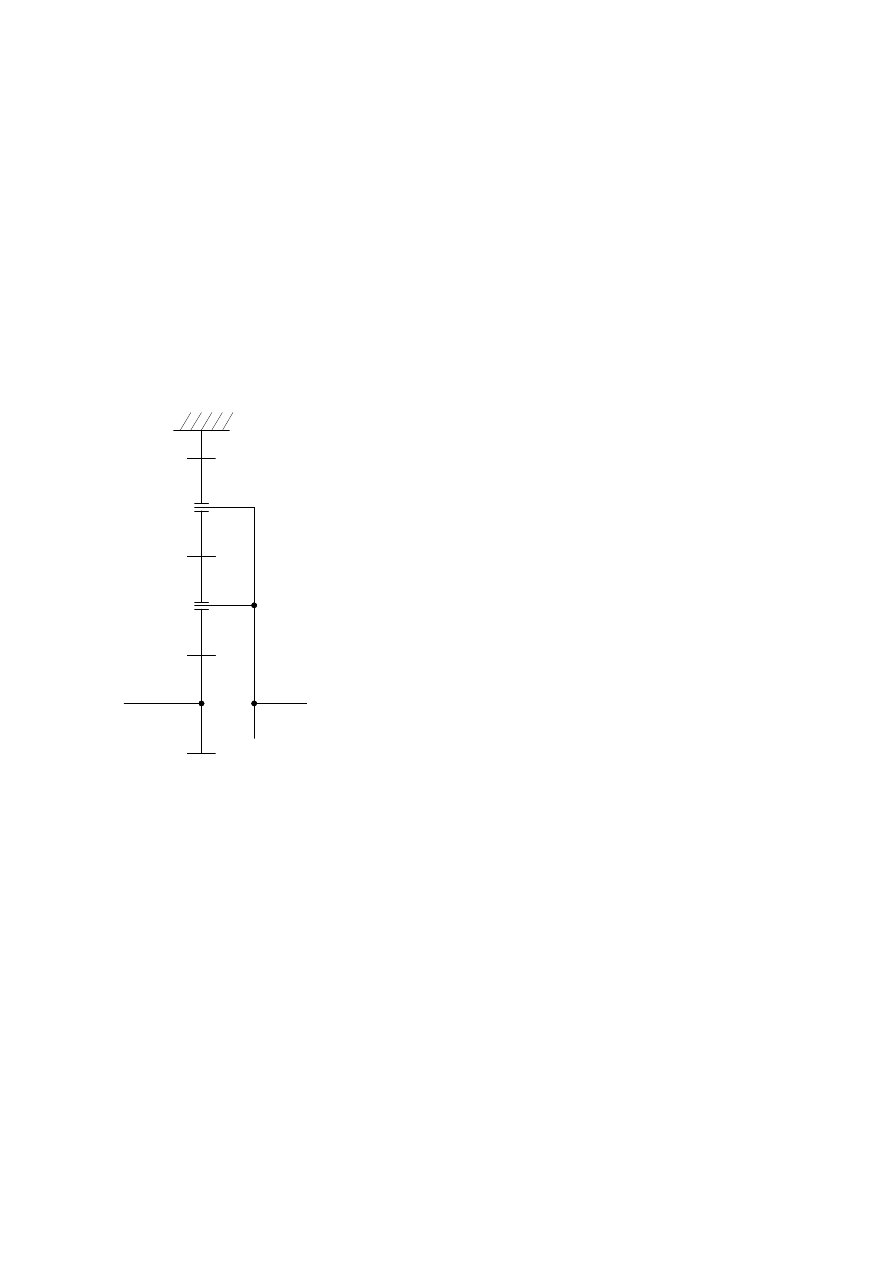
Układy napędowe i ich sterowanie
Przekładnie planetarne
32
Literatura
[1] Chodkowski A. W.: Konstrukcja i obliczanie szybkobieżnych pojazdów gąsienicowych.
WKŁ, Warszawa 1990
[2] Dajniak H.: Ciągniki. Teoria ruchu i konstruowanie. WKŁ, Warszawa 1985
z
1
z
2
Wyszukiwarka
Podobne podstrony:
Projektowanie przekladnie id 40 Nieznany
zelbet www przeklej id 587207 Nieznany
Przekladnie id 404688 Nieznany
6 Wyklad Przekladniki I id 4395 Nieznany (2)
przekladnie cierne id 404815 Nieznany
Przekladnia falowa id 404650 Nieznany
przekladnia rysunek A1 id 40466 Nieznany
Przekladnie mechaniczne id 4047 Nieznany
Przekladnia zebata gotowa id 40 Nieznany
przekladnie zebate id 404821 Nieznany
przekladnie ciegnowe id 404814 Nieznany
PrzekladniaPasowa projekt id 40 Nieznany
przekladnie mechaniczne id 4048 Nieznany
Przekladnia pradowa SN id 40465 Nieznany
fizyka www przeklej pl id 17708 Nieznany
przekladnie cierne id 404815 Nieznany
więcej podobnych podstron