asystent operatora dzwieku 313[06] o1 07 u

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

MINISTERSTWO EDUKACJI
NARODOWEJ

Piotr Ziembicki

Stosowanie urządzeń elektrycznych i sprzętu dźwiękowego
313[06].O1.07

Poradnik dla ucznia

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2007

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Recenzenci:
mgr inż. Jacek Szydłowski
mgr inż. Maciej Szykowny

Opracowanie redakcyjne:
mgr inż. Piotr Ziębicki

Konsultacja:
mgr inż. Joanna Stępień

Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej „Stosowanie urządzeń
elektrycznych i sprzętu dźwiękowego”, zawartego w modułowym programie nauczania dla
zawodu asystent operatora dźwięku

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2007

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

SPIS TREŚCI

1. Wprowadzenie

2. Wymagania wstępne

3. Cele kształcenia

4. Materiał nauczania

4.1. Podstawowe wielkości elektryczne. Prąd elektryczny i jego rodzaje. Obwód

nierozgałęziony prądu stałego i jego elementy. Prawo Ohma. Podstawowe
materiały stosowane w elektrotechnice. Źródła energii elektrycznej

4.1.1. Materiał nauczania

4.1.2. Pytania sprawdzające

4.1.3. Ćwiczenia

4.1.4. Sprawdzian postępów

4.2. Prawa Kirchhoffa dla obwodu prądu stałego – obwód rozgałęziony.
Pole elektryczne. Zjawiska magnetyzmu i elektromagnetyzmu oraz ich
zastosowanie

4.2.1. Materiał nauczania

4.2.2. Pytania sprawdzające

4.2.3. Ćwiczenia

4.2.4. Sprawdzian postępów

4.3. Prąd sinusoidalny jednofazowy. Moc prądu jednofazowego i jej rodzaje.

Budowa i działanie transformatora jednofazowego. Obsługa oscyloskopu

4.3.1. Materiał nauczania

4.3.2. Pytania sprawdzające

4.3.3. Ćwiczenia

4.3.4. Sprawdzian postępów

4.4. Rezonans napięć i prądów. Podstawowe parametry trójfazowego prądu
i napięcia

4.4.1. Materiał nauczania

4.4.2. Pytania sprawdzające

4.4.3. Ćwiczenia

4.4.4. Sprawdzian postępów

4.5. Podstawowe elementy i układy elektroniczne

4.5.1. Materiał nauczania

4.5.2. Pytania sprawdzające

4.5.3. Ćwiczenia

4.5.4. Sprawdzian postępów

4.6. Zasady bezpiecznej obsługi urządzeń elektrycznych. Techniki i metody
pomiarowe stosowane w obwodach prądu stałego i przemiennego

4.6.1 Materiał nauczania

4.6.2 Pytania sprawdzające

4.6.3 Ćwiczenia

4.6.4 Sprawdzian postępów

5. Sprawdzian osiągnięć

6. Literatura

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

1. WPROWADZENIE

Poradnik ten będzie Ci pomocny w kształtowaniu umiejętności z zakresu elektrotechniki.

Zawarto w nim podstawowe pojęcia oraz informacje o elementach obwodów i prawach
obowiązujących w obwodach prądu stałego i przemiennego. Ułatwi Ci to ukształtowanie
umiejętności rozpoznawania elementów obwodów elektrycznych, analizowania zjawisk,
wykonywania pomiarów oraz interpretowania wyników pomiarów przeprowadzanych
w obwodach elektrycznych.

W poradniku zamieszczono:

−

wymagania wstępne – wykaz umiejętności, jakie powinieneś mieć już ukształtowane, abyś
bez problemów mógł korzystać z poradnika,

−

cele kształcenia – wykaz umiejętności, jakie ukształtujesz podczas pracy z poradnikiem,

−

materiał nauczania – wiadomości teoretyczne niezbędne do osiągnięcia założonych celów
kształcenia i opanowania umiejętności zawartych w jednostce modułowej,

−

zestaw pytań, abyś mógł sprawdzić, czy jesteś już przygotowany do wykonywania ćwiczeń,

−

ćwiczenia, które pomogą Ci zweryfikować wiadomości teoretyczne oraz ukształtować
umiejętności praktyczne, w przypadku pytań i ćwiczeń, których rozwiązanie sprawia
Ci trudności, zwracaj się o pomoc do nauczyciela,

−

sprawdziany postępów, czyli zestawy pytań, na które należy odpowiedzieć dla samooceny,

−

test osiągnięć, przykładowy zestaw zadań: pozytywny wynik testu potwierdzi, że dobrze
pracowałeś podczas zajęć i ukształtowałeś umiejętności z tej jednostki modułowej,

−

literaturę, do której należy sięgać dla pogłębienia wiedzy i przygotowania się do zajęć.
Pracując z poradnikiem powinieneś zwrócić uwagę na szczególnie istotne i trudne treści,

a mianowicie:

−

materiały stosowane w elektrotechnice,

−

zjawisko indukcji elektromagnetycznej i jej zastosowanie,

−

podstawy układów elektronicznych,

−

miernictwo elektryczne.

Bezpieczeństwo i higiena pracy

W czasie realizacji zajęć w pracowni pomiarów elektrycznych musisz przestrzegać

regulaminu, stosować się do przepisów bezpieczeństwa i higieny pracy oraz instrukcji
wynikających z rodzaju wykonywanych prac. Regulamin i przepisy poznasz na pierwszych
zajęciach w tej jednostce modułowej.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Schemat układu jednostek modułowych

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

2. WYMAGANIA WSTĘPNE

Przystępując do realizacji programu jednostki modułowej powinieneś, umieć:

−

interpretować podstawowe prawa i zjawiska fizyczne,

−

korzystać z różnych źródeł informacji,

−

współpracować w grupie,

−

uczestniczyć w dyskusji, prezentacji,

−

przestrzegać zasad bezpieczeństwa i higieny pracy podczas wykonywania pomiarów
elektrycznych,

−

stosować prawa i zależności matematyczne opisujące współzależności między wielkościami
fizycznymi,

−

stosować różne metody i środki (symbole, rysunki, zdjęcia itp.) w porozumiewaniu się na
temat zagadnień technicznych.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

3. CELE KSZTAŁCENIA

W wyniku realizacji programu jednostki modułowej powinieneś, umieć:

−

rozróżnić podstawowe wielkości elektryczne,

−

scharakteryzować prąd elektryczny i jego rodzaje,

−

rozróżnić elementy obwodu elektrycznego prądu stałego,

−

rozróżnić podstawowe materiały stosowane w elektrotechnice,

−

scharakteryzować podstawowe elementy i układy elektroniczne,

−

scharakteryzować źródła i rodzaje energii elektrycznej,

−

zdefiniować pojęcie pola elektrycznego,

−

zastosować prawo Ohma i prawa Kirchhoffa dla obwodu prądu stałego,

−

określić wykorzystanie zasad elektrotechniki w urządzeniach dźwiękowych,

−

rozróżnić rodzaje prądu jednofazowego,

−

przedstawić wielkości charakteryzujące prąd sinusoidalny jednofazowy,

−

wykonać obliczenia dotyczące obwodów prądu sinusoidalnego.

−

wykonać połączenia elementów obwodu,

−

scharakteryzować podstawowe zjawiska zachodzące w polu elektrycznym, magnetycznym i
elektromagnetycznym,

−

wyjaśnić zastosowanie magnetyzmu i elektromagnetyzmu w budowie maszyn i urządzeń
elektrycznych,

−

sklasyfikować materiały ze względu na właściwości elektryczne i magnetyczne,

−

dobrać metody i przyrządy do wykonywania pomiarów prądu stałego i przemiennego,

−

posłużyć się woltomierzem, amperomierzem prądu stałego, omomierzem oraz miernikiem
uniwersalnym,

−

dokonać regulacji napięcia i prądu w obwodzie elektrycznym,

−

rozróżnić rodzaje transformatorów,

−

scharakteryzować podstawowe parametry trójfazowego prądu i napięcia,

−

obsłużyć oscyloskop zgodnie z instrukcją,

−

zinterpretować przebieg sygnałów na oscyloskopie,

−

zmierzyć podstawowe wielkości elektryczne i parametry elementów elektrycznych,

−

opracować wyniki pomiarów prądu stałego i przemiennego.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4. MATERIAŁ NAUCZANIA

4.1. Podstawowe wielkości elektryczne. Prąd elektryczny i jego

rodzaje. Obwód nierozgałęziony prądu stałego i jego elementy.
Prawo

Ohma.

Podstawowe

materiały

stosowane

w elektrotechnice. Źródła energii elektrycznej

4.1.1. Materiał nauczania

Prąd elektryczny jest to zjawisko uporządkowanego ruchu elektronów swobodnych lub

jonów. W przewodnikach, w których znajduje się dostateczna liczba elektronów swobodnych,
uporządkowany ruch elektronów - prąd elektryczny, następuje pod wpływem pola
elektrycznego, wytworzonego przez różnicę potencjałów na końcach przewodnika.
W roztworach wodnych kwasów, zasad i soli następuje dysocjacja cząsteczek, a prąd
elektryczny tworzą jony przepływające przez ten roztwór. Podczas analizy obwodów
elektrycznych przyjmuje się zwrot dodatni prądu w obwodzie zewnętrznym jako zgodny
z kierunkiem ruchu ładunków dodatnich, tzn. od zacisku źródła o wyższym potencjale (+) do
zacisku o niższym (-) potencjale.

Napięcie elektryczne jest to różnica potencjałów pomiędzy punktami obwodu

elektrycznego.

Obwód elektryczny jest to zespół elementów tworzących przynajmniej jedną zamkniętą

drogę dla przepływu prądu elektrycznego. Elementami obwodu elektrycznego są: źródło energii
elektrycznej (źródło napięcia), odbiorniki - jako elementy pobierające energię elektryczną,
przewody łączące i wyłączniki służące do zamykania (zwierania) lub przerywania (rozwierania)
obwodu elektrycznego.

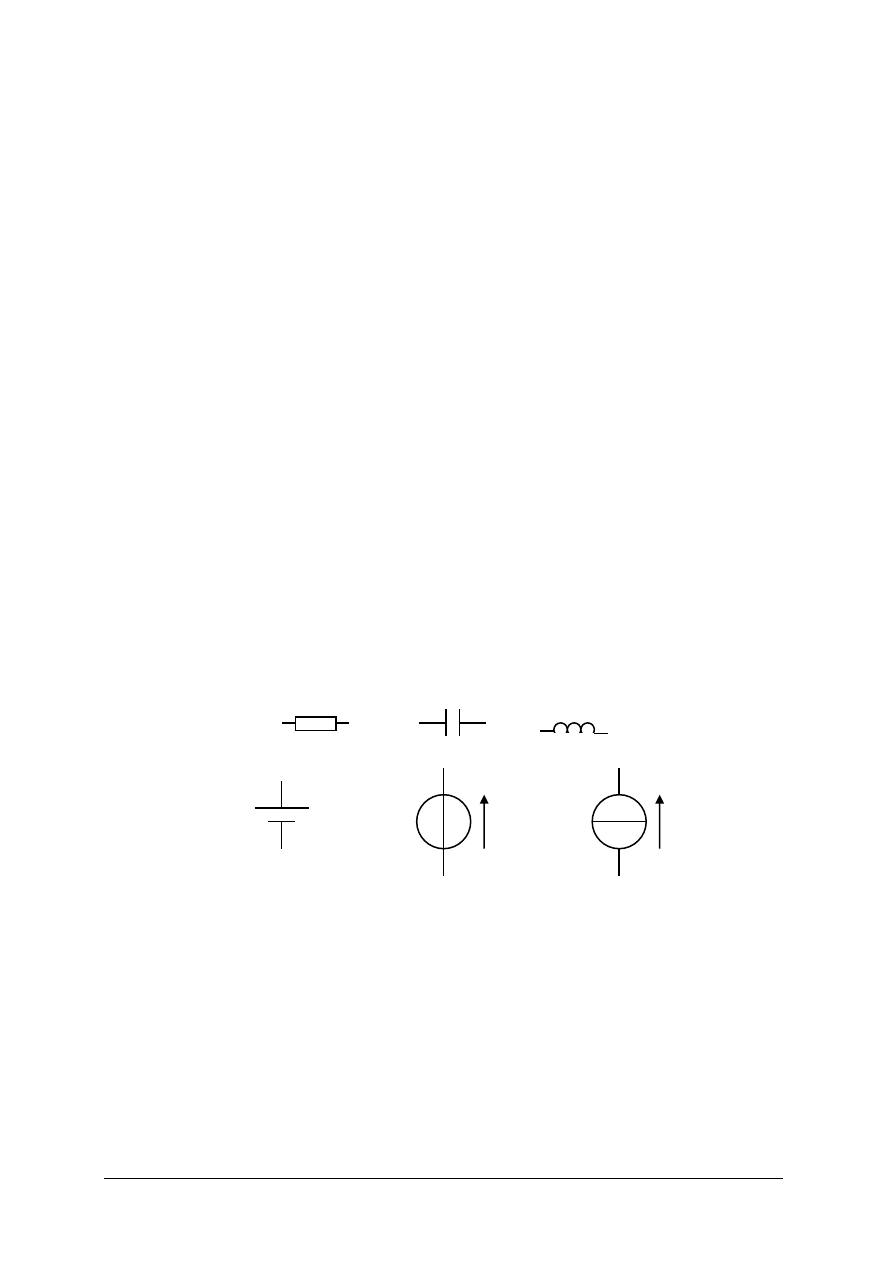
Rys.1. Symbole elementów biernych [8, s. 68

]

Rys. 2. Symbole idealnych źródeł napięcia i prądu [8, s. 69]

Obwody elektryczne przedstawia się na rysunkach za pomocą odpowiednich symboli

elementów obwodu z zaznaczeniem ich połączeń ze sobą. Końcówki elementów obwodu,
służące do połączenia z innymi elementami bezpośrednio lub za pomocą przewodów, nazywa się
zaciskami.

Gałąź obwodu tworzy jeden lub kilka elementów połączonych szeregowo, przez które

przepływa ten sam prąd elektryczny.

Oczkiem obwodu elektrycznego nazywa się zbiór połączonych ze sobą gałęzi, tworzących

nieprzerwaną drogę dla przepływu prądu. Usunięcie dowolnej gałęzi powoduje przerwanie
ciągłości obwodu elektrycznego.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Węzłem obwodu elektrycznego nazywamy zacisk lub końcówkę gałęzi, do której jest

przyłączona inna gałąź lub kilka gałęzi. Węzły obwodu elektrycznego oznaczane są
zaczernionymi punktami.

Rezystancja przewodnika zależy od rodzaju materiału, z jakiego jest wykonany przewodnik,

od jego długości, przekroju i temperatury. Jednostką rezystancji jest jeden ohm (1Ω).
Rezystancja o wartości jednego ohma. (1Ω) istnieje między dwoma punktami prostoliniowego
przewodu, jeżeli doprowadzone do tych punktów napięcie równe jednemu woltowi (1V)
wywołuje przepływ prądu o wartości jednego ampera (1A).

W stałej temperaturze rezystancja R przewodu jest proporcjonalna do jego długości

i odwrotnie proporcjonalna do przekroju poprzecznego

ρ – rezystywność (opór właściwy) [Ω · m]
l – długość przewodu [m]
S – pole przekroju poprzecznego [m

]

Odwrotnością rezystancji jest konduktancja (przewodność)









Ω

Jednostką kondunktancji jest jeden simens (1S), który określa przewodność (konduktancję)
elektryczną przewodu o rezystancji 1Ω.

Rezystancja ciał przewodzących zależy nie tylko od ich wymiarów i rodzaju materiału, lecz

także od czynników zewnętrznych, takich jak temperatura, wilgotność, ciśnienie, pole
magnetyczne. Największy wpływ na wartość rezystancji ma temperatura. Stwierdzono, że
rezystancja metali zwiększa się a rezystancja elektrolitów i półprzewodników maleje przy
podwyższaniu temperatury. Zbadano doświadczalnie, że w zakresie temperatur od 100°C do
+ 150°C przyrost rezystancji metali jest proporcjonalny do przyrostu temperatury.

(

)

]

[

−

∆T = T

– T

oznacza przyrost temperatury,

– rezystancja przewodnika w temperaturze T

, analogicznie R

w temperaturze T

a – współczynnik temperaturowy rezystancji dla danego przewodnika.

Stopy metali odznaczają się małym współczynnikiem temperaturowym rezystancji, tzn. że

ich rezystancja ulega pomijalnie małym zmianom przy zmianach temperatury. Dlatego niektóre
z nich, jak manganin i konstantan są używane do wyrobu oporników laboratoryjnych.

Elektrolity i węgiel odznaczają się ujemnym współczynnikiem temperaturowym rezystancji,

ich rezystancja zmniejsza się z podwyższaniem temperatury.

Przewodniki charakteryzują się małą rezystywnością rządu ρ = (10

-8

÷ 10

-7

) Ωm.

Przewodzą one dobrze prąd. Do przewodników zalicza się materiały, w których przepływ prądu
polega na ruchu elektronów swobodnych (przewodnictwo elektronowe), należą do nich metale.
Do przewodników zalicza się również materiały, w których przepływ prądu polega na ruchu
jonów naładowanych dodatnio lub ujemnie (przewodnictwo jonowe) należą do nich wodne
roztwory kwasów, zasad i soli, w których współczynnik temperaturowy rezystancji jest ujemny.

Izolatory charakteryzują się bardzo dużą rezystywnością, rzędu ρ = (10

÷ 10

) Ω·m. Są to

materiały mające tylko nieznaczną liczbę elektronów swobodnych, wskutek czego praktycznie
prądu nie przewodzą. Dlatego używa się ich jako materiałów izolacyjnych. Należą do nich gazy,
oleje oraz ciała stałe z wyjątkiem przewodników. W elektrotechnice jako materiały izolacyjne są
najczęściej stosowane: tkaniny bawełniane, jedwabne, szklane, porcelana, olej, guma, różne

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

gatunki papierów, mika, igelit itp. W izolatorach na ogół przy wzroście temperatury wraz
z nasileniem ruchu drgającego cząsteczek zwiększa się liczba elektronów swobodnych, co
zwiększa konduktancję materiału. Na skutek tego rezystancja izolatorów maleje, współczynnik
temperaturowy rezystancji jest ujemny.

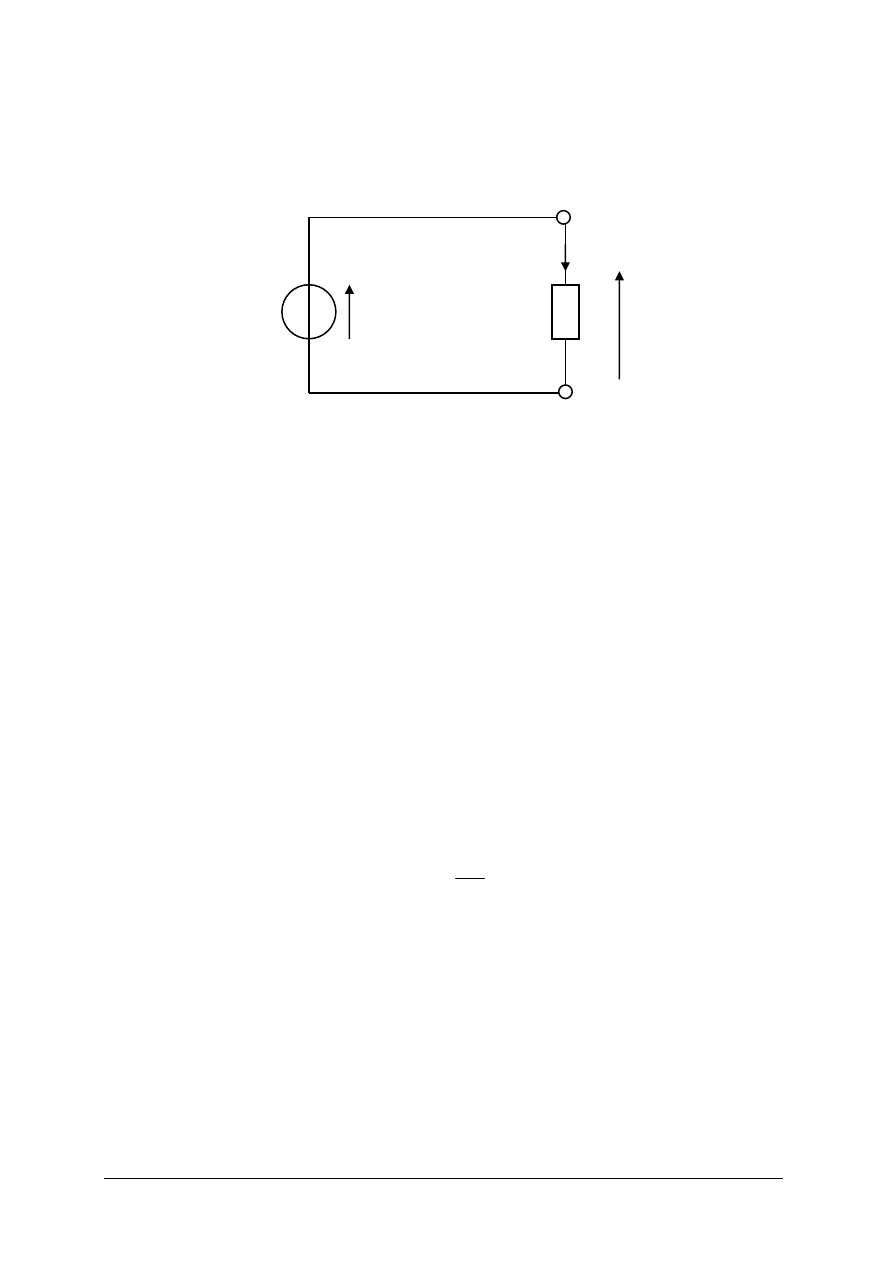
Rys. 3. Schemat najprostszego obwodu elektrycznego nierozgałęzionego [8, s. 69

]

Rozpatrując schemat obwodu z rys. 3 stwierdzamy, że w obwodzie płynie prąd. Jeżeli do

dalszych rozważań weźmiemy pod uwagę część obwodu zawartą między punktami A i B, to
prąd elektryczny płynie od punktu A do B. W punkcie A potencjał jest wyższy niż w punkcie B.
Jeżeli potencjał w punkcie A oznaczymy przez V

, potencjał w punkcie B przez V

, różnicą zaś

potencjałów między punktami A i B przez U

, to otrzymamy napięcie między punktami A i B.

= V

– V

Jednostką napięcia i potencjału jest jeden volt (1 V).

Doświadczenia wykazały, że napięcie U na odcinku AB jest proporcjonalne do prądu

I przepływającego przez ten odcinek oraz do rezystancji R

, a zatem.

= R

Zależność między napięciem, prądem i rezystancją określa prawo Ohma:

Natężenie prądu I płynącego w przewodniku o rezystancji R jest wprost

proporcjonalne do wartości napięcia U a odwrotnie proporcjonalne do rezystancji R.
Rozpatrując obwód elektryczny (rys. 3), w którym uwzględniono również źródło napięcia
(energii elektrycznej) z jego rezystancją wewnętrzną, otrzymamy prawo Ohma w następującej
postaci.

∑

∑R – rezystancja całego obwodu elektrycznego przez który płynie prąd I.

Oporniki, grzejniki, żarówki stawiają przepływowi prądu elektrycznego pewien opór. Do

jego pokonania potrzebne jest napięcie, które musi być dostarczone przez źródło napięcia.

Źródłami napięcia stałego nazywać będziemy układ urządzeń, które daję nam energię

elektryczną w postaci napięcia stałego. W zależności od tego, z jakiej postaci energii otrzymano
energię elektryczną, źródła napięcia stałego dzielimy na: źródła elektromechaniczne, źródła
chemiczne, źródła cieplne, źródła świetlne i źródła piezoelektryczne.
W każdym z powyższych źródeł zachodzi zamiana odpowiedniej postaci energii na energię
elektryczną, objawiającą się napięciem.

Wielkością charakteryzującą każde źródło napięcia jest jego siła elektromotoryczna, czyli

napięcie źródłowe, oznaczane literą E. Należy jednak pamiętać, że w źródłach

A
V

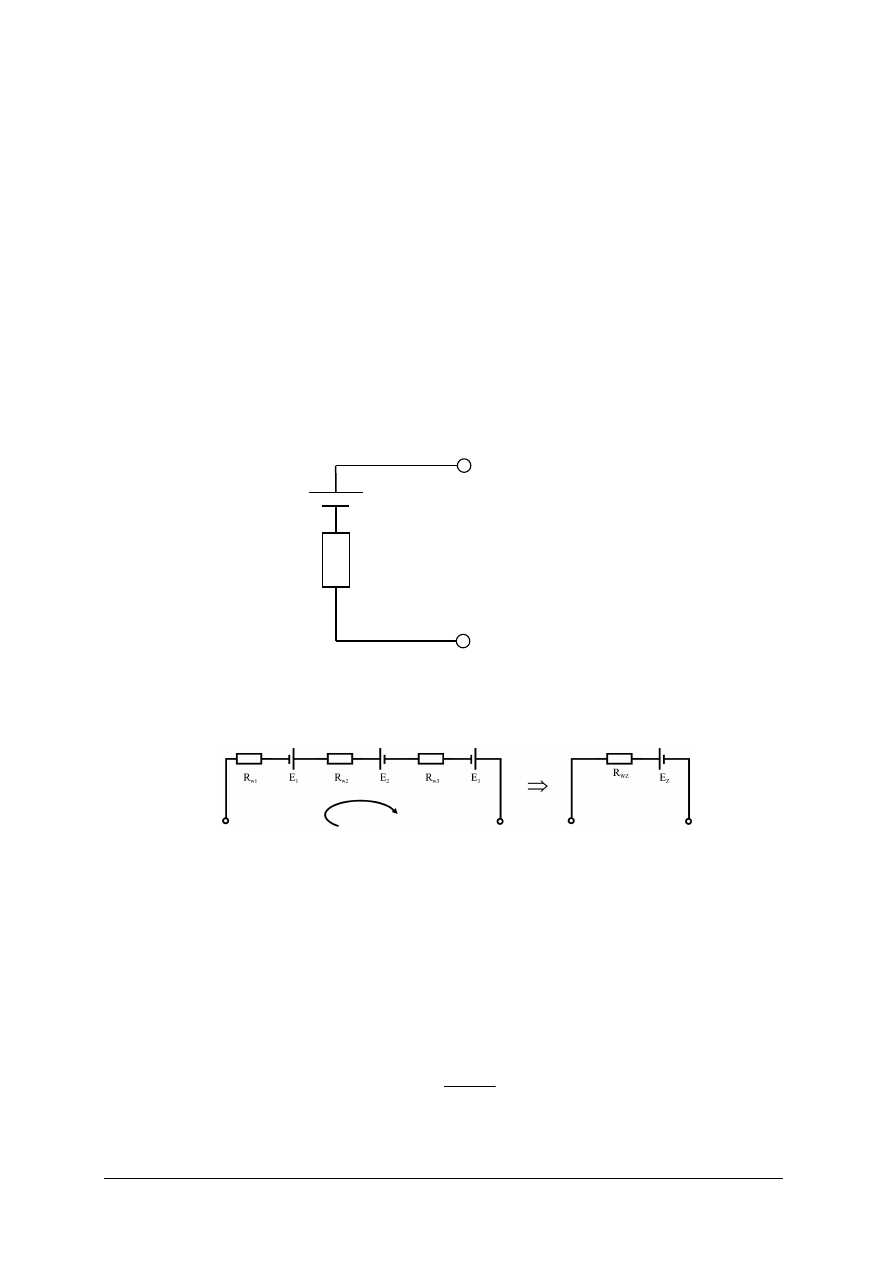
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

elektromaszynowych prąd musi przepływać przez ich uzwojenia, a w źródłach elektro-
chemicznych przez elektrolit. Zarówno uzwojenia jak i elektrolit stawiają przepływowi prądu też
pewien opór zwany oporem wewnętrznym albo rezystancją wewnętrzną źródła, którą
oznaczamy literą R z dodaniem wskaźnika w, a więc R

. W związku z tym zachodzi, wewnątrz

źródła podczas przepływu prądu I strata mocy P = R

, powodująca wydzielanie się w czasie

t ciepła W = R

Idealnym źródłem napięcia można by nazwać takie źródło napięcia, wewnątrz którego nie

występuje strata mocy, co jest możliwe przy R

= 0. Wówczas cała energia wytworzona

w źródle zostaje przekazana odbiornikowi lub układowi odbiorczemu. Do opisania idealnego
źródła napięcia potrzebna jest tylko znajomość jego siły elektromotorycznej.

Rzeczywiste źródło napięcia jest to źródło, do którego opisania potrzebne są dwie

wielkości: siła elektromotoryczna i rezystancja wewnętrzna. W schematach elektrycznych
umieszczamy obok symbolu źródła napięcia oznaczenie E dla źródła idealnego, a E, R

dla

źródła rzeczywistego. Jeszcze wyraźniej można przedstawić w schematach rzeczywiste źródło
napięcia za pomocą źródła idealnego E i połączonego w szereg z nim opornika o rezystancji R

co nazywamy schematem zastępczym rzeczywistego źródła napięcia.

Rys. 4. Rzeczywiste źródło napięcia [4, s. 67]

Jeżeli mamy kilka źródeł napięciowych połączonych szeregowo, to można je zastąpić jednym,
tzw. źródłem zastępczym o rezystancji wewnętrznej R

oraz napięciu źródłowym E

Rys. 5. Połączenie szeregowe źródeł napięcia oraz ich źródło zastępcze [4, s. 72]

Wartość napięcia źródłowego źródła zastępczego E

jest równa sumie algebraicznej napięć

źródłowych E

, E

. Algebraiczna oznacza to, że należy obrać jeden kierunek i te napięcia

źródłowe, które są zgodne z obranym kierunkiem mają znak plus, natomiast te, które są
przeciwne znak minus.

−

Rezystancja wewnętrzna R

jest równa sumie rezystancji wewnętrznych poszczególnych źródeł.

Prąd w obwodzie złożonym z jednego źródła napięcia o danych E, R

i jednego opornika

R wyraża się wzorem i ma zwrot zgodny ze zwrotem siły elektromotorycznej E:

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

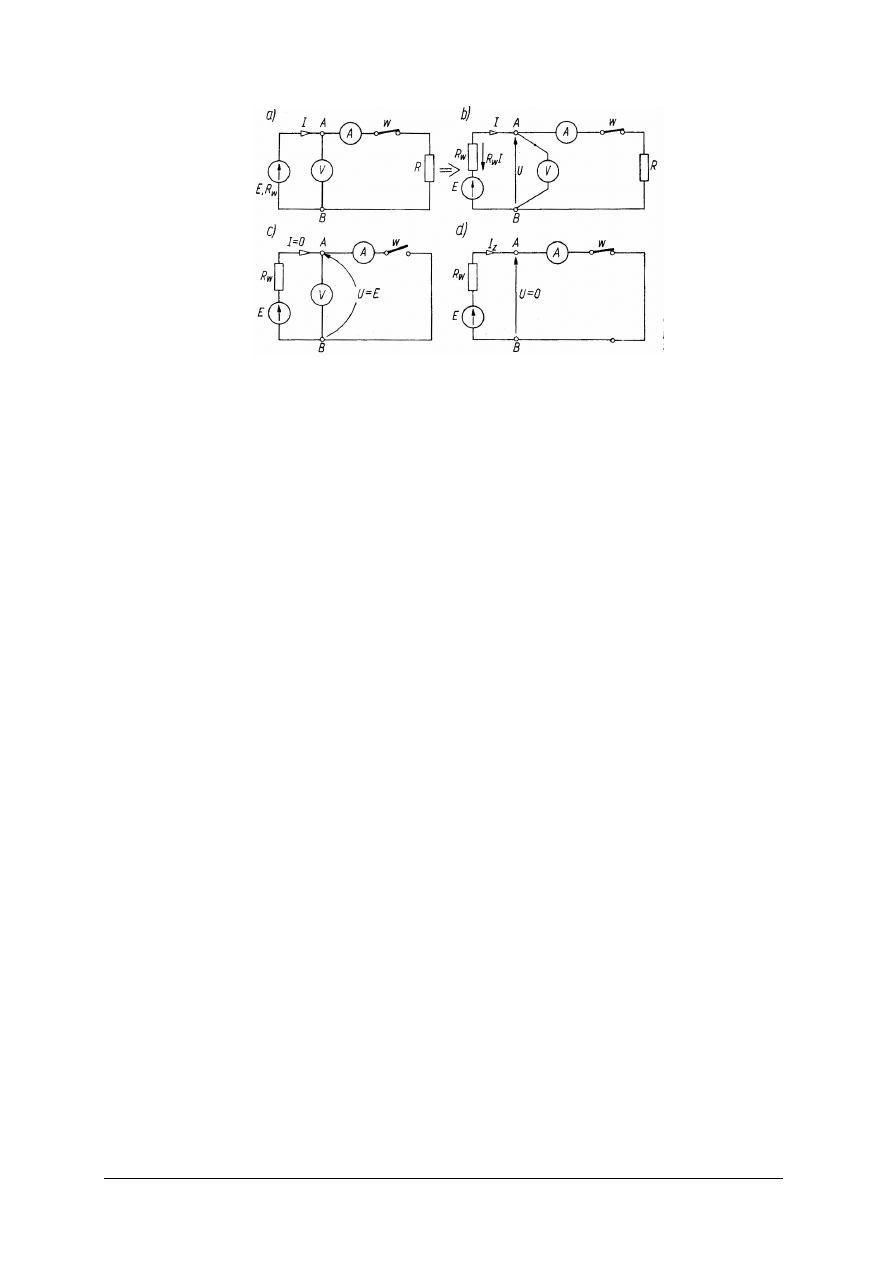
Rys. 6. Rzeczywiste źródło napięcia: a), b) obciążone, c) w stanie jałowym, d) w stanie zwarcia [4, s.79]

Celem określenia wartości napięcia U mierzonego na zaciskach (źródła napięcia

zasilającego odbiornik prądem I) A, B wykonujemy schemat zastępczy źródła napięcia. Między
zaciskami A-B mamy dwa elementy: idealne źródło napięcia E i opornik R

. Na tym oporniku

występuje spadek napięcia R

I o zwrocie skierowanym przeciwnie do zwrotu prądu. Napięcie U

między zaciskami A, B, obliczamy odejmując od siły elektromotorycznej E spadek napięcia R

na rezystancji wewnętrznej źródła.

U = E - R

Stan, w którym źródło napięcia zasila odbiorniki, nazywamy stanem obciążenia źródła
napięcia. Napięcie mierzone na zaciskach źródła obciążonego prądem jest mniejsze od jego siły
elektromotorycznej o spadek napięcia na jego rezystancji wewnętrznej.

Prąd obciążenia źródła zależy od rezystancji R odbiornika, którą możemy zmieniać

w dużych granicach (R = 0 do R = ∞) zmieniając odbiornik lub stosując opornik nastawny.

Nieskończenie wielką wartość rezystancji R osiągamy praktycznie otwierając wyłącznik

w wtedy prąd I = 0, wobec czego nie ma spadku napięcia wewnątrz źródła (R

I = 0), a napięcie

na zaciskach źródła U = E. Stan taki nazywamy stanem jałowym. Napięcie stanu jałowego
oznaczamy zwykle przez U

. Stan jałowy źródła napięcia jest to taki stan, w którym przez

źródło prąd nie płynie: I = 0. Napięcie stanu jałowego U

na zaciskach źródła napięcia jest równe

jego sile elektromotorycznej E.

E=U

Siłę elektromotoryczną źródła napięcia mierzymy praktycznie woltomierzem o bardzo dużej
rezystancji R

(teoretycznie R

= ∞) przyłączonym do zacisków źródła nie obciążonego.

Drugi skrajny przypadek, gdy R = 0, odpowiada połączeniu zacisków źródła tak grubym

i krótkim przewodem, żeby jego rezystancja była znikomo mała. Określamy to jako zwarcie
zacisków źródła napięcia. Wtedy w obwodzie pozostaje tylko rezystancja wewnętrzna źródła,
a prąd osiąga wartość I — I

nazywaną prądem zwarcia. Napięcie na zaciskach źródła jest wtedy

równe zeru. Stan zwarcia źródła napięcia jest to taki stan, w którym napięcie na zaciskach

źródła jest równe zeru. W stanie zwarcia płynie

przez źródło prąd ograniczony tylko rezystancją

wewnętrzną źródła. Niektóre źródła napięcia, np. akumulatory, mają bardzo małą rezystancję
wewnętrzną, tak że prąd zwarcia grozi zniszczeniem źródła napięcia.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Materiały przewodzące i elektroizolacyjne

Materiały używane do budowy sprzętu elektrycznego i elektronicznego dzieli się ze względu

na ich budowę elektronową na trzy grupy: materiały przewodzące, materiały półprzewodnikowe,
materiały elektroizolacyjne – dielektryki.
Materiały przewodzące

Do materiałów przewodzących zalicza się srebro, miedź i aluminium. Srebro ma największą

przewodność elektryczną, jednak charakteryzuje się nie najlepszymi własnościami
mechanicznymi. Łatwo łączy się z siarką i tlenem, po pewnym czasie pokrywa się siarczkami
i tlenkami. Powody te ograniczają zastosowanie srebra w przemyśle elektrotechnicznym. Jako
materiał przewodzący stosowana jest głównie miedź, która ma dobrą przewodność elektryczną,
niezłe własności mechaniczne i jest znacznie tańsza od srebra. Na przewody elektryczne stosuje
się również stopy miedzi, które mają gorszą przewodność elektryczną od miedzi, ale
w znacznym stopniu poprawiają jej własności wytrzymałościowe. Składnikami pogarszającymi
przewodność elektryczną jest fosfor, aluminium, arsen, antymon oraz cyna. Przewody
elektryczne, które powinny mieć większe wymagania wytrzymałościowe wykonuje się ze
stopów miedzi ze srebrem i kadmem, ponieważ w znacznie mniejszym stopniu obniżają
przewodność elektryczną.

Poza miedzią przewody elektryczne wykonuje się z czystego aluminium. Aluminium

posiada dobrą przewodność elektryczną, dobrą odporność chemiczną, małą gęstością, tlenki
aluminium posiadają bardzo dobre własności izolacyjne. Składnik stopowe pogarszają
przewodność elektryczną aluminium, sprzyjają występowaniu korozji elektrochemicznej.

Do materiałów przewodzących drugiej kategorii zalicza się ciecze i gazy. Do cieczy należą

elektrolity, czyli roztwory wodne kwasów, zasad i soli. Niewielka konduktywność zależna jest
od stężenia i ruchliwości jonów w roztworze. W układach prostowniczych dużej mocy stosuje
się gazotron (dwuelektrodowa lampa gazowana) zawierającą katodę tlenkową z niklu, stali lub
grafitu. Gazotron wypełnia się niewielką ilością rtęci (gazotron rtęciowy), z której wytwarzają
się jej pary. Gazotron może być wypełniony gazami obojętnymi (np. neonem, ksenonem). Gazy
wykorzystuje się w gazowanych lampach wskaźnikowych lub lampach zliczających. Świecenie
podczas wyładowania jarzeniowego lub bezelektrodowego jest wizualnym wskaźnikiem sygnału
elektrycznego. Wypełnione są gazami obojętnymi z rodziny helowców, najczęściej neonem,
ksenonem, arsenem.

Materiały półprzewodnikowe

Charakteryzują się średnimi wartościami rezystywności, przy czym ta wielkość zależy od

czynników zewnętrznych: temperatury, napięcia elektrycznego, oświetlenia lub natężenia pola
magnetycznego. Zaliczamy do nich krzem, german. Ze wzrostem temperatury rezystywność
półprzewodników w pewnych zakresach może rosnąć, w innych może maleć.

Niektóre pierwiastki jak np. krzem, german, arsen, selen i tellur charakteryzują się pewnymi

właściwościami zbliżonymi do metali. Materiały zawierające te pierwiastki lub ich związki
mogą odznaczać się słabym przewodnictwem metalicznym (materiały węglowe, grafit). Inne
z nich charakteryzują się przewodnictwem pośrednim pomiędzy metalami, a dielektrykami,
silnie zależnym od czystości lub zawartości celowo wprowadzonych domieszek, i temperatury
(półprzewodniki jak np. krzem, german lub np. arsenek galu GaAs).

Z półprzewodników wykonywane są podzespoły półprzewodnikowe. Do nich należą diody,

rezystory półprzewodnikowe, tranzystory, tyrystory i warystory.

Materiały elektroizolacyjne

Materiały elektroizolacyjne są to dielektryki izolacyjne. Rozróżnia się materiały izolacyjne:

materiały gazowe – gazy elektroizolacyjne (azot, dwutlenek węgla, wodór oraz gazy szlachetne:

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

argon, neon, hel itp.), ciekłe (oleje mineralne, oleje syntetyczne itp.), materiały ciekłe (oleje
pochodzenia mineralnego, oleje syntetyczne), materiały stałe organiczne i nieorganiczne.

Do materiałów izolacyjnych gazowych zaliczamy azot, który jest gazem obojętnym

chemicznie. Stosowany jest często w transformatorach olejowych stanowiąc atmosferę ochronną.
Stosuje się również do wypełniania baniek żarówkowych wraz z argonem.

Dwutlenek węgla wykorzystywany bywa w urządzeniach wymagających intensywnego

chłodzenia jako suchy lód. Wodór stosowany jest jako gaz redukujący w procesach oczyszczania
powierzchni metalowych elementów urządzeń próżniowych. Wraz z tlenem umożliwia
osiągnięcie bardzo wysokiej temperatury, koniecznej przy spawaniu wysokotopliwych metali.
Wykorzystywany bywa w obróbce szkieł kwarcowych. Argon stosuje się w niektórych
żarówkach, lampach wyładowczych, świetlówkach, prostownikach rtęciowych, w bańkach
komórek fotoelektrycznych. Neon ma zastosowanie takie, jak argon oraz w lampach
jarzeniowych. Hel, ze względu na wysoką cenę, ma ograniczone zastosowanie.

Do materiałów izolacyjnych ciekłych zaliczamy przede wszystkim oleje pochodzenia

mineralnego. Otrzymuje się je z ropy naftowej. Są to oleje transformatorowe, kablowe,
kondensatorowe i inne. Duże zastosowanie w elektrotechnice mają obecnie oleje silikonowe,
będące związkami krzemo-organicznymi. Mają dobre własności smarne i izolacyjne, są odporne
na utlenianie.

Do materiałów izolacyjnych stałych organicznie zaliczamy woski oraz dielektryki stałe

z przetworzonej celulozy oraz tworzywa sztuczne. Woski dzielą się na woski właściwe: (wosk
pszczeli, wosk karnauba, wosk motana) i materiały woskowe (woski mineralne oraz woski
syntetyczne). Woski mają zastosowanie jako syciwa materiałów włóknistych oraz składniki
zalew i mas nasycających.

Celulozę otrzymuje się z drewna sosny i świerka lub włókien roślinnych. Służy do produkcji

papieru. Papier przeznaczony do celów elektroizolacyjnych nasyca się olejami, parafiną lub
substancjami asfaltowymi lub laminuje się kilka warstw papieru z użyciem tworzyw sztucznych.
Na produkt laminowany nakłada się cienką folię miedzianą. Wyrób ten służy do produkcji
obwodów drukowanych w aparaturze elektronicznej.

W przemyśle elektrotechnicznym używa się preszpanu i fibry, które wytwarza się przez

prasowanie. Materiały te używa się w elektrycznych indukcyjnych elementach indukcyjnych –
jako korpusy cewek.

Do materiałów izolacyjnych nieorganicznych zalicza się: materiały ceramiczne, szkło

i mika. Do ceramiki należą różnego rodzaju krzemiany, tlenki metali oraz połączenia
krzemianów z tlenkami. Również zaliczamy do nich połączenia węgla, boru, krzemu z innymi
pierwiastkami. Są to węgliki, borki, krzemki. Mogą pracować w podwyższonej temperaturze.

Duże znaczenie wśród materiałów ceramicznych mają materiały o specjalnych

właściwościach. Można je podzielić na:

−

materiały konstrukcyjne ( stosowane na: izolatory wsporcze, przepustowe, korpusy cewek,
korpusy przełączników i wyłączników oraz płyty nośne obwodów wypalanych),

−

materiały kondensatorowe,

−

materiały porowate - do celów próżniowych.
Do tej grupy materiałów zalicza się również:

−

porcelanę elektrotechniczną i radiotechniczną,

−

ceramikę z krzemianów magnezu, tzw. ceramikę steatytową i cyrkonową (kalan, frekwenta,
kalit),

−

ceramikę korundową (keramit, aluminoksyd).
Do ceramiki kondensatorowej zaliczamy: rutyl (MgTiO

), tytanian magnezu (MgTiO

ferrodielektryki np. tytanian baru (BaTiO

). Ceramika porowata, to ceramika szamotowa,

porowaty steatyt, porowata ceramika korundowa przeznaczona do pracy w urządzeniach

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

próżniowych. Podstawowym surowcem w produkcji ceramiki jest glina. Do wyrobu ceramiki,
oprócz gliny używa się skalenia oraz kwarcu.

Szkło jest produktem, który powstaje w wyniku stapiania substancji nieorganicznych.

Wyróżniamy szkła do opakowań, budowlane, gospodarcze oraz szkła techniczne. Ze względu na
skład chemiczny szkło dzielimy na szkło sodowo-wapniowe, krzemionkowe, ołowiowe oraz
boro-krzemowe. Szkło ołowiowe stosuje się w optyce oraz elektronice i chemii do budowy
aparatury. Szkło boro-krzemowe stosuje się je w chemii, elektronice oraz do budowy szklanych
części aparatury pomiarowej. Szkło krzemowe ma zastosowanie głównie do wyrobu aparatury
chemicznej, laboratoryjnej oraz w niektórych urządzeniach próżniowych.

Do szkła elektrotechnicznego zalicza się szkła izolatorowe (tlenki krzemu, baru i glinu),

które używa się do wytwarzania różnego rodzaju izolatorów radiowych i kondensatorów oraz
szkła elektropróżniowe – używanych do wyrobu baniek do żarówek, lamp i przyrządów
elektronowych. Szkło kwarcowe – stopiona krzemionka – służy do wyrobu aparatury chemicznej
oraz w elektronice – lampy kwarcowe. Szkło spiekane – służy do produkcji wyrobów
porowatych (filtrów, sączków) oraz wyrobów nieporowatych (uszczelek).

Szkło metalizowane stosuje się w celu uzyskania warstw przewodzących prąd elektryczny

(podzespoły mikro-elektryczne).

Mika – glinokrzemian potasu, jest materiałem kopalnym, łatwo daje się dzielić na płytki.

Wykorzystywany

jest

w urządzeniach

elektronicznych,

dielektryczne

przekładki

w kondensatorach, oraz w lampach elektronowych na elementy konstrukcyjne.

Materiały magnetyczne twarde i miękkie

Materiały magnetyczne dzielą się ze względu na zachowanie w polu magnetycznym:

−

diamagnetyczne (bizmut, cynk, miedź) – ustawiają się w polu magnetycznym prostopadle
do kierunku linii sił pola,

−

paramagnetyczne (aluminium, chrom, mangan) – ustawiają się w polu magnetycznym
równolegle do kierunku linii sił pola,

−

ferromagnetyczne (stopy i spieki ceramiczne, kobalt, żelazo, stop żelazo-kobalt,).
Materiały ferromagnetyczne dzieli się ze względu na przebieg magnesowania na twarde

i miękkie.

Materiały magnetyczne twarde

Zaliczamy do nich materiały używane na magnesy trwałe, są stosowane w prądnicach,

silnikach prądu stałego, mikrofonach, słuchawkach, głośnikach, busolach, zegarach,
w przyrządach pomiarowych magnetoelektrycznych itp.
Najważniejszymi własnościami materiałów twardych jest natężenie powściągające (stan
naprężeń w sieci krystalicznej) i pozostałość magnetyczna.

Do materiałów magnetycznych twardych należą:

−

stale wysokowęglowe i stopowe (martenzytyczne) – stosowane w urządzeniach prostszych
i mniej ważnych, wykonuje się ze stali wysokowęglowej, stali chromowych i stali
wolframowych (wykorzystywane do produkcji magnesów licznikowych, induktorowych,
głośnikowych i telefonicznych do pracy w temperaturze otoczenia) oraz stali zawierających
kobalt na magnesy do przyrządów pomiarowych, do urządzeń przeciwiskrowych, do
czułych galwanometrów, do przekaźników,

−

stopy utwardzone dyspersyjnie – to stopy kobaltu, stopy żelazo-molidben-kobalt, żelazo-
aluminium-nikiel, żalazo-aluminium-nikiel-kobalt stosowane na magnesy trwałe. Ponadto
magnesy trwałe wykonywane przez spiekanie tlenków żelaza oraz tlenków kobaltu, miedzi,
magnezu, cynku, niklu, manganu stosowane również w urządzeniach wielkiej
częstotliwości,

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

stopy utwardzone przez tworzenie nadstruktury – stopy żelazo-kobalt-wanad oraz stopy
platyny z żelazem lub kobaltem odznaczające się dobrą plastycznością, wytwarzane
w postaci taśm i drutów. Magnesy z proszków żelaza i kobaltu mają bardzo dobre
właściwości magnetyczne twarde – stosuje się na kształtki,

−

ferryty magnetycznie twarde – są zbudowane na osnowie tlenków baru i tlenków żelaza –
zastosowanie w głośnikach. Stosowane są coraz częściej ferryty strontowe.

Materiały magnetyczne miękkie

Zaliczamy do nich czyste żelazo, stal niskowęglową, stopy żelaza z krzemem, żelaza

z aluminium, żelaza z aluminium i krzemem, żelaza z niklem, żelaza z kobaltem oraz ferryty.

Rozróżnia się materiały magnetycznie miękkie:

−

o dużej przenikalności magnetycznej – stosowane w maszynach i aparatach elektrycznych,
transformatorach, przekaźnikach,

−

o stałej przenikalności magnetycznej – materiały używane jako rdzenie w obwodach
telefonicznych i radiowych

Materiały o dużej przenikalności

Czyste żelazo – wykazuje dobre własności ferromagnetyczne. Wadą żelaza jest jego mała

oporność właściwa powodująca znaczne straty wskutek prądów wirowych. W przemyśle
elektrotechnicznym żelaza stosuje się stale niskowęglowe typu „Armco’’, z którego wykonuje
się rdzenie elektromagnesów, nabiegunniki maszyn elektrycznych, osłony magnetyczne, obwody
magnetyczne przekaźników, membrany.

Stale krzemowe. Krzem w tym stopie powoduje zwiększenie oporności elektrycznej. Stali

krzemowych używa się w silnikach elektrycznych, generatorach, transformatorach,
przekaźnikach, w przyrządach pomiarowych.

Stopy żelazo-aluminium. Stosuje się do budowy przekaźników (stopy o zawartości 14 do

16% Al – stopy Alperm).

Stopy żelazo-krzem-aluminium. Znane pod nazwą Sendust lub Alsifer. Stosowane do

wyrobu magneto-dielektryków – materiały na rdzenie do cewek indukcyjnych.

Stopy żelazo-nikiel. Stosowane do budowy przekaźników prądu stałego, ekranów

magnetycznych, dławików, transformatorów pomiarowych, obwodów wielkiej częstotliwości.

Stopy żelazo-kobalt. Stosuje się w obwodach magnetycznych – słuchawkach, głośnikach

dynamicznych, mikrofonach.

Materiały o stałej przenikalności

Stopy nikiel-żelazo-kobalt. Stosuje się stopy obrobione cieplnie: Perminvary lub Mo-

Perminvary zawierające molibden. Zmniejszają one oporność właściwą i używane są do budowy
wzmacniaczy magnetycznych, transformatorów, obwodów wielkiej częstotliwości.

Stopy żelaza i niklu z dodatkiem miedzi lub aluminium. Mają lepsze własności niż

Perminvary, a podobne zastosowanie.

Ferryty magnetycznie miękkie. Są to produkty spiekania tlenków metali dwuwartościowych

z tlenkami żelaza. Stosowane są jako materiały magnetyczne, na nabiegunniki magnesów,
jarzma magnetyczne w radiotechnice, telewizji, teletransmisji przewodowej, automatyce
w dziedzinach techniki małej i wielkiej częstotliwości.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.1.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

Jaka jest definicja następujących pojęć: prąd elektryczny, napięcie, źródło napięcia,
odbiornik, obwód elektryczny?

Jakie elementy wchodzą w skład podstawowego obwodu elektrycznego?

Jakie warunki muszą być spełnione, aby prąd płynął w obwodzie?

W jakich środowiskach może występować przepływ prądu?

Jaka jest interpretacja słowna prawa Ohma?

Jak zastosować prawo Ohma do wykonywania prostych obliczeń – spadków napięcia,
wartości prądu w obwodzie?

Jak dzielą się materiały w elektrotechnice pod względem przenoszenia nośników ładunków
elektrycznych?

Jak można opisać stan jałowy, obciążenia i zwarcia źródła napięcia?

Jakie materiały zaliczamy do materiałów przewodzących?

10.

Który materiał przewodzący metalowy jest używany najczęściej i dlaczego?

11.

Jaki jest podział materiałów elektroizolacyjnych?

12.

Jak dzielą się materiały magnetyczne?

13.

Jakie jest zastosowanie materiałów ferromagnetycznych w elektroakustyce?

14.

Jakie jest zastosowanie materiałów magnetycznych twardych w elektroakustyce?

15.

Jakie są rodzaje źródeł energii i ich zastosowanie w elektroakustyce?

4.1.3

Ćwiczenia

Ćwiczenie 1

Rozpoznaj elementy obwodu elektrycznego na schemacie i w rzeczywistym układzie

elektrycznym.

Opisz przeznaczenie każdego elementu w obwodzie oraz sprawdź działanie

układu.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zapoznać się ze schematem prostego obwodu elektrycznego,

odczytać symbole elektryczne występujące na schemacie,

rozpoznać elementy w rzeczywistym układzie elektrycznym,

opisać zadania jakie spełniają poszczególne elementy w układzie,

sprawdzić działanie układu,

zaplanować i wykonać inny wariant połączenia elementów w obwodzie nierozgałęzionym,

opracować wnioski i zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

schematy elektryczne obwodów,

−

instrukcja do wykonania ćwiczenia,

−

plansza z symbolami elektrycznymi elementów obwodu elektrycznego,

−

zestaw ćwiczeniowy z elementami,

−

literatura zgodna z punktem 6 poradnika dla ucznia,

−

kartka papieru i przybory do pisania.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 2

Wypisz podstawowe wielkości elektryczne oraz podaj ich definicje. Wykonaj przeliczenia

jednostek wielkości elektrycznych.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zapoznać się z jednostkami wielokrotnymi i podwielokrotnymi wielkości elektrycznych,

napisać definicje wielkości elektrycznych,

odczytać z tablicy lub planszy nazwy jednostek z uwzględnieniem przedrostków
i mnożników,

wykonać przeliczenia jednostek mniejszych na większe i na odwrót,

porównać i sprawdzić otrzymane wyniki,

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

kalkulator,

−

plansza z jednostkami miar układu SI,

−

plansza przedstawiająca przedrostki i odpowiadające im mnożniki,

−

zeszyt oraz przybory do pisania,

−

literatura zgodna z punktem 6 poradnika dla ucznia.

Ćwiczenie 3

Zapoznaj się z budową i parametrami źródeł napięcia stałego.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zapisać nazwy i wartości parametrów znamionowych źródeł napięcia,

opisać budowę i zastosowanie tych źródeł w życiu codziennym,

zaprezentować efekty swojej pracy,

Wyposażenie stanowiska pracy:

−

źródła napięcia,

−

informacje katalogowe badanych źródeł,

−

stanowisko komputerowe z dostępem do Internetu.

Ćwiczenie 4

Wykonaj pomiary podstawowych wielkości elektrycznych w obwodzie nierozgałęzionym.

Sprawdź słuszność prawa Ohma.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

dobrać i przygotować mierniki uniwersalne takie jak: woltomierz, amperomierz i omomierz,

narysować schematy do pomiaru napięcia i prądu, przygotować tabelę do wpisywania
wyników pomiarów,

uzgodnić z nauczycielem poprawność narysowanych schematów,

podłączyć woltomierz do źródła i ustawić napięcie U=10V na zasilaczu, nie włączać
zasilania obwodu,

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

uzgodnić z nauczycielem poprawność połączeń elementów obwodu,

następnie wykonać pomiar spadku napięcia na każdym rezystorze (nauczyciel sprawdza
podłączenie amperomierza i woltomierza),

wykonać pomiary prądu płynącego w obwodzie przy różnych napięciach U = 2÷10V, co 2V,

wpisać pomiary do tabeli,

narysować charakterystykę prądowo - napięciową dla każdego rezystora,

10)

rozłączyć obwód i dokonać pomiaru wartości oporności dla każdego rezystora przy U = 0V,

11)

obliczyć wartość oporności każdego rezystora oraz rezystancji zastępczej obwodu,

12)

porównać otrzymane wyniki pomiarów z wynikami obliczeniowymi,

13)

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

zestaw laboratoryjny z wyposażeniem do sprawdzenia prawa Ohma,

−

kalkulator,

−

instrukcja do wykonania ćwiczenia,

−

przybory do pisania, zeszyt do ćwiczeń.

Ćwiczenie 5

Opracuj klasyfikację materiałów magnetycznych ze względu na ich właściwości.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

obejrzeć przezrocza lub film instruktażowy o materiałach magnetycznych i ich
zastosowaniu,

wypisać czynniki, które decydują o właściwościach materiałów,

rozpoznać rodzaje materiałów magnetycznych z próbek tych materiałów, przez naklejenie
właściwej karki z nazwą materiału na próbce,

opisać własności materiałów magnetycznych oraz ich zastosowanie,

sklasyfikować materiały pod różnymi względami: sposobu wytwarzania, właściwości
magnetycznych (przenikalności magnetycznej), zachowania się w polu magnetycznym,

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

stanowisko do wykonania ćwiczenia,

−

przezrocza lub film instruktażowy o materiałach magnetycznych i ich zastosowaniu,

−

próbki materiałów magnetycznych,

−

samoprzylepne kartki z wydrukowanymi nazwami materiałów,

−

arkusz papieru,

−

zeszyt do ćwiczeń, przybory do pisania,

−

literatura zgodna z punktem 6 poradnika dla ucznia.

Ćwiczenie 6

Rozpoznaj przedstawione rodzaje materiałów przewodzących metalowych i opisz ich

własności.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

obejrzeć film instruktażowy o materiałach przewodzących ich zastosowaniu,

rozpoznać rodzaje materiałów przewodzących z próbek tych materiałów,

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

określić własności materiałów przewodzących metalowych,

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

film instruktażowy o materiałach przewodzących ich zastosowaniu,

−

zeszyt do ćwiczeń,

−

odcinki materiałów przewodzących metalowych - przewody i kable,

−

plansze przedstawiające przekroje przewodów i kabli,

−

przybory do pisania.

Ćwiczenie 7

Rozpoznaj przedstawione przez nauczyciela rodzaje materiałów elektroizolacyjnych i określ

ich własności.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

obejrzeć film instruktażowy o materiałach elektroizolacyjnych i ich własnościach,

obejrzeć próbki materiałów elektroizolacyjnych,

dobrać odpowiednie nazwy materiałów elektroizolacyjnych,

nakleić właściwą nazwę materiału przy próbce,

określić własności materiałów elektroizolacyjnych,

przepisać ćwiczenie do zeszytu,

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

film instruktażowy o materiałach elektroizolacyjnych, o ich zastosowaniu,

−

próbki materiałów elektroizolacyjnych,

−

samoprzylepne kartki z wydrukowanymi nazwami materiałów,

−

zeszyt do ćwiczeń,

−

przybory do pisania.

4.1.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

zdefiniować pojęcia: napięcie, prąd elektryczny, źródło napięcia,
obwód elektryczny, odbiornik?

wymienić elementy, które występują w obwodzie elektrycznym?

określić warunki, jakie muszą być spełnione, aby prąd płynął
w obwodzie?

opisać środowiska, w których może przepływać prąd elektryczny?

zastosować prawo Ohma do wykonywania obliczeń wielkości:
napięcia, prądu i rezystancji?

zastosować źródła energii elektrycznej w elektroakustyce?

określić zastosowanie ferromagnetyków w elektroakustyce?

wymienić i scharakteryzować materiały, które przewodzą prąd
elektryczny?

scharakteryzować różne stany źródła napięcia przy pomocy
schematów i równań matematycznych?

10)

sklasyfikować materiały magnetyczne?

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.2. Prawa Kirchhoffa dla obwodu prądu stałego – obwód

rozgałęziony.

Pole

elektryczne.

Zjawiska

magnetyzmu

i elektromagnetyzmu oraz ich zastosowanie

4.2.1 Materiał nauczania

Obwód rozgałęziony prądu stałego

Pierwsze prawo Kirchhoffa dla węzła obwodu prądu stałego można sformułować

następująco: „Dla każdego węzła obwodu elektrycznego suma prądów dopływających do
węzła jest równa sumie prądów odpływających od węzła"

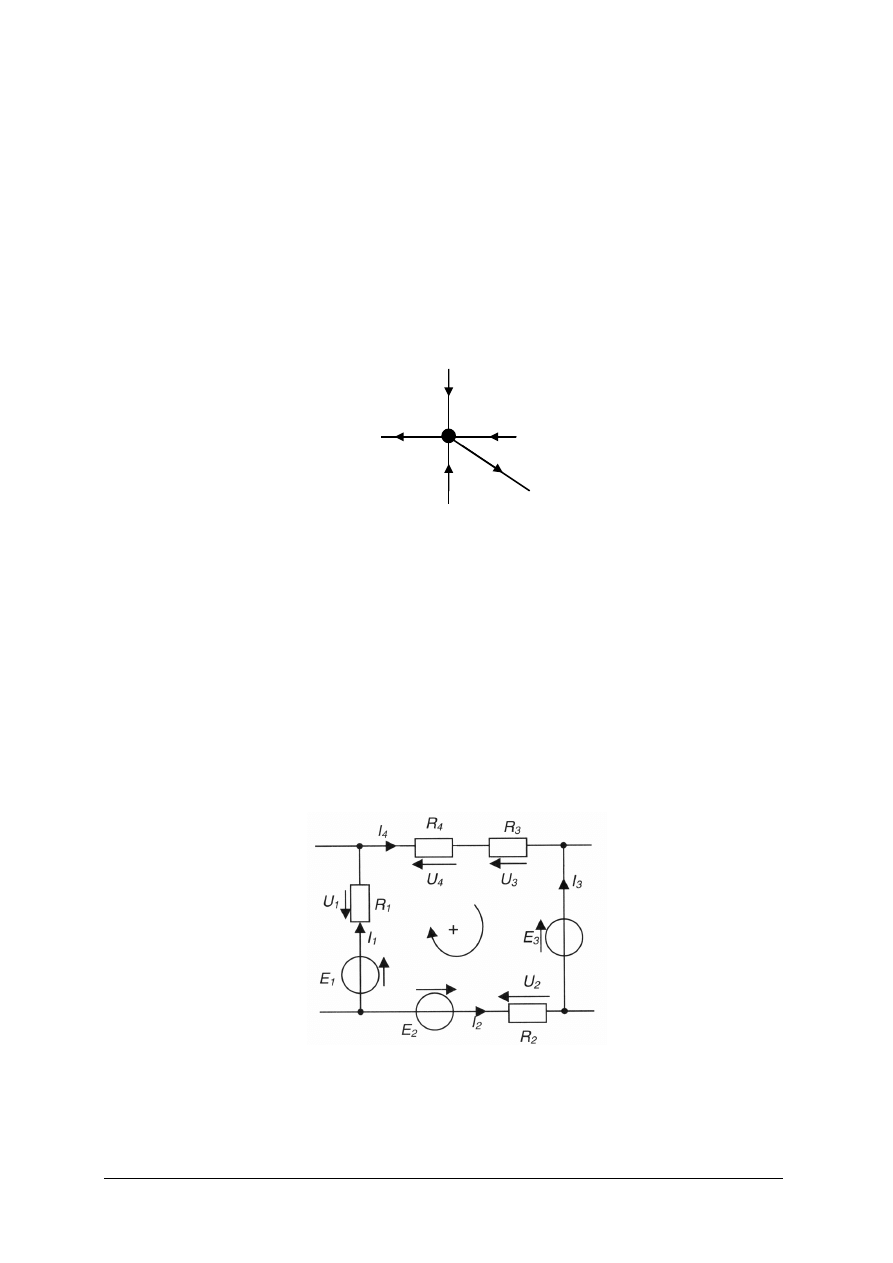
Rys. 7. Węzeł obwodu elektrycznego [4, s. 91]

Dla węzła przedstawionego na rys. 7 pierwsze prawo Kirchhoffa można wyrazić równaniem:

+ I

= I

+ I

Jeżeli wyrazy prawej strony równania przeniesiemy na lewą stronę, otrzymamy równanie:

+ I

– I

= 0

Równanie to wyraża sumę algebraiczną prądów w węźle obwodu elektrycznego, co stanowi

alternatywną treść I prawa Kirchhoffa, mówiącą, że:
„Dla każdego węzła obwodu elektrycznego, algebraiczna suma prądów jest równa zeru’’.

Drugie prawo Kirchhoffa dotyczące bilansu napięć w oczku obwodu elektrycznego prądu

stałego można sformułować następująco: „W dowolnym oczku obwodu elektrycznego prądu
stałego suma algebraiczna napięć źródłowych oraz suma algebraiczna napięć odbiornikowych
występujących na rezystancjach rozpatrywanego oczka jest równa zeru".

Dla zrozumienia sposobu zapisywania II prawa Kirchhoffa w postaci równania rozpatrzymy

dowolne wyodrębnione oczko obwodu elektrycznego (rys. 8).

Rys. 8. Wyodrębnione oczko obwodu elektrycznego [2, s. 26]

W oczku tym oznaczone są zwroty prądów w poszczególnych gałęziach oraz zwroty napięć

na poszczególnych rezystorach (odbiornikach). Napięcia odbiornikowe zgodnie z prawem Ohma
można zapisać jako:

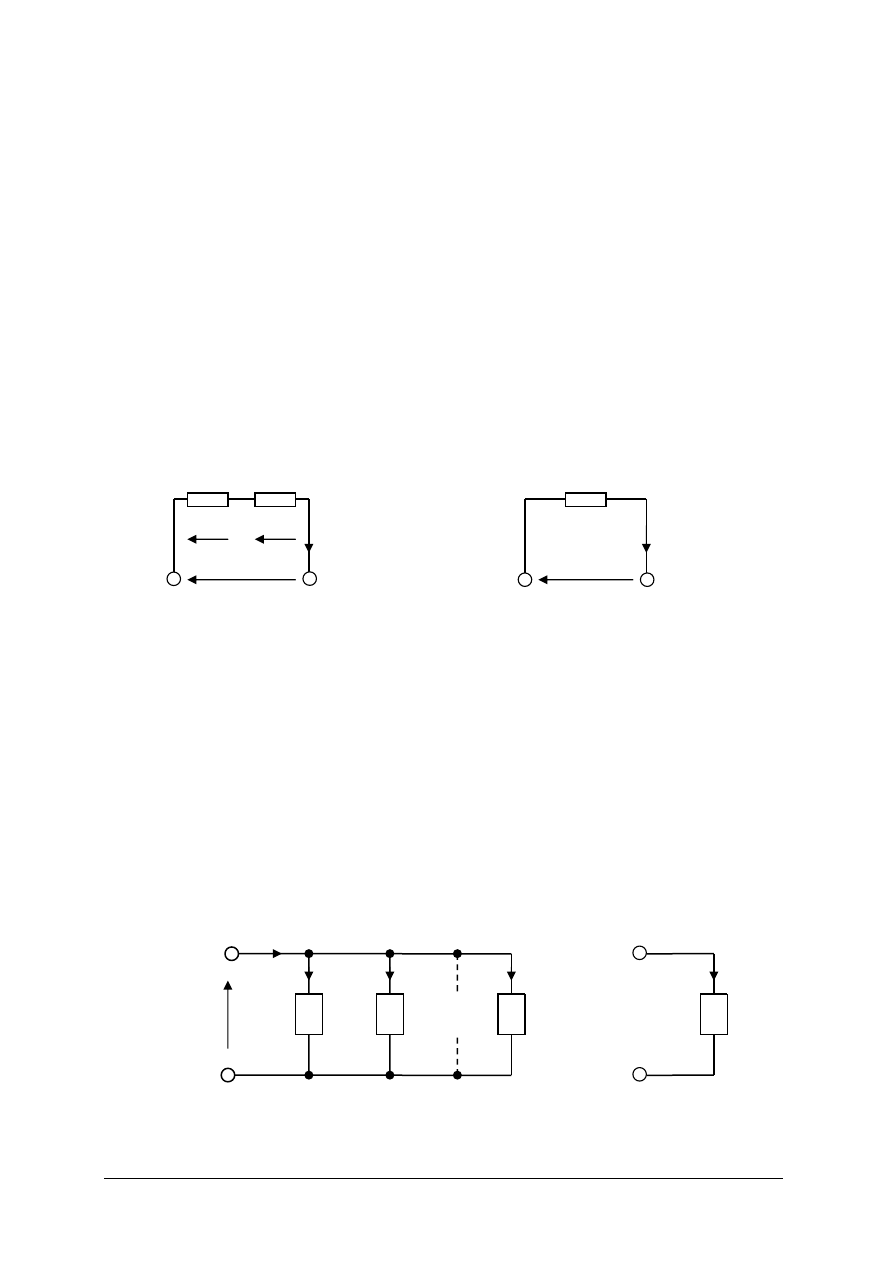
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

= I

· R

= I

· R

= I

· R

= I

· R

Dla zapisania II prawa Kirchhoffa w postaci równania przyjmujemy pewien (dowolny)

zwrot obiegowy oczka oznaczony strzałką wewnątrz oczka. Ten zwrot przyjmujemy za dodatni.
Jeśli zwrot napięcia źródła lub odbiornika jest zgodny z tą strzałką, to te napięcia źródłowe
i odbiornikowe przyjmujemy jako dodatnie. Jeśli zaś zwroty napięć są przeciwne, to znaki
napięcia źródła lub odbiornika przyjmujemy jako ujemne. W rezultacie takich założeń
otrzymujemy równanie:

– E

– U

+ U

– U

= 0

Po przeniesieniu napięć odbiornikowych na prawą stronę równania otrzymamy:

– E

= U

– U

+ U

Oznacza to, że II prawo Kirchhoffa możemy sformułować w postaci odpowiadającej
powyższemu równaniu: „W dowolnym oczku obwodu elektrycznego prądu stałego suma
algebraiczna napięć źródłowych jest równa sumie algebraicznej napięć odbiornikowych".
Szeregowe łączenie rezystorów

Układ dwóch szeregowo połączonych rezystorów R

i R

(rys. 9a) chcemy zastąpić jednym

równoważnym rezystorem R (rys. 9b), takim, który nie zmieni wartości prądu I.
Zgodnie z II prawem Kirchhoffa możemy zapisać: U = U

+ U

Rys. 9. Szeregowe połączenie rezystorów [źródło własne]

Po uwzględnieniu Prawa Ohma: U = I · R

+ I · R

i po podzieleniu stron równania przez

I otrzymamy: U/I = R

+ R

. Po zapisaniu prawa Ohma dla rys. 9b: U/I = R nietrudno zauważyć,

że rezystancja zastępcza dwóch rezystorów połączonych szeregowo wynosi: R = R

+ R

Analogiczna zależność obowiązuje dla dowolnej liczby rezystorów połączonych szeregowo

i by uzyskać rezystancję zastępczą układu należy zsumować rezystancję poszczególnych
rezystorów obwodu.
Napięcie na zaciskach układu szeregowego kilku rezystorów jest równe sumie napięć na
poszczególnych rezystorach

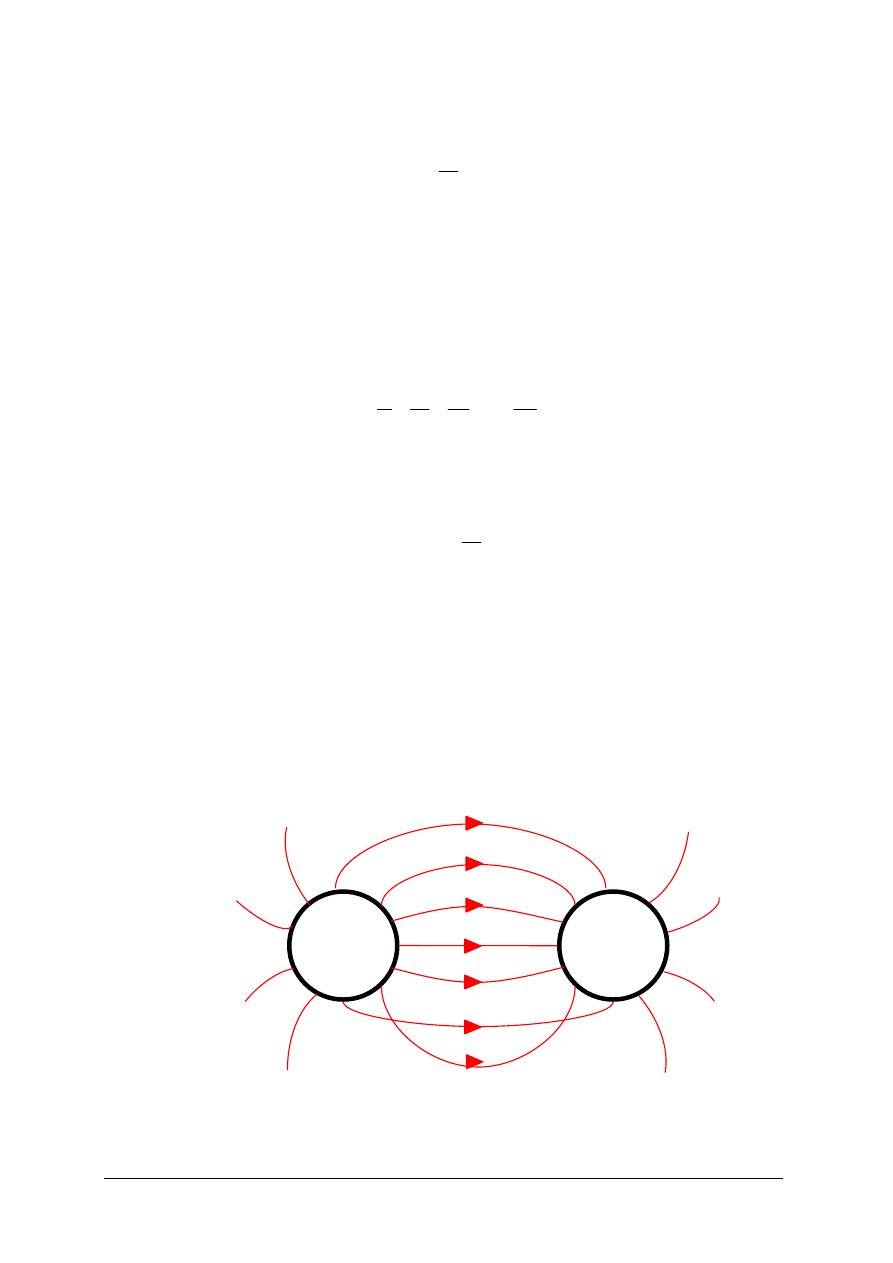
Równoległe łączenie rezystorów

Połączeniem równoległym kilku gałęzi w obwodzie elektrycznym nazywamy takie

połączenie, przy którym na końcach tych gałęzi istnieje wspólne napięcie.
Przykład takiego połączenia pokazano na rys. 10a.

Rys. 10. Równolegle połączenie rezystorów i jego schemat zastępczy [opracowanie własne]

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 12. Pole elektryczne między dwiema elektrodami kulistymi [opracowanie własne]

Prądy płynące poprzez poszczególne rezystory obliczamy dzieląc napięcie przez ich

rezystancje albo mnożąc przez konduktancję:

Prąd wypadkowy I, dopływający do rozpatrywanego układu równoległego, jest równy sumie

prądów w poszczególnych rezystorach.

I = I

+ I

+…+ I

Gdybyśmy chcieli badany układ równoległy rezystorów zastąpić jednym opornikiem, który

by przy tym samym napięciu U pobierał taki sam prąd I, to:

I = G U

G = G

+ G

+…+ G

Wobec powyższego możemy stwierdzić, że konduktancja (przewodność) zastępcza układu

równoległego kilku rezystorów jest równa sumie ich konduktancji.

...

Odwrotność rezystancji zastępczej układu równoległego kilku rezystorów jest równa sumie

odwrotności ich rezystancji.

Przy połączeniu równoległym n jednakowych rezystorów, każdy o rezystancji

ich

rezystancja zastępcza jest

n razy mniejsza niż rezystancja jednego rezystora.

Niekiedy stosuje się szeregowo-równoległe połączenia rezystorów, zwane też połączeniami

mieszanymi. Ze względu na możliwości takich połączeń nie istnieją wzory ogólne na obliczenie
rezystancji zastępczej. Wyznacza się ją zwykle po kolei etapami obliczając rezystancję
poszczególnych układów szeregowych i równoległych.

Pole elektryczne

W przyrodzie istnieje równowaga ładunków elektrycznych w każdym atomie. Powstawanie

ładunku elektrycznego jednego znaku na jakimkolwiek ciele może nastąpić przez przeniesienie
części elektronów z jednego ciała na drugie, wobec czego musi powstać na innych ciałach
ładunek elektryczny przeciwnego znaku o tej samej wartości bezwzględnej.

−

+ Q

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ładunki elektryczne przewodników w stanie statycznym gromadzą się na ich powierzchni.

Jeżeli dwa przewodniki 1 i 2 oddzielone od siebie dielektrykiem połączonym ze źródłem
napięcia o różnicy potencjałów (V

– V

) = U, czyli napięciu na jego zaciskach, to na

przewodnikach tych pojawią się ładunki + Q i – Q równe co do wartości bezwzględnej. Ładunki
te utrzymują się również po odłączeniu od źródła napięcia (rys. 12). Wspomniane przewodniki
nazwiemy elektrodami. Na elektrodzie o potencjale wyższym pojawi się ładunek dodatni, na
elektrodzie drugiej ujemny.

Stwierdzono, że przy danym układzie i kształcie elektrod oraz danym dielektryku,

powstający ładunek Q jest proporcjonalny do różnicy potencjałów elektrod, czyli do napięcia
między elektrodami. Zapiszemy to za pomocą wzoru:

Q = C · (V

– V

)

albo

Q = C · U

Stosunek ładunku Q na dwóch elektrodach oddzielonych dielektrykiem do napięcia

U między tymi elektrodami nazywamy pojemnością elektrostatyczną danego układu elektrod.
Jednostką pojemności jest farad [F].

]

[

]

[

]

[

⋅

Pojemność układu dwóch elektrod jest równa jednemu faradowi, jeżeli przy napięciu

jednego wolta między nimi ładunek na każdej z elektrod jest równy jednemu kulombowi. Farad
jest jednostką bardzo dużą. W praktyce używamy jednostek mniejszych, a mianowicie
milifaradów (1 mF = 10

-3

F), mikrofaradów (1 µF = 10

-6

F), nanofaradów (1 nF = 10

-9

F),

i pikofaradów (1 pF = 10

-12

F).

Dielektrykami nazywamy próżnię i wszystkie ciała nieprzewodzące. Wiemy, że

dielektryków idealnych nie ma. Za taki dielektryk można uważać próżnię doskonałą. Ciała
naładowane utrzymują w próżni swój ładunek bardzo długo po przerwaniu ich połączenia ze
źródłem napięcia.

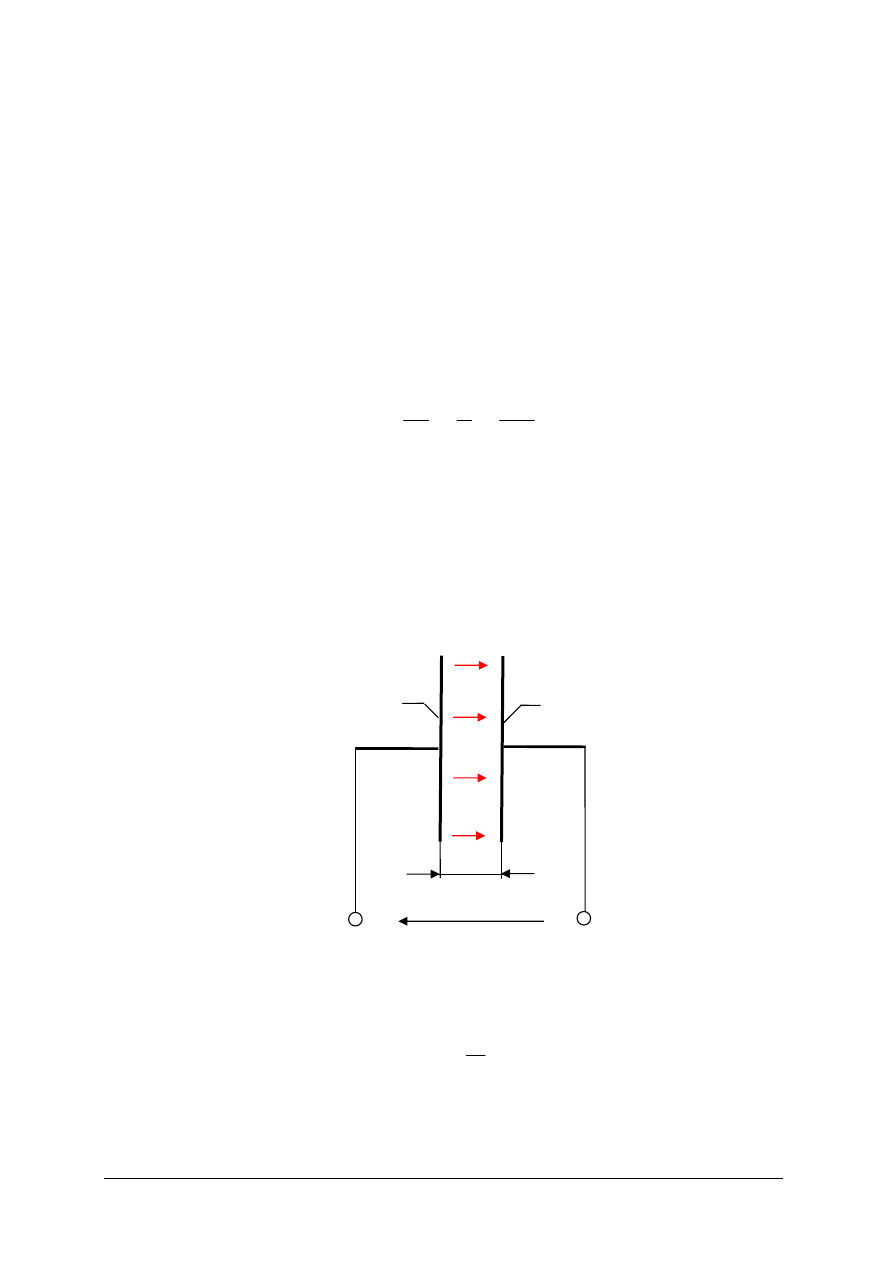
Rys. 13. Układ dwóch elektrod płasko-równoległych [3, s. 125]

Natężenie pola elektrycznego E w przestrzeni międzyelektrodowej obliczymy dzieląc

napięcie przez odległość d.

Z drugiej strony indukcja elektrostatyczna D, a więc i gęstość ładunku σ (sigma), jest równa

ilorazowi ładunku Q na elektrodzie i pola powierzchni S.

−Q

−σ

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Przenikalność elektryczną ε obliczymy z ilorazu D do E.

;

Do wyznaczenia wartości przenikalności próżni, musimy znać pole powierzchni elektrod,

odległość między elektrodami, zmierzyć napięcie U między elektrodami, a następnie zmierzyć
ładunek Q przy rozładowaniu elektrod przez galwanometr. Jednostką przenikalności elektrycznej
jest farad na metr.

Zjawiska magnetyzmu i elektromagnetyzmu zastosowane w urządzeniach dźwiękowych

Znajomość

zrozumienie

zasad

działania

sposobów

podłączeń

aparatury

elektroakustycznej

jest

podstawową

umiejętnością

zapewniającą

poprawność

prac

wykonywanych przez elektroakustyka. Często nie sprzęt, lecz jego nieumiejętne użycie jest
przyczyną pogorszenia jakości nagrania lub nagłośnienia. Podstawowymi urządzeniami toru
akustycznego są: mikrofony, miksery equalizery, kompresory, limitery, ekspandery, bramki,
wzmacniacze i głośniki lub słuchawki. Na parametry dźwięku znaczący wpływ ma dane
urządzenie takie jak: mikrofon, wzmacniacz czy głośnik.

Zjawiska magnetyzmu i elektromagnetyzmu mają zastosowanie w mikrofonach

i głośnikach. Zadaniem mikrofonu jest zamiana fal akustycznych na drgania napięcia
elektrycznego. Ze względu na sposób przetwarzania energii wyróżniamy dwa podstawowe typy
mikrofonów:

−

mikrofony dynamiczne (wykorzystują siłę elektrodynamiczną),

−

mikrofony pojemnościowe (wykorzystują zmianę napięcia na kondensatorze wywołaną
zmianą pojemności).
Mikrofony węglowe czy piezoelektryczne ze względu na wyjątkowo słabe parametry nie

znajdują zastosowania w akustyce.

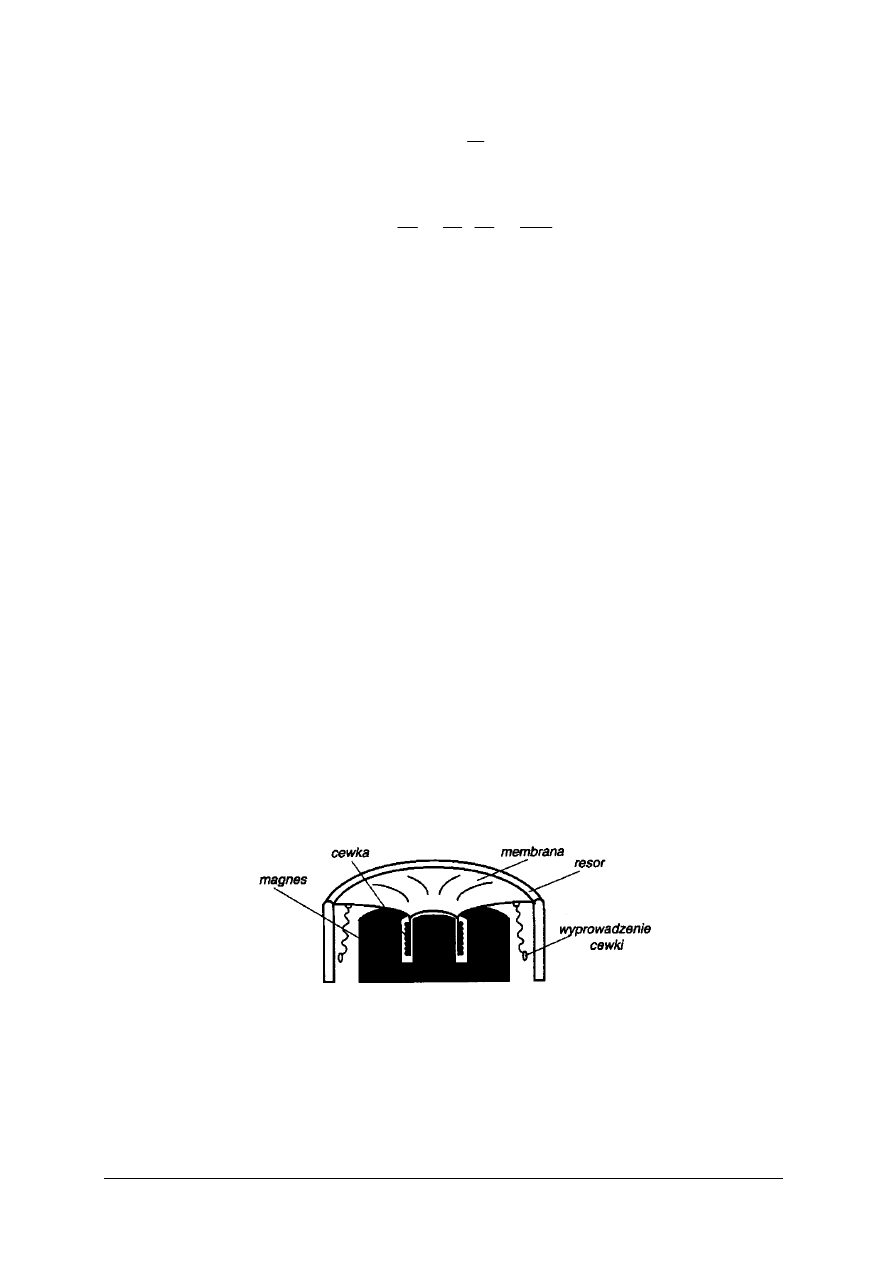
Budowa mikrofonu dynamicznego jest bardzo zbliżona do konstrukcji głośnika. Drgania

powietrza poruszają membranę i połączoną z nią cewkę umieszczoną w silnym polu
magnetycznym wytwarzanym przez magnes.

Rys. 14. Konstrukcja przetwornika w mikrofonie dynamicznym [12, s. 29]

W wyniku tego generowane jest napięcie na zaciskach cewki – siła elektrodynamiczna.

Podstawową zaletą tej konstrukcji jest prostota i brak konieczności zewnętrznego zasilania.
Jednak żeby uzyskać wyższe napięcie na wejściu mikrofonu, należy zastosować cewkę
o większej ilości zwojów, ta z kolei posiada dużą masę i rezystancję, a zatem większą

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

bezwładność i szumy termiczne. W konsekwencji mikrofon będzie miał trudności
z przetwarzaniem wyższych częstotliwości i szybkich impulsów.

Ze względu na nieporównywalnie mniejszą masę elementu drgającego wady tej nie

posiadają mikrofony pojemnościowe. Do przetwarzania fal dźwiękowych na napięcie służy też
specjalnie skonstruowany kondensator, w którym membrana wykonana z bardzo cienkiej
(1-20mikrometrów) i elastycznej folii z napyloną warstwą złota stanowi jedną okładkę, drugą zaś
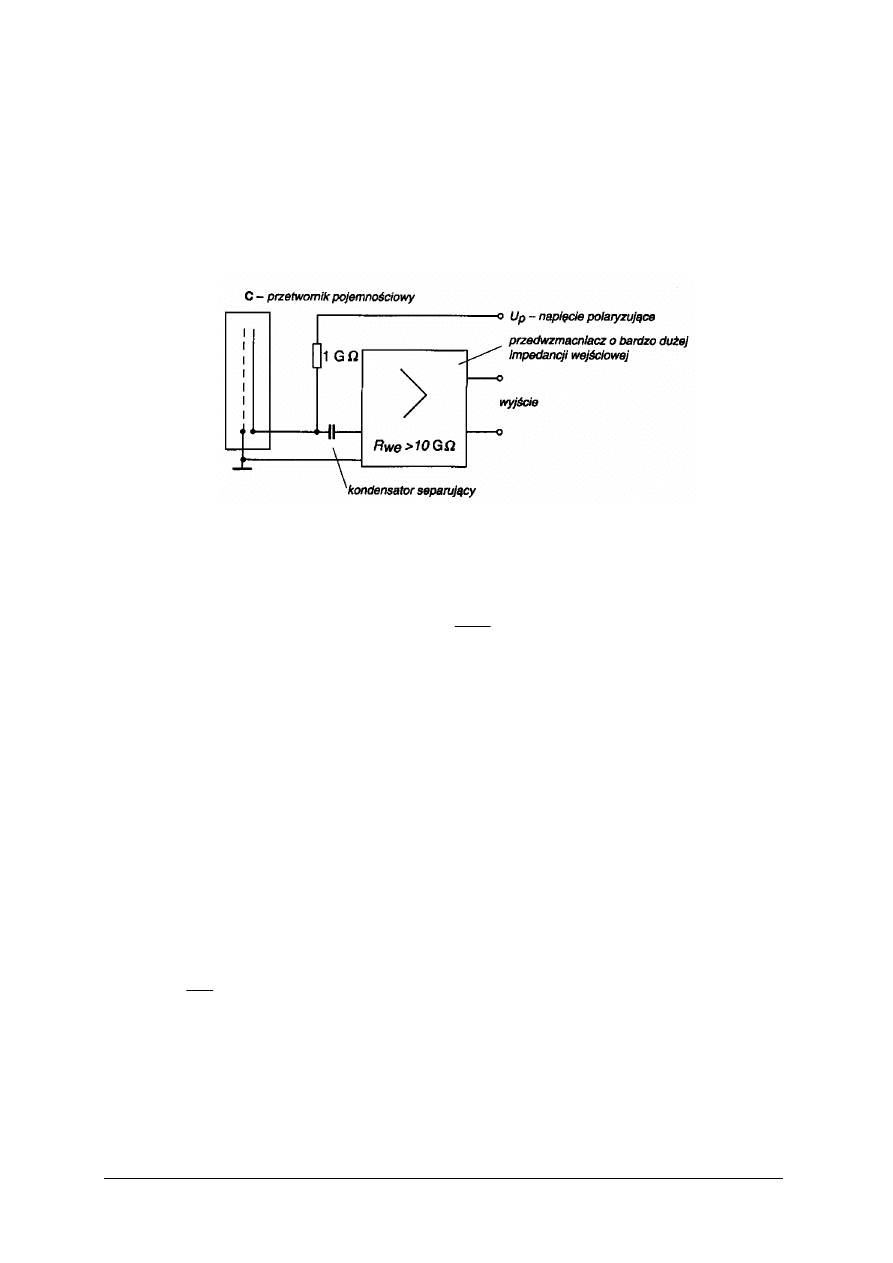
jest umieszczona w niewielkiej odległości drobna siatka metalowa. Uproszczony schemat
blokowy mikrofonu pojemnościowego przedstawia rysunek

Rys. 15. Schemat blokowy mikrofonu pojemnościowego [12, s. 30]

Drgania powietrza wprowadzają w ruch membranę, w wyniku czego zmienia się jej

odległość od drugiej okładki. Zatem pojemność kondensatora będzie również ulegać zmianom
odwrotnie proporcjonalnym do wychylenia membrany, co ilustruje poniższy wzór:

⋅

gdzie:
C – pojemność kondensatora,
E – współczynnik przenikalności dielektrycznej (w tym przypadku powietrza),
S – powierzchnia okładki,
d – odległość między okładkami.

Gdy kondensator C zostanie uprzednio naładowany za pośrednictwem rezystora R=1G

Ω

napięcia polaryzacyjnego Up zgromadzony w nim ładunek Q wyniesie:

⋅

gdzie:
Q – ładunek elektryczny w kulombach [C],
Up – napięcie na kondensatorze w woltach [V],
C – pojemność kondensatora w faradach [F],

Przy ogromnej impedancji przedwzmacniacza i stałej czasowej obwodu ładującego

⋅

znacznie dłuższej do szybkości drgań akustycznych ładunek nie będzie ulegał zmianie,

zaś w wyniku wychyleń membrany zmieniać się będzie napięcie na kondensatorze.

∆

gdzie Q – ładunek zgromadzony na kondensatorze,

∆

C – odchyłka pojemności wywołana ruchami membrany,

∆

U – zmiana napięcia na kondensatorze.

Odseparowanie przetwornika od przedwzmacniacza umożliwia wzmacnianie tylko

wielkości delta U, wynikającej z drgań membrany. Bardziej obrazowo zasadę działania
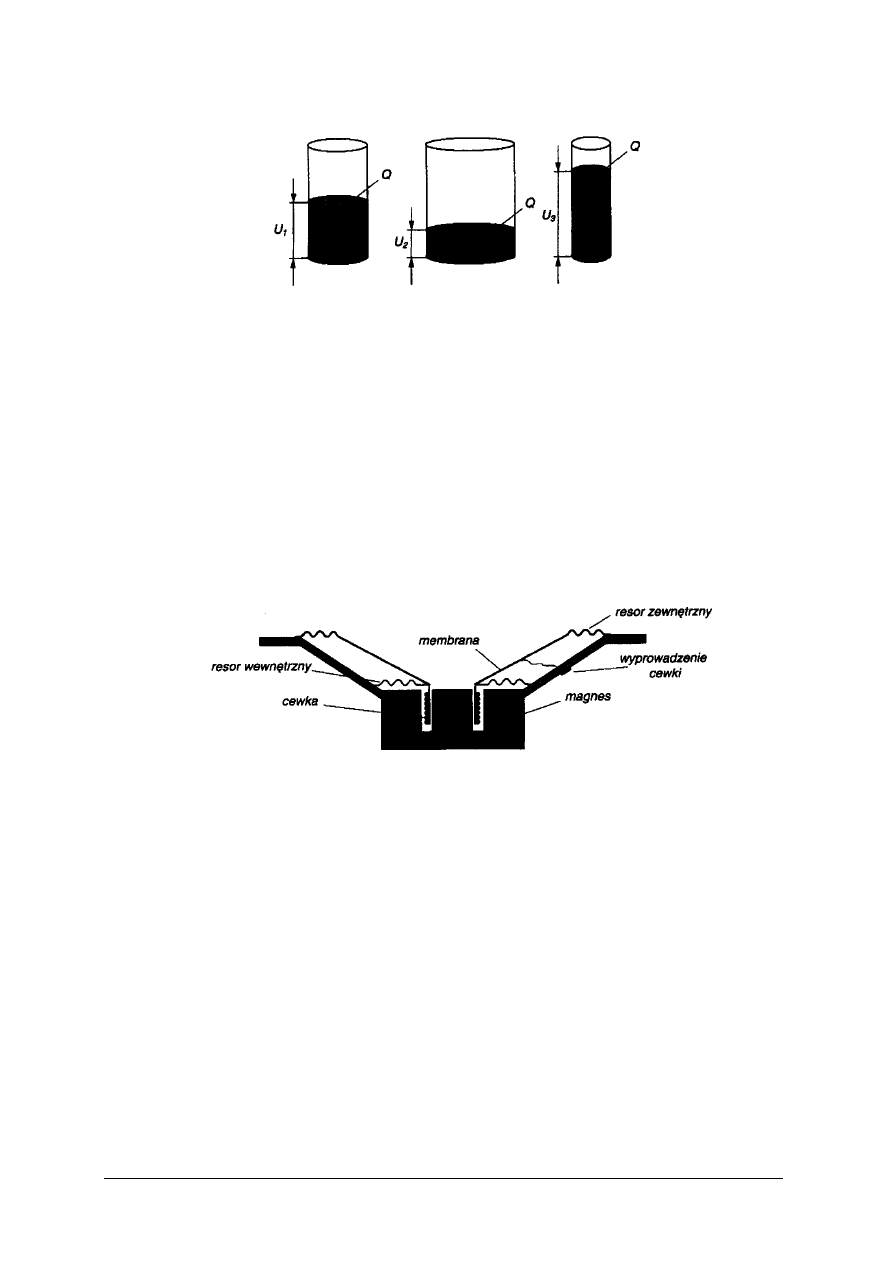
mikrofonu pojemnościowego tłumaczy poniższy rysunek

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 16. Ilustracja zasady działania mikrofonu pojemnościowego [12, s. 31]

Jeśli porównamy pojemność kondensatora do pojemności naczynia, zgromadzony ładunek

do ilości cieczy, a napięcie na kondensatorze do poziomu tej cieczy, to łatwo zauważymy, że ta
sama ilość płynu Q wlana do naczynia o dużej pojemności ustali niższy poziom U

, niż gdy

umieścimy ją w naczyniu o małej pojemności.

Odmianą mikrofonu pojemnościowego jest mikrofon elektretowy. Membrana jest tutaj

powleczona warstwą dielektryka spolaryzowanego (elektretu). Kondensator jest jakby na stałe
naładowany, przez co mikrofon taki nie wymaga dodatkowego zasilania (jedynie dla
przedwzmacniacza).

Zadaniem głośnika jest zamiana energii elektrycznej na akustyczną. W sprzęcie

nagłośnieniowym i odsłuchach studyjnych stosowane są niemal wyłącznie głośniki dynamiczne,
czyli wykorzystujące zjawisko powstawania siły elektrodynamicznej podczas przepływu prądu
w polu magnetycznym. Budowę głośnika dynamicznego ilustruje poniższy rysunek.

Rys. 17. Budowa głośnika dynamicznego [12, s. 92]

Cewka połączona z membraną głośnika umieszczona jest w silnym polu magnesu.

W wyniku przepływu prądu będzie wpychana lub wyciągana ze szczeliny z siłą proporcjonalną
do chwilowej wartości prądu, ruchy membrany będą odwzorowaniem kształtu napięcia
przyłożonego do zacisków głośnika. Rozwiązanie takie ma jedną poważną zaletę – jest bardzo
proste. Jednak uzyskanie dobrych parametrów przysparza wiele kłopotów. Stosunkowo duża
masa obwodu drgającego (cewki i membrany) powoduje znaczną bezwładność, uniemożliwiając
praktycznie odtwarzanie szybkich przebiegów impulsowych.

4.2.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

Jakie są własności połączenia szeregowego rezystorów?

Jakie są własności połączenia równoległego rezystorów?

Jakie obwody nazywa się rozgałęzionymi?

Jak brzmi I i II prawo Kirchhoffa?

Jak zapisuje się równania wyrażające I i II prawo Kirchhoffa?

Jak oblicza się rezystancję zastępczą połączenia szeregowego i równoległego rezystorów?

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Jakie zasady obowiązują podczas określania kierunków prądów i napięć strzałkami?

Jak obliczać wartości prądów i spadków napięć w układach mieszanych rezystorów?

Jaki obraz graficzny ma pole magnetyczne magnesów trwałych?

10.

Jak działa pole magnetyczne na przewodnik z prądem?

11.

Na czym polega zjawisko indukcji elektromagnetycznej?

12.

Jakie zastosowanie mają zjawiska magnetyczne i elektromagnetyczne w przetwornikach
elektroakustycznych?

13.

Jakie są rodzaje kondensatorów?

14.

Jak oblicza się pojemność elektryczną kondensatora?

15.

W jakich jednostkach mierzymy pojemność elektryczną?

4.2.3. Ćwiczenia

Ćwiczenie 1

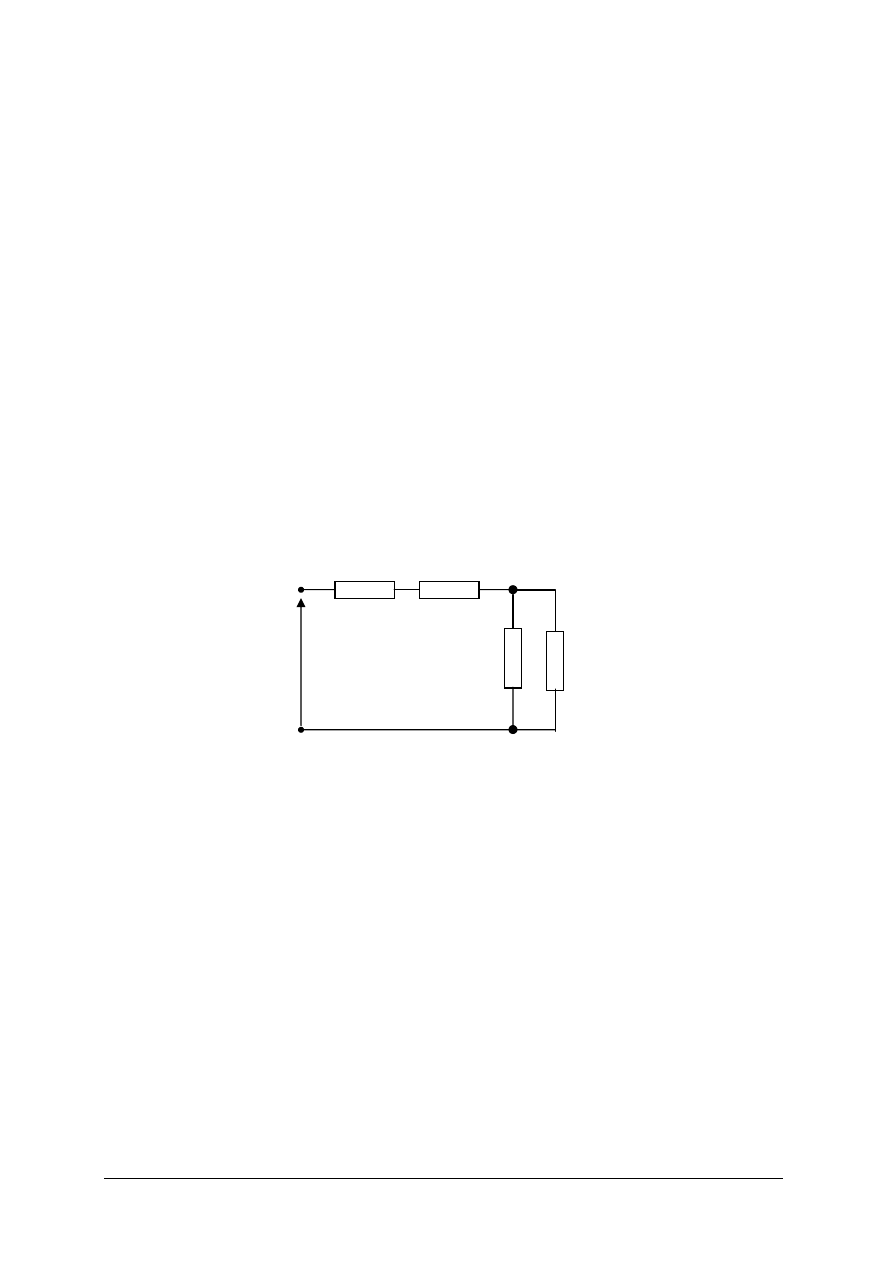
Oblicz wartości prądów w poszczególnych gałęziach układu przedstawionego na rysunku

oraz wartości spadków napięć na wszystkich rezystorach. Obliczenia wykonaj z dokładnością
do 0,01.

DANE:
U=10V,
R

=1Ω, R

=3Ω,

=2Ω, R

=4Ω,

U R

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

wypisać wielkości dane i szukane,

obliczyć rezystancję zastępczą układu,

obliczyć prąd zasilania w układzie,

obliczyć spadki napięć na rezystorach R

i R

obliczyć napięcie na zaciskach ab oraz prądy w gałęziach R

i R

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

literatura wskazana przez nauczyciela lub dotycząca materiału jednostki modułowej,

−

kalkulator,

−

film dydaktyczny przedstawiający łączenie rezystorów,

−

przybory do pisania, zeszyt do ćwiczeń.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

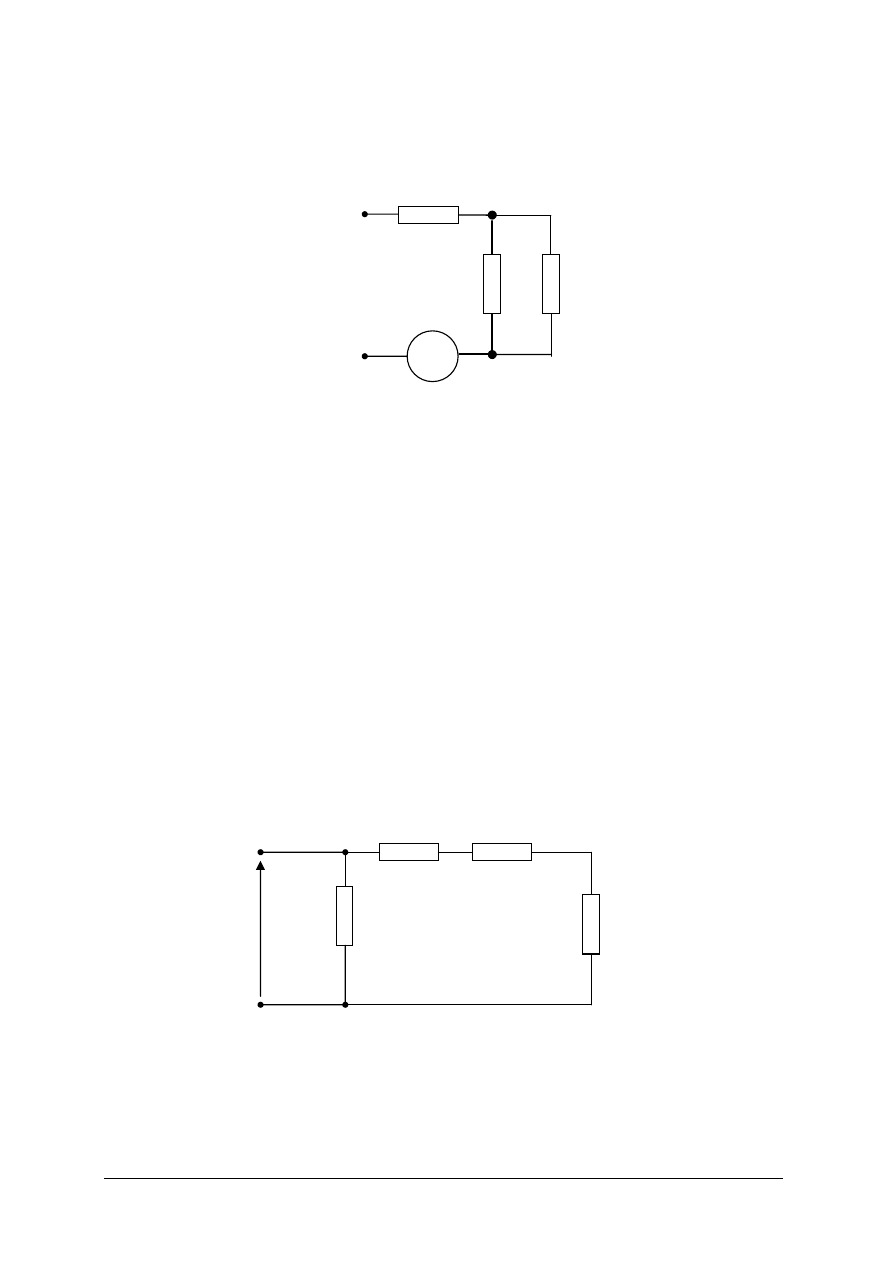
Ćwiczenie 2

Oblicz spadki napięcia na poszczególnych rezystorach w układzie pokazanym na rysunku,

jeżeli amperomierz wskazuje 3A, a rezystancje wynoszą R

=3Ω, R

=2Ω, R

=4Ω.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

wypisać wielkości dane i szukane,

obliczyć rezystancję zastępczą układu,

obliczyć napięcie zasilania,

obliczyć spadki napięcia na poszczególnych rezystorach,

wykonać ćwiczenie innym sposobem (metodą obliczeniową)

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

literatura wskazana przez nauczyciela lub dotycząca materiału jednostki modułowej,

−

kalkulator,

−

film dydaktyczny przedstawiający łączenie rezystorów,

−

przybory do pisania, zeszyt do ćwiczeń,

Ćwiczenie 3

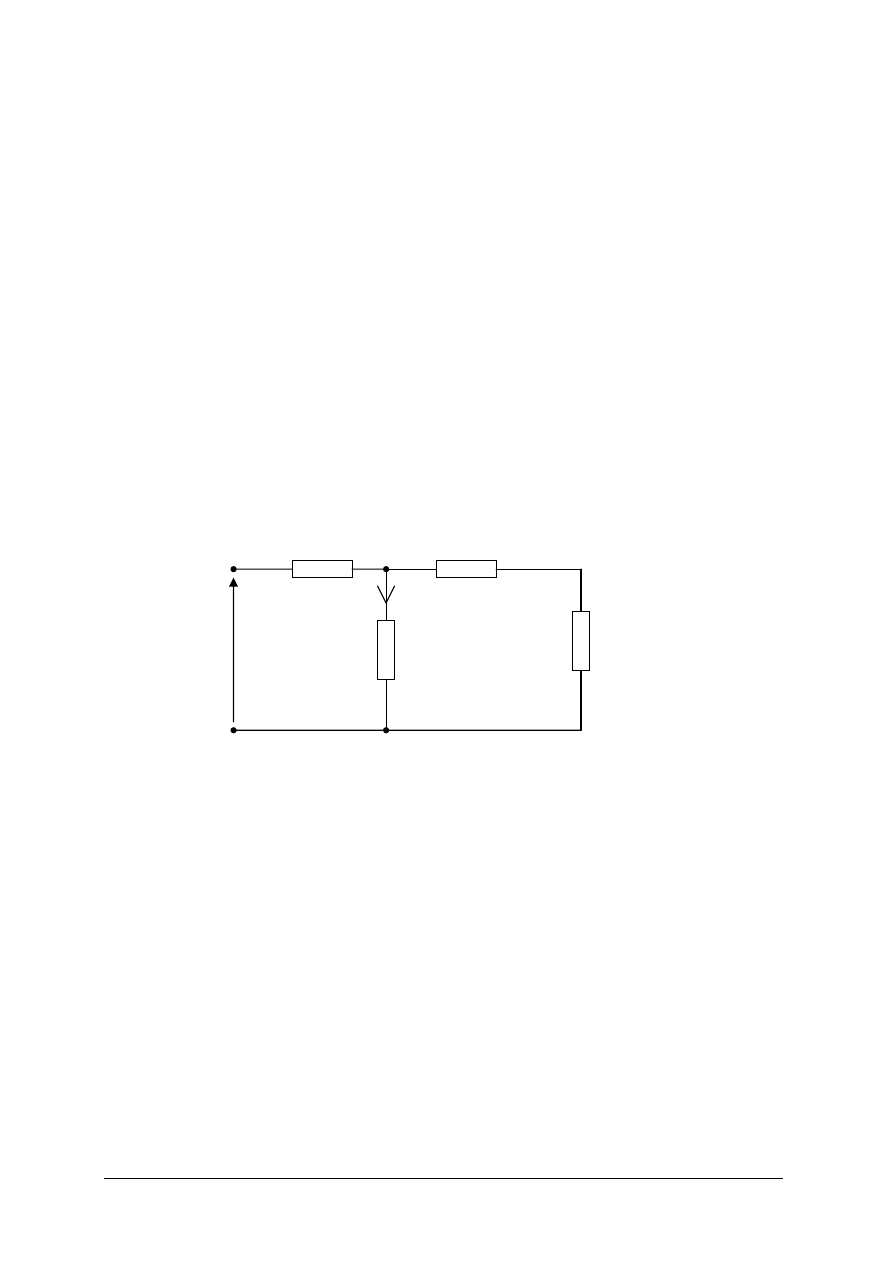
Oblicz w układzie przedstawionym na rysunku wszystkie spadki napięć oraz prądy

w gałęziach. Obliczenia wykonać z dokładnością do 0,01.

U=10V, R

=1Ω, R

=2Ω, R

=3Ω, R

=4Ω,

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

wypisać wielkości dane i szukane,

obliczyć rezystancję zastępczą układu,

obliczyć prąd zasilania,

obliczyć prądy w gałęziach,

obliczyć spadki napięć na rezystorach R2, R3, R4,

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

literatura wskazana przez nauczyciela lub dotycząca materiału jednostki modułowej,

−

kalkulator,

−

film dydaktyczny przedstawiający łączenie rezystorów w układzie mieszanym,

−

przybory do pisania, zeszyt do ćwiczeń,

Ćwiczenie 4

Oblicz napięcie zasilające oraz prądy w pozostałych gałęziach. I

=2A, R

=3Ω, R

=18Ω,

=3Ω, R

=6Ω.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

wypisać wielkości dane i szukane,

obliczyć spadek napięcia na rezystorze R2,

obliczyć wartość prądu płynącego przez rezystory R3 i R4,

obliczyć prąd zasilania układu,

obliczyć napięcie zasilania układu,

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

literatura wskazana przez nauczyciela lub dotycząca materiału jednostki modułowej,

−

kalkulator,

−

przybory do pisania,

−

zeszyt do ćwiczeń.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 5

Scharakteryzuj podstawowe zjawiska zachodzące w polu elektrycznym, magnetycznym

i elektromagnetycznym.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zapoznać się z materiałem nauczania oraz skorzystać z innych źródeł informacji,

opisać następujące zjawiska: pole magnetyczne jako pole elektrokinetyczne, działanie pola
magnetycznego

przewodnik

z prądem

elektrycznym,

zjawisko

indukcji

elektromagnetycznej, napięcie indukowane w przewodzie poruszającym się w polu
magnetycznym, indukcja własna i indukcja wzajemna,

podać przykłady zastosowania powyższych zjawisk w urządzeniach elektrycznych,

opracować wnioski i zaprezentować efekt pracy.

Wyposażenie stanowiska pracy:

−

film dydaktyczny o zjawiskach magnetycznych i elektromagnetycznych,

−

plansze kolorowe przedstawiające zjawiska magnetyczne i elektromagnetyczne,

−

komputer z dostępem do Internetu,

−

zeszyt i przybory do pisania,

−

literatura zgodna z punktem 6 poradnika dla ucznia.

Ćwiczenie 6

Określ i opisz wykorzystanie zjawisk magnetyzmu i elektromagnetyzmu w urządzeniach

dźwiękowych (przetwornikach elektroakustycznych).

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zapoznać się z materiałem nauczania oraz skorzystać z innych źródeł informacji,

wypisać elementy toru fonicznego (akustycznego),

opisać budowę i zasadę działania (ogólnie) tych elementów toru fonicznego, w których
wykorzystuje się zjawiska magnetyzmu i elektromagnetyzmu,

zademonstrować działanie urządzeń przetwarzających dźwięk,

opracować wnioski i zaprezentować efekt pracy.

Wyposażenie stanowiska pracy:

−

zestaw ćwiczeniowy z elementami toru fonicznego,

−

instrukcja do wykonania ćwiczenia,

−

komputer z dostępem do Internetu,

−

literatura zgodna z punktem 6 poradnika dla ucznia,

−

zeszyt i przybory do pisania.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.2.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

zdefiniować pojęcia: napięcie, prąd elektryczny, źródło napięcia,
obwód elektryczny, odbiornik?

wymienić elementy, które występują w obwodzie elektrycznym?

określić warunki, jakie muszą być spełnione, aby prąd płynął
w obwodzie?

opisać środowiska, w których może przepływać prąd elektryczny?

zastosować prawo Ohma do wykonywania obliczeń wielkości:
napięcia, prądu i rezystancji?

zastosować źródła energii elektrycznej w elektroakustyce?

określić zastosowanie ferromagnetyków w elektroakustyce?

wymienić i scharakteryzować materiały, które przewodzą prąd
elektryczny?

scharakteryzować różne stany źródła napięcia przy pomocy
schematów i równań matematycznych?

10)

sklasyfikować materiały magnetyczne?

11)

obliczać napięcie, rezystancję w obwodach stałych prądu?

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.3.

Prąd sinusoidalny jednofazowy. Moc prądu jednofazowego

jej

rodzaje.

Budowa

działanie

transformatora

jednofazowego. Obsługa oscyloskopu

4.3.1. Materiał nauczania

Wytwarzanie prądu sinusoidalnie zmiennego

Prąd nazywamy zmiennym, jeśli zmienia się w nim w czasie przynajmniej jedna

z następujących wielkości: zwrot, wartość. Przykłady prądu zmiennego przedstawiono
na rysunkach poniżej.

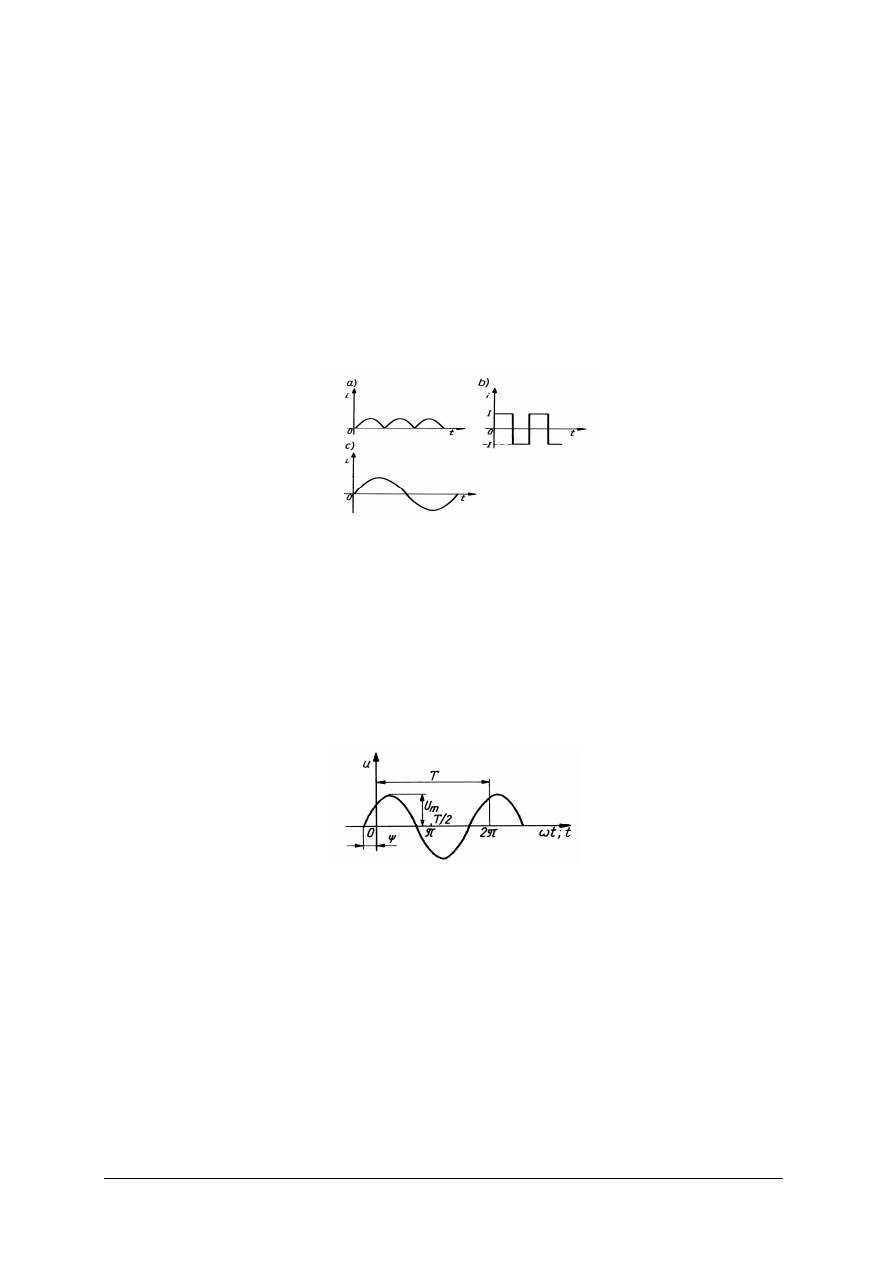
Rys. 18. Przykładowe przebiegi prądów zmiennych w czasie: a)pulsującego jednokierunkowego,

b) dwukierunkowego, c) sinusoidalnego

[źródło własne]

W naszym życiu codziennym wykorzystujemy napięcie sinusoidalnie zmienne, wytwarzane

przez prądnice prądu przemiennego, nazywane generatorami.

Powstałe napięcie ma następującą postać

sinα

– wartość maksymalna SEM nazywana też amplitudą.

Parametry przebiegu sinusoidalnego

Rozpatrzmy wykres napięcia sinusoidalnego.

Rys. 19. Wykres czasowy napięcia sinusoidalnego [4, s. 210]

Rozważania dotyczące przebiegu najczęściej rozpoczynamy w chwili t=0. Omawiany

przebieg jest już wtedy przesunięty o kąt ψ, a jego wartość jest dodatnia. Równanie napięcia ma
postać

ψ)

sin(ω

sinα

∗

u – wartość chwilowa napięcia,
U

– amplituda napięcia (wartość maksymalna napięcia),

T – czas jednego obrotu ramki nazywany okresem napięcia, jednostką jest 1sekunda [1s],
ω – prędkość obrotowa ramki, zwana pulsacją,
α – kąt nazywany fazą napięcia w dowolnej chwili,
ψ – kąt nazywany fazą początkową napięcia, odpowiadającą chwili t=0.

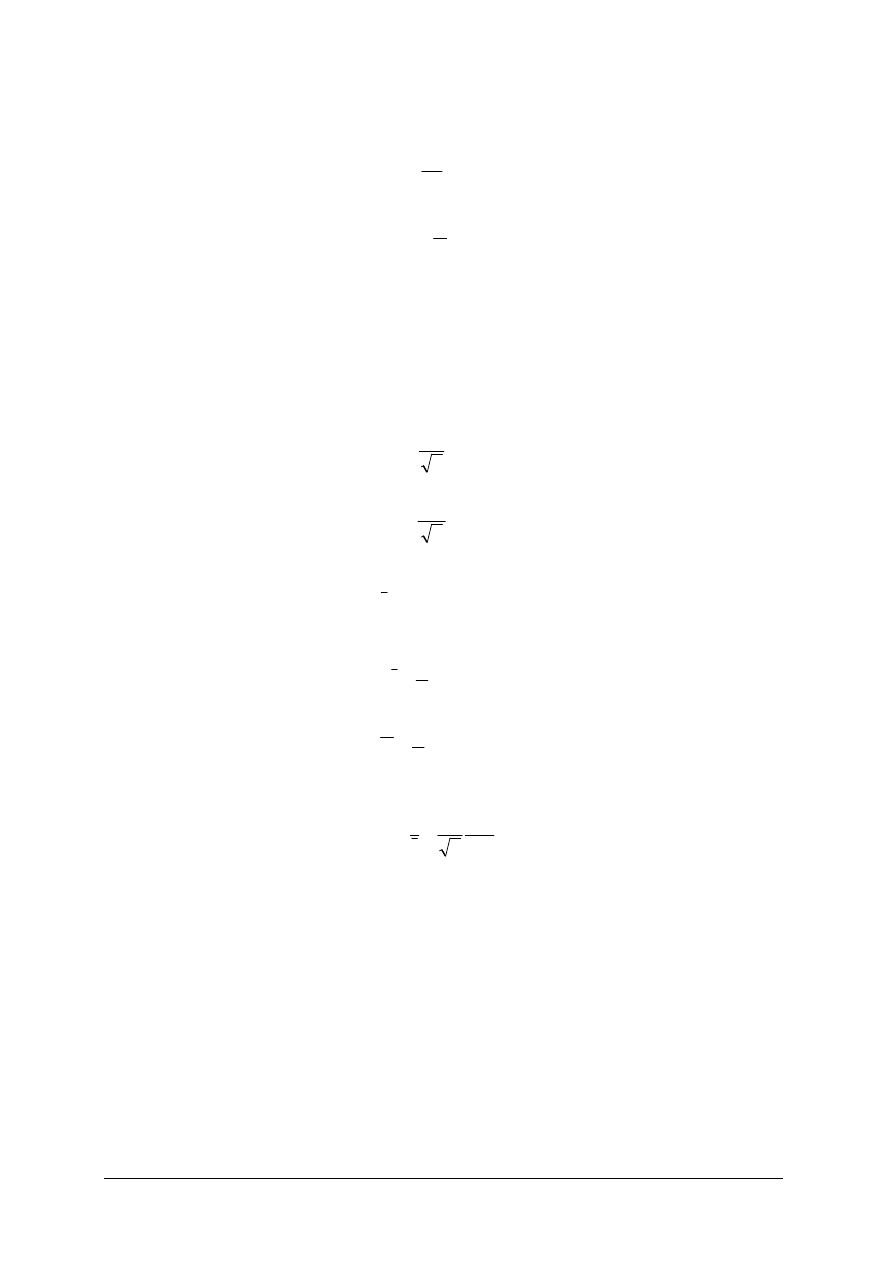
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Wprowadźmy dwa nowe pojęcia:

pulsację

[1rad/s]

2π

oraz częstotliwość f

[1Hz]

Korzystając z powyższych wzorów możemy napisać, że

2π

⋅

Wartość skuteczna i wartość średnia prądu sinusoidalnego

Wartością skuteczną I prądu sinusoidalnego nazywamy taką wartość prądu stałego, który

przepływając przez czas równy okresowi T prądu sinusoidalnego przez stałą rezystancję
R wydzieli w tej rezystancji taką moc, co prąd sinusoidalny w tym samym czasie T.
Można wykazać, że

0,707I

tak samo dla napięcia

0,707U

Wartość średnia za 1okres prądu sinusoidalnego jest równa zeru. Przebieg taki nazywamy

przebiegiem przemiennym.

Wartością średnią półokresową I prądu (napięcia) sinusoidalnego o okresie T, nazywamy

średnią arytmetyczną tego prądu (napięcia) za tę połowę okresu, w której przebieg jest dodatni.
Matematycznie

0,637I

tak samo dla napięcia

0,637U

Współczynnik kształtu przebiegu k

. Jest to stosunek wartości skutecznej do wartości

średniej. Obliczmy ten współczynnik dla prądu sinusoidalnego.

1,11

Przesunięcie fazowe między przebiegami sinusoidalnymi

Przebiegi czasowe o tej samej częstotliwości nazywamy przebiegami synchronicznymi.

Przesunięciem fazowym dwóch przebiegów synchronicznych nazywamy różnicę faz
początkowych tych przebiegów. Przesunięcie fazowe tych przebiegów wynosi (ψ

- ψ

Mówimy też, że napięcie u

wyprzedza w fazie napięci u

(kąt ψ

> ψ

). Odpowiednie równania

opisujące te napięcia mają postać:

sin(ωt+ψ

)

oraz

sin(ωt+ψ

)

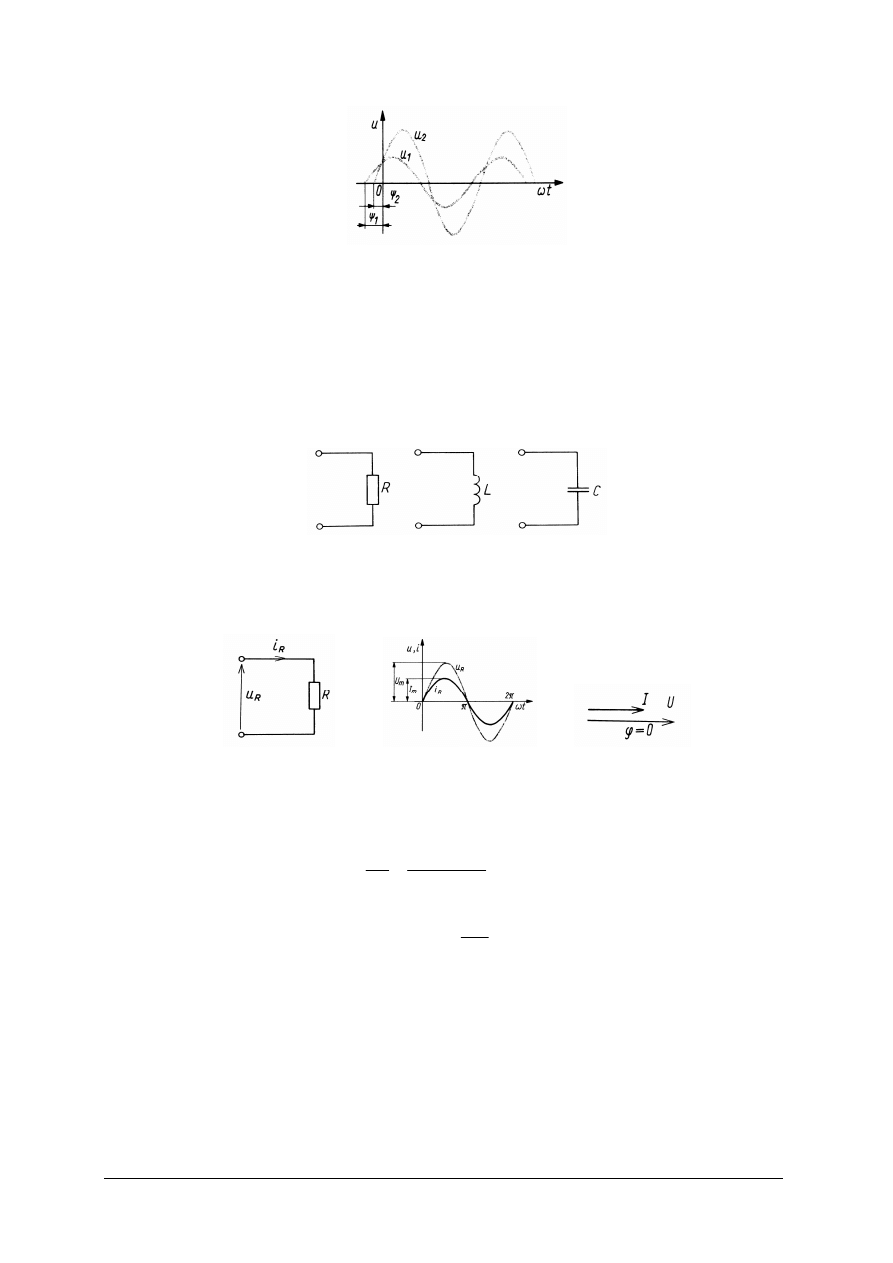
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 20. Wykres czasowy dwóch napięć sinusoidalnych przesuniętych w fazie [4, s. 219]

W ten sam sposób określamy różnicę faz między napięciem i prądem sinusoidalnym, ale

różnicę tę oznaczamy specjalnie małą literą grecką φ (czyt. fi).

Obwód prądu zmiennego z idealnymi elementami RLC

Symbole elementów idealnych stosowane na schematach elektrycznych przedstawiono na

poniższym rysunku. Jak widać każdy z tych elementów ma dwa zaciski i dlatego nazywamy je
dwójnikami.

Rys. 21. Symbole graficzne elementów: rezystora idealnego, cewki idealnej, kondensatora idealnego [4, s. 230]

Idealny element o rezystancji R

Dołączmy do idealnego elementu rezystancyjnego napięcie

sinωt

Rys. 22. Dwójnik o rezystancji R – schemat obwodu, wykres czasowy napięcia i prądu, wykres wektorowy [4, s. 231]

Wartość chwilową prądu wyznaczymy z prawa Ohma

sinω

∗

gdzie amplituda prądu

Można wykazać, że prawo Ohma jest spełnione dla wartości skutecznych i amplitud prądu

i napięcia. Jak wynika z obliczeń oraz wykresów czasowych i wektorowych napięcie u

oraz

natężenie prądu i

mają tę samą fazę początkową, kąt φ=0. O sytuacji takiej mówimy, że prąd

i napięcie są ze sobą w fazie.

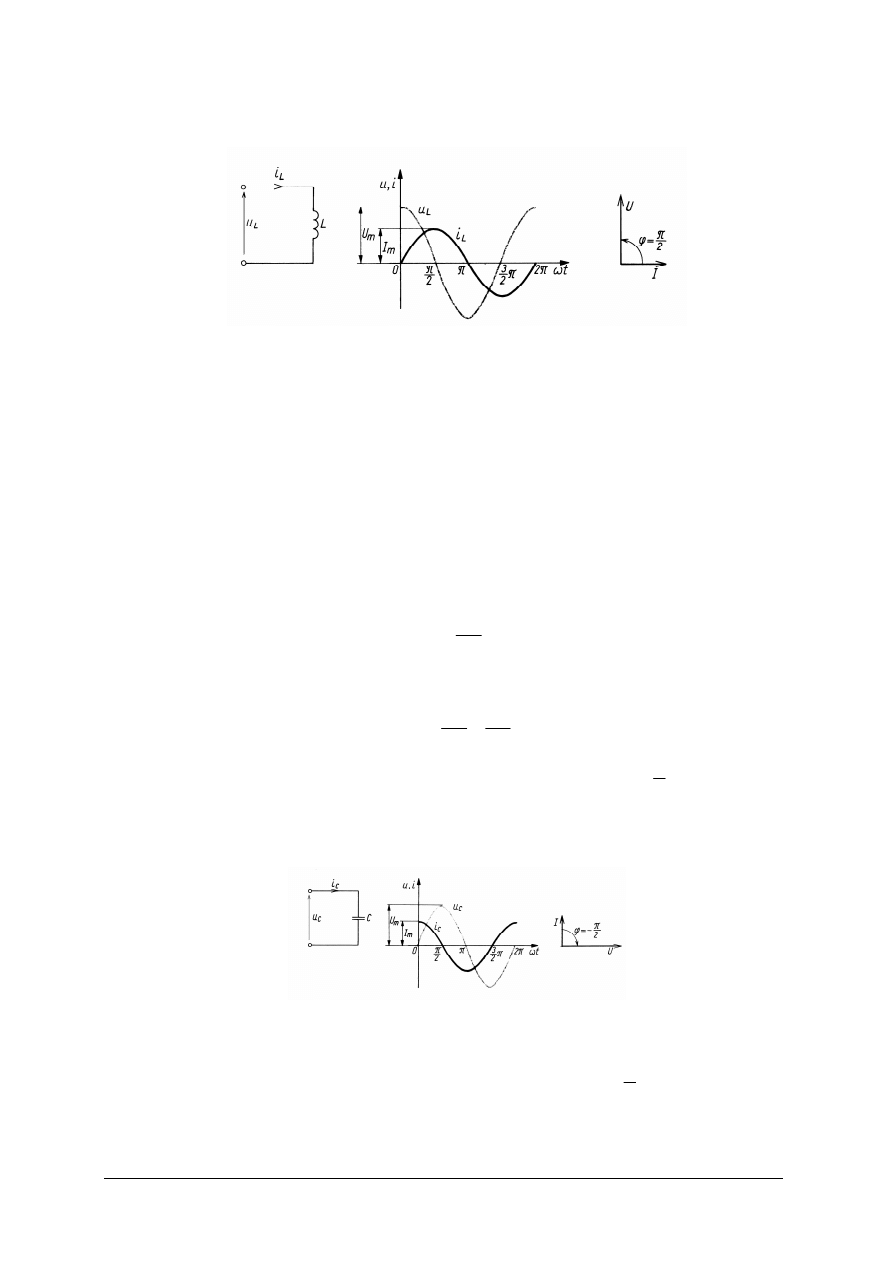
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Idealny element o indukcyjności L

Zasilmy idealny element o indukcyjności L napięciem u

Rys. 23. Dwójnik o indukcyjności L schemat obwodu, wykres czasowy napięcia i prądu, wykres wektorowy

[4, s. 233]

Załóżmy, że przez cewkę płynie prąd i

sinωt.

Przepływ prądu wytwarza siłę elektromotoryczną, której wartość jest równa napięciu u

=ωLI

cosωt=U

sin(ωt+π/2)

stąd wynika, że

ωLI

oraz

U=ωLI

Wprowadźmy oznaczenie

=ωL=2πfL.

Wielkość tę nazywamy reaktancją indukcyjną lub oporem biernym indukcyjnym. Jednostką

jest 1 om [1Ω].

Uwzględniając powyższe rozważania możemy napisać prawo Ohma dla wartości

skutecznych dla cewki idealnej.

Dopełnijmy tok myślenia i wprowadźmy jeszcze odwrotność reaktancji, czyli susceptancję

indukcyjną albo inaczej przewodność bierną indukcyjną B

. Jednostką jest 1 simens [1S].

Zauważmy, że w obwodzie z cewką idealną napięcie wyprzedza prąd o kąt

Idealny element o pojemności C

Zasilmy idealny element o pojemności C napięciem u

sinωt.

Rys. 24. Dwójnik o pojemności C schemat obwodu, wykres czasowy napięcia i prądu, wykres wektorowy

[4, s. 237]

W obwodzie popłynie prąd i

o wartości

)

sin(ω

cos(ω

∗

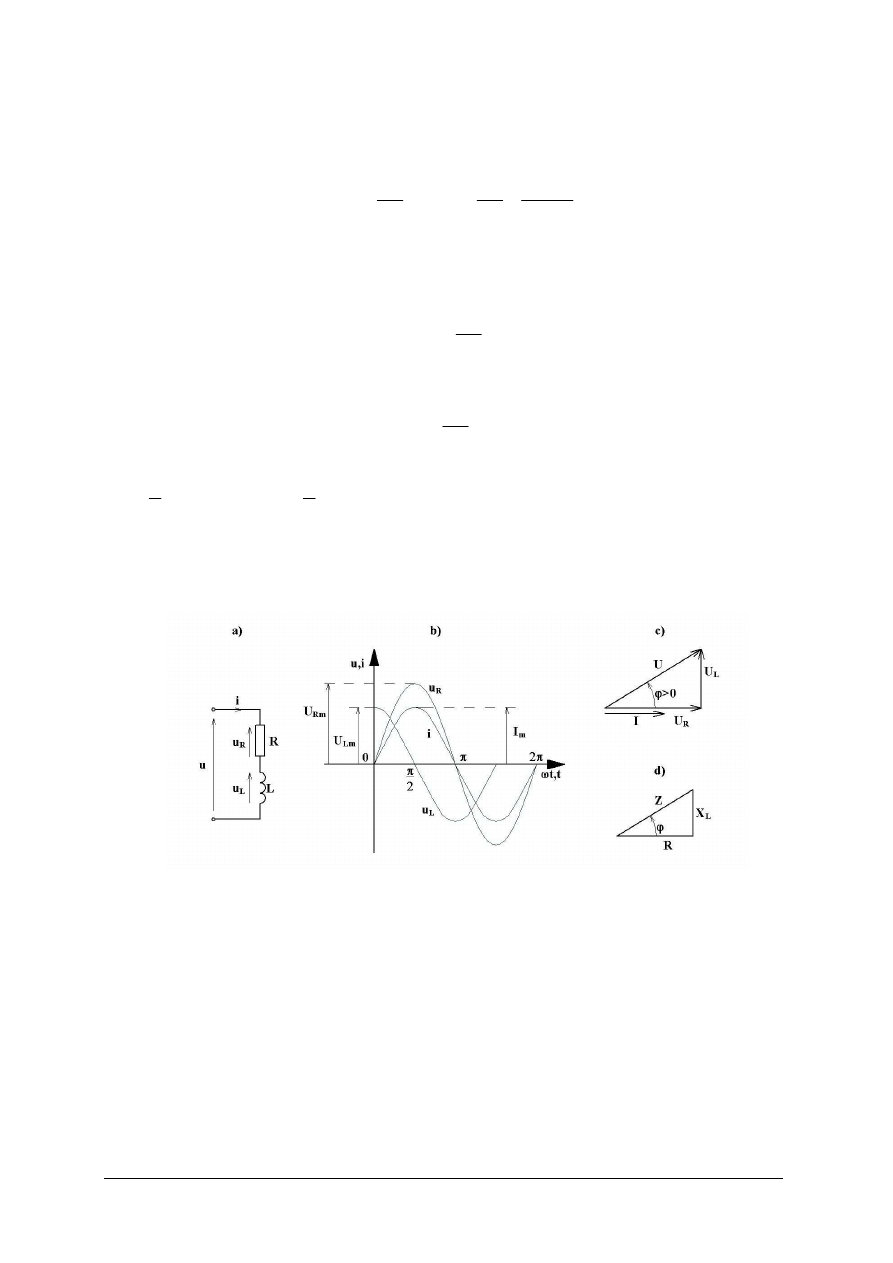
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

stąd wynika, że

ωCU

= I

oraz

I=ωCU

Wprowadźmy oznaczenie

= ωC

2π

ωC

∗

Wielkość tę nazywamy reaktancją pojemnościową lub oporem biernym pojemnościowym.

Jednostką jest 1 om [1Ω].

Uwzględniając powyższe rozważania możemy napisać prawo Ohma dla wartości

skutecznych dla cewki idealnej.

Odwrotność reaktancji nazywamy susceptancją pojemnościową albo inaczej przewodnością

bierną pojemnościową B

. Jednostką jest 1 simens [1S].

Zauważmy, że w obwodzie z pojemnością idealną napięcie opóźnia się względem prądu

o kąt 2

, a zatem kąt

−

Obwód szeregowy RL

Szeregowe połączenie R i L to zarówno połączenie idealnego rezystora z idealną cewką, jak

też schemat zastępczy rzeczywistej cewki o indukcyjności L i rezystancji R (rys. 11).

Rys. 25. Dwójnik szeregowy R, L: a) schemat dwójnika, b) wykres czasowy napięć i prądu, c) wykres wektorowy

napięć, d) trójkąt impedancji [4, s. 241]

W tym obwodzie:

u = u

+ u

Jeżeli:

i = I

sinωt,

to: u = R I

sinωt + ωLIm sin(ωt + π/2)

= U

sinωt + U

sin(ωt + π/2) = U

sin(ωt +φ)

Dodawaniu wartości chwilowych napięć zgodnie z drugim prawem Kirchhoffa odpowiada

dodawanie geometryczne wektorów odwzorowujących te napięcia:
wartości maksymalnych:

= U

+ U

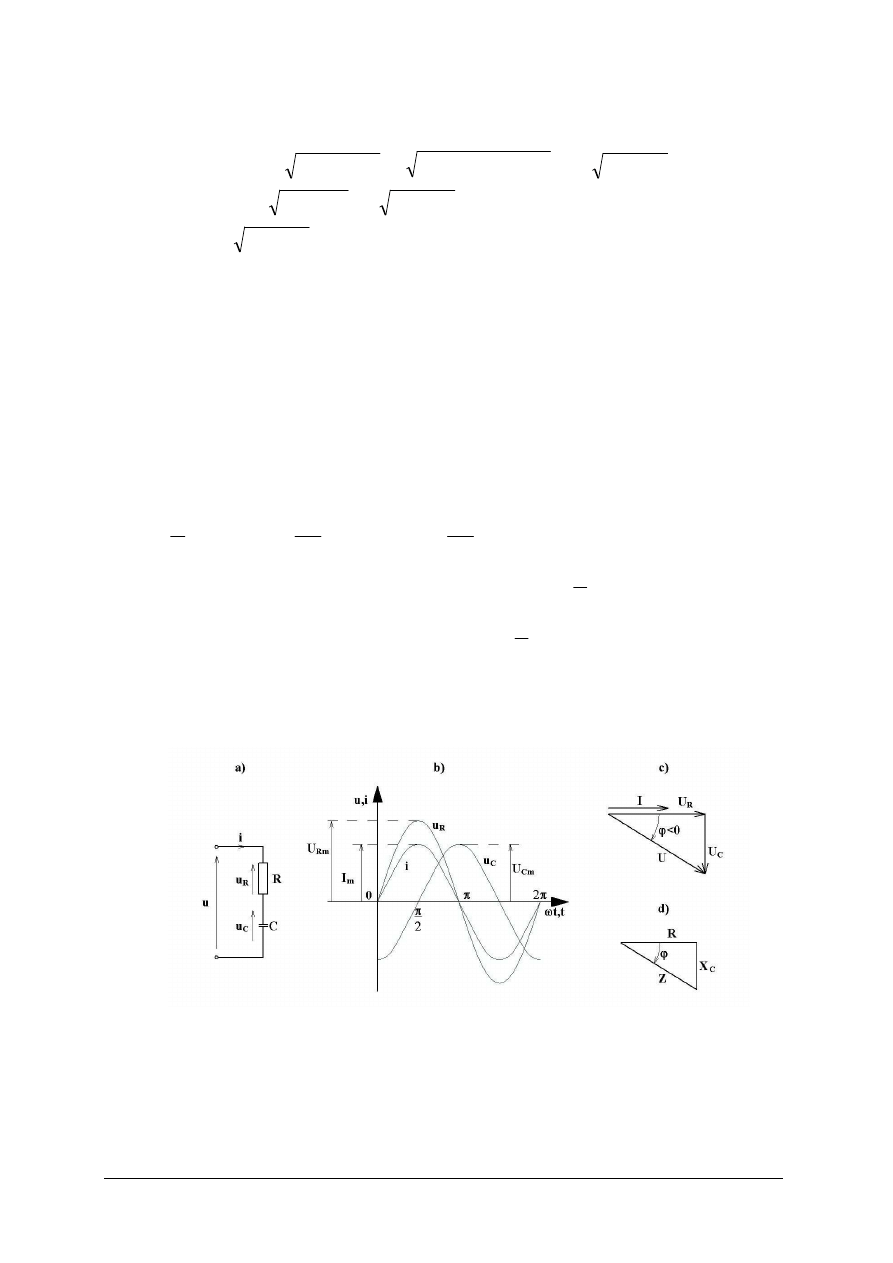
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

wartości skutecznych:

U = U

+ U

2
Lm

2
Rm

)

(

)

(

= I

oraz:

U =

2
L

2
R

= I

Oznaczamy: Z =

Z – impedancja ( opór pozorny ) dwójnika szeregowego RL, jednostką impedancji jest 1 ohm
(1 Ω).
φ

– kąt przesunięcia fazowego: φ = φ

– φ

Prawo Ohma dla dwójnika RL zasilanego napięciem sinusoidalnym:

U = IZ

Ponieważ moduły napięć są proporcjonalne do prądu, czyli: U

= IR, U

= I X

U = IZ, to

po podzieleniu boków trójkąta napięć przez prąd I otrzymujemy trójkąt impedancji o bokach R,
X

, Z, który jest trójkątem podobnym do trójkąta napięć. Wynika z niego, że:

R = Z cos φ
X

= Z sin φ

cos φ

sin φ

tg φ

Kąt φ dla dwójnika RL jest dodatni zawarty w przedziale 0≤ φ ≤ 2

Dla φ = 0 dwójnik jest idealnym dwójnikiem R, dla φ = 2

– idealny dwójnik L.

Obwód szeregowy RC

Szeregowe połączenie rezystora o rezystancji R i kondensatora o pojemności C zasilanych

napięciem sinusoidalnym oraz wykresy dla tego dwójnika przedstawia (rys. 12).

Rys. 26. Dwójnik szeregowy RC: a) schemat dwójnika, b) wykres czasowy napięć i prądu, c) wykres wektorowy

napięć, d) trójkąt impedancji [4, s. 247]

W tym obwodzie:

u = u

+ u

Jeżeli:

i = I

sinωt,

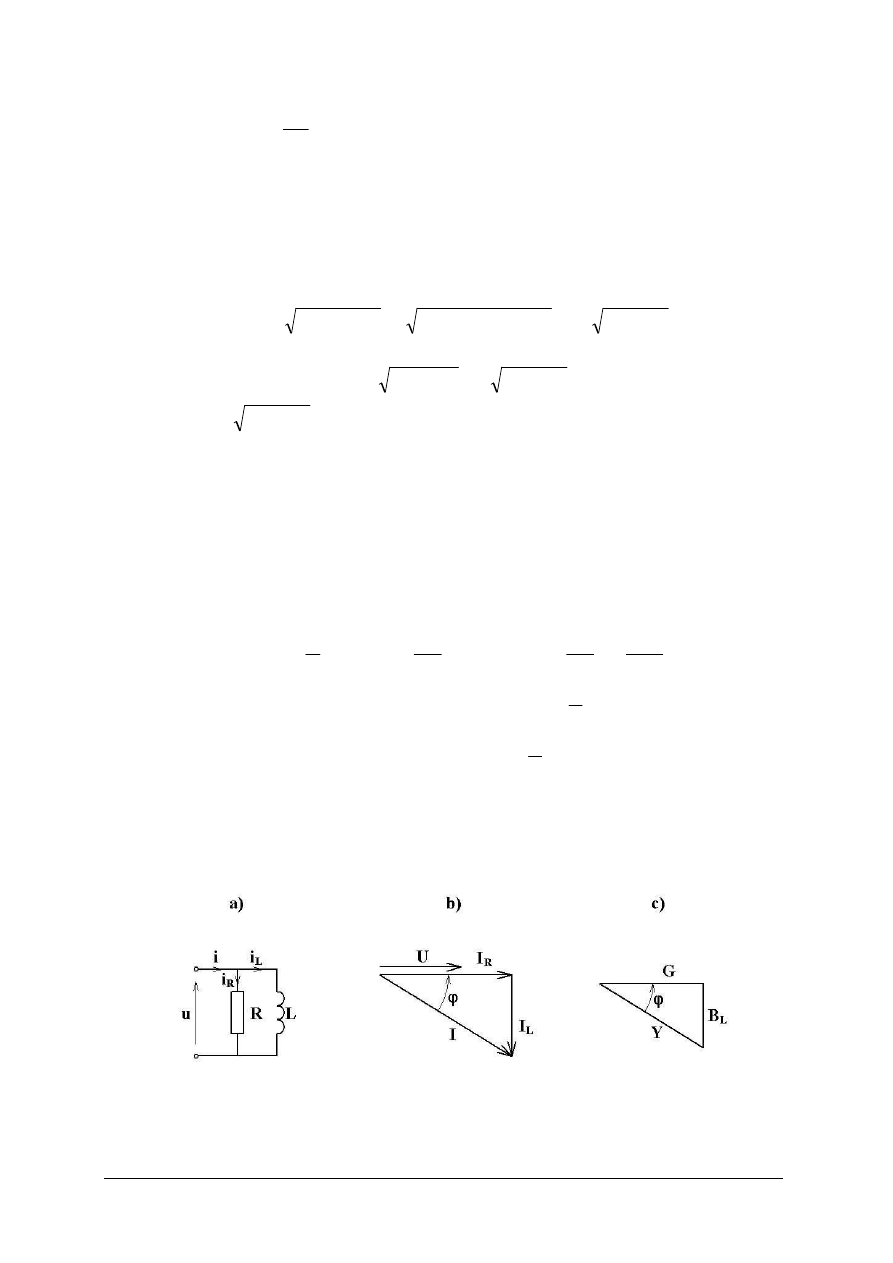
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

to: u = R I

sinωt + C

Im sin(ωt – π/2)

= U

sinωt + U

sin(ωt – π/2) = U

sin(ωt +φ).

Dodawaniu wartości chwilowych napięć zgodnie z drugim prawem Kirchhoffa odpowiada

dodawanie geometryczne wektorów odwzorowujących te napięcia:

−

wartości maksymalnych:

= U

+ U

−

wartości skutecznych:

U = U

+ U

2
Cm

2
Rm

)

(

)

(

= I

oraz:

U =

2
C

2
R

= I

Oznaczamy: Z =

Z – impedancja (opór pozorny) dwójnika szeregowego RC, jednostką impedancji jest
1 ohm (1Ω).
φ

– kąt przesunięcia fazowego: φ = φ

– φ

Prawo Ohma dla dwójnika RL zasilanego napięciem sinusoidalnym:

U = IZ

Moduły napięć są proporcjonalne do prądu, czyli: U

= I*R, U

= I*X

U = I*Z. Trójkąt

impedancji o bokach R, X

, Z jest trójkątem podobnym do trójkąta napięć. Wynika z niego, że:

R = Z cos φ

= – Z sin φ

cos φ

sin φ

= –

tg φ

= –

−

Kąt φ dla dwójnika RC jest ujemny, zawarty w przedziale

– 2

≤

φ≤ 0

Dla φ = 0 dwójnik jest idealnym dwójnikiem R, dla φ = – 2

– idealny dwójnik C (R = 0).

Równoległe połączenie R i L

Dla równoległego połączenia R i L (rys. 14) , zgodnie z I prawem Kirchhoffa

i = i

+ i

Rys. 27. Układ równoległy R,L: a)schemat, b) wykres wektorowy, c) trójkąt admitancji [4, s. 258

]

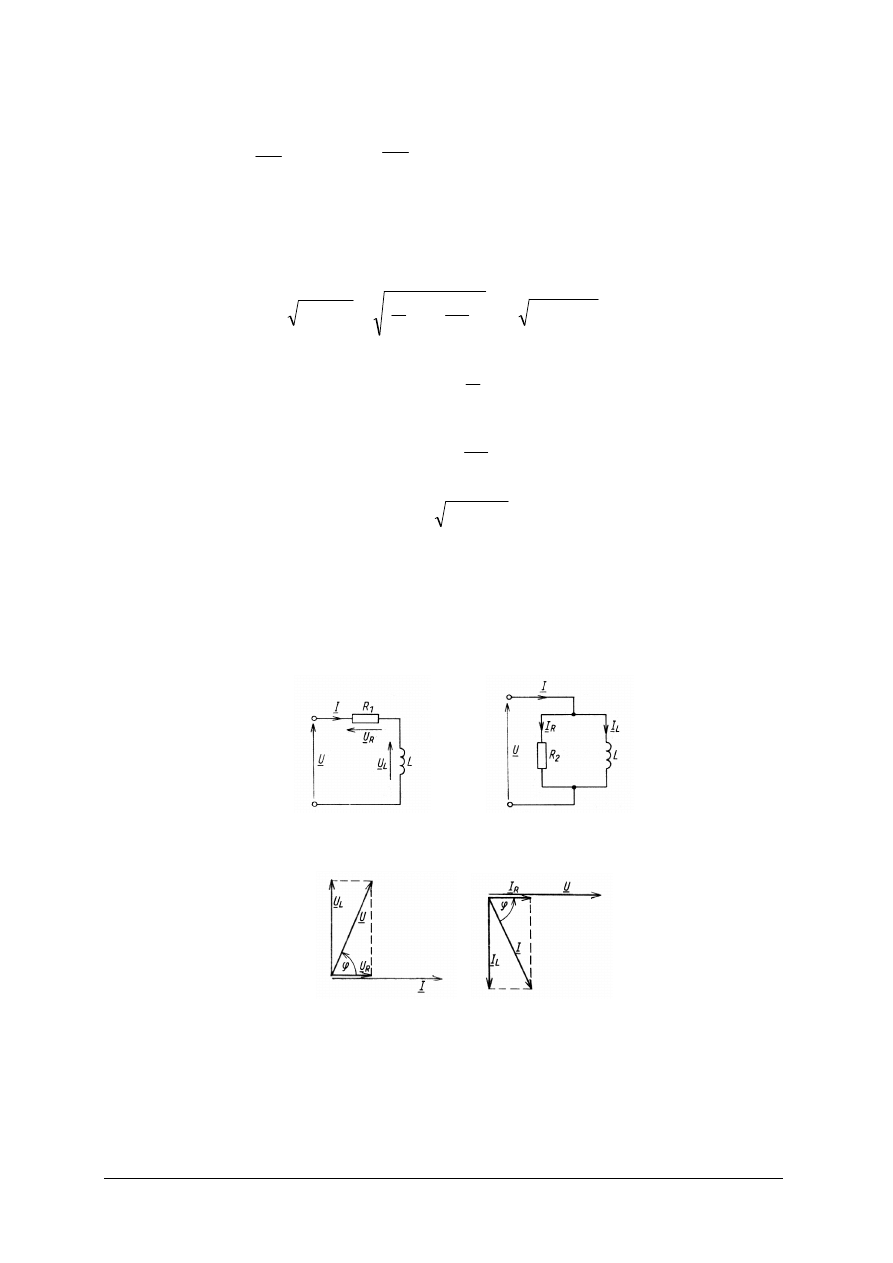
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Jeżeli napięcie zasilające dwójnik ma wartość: u = U

sinωt, to:

= R

sinωt, i

sin(ωt – π/2),

i = I

sin(ωt – φ),

φ – kąt przesunięcia fazowego: φ = φ

– φ

Wektor prądu I pobieranego przez dwójnik RL: I = I

+ I

Dla wartości maksymalnych: I

= I

+ I

Moduł wartości skutecznej prądu (długość wektora I ):

)

(

)

(

gdzie:

−

konduktancja (przewodność czynna): jednostką konduktancji jest 1S (simens),

−

susceptancja (przewodność bierna), jednostką konduktancji jest 1 S (simens),

−

admitancja (przewodność pozorna).
Dla równoległego połączenia R i L można wykreślić trójkąt admitancji, którego boki są

proporcjonalne do odpowiednich boków trójkąta prądów (rys. 14), ponieważ:

= UG,

= U B

I = UY

Rzeczywistą cewkę (przy pominięciu pojemności międzyzwojowej i pojemności względem

ziemi) można przedstawić jako szeregowe bądź równoległe połączenie idealnych elementów
R i L (rys. 15) i odpowiadające tym schematom zastępczym wykresy wektorowe – (rys. 16).

Rys. 28. Schematy zastępcze cewki rzeczywistej: a) schemat szeregowy, b) schemat równoległy [4, s. 261]

Rys. 29. Wykresy wektorowe napięć i prądów dla cewki rzeczywistej: a) wykres dla schematu szeregowego,

b) wykres dla schematu równoległego [4, s. 262

]

Tangens kąta φ nazywamy dobrocią cewki i oznaczamy Q

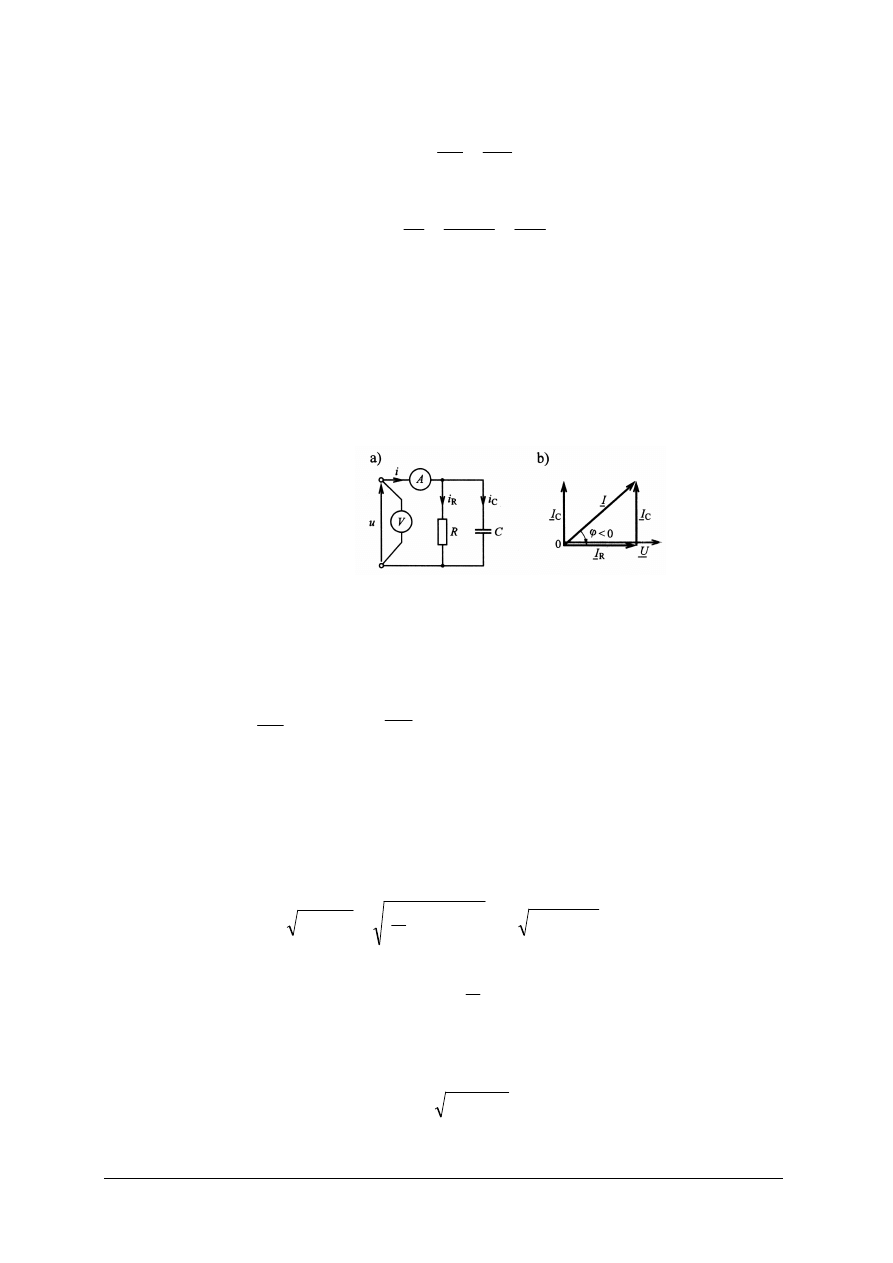
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Dla schematu szeregowego:

Dla schematu równoległego:

Im mniejsza rezystancja cewki, tym większa jej dobroć.

Równoległe połączenie R i C

Dla równoległego połączenia R i C (rys. 17) zgodnie z I prawem Kirchhoffa:

i = i

+ i

Rys. 30. Układ równoległy RC zasilany napięciem sinusoidalnym: a) schemat obwodu, b) wykres wektorowy [4, s. 259]

Jeżeli napięcie zasilające dwójnik ma wartość:

u = U

sinωt,

to:

= R

sinωt, i

sin(ωt + π/2)

i = I

sin(ωt + φ)

Wektor prądu I pobieranego przez dwójnik RC:

I = I

+ I

Dla wartości maksymalnych:

= I

Moduł wartości skutecznej prądu (długość wektora I ):

)

(

)

(

gdzie:

−

konduktancja (przewodność czynna): jednostką konduktancji jest 1 simens (1S),

−

susceptancja (przewodność bierna), jednostką konduktancji jest 1 simens (1S),

−

admitancja (przewodność pozorna).

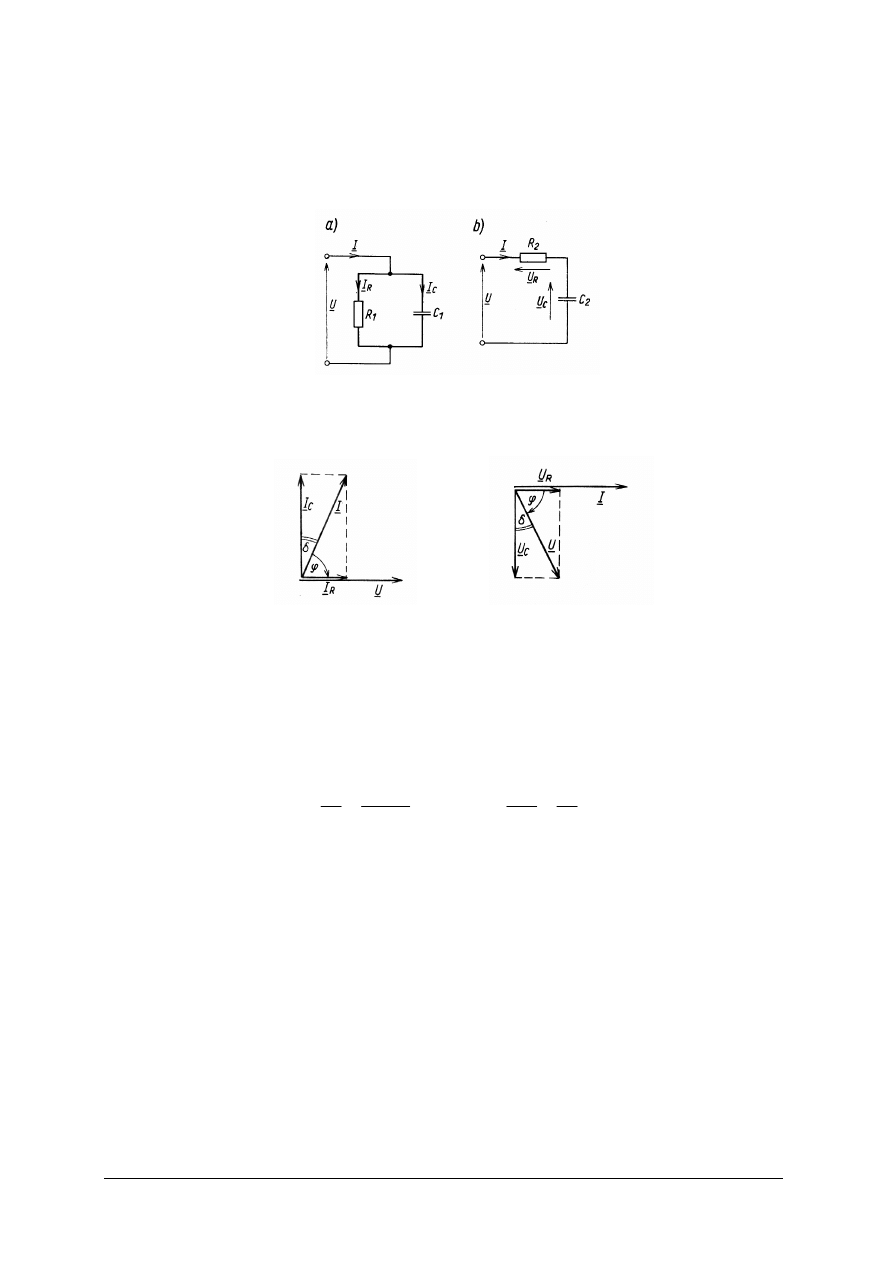
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Dla równoległego połączenia R i C można wykreślić trójkąt admitancji, którego boki są

proporcjonalne do odpowiednich boków trójkąta prądów, ponieważ:

= U*G,

= U*B

, I = U*Y.

Schemat zastępczy rzeczywistego kondensatora można przedstawić jako równoległe lub

szeregowe połączenie R i C (rys. 18).

Rys. 31. Schematy zastępcze kondensatora rzeczywistego: a) schemat równoległy, b) schemat szeregowy [4, s. 265

]

Dla rzeczywistego kondensatora słuszne są wykresy przedstawione na rys. 32.

Rys. 32. Wykresy wektorowe prądów i napięć dla kondensatora rzeczywistego: a) wykres dla schematu

równoległego, b) wykres dla schematu szeregowego [4, s. 266

]

Oznaczenia:

– kąt strat dielektrycznych,

– współczynnik strat dielektrycznych.

Odwrotność współczynnika strat dielektrycznych nazywamy dobrocią kondensatora

i oznaczamy Q

. Dla schematu równoległego:

Moc prądu jednofazowego

W obwodzie prądu sinusoidalnego zasilonym napięciem o wartości chwilowej u,

pobierającym prąd o wartości chwilowej, wartość chwilowa mocy jest równa iloczynowi prądu
i napięcia:

p = ui

Ponieważ w obwodzie prądu zmiennego napięcie i prąd zmieniają w czasie swoją wartość

oraz znak, moc chwilowa ma wartość dodatnią w tych przedziałach czasu, w których wartości
chwilowe prądu i napięcia mają te same znaki, oraz ujemną, w przedziałach czasu, gdzie
napięcie i prąd mają znaki przeciwne.

Jeżeli p>0, to energia jest dostarczana ze źródła do odbiornika, jeżeli p<0, to energia jest

zwracana przez odbiornik do źródła.

Na rys. 33 przedstawiono przebiegi prądu, napięcia i mocy dla dwójnika zasilanego

napięciem o wartości chwilowej u = U

sinωt , pobierającego prąd i = I

sin(ωt – φ).

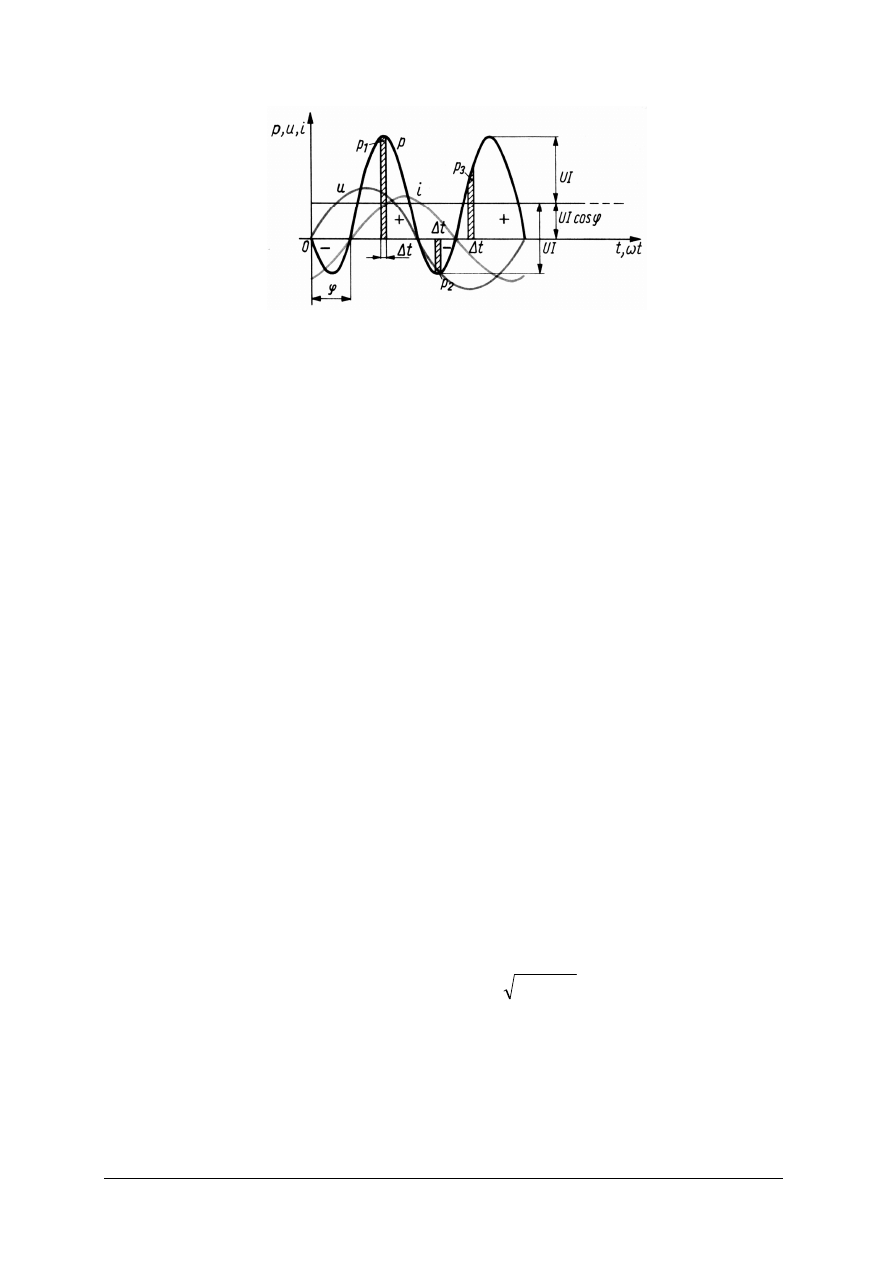
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 33. Przebiegi wartości chwilowej napięcia, prądu i mocy [4, s. 265]

Moc chwilowa, po przekształceniach trygonometrycznych:

p = ui = UIcos φ – UI cos(2ωt – φ).

Moc chwilowa ma dwie składowe:

−

składową stałą (nie zmieniającą się w czasie): UIcos φ,

−

składową sinusoidalnie zmienną: UI cos(2ωt – φ), której częstotliwość jest dwukrotnie
większa od częstotliwości napięcia i prądu.
Energia dostarczana do odbiornika w równych przedziałach czasu ∆t jest różna, ponieważ

wartość chwilowa mocy dla poszczególnych przedziałów czasu jest różna. Energia w czasie ∆t
wynosi:

∆W = p∆t.

Graficznie tę energię ilustruje pole powierzchni paska o podstawie ∆t. Sumując iloczyny p∆t

w ciągu całego okresu otrzymamy energię pobraną w ciągu okresu T:

W = Pt

Po podzieleniu przez T otrzymujemy wartość średnią mocy chwilowej za okres:

P = UIcos φ

U – wartość skuteczna napięcia sinusoidalnego, I – wartość skuteczna prądu sinusoidalnego,
cosφ – współczynnik mocy (cos kąta przesunięcia fazowego).

Mocą czynną P nazywamy wartość średnią mocy chwilowej. Jednostką mocy czynnej jest

1 wat (1W).

Dla urządzeń elektrycznych o określonych wartościach znamionowych napięcia U oraz

prądu I określamy moc pozorną S:

S = UI

Moc pozorna jest iloczynem wartości skutecznych napięcia i prądu.

Jednostką mocy pozornej jest 1 woltoamper (1VA). Moc pozorna jest równa największej
wartości mocy czynnej. Zachodzi to przy cosφ = 1 (φ = 0).

W obwodach prądu sinusoidalnego określa się także moc bierną Q:

Q = UIsinφ

Moc bierna jest iloczynem wartości skutecznych napięcia i prądu oraz sinusa kąta

przesunięcia fazowego. Jednostką mocy biernej jest 1 war(1 var).

Pomiędzy mocami: czynną, bierną i pozorną zachodzi zależność:

= P

+ Q

, stąd:

Dla każdego dwójnika RLC możemy narysować trójkąt mocy (rys. 23), który jest trójkątem

podobnym do trójkąta impedancji (admitancji) dla danego dwójnika:

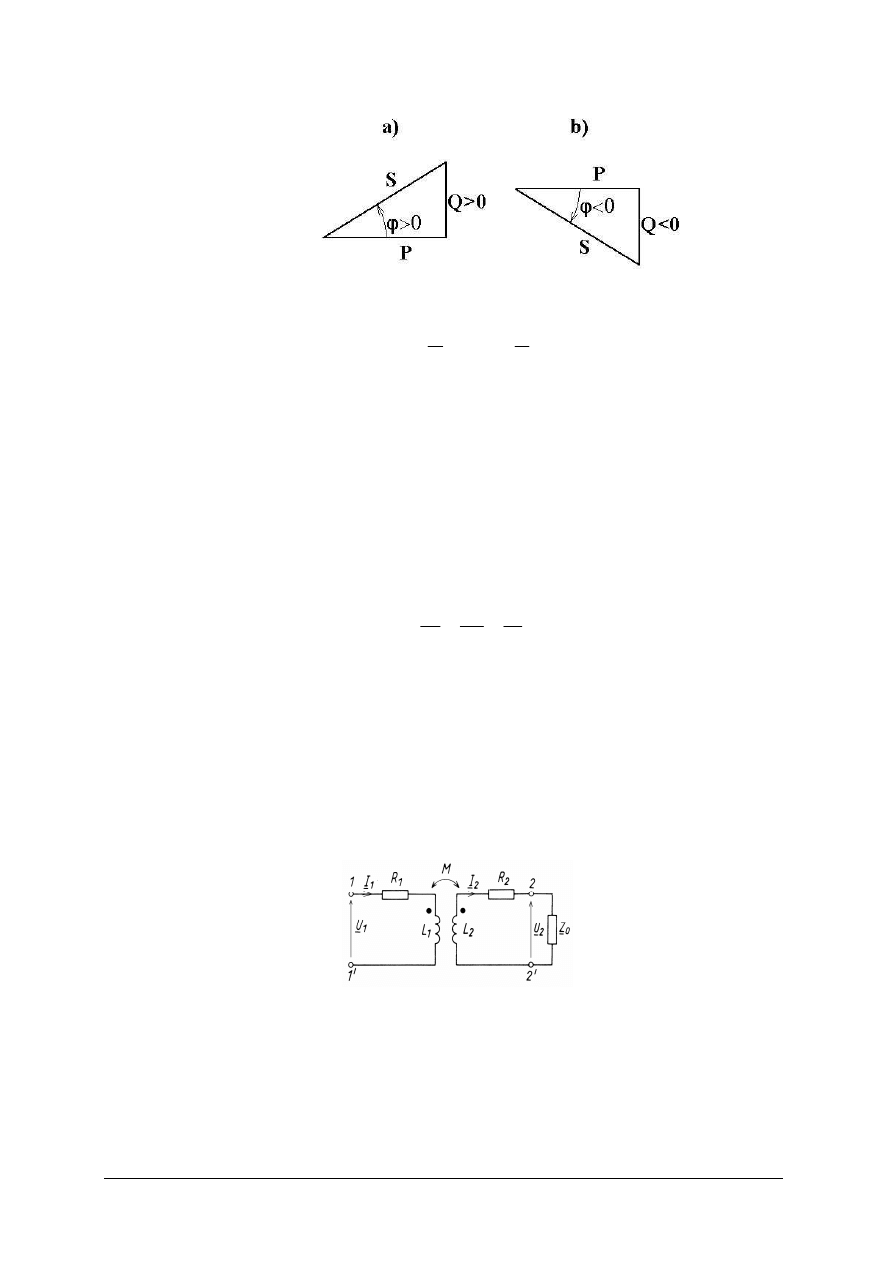
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 34. Trójkąty mocy a) dla Q > 0, b) dla Q < 0 [4, s. 273]

Funkcje kąta φ można określić z zależności:

cos

Transformator

Transformator jest urządzeniem elektrycznym, w którym energia elektryczna jest

przekazywana z jednego obwodu do drugiego za pośrednictwem pola elektromagnetycznego.

Najprostszy transformator ma dwa uzwojenia, z których jedno nazywamy uzwojeniem

pierwotnym, a drugie uzwojeniem wtórnym. Taki transformator nazywamy dwuuzwojeniowym.
Są też transformatory wielouzwojeniowe. W zależności od tego, czy sprzężenie uzwojeń odbywa
się przez powietrze, czy za pośrednictwem rdzenia ferromagnetycznego rozróżniamy
transformatory powietrzne i z rdzeniem ferromagnetycznym.

Przekładnię zwojową transformatora n. nazywamy stosunek liczby zwojów uzwojenia

pierwotnego N

do liczby zwojów uzwojenia wtórnego N

Rozróżnia się trzy stany pracy transformatora:

stan biegu jałowego, kiedy Z

∞

, I

stan zwarcia, kiedy Z

=0, U

stan obciążenia, kiedy Z

≠

Transformator powietrzny

Transformator powietrzny ma dwa uzwojenia sprzężone przez powietrze. Sprzężenie to

zwykle nie jest dobre. Transformatory powietrzne mają duży strumień rozproszenia.
Schemat zastępczy takiego transformatora jest następujący.

Rys. 35. Schemat zastępczy transformatora powietrznego dwuuzwojeniowego [3, s. 48]

Przez R

oznaczyliśmy rezystancje uzwojeń, przez L

i L

oznaczyliśmy indukcyjności

własne uzwojeń, przez M – indukcyjność wzajemną.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Transformator z rdzeniem ferromagnetycznym

Transformator taki ma dwa uzwojenia nawinięte na rdzeniu wykonanym z materiału

ferromagnetycznego, co powoduje, że strumień główny jest duży, a strumień rozproszenia mały.
Ze względu na budowę rdzenia rozróżniamy transformatory rdzeniowe i płaszczowe.

Rys. 36. Budowa transformatora: a)rdzeniowego, b) płaszczowego

[3, s. 49]

W celu zmniejszenia strat na prądy wirowe w rdzeniu transformatora, ten ostatni wykonany

jest z blach jednostronnie izolowanych lakierem izolacyjnym.
Ze względu na sposób chłodzenia transformatory dzielimy na suche i olejowe.

4.5.2 Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonywania ćwiczeń.

Jaki prąd nazywa się prądem zmiennym?

Jaka maszyna elektryczna wytwarza prąd zmienny?

Jakie są parametry przebiegu sinusoidalnego?

Co to jest pulsacja?

Jaka jest częstotliwość napięcia w sieci przemysłowej?

Jakim wzorem ogólnym określone jest napięcie sinusoidalne?

W jakich jednostkach mierzy się okres napięcia?

Jak określa się skuteczną napięcia sinusoidalnego.

Jaka jest wartość średnia napięcia sinusoidalnego za okres przebiegu?

10.

Jaka jest wartość średnia półokresowa napięcia sinusoidalnego?

11.

Jaki wykres nazywa się wektorowym, a jaki czasowym?

12.

Jak rysuje się wykres wektorowy?

13.

Jakie jest przesunięcie fazy między prądem i napięciem na idealnej rezystancji?

14.

Jakie jest przesunięcie fazy między prądem i napięciem na idealnej cewce?

15.

Jakie jest przesunięcie fazy między prądem i napięciem na idealnym kondensatorze?

16.

Jak oblicza się reaktancję indukcyjną i pojemnościową?

17.

Jak zmienia się reaktancja indukcyjna cewki w zależności od częstotliwości?

18.

Jak zmienia się reaktancja pojemnościowa kondensatora w zależności od częstotliwości?

19.

Jaki znak ma kąt φ przesunięcia fazowego napięcia względem prądu w dwójniku
szeregowym RL? W jakich granicach zmienia się ten kąt?

20.

Jaki znak ma kąt φ przesunięcia fazowego napięcia względem prądu w dwójniku
szeregowym RC?

21.

Jakie dwie składowe ma moc chwilowa prądu sinusoidalnego?

22.

Jaka jest zależność między mocą czynną, mocą bierną i mocą pozorną prądu
sinusoidalnego?

23.

Jaką moc pobiera rezystor idealny, a jaką cewka idealna?

24.

Jaką maszynę nazywa się transformatorem?

25.

Jak zbudowany jest transformator?

26.

Jak dzieli się transformatory?

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

27.

Co to jest przekładnia napięciowa transformatora?

28.

Co to jest przekładnia prądowa transformatora?

29.

Co to jest przekładnia zwojowa transformatora?

30.

Jakie są związki między przekładniami transformatora?

4.3.3 Ćwiczenia

Ćwiczenie 1

Zapoznaj się z płytą czołową oscyloskopu oraz przeznaczeniem elementów regulacyjnych.

Przeprowadź obserwację przebiegów na ekranie oscyloskopu.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zapoznać się z położeniem i funkcjami następujących regulatorów, przełączników i gniazd
na płycie czołowej oscyloskopu: Jaskrawość (INTENSITY) i ostrość (FOCUS), BLOK
ODCHYLANIA PIONOWEGO (VERTIKAL), BLOK ODCHYLANIA POZIOMEGO
(HORIZONTAL), BLOK WYZWALANIA (TRIGGER).

doprowadzić do wejścia A oscyloskopu sygnał sinusoidalny o częstotliwości 1 kHz,
amplitudzie 2 V z niewielką dodatnią składową stałą.

uzyskać na ekranie oscyloskopu stabilny obraz dwóch okresów. Zanotować ustawienia
wszystkich regulatorów i przełączników wymienionych w punkcie 1. Sprawdzić
regulację jaskrawości i ostrości, dobrać warunki optymalne i przerysować przebieg.

ustawić przełącznik wyboru trybu pracy odchylania pionowego na INT, a następnie:

−

sprawdzić możliwość regulacji (i jej efekty) czułości skokowej i płynnej wzmacniacza
odchylania pionowego oraz ewentualne jej mnożniki (x10, x2, x1 itp.),

−

wyłączyć regulację płynną, a skokową ustawić tak aby badany przebieg mieścił się na
ekranie,

−

ustawić przełącznik wyboru sprzężenia sygnału wejściowego ze wzmacniaczem
odchylania pionowego w pozycję GND i regulatorem położenia przebiegu w kierunku
pionowym ustawić poziomą linię na najbliższą pełną działkę (w przypadku braku obrazu
ustawić tryb wyzwalania na AUTO). Następnie przełączając sprzężenie na AC i DC
zaobserwować efekty i dokonać pomiaru amplitudy i składowej stałej sygnału mnożąc
odczyty w działkach (DIV) przez ustawioną czułość (VOLTS/DIV),

−

pomiary amplitudy i składowej stałej powtórzyć dla kilku różnych ustawień tych
parametrów na generatorze.

przy sprzężeniu AC ustawić przebieg w środkowej części ekranu (w pionie) oraz:

−

sprawdzić regulację (i jej efekty) podstawy czasu regulowanej i ciągłej (płynnej) oraz
ewentualnych jej mnożników,

−

ustawić mnożniki na x1, wyłączyć regulację płynną, a regulację skokową ustawić tak
aby na ekranie widoczny był przynajmniej jeden okres,

−

dokonać pomiaru okresu sygnału (przy odczycie skorzystać z regulatora położenia
przebiegu w kierunku poziomym) dla kilku różnych wartości częstotliwości ustawianych
na generatorze (b. małej, b. dużej i pośrednich),

przy pośredniej częstotliwości sygnału badanego, trybie pracy odchylania pionowego-A,
sprzężeniu - AC, trybie wyzwalania - AUTO i źródle wyzwalania - INT:

−

sprawdzić regulację (i jej efekty) poziomu wyzwalania (zwrócić uwagę na początek
obrazu sygnału na ekranie),

−

przy stabilnym obrazie sprawdzić działanie przełącznika zbocza wyzwalającego.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

przy stabilnym obrazie przełączyć tryb wyzwalania na NORM i ponownie obserwować,
co daje regulacja poziomem wyzwalania,

−

sprawdzić wpływ ustawienia regulatora czułości wzmacniacza odchylania pionowego na
regulację poziomu wyzwalania,

−

przy stabilnym obrazie, w trybie wyzwalania AUTO (a następnie NORM)
zmienić źródło wyzwalania. Opisać, co się dzieje i dlaczego,

−

przy niestabilnym obrazie, w trybie wyzwalania AUTO zmieniać płynnie regulację
podstawy czasu. Czy przy pomocy tego pokrętła jest możliwe uzyskanie stabilnego
obrazu? - uzasadnić odpowiedź,

podłączyć dwa różne sygnały do wejść A i B a następnie:

−

sprawdzić możliwość obserwacji raz jednego raz drugiego i obu na raz (wybór trybu
pracy odchylania pionowego),

−

sprawdzić możliwość obserwacji jednego kanału przy wyzwalaniu z drugiego. Czy
rodzaj sprzężenia ma wpływ na regulację poziomu wyzwalania,

−

w dwukanałowym (wciśnięte przyciski A oraz B) trybie pracy odchylania
pionowego zaobserwować pracę w trybie ALT i CHOP. Czy musimy zmieniać nastawy
jaskrawości czy też nastawione na początku wystarczająco dobrze nadają się do każdych
pomiarów,

−

sprawdzić jak działa oscyloskop w trybie X-Y,

−

uporządkować nabytą wiedzę i opisać przeznaczenie i działanie każdego z poznanych
elementów regulacyjnych oscyloskopu oraz podać sposoby (przykłady) ich
wykorzystania np. praca w trybie ALT nadaje się głównie do badania przebiegów
o dużych częstotliwościach lub tryb AUTO umożliwia szybką orientację co do położenia
(w pionie) i istnienia sygnału, itp.

opisać znaczenie poszczególnych pozycji od 1 do 29 na załączonym rysunku,

zaprezentować wyniki swojej pracy i zapisać wnioski.

Wyposażenie stanowiska pracy:

−

literatura zgodna z punktem 6 poradnika dla ucznia,

−

oscyloskop,

−

generator funkcyjny,

−

przewody BNC,

−

miernik uniwersalny,

−

częstościomierz,

−

zeszyt, przybory do pisania.

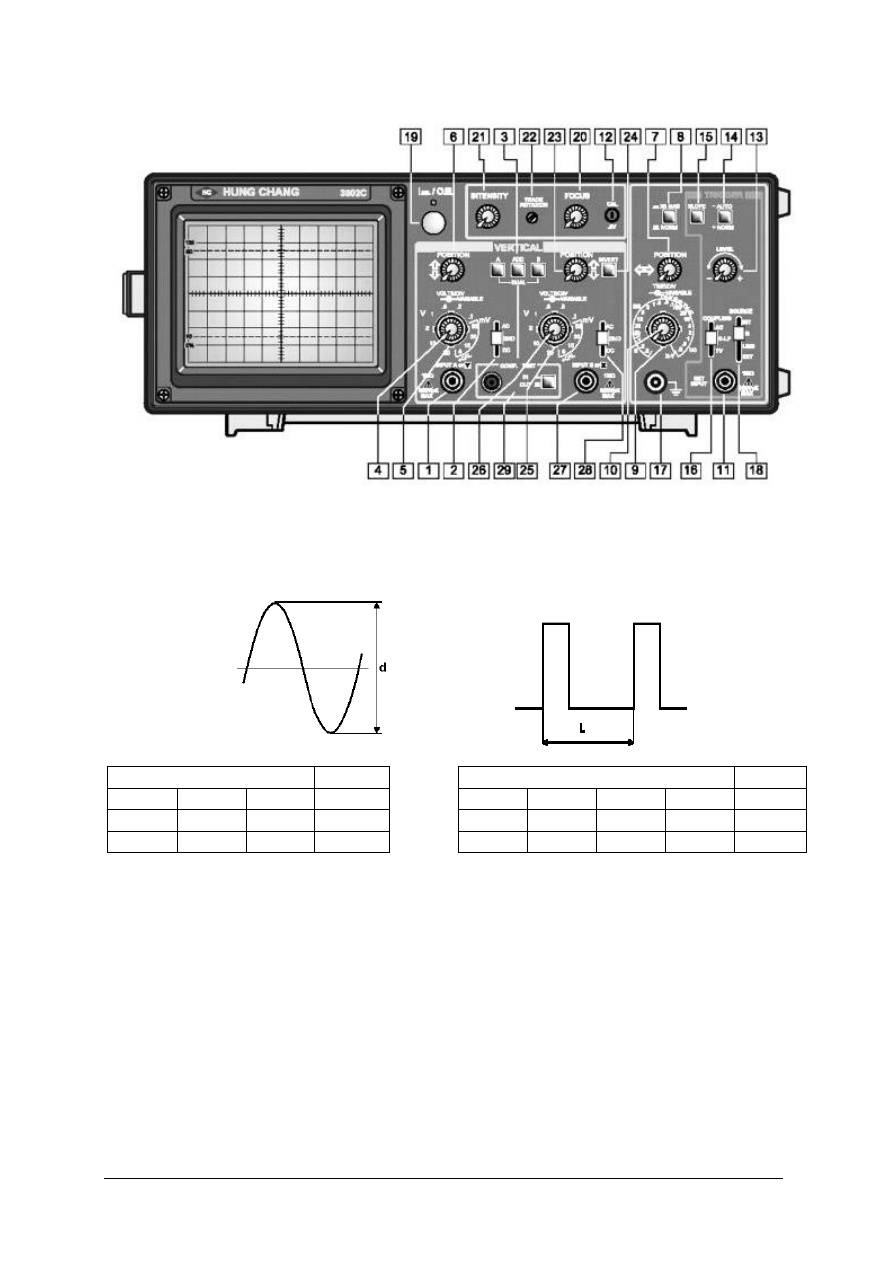
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 2

Wykonaj podstawowe pomiary przy pomocy oscyloskopu.

Sposób wykonania ćwiczenia

Pomiar oscyloskopem

Miernik

Pomiar oscyloskopem

miernik

Działki

V/dz

działki

ms/dz

Aby wykonać ćwiczenie, powinieneś:

przygotować oscyloskop do pracy: w tym celu należy zmniejszyć do minimum jasność oraz
ustawić maksymalną wartość podstawy czasu i minimalne wzmocnienie sygnału
wejściowego. Następnie pokrętła płynnej regulacji wzmocnienia i podstawy czasu trzeba
ustawić w pozycji CAL. Z kolei pokrętła ostrości oraz położenia poziomego i pionowego
należy ustawić w położeniach środkowych. Po wykonaniu opisanych czynności wstępnych
można włączyć zasilanie oscyloskopu i odczekać chwilę, aby oscyloskop się nagrzał. Po
wygrzaniu przełącznik typu sygnału należy ustawić w pozycji GND, po czym należy
skorygować położenie oraz jaskrawość i ostrość obserwowanego na ekranie obrazu,

ustawić w skrajnej pozycji obracając w lewą stronę pokrętło jasności (21) oraz przełączniki
skokowej zmiany podstawy czasu (9) i skokowej zmiany wzmocnienia sygnału
wejściowego (25),

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

ustawić w pozycji CAL przez obracanie w prawą stronę pokrętła płynnej regulacji
wzmocnienia (4 i 26) i podstawy czasu (10) ustawić,

ustawić w położeniach środkowych pokrętła ostrości (20), położenia poziomego (7)
i pionowego (6 i 23),

sprawdzić czy przycisk (8) jest wyciśnięty.

uzyskać zezwolenie na włączenie oscyloskopu i po włączeniu odczekać min. 30 sekund,
aby oscyloskop się nagrzał.

ustawić: przełącznik źródła sygnału wejściowego (18) w położeniu INT, przełącznik trybu
wyzwalania (14) w pozycji AUTO, a przełącznik typu sygnału (2 i 28) w pozycji środkowej
GND.

skorygować pokrętłami jasności (21) i ostrości (20) jaskrawość i ostrość obserwowanego na
ekranie obrazu (powinna być widoczna ostra linia pozioma), a następnie pokrętłami
położenia (7 i (23) przesunąć obraz na środek ekranu.

połączyć wyjście generatora funkcji z wejściem B (27) oscyloskopu, przełącznikiem rodzaju
sygnału wejściowego (28) wybrać sygnał zmienny (AC), ustawić na generatorze
częstotliwość f = 1 kHz oraz amplitudę sygnału na wartość Uwe=0.1V (odczyt amplitudy
i okresu powinien być dokonany z ekranu oscyloskopu),

10)

zbadać przebieg sinusoidalnie zmienny i prostokątny

11)

odczytać z ekranu oscyloskopu wartości amplitudy sygnału wejściowego Uwe dla
4 wskazanych przez nauczyciela wartości częstotliwości (np.: f = 2, 50, 100, 500 kHz),
odczyt amplitudy i okresu powinien być dokonywany z ekranu oscyloskopu, przerysować
wybrane przez nauczyciela oscylogramy.

12)

powtórzyć czynności z punktu 10 dla dwu innych wskazanych przez nauczyciela wartości
amplitudy sygnału wejściowego, np.: Uwe = 1V, 5V.

13)

wybrać przebieg sinusoidalny przełącznikiem rodzaju przebiegu na generatorze i ustawić
częstotliwość i amplitudę tego sygnału na wartości f = 0,5 kHz, Uwe = 0,1 V, wykonać
powtórnie czynności z punktu 11 i 12.

14)

wybrać przebieg trójkątny przełącznikiem rodzaju przebiegu na generatorze i ustawić
częstotliwość i amplitudę tego sygnału na wartości f = 0,1 kHz, Uwe = 0,1 V. powtórzyć
czynności z punktu 11 i 12.

15)

wyłączyć oscyloskop po zakończeniu pomiarów,

16)

zaprezentować wyniki pomiarów.

Wyposażenie stanowiska pracy:

−

zeszyt przedmiotowy i przybory do pisania, rysunek płyty czołowej oscyloskopu,

−

oscyloskop,

−

generator funkcyjny,

−

przewody BNC,

−

miernik uniwersalny,

−

częstościomierz,

−

literatura zgodna z punktem 6 poradnika dla ucznia.

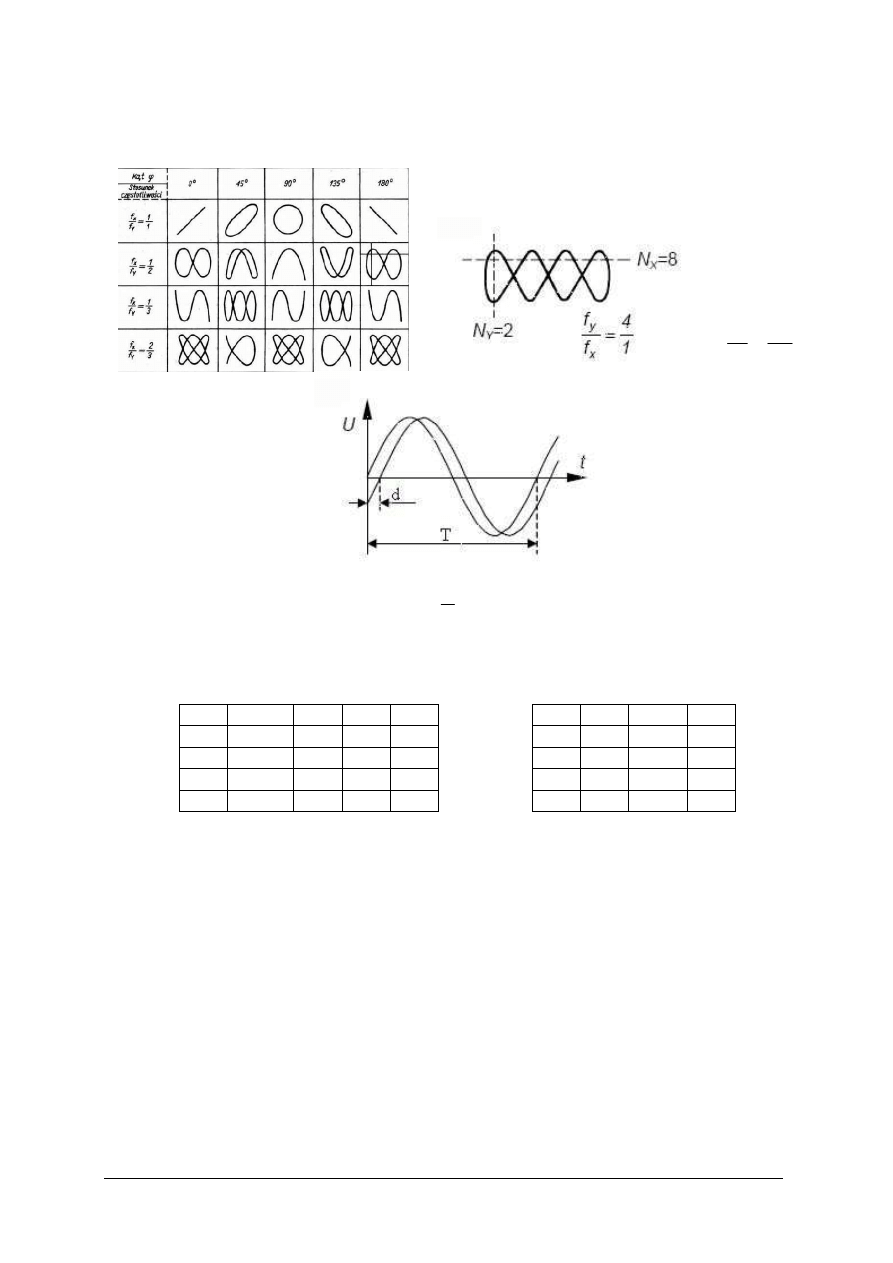
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 3

Wykonaj pomiar częstotliwości i przesunięcia fazowego przy pomocy oscyloskopu.

360

∗

Tabele pomiarowe

Tabela 1

Tabela 2

Lp.

figura

ms/dz

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

przygotować oscyloskop do pracy,

połączyć układ według schematu pomiarowego, do zbadania przesunięcia fazowego metodą
bezpośrednią i metodą figur Lissajous,

wykonać pomiary, zapisać wyniki w tabelach, obliczyć wartości końcowe,

wykonać szkice z ekranu oscyloskopu,

zaprezentować wyniki pomiarów.

Wyposażenie stanowiska pracy:

−

instrukcja do ćwiczenia,

−

zeszyt przedmiotowy i przybory do pisania,

−

oscyloskop,

−

generator funkcyjny Maxcom,

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

przesuwnik fazy,

−

przewody BNC,

−

miernik uniwersalny,

−

częstościomierz,

−

literatura zgodna z punktem 6 poradnika dla ucznia.

Ćwiczenie 4
Do uzwojenia pierwotnego transformatora jednofazowego doprowadzono napięcie U

=230V.

Liczby zwojów uzwojeń: z

=1320 i z

=60. Oblicz przekładnię n transformatora oraz wartość

napięcia wtórnego U

transformatora.

Sposób wykonania ćwiczeń

Aby wykonać ćwiczenia, powinieneś:

zapoznać się z treścią zadania,

wypisać dane wielkości i szukane,

wypisać wzory matematyczne, które opisują zależności między wielkościami danymi
i szukanymi,

opracować plan rozwiązania zadania,

podstawić dane do wzorów i wykonać obliczenia,

opracować wnioski do zadań.

Wyposażenie stanowiska pracy:

−

literatura zgodna z punktem 6 poradnika dla ucznia,

−

kalkulator,

−

zeszyt i przybory do pisania.

Ćwiczenie 5

Dane znamionowe transformatora bezpieczeństwa są następujące: napięcie na uzwojeniu

pierwotnym U

=230V, napięcie na uzwojeniu wtórnym U

=24V, moc pozorna S=100VA.

Oblicz przekładnię n transformatora oraz wartości prądów znamionowych: pierwotnego I

i wtórnego I

. Oblicz ponadto średnice drutów nawojowych, przyjmując gęstość prądu

w uzwojeniach J=2*10

A/m

=2A/mm

Sposób wykonania ćwiczeń

Aby wykonać ćwiczenia, powinieneś:

zapoznać się z treścią zadania,

wypisać dane wielkości i szukane,

wypisać wzory matematyczne, które opisują zależności między wielkościami danym
i szukanymi,

opracować plan rozwiązywania zadań,

podstawić dane do wzorów i wykonać obliczenia,

opracować wnioski do zadań.

Wyposażenie stanowiska pracy:

−

literatura zgodna z punktem 6 poradnika dla ucznia,

−

zeszyt i przybory do pisania.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 6

Oblicz wartości: impedancji Z obwodu, prądu I płynącego w obwodzie złożonym z rezystora

o rezystancji R=120Ω i cewki o indukcyjności L=0,51H połączonych szeregowo oraz napięć U

, U

. Do obwodu doprowadzono napięcie z sieci (230V, 50 Hz). Sporządź wykres wektorowy

i trójkąt impedancji.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

wypisać dane wielkości z zadania oraz wielkość (wielkości) szukane,

przeczytać ze zrozumieniem treść zadania (zadań),

wypisać wzory matematyczne, które przedstawiają zależności między wielkościami danymi,
a wielkością (wielkościami) szukaną,

opracować plan rozwiązania zadania,

podstawić do wzorów dane wielkości i wykonać obliczenia,

opracować wnioski i zaprezentować efekt pracy.

Wyposażenie stanowiska pracy:

−

literatura zgodna z punktem 6 poradnika dla ucznia,

−

kalkulator,

−

zeszyt i przybory do pisania.

Ćwiczenie 7

Oblicz wartość prądu płynącego przez rezystor oraz narysuj trójkąt prądów w obwodzie

równoległym RC, jeżeli prąd całkowity I=2,5A, a prąd płynący przez kondensator I

=1,2 A.

Sposób wykonania ćwiczeń

Aby wykonać ćwiczenia, powinieneś:

wypisać dane wielkości z zadania oraz wielkość (wielkości) szukane,

przeczytać ze zrozumieniem treść zadania (zadań),

wypisać wzory matematyczne, które przedstawiają zależności między wielkościami danymi,
a wielkością (wielkościami) szukaną,

opracować plan rozwiązania zadania,

podstawić do wzorów dane wielkości i wykonać obliczenia,

opracować wnioski i zaprezentować efekt pracy.

Wyposażenie stanowiska pracy:

−

literatura zgodna z punktem 6 poradnika dla ucznia,

−

kalkulator,

−

zeszyt i przybory do pisania.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.3.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

definiować pojęcia: prąd zmienny, prąd przemienny, pulsacja, okres,
amplituda?

obliczyć wartość skuteczną prądu sinusoidalnego?

obliczyć wartość średnią prądu sinusoidalnego?

napisać wzór na przebieg napięcia sinusoidalnego?

opisać jakie przebiegi nazywamy synchronicznymi?

określić przesunięcie fazowe?

podać jednostkę częstotliwości?

określić przeznaczenie regulatorów, przycisków i gniazd na płycie czołowej
oscyloskopu?

przeprowadzić obserwację przebiegów na ekranie oscyloskopu?

10)

wykonać podstawowe pomiary przy pomocy oscyloskopu?

11)

wykonać pomiar częstotliwości i przesunięcia fazowego przy pomocy
oscyloskopu?

12)

wykazać różnicę między prądem zmiennym, a przemiennym?

13)

podać interpretację fizyczną wartości średniej prądu?

14)

obliczyć reaktancję indukcyjną oraz wartość skuteczną napięcia na cewce?

15)

obliczyć reaktancję pojemnościową oraz wartość skuteczną prądu i napięcia
na kondensatorze?

16)

opisać jak zmienia się reaktancja pojemnościowa i indukcyjna w zależności od
częstotliwości?

17)

obliczyć impedancję gałęzi szeregowej RL i RC?

18)

obliczyć wartości prądów w układach równoległych RL i RC?

19)

obliczyć wartość maksymalną prądu sinusoidalnego, znając jego wartość
skuteczną?

20)

określić przesunięcie fazowe na podstawie pomiaru mocy czynnej i pozornej
prądu sinusoidalnego jednofazowego?

21)

narysować wykres wektorowy prądu i napięcia dla idealnych elementów RLC?

22)

wyznaczyć przesunięcie fazowe między prądem, a napięciem na elementach
idealnych: rezystorze, cewce, kondensator?

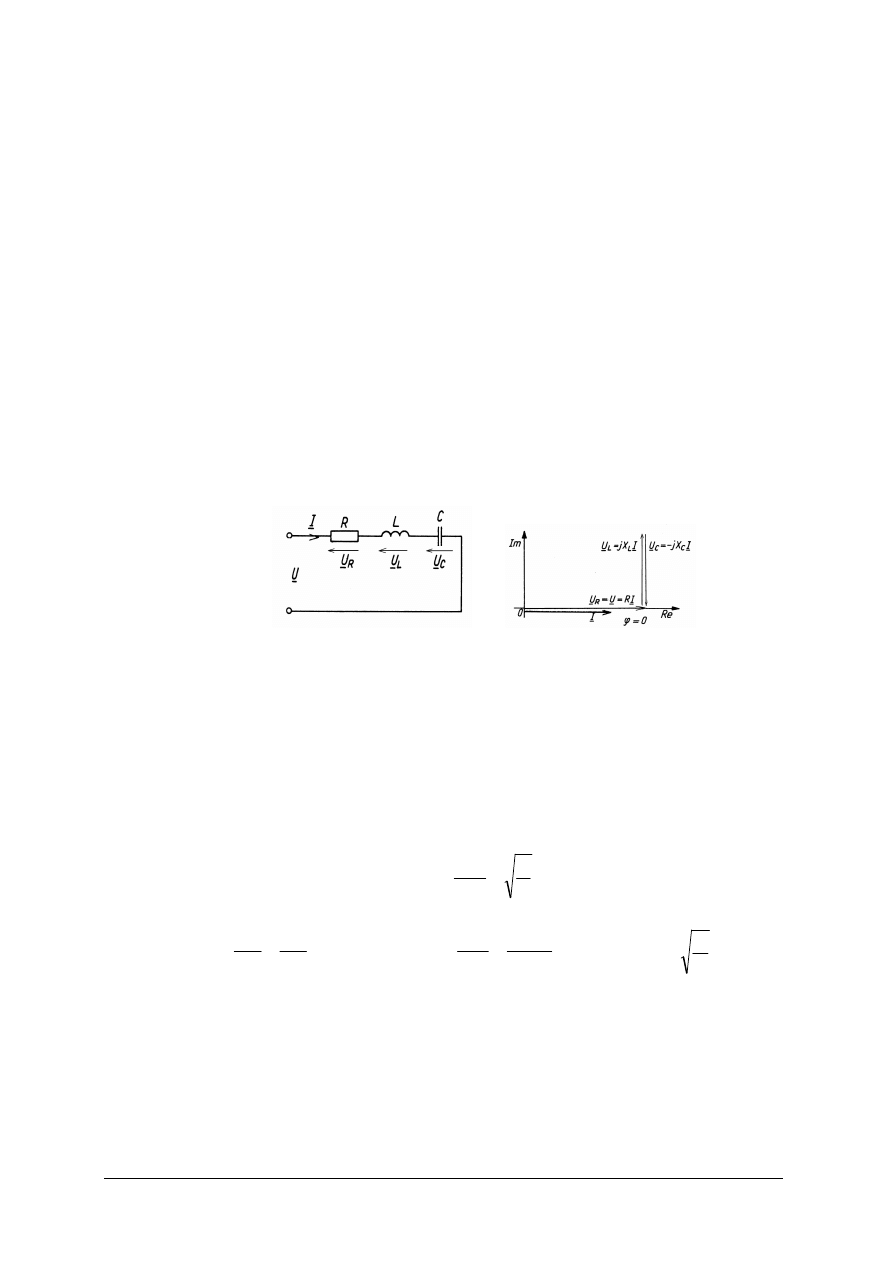
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.4. Rezonans napięć i prądów. Podstawowe parametry

trójfazowego prądu i napięcia

4.4.1. Materiał nauczania

Rezonans w obwodach elektrycznych

Rezonans zachodzi w obwodach elektrycznych, w których susceptancja lub reaktancja

wypadkowa jest równa zeru. Oznacza to, że w obwodzie będącym w rezonansie prąd i napięcie
na jego zaciskach są w fazie ze sobą. Oznacza to również, że taki obwód ma charakter wyłącznie
rezystancyjny. Częstotliwość, dla której zachodzi zjawisko rezonansu, nazywamy
częstotliwością rezonansową. W zależności od sposobu połączenia elementów R, L, C, mówimy
o rezonansie napięć lub prądów.

Rezonans napięć

Rezonans napięć zachodzi przy szeregowym połączeniu elementów R, L, C. Z warunku

rezonansu wynika, że X

. Wynika stąd, że napięcia na L i C są sobie równe, lecz przeciwnie

skierowane. Rozpocznij konstrukcję wykresu wektorowego od wektora wspólnego, którym jest
natężenie prądu I. Przyjmij, że faza początkowa prądu φ=0.

Rys. 37. Rezonans napięć w dwójniku szeregowym–schemat obwodu, wykres wektorowy dla stanu rezonansu

[3, s. 252]

Zapamiętaj, że w stanie rezonansu napięć:

−

reaktancja pojemnościowa jest równa reaktancji indukcyjnej,

−

impedancja jest równa rezystancji,

−

napięcie na cewce jest co do wartości równe napięciu na kondensatorze, a ich suma
geometryczna wynosi zero,

−

ponieważ X=0, prąd w obwodzie ma wartość największą.
Impedancją falową ρ nazywamy reaktancję indukcyjną lub pojemnościową obwodu R, L, C

przy częstotliwości rezonansowej.

Określmy także dobroć Q obwodu rezonansowego.

czyli

lub

Rezonans prądów

Rezonans prądów zachodzi przy równoległym połączeniu elementów R, L, C. Z warunku

rezonansu wynika, że B

. Wynika stąd, że prądy płynące przez L i C są sobie równe, lecz

przeciwnie skierowane. Rozpocznij konstrukcję wykresu wektorowego od wektora wspólnego,
którym jest napięcie U. Przyjmij, że faza początkowa napięcia φ=0.

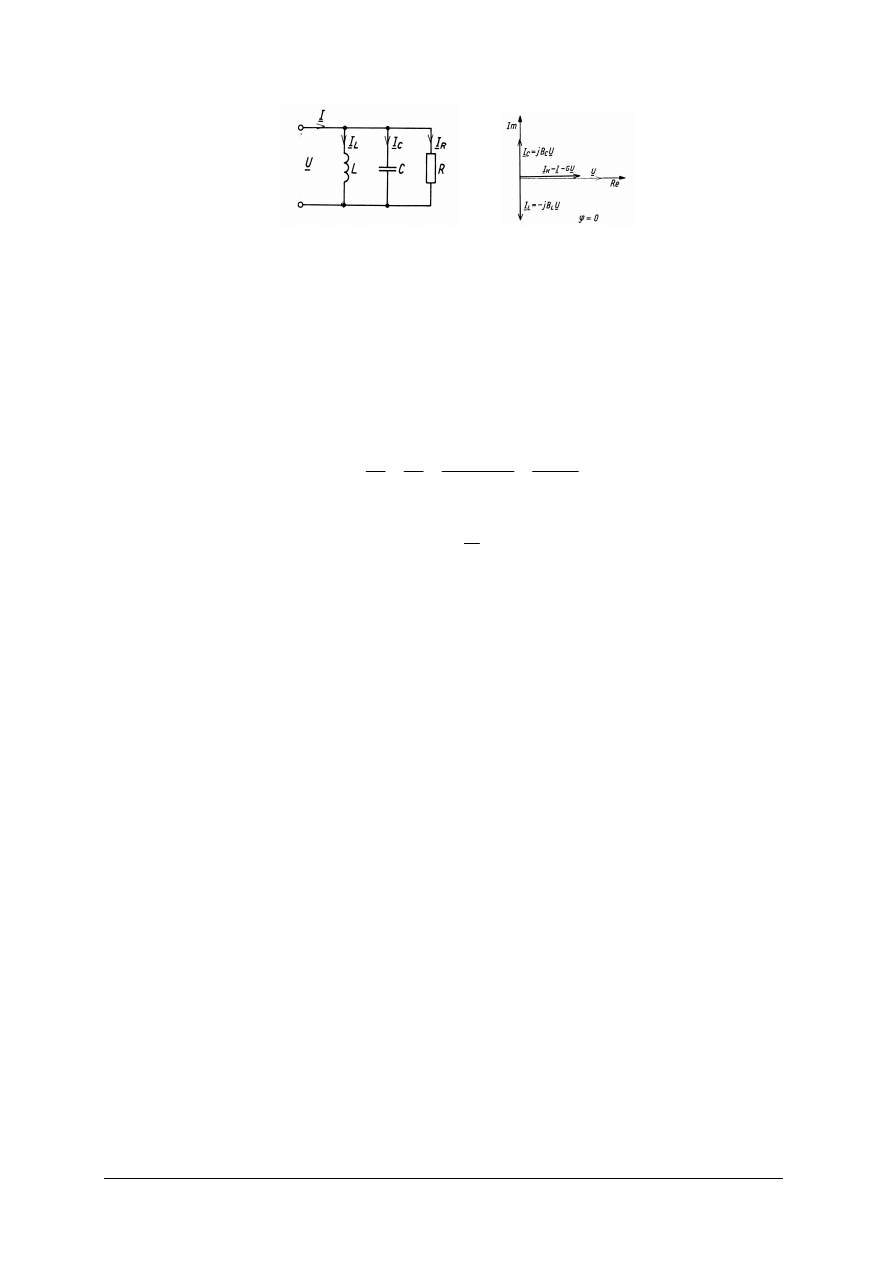
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 38. Rezonans prądów w dwójniku równoległym – schemat obwodu, wykres wektorowy dla stanu rezonansu

[3, s. 263]

Można stwierdzić, że w stanie rezonansu prądów:

−

susceptancja pojemnościowa jest równa susceptancji indukcyjnej,

−

admitancja obwodu jest równa konduktancji,

−

natężenie prądu w gałęzi z kondensatorem jest równe natężeniu prądu w gałęzi z cewką,
a suma geometryczna tych prądów jest równa zeru,

−

wobec B=0, prąd całkowity ma najmniejszą wartość, a źródło pracuje w stanie zbliżonym do
biegu jałowego.
Podobnie jak poprzednio zdefiniujmy pojęcie dobroci Q obwodu rezonansowego.

∗

ostatecznie po przekształceniach otrzymamy

Z definicji dobroci Q wynika, że im Q jest większa, tym większe są przetężenia w obwodzie

rezonansu prądów. Przetężeniem nazywamy stan, w którym prądy w gałęziach indukcyjnej
i pojemnościowej są Q razy większe niż prąd dopływający do obwodu rezonansowego.

Wytwarzanie prądu trójfazowego

Prąd przemienny jest dzisiaj wytwarzany z reguły jako trójfazowy, a użytkowany jako prąd

trójfazowy lub jednofazowy.

Prąd trójfazowy jest to prąd przemienny, który ma trzy jednakowe sinusoidalne przebiegi

przesunięte względem siebie kolejno o 120°.

Prąd taki możemy wytworzyć, umieszczając trzy jednakowe, niezależne uzwojenia,

przesunięte względem siebie kolejno o 120°, w polu. tej samej magneśnicy. Te trzy uzwojenia,
zwane fazami prądnicy, mają sześć końcówek o znormalizowanych oznaczeniach:
U — X przynależne do fazy L

V — Y przynależne do fazy L

W — Z przynależne do fazy L

U,V,W — początki, natomiast X, Y, Z — końce uzwojeń.

W czasie ruchu obrotowego wirnika prądnicy, wskutek przecinania linii sił pola

magnetycznego, w każdym uzwojeniu fazowym indukują się siły elektromotoryczne
o jednakowych częstotliwościach, amplitudach i o fazach przesuniętych względem siebie o 120°.
Każdą z faz prądnicy trójfazowej możemy wykorzystać jako oddzielne źródło napięcia,
zasilające przyłączone do niego odbiorniki. Taki układ nazywamy układem trójfazowym
nieskojarzonym. W układzie tym każda faza wraz z jej odbiornikiem stanowi niezależny obwód
elektryczny. Do dokonania połączeń poszczególnych faz z ich odbiornikami trzeba użyć aż
sześciu przewodów.

Liczbę przewodów koniecznych do rozprowadzenia prądu trójfazowego możemy

zmniejszyć do trzech lub czterech, łącząc uzwojenia trójfazowe między sobą w gwiazdę lub
trójkąt.

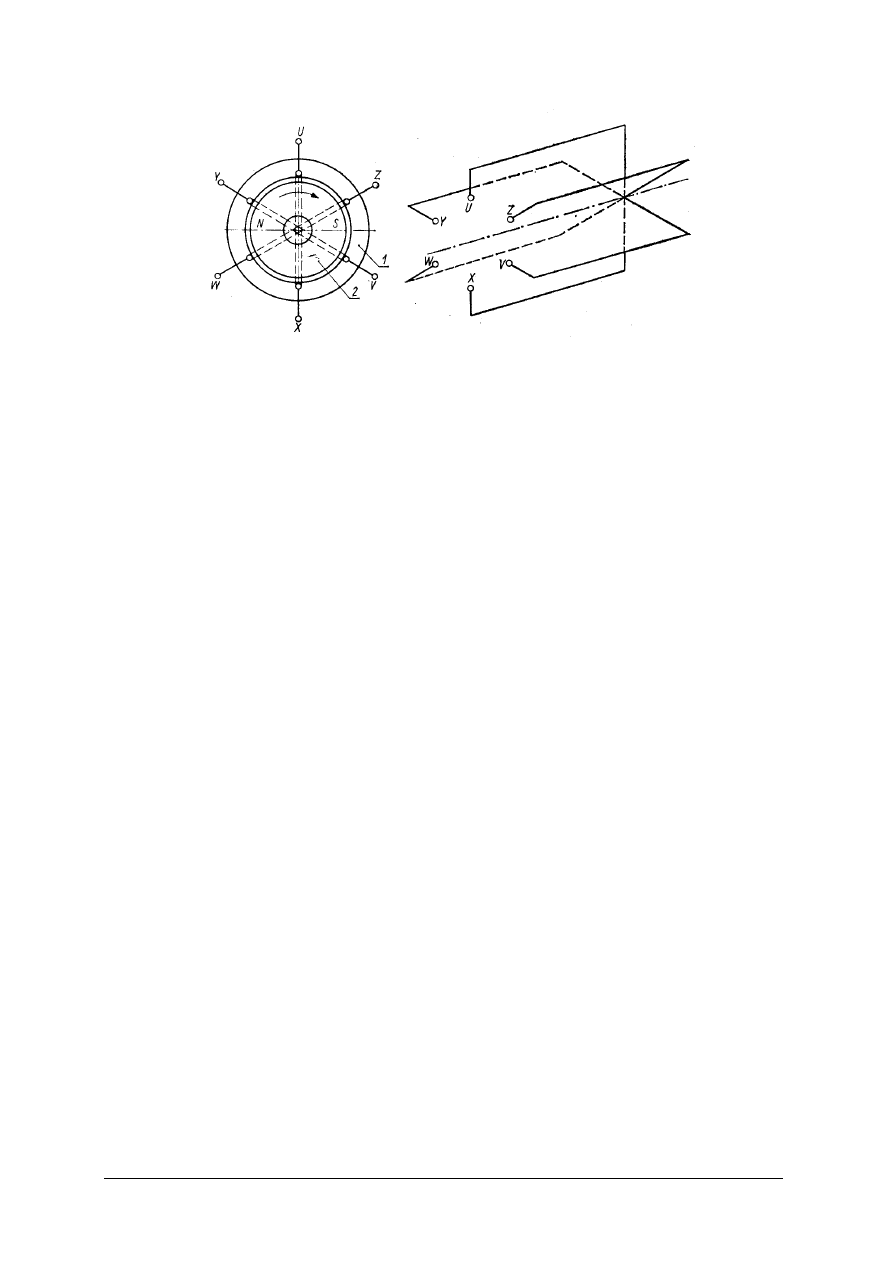
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 39. Zasada działania prądnicy trójfazowej: a) schemat prądnicy, b) schemat rozmieszczenia uzwojeń stojana

1 – stojan, 2 – magneśnica [3, s. 7]

Jeśli końce X, Y, Z uzwojeń trzech faz połączymy razem w jeden wspólny punkt, zwany

punktem neutralnym N (zerowym), natomiast od początków U, V, W odprowadzimy trzy
przewody L

zwane przewodami fazowym to otrzymamy układ połączeń w gwiazdę,

trójprzewodowy.

Taki układ stosuje się w prądnicach wysokiego napięcia i do zasilania odbiorników

powodujących równomierne (symetryczne) obciążenie faz. Jeśli od punktu neutralnego
N odprowadzimy czwarty przewód, to otrzymamy układ połączeń w gwiazdę,
czteroprzewodowy. Punkt neutralny najczęściej uziemiamy, a wtedy przewód odprowadzony od
tego punktu nazywamy przewodem zerowym i oznaczamy go przez N.

Napięcie występujące na jednym uzwojeniu fazowym, czyli pomiędzy dowolnym

przewodem fazowym a przewodem zerowym, nazywamy napięciem fazowym U

. Natomiast

napięcie występujące między dwoma przewodami fazowymi nazywamy napięciem
międzyfazowym (przewodowym) U.

Przy połączeniu w gwiazdę i układzie czteroprzewodowym mamy do dyspozycji dwa

napięcia: fazowe i międzyfazowe, przy czym to ostatnie w tym połączeniu wynosi U = 1,73 U

Przy równomiernym obciążeniu faz suma prądów chwilowych jest równa zeru, a więc nie płynie
prąd przewodem zerowym. Jeśli jednak fazy będą obciążone niesymetrycznie, wówczas
przewodem zerowym popłynie prąd, który nazywamy prądem wyrównawczym. Prąd ten jest
zawsze mniejszy od prądu fazowego I

płynącego w uzwojeniu jednej fazy, i dlatego przewód

zerowy może mieć mniejszy przekrój od przewodów fazowych.

Prąd płynący przewodem fazowym nazywamy prądem przewodowym I. Prąd ten

w połączeniu w gwiazdę jest równy prądowi fazowemu I

= If.

Układy trójfazowe mogą być symetryczne i niesymetryczne.

W układach trójfazowych rozróżniamy dwa rodzaje prądów:

−

prądy przewodowe – są to prądy płynące w przewodach fazowych,

−

prądy fazowe – prądy płynące w fazach odbiornika,

i dwa rodzaje napięć:

−

napięcia fazowe źródła – są to napięcia występujące między punktem neutralnym prądnicy
oraz jej zaciskiem, oznaczamy je E

, E

−

napięcia fazowe odbiornika jak wyżej, oznaczamy je: U

, U

−

napięcia międzyfazowe (inna nazwa napięcia liniowe) – są to napięcia występujące między
kolejnymi zaciskami prądnicy lub odbiornika.

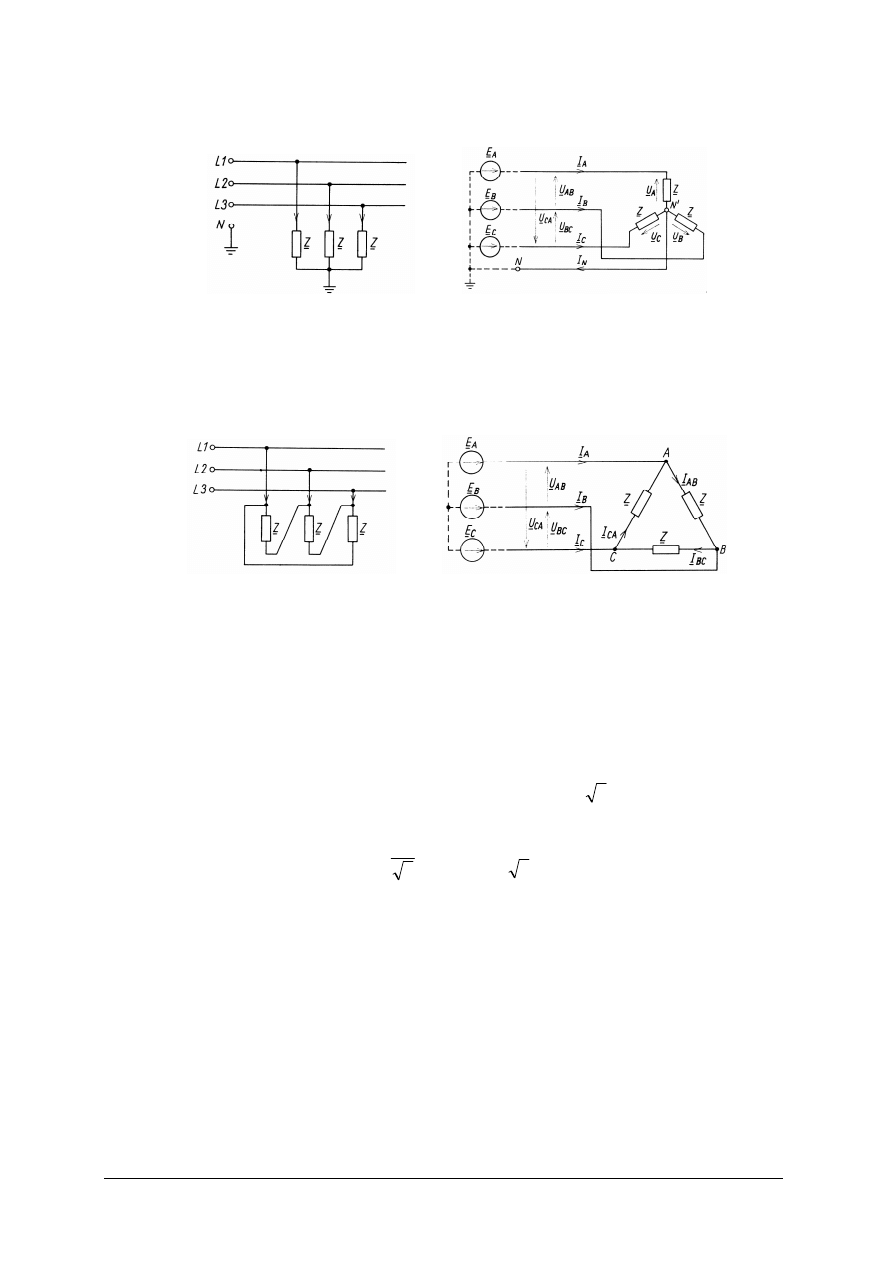
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Odbiornik połączony w gwiazdę

Rys. 40. Układ trójfazowy symetryczny z odbiornikiem połączonym w gwiazdę z uziemionym punktem neutralnym:

a) odbiornik dołączony do sieci trójfazowej, b) ten sam odbiornik z dorysowanym schematem źródła [3, s. 11]

Układ trójfazowy trójprzewodowy – a, oraz układ trójfazowy czteroprzewodowy – b.

Odbiornik połączony w trójkąt

Rys. 41. Układ trójfazowy symetryczny z odbiornikiem połączonym w trójkąt: a) odbiornik dołączony do sieci

trójfazowej, b) ten sam odbiornik z dorysowanym schematem źródła [3, s. 25]

−

napięcia międzyfazowe źródła są równe napięciom fazowym odbiornika,

−

suma wartości skutecznych zespolonych napięć fazowych odbiornika jest równa zeru (suma
wektorowa napięć fazowych odbiornika jest równa zeru),

−

moduły prądów fazowych odbiornika są sobie równe,

−

suma wartości skutecznych zespolonych prądów fazowych jest równa zeru,

−

suma wartości skutecznych zespolonych napięć międzyfazowych jest równa zeru,

−

wartość skuteczna (moduł) prądów przewodowych I

jest 3 razy większy od wartości

skutecznej prądu fazowego I

lub I

−

napięcia fazowe odbiornika są równe napięciom międzyfazowym,

= U

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.4.2 Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

W jakich obwodach zachodzi rezonans?

Jakie znane są rezonanse elektryczne?

Jak wyznacza się dobroć obwodu rezonansowego?

Jakie cechy ma prąd przemienny trójfazowy?

Jak można skojarzyć układy trójfazowe?

Jaka jest różnica między wielkościami fazowymi, a przewodowymi?

Kiedy układ trójfazowy jest symetryczny?

Jakie rozróżnia się połączenia w gwiazdę?

Jaka jest zależność między wartościami skutecznymi napięć fazowych i międzyfazowych
w układzie trójfazowym symetrycznym?

10.

Na czym polega połączenie uzwojeń w trójkąt?

11.

Jaką wartość ma suma sił elektromotorycznych w układzie trójfazowym symetrycznym?

12.

Czy odbiorniki trójfazowe mogą być łączone dowolnie, tj. w trójkąt albo w gwiazdę?

13.

Jakie są zależności między: prądami fazowymi i prądami liniowymi oraz napięciami
fazowymi

napięciami

liniowymi

przy

symetrycznym

obciążeniu

układu

czteroprzewodowego?

4.4.3 Ćwiczenia

Ćwiczenie 1

Obliczyć moc pieca elektrycznego i energię elektryczną zużytą podczas pracy pieca w ciągu

4 godzin. Piec ma grzałki oporowe połączone w trójkąt. Przy napięciu fazowym 230V piec
pobiera prąd o natężeniu I=15A, przy czym cos φ= 1.

Sposób wykonania ćwiczeń

Aby wykonać ćwiczenia, powinieneś:

przeczytać ze zrozumieniem treść zadań,

wypisać wzory matematyczne, które przedstawiają zależność wielkości szukanych i danych
w zadaniu,

wstawić dane do wzoru (wzorów) i wykonać obliczenia,

opracować wnioski z wykonanych obliczeń i zaprezentować efekt pracy.

Wyposażenie stanowiska pracy:

−

literatura zgodna z punktem 6 poradnika dla ucznia,

−

kalkulator,

−

zeszyt i przybory do pisania.

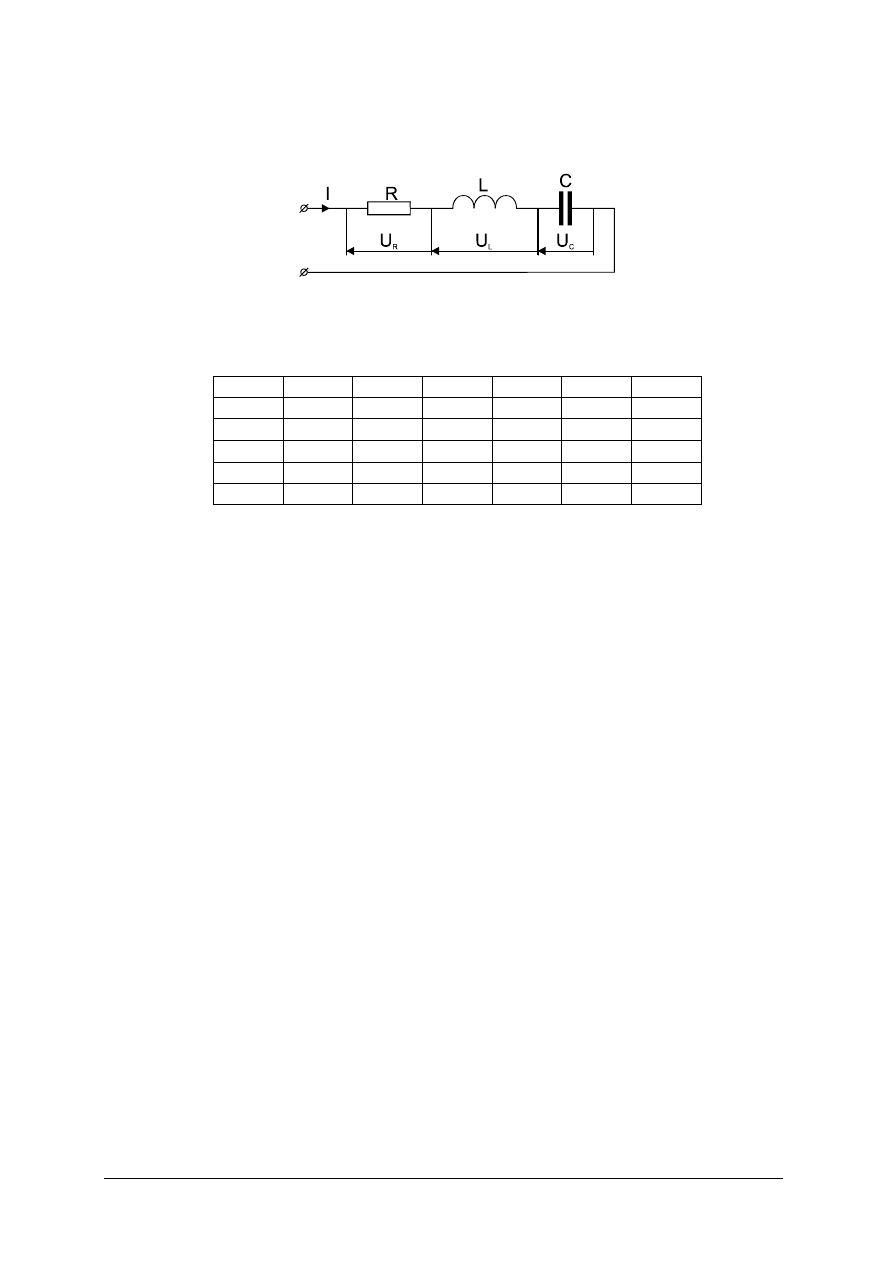
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 2

Wykonaj badanie szeregowego obwodu RLC dokonując zmiany częstotliwości napięcia

zasilającego.

Obwód szeregowy RLC w stanie rezonansu napięć

Wyniki pomiarów wpisz do tabeli.

Tabela 1 Tabela wyników pomiarów ćwiczenie 1

Ω

1600

3600

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zgromadzić następujące przyrządy pomiarowe sprzęt i materiały: cewkę L=4mH,
kondensator C=1x10

-6

F, rezystor R=32Ω, przewody połączeniowe, 5 mierników

uniwersalnych, wyłącznik,

połączyć wyżej wymienione elementy według wskazań nauczyciela,

ustawić odpowiednie zakresy na miernikach uniwersalnych,

pokazać nauczycielowi układ gotowy do podłączenia w celu sprawdzenia prawidłowości
połączeń i nastaw,

zaplanować ilość pomiarów i wykonać pomiary,

ustalić częstotliwość rezonansową doświadczalnie (U

) oraz obliczeniowo,

zapisać wyniki pomiarów w tabeli,

wykonać potrzebne obliczenia końcowe, wykonać wykresy wektorowe,

wykonać ćwiczenie w zespole.

Wyposażenie stanowiska pracy:

−

zeszyt i przybory do pisania, kalkulator,

−

cewka L=4mH, kondensator C=1x10

-6

F, rezystor R=32Ω,

−

generator sinusoidalny,

−

mierniki uniwersalne,

−

wyłącznik,

−

przewody połączeniowe.

Ćwiczenie 3

Wykonaj badanie równoległego obwodu RLC poprzez zmianę częstotliwości napięcia

zasilającego.

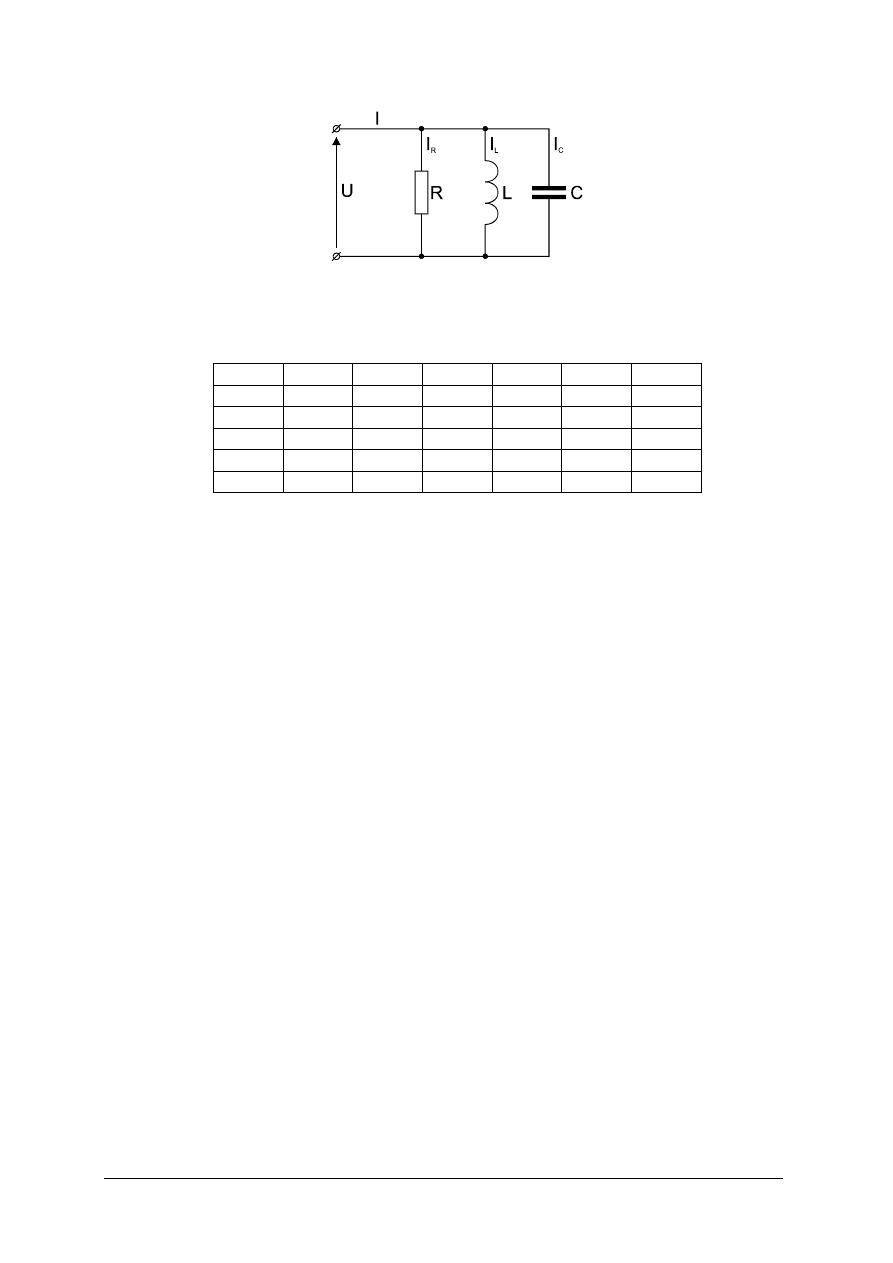
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Równoległy obwód R, L, C w stanie rezonansu prądów

Wyniki pomiarów wpisz do tabeli.

Tabela 1 Tabela wyników pomiarów ćwiczenie 2

Ω

1600

3600

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zgromadzić następujące przyrządy pomiarowe sprzęt i materiały: cewkę L=4mH,
kondensator C=1x10

-6

F, rezystor R=32Ω, przewody połączeniowe, 5 mierników

uniwersalnych, wyłącznik, ,

połączyć wyżej wymienione elementy według schematu,

ustawić odpowiednie zakresy na miernikach uniwersalnych,

pokazać nauczycielowi układ gotowy do podłączenia w celu sprawdzenia prawidłowości
połączeń i nastaw,

zaplanować ilość pomiarów i wykonać pomiary,

ustalić częstotliwość rezonansową doświadczalnie (I

) oraz obliczeniowo,

zapisać wyniki pomiarów w tabeli,

wykonać potrzebne obliczenia końcowe, wykonać wykresy wskazane przez nauczyciela,

wykonać ćwiczenie w zespole.

Wyposażenie stanowiska pracy:

−

zeszyt i przybory do pisania, kalkulator,

−

cewka L=4mH, kondensator C=1x10

-6

F, rezystor R=32Ω,

−

generator sinusoidalny

−

mierniki uniwersalne,

−

wyłącznik,

−

przewody połączeniowe.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.4.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

odróżnić obwód rezonansu napięć od obwodu rezonansu prądów?

określić przesunięcie fazowe napięć w symetrycznym układzie trójfazowym?

wypisać zależności między wielkościami fazowymi i przewodowymi w
układzie trójfazowym symetrycznym skojarzonym w trójkąt i w gwiazdę?

wymienić cechy charakteryzujące obwód, w którym zachodzi rezonans napięć?

wymienić cechy charakteryzujące obwód, w którym zachodzi rezonans
prądów?

wyznaczyć częstotliwość i dobroć rezonansową obwodu?

określić różnice między wielkościami fazowymi, a przewodowymi?

rozróżnić połączenie faz w trójkąt i w gwiazdę?

określić zależność między wartościami skutecznymi napięć fazowych
i międzyfazowych w układzie trójfazowym symetrycznym?

10)

rozróżnić połączenie faz w gwiazdę ze względu na ilość przewodów?

11)

wymienić cechy prądu przemiennego trójfazowego?

12)

określić wartość sumy sił elektromotorycznych w układzie trójfazowym
symetrycznym?

13)

zastosować na obliczanie mocy: czynnej, biernej i pozornej prądu
przemiennego trójfazowego?

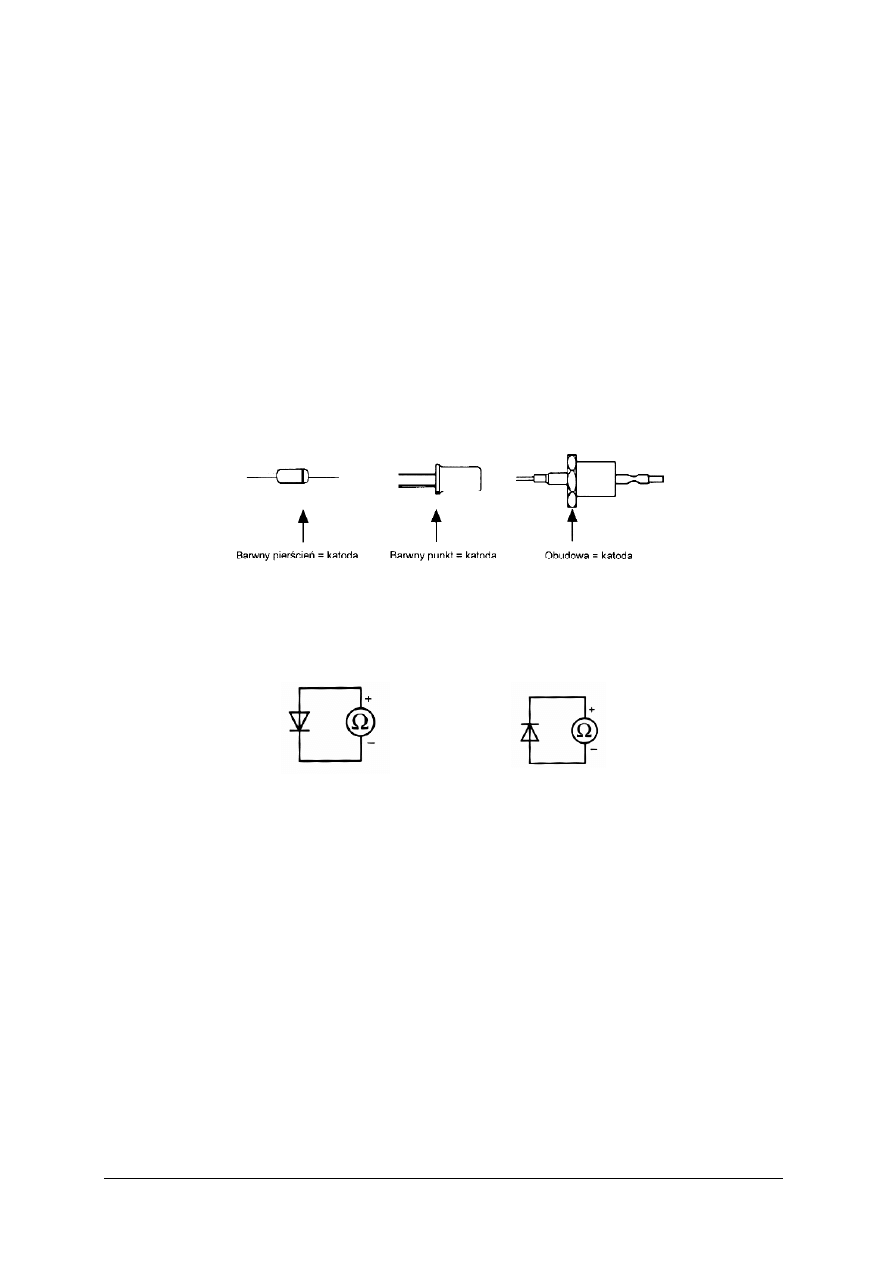
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.5. Podstawowe elementy i układy elektroniczne

4.5.1. Materiał nauczania

Elementy półprzewodnikowe i elementy optoelektroniczne

Do podstawowych elementów elektronicznych półprzewodnikowych zalicza się diodę,

tranzystor, tyrystor oraz elementy optoelektroniczne.

W diodach dla prądu elektrycznego istnieje kierunek przewodzenia i kierunek zaporowy.

Jeżeli strzałka w symbolu graficznym diody (rys. 42) wskazuje umowny kierunek prądu, to
dioda jest połączona w kierunku przewodzenia. W kierunku przewodzenia w diodzie powstaje
napięcie ok. 0,7 V, które nazywa się napięciem progowym.

W kierunku zaporowym napięcie nie może przekroczyć dopuszczalnej wartości,

a w kierunku przewodzenia prąd nie może przekroczyć prądu dopuszczalnego. Praca diody
w zbyt dużej temperaturze powoduje zniszczenie diody. Oznaczenie diody przedstawia (rys. 42)

Rys. 42. Oznaczenie katody na diodzie [8, s. 89]

Sprawdzenie diody można dokonać miernikiem uniwersalnym (rys. 11). Należy zmierzyć

rezystancję diody krzemowej w kierunku przewodzenia i zaporowym, wykorzystując różne
zakresy pomiarowe.

Rys. 43. Sprawdzenia diody: z lewej – w kierunku przewodzenia, z prawej – zaporowym [8, s. 83]

Diody mają bardzo szerokie zastosowanie, są stosowane do prostowania prądu.

Tranzystor

Tranzystor to trójelektrodowy półprzewodnikowy element elektroniczny, posiadający

zdolność wzmacniania sygnału elektrycznego.

Tranzystor ze względu na swoje właściwości wzmacniające znajduje bardzo szerokie

zastosowanie. Stosowany jest do budowy różnego rodzaju wzmacniaczy: różnicowych,
operacyjnych, mocy (akustycznych), selektywnych, pasmowych. Jest kluczowym elementem
w konstrukcji wielu układów elektronicznych, takich jak źródła prądowe, stabilizatory,
przerzutniki, generatory, przesuwniki napięcia, klucze elektroniczne.

Dzięki rozwojowi technologii oraz ze względów ekonomicznych większość wymienionych

wyżej układów tranzystorowych realizuje się w postaci układów scalonych. Z tranzystorów
zbudowane są mikroprocesory (liczące miliony tranzystorów).

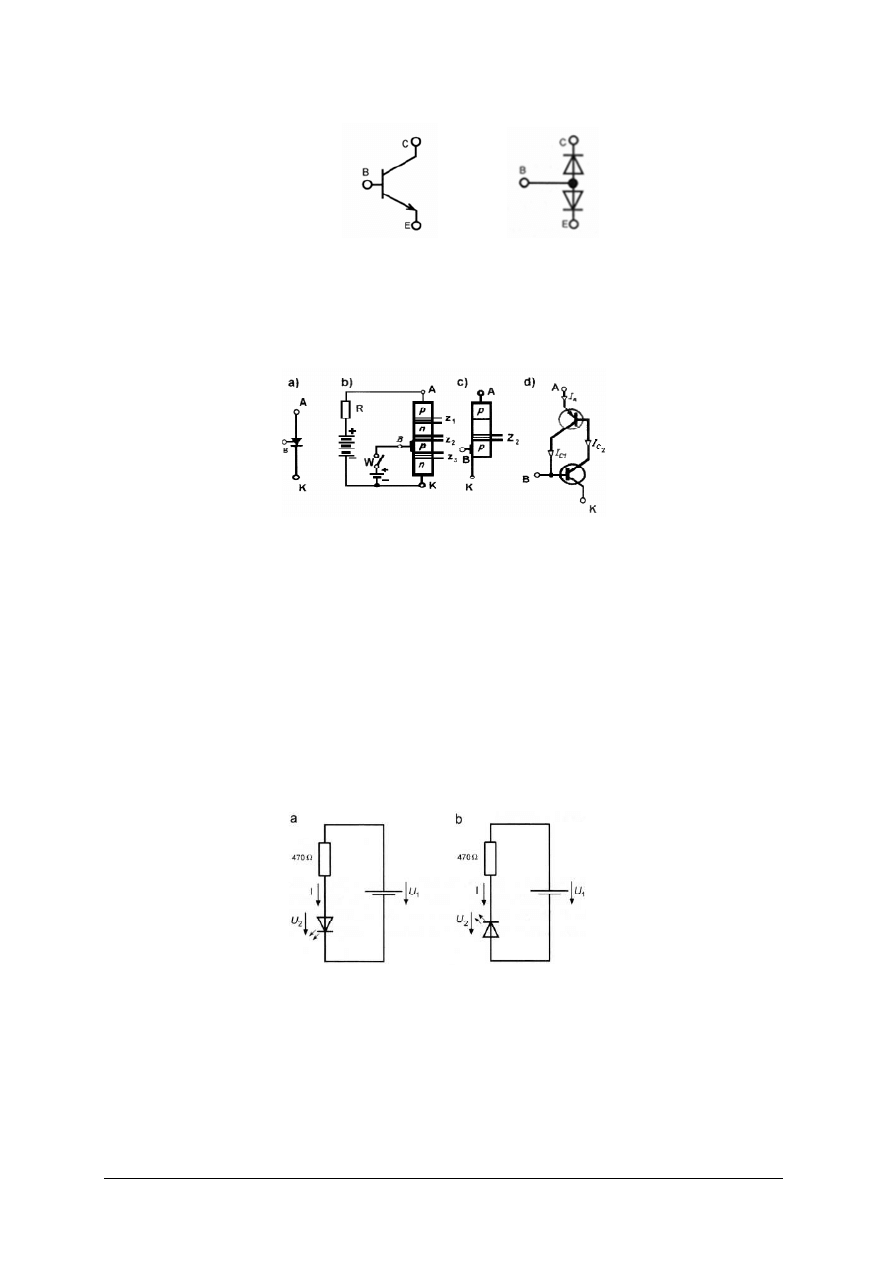
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 44. a) Oznaczenie schematyczne tranzystora, b) tranzystor jako otwarty zestyk [8, s. 99]

Tyrystor – dioda sterowana, tu półprzewodnik o strukturze czterowarstwowej p-n-p-n

(rys. 45). Końcówki przyłączone do warstw zewnętrznych p i n stanowią anodę i katodę,
a końcówka przyłączona do warstwy wewnętrznej p stanowi elektrodę sterującą, zwanej bramką.

Rys. 45. Tyrystor : a) symbol graficzny, b) struktura czterowarstwowa, c) schemat zastępczy, d) analogia

dwutranzystorowa [8, s. 252]

Zasadę działania tyrystora o strukturze czterowarstwowej p-n-p-n można wyjaśnić poprzez

zastosowanie analogii z dwoma tranzystorami p-n-p oraz n-p-n (jak na rys. 45 d). Gdy do
tyrystora doprowadzone jest napięcie polaryzujące dodatnio anodę względem katody,
zewnętrzne złącza z

i z

są spolaryzowane w kierunku przewodzenia, złącze z

jest

spolaryzowane zaporowo.

Dioda LED (Light-Emiting-Diode)

Dioda elektroluminescencyjna LED (ang. Light Emitting Diode) – zaliczana jest do

półprzewodnikowych przyrządów optoelektronicznych, emitujących promieniowanie w zakresie
światła widzialnego i podczerwieni.

Rys. 46. Dioda świecąca a) kierunek przewodzenia, b) kierunek zaporowy. U

– napięcie zasilania, U

– napięcie na

diodzie świecącej, I – prąd płynący przez diodę świecącą. [8, s. 92]

Napięcie przewodzenia diody świecącej wynosi ok. 1,6 do 4 V, a prąd przewodzenia tylko

4 do 20 mA, w zależności od rodzaju diody oraz wartości rezystancji obciążenia.

Napięcie przewodzenia diod LED wynosi, dla diod o barwie:

−

czerwonej ok. 1,6 V,

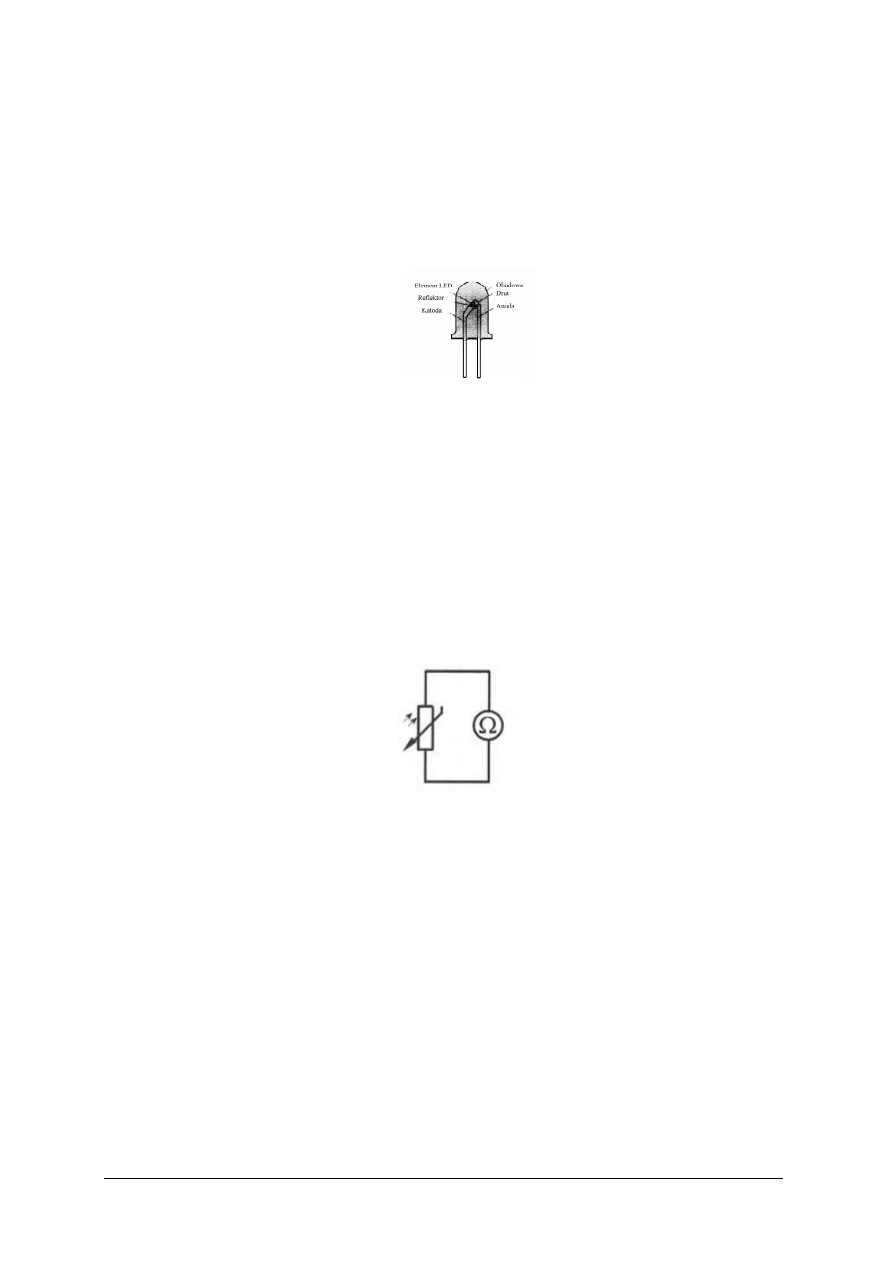
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

pomarańczowej ok. 2,2V,

−

zielonej ok. 2,7 V,

−

żółtej ok. 2,4 V,

−

niebieskiej ok. 4,0 V.
Diody świecące wykonuje się z połączonych elementów półprzewodnikowych jak:

GaP = gal-fosfor, GaN = gal-azot, GaAsP = gal-arsen-fosfor. Budowę diody świecącej
przedstawia rysunek 47.

Rys. 47. Budowa diody LED [8, s. 93]

Diody świecące stosuje się jako próbnik kontrolny. Próbnik ustala rodzaj napięcia, a przy

napięciu stałym – biegunowość. Diody świecące są stosowane jako zapory świetlne
w czujnikach mających nadajnik światła i światłoczuły odbiornik. Bywają stosowane jako
wyświetlacze siedmiosegmentowe.

Fotorezystor (LDR) (Light-Depedent-Resistor)

W materiałach półprzewodnikowych po doprowadzeniu energii można wyrwać elektrony

z ich połączeń, a tym samym zwiększyć przewodność materiału. Światło jest tą energią i można
nim wpływać na przewodność materiału. Ze wzrostem strumienia światła zmniejsza się
rezystancja fotorezystora (LDR). Na (rys. 48) przedstawiono obwód z fotorezystorem.

Rys. 48.

Obwód z fotorezystorem LDR [8, s. 204]

Fotorezystor stosowany bywa do:

−

regulacji intensywności oświetlenia np. zestawu wskaźników,

−

jako odbiornik w zaporze świetlnej np. w urządzeniu włączającym.

Wzmacniacz

Wzmacniacz jest to urządzenie elektroniczne, którego zadaniem jest zwiększenie poziomu

sygnału elektrycznego przy użyciu energii źródła zasilającego.

Wzmacniacze możemy podzielić na:

Ze względu na rodzaj wzmacnianego sygnału:

−

prądu stałego (wzmacniają tylko sygnały prądu stałego lub wolno zmieniające się),

−

prądu przemiennego (wzmacniają w pewnych granicach sygnały prądu zmiennego,
występują tu wzmacniacze m.cz. - małej częstotliwości i w.cz. - dużej częstotliwości).

Ze względu na pasmo częstotliwości:

−

wąskopasmowe - zwane selektywnymi,

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

szerokopasmowe.

Ze względu na rodzaj i sposób włączenia elementu obciążającego:

−

oporowe,

−

transformatorowe,

−

rezonansowe.

Ze względu na liczbę i sposób włączenia urządzeń wzmacniających (tranzystorów):

−

jednostopniowe (w ich skład wchodzi tylko jeden element wzmacniający),

−

wielostopniowe,

Ze względu na rodzaj wielkości, która podlega wzmocnieniu:

−

wzmacniacze napięciowe,

−

wzmacniacze prądowe,

−

wzmacniacze mocy.

Ze względu na punkt pracy tranzystora wzmacniacza:

−

wzmacniacze klasy A,

−

wzmacniacze klasy B,

−

wzmacniacze klasy C,

−

wzmacniacze klasy D,

−

wzmacniacze klasy AB.

Najważniejszymi parametrami wzmacniaczy elektronicznych są:

Współczynnik wzmocnienia. Można wyróżnić wzmocnienie napięciowe, prądowe,
oraz mocy. Każdy z tych parametrów definiowany jest jako stosunek wartości sygnału
wyjściowego do wejściowego, i tak wzmocnienie napięciowe jest to iloraz napięcia
wyjściowego do napięcia wejściowego.

Identycznie wzmocnienie prądowe będzie stosunkiem prądu wyjściowego do wejściowego.

Mnożąc współczynnik wzmocnienia napięciowego i prądowego uzyskamy współczynnik
wzmocnienia mocy.

⋅

Inaczej wzmocnieniem mocy nazywamy stosunek mocy, która wydziela się w obciążeniu do
mocy dostarczonej przez źródło sygnału

Impedancja wejściowa czyli stosunek napięcia wejściowego do prądu wejściowego.

Impedancja wyjściowa czyli stosunek zmiany napięcia wyjściowego do zmiany prądu
wyjściowego wywołanych zmianą obciążenia wzmacniacza. Impedancja wejściowa
i wyjściowa to parametry, mające duży wpływ na współpracę wzmacniacza, ze źródłem
sygnału i odbiornikiem sygnału (obciążeniem wzmacniacza).

∆

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Pasmo przenoszenia wzmacniacza jest to parametr wynikający z faktu, że dany wzmacniacz
elektroniczny nie wzmacnia w taki sam sposób sygnałów o różnych częstotliwościach.
Określenie pasma jest możliwe na podstawie charakterystyk częstotliwościowych.

Zniekształcenia nieliniowe. Przyczyną zniekształceń nieliniowych są nieliniowe
charakterystyki prądowo-napięciowe elementów (głównie tranzystorów) wchodzących
w skład układu wzmacniającego. Sygnał przepływając przez element nieliniowy ulega
zniekształceniu, przez co na wyjściu, oprócz wszystkich częstotliwości, z jakich składa się
przebieg wejściowy, pojawią się dodatkowe składowe sygnału o częstotliwości, których
uprzednio nie było. Te dodatkowe składowe napięcia sygnału to tzw. wyższe harmoniczne.
Im większe są amplitudy poszczególnych harmonicznych, tym większa jest wartość
zniekształceń nieliniowych. W technice poziom zniekształceń nieliniowych określany jest
współczynnikiem zawartości harmonicznych.

Wzmacniacze operacyjne są najbardziej rozpowszechnionym analogowym układem

elektronicznym, realizowanym obecnie w postaci monolitycznych układów scalonych. Wielka
uniwersalność, przy jednoczesnym wykorzystaniu istotnych właściwości układów scalonych,
daje możliwość stosowania ich w rozmaitych układach, urządzeniach i systemach
elektronicznych.

Wzmacniacz operacyjny posiada dwa wejścia: odwracające (oznaczane symbolem '-',

napięcie na tym wejściu U

) i nieodwracające (oznaczane symbolem '+', napięcie na tym

wejściu U

), oraz jedno wyjście (napięcie na wyjściu U

, lub U

). Różnica napięć wejściowych

nazywa się napięciem różnicowym (U

= U

− U

Idealny wzmacniacz charakteryzuje się:

−

nieskończenie dużym różnicowym wzmocnieniem napięciowym,

−

zerowym wzmocnieniem sygnału wspólnego,

−

nieskończenie dużą impedancją wejściową,

−

zerową impedancją wyjściową,

−

nieskończenie szerokim pasmem przenoszonych częstotliwości,

−

nieskończenie dużym zakresem dynamicznym sygnału.

Zasilanie
+15V

Zasilanie
-15V

Rys. 49. Wzmacniacz operacyjny [opracowanie własne]

Parametry rzeczywistego wzmacniacza odbiegają od tych założeń, i tak:

−

wzmocnienie napięciowe sygnału różnicowego nie jest nieskończenie wielkie, choć bardzo
duże - µA741 – 2×10

V/V],

−

impedancja wejściowa nie jest nieskończenie wielka, choć bardzo duża - rzędu megaomów -
µA741 – 2MΩ, wzmacniacz stanowi niewielkie obciążenie dla źródła sygnału prądy
wejściowe są rzędu nano lub nawet pikoamperów - µA741 – 20nA,

−

impedancja wyjściowa nie jest równa zeru a rzędu kilkuset omów - µA741 – 75Ω,

−

pasmo przenoszenia sygnałów nie jest nieograniczone, powyżej częstotliwości granicznej
wzmocnienie zaczyna spadać - µA741 – 1MHz,

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

wejścia wzmacniacza nie są idealnie symetryczne, ze względu na ich asymetrię definiuje się
tzw. wejściowe napięcie niezrównoważenia - jest to napięcie różnicowe (1 mikro do kilku
miliwoltów - µA741 – 1mV), jakie trzeba podać na wejścia, aby napięcie wyjściowe było
równe zero.

Generatory

Generatory są to układy elektroniczne wytwarzające sygnały zmienne o określonym

kształcie i częstotliwości kosztem energii pobieranej ze źródła zasilającego, bez konieczności
doprowadzania z zewnątrz jakiegokolwiek sygnału sterującego. Pracują one przy wykorzystaniu
dodatniego sprzężenia zwrotnego. Podstawowymi parametrami generatora są:

−

wartość częstotliwości,

−

kształt przebiegu generowanego,

−

moc sygnału generowanego.
Ze względu na kształt generowanego przebiegu możemy je podzielić na: generatory drgań

sinusoidalnych i niesinusoidalnych.

−

sinusoidalne,

−

impulsowe,

−

przebiegu prostokątnego,

−

przebiegu liniowego (trójkątnego, piłokształtnego).
Pod względem rodzaju elementów decydujących o częstotliwości generowanego przebiegu

możemy je podzielić na trzy grupy:
1)

RC,

LC,

kwarcowe.
Parametrem generatorów jest stałość częstotliwości generowanego przebiegu – stosunek

średniej wartości odchyłki częstotliwości do wartości nominalnej (f

) częstotliwości. Wyrażana

jest liczbą niemianowaną. W zależności od tego, za jaki okres czasu wyznacza się średnią
wartość odchyłki częstotliwości, wyróżnia się stałość krótko- i długoterminową.

Innym ważnym parametrem jest również współczynnik zawartości harmonicznych,

oraz zakres i charakter przestrajania generatora. Generatory mogą być przestrajane napięciem,
prądem lub zmianą punktu pracy elementów aktywnych albo zmianą parametrów sprzężenia
zwrotnego.

Przed realizacją ćwiczeń należy zapoznać się z treściami dotyczącymi podstaw elektroniki,

umieszczonymi na stronach internetowych, np. WWW.wikipedia.org/

4.5.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

Jakie elementy elektroniczne zalicza się do elementów półprzewodnikowych?

Co to jest napięcie progowe?

Jak oznaczona jest katoda w diodzie?

W jaki sposób sprawdza się diody w kierunku przewodzenia i kierunku zaporowym?

Jak nazywają się końcówki tyrystora?

Jaką strukturę posiada tyrystor?

Jakie zastosowanie mają diody elektroluminescencyjne (LED)?

Z jakich materiałów wykonuje się diody świecące?

Jak działa fotorezystor?

10.

Jakie ma zastosowanie fotorezystor?

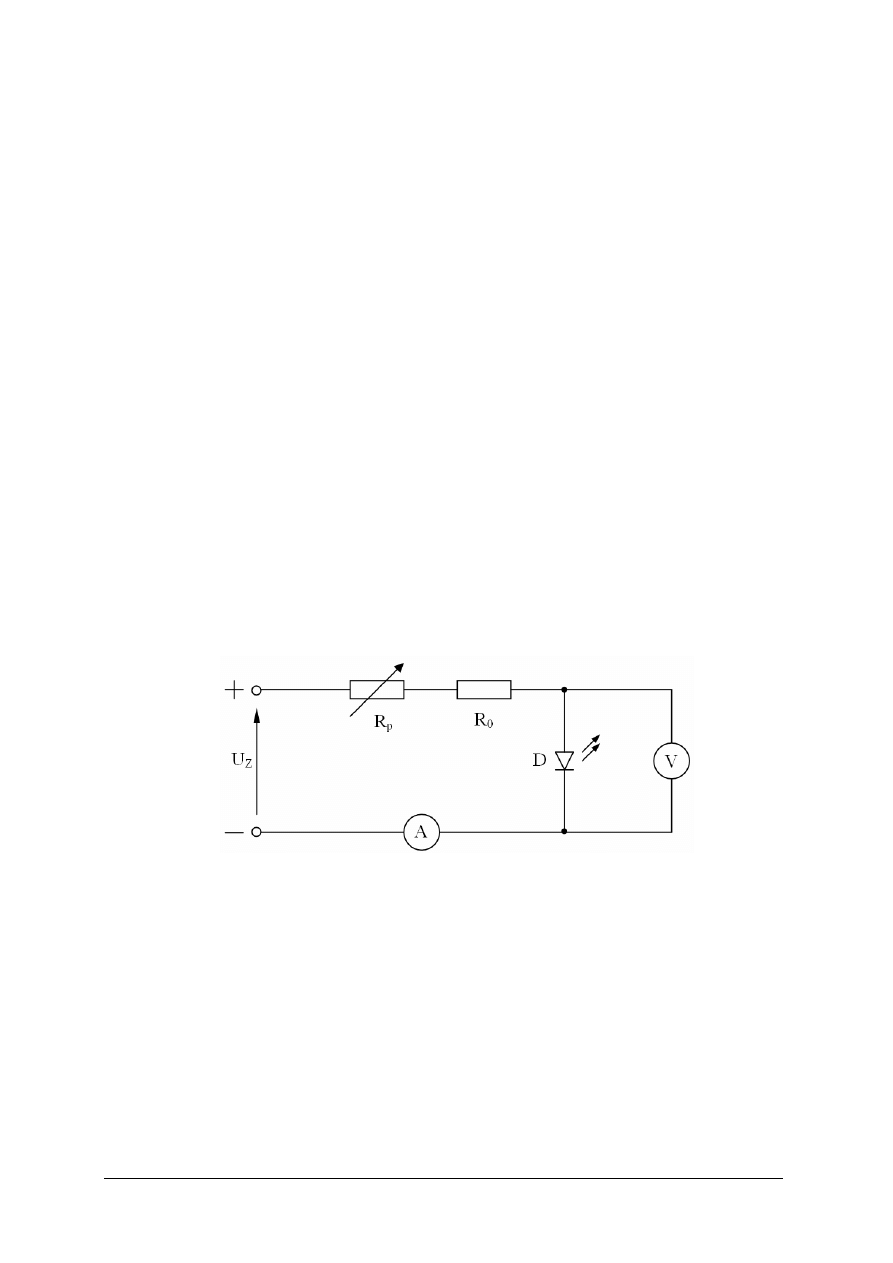
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.5.3. Ćwiczenia

Ćwiczenie 1

Sklasyfikuj diody na podstawie ich oznaczeń i pomiarów.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zorganizować stanowisko pracy,

zapoznać się z katalogami diod półprzewodnikowych,

rozpoznać diody po ich oznaczeniach,

wykonać pomiary rezystancji diod w kierunku przewodzenia i zaporowym,

zaprezentować wykonane ćwiczenie.

Wyposażenie stanowiska pracy:

−

instrukcje i przewodnie teksty do ćwiczeń,

−

diody,

−

miernik uniwersalny,

−

dokumentacje techniczne, katalogi, normy ISO,

−

zeszyt do ćwiczeń,

−

przybory do pisania,

−

zestaw komputerowy z dostępem do Internetu.

Ćwiczenie 2

Przeprowadź badanie diody elektroluminescencyjnej LED.

Schemat układu pomiarowego

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zapoznać się z instrukcją do ćwiczenia,

zorganizować stanowisko do wykonania pomiarów diody LED,

zapoznać się z parametrami diod elektroluminescencyjnych,

połączyć układ pomiarowy według schematu układu pomiarowego,

wykonać pomiary, z uwzględnieniem I

max

≤

20mA,

wykreślić charakterystyki I = f(U) dla różnych rodzajów diod w jednym układzie
współrzędnych,

zaprezentować efekty pracy.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Wyposażenie stanowiska pracy:

−

instrukcja do wykonania ćwiczenia,

−

zasilacz stabilizowany napięcia stałego,

−

mierniki uniwersalne,

−

diody elektroluminescencyjne,

−

przewody elektryczne,

−

dokumentacje techniczne, katalogi, normy ISO,

−

zeszyt do ćwiczeń,

−

przybory do pisania.

Ćwiczenie 3

Rozpoznaj elementy optoelektroniczne – fotodiodę i fotorezystor na podstawie oznaczeń

i pomiarów.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zapoznać się z instrukcją do ćwiczenia,

zorganizować stanowisko pracy zgodnie z zasadami ergonomii i przepisami bhp,

zaproponować układ do wykonywania pomiarów i przedstawić go nauczycielowi do
akceptacji,

dobrać narzędzia pomiarowe do wykonania pomiarów fotodiody i fotorezystora,

wykonać połączenia obwodu elektrycznego z fotodiodą i obwodu elektrycznego
z fotorezystorem ,

wykonać pomiary wartości prądu od napięcia przy różnych warunkach oświetlenia
fotodiody,

wykonać pomiary rezystancji fotorezystora w zalezności od natężenia oświetlenia
zewnętrznego,

wykreślić charakterystyki I = f(U) dla fotodiody oraz R = f(E) dla fotorezystora,

zaprezentować efekty pracy.

Wyposażenie stanowiska pracy:

−

instrukcja do ćwiczeń, teksty przewodnie,

−

zasilacz stabilizowany napięcia stałego i zasilacz napięcia zmiennego,

−

miernik uniwersalny,

−

źródło oświetlenia,

−

miernik natężenia oświetlenia,

−

przewody elektryczne,

−

fotodiody i fotorezystory,

−

dokumentacje techniczne, katalogi, normy ISO,

−

zeszyt do ćwiczeń,

−

przybory do pisania.

Ćwiczenie 4

Zbadaj tranzystor w podstawowym układzie wzmacniającym (OE).

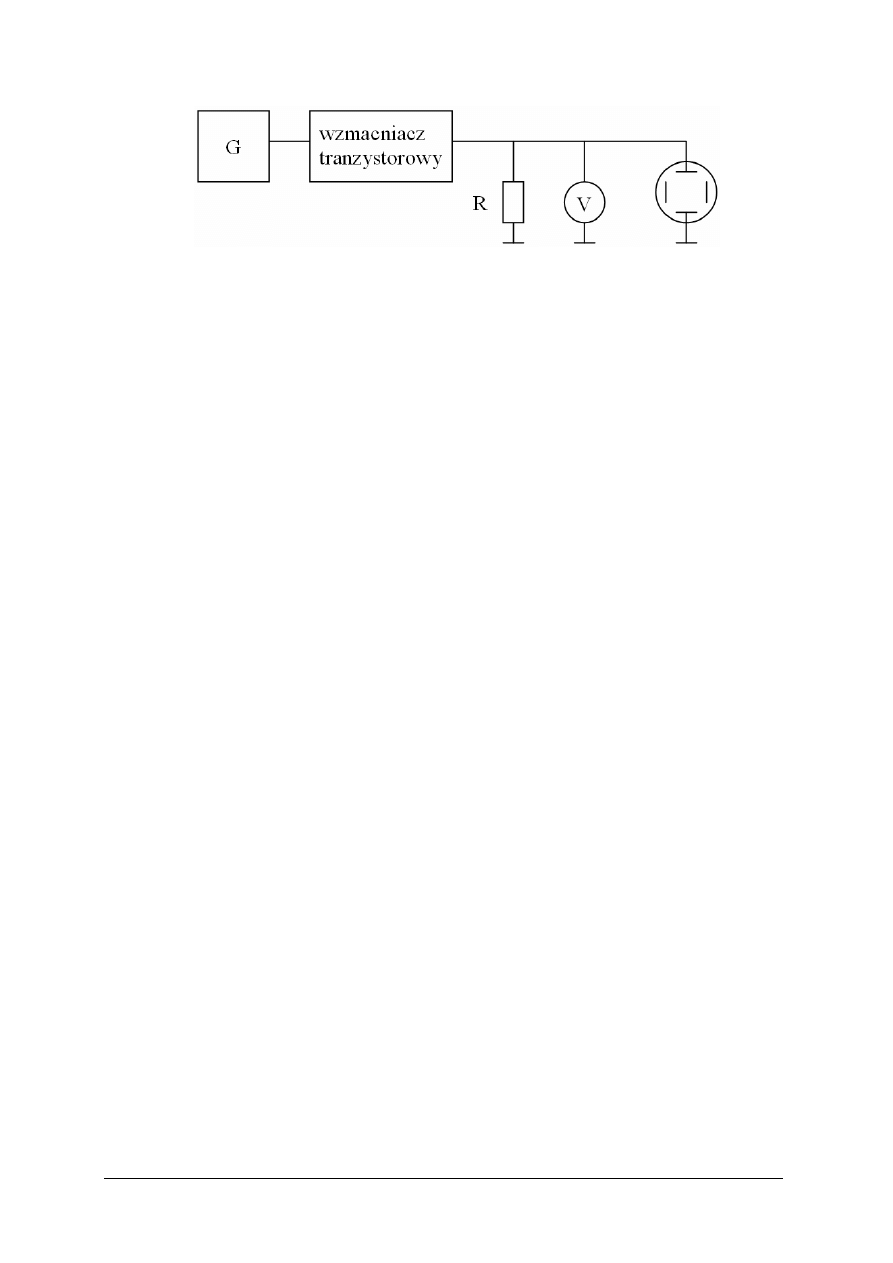
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Schemat układu pomiarowego

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zapoznać się z instrukcją do ćwiczenia,

zorganizować stanowisko pracy zgodnie z zasadami ergonomii i przepisami bhp,

dobrać narzędzia pomiarowe do wykonania pomiarów,

wykonać połączenia obwodu elektrycznego,

wykonać pomiary,

wykreślić charakterystyki U

= f(U

) przy f = 1kHz oraz U

= f(f) przy U

= 10mV,

zaprezentować efekty pracy.

Wyposażenie stanowiska pracy:

−

instrukcja do ćwiczeń, teksty przewodnie,

−

generator,

−

wzmacniacz tranzystorowy,

−

obciążenie rezystancyjne,

−

miernik uniwersalny,

−

oscyloskop,

−

przewody elektryczne i koncentryczne,

−

dokumentacje techniczne, katalogi, normy ISO,

−

zeszyt do ćwiczeń,

−

przybory do pisania.

4.5.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

rozpoznać elementy elektroniczne półprzewodnikowe?

odczytać oznaczenia na obudowie diody?

określić wartość napięcia między bazą, a emiterem w tranzystorze?

zorganizować stanowisko do wykonania pomiarów elementów
optoelektronicznych?

rozpoznać końcówki tyrystora?

określić z jakich materiałów półprzewodnikowych wykonuje się diody
świecące?

określić zastosowanie diod świecących?

rozpoznać fotorezystory?

wyznaczyć podstawowe parametry diody?

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.6. Zasady bezpiecznej obsługi urządzeń elektrycznych. Techniki

i metody pomiarowe stosowane w obwodach prądu stałego
i przemiennego

4.6.1. Materiał nauczania

Przed przystąpieniem do naprawy, konserwacji lub innych prac związanych z obsługą

urządzeń elektrycznych należy odłączyć urządzenie od sieci zasilającej i skutecznie
zabezpieczyć, postępując według reguł bezpieczeństwa w ustalonej kolejności.

Reguła 1: Wyłączyć napięcie
Przed rozpoczęciem pracy należy wyłączyć wszystkie obwody doprowadzające napięcie do

miejsca pracy. Samo naciśnięcie wyłącznika w tym przypadku nie wystarcza. W obwodach
zawierających kondensatory trzeba się upewnić, czy po wyłączeniu zostały one rozładowane
przez odpowiednie urządzenia, np. przez wbudowane rezystory. Napięcie na kondensatorach
musi obniżyć się w ciągu minuty do wartości poniżej 50 V.

Reguła 2: Zabezpieczyć przed powtórnym załączeniem
Urządzenia, za pomocą których instalację wyłączono spod napięcia, np. bezpieczniki

i wyłączniki, należy natychmiast po wyłączeniu zabezpieczyć w sposób pewny przed ponownym
załączeniem. Odłączniki główne, które można unieruchomić w stanie otwartym, należy
zablokować za pomocą kłódek. Jeżeli na przykład przy urządzeniu grzewczym pracują
jednocześnie elektrycy i hydraulicy, każda grupa powinna niezależnie zablokować wyłącznik
własną kłódką. W ten sposób zabezpieczą się przed mimowolnym załączeniem urządzenia.
Urządzenie może być ponownie uruchomione dopiero po usunięciu wszystkich kłódek. Oprócz
blokady napędu można również usunąć płytkę izolacyjną pomiędzy otwarte styki odłącznika.
Miejsca załączania, nawet te, które znajdują się w bezpośrednim sąsiedztwie miejsca, gdzie
prowadzi się prace, należy zaopatrzyć w tablicę Nie włączać - pracują ludzie.

Reguła 3: Sprawdzić brak napięcia
Po wyłączeniu należy potwierdzić przez pomiar w miejscu wykonywania prac, że

rzeczywiście napięcie nie występuje. Tylko w ten sposób można sprawdzić, czy przez pomylenie
bezpieczników lub wyłączników nie wyłączono innego obwodu.

Reguła 4: Uziemić i zewrzeć
Urządzenia uziemiające i zwierające należy zawsze łączyć najpierw z uziemieniem

a dopiero później z częścią urządzenia, która ma być uziemiona i zwarta na krótko. Urządzenie
do uziemiania i zwierania musi być widoczne z miejsca, w którym wykonuje się pracę.
W sytuacji, gdy jest to technicznie niemożliwe, wolno uziemić i zewrzeć także poza miejscem
pracy, najbliżej tego miejsca. Należy zwracać uwagę na pewny kontakt urządzeń uziemiających
i zwierających z uziomem, ponieważ urządzenia te w różnych warunkach muszą przewodzić
prądy zwarciowe o dużym natężeniu

Reguła 5: Osłonić i oddzielić sąsiadujące elementy znajdujące się pod napięciem
W pobliżu wyłączonego miejsca pracy mogą się znajdować elementy instalacji, których nie

można wyłączyć z uwagi na pewność ruchu albo przewidywane straty materialne. W tym
przypadku elementy znajdujące się pod napięciem należy w taki sposób osłonić i zabezpieczyć,
żeby nie można było ich dotknąć ciałem lub narzędziem. Miejsce pracy musi być oznaczone
tablicą ostrzegawczą z napisem Miejsce pracy.

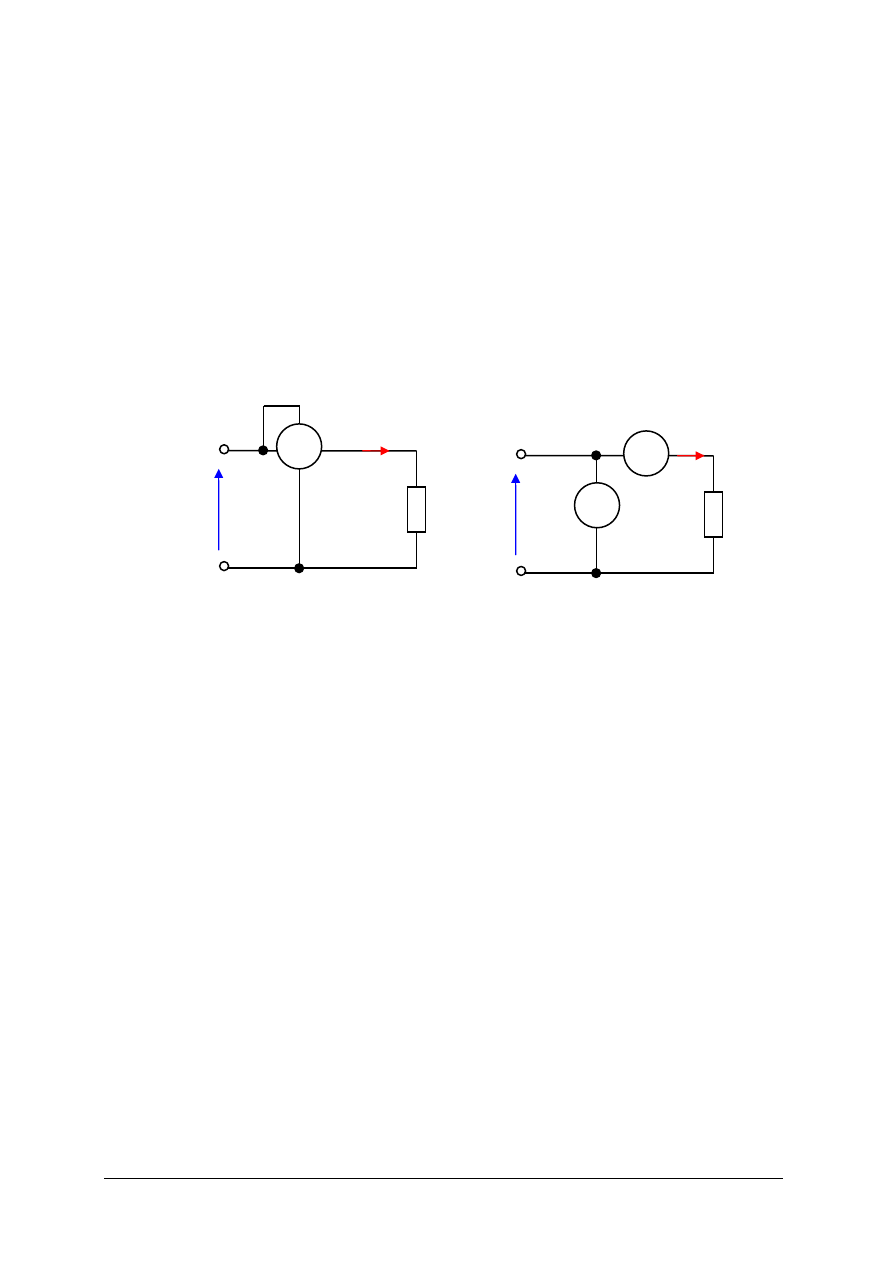
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Przyrządy pomiarowe i błędy pomiarowe. Pomiary oraz regulacja napięcia i natężenia
prądu. Pomiar rezystancji

Wzorzec miary jest to narzędzie pomiarowe odtwarzające z określoną dokładnością jedną

wartość wielkości, kilka, lub ściśle określone wartości ciągłe w pewnym zakresie.

Metoda pomiarowa określa sposób porównania wielkości mierzonej z wzorcem tej

wielkości zastosowanym w pomiarach, celem wyznaczenia wyniku pomiaru. Stosuje się różne
metody w zależności od: rodzaju wielkości mierzonej, wymaganej dokładności, sposobu
opracowania wyników, warunków

pomiaru (laboratoryjne, przemysłowe, terenowe). Tę samą

wielkość (np. rezystancję) można mierzyć różnymi metodami.

W metodzie pomiarowej bezpośredniej wartość wielkości mierzonej otrzymuje się

bezpośrednio bez dodatkowych obliczeń, np.: pomiar prądu elektrycznego – amperomierzem,
mocy elektrycznej – watomierzem, rezystancji elektrycznej – omomierzem.

Rys. 50. Metody pomiaru mocy: a) bezpośrednia, b) pośrednia [1, s. 207]

W metodzie pomiarowej pośredniej mierzy się bezpośrednio nie wielkość badaną Y, lecz

wielkości A, B, C, ... związane z wielkością Y zależnością funkcyjną: Y = f(A, B, C,...), ustaloną
teoretycznie lub doświadczalnie. Przykładem jest pomiar mocy P lub pomiar rezystancji R za
pomocą woltomierza (napięcie U) i amperomierza (prąd I), a następnie obliczenie P = U·I
(rys. 50 b) lub R = U/I.

Narzędzia pomiarowe są to środki techniczne służące do bezpośredniego porównania

mierzonych wielkości z jednostkami miary tych wielkości. Są to wzorce, przyrządy pomiarowe,
przetworniki pomiarowe.

Przyrząd pomiarowy jest to narzędzie pomiarowe służące do przetwarzania wielkości

mierzonej na wskazania lub równoważną informację. Nazwa przyrządu pochodzi od wielkości
mierzonej (np.: częstościomierz, fazomierz), jednostki miary (np.: amperomierz, omomierz),
zasady działania (np. kompensator, komparator) lub od nazwiska wynalazcy (np.: mostek
Wheatstone’ a, mostek Wiena).

Przyrządy pomiarowe klasyfikuje się wg różnych kryteriów. Na przykład wg spełnianych

funkcji przyrządy pomiarowe dzieli się na: mierniki, rejestratory, liczniki i detektory zera.
Mierniki są to przyrządy pomiarowe wyskalowane w jednostkach miary wielkości mierzonej.
Rejestratory są to przyrządy pomiarowe umożliwiające zapis mierzonej wielkości w funkcji
czasu (rejestratory X-t) lub w funkcji innej wielkości (rejestratory X-Y). Detektory zera są to
przyrządy umożliwiające stwierdzenie zaniku wielkości (np.: prądu, strumienia magnetycznego).

Przetwornik pomiarowy służy do przetwarzania wartości wielkości mierzonej na

proporcjonalną wartość innej wielkości (np.: termoelement) lub inną wartość tej samej wielkości
(np.: przekładnik prądowy, dzielnik napięcia).

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ważniejsze pojęcia techniki pomiarowej
Pojęcie

Objaśnienie

Przykłady

Wielkość
pomiarowa

Mierzona wielkość fizyczna.

Napięcie, natężenie prądu, czas.

Wartość
zmierzona

Wartość odczytana ze wskaźnika przyrządu
pomiarowego pomnożona przez jednostkę
przyjętą za jednostkę miary

U =(230 ·1) V = 230V
I =(10 ·1) µA = 10µA

Wynik
pomiaru

Wartość zmierzona otrzymana z jednego lub
więcej pomiarów. Wyniki pomiarów mogą
być także obliczane w sposób pośredni.

U =230V, / = 2,5A,
P = UI = 575W

Ustrój
pomiarowy

Elementy,

które

wytwarzają

moment

obrotowy i powodują ruch wskazówki.

Ustrój magnetoelektryczny, ustrój
elektrodynamiczny

Miernik

Ustrój pomiarowy wraz z obudową, skalą
i wbudowanymi elementami, np. rezystorami
połączonymi szeregowo i lub równolegle.

Multimetr, częstotliwościomierz

Przyrząd
pomiarowy

Miernik wraz z całym wyposażeniem,
również odłączanym, jak np. przewody
pomiarowe, głowice i przekładniki. Przyrząd
pomiarowy jest kompletnym urządzeniem.

Miernik z oddzielnym dzielnikiem,
przekładnikiem

prądowym,

przekładnikiem napięciowym lub
czujnikiem temperatury.

Metoda
pomiaru

Sposób przeprowadzenia pomiaru.

Pomiar bezpośredni lub pośredni.
Metoda

techniczna,

metoda

mostkowa.

Pomiar
bezpośredni

Szukana

wartość

jest

określana

(bezpośrednio) przez pomiar.

Pomiar

prądu

amperomierzem,

pomiar napięcia woltomierzem.

Pomiar
pośredni

Szukana wartość wielkości mierzonej jest
określana na podstawie kilku wartości
ustalonych bezpośrednio.

Obliczanie wartości rezystancji lub
mocy

podstawie

wartości

otrzymanych z pomiarów napięcia
i prądu.

Dla przyrządów i przetworników sprecyzowano warunki pracy (temperatura, wilgotność,

i inne). Błąd przetwarzania narzędzia pomiarowego wyznaczony w warunkach odniesienia
(znamionowych) nazywa się błędem podstawowym.

Błędy powstające w samym przyrządzie zależą od konstrukcji przyrządu, np.: od rodzaju

ułożyskowania ustroju pomiarowego i zależnego od niego tarcia w łożyskach. W przypadku
mierników wskazówkowych błąd wskazań przyrządu jest podany na skali jako wartość liczbowa
wyrażonego w procentach stosunku maksymalnego błędu bezwzględnego do największego
wskazania. Wartość tę nazywa się klasą dokładności przyrządu. Błąd bezwzględny to różnica
między wynikiem pomiaru a przyjętą za wzorcową

Na uchyby pomiaru składają się: błąd odczytu, błędne posługiwanie się miernikiem, błędne

przyłączenie miernika, błędy wynikające z klasy miernika i wpływy zewnętrzne.

Jeżeli narzędzie będzie stosowane w warunkach różnych od warunków znamionowych, to

wynik pomiaru będzie ponadto obarczony błędami dodatkowymi spowodowanymi
wielkościami wpływowymi (np.: temperaturą – błąd temperaturowy, częstotliwością – błąd
częstotliwościowy).

Ograniczona dokładność narzędzia pomiarowego powoduje, że wskazanie narzędzia różni

się od wartości prawdziwej wielkości mierzonej. Różnicę między tymi wartościami nazywa się
błędem pomiaru. Rozróżnia się wiele składowych błędów – np.: błędy przyrządowe
(podstawowy i dodatkowe), błąd metody – spowodowany zastosowaniem nieodpowiedniej
metody pomiaru z uwagi na właściwości użytych narzędzi pomiarowych. Inne podziały, błędy
bezwzględni i względne, błędy systematyczne, przypadkowe i nadmierne.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Błędy powstające w samym przyrządzie zależą od konstrukcji przyrządu, np.: od rodzaju

wartością mierzonej wielkości.

Błąd bezwzględny ∆ jest różnicą między wynikiem pomiaru x a wartością prawdziwą

(rzeczywistą) wielkości mierzonej v czyli

∆ = x - v

Błąd bezwzględny ∆, zawsze wyrażony w jednostkach wielkości mierzonej, konkretny znak:

plus ( + ) lub minus (–).

Wskazanie narzędzia pomiarowego x jest nazywane niekiedy surowym wynikiem pomiaru.

Wartość prawdziwa v jest w praktyce nieznana. W pomiarach można zastąpić względnie
dokładnym przybliżeniem, tzw. wartością poprawną x

, otrzymaną za pomocą wzorcowego

narzędzia pomiarowego. Błąd bezwzględny ∆, lecz ze znakiem przeciwnym, nazywa się
poprawką.

p = - ∆

Dodając algebraicznie poprawkę p do wartości x uzyskanej z pomiarów, otrzymuje się

wynik poprawiony, równy wartości poprawnej.

= x + p

Wprowadza się też pojęcie błędu względnego δ. Jest to stosunek błędu bezwzględnego ∆ do

wielkości mierzonej v, czyli:

−

∆

Lub wyrażonego w procentach:

100

⋅

∆

Błędy systematyczne są to błędy, które przy wielu pomiarach tej samej wartości określonej

wielkości, wykonanych w tych samych warunkach, są stałe lub zmieniają się wg określonego
prawa wraz ze zmianą warunków. Błędy systematyczne stałe mają tę samą wartość i znak przy
każdym pomiarze. Powstają np.: przy użyciu narzędzi pomiarowych w warunkach różnych od
warunków odniesienia, przy użyciu miernika z przesuniętym położeniem zerowym lub błędnie
wykonaną działką. Błędy systematyczne zmienne mają różne wartości w funkcji czasu, lub
w funkcji innej wielkości (np.: mierzonej). Na przykład mierzony prąd nagrzewa sprężyny
wytwarzające moment zwrotny miernika, a to powoduje wzrost wychylenia wskazówki tego
miernika. Wykrycie błędów systematycznych jest trudne. Wielokrotne powtarzanie pomiarów
nie umożliwia ich wykrycia ani wyeliminowania. Istnienie błędów systematycznych można
stwierdzić w wyniku zastosowania innej metody pomiarowej lub zastosowania innego narzędzia
pomiarowego.

Błędy przypadkowe są to błędy zmieniające się w sposób nieprzewidziany (przypadkowy,

losowy), zarówno co do znaku, jak i wartości bezwzględnej, przy powtarzaniu pomiarów tej
samej wielkości mierzonej w warunkach praktycznie niezmiennych. Błędów przypadkowych nie
można usunąć z wyników pomiarów przez dodanie poprawek, ponieważ wartości tych poprawek
są nieznane. Na podstawie serii pomiarów i rachunku prawdopodobieństwa ustala się granice,
w których znajdują się błędy przypadkowe (przedział niepewności końcowego wyniku pomiaru).
Podział błędów na systematyczne, przypadkowe i

nadmierne ilustruje np. wynik strzelania do

trzech tarcz (rys. ). Odległość od przestrzeliny do środka tarczy jest błędem bezwzględnym. Na
tarczy przedstawionej na rys. a przestrzeliny są rozproszone wokół środka tarczy. Jest to
ilustracja błędów przypadkowych. Przestrzelina w prawym górnym rogu tarczy ilustruje błąd
nadmierny. Na rysunku b przedstawiono przesunięcie środka rozrzutu przestrzelin względem

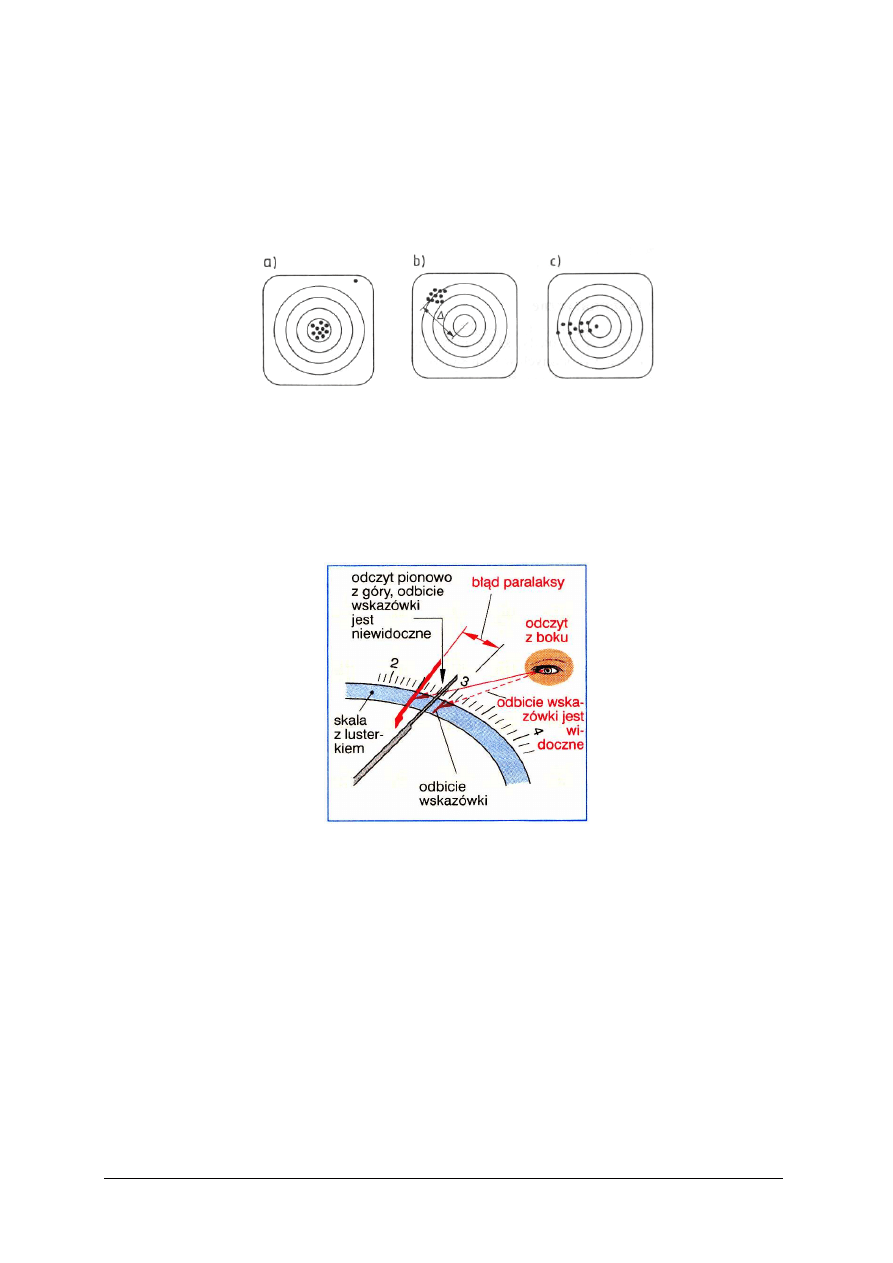
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

środka tarczy (spowodowane np.: źle nastawionym urządzeniem celowniczym). Przesunięcie
∆ przedstawia błąd systematyczny stały. Na rysunku c przedstawiono błąd systematyczny
zmienny (spowodowany np.: przez nasilający się proporcjonalnie do czasu strzelania wiatr
wiejący z prawej strony). Analogicznie w pomiarach elektrycznych podobny wpływ na uzyskany
wynik może mieć: uszkodzenie miernika (zawyża bądź zaniża wskazanie), niewłaściwa
temperatura, wilgotność, metoda pomiaru.

Rys. 51. Wyniki strzelania do trzech tarcz, a) ilustracja błędów przypadkowych i błędu nadmiernego, b) ilustracja
błędu systematycznego stałego i błędów przypadkowych, c) ilustracja błędu systematycznego zmiennego i błędów

przypadkowych [3, s. 52]

Błędy odczytu powstają, gdy wynik pomiaru z miernika wskazówkowego odczytuje się

patrząc na skalę nieco z boku. Błędu paralaksy można uniknąć stosując skalę z lusterkiem.
Przed każdym pomiarem należy sprawdzić prawidłowość zerowego położenia wskazówki.

Rys. 52. Błąd paralaksy [1, s. 161]

Błędy związane z niewłaściwym posługiwaniem się przyrządem polegają m.in. na

nieodpowiednim ustawieniu zakresu pomiarowego albo rodzaju pracy . Inną przyczyną może
być niewłaściwe położenie miernika. Prawidłowe położenie przyrządu jest oznaczone na skali.
Przyrządy tablicowe pracują w położeniu pionowym (oznaczenie: ┴), przyrządy wielozakresowe
w położeniu poziomym (oznaczenie: ┌┐).

Przyrządem pomiarowym jest narzędzie pomiarowe, które przetwarza mierzoną wielkość

(np.: prąd, napięcie) na wskazanie proporcjonalne do wartości wielkości mierzonej.

Rozróżnia się przyrządy o działaniu bezpośrednim i pośrednim. W przyrządach o działaniu

bezpośrednim (o strukturze otwartej) energia zużywana na wychylenie ruchomego elementu
przyrządu jest pobierana bezpośrednio z obiektu badanego. W przyrządach o działaniu
pośrednim (o strukturze zamkniętej) energia potrzebna do przemieszczenia ruchomego elementu
przyrządu jest dostarczana ze źródła pomocniczego (są to przyrządy elektroniczne). Przyrząd
pomiarowy określający wartość wielkości mierzonej tylko za pomocą jednego wskazania

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

nazywa się miernikiem. Mierniki, w których wskazania są ciągłą funkcją wartości wielkości
mierzonej, nazywa się miernikami analogowymi (np.: amperomierz wskazówkowy).

Błędy w układzie pomiarowym powstają wskutek niewłaściwego przyłączenia przyrządu,

np.: gdy miernik napięcia włączono tak jak miernik prądu, tzn. szeregowo z odbiornikiem. Także
wskutek niewłaściwej metody pomiaru. Błędy w układzie pomiarowym mogą prowadzić nie
tylko do błędnych wyników, ale także do uszkodzenia przyrządu pomiarowego.

Przyrządy pomiarowe są wykonywane jako : laboratoryjne (w klasach dokładności: 0,1, 0,2,

0,5) i warsztatowe (w klasach dokładności: 1, 1,5, 2,5, 5).
Multimetrami lub miernikami uniwersalnymi nazywa się mierniki wielofunkcyjne
(np.: umożliwiające pomiary prądu i napięcia stałego oraz przemiennego, pomiar rezystancji).
W celu zabezpieczenia przed przeciążeniem przyrządy wielozakresowe mają najczęściej
wbudowany bezpiecznik aparatowy albo elektroniczny wyłącznik ochronny. Nowoczesne
multimetry są z reguły wyposażone w testery przejścia. Funkcja ta jest często łączona z funkcją
testera diod, stan przejścia można ocenić na podstawie wskazania spadku napięcia lub jest
sygnalizowane tonowo.

Przyrządy wielozakresowe wskazówkowe mają ustrój pomiarowy z ruchomą cewką, który

przy pomiarze wielkości prądu przemiennego włączany jest przez prostownik. Do rozszerzania
zakresów pomiarowych służą wbudowane rezystory połączone szeregowo, lub równolegle.
Przełącznik zakresów pozwala na nastawianie potrzebnego zakresu pomiarowego, np. 100 V. Do
omomierza i do zasilania wzmacniacza pomiarowego w przyrządzie jest zainstalowane
wewnętrzne źródło prądu, np. bateria 9 V.

Przyrządy wielozakresowe cyfrowe mają zamiast ustroju pomiarowego przetwornik

analogowo-cyfrowy. Wynik pomiaru jest wyświetlany w postaci cyfrowej z uwzględnieniem
miejsc dziesiętnych i znaku. Nowoczesne multimetry zapewniają znaczny komfort obsługi.
Układ automatycznego wybierania zakresu wybiera np. zakres pomiarowy o najlepszej
rozdzielczości, zależnie od wartości doprowadzonej wielkości mierzonej. Pamięć wartości
zmierzonej pozwala na odczytywanie wyniku również po zakończeniu pomiarów. Dzięki
dodatkowemu wskaźnikowi analogowemu łatwiej jest obserwować zmiany wartości mierzonej,
np. przy zdejmowaniu charakterystyk.

Wyświetlacz LCD (ciekłokrystaliczny) najczęściej stosowany w multimetrach pobiera mały

prąd, ale jest czuły na niskie temperatury. Dlatego należy unikać wykonywania pomiarów
w temperaturach poniżej 0°C.

Przyrządy analogowe to wszystkie przyrządy wskazówkowe, w których wskazówka

poruszana jest przez mechaniczny ustrój pomiarowy. Wskaźnik analogowy przedstawia wynik
pomiaru w postaci długości, jak np.: w przypadku termometru, albo w postaci kąta, jak
np. w przyrządach ze skalą i wskazówką.

Rys. 53. Skala analogowego przyrządu pomiarowego [1, s. 160

]

Przyrządy cyfrowe służące do pomiaru wielkości fizycznych analogowych mają zamiast

ustroju pomiarowego przetwornik analogowo cyfrowy (przetwornik A/C). Wartość zmierzona

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

pokazywana jest w postaci cyfrowej, np.: na wyświetlaczach 7-segmentowych. Wyświetlacz
pełny może wyświetlać wszystkie cyfry od 0 do 9. Jeśli na pierwszej pozycji (miejscu)
wyświetlacza mogą się wyświetlić tylko cyfry 0 lub 1, mówi się, że jest wyświetlane 1 /2 cyfry.
Cyfrowe przyrządy pomiarowe pozwalają na uniknięcie błędów odczytu, które popełnia się
odczytując wskazanie ze skali analogowej. Cyfrowe przyrządy pomiarowe mają często oprócz
wskaźnika cyfrowego dodatkowo wskaźnik analogowy, np.: w postaci linii. Dzięki temu łatwiej
jest obserwować zmiany wartości wielkości mierzonej, np.: przy strojeniu obwodów. Cyfrowe
przyrządy pomiarowe nie mają mechanizmów ruchomych tylko przetwornik analogowo
cyfrowy, który przetwarza analogowe wielkości fizyczne na sygnały cyfrowe. Często mają także
wbudowany wzmacniacz pomiarowy. Przetwornik A/C przetwarza tylko napięcia naprzemienne.
Z tego powodu napięcia i prądy przemienne muszą być najpierw wyprostowane. Dokładność
pomiarów przy prądzie przemiennym jest mniejsza niż przy prądzie stałym.

Rys. 54. Wyświetlacz siedmiosegmentowy 3 ½ cyfry (po lewo) i cyfrowy wyświetlacz przyrządu

wielozakresowego (po prawo) [1, s. 160]

Mierniki cyfrowe mają uchyb składający się z odchyłki własnej i błędu kwantyzacji.

Odchyłka własna (dokładność) w odniesieniu do wskazywanej wartości mierzonej zawiera się
w przedziale od ± 0,1 % do ± 1,5 %. Błąd kwantyzacji (niedokładność wskazania na ostatniej
pozycji) wynika z rozdzielczości przetwornika A/C i jest podawany w jednostkach wyświetlanej
liczby. Wynosi on, co najmniej ± 1 jednostkę. Błąd wskazań miernika cyfrowego składa się
z odchyłki własnej i błędu kwantyzacji.

Rys. 55. Obliczanie błędów przyrządu wskazówkowego (po lewo), oraz przyrządu cyfrowego [1, s. 162]

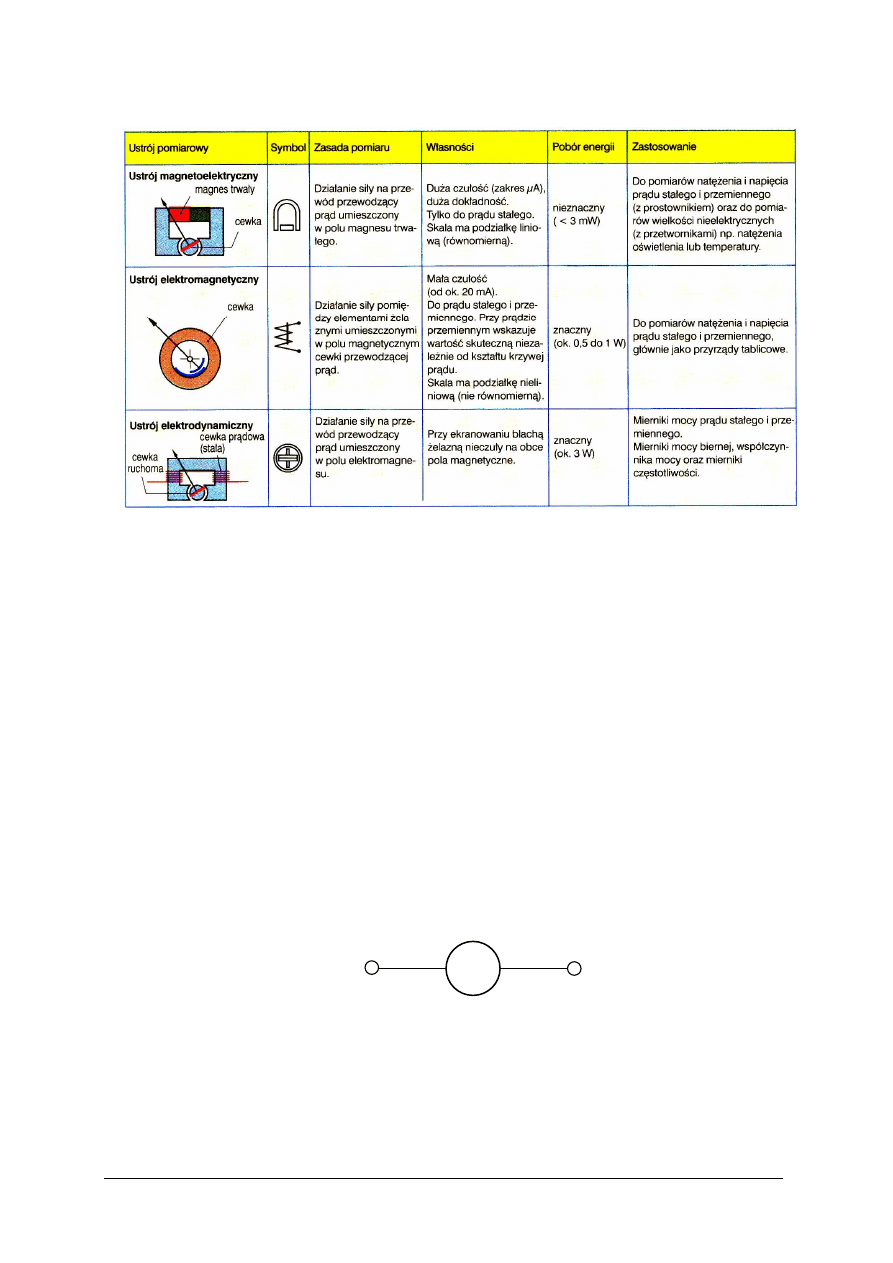
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 56. Podstawowe ustroje pomiarowe [1, s. 161]

Dwubiegunowe próbniki napięcia mogą być stosowane do napięć stałych i przemiennych.

Przy prądzie stałym wskazują również biegunowość. Próbniki dwubiegunowe mają najczęściej
wskaźnik z diodami LED. Diody te wskazują zakres występującego napięcia, np.: 12V, 50V,
albo 500V. Nowoczesne próbniki napięć nadają się również do sprawdzania ciągłości obwodu.
Ciągłość sygnalizowana jest przez diodę świecącą oraz dźwięk. Jasność świecenia i wysokość
tonu zależy przy tym od oporności obwodu.

Tester przejścia ma własne, wewnętrzne źródło prądu. Tester przejścia ze wskaźnikiem

akustycznym ma brzęczyk. Zaletą tego testera jest to, że podczas pomiaru nie trzeba odczytywać
wskazań przyrządu. W elektronicznych testerach przejścia wysokość emitowanego dźwięku
zależy

rezystancji

mierzonego

obwodu.

Można

stosować

obwodów

nisko i wysokoomowych. Testery przejścia ze wskaźnikami optycznymi są często niskoomowe,
tzn. generują sygnał wyjściowy tylko wtedy, gdy kontrolowany przewód ma małą rezystancję.

Przyrządy wielozakresowe nie wymagają specjalnej konserwacji. Zaleca się jednak

sprawdzenie stanu naładowania baterii przed każdą serią pomiarów. Baterii rozładowanej albo
cieknącej nie wolno pozostawiać w przyrządzie. Baterii i bezpiecznika ochronnego, wskazanych
przez producenta, nie wolno zastępować elementami o innych danych znamionowych.

Do pomiaru napięcia (różnicy potencjałów) służy miernik elektryczny zwany

woltomierzem. Woltomierz za pomocą przewodów podłączamy do obwodu równolegle, czyli
między zaciski elementu lub grupy elementów, na których mierzymy napięcie.

Rys. 57. Symbol graficzny woltomierza [3, s. 206]

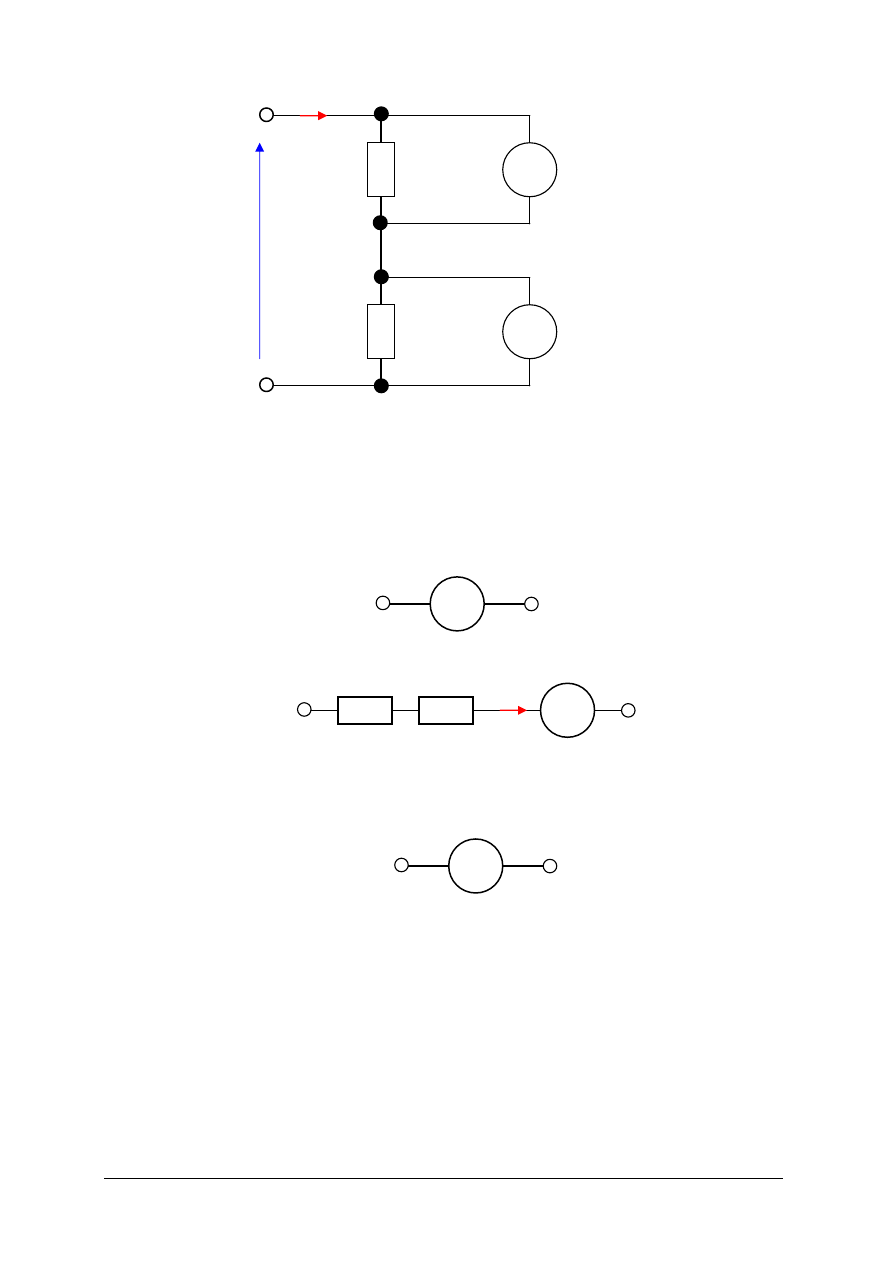
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 58. Przykład schematu obwodu z woltomierzem. Woltomierz V

mierzy spadek napięcia na rezystorze R

zaś woltomierz V

spadek napięcia na rezystorze R

[3, s. 205

]

Pomiar prądu w obwodzie wykonujemy amperomierzem. Pomiar ten możemy porównać

z pomiarem przepływającej wody w rurociągu. Aby zmierzyć ilość przepływającej wody, należy
przeciąć rurociąg i w miejscu przecięcia zainstalować wodomierz. Podobnie, aby zmierzyć prąd,
należy przerwać obwód elektryczny i podłączyć końce przewodów w miejscu przerwy
z amperomierzem. W taki sposób zostanie stworzona dla elektronów droga przejścia przez
amperomierz.

Rys. 59. Symbol graficzny amperomierza [3, s. 204]

Rys. 60. Przykład podłączenia amperomierza [3, s. 203]

Pomiar rezystancji wykonujemy omomierzem. Omomierz podłączamy za pomocą

przewodów do obwodu szeregowo lub równolegle.

Rys. 61. Symbol graficzny omomierza [3, s. 202

]

Jeżeli biegniemy szybko ulicą, napotykamy opór powietrza hamującego nasz bieg. Jeśli

natomiast biegniemy w wodzie, napotykamy jeszcze większy opór. Widzimy, więc, że przy
poruszaniu się różne środowiska stawiają różny opór. Podobnie dzieje się z ruchem elektronów
w przewodnikach. Tę własność przewodników nazywamy opornością (rezystancją) elektryczną.
Jednostkę oporności (rezystancji) nazywamy omem [Ω]. Rezystancję 1 oma ma przewód,
w którym przepływa prąd o natężeniu jednego ampera, pod wpływem napięcia jednego wolta.

Rezystancję rezystora można tez obliczyć korzystając z prawa Ohma na podstawie

jednocześnie zmierzonych wartości napięcia i natężenia prądu. Zależnie od sposobu połączenia
amperomierza i woltomierza w obwodzie pomiarowym powstają błędy zniekształcające wynik
pomiaru. Uchyb metody zależny od sposobu połączenia mierników jest maty, gdy przy dużych

Ω

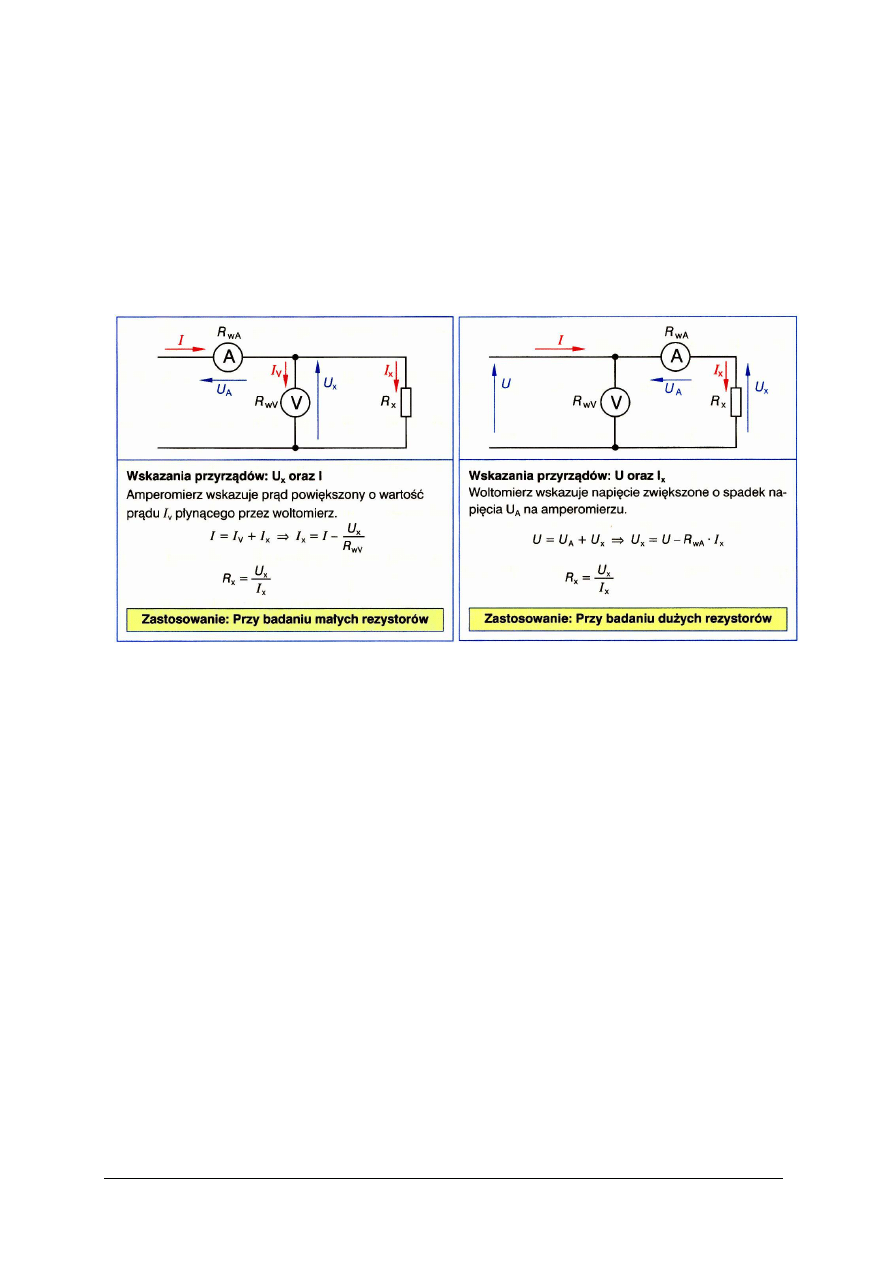
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

rezystancjach rezystorów mierzonych stosuje się układ z dokładnym pomiarem prądu
odbiornika, a przy małych układ z dokładnym pomiarem napięcia odbiornika. Na wybór
właściwego układu należy zwracać uwagę szczególnie przy zdejmowaniu charakterystyk
elementów, np. rezystorów nieliniowych lub elementów półprzewodnikowych.

Układ z dokładnym pomiarem prądu odbiornika. W tym układzie prąd I

płynący przez

badany rezystor jest mierzony dokładnie. Woltomierz wskazuje napięcie większe, gdyż
uwzględnia spadek napięcia U

na rezystancji wewnętrznej amperomierza. Tak wyznaczona

wartość rezystancji jest większa od wartości rzeczywistej, bo jest powiększona o rezystancję
wewnętrzną R

amperomierza.

Rys. 62. Układ z dokładnym pomiarem napięcia (po lewo) i prądu (po prawo) [1, s. 167]

Amperomierze mają małą oporność wewnętrzną, więc duże wartości rezystancji można mierzyć bez uwzględniania

poprawki

Układ z dokładnym pomiarem napięcia odbiornika. W tym układzie napięcie U

zaciskach rezystora R

jest mierzone dokładnie. Zmierzony prąd I jest większy od prądu

w rezystorze R

o wartość prądu I

, płynącego przez woltomierz. Obliczona wartość rezystancji

jest w tym wypadku mniejsza od wartości rzeczywistej.

Woltomierze mają duże rezystancje wewnętrzne, więc przy mierzeniu małych rezystancji

błąd może być pominięty.

Pomiar multimetrem:

−

Nastawić rodzaj mierzonej wielkości i zakres pomiarowy.

−

Przy przyrządach wskazówkowych wybierać zawsze największy zakres pomiarowy.

−

Przewody pomiarowe przyłączać najpierw do przyrządu, a potem do punktu pomiaru.

−

Przy pomiarach prądu i rezystancji najpierw wyłączyć zasilanie.

−

Przy pomiarze prądu ponownie włączyć zasilanie.

−

Pomiary rezystancji przeprowadzać zawsze w stanie bezprądowym.

−

Wykonać pomiar i odczytać wartość zmierzoną.

−

Przy przyrządach wskazówkowych wybierać taki zakres pomiarowy, żeby wskazanie
pomiarowe znajdowało się powyżej połowy skali.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Po zakończeniu pomiaru:

−

Wyłączyć zasilanie (przy pomiarze prądu) i rozłączyć układ pomiarowy.

−

Przy przyrządach wskazówkowych przestawić przełącznik zakresów ponownie na
największy zakres.

4.7.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

Czym różni się wskaźnik analogowy od cyfrowego?

W której części skali przyrząd wskazówkowy ma największą dokładność?

Wskutek czego mogą powstać błędy?

Co się stanie gdy przez pomyłkę użyje się do pomiaru prądu woltomierza?

Jaka jest różnica pomiędzy układem z dokładnym pomiarem prądu odbiornika, a dokładnym
pomiarem napięcia?

4.7.3.

Ćwiczenia

Ćwiczenie 1

Wykonaj pomiary napięcia i prądu dokonując zmiany napięcia opornicą suwakową

włączoną do obwodu potencjometrycznie z obciążeniem R

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

połączyć układ według schematu,

ustawić suwak w skrajne położenie,

załączyć napięcie do układu,

przesuwać suwak w równych odstępach i odczytywać wskazania mierników dla 10 położeń,

zapisać wyniki pomiarów w tabeli,

sporządzić na podstawie wyników pomiarów charakterystykę U=f(x), oraz I=f(x), gdzie
x jest przesunięciem suwaka (charakterystykę utworzyć za pomocą arkusza kalkulacyjnego),

przeanalizować uzyskane charakterystyki,

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

zestaw laboratoryjny do wykonywania ćwiczeń,

−

komputer z arkuszem kalkulacyjnym,

−

instrukcja do ćwiczenia,

−

przybory do pisania, zeszyt do ćwiczeń.

Ćwiczenie 2

Wykonaj pomiary napięcia i prądu w układzie z potencjometrami połączonymi szeregowo

z obciążeniem R

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

połączyć układ według schematu,

ustawić suwaki w położenie z godnie z instrukcją,

załączyć napięcie do układu,

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

przesuwać suwak w równych odstępach i odczytywać wskazania mierników dla 10 położeń,

wyniki pomiarów zapisać w tabeli,

sporządzić na podstawie wyników pomiarów charakterystykę U=f(x), oraz I=f(x), gdzie
x jest przesunięciem suwaka (charakterystykę utworzyć za pomocą arkusza kalkulacyjnego),

przeanalizować uzyskane charakterystyki,

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

zestaw laboratoryjny do wykonywania ćwiczeń,

−

komputer z arkuszem kalkulacyjnym,

−

instrukcja do ćwiczenia,

−

przybory do pisania,

−

zeszyt do ćwiczeń.

Ćwiczenie 3

Wykonaj pomiary napięcia zmieniając jego wartości za pomocą dzielnika napięcia.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

połączyć układ według schematu,

ustawić suwak w skrajne położenie,

załączyć napięcie do układu,

przesuwać suwak w równych odstępach i odczytywać wskazania miernika dla 10 położeń,

wyniki pomiarów zapisać w tabeli,

sporządzić na podstawie wyników pomiarów charakterystykę U=f(x), gdzie x przesunięciem
suwaka (charakterystykę utworzyć za pomocą arkusza kalkulacyjnego),

przeanalizować uzyskaną charakterystykę,

zaprezentować efekty swojej pracy.

Wyposażenie stanowiska pracy:

−

zestaw laboratoryjny do wykonywania ćwiczeń,

−

komputer z arkuszem kalkulacyjnym,

−

instrukcja do ćwiczenia,

−

przybory do pisania,

−

zeszyt do ćwiczeń.

4.7.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

zinterpretować otrzymane wyniki pomiarów?

wykorzystać komputer do opracowywania wyników?

dobrać odpowiednią metodę pomiaru?

wykonać pomiar napięcia?

wykonać pomiar natężenia prądu?

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5. SPRAWDZIAN OSIĄGNIĘĆ

INSTRUKCJA DLA UCZNIA

Przeczytaj uważnie instrukcję.

Zapoznaj się z zestawem zadań testowych.

Udzielaj odpowiedzi na załączonej karcie odpowiedzi.

Test składa się z 20 zadań.

Za każde poprawnie rozwiązane zadanie uzyskasz 1 punkt.

Dla każdego zadania podane są cztery możliwe odpowiedzi: a, b, c, d.

Tylko jedna odpowiedź jest poprawna.

Wybraną odpowiedz zaznacz X.

Staraj się wyraźnie zaznaczać odpowiedzi. Jeżeli się pomylisz i błędnie zaznaczysz
odpowiedź, otocz ją kółkiem i zaznacz odpowiedź, którą uważasz za prawdziwą.

10.

Przed wykonaniem każdego zadania przeczytaj bardzo uważnie polecenie.

11.

Czas na rozwiązanie testu 60 minut.

Powodzenia

ZESTAW ZADAŃ TESTOWYCH

1. Jeżeli zastosujemy jeden z dwóch przewodów elektrycznych z tego samego materiału,

o takiej samej długości, ale o większym przekroju, to droga po której przesuwają się
elektrony swobodne rozszerza się stawiając tym samym
a)

mniejszy opór przepływowi prądu elektrycznego.

taki sam opór w obu przewodnikach.

większy opór przepływowi prądu elektrycznego.

opór odwrotnie proporcjonalny do przekroju przewodu.

2. Rezystancję przewodu obliczamy znając jego wymiary i rezystywność. Rezystancja ta

zależy od długości przewodu
a)

odwrotnie proporcjonalnie.

wprost proporcjonalne.

nie zależy od długości przewodu.

im krótszy, tym większa rezystancja.

3. Jednostką rezystywności w układzie SJ jest

Ω

m2.

VA.

Ω

S m/mm2.

4. Stan zwarcia źródła napięcia jest to taki stan, w którym

U=E-Rw I i I>0.

Uo=E i I=0.

U>E i I<0.

Iz=E/Rw i U=0.

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5. Natężenie prądu w obwodzie nierozgałęzionym zasilanym z jednego źródła napięcia stałego,

w którym występuje 3 rezystory (połączone szeregowo) jest
a)

różny (pod względem wartości) w każdym punkcie obwodu.

jednakowy (pod względem wartości) w każdym punkcie obwodu.

zależny od różnicy potencjałów na zaciskach każdego rezystora.

równy różnicy potencjałów na zaciskach każdego rezystora.

6. Napięcie na zaciskach każdego z 3 rezystorów połączonych równolegle, które są zasilane

z jednego źródła jest
a)

różne.

zależne od wartości rezystancji zastępczej układu.

jednakowe.

niezależne od wartości rezystancji każdego z tych rezystorów.

W obwodach elektrycznych rozgałęzionych oczkiem nazywamy
a)

miejsce rozgałęzienia się przewodów w układzie.

drogę dla przepływu prądu, łączącą bezpośrednio dwa węzły.

sumę algebraiczną prądów schodzących się w dowolnym węźle.

zbiór gałęzi tworzących jedną zamkniętą drogę dla przepływu prądu.

8. W stanie zwarcia wartość napięcia na zaciskach źródła napięcia jest

U>E.

U<E.

U=0.

U=E.

9. Silnik elektryczny prądu stałego działa na zasadzie oddziaływania pola magnetycznego na

przewodnik z prądem umieszczony w tym polu. Posługując się „regułą lewej dłoni”
możemy wyznaczyć
a)

kierunek pola magnetycznego w solenoidzie.

kierunek wektora indukcji B w polu wytworzonym przez prąd elektryczny.

kierunek siły oddziaływania pola magnetycznego na prąd płynący w przewodniku
umieszczony w tym polu.

kierunek prądu w przewodniku umieszczonym w tym polu.

10. Do wyznaczenia wartości prądu płynącego przez rezystor o znanej wartości rezystancji

R i przy znanym spadku napięcia U zastosujesz
a)

II prawo Kirchhoffa.

I prawo Kirchhoffa.

prawo Coulomba.

prawo Ohma.

11. Błąd (uchyb) bezwzględny pomiaru to

uchyb miernika wyrażony w % wartości zmierzonej.

różnica między wartością zmierzoną (wskazaną), a rzeczywistą.

różnica między wartością rzeczywistą, a zmierzoną.

wartość, którą należy dodać do wyniku pomiaru, aby uzyskać wartość rzeczywistą.

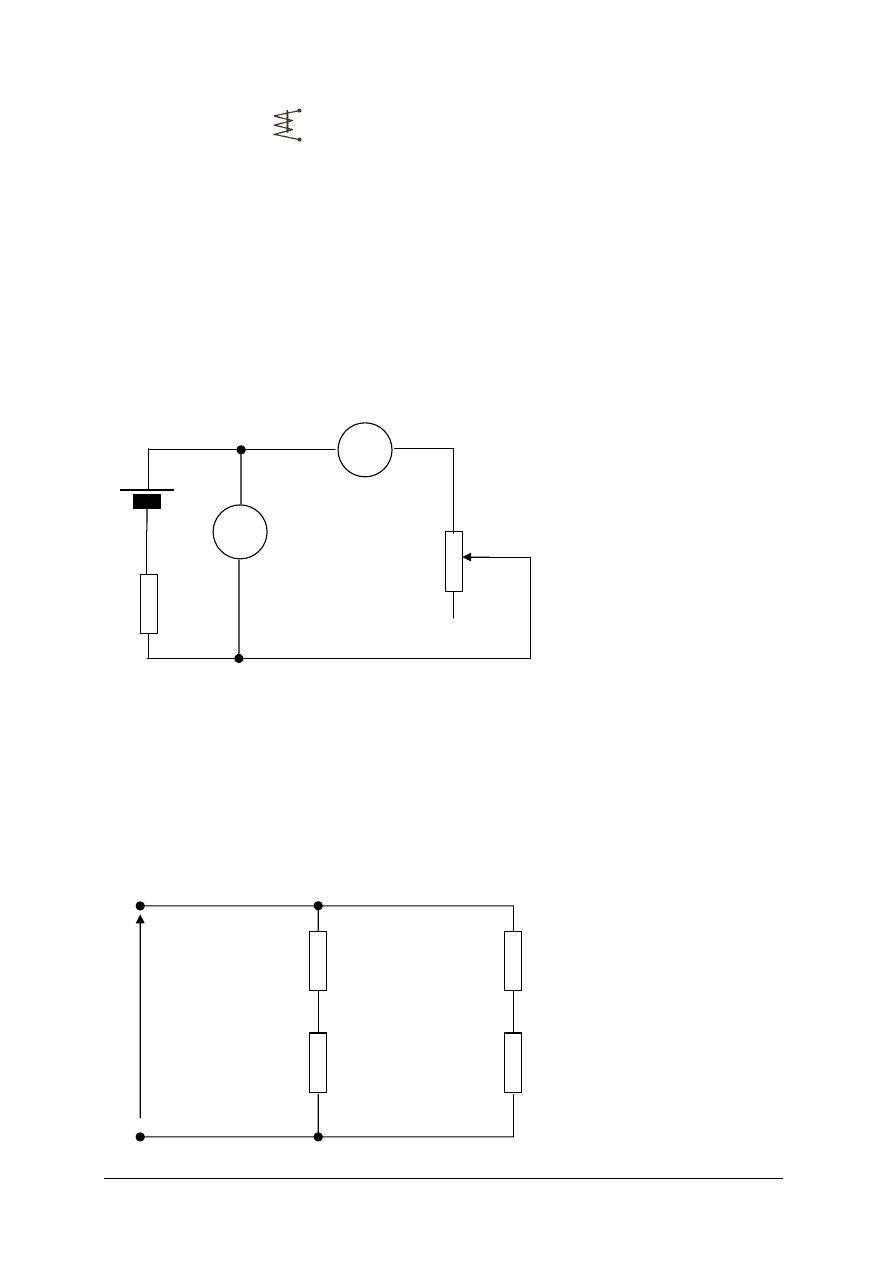
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

12. Symbol graficzny

na tablicy podziałowej miernika analogowego oznacza

ustrój elektrodynamiczny.

ustrój magnetyczny.

ustrój elektromagnetyczny.

ustrój magnetoelektryczny.

13. Wielkością charakteryzującą pole magnetyczne i określające jego intensywność jest

natężenie pola magnetycznego.

przenikalność magnetyczna.

indukcja magnetyczna.

Siła elektrodynamiczna.

14. Jak zmienią się wskazania mierników, jeżeli przesuniemy suwak rezystora w kierunku

punktu A

Wskazania woltomierza Wskazanie amperomierza

nie zmieni się wzrośnie.

zmaleje zmaleje.

zmaleje wzrośnie.

wzrośnie wzrośnie.

15. Na którym rezystorze wystąpi najmniejszy spadek napięcia

tj. na rezystorze A.

tj. na rezystorze B.

tj. na rezystorze C.

tj. na rezystorze D.

5Ω C 3Ω

60V

7Ω D 7Ω

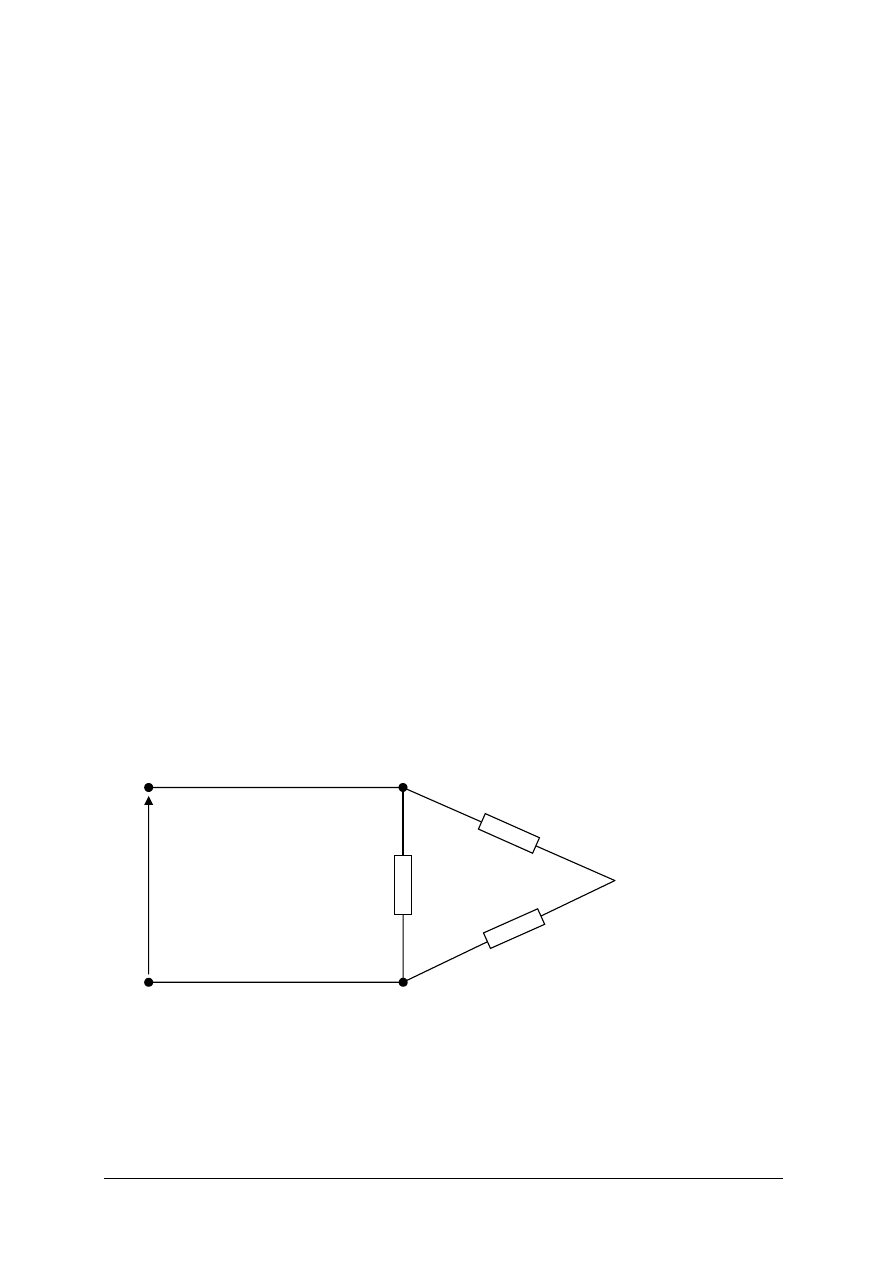
,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

16. Woltomierz mierzący napięcie akumulatora w samochodzie osobowym powinien mieć

ustawiony zakres
a)

0 – 20V AC.

0 – 20 V DC.

0 – 200V AC.

0 – 200V DC.

17. Siłę elektromotoryczną indukowaną w przewodach o danej długości obliczamy za pomocą

wzoru
a)

e=Blv.

e=Blvsin α.

e=+/-∆Φ/t.

e=+/-∆B/∆t.

18. W układzie SJ jednostką indukcji magnetycznej jest

1Vs/m2.

1Vs/Am2.

1Vs.

1A/m.

19. Magnetowodem nazywamy

zespół elementów służących do wytwarzania strumienia magnetycznego.

cewkę pierścieniową nawiniętą nierównomiernie z rdzeniem.

zespół elementów, wzdłuż których zamyka się strumień magnetyczny.

zespół elementów służących do wytwarzania indukcji magnetycznej.

20. W obwodzie pokazanym na rysunku określ (dla każdej odpowiedzi a, b i c przyporządkuj

odpowiedni opornik A, B lub C)
a)

przez który opornik przepływa prąd o największym natężeniu.

który opornik znajduje się pod największym napięciem.

który opornik znajduje się pod najniższym napięciem.

10Ω

24V

4Ω

5Ω

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

KARTA ODPOWIEDZI

Imię i nazwisko........................................................

Stosowanie urządzeń elektrycznych i sprzętu dźwiękowego

Zakreśl poprawną odpowiedź.

Zadania

Odpowiedź

Punkty

Razem:

,,Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

6. LITERATURA

Bastion P., Schuberth G., Spievogel O., Steil H., Tkotz K., Ziegler K.: Praktyczna
elektrotechnika ogólna. REA, Warszawa 2003

Bolkowski S.: Podstawy elektrotechniki. WSiP, Warszawa 1995

Kammerer J., Oberthur W., Zastow P. (tłumaczenie Rodak A.).: Pracownia podstaw
elektrotechniki i elektroniki. WSiP, Warszawa 2000

Kurdziel R.: Elektrotechnika dla szkoły zasadniczej. Dwie części. WSiP, Warszawa 1995

Latek W.: Maszyny elektryczne w pytaniach i odpowiedziach. WNT, Warszawa 1995

Mac St., Leowski J.: Bezpieczeństwo i higiena pracy dla szkół zasadniczych. WSiP,
Warszwa 1999

Markiewicz A.: Zbiór zadań z elektrotechniki. WSiP, Warszawa 2003

Marusak A.: Urządzenia elektroniczne. Trzy części. WSiP Warszawa 2000

Okoniewski S.: Technologia dla elektroników. WSiP, Warszawa 2000

10.

Pilawski M.: Pracownia elektryczna dla ZSE. WSiP, Warszawa 1999

11.

Przybyłowska-Łomnicka P.: Pomiary elektryczne - obwody prądu przemiennego. PWN,
Warszawa 1999

12.

Sztekmiler K.: Podstawy nagłośnienia i realizacji nagrań. Narodowe Centrum Kultury,
Warszawa 2003