Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 1

Opracowali: J. Felis, H. Jaworowski

WYRÓWNOWAŻANIE MASZYN I MECHANIZMÓW.

J

ak wiadomo, każde ogniwo łańcucha kinematycznego poruszającego się

mechanizmu lub maszyny posiada określone przyśpieszenia liniowe i kątowe.
Zgodnie z zasadą d’Alemberta przyspieszenia te powodują powstanie
uogólnionych sił bezwładności, które nakładając się na istniejący układ sił
zewnętrznych powodują na ogół zwiększenie reakcji w parach
kinematycznych mechanizmu lub maszyny.

Jeżeli reakcję w parze kinematycznej ( i, j ) w nieruchomym mechanizmie

czyli tzw. reakcję statyczną oznaczymy przez

st

ij

R , to reakcję dynamiczną

w tej parze

dyn

ij

R

, czyli reakcję w ruchomym łańcuchu kinematycznym

możemy zapisać:

dyn

ij

st

ij

dyn

ij

R

R

R

∆

+

=

(1)

gdzie:

dyn

ij

R

∆

- jest to przyrost reakcji (nadwyżka dynamiczna) w parze

kinematycznej spowodowany siłami bezwładności członów ruchomych
mechanizmu.

Reakcje dynamiczne są obciążeniami okresowo zmiennymi ze względu na

cykliczność ruchu maszyny i wywołują wiele bardzo niekorzystnych zjawisk,
takich jak: drgania elementów i naprężenia zmęczeniowe, nadmierne
zużywanie się łożysk, drgania korpusów, fundamentów i otoczenia maszyny
oraz związany z tymi zjawiskami hałas. Aby wyeliminować choćby częściowo
te bardzo niepożądane zjawiska, stosuje się odpowiednią korekcję rozkładu
mas elementów maszyn zwaną wyrównoważaniem lub wyważaniem.

Wyrównoważanie przebiega w dwóch etapach:
- konstrukcyjnym,
- technologicznym.
Wyrównoważanie konstrukcyjne przeprowadza się podczas

konstruowania (projektowania) maszyn. Staramy się wtedy zapewnić
poszczególnym członom i całej maszynie prawidłowe lub co najmniej
wystarczające rozłożenie mas ze względu na wyrównoważenie. Jednak na
skutek wad materiałowych, błędów wykonawczych, naprężeń wewnętrznych,
błędów montażowych oraz efektów eksploatacji (zużycie, uszkodzenie,
korozja, osady mechaniczne) stan wyrównoważenia może być
niezadowalający i wówczas układ mas wymaga korekty na drodze
pomiarowej.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 2

Opracowali: J. Felis, H. Jaworowski

Wyrównoważenie technologiczne jest korektą mas wytworzonych już

części maszyn. Takie wyrównoważanie przeprowadza się na ogół w trakcie
procesu technologicznego na specjalnych maszynach zwanych
wyważarkami, na których na drodze pomiarowej zostaje ustalone miejsce
oraz ilość zbędnego lub brakującego materiału. Przykładem jest
wyrównoważanie wirników silników elektrycznych czy wirników wentylatorów.
Oczywiście można również wyważać w ten sposób części maszyn, które
uległy zużyciu bądź uszkodzeniu w trakcie eksploatacji np. koła
samochodowe.

Maszyny o dużych wymiarach, ciężkie, trudne do demontażu można

wyważać w trakcie eksploatacji korzystając z przenośnej aparatury
pomiarowej.

W przemyśle pracują również takie maszyny, w których wirujący człon

roboczy zużywa się nierównomiernie podczas pracy, wywołując stan
niewyrównoważenia. Szczególnym przypadkiem takich maszyn są precyzyjne
szlifierki tarczowe. W takich przypadkach do wyrównoważania są stosowane
specjalne głowice zabudowane na stałe bezpośrednio na wirniku (tarczy
ściernicy), które umożliwiają korektę jego masy w trakcie ruchu..

Jedną z cech postępu technicznego jest ciągły wzrost prędkości

obrotowych maszyn i urządzeń, ponieważ szybkoobrotowe maszyny są
bardziej wydajne i lżejsze od maszyn wolnoobrotowych. Przykładowo
prędkości obrotowe turbin parowych i gazowych przekraczają 10 000
obr./min., wirniki silników elektrycznych o dużych częstotliwościach zasilania
osiągają 100 000 obr./min., a niektóre ultrawirniki wirują z prędkościami rzędu
500

000 obr./min. Dla tego typu maszyn wyrównoważanie staje się

koniecznością. Można wykazać, że już przy prędkości obrotowej 3000
obr./min. przesunięcie środka ciężkości wirnika o 100

µµµµ

m wywołuje

w łożyskach reakcje dynamiczne równe w przybliżeniu ciężarowi
wirnika. Ponieważ reakcje dynamiczne rosną z kwadratem prędkości
obrotowej, to przy prędkościach rzędu 30 000 obr./min. reakcje dynamiczne
są 100 razy większe od statycznych.

Problemy wyrównoważania możemy podzielić na dwie grupy:
- wyrównoważanie wirników sztywnych (pojedynczych członów)
- wyrównoważanie mechanizmów i maszyn złożonych z układów członów
sztywnych.
W pierwszym przypadku chodzi o sprowadzenie do zera nadwyżek

dynamicznych reakcji działających na łożyska wirującego członu. W drugim
przypadku dążymy do minimalizacji reakcji dynamicznych przenoszonych na
podstawę maszyny (ostoję), co na ogół wiąże się ze zwiększeniem reakcji

dynamicznych w parach kinematycznych pomiędzy ruchomymi członami nie
związanymi z podstawą.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 3

Opracowali: J. Felis, H. Jaworowski

Podstawy teoretyczne wyrównoważania wirników sztywnych.

Wirnik sztywny w trakcie pracy jest podtrzymywany na powierzchniach

nośnych za pomocą podpór łożyskowych. Powierzchnie nośne wirnika
przenoszą obciążenia na podpory łożyskowe za pośrednictwem łożysk
tocznych lub ślizgowych, strumieni gazów lub cieczy, pól magnetycznych lub
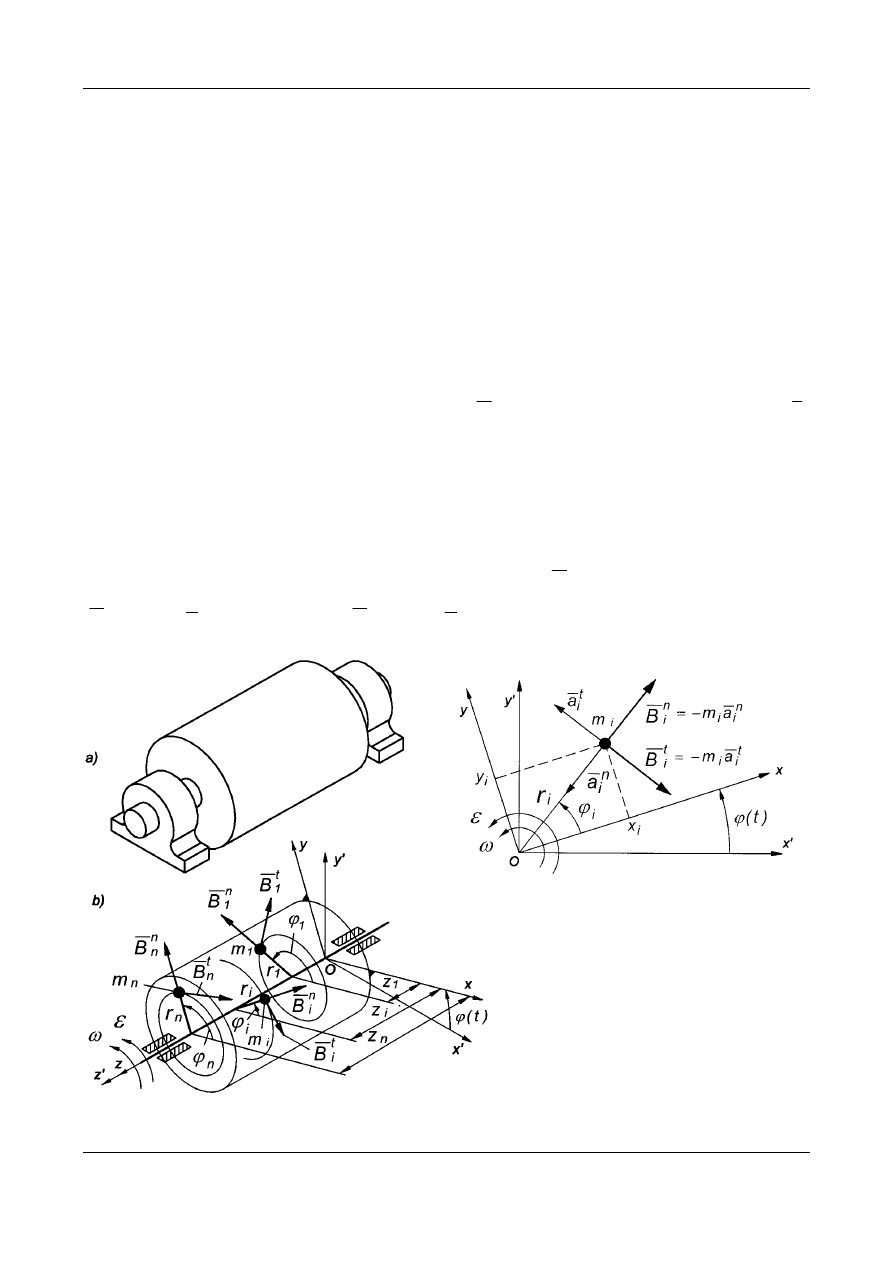
elektrycznych itp. Rozpatrzymy warunki wyrównoważenia wirnika sztywnego
zamodelowanego układem dyskretnych mas skupionych (Rys. 1).

Oznaczenia na Rys. 1:
Ox’y’z’ - nieruchomy układ współrzędnych, oś Oz’ pokrywa się z osią
obrotu wirnika,
Oxyz - ruchomy układ współrzędnych sztywno związany z wirnikiem
obracający się z prędkością kątową

ω

i przyspieszeniem kątowym

ε

względem osi Oz, która pokrywa się z osią Oz’,

n

i

1

m

,...

m

,...

m

- elementarne masy skupione,

n

i

1

r

,...

r

,...

r

- odległości mas od obrotu wirnika,

)

z

,

sin

r

y

,

cos

r

x

(

i

i

i

i

i

i

i

ϕ

ϕ

=

=

- współrzędne i-tej masy w układzie

ruchomym Oxyz.

Na każdą z mas układu działa siła bezwładności

i

B o składowych normalnej

n

i

i

n

i

a

m

B

⋅

−

=

oraz stycznej

t

i

i

t

i

a

m

B

⋅

−

=

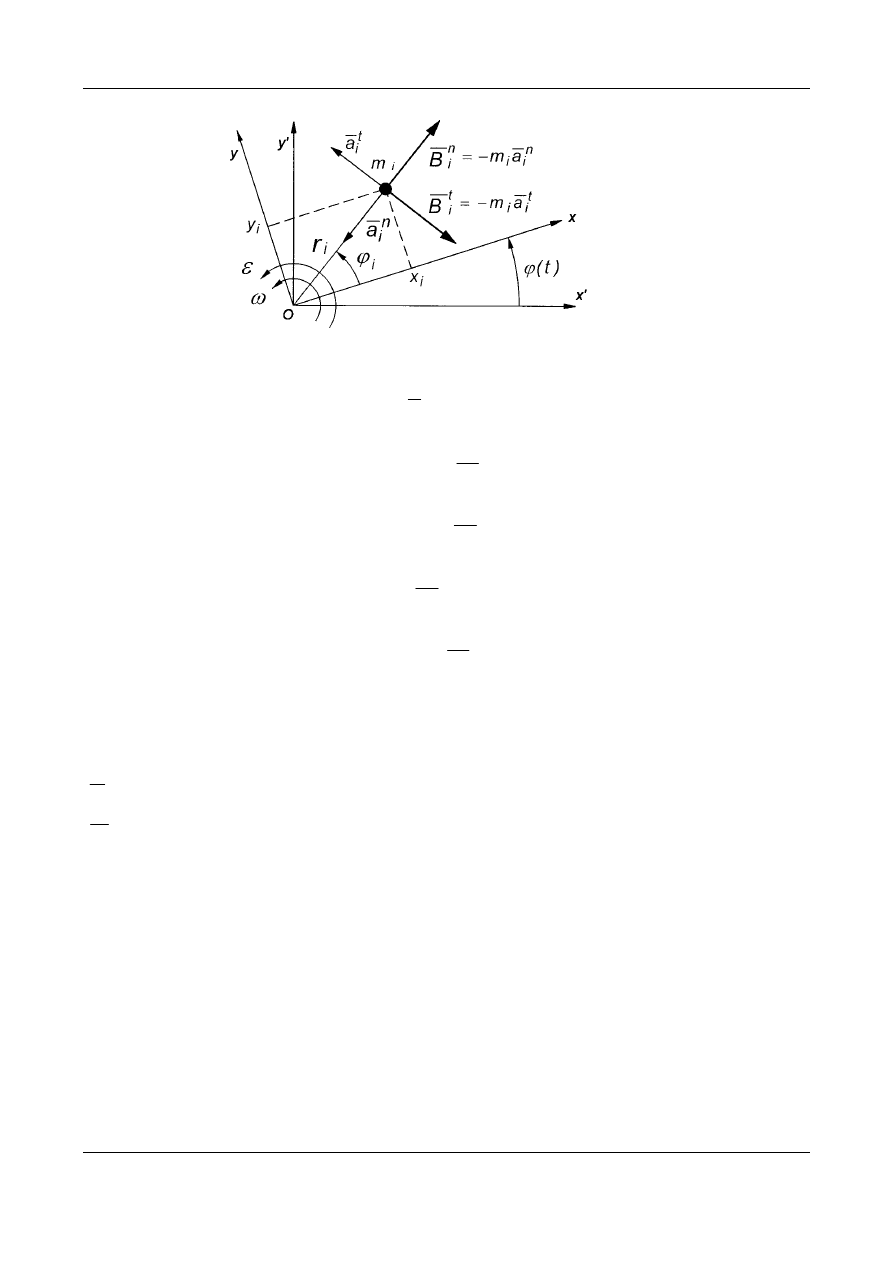
zgodnie z Rys. 2.

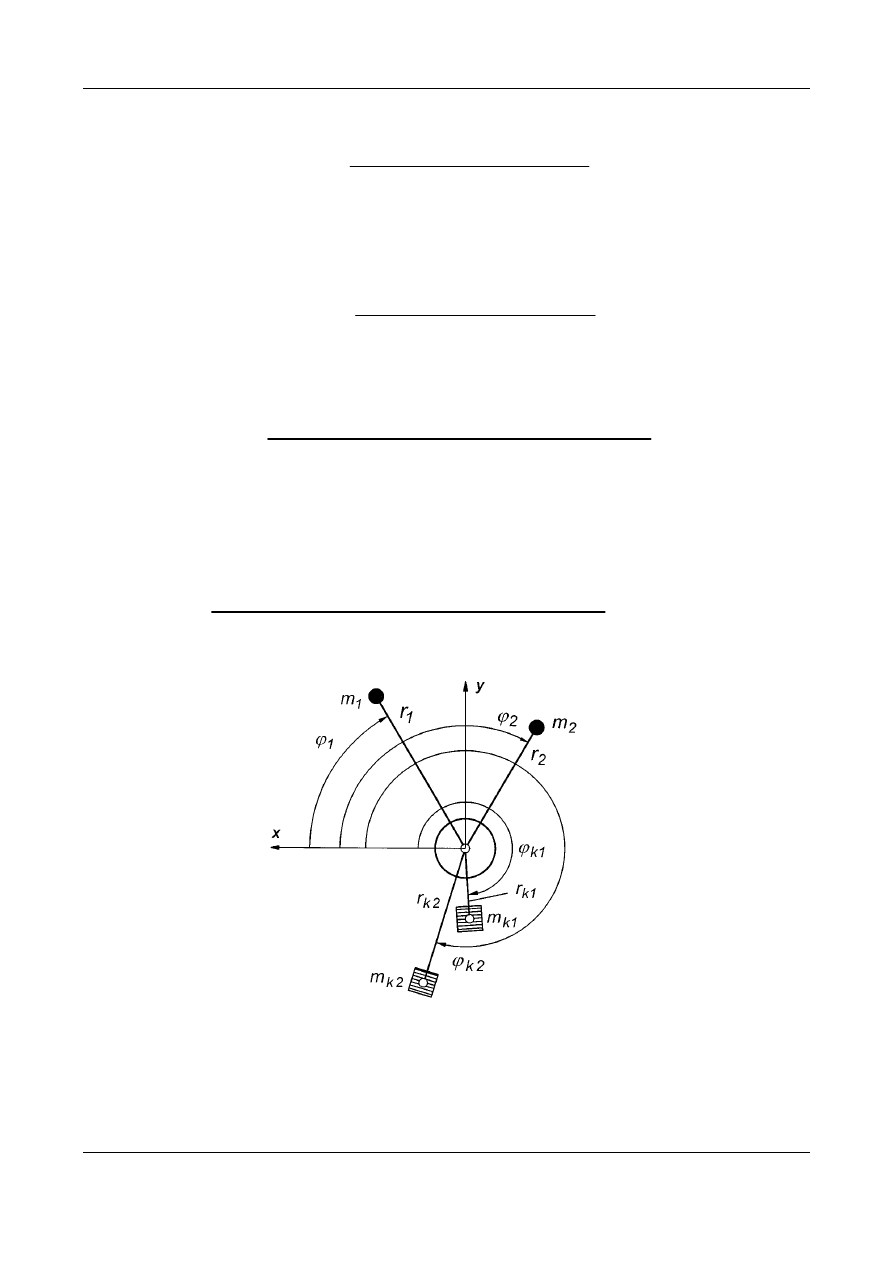
Rys. 2. Składowe siły bezwładności
działające na pojedynczą masę
skupioną

i

m

Rys. 1. Model wirnika sztywnego w postaci układu mas skupionych

`

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 4

Opracowali: J. Felis, H. Jaworowski

Rys. 2 (powtórzony). Składowe siły bezwładności działające na pojedynczą masę
skupioną

i

m

Współrzędne siły bezwładności

i

B

wynoszą odpowiednio:

,

x

m

r

x

r

m

cos

r

m

B

,

y

m

r

y

r

m

sin

r

m

B

,

y

m

r

y

r

m

sin

r

m

B

,

x

m

r

x

ir

i

m

cos

r

m

B

i

i

i

i

i

i

i

i

i

t

iy

i

i

i

i

i

i

i

i

i

t

ix

2

i

i

i

i

2

i

i

i

2

i

i

n

iy

2

i

i

i

i

2

i

2

i

i

n

ix

ε

ε

ϕ

ε

ε

ε

ϕ

ε

ω

ω

ϕ

ω

ω

ω

ϕ

ω

−

=

−

=

−

=

=

=

=

=

=

=

=

=

=

(2)

Należy zauważyć, że

0

B

B

t

iz

n

iz

=

=

, ponieważ siły bezwładności działają

w płaszczyznach prostopadłych do osi wirnika.

Aby wyznaczyć współrzędne wektora głównego sił bezwładności

)

B

,

B

,

B

(

B

z

y

x

oraz momentu głównego sił bezwładności

)

M

,

M

,

M

(

M

Bz

By

Bx

B

należy przeprowadzić sumowanie sił i momentów dla

wszystkich mas układu.

Wprowadzimy dodatkowo oznaczenia:

i

n

1

i

i

S

x

i

n

1

i

i

S

y

y

m

My

S

,

x

m

Mx

S

∑

=

=

∑

=

=

=

=

(3)

i

i

n

1

i

i

yz

i

i

n

1

i

i

xz

z

y

m

D

,

z

x

m

D

∑

=

∑

=

=

=

(4)

(

)

2

i

2

i

n

1

i

i

z

y

x

m

J

+

∑

=

=

(5)

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 5

Opracowali: J. Felis, H. Jaworowski

gdzie:

y

x

S

,

S

- momenty statyczne wirnika względem osi Ox, Oy ,

yz

xz

D

,

D

- momenty dewiacji wirnika względem płaszczyzn Oxz, Oyz,

z

J - moment bezwładności wirnika względem osi Oz,

M - masa całkowita wirnika

S

S

y

,

x

- współrzędne środka masy wirnika.

Na podstawie (2), (3), (4) i (5) współrzędne wektora głównego sił

bezwładności

∑

=

=

n

1

i

i

z

y

x

B

)

B

,

B

,

B

(

B

wynoszą:

(

)

(

)

∑

=

−

=

∑

−

∑

=

∑

+

∑

∑

=

=

+

=

∑

+

∑

=

∑

+

∑

∑

=

=

=

=

=

=

=

=

=

=

=

=

=

n

1

i

iz

z

S

2

S

i

n

1

i

i

i

n

1

i

i

2

n

1

i

t

iy

n

1

i

n

1

i

n

iy

iy

y

S

2

S

i

n

1

i

i

i

n

1

i

i

2

n

1

i

t

ix

n

1

i

n

1

i

n

ix

ix

x

B

B

x

y

M

x

m

y

m

B

B

B

B

y

x

M

y

m

x

m

B

B

B

B

ε

ω

ε

ω

ε

ω

ε

ω

(6)

Współrzędne momentu głównego sił bezwładności wyznaczymy na

podstawie:

(

)

(

)

(

)

∑

∑

∑

∑

∑

∑

=

−

−

=

=

=

−

+

+

−

=

=

=

×

=

=

n

1

i

i

ix

i

iy

n

1

i

i

ix

n

1

i

i

iy

n

1

i

iy

ix

i

i

i

i

n

1

i

i

n

1

i

Bi

B

y

B

x

B

k

z

B

j

z

B

i

0

B

B

z

y

x

k

j

i

B

M

M

ρ

(7)

gdzie

i

ρ

- wektor promień łączący biegun redukcji (środek układu

współrzędnych Oxyz) z masą

i

m .

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 6

Opracowali: J. Felis, H. Jaworowski

Na podstawie (7) mamy:

(

)

(

)

(

)

(

)

z

n

1

i

2

i

2

i

i

n

1

i

n

1

i

2

i

i

i

i

i

2

2

i

i

i

i

i

2

Biz

Bz

yz

xz

2

n

1

i

n

1

i

i

i

i

i

i

i

2

n

1

i

i

i

i

i

i

i

2

n

1

i

Biy

By

yz

2

xz

n

1

i

n

1

i

i

i

i

i

i

i

2

n

1

i

i

i

i

i

i

i

2

n

1

i

Bix

Bx

J

y

x

m

y

m

y

x

m

x

m

x

y

m

M

M

,

D

D

z

y

m

z

x

m

z

y

m

z

x

m

M

M

D

D

z

x

m

z

y

m

z

x

m

z

y

m

M

M

ε

ε

ε

ω

ε

ω

ε

ω

ε

ω

ε

ω

ω

ε

ε

ω

ε

ω

−

=

∑

+

−

=

=

∑

∑

−

−

−

=

=

+

=

=

∑

∑

+

=

∑

+

−

=

∑

=

−

=

=

∑

∑

+

−

=

∑

−

−

=

∑

=

=

=

=

=

=

=

=

=

=

=

=

(8)

Jeśli wektor główny sił bezwładności jest równy zero,

0

B

i

=

oraz

moment główny sił bezwładności jest równy zero,

0

M

B

=

, to reakcje

dynamiczne na podporach łożyskowych nie występują.

Aby wektor główny sił bezwładności był równy zero muszą być spełnione

na podstawie (6) następujące warunki:

,

0

y

m

My

,

0

x

m

Mx

n

1

i

i

i

S

n

1

i

i

i

S

=

∑

=

=

∑

=

=

=

(9)

czyli

0

x

S

=

oraz

0

y

S

=

Oś obrotu przechodząca przez środek masy wirnika nazywa się osią

centralną. Warunek (9) oznacza, że środek masy wirnika znajduje się na osi
obrotu. Wirnik jest w tym wypadku wyrównoważony statycznie.

Moment główny sił bezwładności jest równy zero jeśli spełnione są warunki

(na podstawie (8)):

∑

=

=

=

n

1

i

i

i

i

xz

0

z

x

m

D

oraz

∑

=

=

=

n

1

i

i

i

i

yz

0

z

y

m

D

(10)

Spełnienie przez układ mas dyskretnych warunku (10) oznacza, że oś

obrotu jest główną osią bezwładności.

Jeśli spełnione są równocześnie warunki (9) i (10) wówczas oś obrotu

jest główną centralną osią bezwładności i wirnik jest wyrównoważony
dynamicznie (zupełnie).

Składowa

Bz

M

momentu głównego sił bezwładności równoważy się

z momentem napędowym oraz momentem oporu i nigdy nie powoduje
obciążeń dynamicznych łożysk, nie ma zatem wpływu na stan
wyrównoważenia.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 7

Opracowali: J. Felis, H. Jaworowski

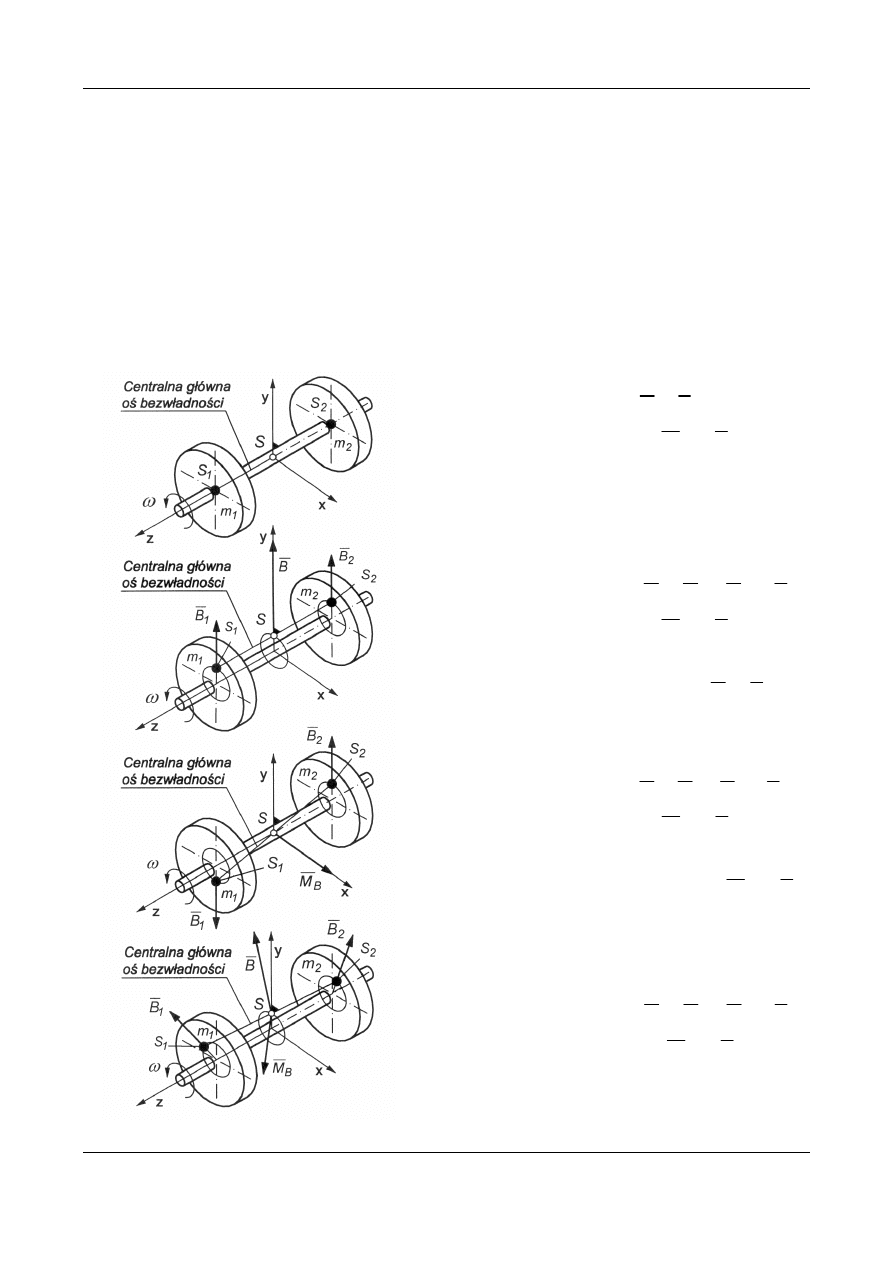
Warianty stanu wyrównoważenia wirnika

Różne możliwe warianty stanu wyrównoważenia przeanalizujemy na

przykładzie wirnika składającego się z wału i osadzonych na nim dwóch
cienkich tarcz, które zamodelujemy w postaci układu mas skupionych

2

1

m

,

m

. Założymy, że wał wirnika jest konstrukcyjnie i technologicznie

wyrównoważony. Stan wyrównoważenia wirnika będzie zatem wynikał
z położenia środków mas

2

1

S

,

S

. Uwzględniając położenie środków mas

2

1

S

,

S

otrzymamy cztery warianty stanu wyrównoważenia (Rys. 3-6).

0

B

,

0

y

,

0

x

S

S

=

=

=

0

M

,

0

D

,

0

D

B

yz

xz

=

=

=

Rys. 3. Wirnik wyrównoważony

0

B

B

B

,

0

y

,

0

x

2

1

S

S

≠

+

=

≠

=

0

M

,

0

D

,

0

D

B

yz

xz

=

=

=

Rys. 4. Wirnik niewyrównoważony

0

B

≠

- niewyrównoważenie siłowe

0

B

B

B

,

0

y

,

0

x

2

1

S

S

=

+

=

=

=

0

M

,

0

D

,

0

D

B

yz

xz

≠

≠

=

Rys. 5. Wirnik niewyrównoważony

0

M

B

≠

- niewyrównoważenie momentowe

0

B

B

B

,

0

y

,

0

x

2

1

S

S

≠

+

=

≠

≠

0

M

,

0

D

,

0

D

B

yz

xz

≠

≠

≠

Rys. 6. Wirnik niewyrównoważony przypadek ogólny

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 8

Opracowali: J. Felis, H. Jaworowski

Twierdzenie o wyrównoważaniu wirników.

Udowodnimy obecnie twierdzenie o warunkach wyrównoważenia dla

modelu wirnika z masą rozłożoną w sposób ciągły, które ma duże znaczenie
praktyczne, gdyż pokazuje, w jaki sposób należy przeprowadzać
wyrównoważanie maszyn wirnikowych. Twierdzenie to jest również słuszne
dla przypadku, gdy wirnik modeluje się układem mas dyskretnych.
Twierdzenie: Dowolny wirnik można całkowicie wyrównoważyć dynamicznie
poprzez umieszczenie dwóch mas korekcyjnych w dwóch dowolnych nie
pokrywających się płaszczyznach prostopadłych do osi obrotu wirnika.
Położenia kątowe tych mas oraz promienie, na których powinny być
umieszczone zależą od wielkości niewyrównoważenia wirnika.
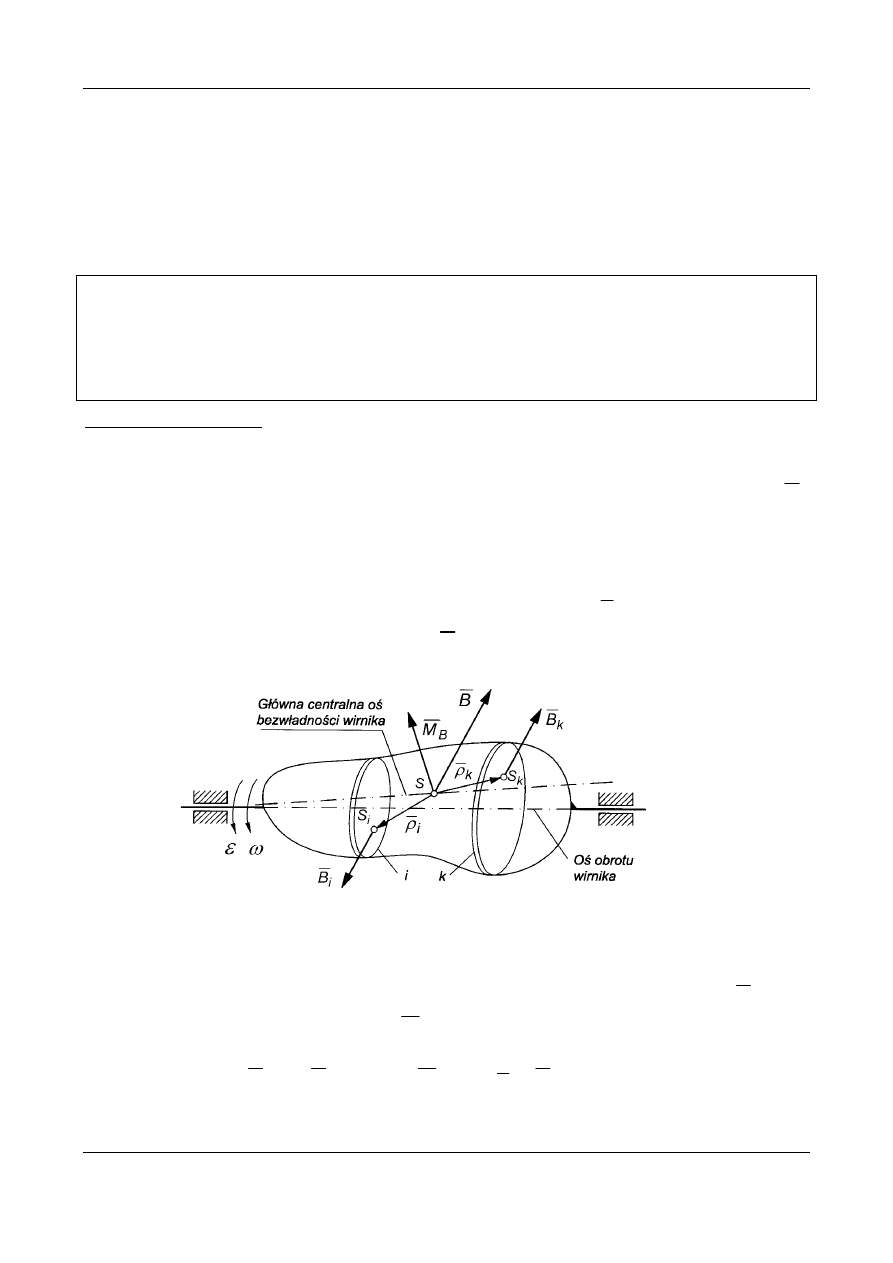
Dowód twierdzenia

Przyjmiemy, że wirnik składa się z cienkich niewyrównoważonych tarcz

prostopadłych do osi obrotu. Na każdą tarczę działa siła bezwładności

i

B

przyłożona w jej środku masy

i

S . (Rys. 7).

Przeprowadzamy redukcję zadanego układu sił bezwładności przyjmując

za biegun redukcji środek masy wirnika S. Przez

i

ρ

oznaczono wektor

punktu przyłożenia siły bezwładności

i

B .

Rys. 7. Model fizyczny niewyrównoważonego wirnika.

W wyniku redukcji otrzymujemy wektor główny sił bezwładności B oraz
moment główny sił bezwładności

B

M

przyłożone w środku masy wirnika S:

∑

∑

=

=

×

=

=

n

1

i

i

i

B

n

1

i

i

B

M

;

B

B

ρ

(11)

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 9

Opracowali: J. Felis, H. Jaworowski

Wektor główny sił bezwładności

B

jest prostopadły do osi wirnika

i przechodzi przez jego środek masy S. Moment główny sił bezwładności

B

M

jest prostopadły do głównej centralnej osi bezwładności oraz do osi wirnika
i przechodzi przez jego środek masy S. Ponieważ wirnik jest
niewyrównoważony dynamicznie, oś obrotu wirnika oraz główna centralna oś
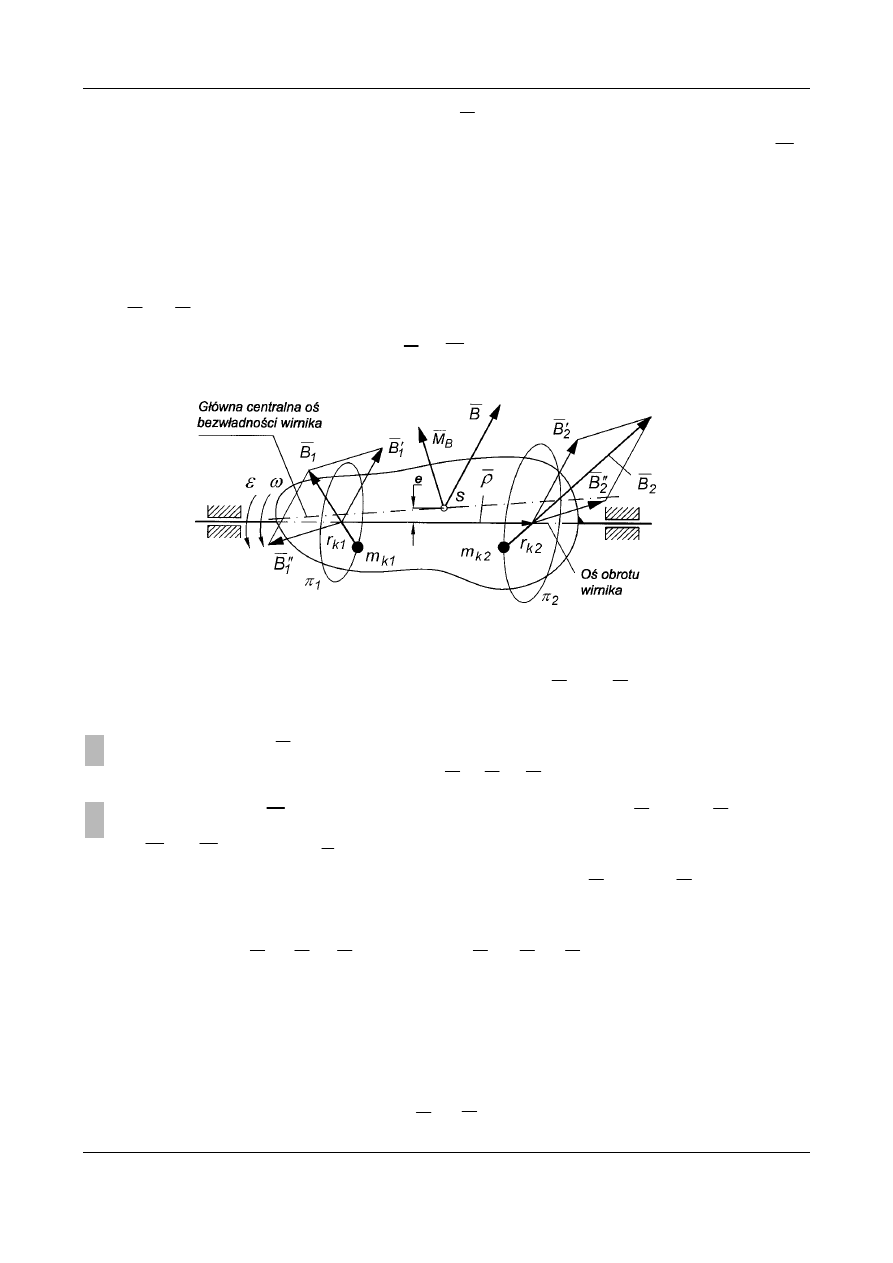
bezwładności wirnika są prostymi skośnymi. Przyjmujemy dwie dowolne
płaszczyzny

1

π

i

2

π

prostopadłe do osi wirnika, w których przyłożymy dwie

siły

1

B i

2

B bezwładności w taki sposób, aby nowy układ sił był statycznie

równoważny zadanemu układowi

B

i

B

M

co przedstawiono na Rys. 8

Rys. 8. Wektor główny sił bezwładności i moment główny sił bezwładności oraz
równoważny układ sił bezwładności w płaszczyznach korekcyjnych.

W celu ustalenia kierunków i wartości sił

1

B i

2

B przeprowadzimy

następujące kroki:
!

wektor główny

B

rozkładamy na dwie siły równoległe działające

w płaszczyznach

1

π

i

2

π

takie, że

2

1

B

B

B

′

+

′

=

,

!

moment główny

B

M

przedstawiamy w postaci pary sił

1

B

′′

oraz

2

B

′′

takich,

że:

(

)

1

2

1

B

B

B

B

,

B

M

M

′′

×

=

′′

′′

=

ρ

Otrzymujemy ostatecznie dwie siły bezwładności

1

B oraz

2

B działające

w płaszczyznach

1

π

i

2

π

:

1

1

1

B

B

B

′′

+

′

=

2

2

2

B

B

B

′′

+

′

=

(12)

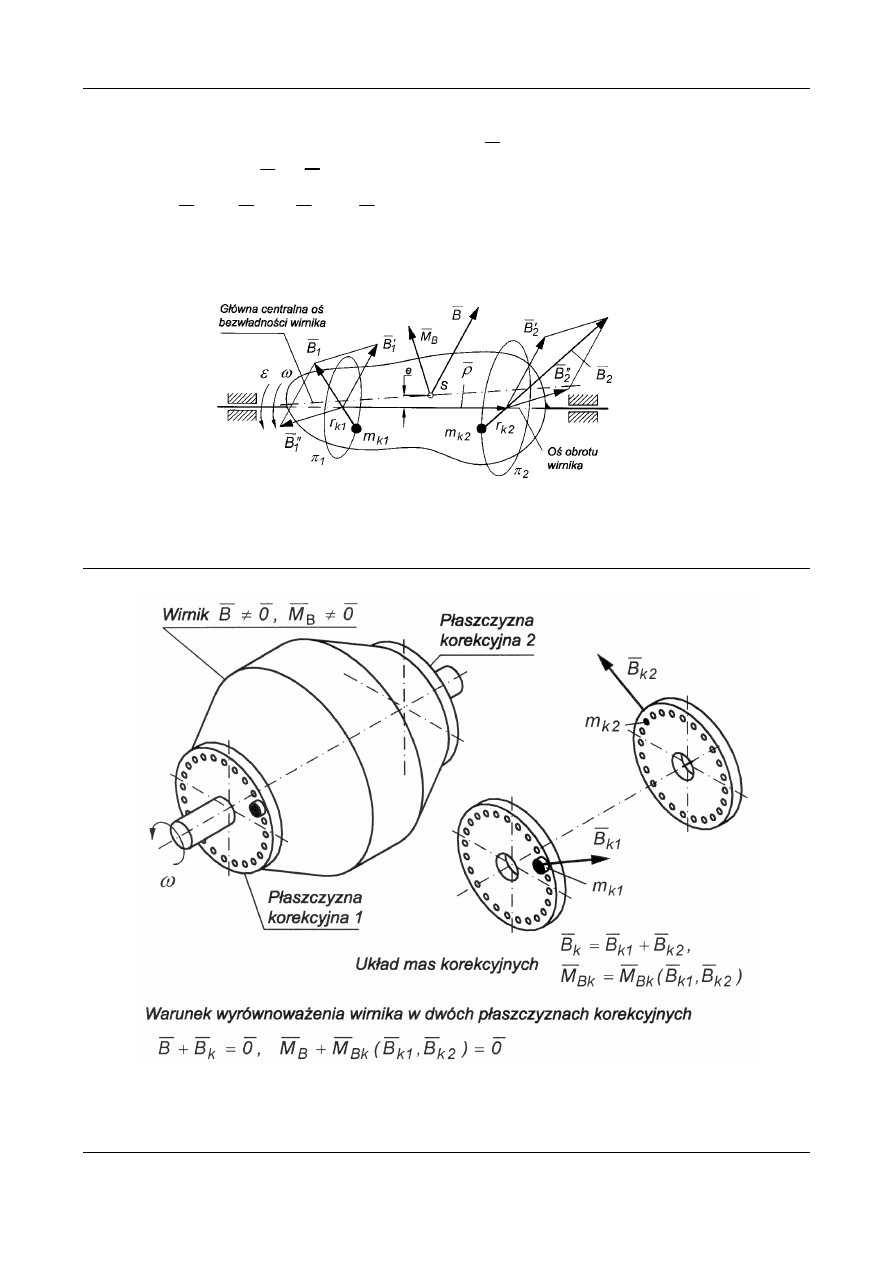
Aby zatem wirnik wyrównoważyć dynamicznie, należy

w płaszczyznach

1

π

i

2

π

zwanych płaszczyznami korekcyjnymi (lub

płaszczyznami wyważania) umieścić masy korekcyjne

1

k

m i

2

k

m

na

promieniach korekcyjnych

1

k

r i

2

k

r (Rys. 8), obróconych o kąt 180

°°°°

w stosunku do sił bezwładności

1

B i

2

B , co kończy dowód twierdzenia.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 10

Opracowali: J. Felis, H. Jaworowski

Masy korekcyjne

1

k

m i

2

k

m na promieniach korekcyjnych

1

k

r i

2

k

r

przy

obrocie wału z prędkością kątową

ω

wywołują siły bezwładności

równoważące siły

1

B i

2

B , muszą być zatem spełnione równania:

2

k

2

1

k

1

B

B

,

B

B

−

=

−

=

2

1

k

1

k

1

k

r

m

B

ω

=

,

2

2

k

2

k

2

k

r

m

B

ω

=

(13)

Rys. 8 (powtórzony). Wektor główny sił bezwładności i moment główny sił bezwładności
oraz równoważny układ sił bezwładności w płaszczyznach korekcyjnych.

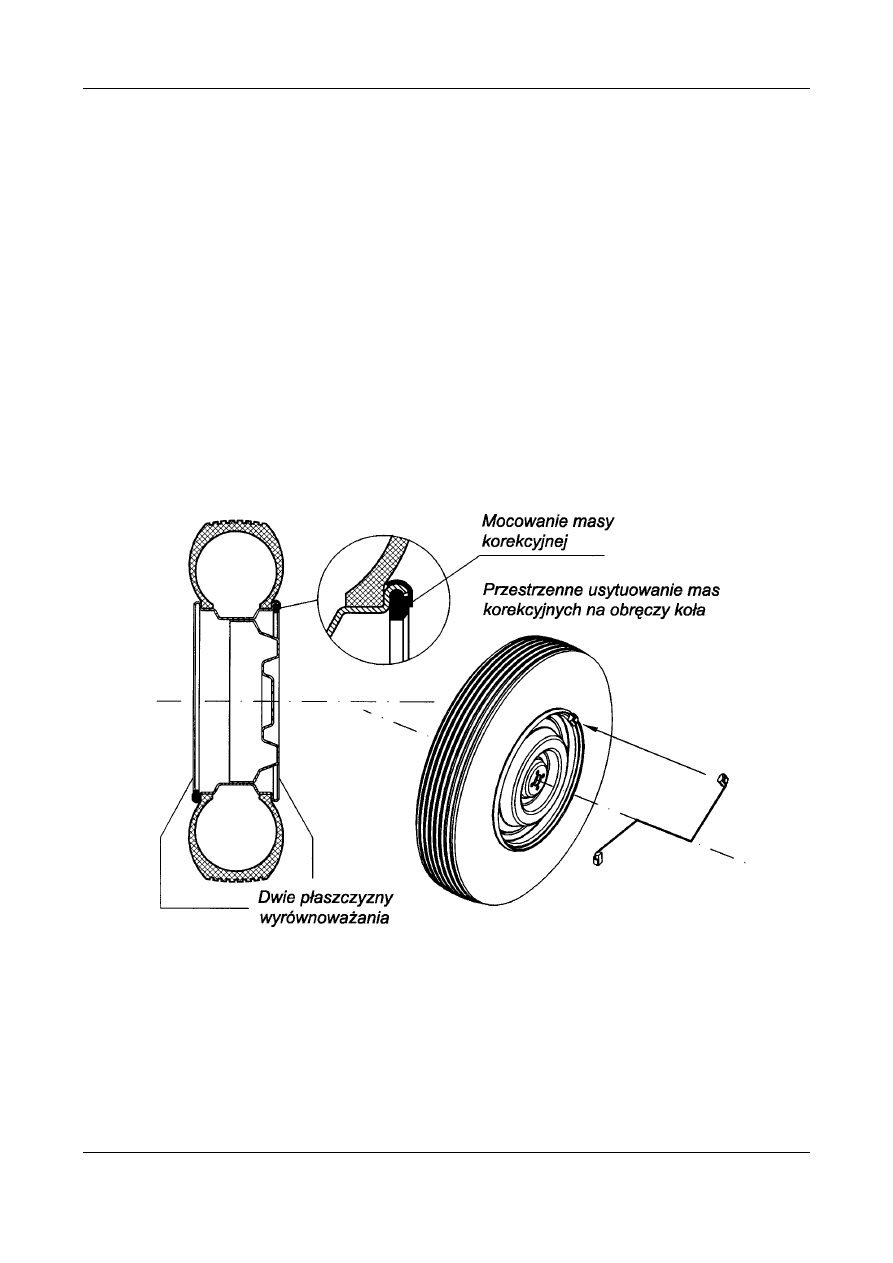
Rys. 9. Praktyczne wyrównoważanie wirnika w dwóch płaszczyznach korekcyjnych

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 11

Opracowali: J. Felis, H. Jaworowski

Przedstawiona teoria znajduje zastosowanie przy wyrównoważaniu

wirników silników elektrycznych, wentylatorów, turbin itp.

Charakterystycznym przykładem jest dynamiczne wyrównoważanie kół

pojazdów samochodowych.

Na Rys. 10 wybór płaszczyzn korekcyjnych oraz sposób mocowania mas

korekcyjnych na obręczy koła.

Przyczyny niewyrównoważenia kół pojazdów samochodowych:

- niewyrównoważenie obręczy koła,
- niewyrównoważenie opony,
- niewyrównoważenie powstałe przy montażu opony na obręczy,
- nierównomierne zużycie bieżnika opony,
- uszkodzenie lub skrzywienie obręczy.

Rys. 10.

Wyważanie dynamiczne kół pojazdów samochodowych.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 12

Opracowali: J. Felis, H. Jaworowski

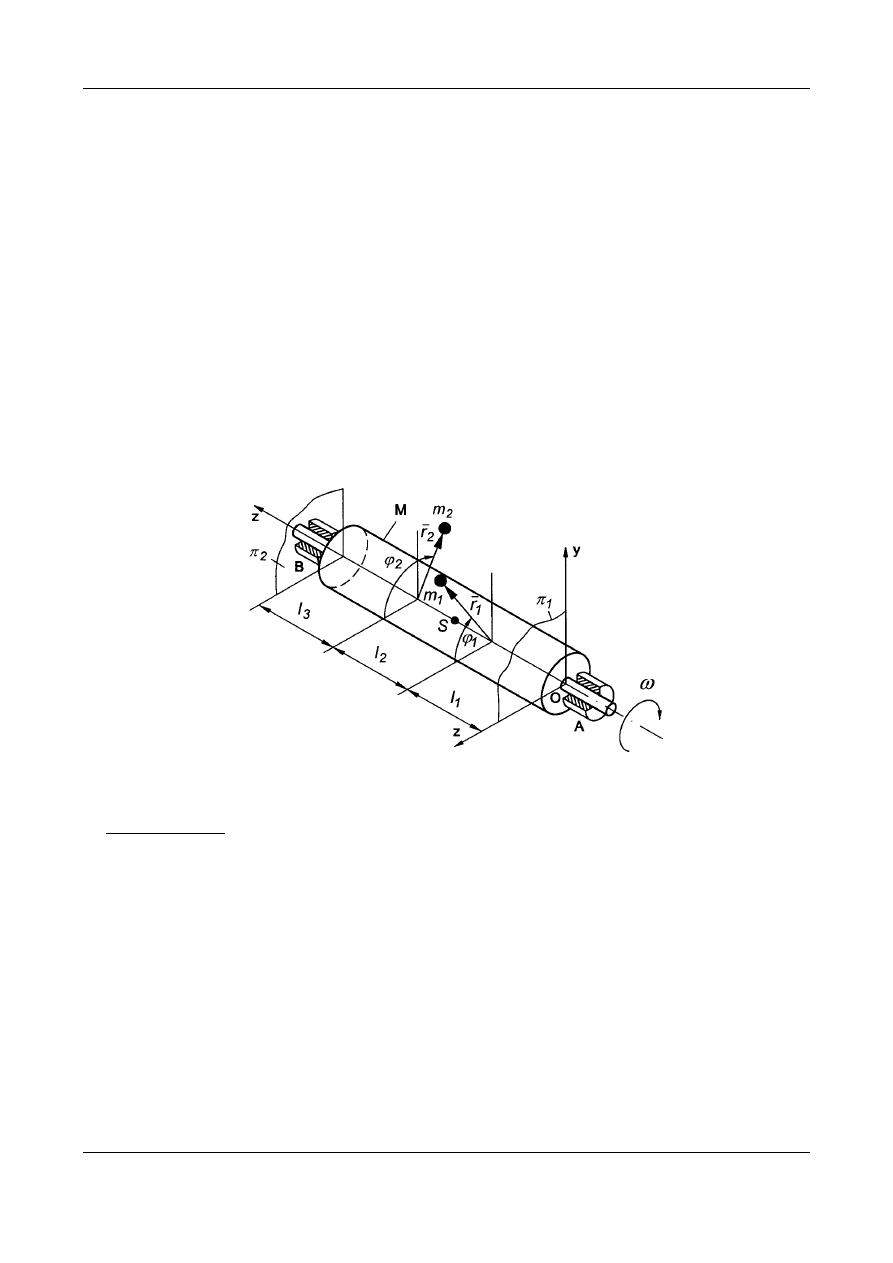
Przykład 1

Dany jest wał o masie M i środku ciężkości S leżącym na osi obrotu Oz

wirujący wokół tej osi z prędkością kątową

ω

(Rys. 11), dla którego

0

D

xz

=

i

0

D

yz

=

. Niewyrównoważenie wału spowodowane jest układem dwóch

mas

g

10

m

1

=

i

g

20

m

2

=

umieszczonych odpowiednio na promieniach

50

r

1

=

mm,

40

r

2

=

mm, pod kątami

°

=

60

1

ϕ

,

°

=

120

2

ϕ

, mierzonymi

w układzie ruchomym Oxyz związanym z wałem. Dane są odległości:

mm

200

l

l

l

l

3

2

1

=

=

=

=

. Położenie płaszczyzn korekcyjnych

2

1

,

π

π

jak na

rysunku.
Należy wyznaczyć masy korekcyjne

2

k

1

k

m

,

m

oraz ich położenie

2

k

1

k

,

ϕ

ϕ

tak, aby wyrównoważyć dynamicznie wał z zadanymi masami. Promienie
korekcji wynoszą:

mm

20

r

1

k

=

,

mm

40

r

2

k

=

.

Rys. 11. Wyrównoważanie wału z układem mas skupionych

Rozwiązanie
Warunki wyrównoważenia dynamicznego układu mają postać:

∑

∑

∑

∑

=

=

=

=

=

⋅

+

⋅

⋅

+

=

=

⋅

+

⋅

⋅

+

=

=

+

+

+

=

=

+

+

+

=

n

1

i

2

k

2

k

2

k

2

2

2

1

1

k

1

i

i

i

n

1

i

2

k

2

k

2

k

2

2

2

1

1

1

i

i

i

n

1

i

2

k

2

k

2

k

2

2

2

1

1

1

1

k

1

k

1

k

i

i

n

1

i

2

k

2

k

2

k

2

2

2

1

1

1

1

k

1

k

1

k

i

i

0

sin

l

3

r

m

sin

l

2

r

m

sin

l

r

m

z

y

m

0

cos

l

3

r

m

cos

l

2

r

m

cos

l

r

m

z

x

m

0

sin

r

m

sin

r

m

sin

r

m

sin

r

m

y

m

0

cos

r

m

cos

r

m

cos

r

m

cos

r

m

x

m

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

(P1.1)

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 13

Opracowali: J. Felis, H. Jaworowski

Z trzeciego i czwartego równania (P1.1) mamy:

306

,

3

cos

r

m

2

cos

r

m

sin

r

m

2

sin

r

m

tg

2

2

2

1

1

1

2

2

2

1

1

1

2

k

−

=

+

+

=

ϕ

ϕ

ϕ

ϕ

ϕ

(P1.2)

stąd:

°

=

82

,

286

2

k

ϕ

Z czwartego równania (P1.1) mamy:

g

83

,

15

sin

r

3

sin

r

m

2

sin

r

m

m

2

k

2

k

2

2

2

1

1

1

2

k

=

−

−

=

ϕ

ϕ

ϕ

(P1.3)

Z pierwszego i drugiego równania (P1.1) mamy:

615

,

15

cos

r

m

cos

r

m

cos

r

m

sin

r

m

sin

r

m

sin

r

m

tg

2

k

2

k

2

k

2

2

2

1

1

1

2

k

2

k

2

k

2

2

2

1

1

1

1

k

=

+

+

+

+

=

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

(P1.4)

stąd:

°

=

33

,

266

1

k

ϕ

Z drugiego równania (P1.1) mamy:

g

03

,

26

sin

r

sin

r

m

sin

r

m

sin

r

m

m

1

k

1

k

2

k

2

k

2

k

2

2

2

1

1

1

1

k

=

−

−

−

=

ϕ

ϕ

ϕ

ϕ

(P1.5)

Rys. 12. Rozmieszczenie mas korekcyjnych.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 14

Opracowali: J. Felis, H. Jaworowski

WYRÓWNOWAŻANIE MECHANIZMÓW DŹWIGNIOWYCH

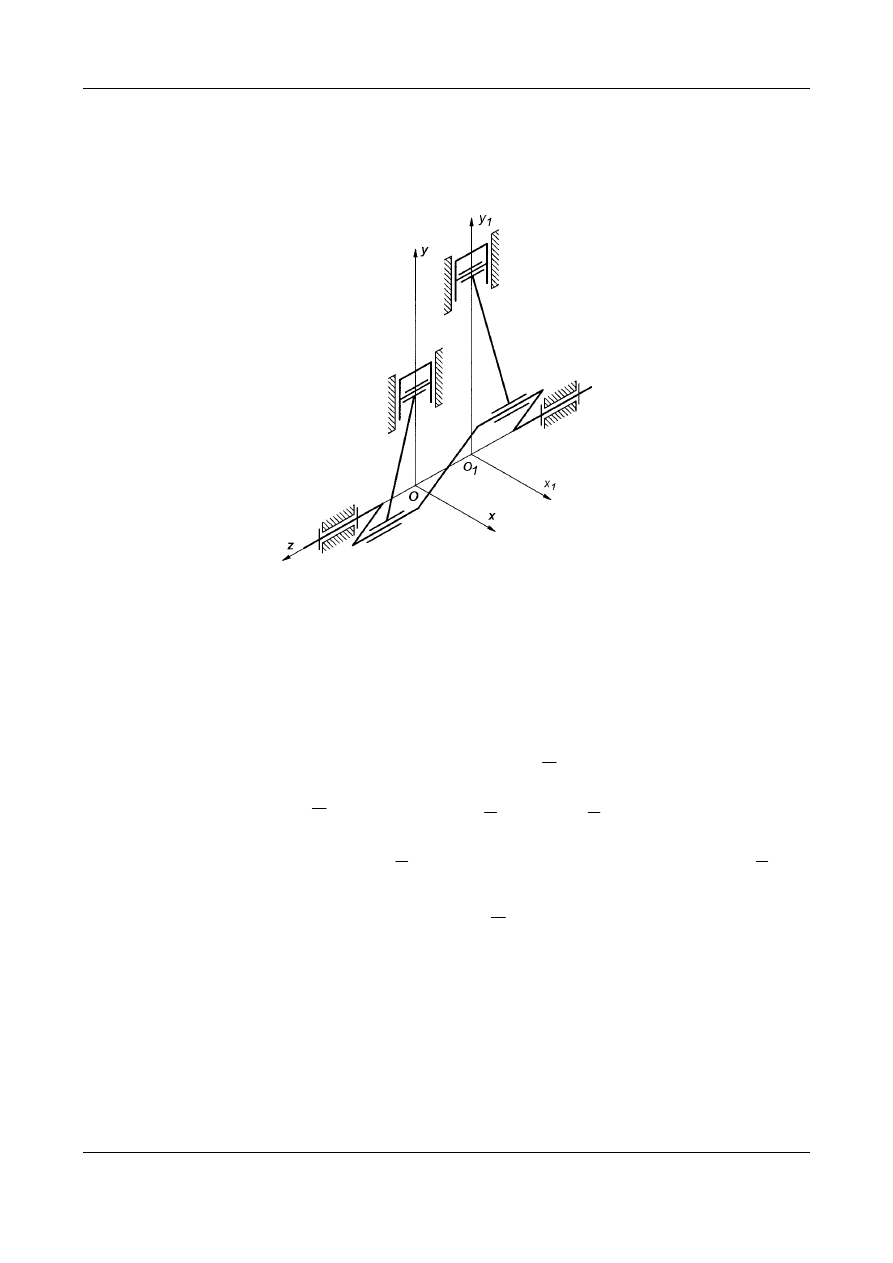
Mechanizmy dźwigniowe w ogólnym przypadku są mechanizmami

przestrzennymi. Ich człony poruszają się w płaszczyznach równoległych do
pewnej płaszczyzny kierowniczej.

Rys. 13. Dwucylindrowy silnik w układzie rzędowym

Przyjęto, że główna płaszczyzna ruchu Oxy (płaszczyzna kierownicza)

przechodzi przez oś pierwszego cylindra. Oś drugiego cylindra jest
przesunięta i przechodzi przez nią płaszczyzna Ox

1

y

1

. Przy tak przyjętym

układzie współrzędnych, współrzędne wszystkich ruchomych członów
z

i

= const, zatem również współrzędna środka masy z

S

= const.

Obliczymy teraz wektor główny sił bezwładności B dla mechanizmu. Mamy:

∑

−

=

−

=

=

n

1

i

Si

i

S

z

y

x

a

m

a

M

)

B

,

B

,

B

(

B

(14)

gdzie: M - masa całkowita,

S

a - przyspieszenie środka masy,

Si

a -

przyspieszenie środka masy i - tego członu.

Na podstawie (14) współrzędne wektora B wynoszą:

0

z

m

z

M

B

,

y

m

y

M

B

,

x

m

x

M

B

n

1

i

i

i

S

z

n

1

i

i

S

y

n

1

i

i

i

S

x

=

∑

−

=

−

=

∑

−

=

−

=

∑

−

=

−

=

=

=

=

&&

&&

&&

&&

&&

&&

(15)

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 15

Opracowali: J. Felis, H. Jaworowski

Moment główny sił bezwładności

B

M

obliczamy ze wzoru:

∑

∑

−

−

=

×

=

=

=

n

1

i

n

1

i

i

i

i

i

i

i

i

B

0

y

m

x

m

z

y

x

k

j

i

B

M

&&

&&

ρ

(16)

stąd współrzędne momentu wynoszą:

(

)

.

y

x

m

y

x

m

M

,

dt

D

d

z

x

m

M

,

dt

D

d

z

y

m

M

n

1

i

i

i

i

i

i

i

Bz

n

1

i

2

xz

2

i

i

i

By

n

1

i

2

yz

2

i

i

i

Bx

∑

−

=

∑

−

=

=

∑

=

=

=

=

=

&&

&&

&&

&&

(17)

Warunkiem wyrównoważenia całkowitego mechanizmu jest,

0

B

=

oraz

0

M

B

=

Na podstawie (15) otrzymujemy:

0

B

=

dla

0

a

S

=

(18)

Przyspieszenie

0

a

S

=

dla

const

v

S

=

lub

0

v

S

=

.

Jednak ze względu na cykliczność ruchu mechanizmu nie jest możliwy

jednostajny prostoliniowy ruch środka masy względem nieruchomej
podstawy. Dlatego w rzeczywistości musi być spełniony warunek:

const

x

S

=

oraz

const

y

S

=

(19)

Podobnie na podstawie (17) otrzymujemy:

0

M

Bx

=

dla

const

D

yz

=

(20)

0

M

By

=

dla

const

D

xz

=

(21)

Wyzerowanie współrzędnej

Bz

M

nie jest możliwe i współrzędna ta jest

przedmiotem odrębnej analizy w rozdziale dotyczącym równań dynamicznych
maszyny. Współrzędna

Bz

M

powoduje zjawisko „kołysania się silnika”.

Jeśli spełnione są warunki (18) przestrzenny mechanizm dźwigniowy

jest wyrównoważony statycznie.

Jeśli spełnione są równocześnie warunki (18), (20) i (21) przestrzenny

mechanizm dźwigniowy jest wyrównoważony dynamicznie (całkowicie).

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 16

Opracowali: J. Felis, H. Jaworowski

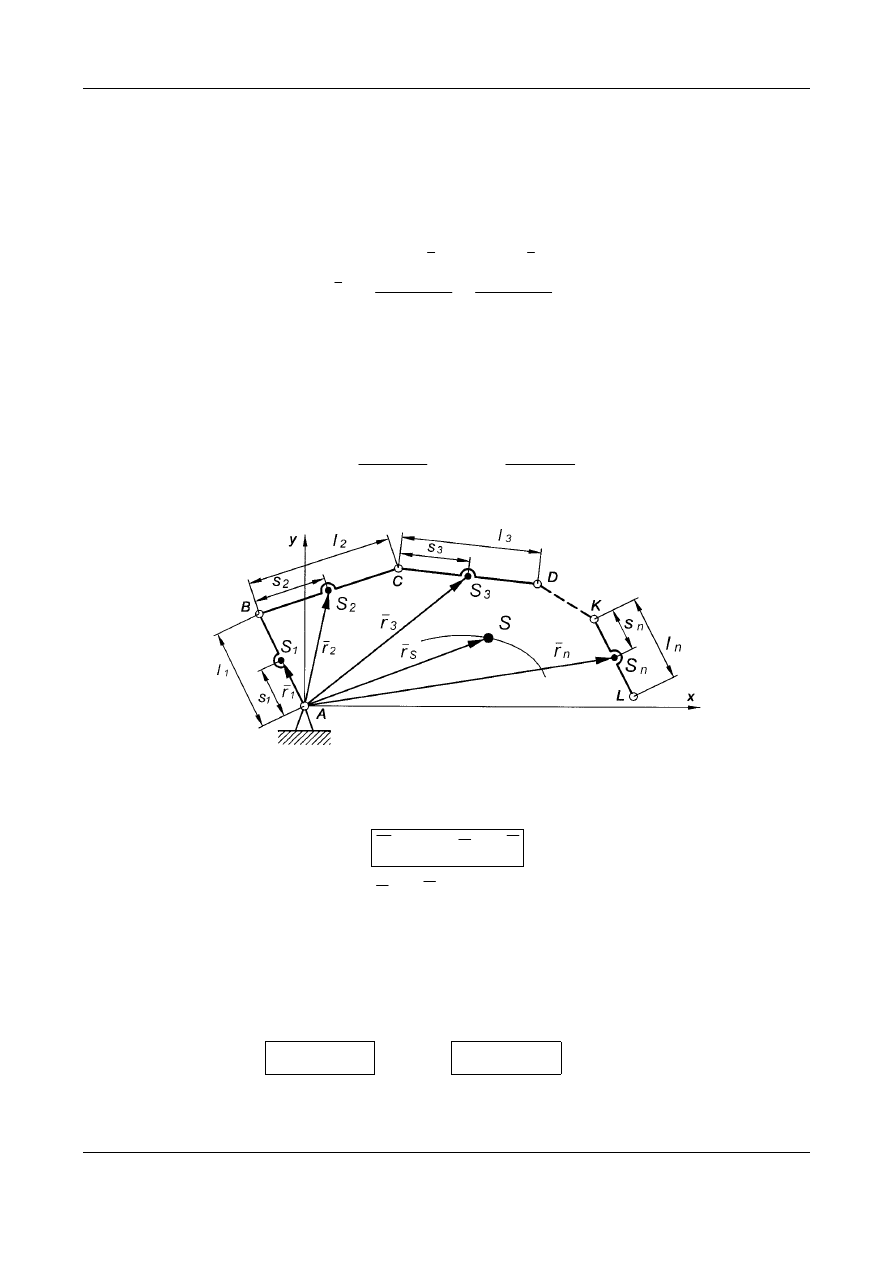
Wyrównoważanie statyczne płaskich mechanizmów dźwigniowych.

Dany jest płaski mechanizm dźwigniowy (Rys. 14), dla którego

wyznaczymy położenie środka masy. Promień wektor środka masy
wyznaczamy z zależności:

M

r

m

m

r

m

r

n

1

i

Si

i

n

1

i

i

n

1

i

Si

i

S

∑

∑

∑

=

=

=

=

=

(22)

W trakcie ruchu niewyrównoważonego mechanizmu środek masy porusza

się po torze o współrzędnych:

M

y

m

y

;

m

x

m

x

n

1

i

i

i

S

n

1

i

i

n

1

i

i

i

S

∑

∑

∑

=

=

=

=

=

(23)

Rys. 14. Wyznaczanie środka masy płaskiego mechanizmu dźwigniowego

Warunek statycznego wyrównoważenia mechanizmu płaskiego ma postać:

0

a

M

B

S

=

⋅

−

=

(24)

Ponieważ

0

M

≠

, natomiast

0

a

S

=

jeżeli:

a) środek masy mechanizmu porusza się ruchem jednostajnym

prostoliniowym.

b) środek masy mechanizmu jest nieruchomy.
W mechanizmach dźwigniowych wykonujących ruch okresowy możliwy jest

jedynie drugi przypadek tzn.:

const

x

S

=

oraz

const

y

S

=

(25)

Zależność (25) jest warunkiem koniecznym i wystarczającym

statycznego wyrównoważenia mechanizmu płaskiego.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 17

Opracowali: J. Felis, H. Jaworowski

Przykład 2
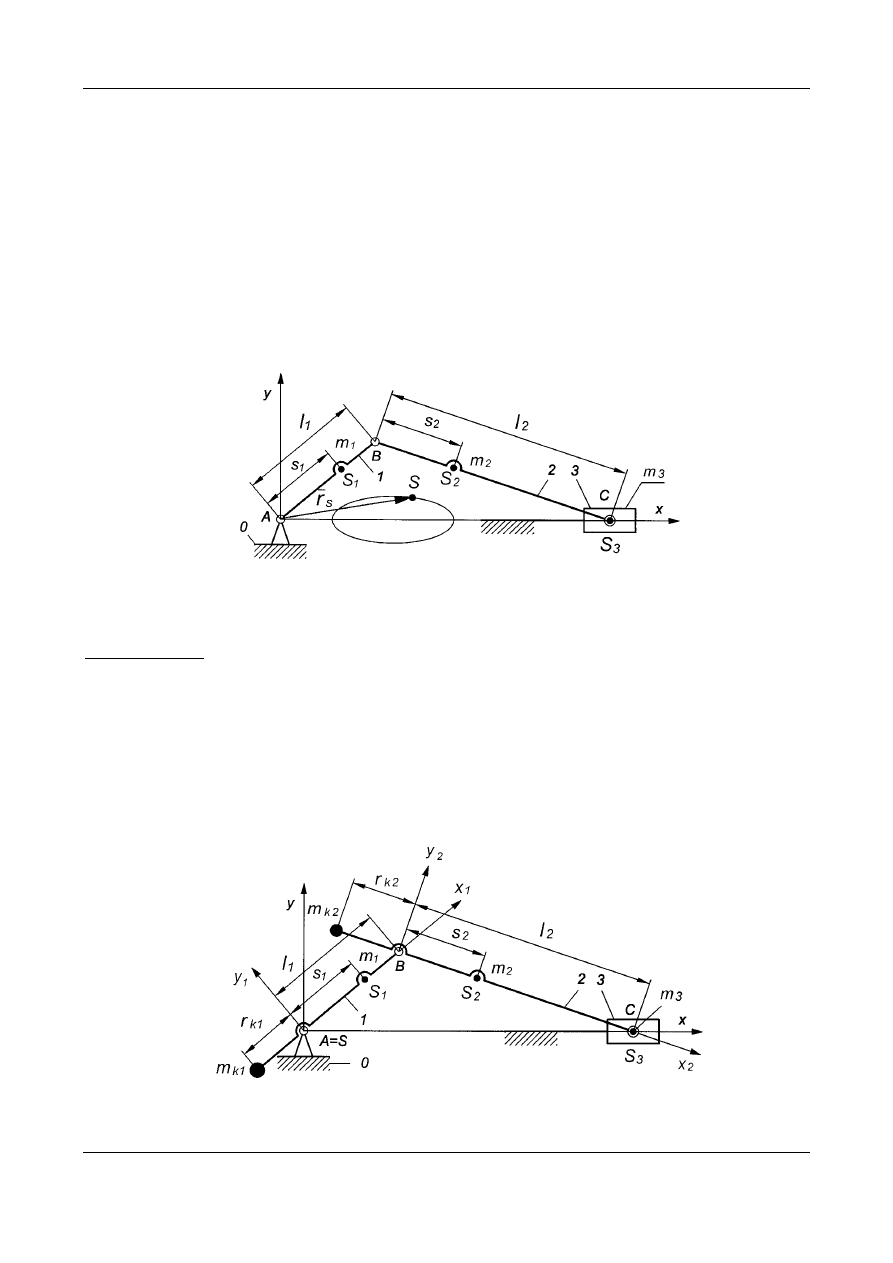
Wyrównoważanie statyczne całkowite mechanizmu korbowo - suwakowego.

Dany jest niewyrównoważony mechanizm korbowo - suwakowy, którego

środek masy S porusza się po torze pokazanym na Rys. 15. Dane są masy
członów

kg

2

m

,

kg

1

m

m

2

3

1

=

=

=

umieszczone w środkach mas

3

2

1

S

,

S

,

S

oraz długości

m

2

,

0

s

,

m

4

,

0

l

,

m

1

,

0

s

,

m

2

,

0

l

2

2

1

1

=

=

=

=

. Przeprowadzić

całkowite statyczne wyrównoważenie mechanizmu wprowadzając
odpowiednie masy korekcyjne (przeciwciężary).

Rys. 15. Niewyrównoważony mechanizm korbowo-suwakowy

Rozwiązanie

Dla statycznego całkowitego wyrównoważenia mechanizmu korbowo -

suwakowego niezbędne jest, aby jego środek masy trakcie ruchu
mechanizmu pozostawał nieruchomy. W przypadku tego mechanizmu
oznacza to, że jego środek masy powinien znajdować się w punkcie A.
Przeniesienie środka masy do nieruchomego punktu A uzyskamy po
wprowadzeniu dodatkowych mas tzw. mas korekcyjnych (przeciwciężarów),
co przedstawiono na Rys. 16.

Rys. 16. Wyrównoważanie całkowite mechanizmu korbowo-suwakowego

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 18

Opracowali: J. Felis, H. Jaworowski

Krok pierwszy polega na sprowadzeniu środków mas członów 2 i 3 do

punktu B poprzez umieszczenie na przedłużeniu członu 2 masy korekcyjnej

2

k

m

na promieniu

2

k

r

.

W celu obliczenia współrzędnych środka ciężkości mas

3

2

m

,

m

oraz

2

k

m

wygodnie jest przyjąć układ współrzędnych w ten sposób, aby początek
układu znajdował się w punkcie, do którego chcemy sprowadzić środek
ciężkości układu mas (czyli punkt B), oś

2

Bx winna pokrywać się z osią

członu, natomiast

2

By powinna być do niej prostopadła. Wtedy współrzędna

S

y środka masy równa jest zero. Współrzędna

S

x również ma być równa

zero, co pozwala na zapisanie warunku zerowania się momentu statycznego

2

y

S

:

0

l

m

s

m

r

m

x

m

S

2

3

2

2

2

k

2

k

n

1

i

i

i

2

y

=

+

+

∑

−

=

=

=

(P2.1)

stąd

0

l

m

s

m

r

m

S

2

3

2

2

2

k

2

k

2

k

=

+

=

=

(P2.2)

gdzie:

2

k

S

- moment statyczny przeciwciężaru.

Możemy dobrać

2

k

m

i

2

k

r w ten sposób, aby zależność (P2.2) była

spełniona.

W kroku drugim sprowadzamy środek ciężkości układu mas

1

m

oraz masy

znajdującej się obecnie w punkcie B:

2

k

3

2

B

m

m

m

m

+

+

=

do punktu A

poprzez umieszczenie na przedłużeniu członu 1 masy korekcyjnej

1

k

m na

promieniu

1

k

r . Przyjmujemy w tym celu układ współrzędnych

1

1

y

Ax

o

początku w punkcie A. Obliczamy moment statyczny:

∑

=

+

+

−

=

=

=

n

1

i

1

B

1

1

1

k

1

k

i

i

1

y

0

l

m

s

m

r

m

x

m

S

(P2.3)

stąd:

(

)

1

2

k

3

2

1

1

1

B

1

1

1

k

1

k

1

k

l

m

m

m

s

m

l

m

s

m

r

m

S

+

+

+

=

+

=

=

(P2.4)

Możemy dobrać

1

k

m i

1

k

r w ten sposób, aby była spełniona zależność

(P2.4). Przyjmiemy promienie korekcyjne:

m

2

,

0

r

,

m

2

,

0

r

2

k

1

k

=

=

i następnie obliczymy masy korekcyjne:

kg

5

,

7

2

,

0

2

,

0

)

8

1

2

(

1

,

0

1

r

l)

m

m

m

(

s

m

m

kg

4

2

,

0

4

,

0

1

2

,

0

2

r

l

m

s

m

m

1

k

1

2

k

3

2

1

1

1

k

2

k

2

3

2

2

2

k

=

⋅

+

+

+

⋅

=

+

+

=

=

⋅

+

⋅

=

+

=

(P2.5)

W ten sposób mechanizm został wyrównoważony statycznie całkowicie.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 19

Opracowali: J. Felis, H. Jaworowski

Masa mechanizmu przed wyrównoważeniem:

kg

4

m

m

m

M

3

2

1

p

=

+

+

=

(P2.6)

Masa mechanizmu po wyrównoważeniu:

kg

5

,

15

m

m

m

m

m

M

2

k

1

k

3

2

1

w

=

+

+

+

+

=

(P2.7)

W wyniku w wyrównoważenia statycznego całkowitego uzyskaliśmy

wprawdzie wektor

0

B

=

, lecz masa mechanizmu wzrosła prawie

czterokrotnie. Dodatkowo wzrosną wartości momentów bezwładności

1

S

J

i

2

S

J

członów 1 i 2, co spowoduje znaczny wzrost momentu bezwładności

całego mechanizmu.

W praktyce rzadko stosuje się całkowite wyrównoważanie statyczne.

Stosuje się natomiast wyrównoważanie statyczne częściowe, które polega na
tym, że nie sprowadza się wektora głównego sił bezwładności do zera, lecz
dąży się do zmniejszenia jego wartości oraz odpowiedniego doboru jego
kierunku .
Przykład 3
Wyrównoważanie statyczne częściowe mechanizmu korbowo - suwakowego.

Dany jest niewyrównoważony mechanizm korbowo - suwakowy jak

w Przykładzie 2. Przeprowadzić wyrównoważenie statyczne częściowe
mechanizmu.

Rozwiązanie
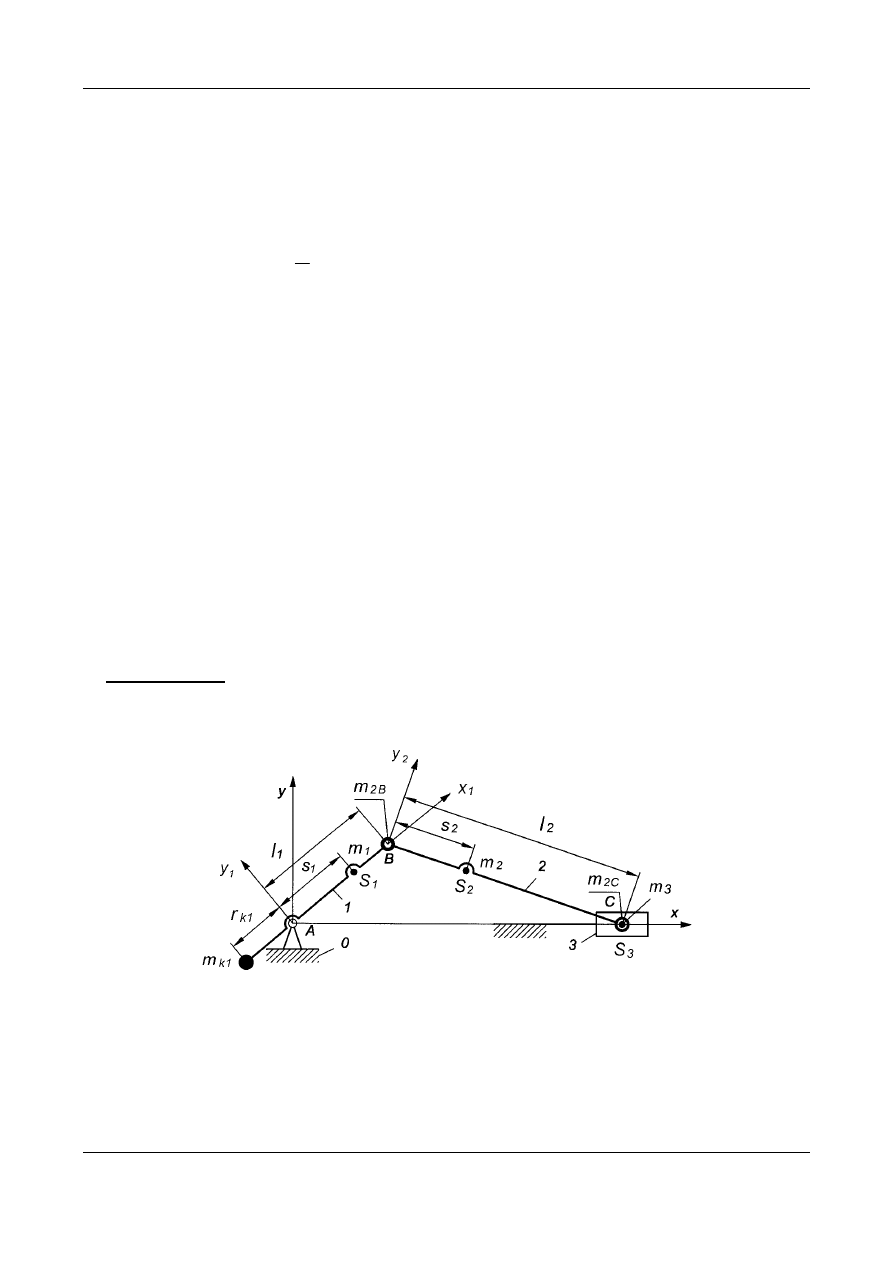
Do wyrównoważenia mechanizmu zastosujemy tylko jedną masę

korekcyjną umieszczoną na przedłużeniu korby (Rys. 17).

Rys. 17. Częściowe wyrównoważanie mechanizmu korbowo-suwkowego

W kroku pierwszym wyrównoważania zastępujemy masę członu 2 układem

dwóch mas

B

2

m

i

C

2

m

skupionych w punktach B i C.

Wykorzystamy w tym celu metodę mas zastępczych.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 20

Opracowali: J. Felis, H. Jaworowski

Metoda mas zastępczych polega na zastąpieniu mas niektórych członów

(brył sztywnych o ciągłym rozkładzie masy) skończonym zbiorem mas
punktowych skupionych w wybranych z góry punktach.

Warunki równoważności masy członu rozłożonej w sposób ciągły oraz

zbioru mas skupionych dla układu płaskiego są następujące:
- masa

układu pozostaje niezmieniona:

m

m

n

1

i

i

=

∑

=

,

(P3.5)

- środek masy nie zmienia swego położenia:

S

n

1

i

i

i

S

n

1

i

i

i

my

y

m

;

mx

x

m

=

=

∑

∑

=

=

(P3.26)

- moment

bezwładności względem środka masy pozostaje niezmieniony:

(

)

S

n

1

i

2

i

2

i

i

J

y

x

m

=

+

∑

=

(P3.37)

W przypadku pręta (członu jednowymiarowego) warunek (P3.2) redukuje

się do postaci:

0

x

m

n

1

i

i

i

=

∑

=

(P3.4)

Dla członu jednowymiarowego otrzymujemy zatem 3 warunki równoważności:
(P3.1), (P3.2) i (P3.3). Ponieważ powyższy układ równań musi być
oznaczony, minimalna liczba skupionych mas zastępczych wynosi 3.

W niniejszym przykładzie zastępujemy masę członu 2 jedynie dwiema

masami skupionymi, rezygnując ze spełnienia warunku (P3.3).

Na podstawie (P3.1) oraz (P3.4) otrzymujemy zależności:

(

)

0

s

l

m

s

m

m

m

m

2

2

C

2

2

B

2

C

2

B

2

2

=

−

+

−

+

=

(P3.5)

stąd obliczamy:

(

)

2

2

2

2

B

2

s

l

l

m

m

−

=

oraz

2

2

2

C

2

s

l

m

m

=

(P3.6)

Zastąpienie członu 2 dwiema masami zastępczymi

B

2

m

,

C

2

m

nie zmienia

jego masy, jak również położenia środka masy

2

S . Natomiast moment

bezwładności układu mas zastępczych różni się od momentu bezwładności
członu 2 i dlatego jest to model przybliżony, nie w pełni ekwiwalentny.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 21

Opracowali: J. Felis, H. Jaworowski

Masa

B

2

m

traktowana jako punkt materialny porusza się razem z członem

1, który wykonuje ruch obrotowy, natomiast masa

C

2

m

porusza się wraz z

członem 3 ruchem postępowym.

W drugim kroku wyrównoważania sprowadzamy środek ciężkości układu

mas

1

m i

B

2

m

do osi obrotu korby (punkt A) umieszczając na jej przedłużeniu

masę korekcyjną

1

k

m .

Mamy obecnie:

1

k

1

B

2

1

1

1

k

1

B

2

1

1

1

k

1

k

n

1

i

i

i

1

y

r

l

m

s

m

m

0

l

m

s

m

r

m

x

m

S

+

=

=

+

+

−

=

∑

=

=

(P3.7)

Po uwzględnieniu danych jak w Przykładzie 3.19 mamy:

(

)

kg

1

)

2

,

0

4

,

0

(

4

,

0

2

s

l

l

m

m

2

2

2

2

B

2

=

−

=

−

=

(P3.8)

kg

1

2

,

0

4

,

0

2

s

l

m

m

2

2

2

C

2

=

=

=

(P3.9)

kg

5

,

1

2

,

0

1

,

0

1

1

,

0

1

r

l

m

s

m

m

1

k

1

B

2

1

1

1

k

=

⋅

+

⋅

=

+

=

(P3.10)

Masa w punkcie C:

kg

2

1

1

m

m

m

C

2

3

C

=

+

=

+

=

(P3.11)

Masa mechanizmu przed wyrównoważaniem:

kg

4

m

m

m

M

3

2

1

p

=

+

+

=

(P3.12)

Masa mechanizmu po wyrównoważeniu częściowym:

kg

5

,

5

m

m

m

m

M

1

k

3

2

1

w

=

+

+

+

=

(P3.13)

Jak widać, stosując tę metodę wyrównoważania całkowity wzrost masy

częściowo wyrównoważonego mechanizmu jest nieduży. Jednakże
wykonująca ruch postępowy masa

C

2

3

C

m

m

m

+

=

pozostaje

niewyrównoważona i dlatego środek masy mechanizmu porusza się po linii
prostej (po osi Ox).

W tym przypadku wyrównoważona została składowa pionowa wektora

głównego sił bezwładności

0

B

y

=

, natomiast składowa pozioma pozostaje

różna od zera

0

B

x

≠

.

Teoria maszyn i mechanizmów Dynamika Mechanizmów. Wyrównoważanie 22

Opracowali: J. Felis, H. Jaworowski

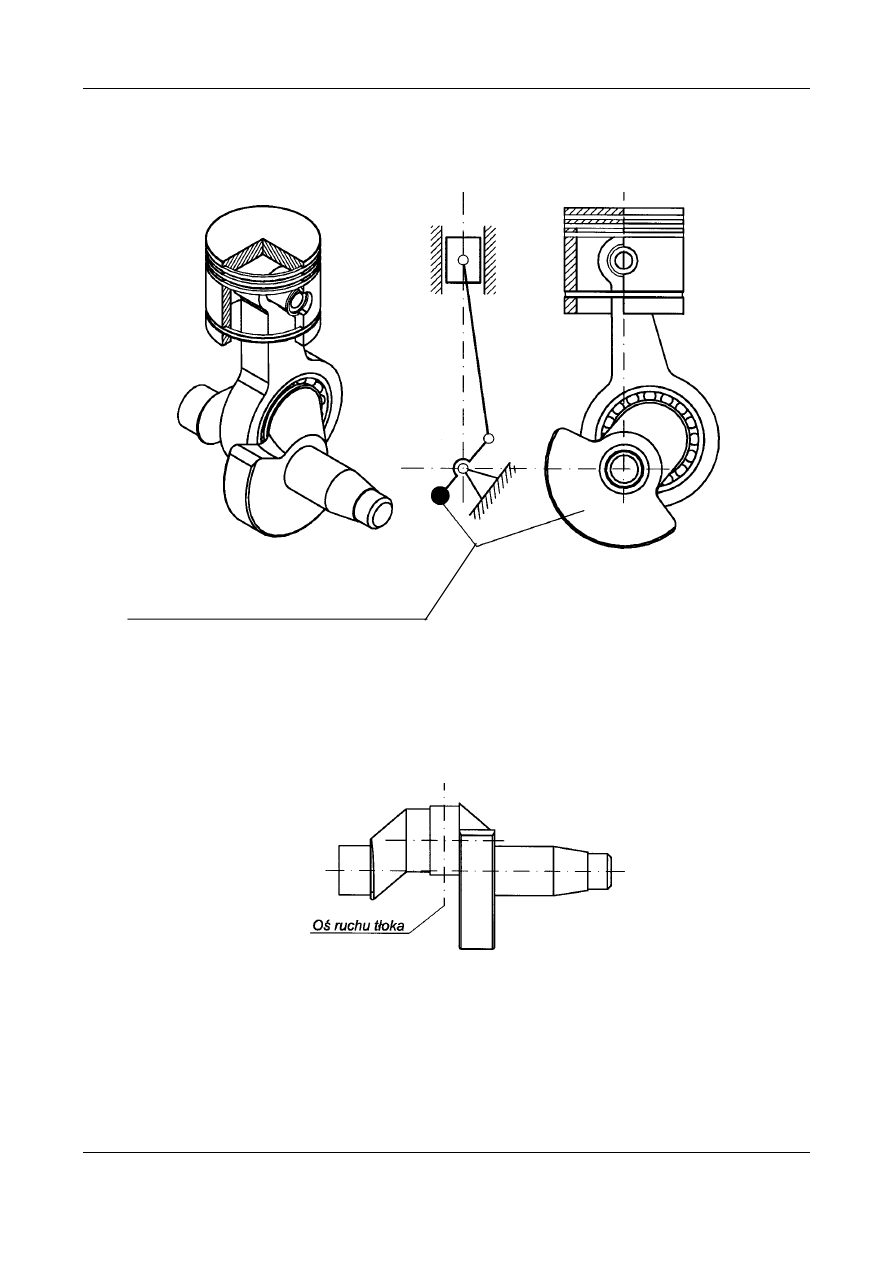
Wyrównoważanie konstrukcyjne sprężarki tłokowej jednocylindrowej

Masa korekcyjna (przeciwciężar)

Rys. 18. Wyrównoważanie mechanizmu korbowo-suwakowego sprężarki tłokowej
jednocylindrowej - schemat rozmieszczenia przeciwciężaru.

Rys. 19. Wyrównoważanie mechanizmu korbowo-suwakowego sprężarki tłokowej
jednocylindrowej - konstrukcja wału korbowego z przeciwciężarem