Instytut

Spawalnictwa

w Gliwicach

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii

układów konstrukcji

3.1

opracował:

dr inż. Piotr Sędek

Nowelizacja materiału: 01. 2012 r.

2

1. Siły jako oddziaływania mechaniczne

Z oddziaływaniem mechanicznym najpro

ś

ciej jest zwi

ą

za

ć

poj

ę

cie siły. Siła jest

miar

ą

oddziaływa

ń

(mechanicznych) działaj

ą

cych na ciało. Im wi

ę

ksze oddziaływanie

(czyli wi

ę

ksza siła) tym wi

ę

ksze wywołuje ono skutki – mocniej przyspiesza (lub

zwalnia ciało), silniej go odkształca. Trzecia zasada dynamiki Newtona mówi o wza-
jemno

ś

ci oddziaływa

ń

. Jest ona cz

ę

sto nazywana zasad

ą

akcji i reakcji. Sformuło-

wanie III zasady dynamiki:
Je

ż

eli ciało A działa na ciało B sił

ą

F

AB

, to ciało B działa na ciało A sił

ą

F

BA

, o taki,

samym kierunku i warto

ś

ci jak F

AB

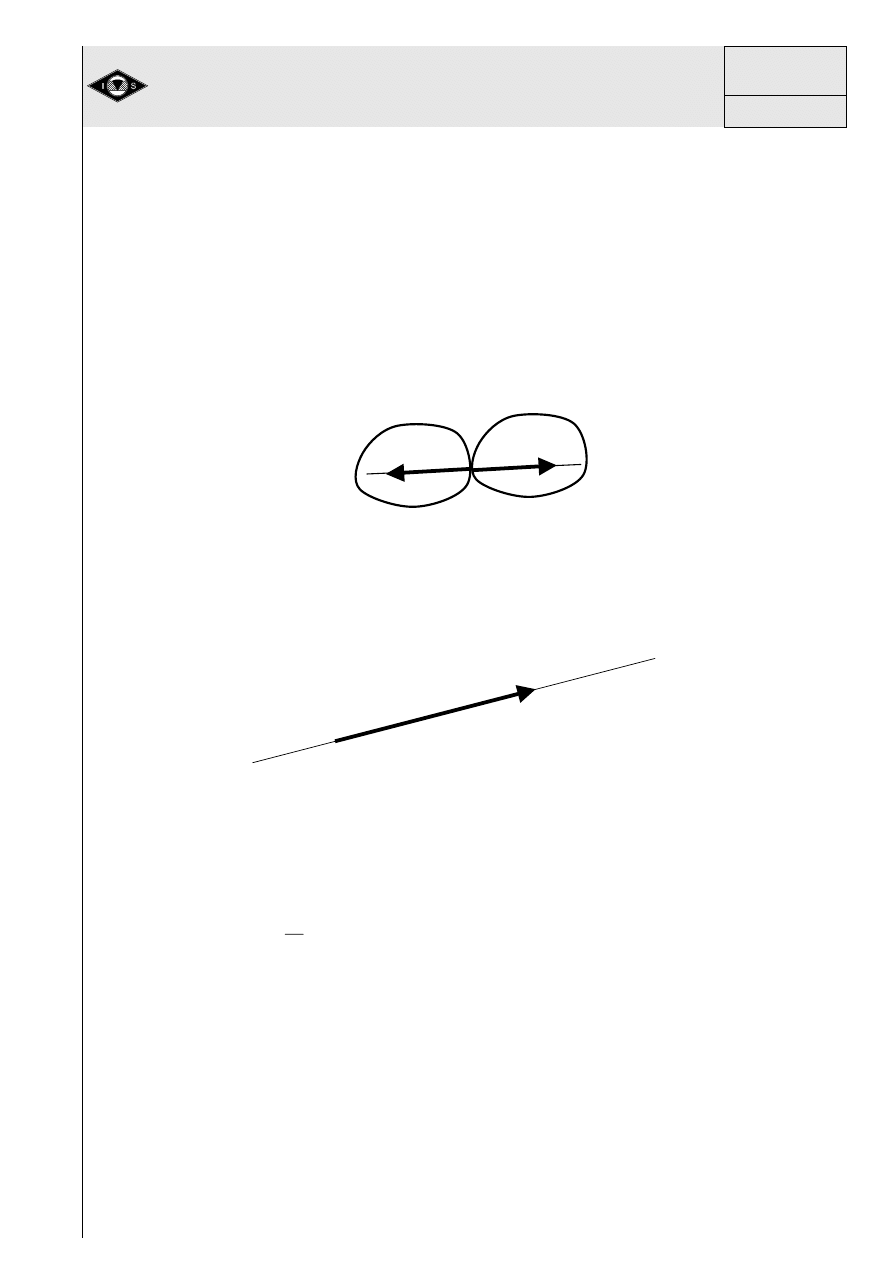
, ale przeciwnym zwrocie (rys. 1 ) .

Rys. 1 Siła jako oddziaływanie mechaniczne

Poj

ę

cie siły nierozerwalnie ł

ą

czy si

ę

z wektorem, który jest okre

ś

lony jako tzw. odci-

nek skierowany i jest graficznym odzwierciedleniem siły. Posiada on nast

ę

puj

ą

ce ce-

chy: kierunek, zwrot i warto

ść

. Na rys.2 pokazano wektor siły i okre

ś

lono jego cechy.

Rys.2 Wektor jako graficzne przedstawienie siły

Kierunek wektora okre

ś

la linia prosta, wzdłu

ż

której on działa, zwrot okre

ś

lony jest

poło

ż

eniem grota strzałki, a warto

ść

długo

ś

ci

ą

odcinka wyra

ż

on

ą

jednostkami siły

odniesionymi do jednostek długo

ś

ci np. 1 cm = 1kN.

Jednostkami siły s

ą

N (niuton), kN (kiloniuton), rzadziej MN (meganiuton). Wg defini-

cji , siła

2

1

1

1

s

m

kg

N

=

co oznacza,

ż

e siła jednego niutona wyst

ą

pi wtedy, kiedy masie

1 kg nada si

ę

przyspieszenie 1 m/s

2

.

1.1 Sumowanie i odejmowanie sił

Wektorowe przedstawianie sił umo

ż

liwia szereg działa

ń

takich jak: sumowanie

(składanie) i rozkład. W wyniku sumowania si

ę

sił otrzymujemy sił

ę

wypadkow

ą

, a

wyniku rozkładania otrzymuje si

ę

siły składowe. Na rys.3 pokazano podstawowe

działania na siłach jako wektorach. Z wielko

ś

ciami wektorowymi nierozerwalnie zwi

ą

-

zane jest poj

ę

cie układu współrz

ę

dnych. Prostok

ą

tny układ współrz

ę

dnych umo

ż

liwia

w sposób analityczny zorientowanie na płaszczy

ź

nie lub w przestrzeni odcinka wek-

tora. Ułatwia prowadzenie działa

ń

na wektorach. Na rys.3 pokazano przykłady dzia-

ła

ń

graficznych i analitycznych prowadzonych na wektorach.

A

B

AB

F

r

BA

F

r

l

F

r

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 1

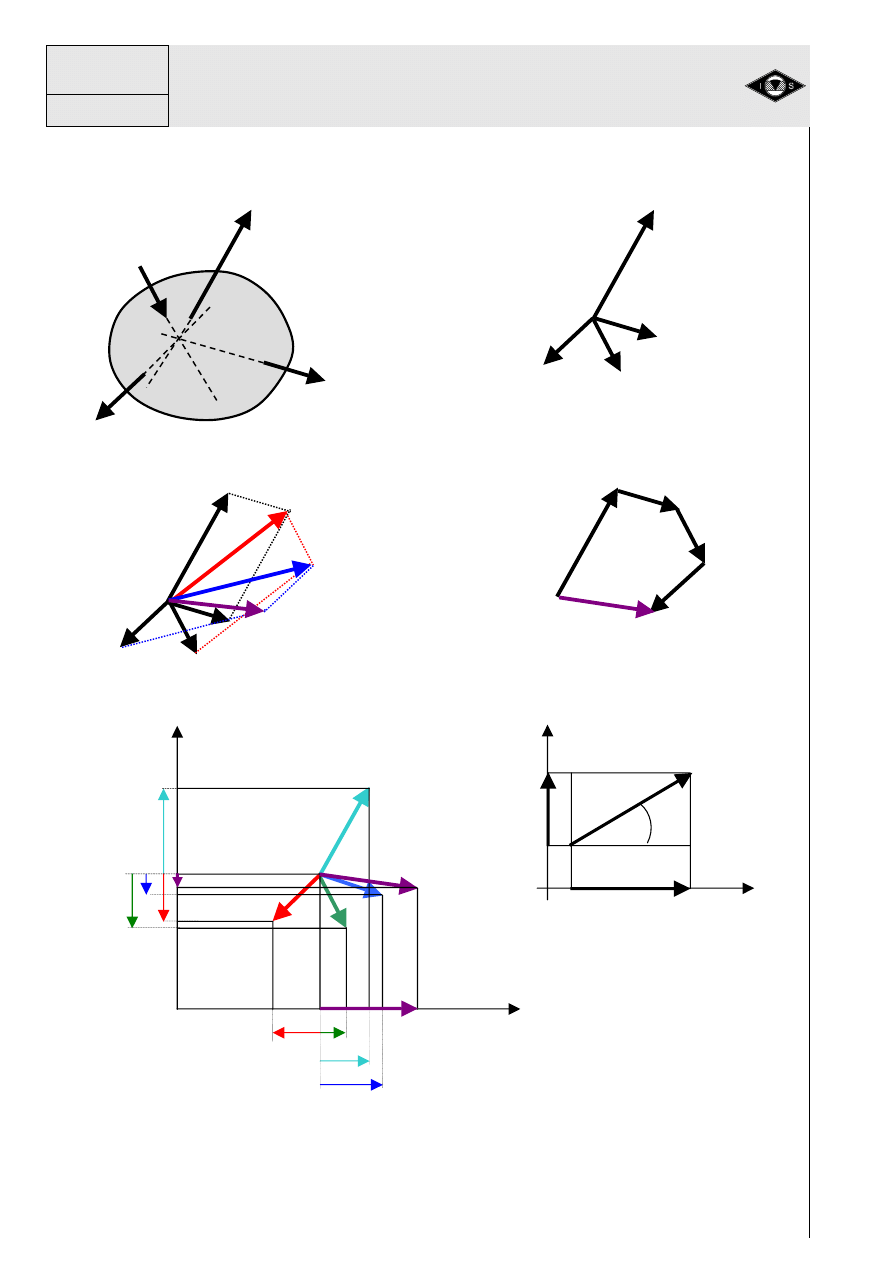
3

Sumowanie sił

Układ zbie

ż

ny

Rys.3. Sposoby składania sił (wektorów)

Na rys.3 na przykładzie układu zbie

ż

nego sił pokazano ró

ż

ne rodzaje działa

ń

na si-

łach a

ś

ci

ś

lej na wektorach. I tak na rys.3a układ sił zbie

ż

nych działa na ciało sztyw-

ne; ka

ż

da z sił działa wzdłu

ż

prostej (kierunku). Na rys.3b pokazano schemat sił w

Siły zbie

ż

ne działaj

ą

ce na

ciało sztywne

Schemat sił zbie

ż

nych

Składanie sił metod

ą

równoległoboku

Składanie sił metod

ą

wieloboku

P

1

P

2

P

3

O

P

4

P

123

P

1

P

2

P

12

O

R=P

1234

O

P

1

P

2

P

3

P

4

R

Składanie sił metod

ą

analityczn

ą

rzuto-

wania w układzie współrz

ę

dnych pro-

stok

ą

tnych

a)

P

1

P

2

P

3

P

4

O

b)

c)

d)

y

x

P

2x

P

3y

P

1

P

2

P

3

P

i

0

P

1y

P

2y

P

iy

P

1x

P

ix

P

3x

R

e)

R

y

R

x

y

x

α

P

r

x

P

r

y

P

r

f)

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 2

4

układzie zbie

ż

nym przecinaj

ą

cych si

ę

w jednym punkcie. Układ sił, w tym układ sił

zbie

ż

nych mo

ż

na zast

ą

pi

ć

jedn

ą

sił

ą

wypadkow

ą

R, która jest rezultatem sumowania

wektorowego. Jednym ze sposobów jest składanie sił metod

ą

równoległoboku, któ-

rego przykład podano na rys. 3c. Zasada polega na tym,

ż

e do danej pierwszej siły w

układzie dodaje si

ę

nast

ę

pn

ą

składaj

ą

c je w postaci równoległoboku np. P

1

+ P

2

.

Suma wektorowa P

12

jest wektorem – odcinkiem (przek

ą

tna równoległoboku) prze-

biegaj

ą

cym od punktu przeci

ę

cia si

ę

składanych sił do wierzchołka utworzonego

przez przeci

ę

cie si

ę

odcinków równoległych do składanych sił

(boków równoległo-

boku). Nale

ż

y przestrzega

ć

zasady,

ż

e długo

ś

ci odcinków musz

ą

by

ć

proporcjonalne

do warto

ś

ci sił i kierunki działania sił musz

ą

by

ć

niezmienne podczas konstruowania

równoległoboku. Najbardziej rozpowszechnion

ą

metod

ą

składania sił przedstawio-

nych w postaci wektorów jest metoda analityczna. Jest wygodna poniewa

ż

nie wy-

maga tworzenia precyzyjnych konstrukcji geometrycznych, które w rzeczywisto

ś

ci

obarczone s

ą

znacznym bł

ę

dem. Przedstawiona j

ą

na rys. 3e. Przykładowo dla

uproszczenia posłu

ż

ono si

ę

płaszczyzn

ą

, na której rozmieszczone s

ą

siły P

1

… P

i

.

Naszym zadaniem jest wyznaczenie siły wypadkowej R, która b

ę

dzie sum

ą

wektoro-

w

ą

sił podanych sił składowych.

i

P

P

P

P

R

r

L

r

r

r

r

3

2

1

+

+

=

(1)

Przestrze

ń

, a wła

ś

ciwie w naszym przypadku płaszczyzna zdefiniowana b

ę

dzie ukła-

dem współrz

ę

dnych prostok

ą

tnych, przy pomocy którego mo

ż

na posługiwa

ć

si

ę

po-

j

ę

ciem rzutu na osie tego układu. Wszystkie siły składowe jako kategorie geome-

tryczne mog

ą

w układzie współrz

ę

dnych podlega

ć

wszystkim zasadom geometrii i

trygonometrii. I tak ka

ż

da z sił (wektorów) b

ę

dzie tworzy

ć

na osiach rzuty (rys.3f),

które b

ę

d

ą

podlega

ć

zasadom sumowania wektorowego (rys. 3f).

y

x

P

P

P

r

r

r

++++

====

(2)

Wykorzystuj

ą

c zasady trygonometrii mo

ż

emy przedstawi

ć

rzuty w postaciach:

αααα

cos

P

P

x

====

r

i

αααα

sin

P

P

y

====

r

(3)

Z twierdzenia Pitagorasa mo

ż

na okre

ś

li

ć

zale

ż

no

ść

pomi

ę

dzy wymiarami rzutów:

2

2

y

x

P

P

P

r

r

++++

====

(4)

Sumowanie analityczne b

ę

dzie zatem polega

ć

na wyznaczeniu analitycznym warto-

ś

ci poszczególnych rzutów na obie osie współrz

ę

dnych. Po ich algebraicznym zsu-

mowaniu z uwzgl

ę

dnieniem znaków (zwrotów) otrzymamy warto

ś

ci rzutów siły wy-

padkowej na obie osie współrz

ę

dnych.

∑

∑

∑

∑

====

====

i

i

ix

x

P

R

1

∑

∑

∑

∑

====

====

i

i

iy

y

P

R

1

-

rzuty wypadkowej

(5)

2

2

y

x

R

R

R

++++

====

-

długo

ść

(warto

ść

wypadkowej)

(6)

αααα

====













x

y

R

R

tg

arc

- k

ą

t orientacji do osi x

(7)

Analityczna zasada sumowania sił (wektorów nie dotyczy tylko układu zbie

ż

nego sił.

Mo

ż

na j

ą

wykorzystywa

ć

równie

ż

w przypadku rozpatrywania układów dowolnych,

przy wyznaczaniu warunków równowagi sił. Zasada ta jest równie

ż

stosowana przy

rozpatrywaniu układów przestrzennych. W celu uproszczenia przedstawiono j

ą

dla

przypadku układu płaskiego (dwuwymiarowego). Siły mo

ż

na równie

ż

odejmowa

ć

.

Polega to na tym,

ż

e wektor odjemnika dodaje si

ę

do wektora z przeciwnym zwrotem

(rys. 4).

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 3

5

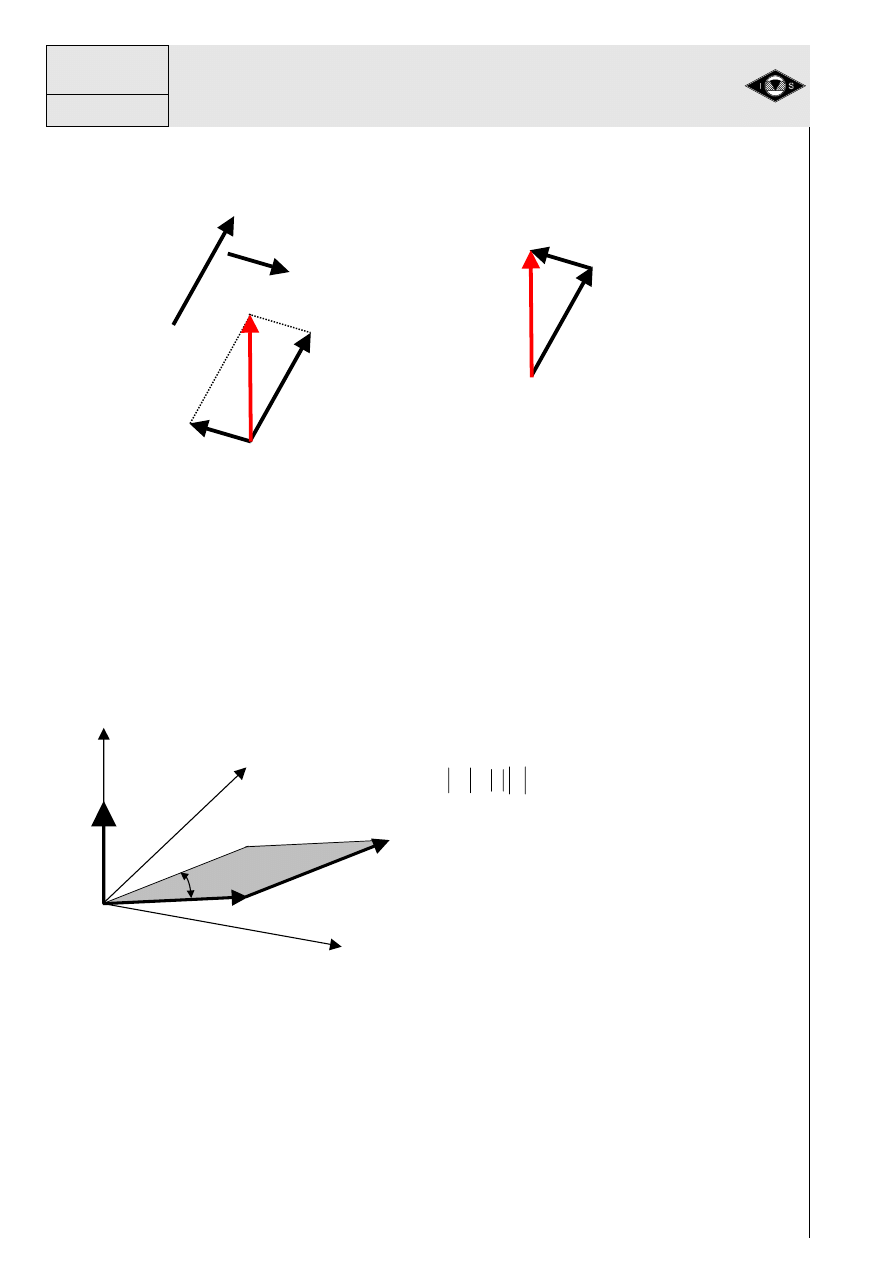
Rys.4 Odejmowanie sił

a) Metod

ą

równoległoboku

b) Metod

ą

wieloboku

1.2 Moment siły

W statyce oprócz sił wyst

ę

puje jeszcze poj

ę

cie momentu siły. Moment siły zdefi-

niowany jest wraz z ramieniem na jakim ta siła oddziaływuje oraz punktem O - biegu-
nem. Moment siły wzgl

ę

dem bieguna O na ramieniu r jest iloczynem wektorowym

wektora siły przez wektor ramienia.

P

r

M

r

r

r

××××

====

(8)

Graficznie iloczyn wektorowy przedstawiono na rys.5.



(9)









Rys. 5 Konstrukcja wektora momentu

Wektor moment skierowany jest prostopadle do płaszczyzny xy, na której le

ż

a wekto-

ry ramienia i siły. Warto

ść

– jego długo

ść

, jest równa powierzchni równoległoboku

okre

ś

lonego wektorami r i P (rys.5). Warto

ść

momentu mo

ż

na wyznaczy

ć

w sposób

analityczny. Przedstawiono to na rys.6

y

x

r

r

P

r

M

r

z

α

αααα

sin

P

r

M

r

r

v

====

Zwrot wektora momentu okre

ś

la reguła

ś

ruby o

gwincie prawoskr

ę

tnym. Je

ś

li na płaszczy

ź

nie

wyznaczonej przez r i P, siła P powoduje obrót
przeciwnie do kierunku wskazówek zegara to ob-
racaj

ą

c

ś

rub

ę

o osi prostopadłej do tej płaszczy-

zny powoduje jej „wykr

ę

canie”. Kierunek prze-

suwania si

ę

ś

ruby okre

ś

la zwrot wektora.

P

1

P

2

P

12

= P

1

– P

2

O

P

1

- P

2

O

P

1

P

2

P

12

= P

1

– P

2

a)

b)

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 4

6

(10)

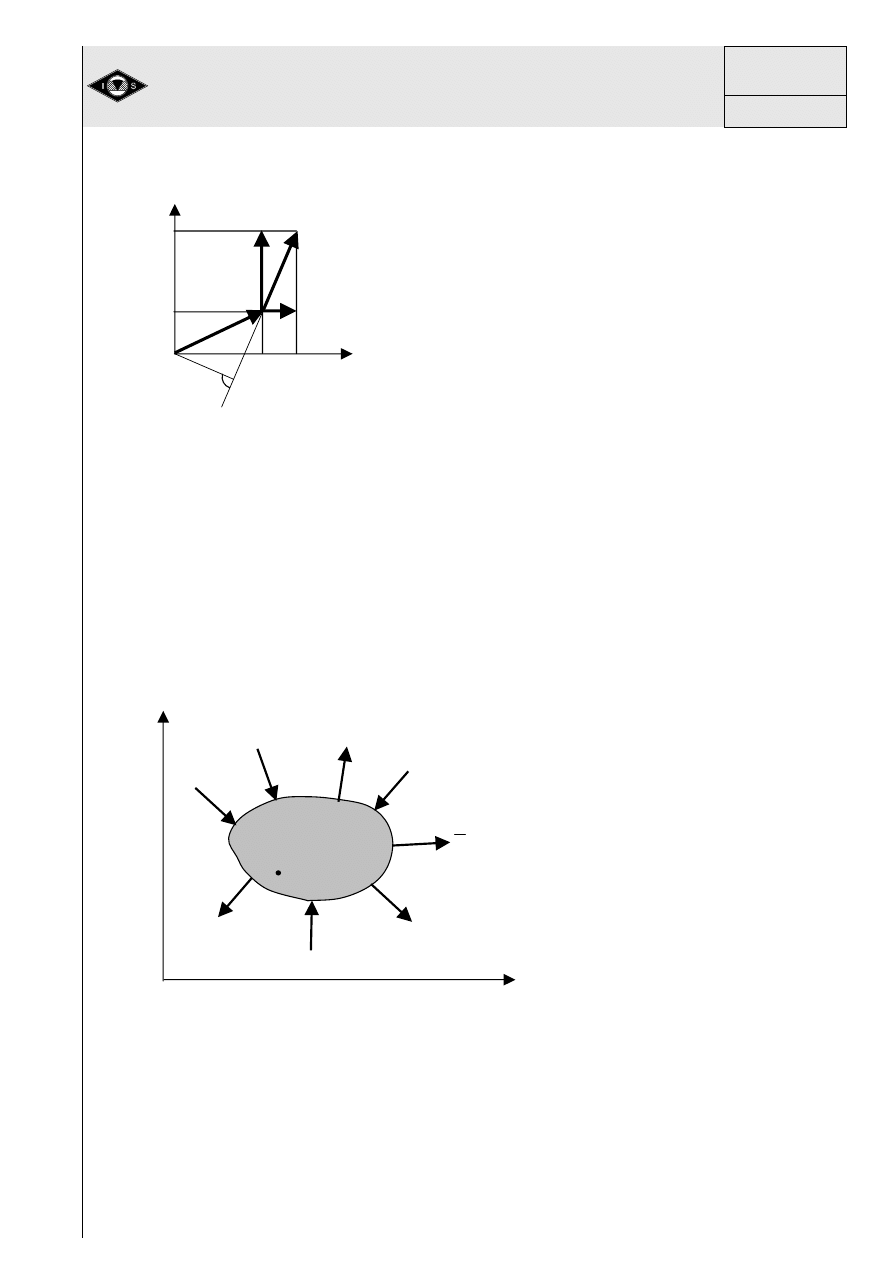
Rys.6 Wyznaczenie warto

ś

ci momentu w układzie współrz

ę

dnych.

1.3 Równowaga sił i momentów

Podstawowym warunkiem rozpatrywania zagadnie

ń

statyki jest równowaga

wszystkich sił działaj

ą

cych na układ. Siły czynne P

k

(oddziaływania i ci

ęż

ar własny)

oraz bierne R

l

(reakcje) musz

ą

si

ę

wzajemnie równowa

ż

y

ć

. Ka

ż

dy układ sił rozpa-

trywa

ć

nale

ż

y w układzie współrz

ę

dnych. Na rys.7 przedstawiono przykładowy układ

sił umieszczony w układzie współrz

ę

dnych. Nale

ż

y podkre

ś

li

ć

,

ż

e przy rozwi

ą

zywaniu

danego zagadnienia nale

ż

y zało

ż

y

ć

układ, którego nie mo

ż

na zmienia

ć

. Zastosowa-

nie układu współrz

ę

dnych umo

ż

liwia przeprowadzenie rzutowania sił wzgl

ę

dem osi

oraz wyznaczenia równowagi momentów wzgl

ę

dem ustalonych w tym układzie punk-

tów. Prawidłowo zało

ż

ony układ statyczny musi zapewni

ć

równowag

ę

sił czynnych i

biernych.

Warunek równowagi rzutów sił na o

ś

x

0

1

1

====

++++

∑

∑

∑

∑

∑

∑

∑

∑

====

====

m

l

lx

n

k

kx

R

P

(11)

Warunek równowagi rzutów sił na o

ś

y

0

1

1

====

++++

∑

∑

∑

∑

∑

∑

∑

∑

====

====

m

l

ly

n

k

ky

P

P

(12)

Warunek równowagi momentów wzgl.
obranego punktu B

(((( ))))

(((( ))))

0

1

1

====

++++

∑

∑

∑

∑

∑

∑

∑

∑

====

====

l

m

l

B

k

n

k

B

R

M

P

M

(13)

Rys.7 Warunki równowagi sił w układzie współrz

ę

dnych

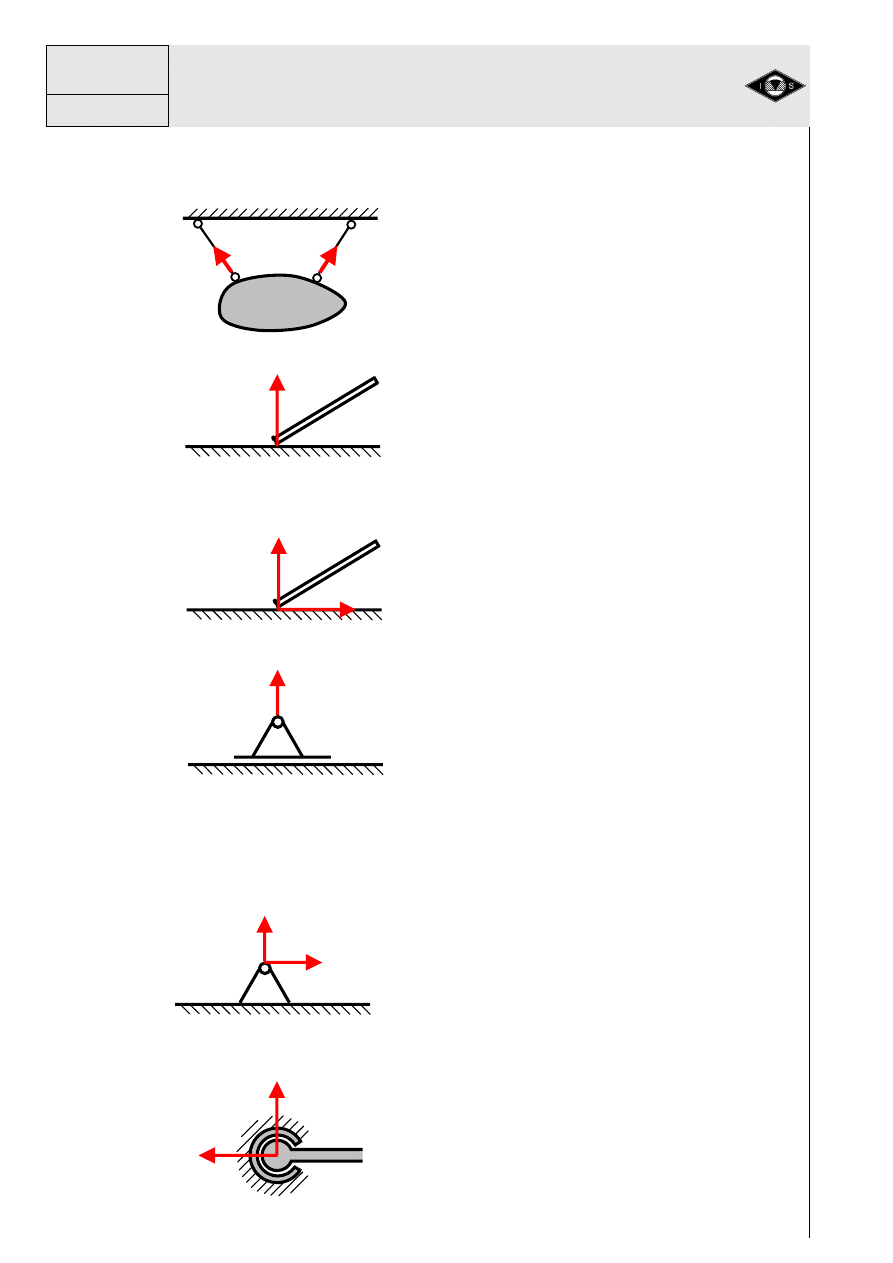
2. Podpory i wi

ę

zy

Podpory oraz wi

ę

zy słu

żą

do utrzymania układu sztywnego w bezruchu; s

ą

zatem

miejscami przyło

ż

enia sił biernych. Prawidłowe zało

ż

enie podpory jest jednym z

czynników tworzeniu modelu statycznego. Od tego zale

ż

y prawidłowe przedstawienie

rzeczywistego układu oddziaływa

ń

i reakcji. Najcz

ęś

ciej spotykane rodzaje podpór to

podpory kierunkowe i przegubowe. Podpory kierunkowe z definicji posiadaj

ą

znane

kierunki reakcji.

h

P

y

P

x

P

M

P

x

P

Y

o

====

−−−−

====

r

r

x

y

P

r

O

x

P

y

P

p

x

p

y

h

x

1

P

r

2

P

r

3

P

r

n

P

y

0

k

P

r

1

R

r

m

R

r

l

R

r

B

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 5

7

a)
Ci

ę

gna

b)
Podpory gładkie




c)
Podpora chropowata (z tarciem)






d)
Podpora przegubowa ruchoma

Rys. 8 Zbiór podpór kierunkowych

a)
Podpora przegubowa stała






b)
Przegub walcowy

1

S

r

2

S

r

Ci

ę

gnami s

ą

liny i ła

ń

cuchy. Kierunki działa-

nia reakcji s

ą

znane

R

Prosta działania reakcji jest prostopa-
dła do powierzchni

N

T

Wyst

ę

puj

ą

dwie reakcje o znanych kie-

runkach. Normalna do powierzchni N i
styczna siła tarcia T.

R

Wektor reakcji jest prostopadły do kie-
runku mo

ż

liwego ruchu.

y

R

x

R

Wektor reakcji a

ś

ci

ś

lej jego kierunek jest nie-

znany. Okre

ś

la si

ę

go po obliczeniu R

y

i R

x

x

R

y

R

Kierunek wektora reakcji jest nieznany .
Wynika z warto

ś

ci składowych R

x

i R

y

.

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 6

8

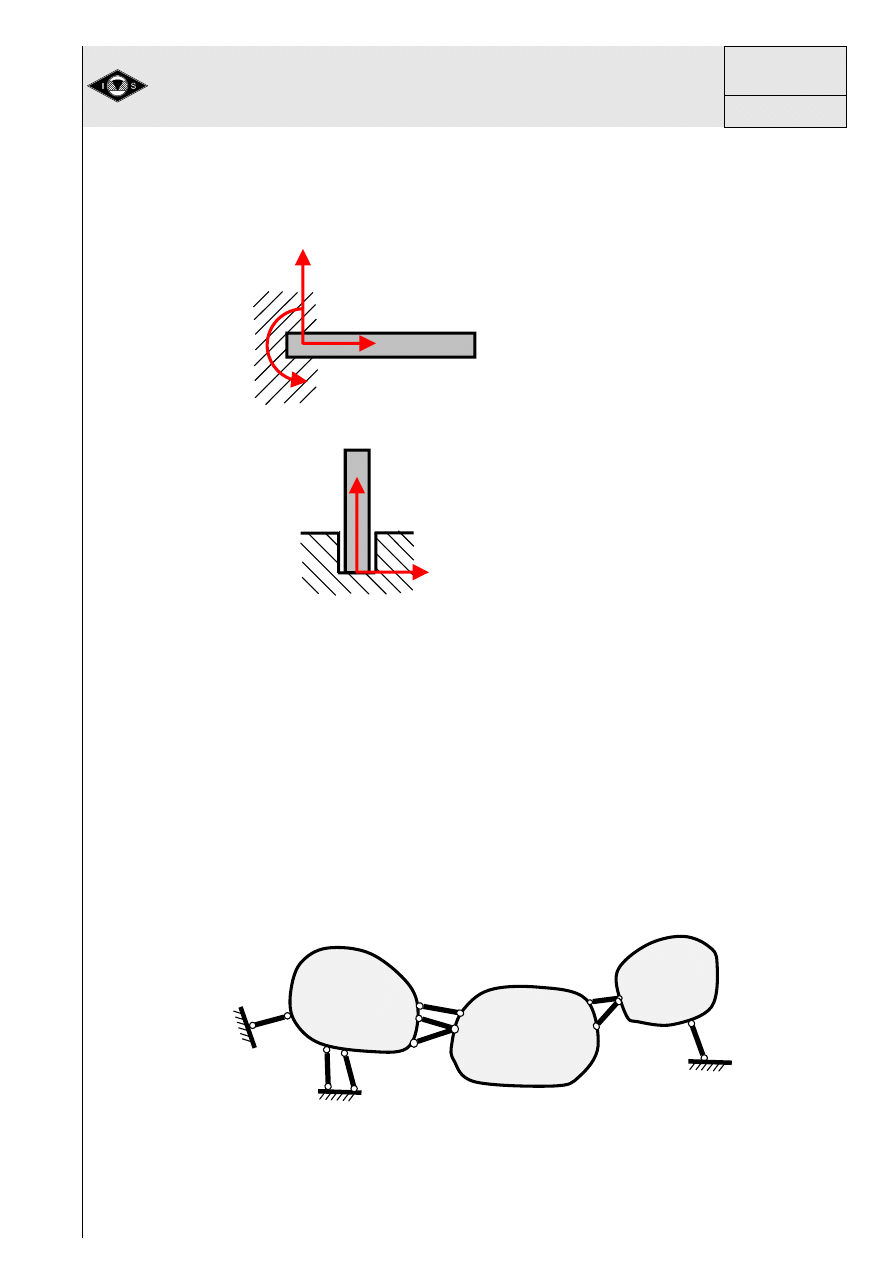
c)
Utwierdzenie








d)
Ło

ż

ysko stopowe

Rys. 9 Podpory przegubowe

3. Geometryczna niezmienno

ść

układu

W układach statycznych cz

ę

sto wyst

ę

puj

ą

elementy materialne poł

ą

czone ze so-

b

ą

strukturami podatnymi posiadaj

ą

cymi mo

ż

liwo

ść

obrotu i przesuni

ę

cia. Cz

ę

sto s

ą

to przeguby. Aby spełni

ć

warunek równowagi statycznej musz

ą

by

ć

one nieruchome

wzgl

ę

dem ł

ą

czonych tych elementów. Aby unieruchomi

ć

elementy w układzie nale-

ż

y poł

ą

czy

ć

go z podło

ż

em trzema pr

ę

tami, nie przecinaj

ą

cymi si

ę

w jednym punkcie

i nierównoległymi. Je

ś

li do takiego systemu doł

ą

czymy nast

ę

pny element poł

ą

czony

równie

ż

trzema pr

ę

tami (tylko z poprzednim elementem albo z elementem i podło-

ż

em) nie przecinaj

ą

cymi si

ę

w jednym punkcie i nierównoległymi, to układ takich

elementów b

ę

dzie geometrycznie niezmienny (rys. 10). W ten sposób układ system

mo

ż

emy rozbudowa

ć

.

Rys. 10 Układ elementów niezmiennych geometrycznie

y

R

x

R

a

M

Kierunek wektora reakcji jest niezna-
ny. Wynika z warto

ś

ci składowych R

x

i

R

y.

. Dodatkowo wyst

ą

pi reakcja mo-

mentu M

a

.

x

R

y

R

Kierunek reakcji wyznaczaj

ą

warto

ś

ci

składowych R

y

i R

y

. Punkt zaczepienie

reakcji jest znany (styk słupa z podło

ż

em)

T-1

T-2

T-3

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 7

9

Poł

ą

czenie elementów T-2 i T-3 za pomoc

ą

dwóch pr

ę

tów nierównoległych mo

ż

na

traktowa

ć

jako przegub, natomiast poł

ą

czenie elementów T-1 i T-2 trzema pr

ę

tami

nierównoległymi i nie przecinaj

ą

cymi si

ę

w jednym punkcie jest poł

ą

czeniem sztyw-

nym. Bior

ą

c powy

ż

sze pod uwag

ę

, mo

ż

na wyprowadzi

ć

prosty wzór okre

ś

laj

ą

cy

geometryczn

ą

niezmienno

ść

układu konstrukcyjnego. Do unieruchomienia jednego

elementu potrzeba trzech pr

ę

tów ł

ą

cz

ą

cych go z podło

ż

em lub z podło

ż

em i z innym

elementem. Zatem w układzie geometrycznie niezmiennym liczba pr

ę

tów musi by

ć

równa trzykrotnej liczbie elementów. Je

ż

eli przez t oznaczymy liczb

ę

elementów, a

przez p liczb

ę

pr

ę

tów to mo

ż

emy napisa

ć

:

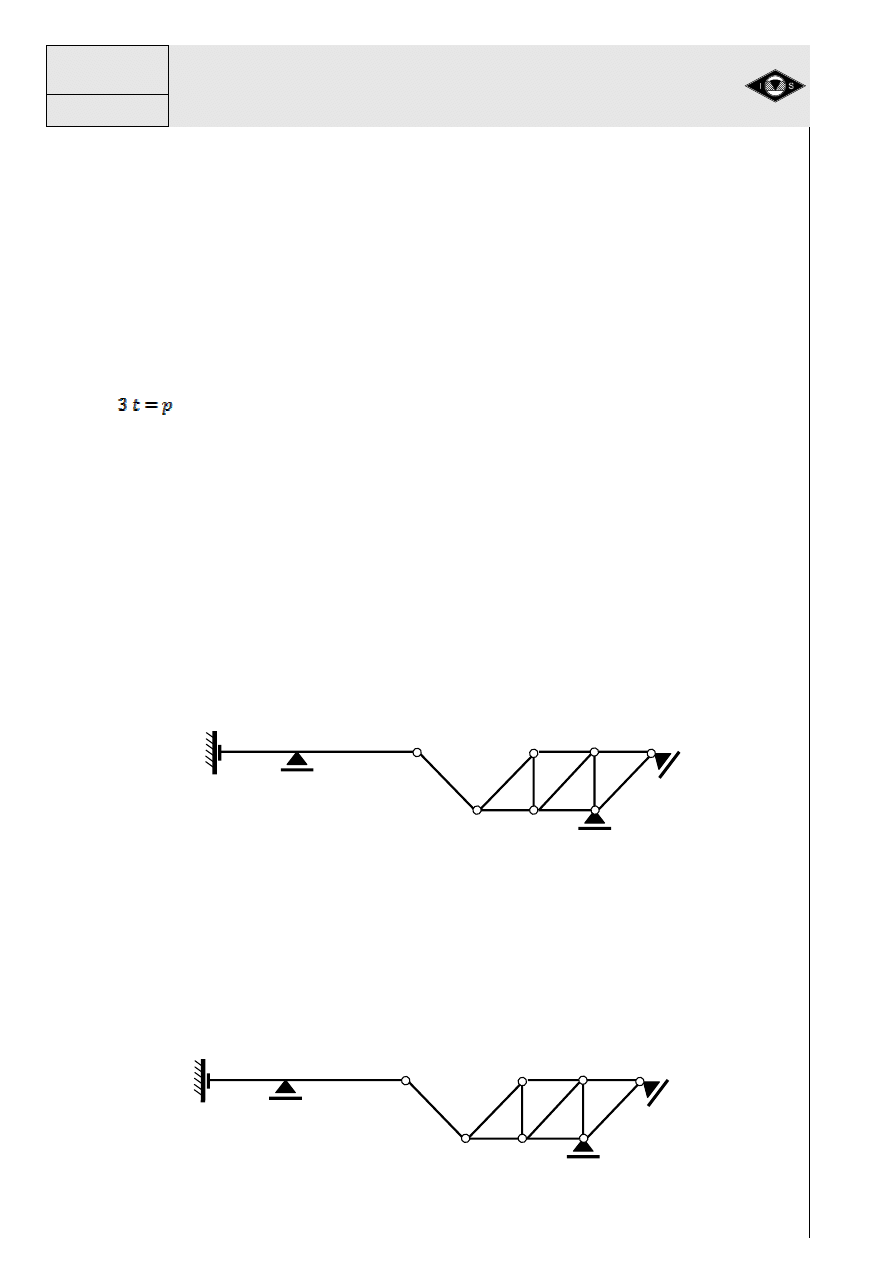
(14)

Spełnienie powy

ż

szego równania jest warunkiem koniecznym, ale nie wystarczaj

ą

-

cym geometrycznej niezmienno

ś

ci układu. Wystarczy bowiem w układzie na rysunku

powy

ż

ej usun

ąć

pr

ę

t ł

ą

cz

ą

cy element T-3 z podło

ż

em i przyło

ż

y

ć

go do elementu T-

2. Liczba pr

ę

tów i tarcz w układzie nie ulegnie zmianie, tak wi

ę

c równanie powy

ż

sze

b

ę

dzie spełnione, chocia

ż

układ b

ę

dzie geometrycznie zmienny (chwiejny). Tarcza T-

3 ma bowiem mo

ż

liwo

ść

obrotu w przegubie.

Buduj

ą

c pr

ę

towe układy konstrukcyjne np. kratownice, post

ę

powa

ć

b

ę

dziemy według

powy

ż

szych zasad, traktuj

ą

c ka

ż

dy pr

ę

t jak wspomniany element. Pami

ę

tamy rów-

nie

ż

o tym,

ż

e trzy pr

ę

ty nierównoległe i nie przecinaj

ą

ce si

ę

w jednym punkcie, pod-

pieraj

ą

ce belk

ę

na jej ko

ń

cu to utwierdzenie, podparcie belki dwoma przecinaj

ą

cymi

si

ę

pr

ę

tami to podpora przegubowa, a podparcie jednym pr

ę

tem - podpora przegu-

bowo przesuwna.
Przykład: Sprawdzi

ć

geometryczn

ą

niezmienno

ść

podanego układu pr

ę

towego (11).

Rys. 11 Układ pr

ę

towy

Ka

ż

d

ą

cz

ęść

układu oddzielon

ą

przegubami traktujemy jako tarcz

ę

(wspomniany ju

ż

element). Liczba tarcz wynosi zatem t = 11. Liczba pr

ę

tów, którymi mo

ż

emy zast

ą

pi

ć

podpory wynosi 2 + 3 = 5. Ka

ż

dy przegub w którym schodz

ą

si

ę

dwie tarcze zast

ę

pu-

jemy dwoma pr

ę

tami, je

ż

eli w przegubie schodzi si

ę

wi

ę

cej tarcz do dla ka

ż

dej tarczy

powy

ż

ej dwóch dodajemy dwa pr

ę

ty. Tak wi

ę

c w naszym układzie liczba pr

ę

tów, któ-

rymi zast

ę

pujemy przeguby jest nast

ę

puj

ą

ca: 2 + 4 + 6 + 4 + 2 + 6 + 4 = 28 (rys.12).

Mamy wi

ę

c: liczba pr

ę

tów 5 + 28 = 33 co jest równe liczbie tarcz pomno

ż

onej przez

trzy. Warunek konieczny geometrycznej niezmienno

ś

ci jest wi

ę

c spełniony.

Rys. 12 Analiza układu pr

ę

towego

2

1

1

1

2

2

4

4

4

6

6

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 8

10

Trzy pr

ę

ty nie przecinaj

ą

ce si

ę

w jednym punkcie i nierównoległe tworz

ą

układ geo-

metrycznie niezmienny. Je

ż

eli taki układ rozbudujemy, doł

ą

czaj

ą

c po dwa pr

ę

ty, tak

aby układ trójk

ą

tów był zachowany, to układ taki dalej b

ę

dzie geometrycznie nie-

zmienny. W ten sposób konstruuje si

ę

kratownice. Układ, b

ę

d

ą

cy kratownic

ą

, mo

ż

na

zatem traktowa

ć

jako jedn

ą

tarcz

ę

. Bior

ą

c to pod uwag

ę

do analizy naszego przykła-

du mo

ż

na by wzi

ąć

trzy tarcze, jak na rysunku poni

ż

ej.

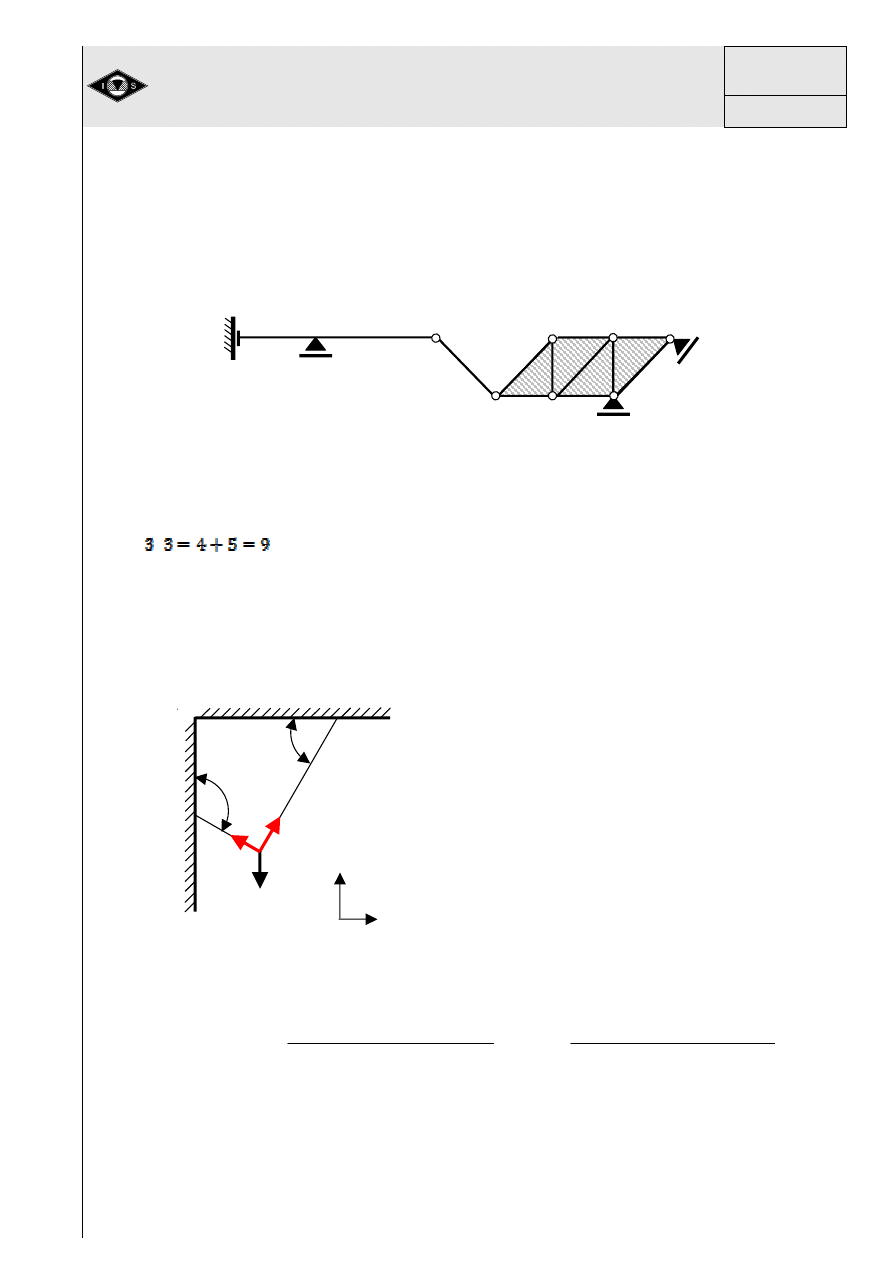
Rys. 13 Układ pr

ę

towo tarczowy

Przy takim podziale równie

ż

spełniony jest warunek geometrycznej niezmienno

ś

ci wg

( 14 ):

4. Przykłady

Przykład 1
1)

Dane: Q,

α

,

β

Szukane: T

A

, T

C

Rozwi

ą

zanie:

Warunki równowagi:

Rzutów sił na o

ś

x:

Rzutów sił na o

ś

y:

Rys. 14 Układ ci

ę

gnowy

Wynik:

x

y

Q

T

A

T

C

A

C

β

α

B

∑

∑

∑

∑

====

====

i

i

ix

P

1

0

,

((((

))))

0

cos

90

cos

====

++++

−−−−

−−−−

αααα

ββββ

A

o

C

T

T

0

1

====

∑

∑

∑

∑

====

i

i

iy

P

,

((((

))))

0

sin

90

sin

====

−−−−

++++

−−−−

Q

T

T

A

o

C

αααα

ββββ

((((

))))

((((

))))

o

o

C

Q

T

90

cos

90

sin

cos

−−−−

++++

−−−−

====

ββββ

ββββ

αααα

,

((((

))))

((((

))))

((((

))))

o

o

o

A

Q

T

90

cos

90

sin

90

cos

−−−−

++++

−−−−

−−−−

====

ββββ

ββββ

ββββ

2

1

1

1

2

2

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 9

11

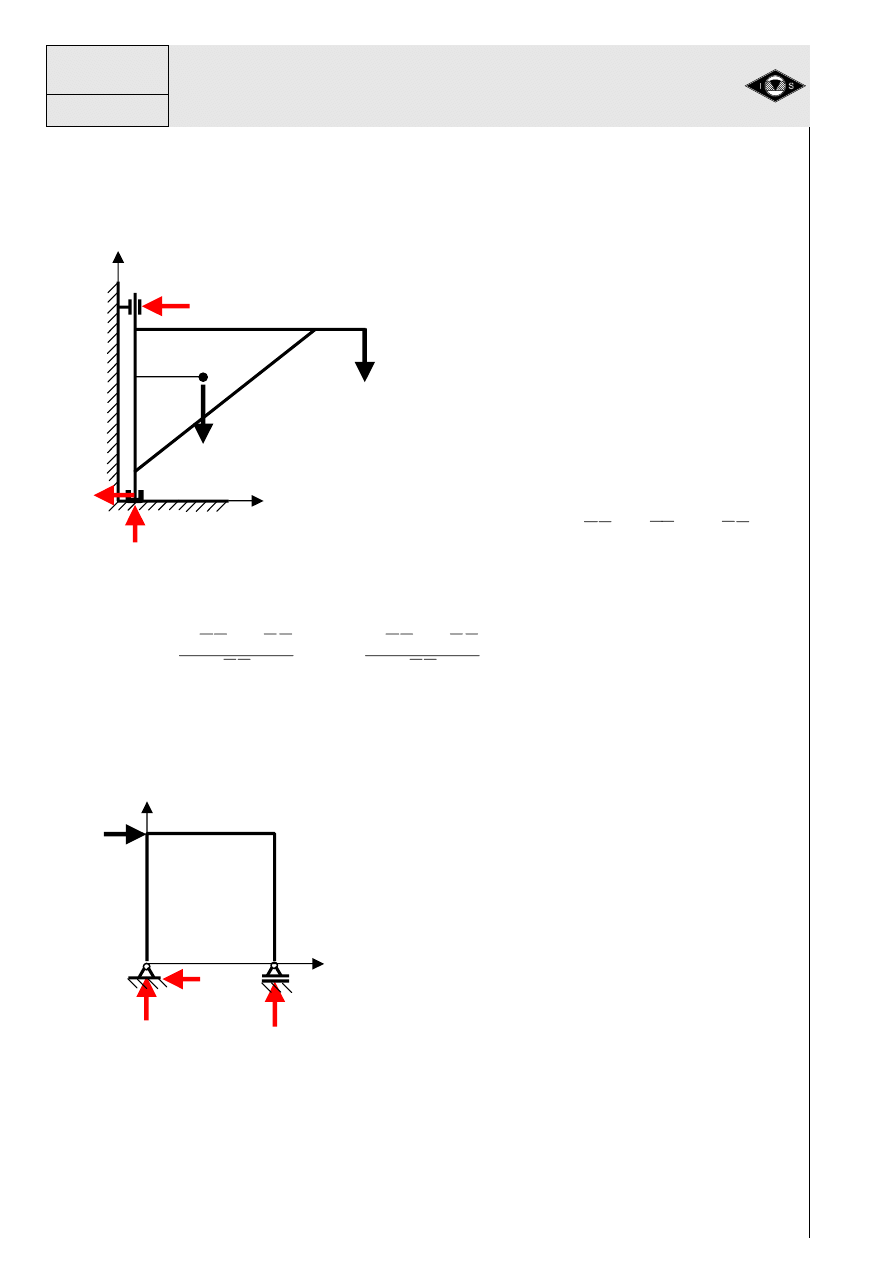
Przykład 2

Dane:

Q, P, wymiary

Szukane:

R

A

, R

B

Warunki równowagi

Rzutów na os x:

Rzutów na o

ś

y:

Momentów wzgl. punktu B:

Rys. 15 Wysi

ę

gnik

Wynik:




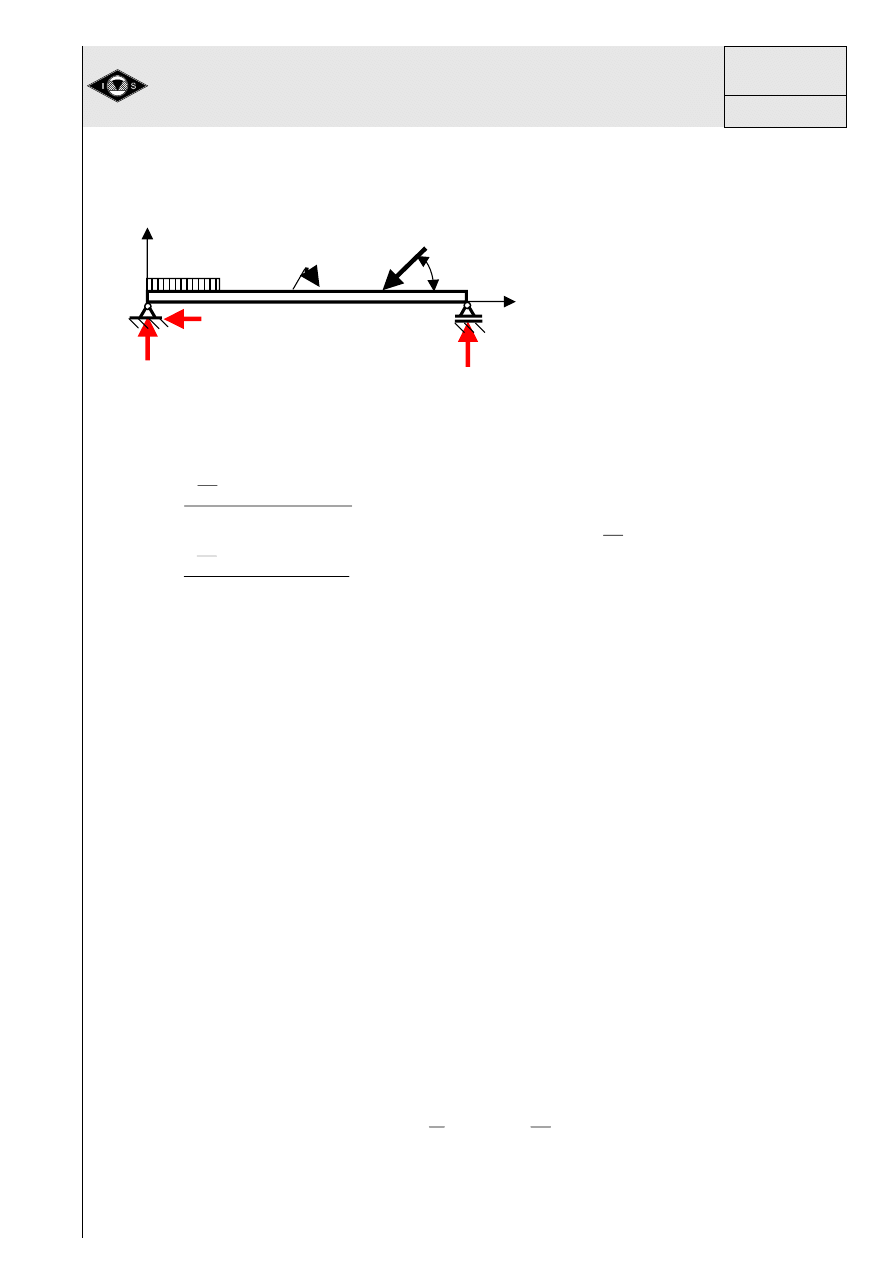
Przykład 3

Dane:

P, AB, BC, CD = a
Szukane:
R

Ay

, R

Ax

, R

Dy

Warunki równowagi

Rzutów na os x:

Rzutów na o

ś

y:

Momentów wzgl. punktu B:

Wynik: R

Ay

= R

Ax

= R

Dy

= P

A

R

A

y

B

R

Bx

R

By

D

Q

C

P

x

E

0

,

0

1

====

−−−−

====

∑

∑

∑

∑

====

i

i

Bx

A

ix

R

R

P

0

,

0

1

====

++++

−−−−

−−−−

====

∑

∑

∑

∑

====

By

i

i

iy

R

P

Q

P

∑

∑

∑

∑

====

====

++++

−−−−

−−−−

====

i

i

A

iB

B

A

R

A

C

P

E

D

Q

M

1

0

,

0

P

Q

R

B

A

C

A

P

E

D

Q

R

B

A

C

A

P

E

D

Q

R

By

Bx

A

++++

====

++++

====

++++

====

,

,

0

,

0

1

====

−−−−

====

∑

∑

∑

∑

====

i

i

Ax

ix

R

P

P

0

,

0

1

====

++++

====

∑

∑

∑

∑

====

Dy

Ay

i

i

iy

R

R

P

∑

∑

∑

∑

====

====

−−−−

====

i

i

Dy

iA

a

P

a

R

M

1

0

,

0

A

R

Ay

R

Ax

D

R

Dy

P

B

C

y

x

Rys. 16 Rama

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 10

12

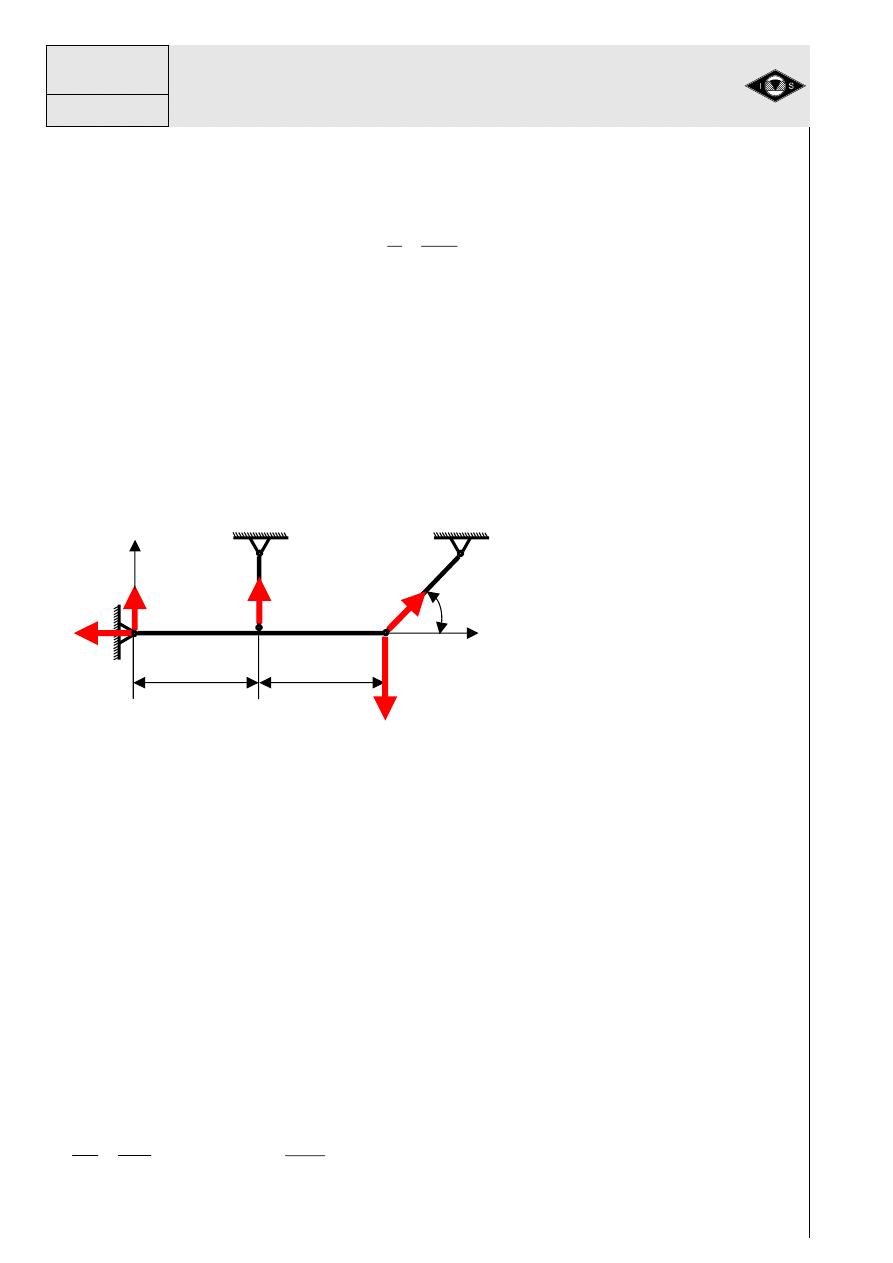
Przykład 4

Dane:

Q, M, P, AB=BC=CD=DE=a

Szukane:

R

Ay

, R

Ax

, R

Ey

Warunki równowagi
Rzutów na os x:

Rzutów na o

ś

y:

Momentów wzgl. punktu A:

5. Układy statycznie niewyznaczalne

W przypadku, kiedy liczba równa

ń

równowagi jest mniejsza od liczby sił we-

wn

ę

trznych, to konstrukcje takie s

ą

nierozwi

ą

zywalne przy zastosowaniu trzech rów-

na

ń

równowagi statyki ciał doskonale sztywnych i nosz

ą

nazw

ę

układów statycznie

niewyznaczalnych.
Do obliczenia niewiadomych sił nale

ż

y wtedy dodatkowo uwzgl

ę

dni

ć

odkształcenia i

przemieszczenia pr

ę

tów. Uzyskane w ten sposób dodatkowe równania współzale

ż

-

no

ś

ci odkształce

ń

stanowi

ą

zale

ż

no

ś

ci o charakterze geometrycznym i uzupełniaj

ą

liczb

ę

równa

ń

. W celu poł

ą

czenia równa

ń

równowagi z równaniami geometrycznymi

nale

ż

y posłu

ż

y

ć

si

ę

zwi

ą

zkami fizycznymi uzale

ż

niaj

ą

cymi wzajemnie siły wewn

ę

trz-

ne i przemieszczenia. W przypadku materiałów liniowo spr

ęż

ystych zwi

ą

zki te wyni-

kaj

ą

bezpo

ś

rednio z prawa Hooke'a.

Prawo Hooke’a jest podstaw

ą

zale

ż

no

ś

ci

ą

teorii spr

ęż

ysto

ś

ci, która wi

ąż

e zale

ż

no-

ś

ci

ą

proporcjonalno

ś

ci odkształcenie i siły. Podstawowa zale

ż

no

ść

przedstawia si

ę

nast

ę

puj

ą

co:

εεεε

σσσσ

E

====

(15)

gdzie:

σ

- napr

ęż

enie [MPa],

E – [MPa] wsp. proporcjonalno

ś

ci; moduł spr

ęż

ysto

ś

ci podłu

ż

nej

(moduł Younge’a)

ε

- wielko

ść

bezwymiarowa odkształcenie wzgl

ę

dne

Przedstawione wielko

ś

ci mo

ż

na przedstawia

ć

w ró

ż

ny sposób:

A

P

====

σσσσ

oraz

l

l

∆∆∆∆

====

εεεε

(16)

gdzie: P – siła [N]

A- pole powierzchni przekroju [mm

2

]

∆

l – wydłu

ż

enie elementu pod działaniem siły P [mm]

0

cos

,

0

1

====

−−−−

−−−−

====

∑

∑

∑

∑

====

αααα

P

R

P

i

i

Ax

ix

0

sin

,

0

1

====

++++

−−−−

−−−−

====

∑

∑

∑

∑

====

Ey

Ay

i

i

iy

R

P

a

q

R

P

αααα

∑

∑

∑

∑

====

====

++++

−−−−

−−−−

−−−−

====

i

i

Ey

iA

a

R

a

P

M

a

q

M

1

2

0

4

3

sin

2

,

0

αααα

Wynik:

αααα

cos

P

R

Ax

====

a

a

P

M

a

q

R

Ey

4

3

sin

2

2

αααα

++++

++++

====

αααα

αααα

sin

4

3

sin

2

2

P

qa

a

a

P

M

a

q

R

Ay

++++

++++

++++

++++

====

x

A

R

Ay

R

Ax

E

R

Ey

q

M

P

B

C

D

α

y

Rys. 17 Belka

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 11

13

l – długo

ść

pocz

ą

tkowa elementu [mm]

Prawo Hooke’a mo

ż

na przedstawi

ć

w rozwini

ę

tej formie:

l

l

E

A

P

∆

=

(17)

Układy statyczne, w których liczba niewiadomych (składowych reakcji) jest wi

ę

ksza

od liczby równa

ń

równowagi nazywamy statycznie niewyznaczalnymi. Przykładami

takich układów b

ę

d

ą

: belki wieloprz

ę

słowe (o trzech lub wi

ę

cej podporach), belki

dwustronnie utwierdzone, belki jednym ko

ń

cem utwierdzone, a na drugim podparte

etc. W tych belkach okre

ś

lenie reakcji b

ą

d

ź

sił wewn

ę

trznych tylko na podstawie

równa

ń

równowagi nie jest mo

ż

liwe. Do ich wyznaczenia nale

ż

y uwzgl

ę

dni

ć

od-

kształcenie tych konstrukcji wykorzystuj

ą

c zale

ż

no

ś

ci geometryczne pomi

ę

dzy tymi

odkształceniami. Najlepiej zilustrowa

ć

to na przykładzie.

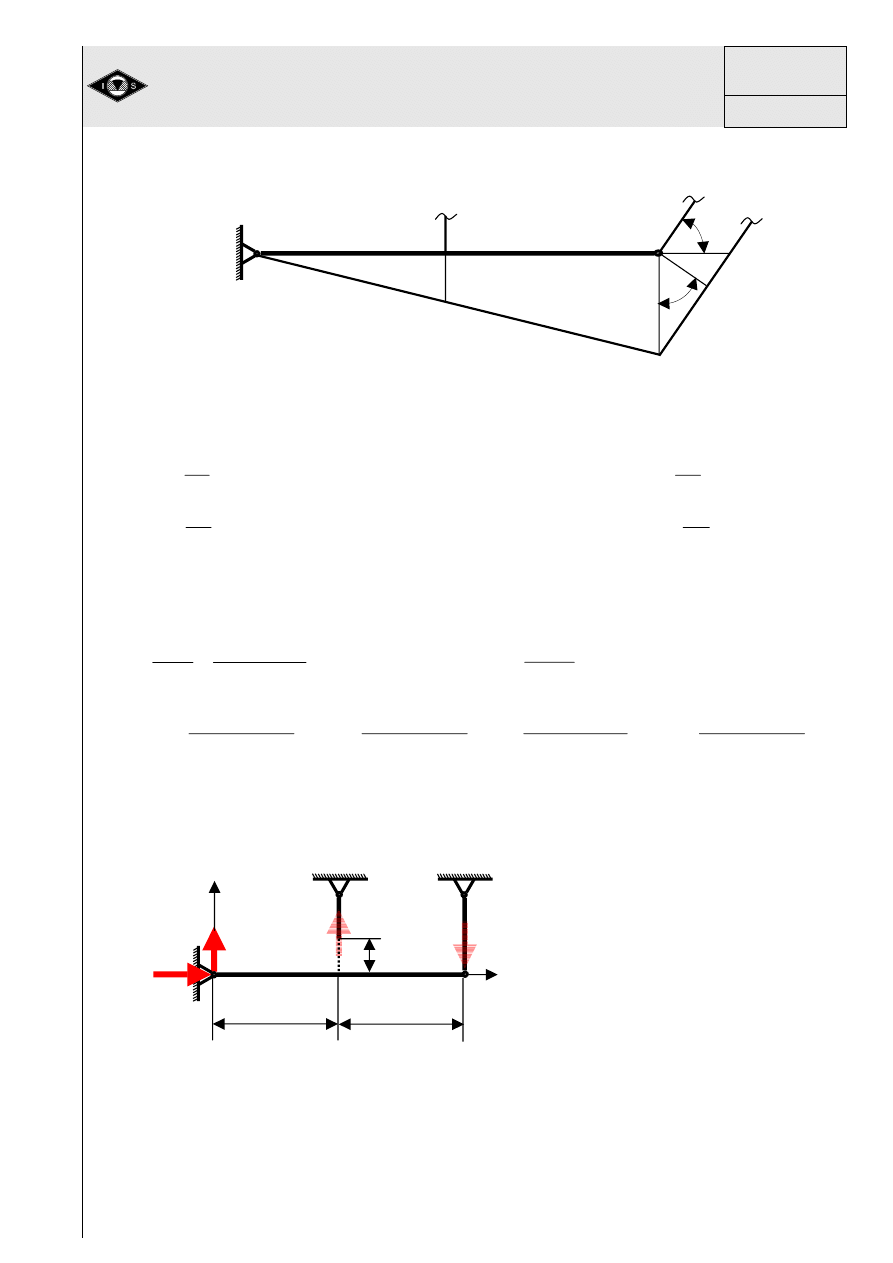
Przykład 5











Przykład stanowi pr

ę

t umocowany przegubowo w podporze stałej O, zawieszony na

dwóch sztywnych ci

ę

gnach 1 i 2 równie

ż

umocowanych przegubowo.

Warunki równowagi:

0

cos

,

0

2

1

====

++++

−−−−

====

∑

∑

∑

∑

====

αααα

N

R

P

i

i

x

ix

(a)

0

sin

,

0

2

1

1

====

−−−−

++++

++++

====

∑

∑

∑

∑

====

P

N

N

R

P

i

i

y

iy

αααα

(b)

∑

∑

∑

∑

====

====

−−−−

++++

====

i

i

iO

a

P

a

N

a

N

M

1

2

1

0

2

2

sin

,

0

αααα

(c)

Dla wyznaczenia czwartego równania wykorzysta

ć

nale

ż

y podstawowy zwi

ą

zek teorii

spr

ęż

ysto

ś

ci, mianowicie prawo Hooke’a. Wi

ąż

e ono w zale

ż

no

ść

proporcjonalno

ś

ci

napr

ęż

enia i odkształcenia. Nale

ż

y zatem przy pomocy zale

ż

no

ś

ci geometrycznych

wyznaczy

ć

przemieszczenia, które wyst

ą

piły w elemencie pod działaniem sił.

Pod działaniem siły P pr

ę

t OAB ulega przemieszczeniu do pozycji O A

1

B

1

. Przy za-

ło

ż

eniu pełnej sztywno

ś

ci i jego nieodkształcalno

ś

ci po odkształceniu jest on lini

ą

prost

ą

. Ci

ę

gna N

1

i N

2

wydłu

żą

si

ę

odpowiednio o

∆

l

1

i

∆

l

2

. Mamy wtedy zale

ż

no

ś

ci

geometryczne wynikaj

ą

ce z twierdzenia Talesa:

a

BB

a

l

2

1

1

====

∆∆∆∆

odcinek

ββββ

sin

2

1

l

BB

∆∆∆∆

====

Rys. 18 Układ pr

ę

towy sta-

tycznie niewyznaczalny

a

a

1

2

N

1

N

2

R

y

R

x

y

x

α

P

O

Istniej

ą

zatem trzy równania równowagi ale

cztery niewiadome: R

x

, R

y

, N

1

, i N

2

. Dla

wyznaczenia

wszystkich

niewiadomych

konieczne jest jeszcze znalezienie jednego
czwartego równania.

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 12

14

Rys.19 Zale

ż

no

ś

ci geometryczne przemieszcze

ń

Napr

ęż

enia w pr

ę

tach wynios

ą

odpowiednio:

1

1

1

A

N

====

σσσσ

a wykorzystuj

ą

c prawo Hooke’a,

1

1

εεεε

σσσσ

E

====

i dalej,

1

1

1

l

l

E

∆∆∆∆

====

σσσσ

1

2

2

A

N

====

σσσσ

a wykorzystuj

ą

c prawo Hooke’a,

2

2

εεεε

σσσσ

E

====

i dalej,

2

2

2

l

l

E

∆∆∆∆

====

σσσσ

Zakładaj

ą

c,

ż

e materiał pr

ę

tów 1 i 2 ma taki sam moduł spr

ęż

ysto

ś

ci podłu

ż

nej i ten

sam przekrój A, po przekształceniu otrzymamy zwi

ą

zek fizyczny pomi

ę

dzy siłami N

1

a N

2

, który b

ę

dzie czwartym równaniem uzupełniaj

ą

cym układ utworzony z warun-

ków równowagi sił:

EA

a

l

N

EA

a

l

N

αααα

sin

2

2

2

1

1

====

a po uproszczeniu

αααα

sin

2

2

2

1

1

l

N

l

N

====

(d)

Rozwi

ą

zuj

ą

c układ równa

ń

(a, b, c, d) o czterech niewiadomych otrzymamy wyniki:

αααα

2

1

2

2

1

sin

4

2

l

l

l

P

N

++++

====

,

αααα

2

1

2

1

1

sin

4

4

l

l

l

P

N

++++

====

,

αααα

αααα

2

1

2

1

sin

4

2

sin

4

l

l

l

P

R

x

++++

====

,

αααα

2

1

2

2

sin

4

l

l

l

P

R

y

++++

−−−−

====

Kolejny przykład dotyczy napr

ęż

e

ń

monta

ż

owych wynikaj

ą

cych z niedokładno

ś

ci

elementów składowych. Na rys. 20 pokazano schemat układu pr

ę

towego z pokaza-

nymi niedokładno

ś

ciami poszczególnych elementów.

Rys.20 Schemat układu monta

ż

owego

0

,

0

1

====

====

∑

∑

∑

∑

====

i

i

x

ix

R

P

(a’)

0

,

0

2

1

1

====

−−−−

++++

====

∑

∑

∑

∑

====

N

N

R

P

i

i

y

iy

(b’)

∑

∑

∑

∑

====

====

−−−−

====

i

i

iO

a

N

a

N

M

1

2

1

0

2

,

0

(c’)

α

O

α

A

1

A

B

1

B

C

∆

l

1

∆

l

2

1

2

a

a

1

2

N

1

N

2

R

y

R

x

y

O

δ

A

B

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 13

15

Jak wida

ć

na rys. 20 niedokładno

ść

monta

ż

owa

δ

wynika z zastosowania zbyt krót-

kiego pr

ę

ta 1. Naci

ą

gni

ę

cie tego pr

ę

ta do utworzenia poł

ą

czenia z belk

ą

OAB spo-

woduje napi

ę

cia N

1

i N

2

w pr

ę

tach 1 i 2 oraz przemieszczenie belki. Wyst

ą

pi

ą

nie-

wiadome reakcje w podporze O i wspomniane ju

ż

napi

ę

cia. I w tym przypadku ujaw-

nia si

ę

układ statycznie niewyznaczalny. Mamy trzy równania równowagi i cztery nie-

wiadome: R

x

, R

y

, N

1

i N

2

. Konieczna jest zatem dodatkowa zale

ż

no

ść

wi

ążą

ca wa-

runki geometryczne i siłowe. Zakładamy,

ż

e belka OAB jest nieodkształcalna i nie-

wa

ż

ka, natomiast pr

ę

ty 1 i 2 o tej samej długo

ś

ci, przekroju i z tego samego materia-

łu s

ą

niewa

ż

kie ale odkształcalne w zale

ż

no

ś

ci liniowej Hooke’a. Po naci

ą

gni

ę

ciu

pr

ę

ta 1 układ przedstawiony na rys.20 przyjmie posta

ć

(rys.21).

Zale

ż

no

ś

ci geometryczne:

1

l

∆∆∆∆

−−−−

====

∆∆∆∆

δδδδ

a

l

a

l

2

2

1

∆∆∆∆

====

∆∆∆∆

−−−−

δδδδ

(d’)

Zale

ż

no

ś

ci fizyczne:

EA

l

N

l

1

1

====

∆∆∆∆

,

EA

l

N

l

2

2

====

∆∆∆∆

Rys.12 Układ statycznie niewyznaczalny po zaczepieniu ci

ę

gien 1 i 2 do belki.

Do równania (d’) tworz

ą

cego zale

ż

no

ść

geometryczn

ą

nale

ż

y podstawi

ć

zale

ż

no

ś

ci

fizyczne i nast

ę

pnie rozwi

ą

za

ć

układ równa

ń

a’, b’, c’ i d’. Wynik przyjmie posta

ć

:

0

====

x

R

,

EA

l

R

y

δδδδ

5

2

−−−−

====

,

EA

l

N

δδδδ

5

4

1

====

,

EA

l

N

δδδδ

5

2

2

====

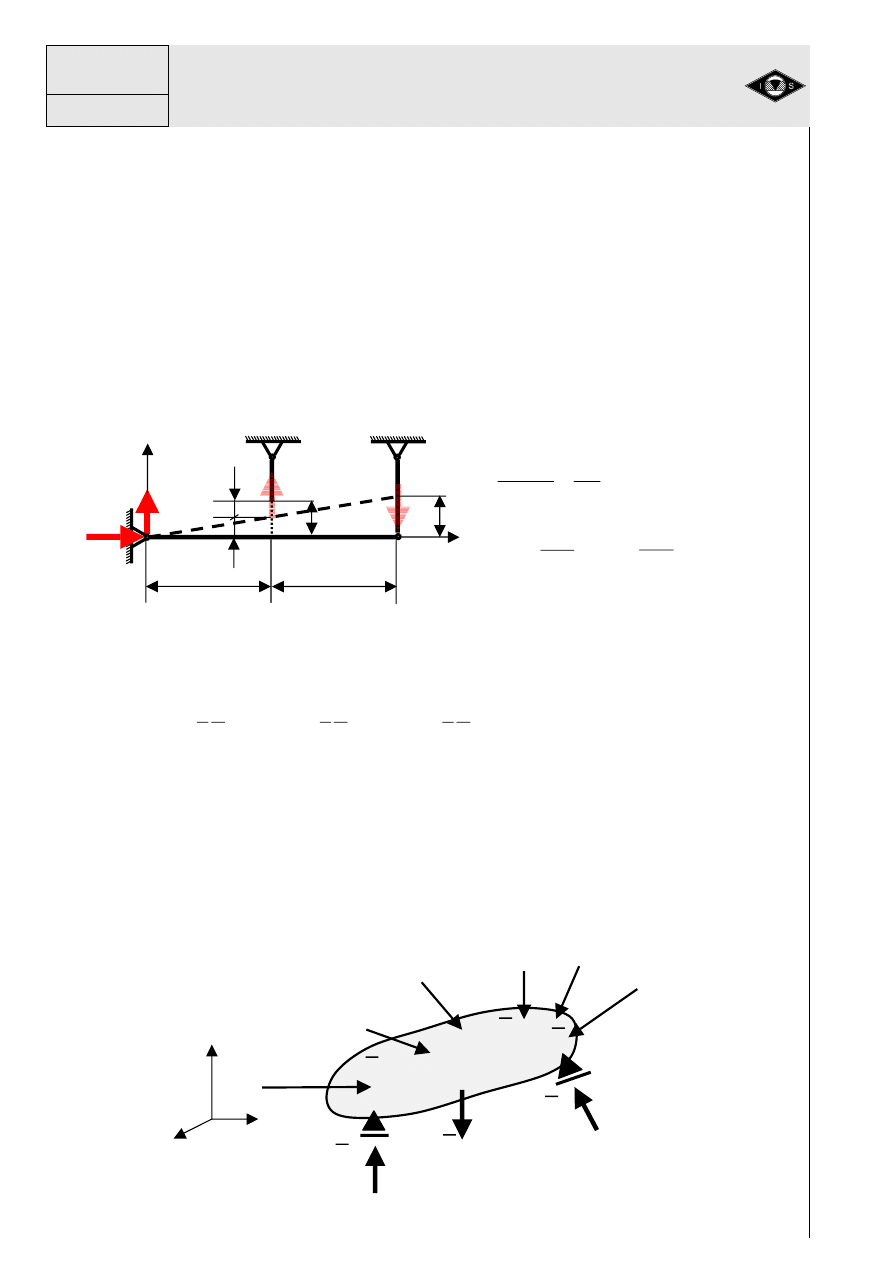
6. Napr

ęż

enia jako efekt obci

ąż

e

ń

zewn

ę

trznych

Siłami zewn

ę

trznymi nazywamy siły, które zast

ę

puj

ą

działanie sił oddziałuj

ą

-

cych na rozpatrywane ciało, przy izolowaniu tego ciała od innych, pierwotnie z nim
poł

ą

czonych. Wyst

ę

puj

ą

one jako tzw. siły czynne obci

ąż

aj

ą

ce ciało i jako reakcje

wi

ę

zów, tzw. siły bierne. Siłami czynnymi b

ę

d

ą

: ci

ęż

ar całkowity ciała stałego lub ci

ę

-

ż

ary cz

ą

stkowe w zło

ż

onych układach mechanicznych, siły dynamiczne działaj

ą

ce

przez okre

ś

lony czas i wynikaj

ą

ce z ruchu mas. Siłami biernymi s

ą

reakcje w wi

ę

zach

i podporach. Na rys. 22 pokazano uogólniony układ mechaniczny b

ę

d

ą

cy w równo-

wadze statycznej.

Rys.22 Uogólniony układ mechaniczny w równowadze statycznej

a

a

1

2

N

1

N

2

R

y

R

x

y

O

δ

A

B

∆

l

1

∆

∆

l

2

B’

A’

P

1

P

n

P

i

x

y

x

R

A

Q

R

B

A

B

O

G

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 14

16

W przestrzeni opisanej układem współrz

ę

dnych prostok

ą

tnych O,x,y,x istnieje ciało

stałe Q, na które oddziaływaj

ą

siły zewn

ę

trzne P

1

… P

n

, ci

ęż

ar własny G i reakcje R

A

i R

B

, b

ę

d

ą

ce w równowadze statycznej. Ciało stałe Q jako pewna ci

ą

gło

ść

materialna

jest elementem ł

ą

cz

ą

cym obszar oddziaływania wszystkich sił. W rezultacie w jego

obj

ę

to

ś

ci wyst

ą

pi

ą

jakie

ś

siły, które b

ę

d

ą

ł

ą

czy

ć

układ w pewn

ą

zrównowa

ż

on

ą

ca-

ło

ść

. Siły te nazywa si

ę

siłami wewn

ę

trznymi lub napi

ę

ciami. Aby je wyznaczy

ć

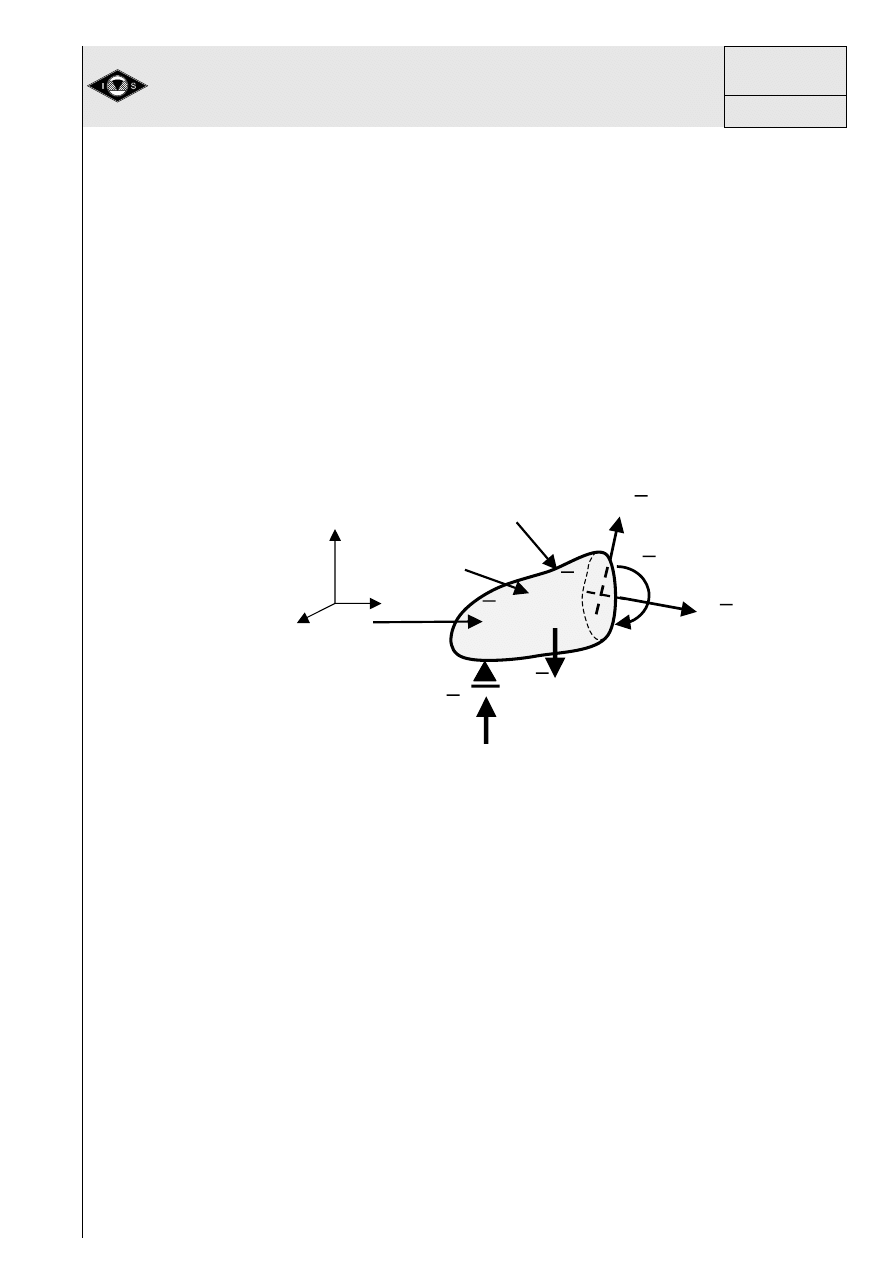
nale-

ż

y je „uzewn

ę

trzni

ć

” poprzez przeci

ę

cie ciała Q, odrzucenie odci

ę

tej cz

ęś

ci i zało

ż

e-

nie w przekroju sił wewn

ę

trznych (rys.23). Po odrzuceniu, w naszym przypadku cz

ę

-

ś

ci lewej, nale

ż

y w utworzonym przekroju zało

ż

y

ć

siły wewn

ę

trzne: normaln

ą

N,

styczn

ą

T i moment M. Nowy układ musi równie

ż

spełnia

ć

warunki równowagi sta-

tycznej. Mo

ż

na z tego wywnioskowa

ć

,

ż

e w ró

ż

nych przekrojach i ich poło

ż

eniach siły

wewn

ę

trzne mog

ą

si

ę

ró

ż

ni

ć

. Wykonuj

ą

cy obliczenia sprawdzaj

ą

ce musi zatem wy-

bra

ć

przekrój, w którym te siły mog

ą

by

ć

najwi

ę

ksze – b

ę

dzie to przekrój niebez-

pieczny. Jest najwa

ż

niejszy element pracy projektanta i decyduj

ą

cy o bezpiecze

ń

-

stwie eksploatacji konstrukcji.

Rys.23 Ujawnienie sił wewn

ę

trznych

Dla wygody i zwi

ę

kszenia wydajno

ś

ci oblicze

ń

siły wewn

ę

trzne odnosi si

ę

do rozpa-

trywanego przekroju. Tak przekształcone siły wewn

ę

trzne nazywamy napr

ęż

eniami.

Jednostkami napr

ęż

e

ń

s

ą

: MPa, N/mm

2

. W napr

ęż

eniach i ich jednostkach wyra

ż

ane

s

ą

parametry materiałowe takie jak: granica plastyczno

ś

ci lub wytrzymało

ść

na roz-

ci

ą

ganie. Mo

ż

na wtedy łatwo porówna

ć

wyniki oblicze

ń

wytrzymało

ś

ciowych z warto-

ś

ciami granicznymi dla danych materiałów rzeczywistych.

W odniesieniu do przekroju wyst

ę

puj

ą

dwa rodzaje napr

ęż

e

ń

: napr

ęż

enia normalne

(

σ)

i styczne (

τ).

Okre

ś

lenie warto

ś

ci napr

ęż

e

ń

normalnych

σσσσ

i stycznych

ττττ

w po-

szczególnych punktach przekroju jest podstawowym zadaniem wytrzymało

ś

ci mate-

riałów. Cz

ę

sto rozkład tych napr

ęż

e

ń

nie jest równomierny na przekroju i wtedy nale-

ż

y wyznaczy

ć

funkcje, które okre

ś

laj

ą

warto

ś

ci tych napr

ęż

e

ń

w ró

ż

nych punktach

przekroju.
Siły wewn

ę

trzne b

ę

d

ą

zale

ż

e

ć

od rozkładu i warto

ść

i oddziaływa

ń

zewn

ę

trznych.

Jednym z zada

ń

statyki jest wyznaczenie rozkładów i warto

ś

ci sił wewn

ę

trznych, któ-

re jest kolejnym krokiem w wyznaczaniu stanów napr

ęż

e

ń

w poszczególnych prze-

krojach.
Jednym z najprostszych stanów napr

ęż

e

ń

jest stan napr

ęż

e

ń

rozci

ą

gaj

ą

cych. Jest

wynikiem oddziaływania sił rozci

ą

gaj

ą

cych na element ci

ę

gnowy sztywny lub wiotki.

Warunkiem jednoosiowego stanu napr

ęż

e

ń

jest poło

ż

enie siły czynnej i biernej w

jednej osi prostopadle do przekroju niebezpiecznego (rys.24).

P

i

T

M

x

y

x

O

R

A

A

P

1

N

G

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 15

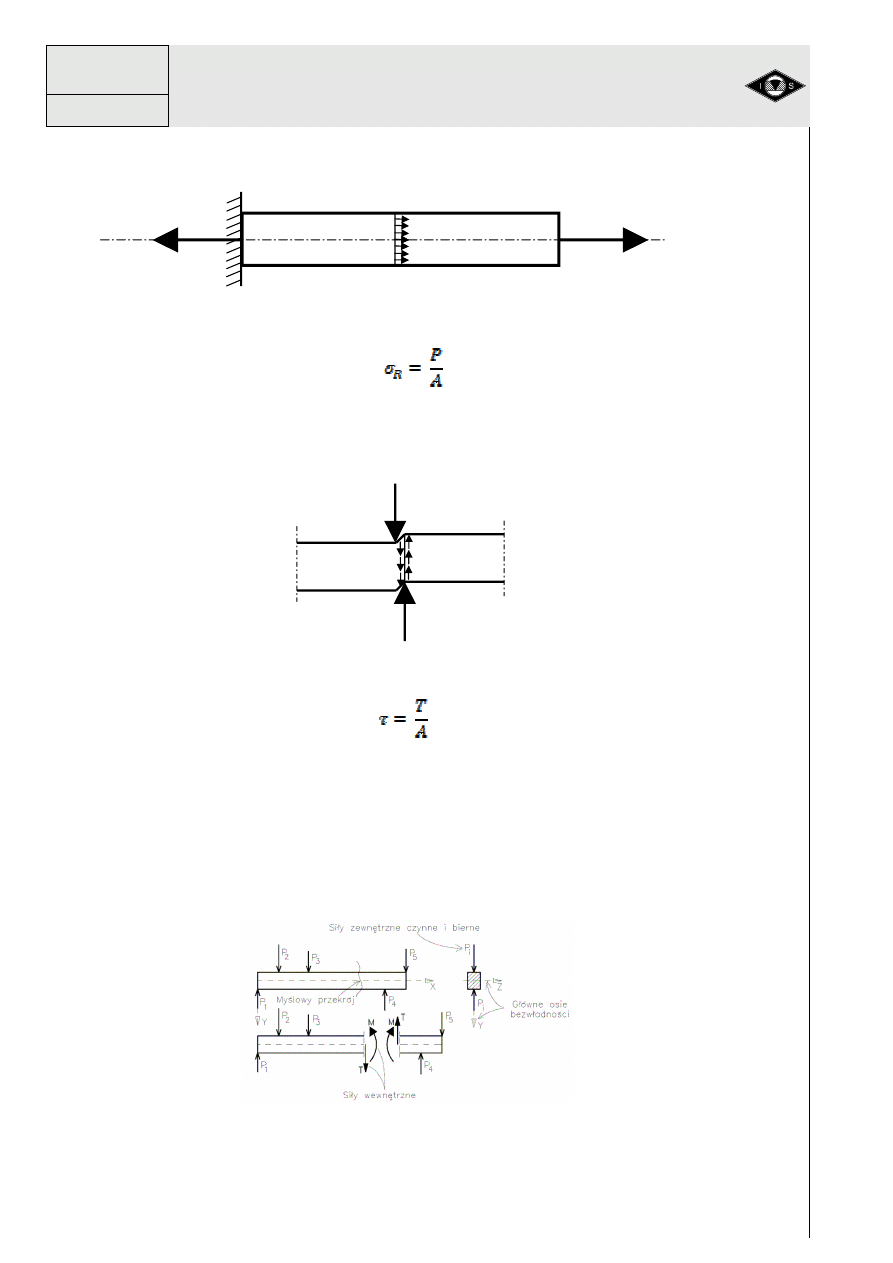
17

Rys.24 Stan napr

ęż

e

ń

rozci

ą

gaj

ą

cych

Zjawisko

ś

ciskania zachodzi w taki sam sposób jak rozci

ą

ganie z t

ą

ró

ż

nic

ą

,

ż

e siły

czynne oddziaływaj

ą

z przeciwnym zwrotem.

Zjawisko

ś

cinania zwi

ą

zane jest z napr

ęż

eniami

ś

cinaj

ą

cymi - stycznymi. Siły we-

wn

ę

trzne tworz

ą

ce ten stan s

ą

ukierunkowane stycznie do rozpatrywanego przekro-

ju.

Rys. 25 Stan napr

ęż

e

ń

stycznych przy

ś

cinaniu

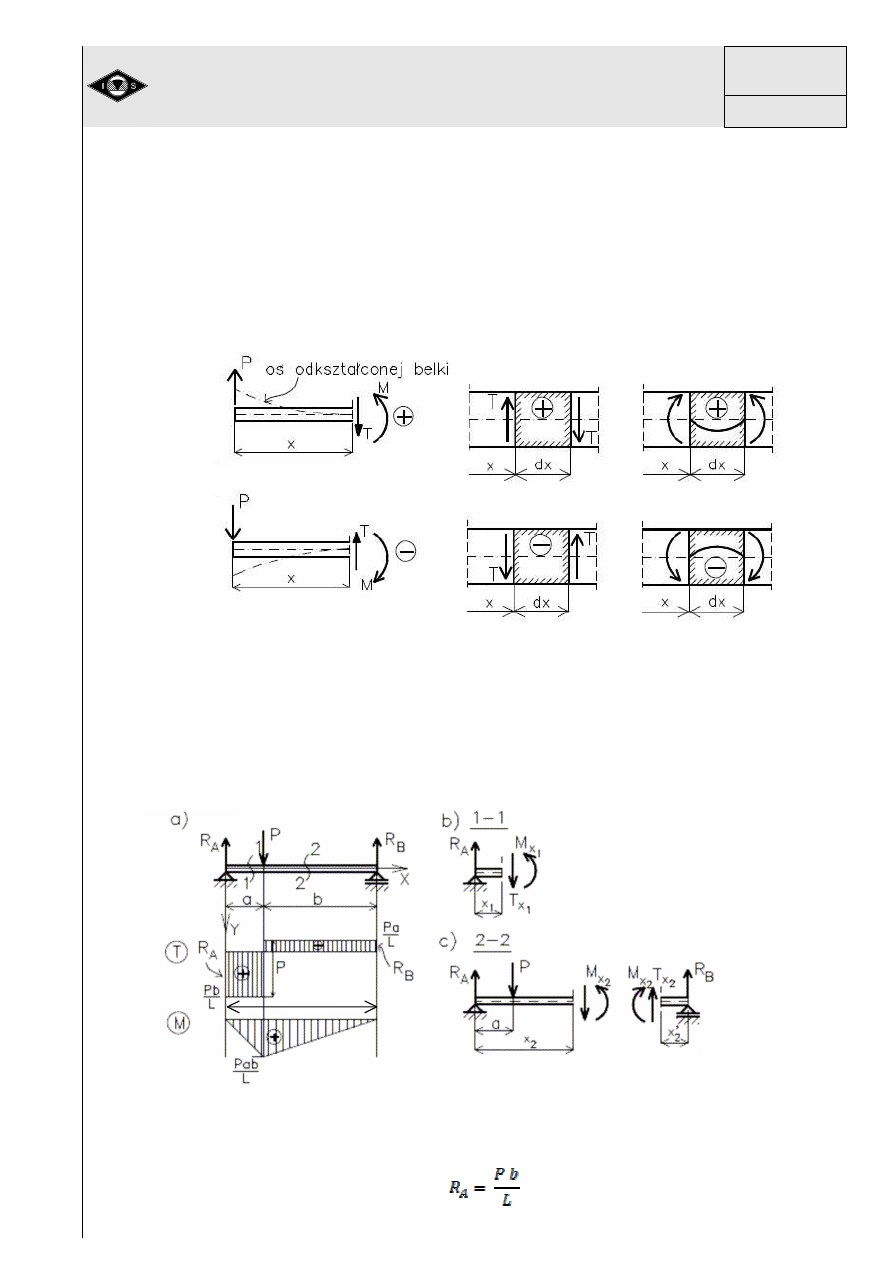
7. Zginanie

Zjawisko zginania jest efektem oddziaływania sił wewn

ę

trznych w postaci mo-

mentów gn

ą

cych oraz cech geometrycznych przekroju poprzecznego elementu zgi-

nanego. Dla uproszczenia element zginany zostanie nazwany belk

ą

. Do wyznacza-

nia sił wewn

ę

trznych wykorzystuje si

ę

metod

ę

my

ś

lowych przekrojów. Przy stałym

przekroju belki granicami odcinków, w których nale

ż

y dokona

ć

my

ś

lowych przekro-

jów, s

ą

punkty przyło

ż

enia sił zewn

ę

trznych – czynnych i biernych (reakcji podporo-

wych).

Rys. 26 Momenty gn

ą

ce jako ujawnione siły wewn

ę

trzne

Na rys.26 pokazano zastosowanie metody my

ś

lowych przekrojów, układ współrz

ę

d-

nych (o

ś

Y skierowana jest w dół, o

ś

X wzdłu

ż

osi belki) oraz siły wewn

ę

trzne w bel-

ce.

P

R

σ

R

A – pole powierzchni

T

T

τ

A

(18)

(19)

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 16

18

7.1 Siły wewn

ę

trzne

W zginaniu wyst

ę

puj

ą

dwie siły wewn

ę

trzne – siła poprzeczna T w płaszczy

ź

-

nie obci

ąż

enia XY oraz moment zginaj

ą

cy M, którego wektor jest prostopadły do

płaszczyzny XY. W obliczeniach wytrzymało

ś

ciowych belek rzecz

ą

podstawow

ą

jest

wyznaczenie rozkładów T i M. Maksymalne warto

ś

ci tych sił wskazuj

ą

na przekroje

najbardziej obci

ąż

one, na przekroje niebezpieczne. Umowne okre

ś

lenie znaków sił

wewn

ę

trznych pokazano na rys 27.

Rys.27 Okre

ś

lenie znaków sił wewn

ę

trznych przy zginaniu

Przykład 7

Dla belki przedstawionej na rys.28 wykona

ć

wykresy sił poprzecznych i momentów zgi-

naj

ą

cych. Zadanie jest statycznie wyznaczalne.

Rys.28 Wykresy momentów gn

ą

cych i sił poprzecznych (tn

ą

cych)

w belce obci

ąż

onej siła skupion

ą

Reakcje podporowe (siły bierne) wynosz

ą

odpowiednio:

L

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 17

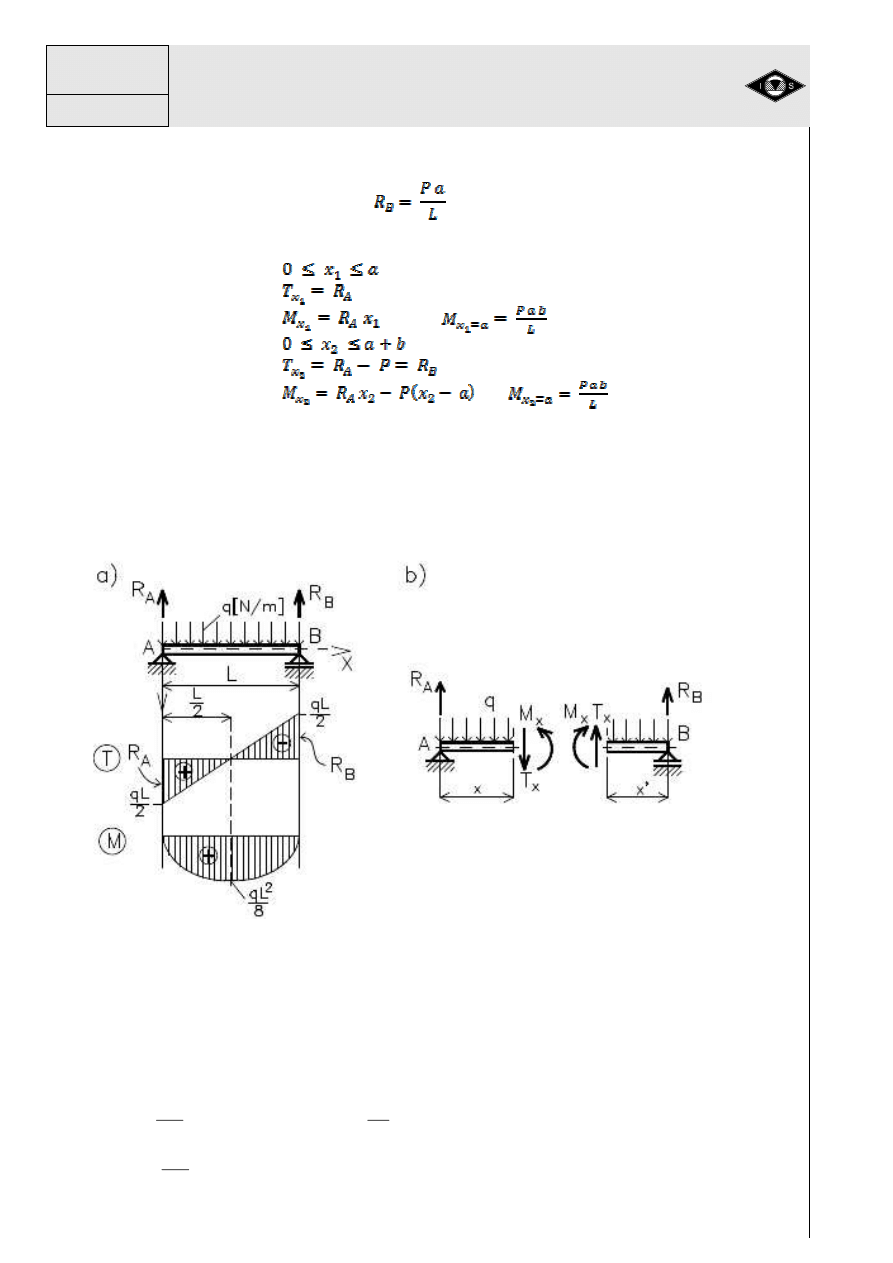
19

Poniewa

ż

belka ma stały przekrój poprzeczny, my

ś

lowe przekroje wyznacza si

ę

w prze-

działach ograniczonych punktami przyło

ż

enia obci

ąż

e

ń

(rys. 28 b,c):

Dla przedziału 1-1

Siła poprzeczna

Moment gn

ą

cy

dla

Dla przedziału 2-2

Siła poprzeczna

Moment gn

ą

cy

dla

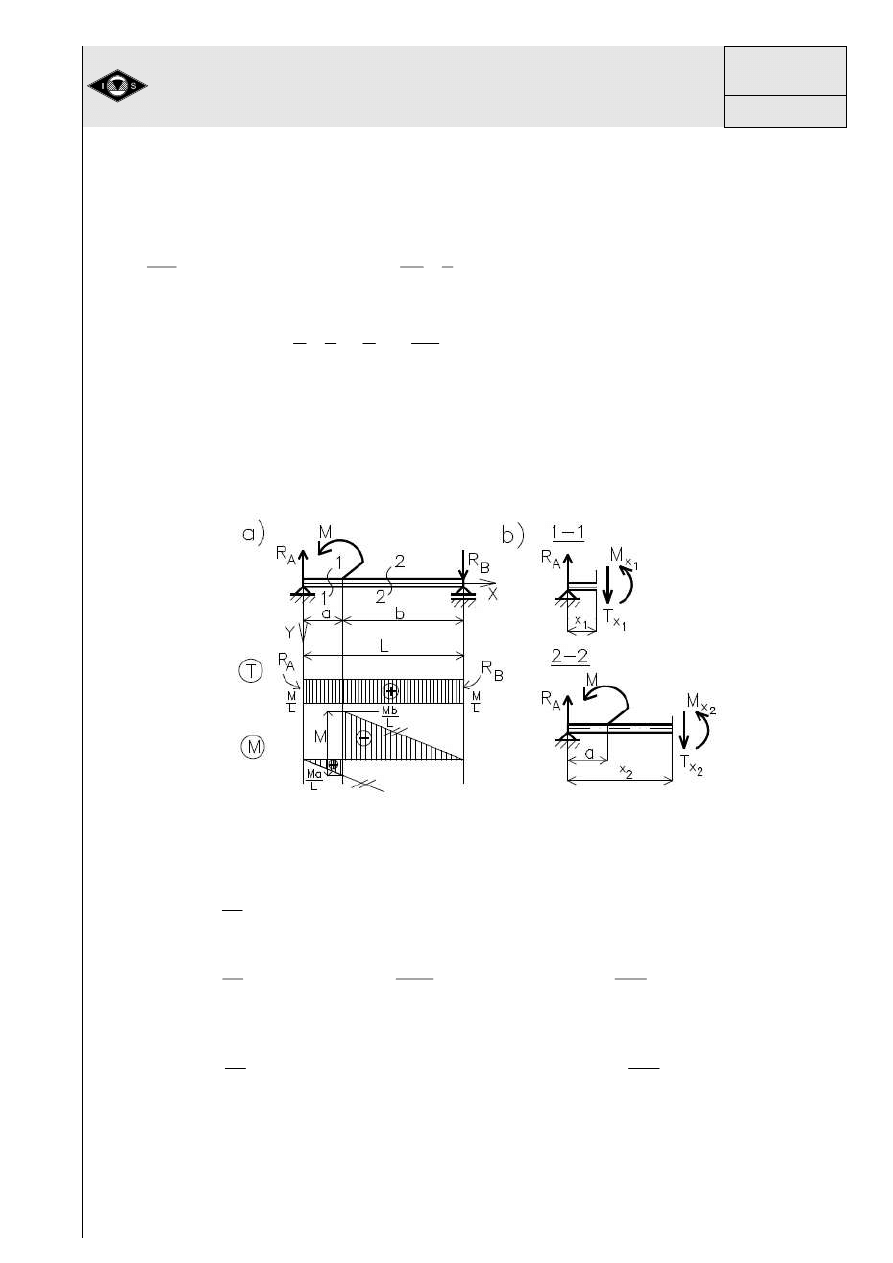
Przykład 8

Dla belki obci

ąż

onej w sposób ci

ą

gły obci

ąż

eniem o stałej intensywno

ś

ci q wykona

ć

wykresy sił poprzecznych i momentów zginaj

ą

cych (rys.29).

Rys. 29 Zginanie belki obci

ąż

onej sił

ą

równomiernie rozło

ż

on

ą

Obci

ąż

enie ci

ą

głe q = const działaj

ą

ce na odcinku L mo

ż

na zast

ą

pi

ć

sił

ą

wypadkow

ą

q L,

przyło

ż

on

ą

w połowie długo

ś

ci odcinka (wypadkowa układu sił równoległych). Z sumy

momentów wzgl

ę

dem podpór A i B otrzymuje si

ę

R

A

= R

B

= qL/2 (rys. 20 a). W belce wy-

starczy rozpatrzy

ć

tylko jeden przedział 0

≤

x

≤

L, w którym

qx

R

T

A

x

−

=

2

0

L

q

R

T

A

x

=

=

=

,

2

qL

qL

R

T

A

L

x

−

=

−

=

=

2

2

qx

x

R

M

A

x

−

=

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 18

20

Wykres momentów gn

ą

cych jest parabol

ą

i ma warto

ś

ci zerowa w podporach belki.

Dla wyznaczenia ekstremum funkcji - w rozpatrywanym przypadku jej maksimum na-
le

ż

y zró

ż

niczkowa

ć

równanie momentów gn

ą

cych.

L

q

R

x

T

qx

R

dx

dM

A

m

x

A

2

1

0

=

=

→

=

=

−

=

8

2

2

1

2

2

2

max

qL

L

q

L

R

M

M

A

x

x

m

=













−

=

=

=

Przykład 9

Dla belki obci

ąż

onej momentem skupionym M wykona

ć

wykresy sił poprzecznych i

momentów zginaj

ą

cych (rys.30).

Rys.30 Zginanie belki obci

ąż

onej momentem skupionym

Z równa

ń

równowagi statycznej mo

ż

na wyliczy

ć

reakcje podporowe:

L

M

R

R

B

A

=

=

W przedziale 1-1 (0

≤

x

1

≤

a) siły wewn

ę

trzne

L

M

R

T

A

x

=

=

1

,

L

x

M

x

R

M

A

X

1

1

1

=

=

,

0

0

1

=

=

x

M

,

L

a

M

M

a

x

=

=

1

W przedziale 2-2 ( 0

≤

x

2

≤

L)

L

M

R

T

A

x

=

=

2

,

M

x

R

M

A

X

−

=

2

2

,

0

2

=

=

L

x

M

,

L

b

M

M

a

x

−

=

=

2

Na rys. 30 pokazano wykresy sił wewn

ę

trznych.

Przykład 10

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 19

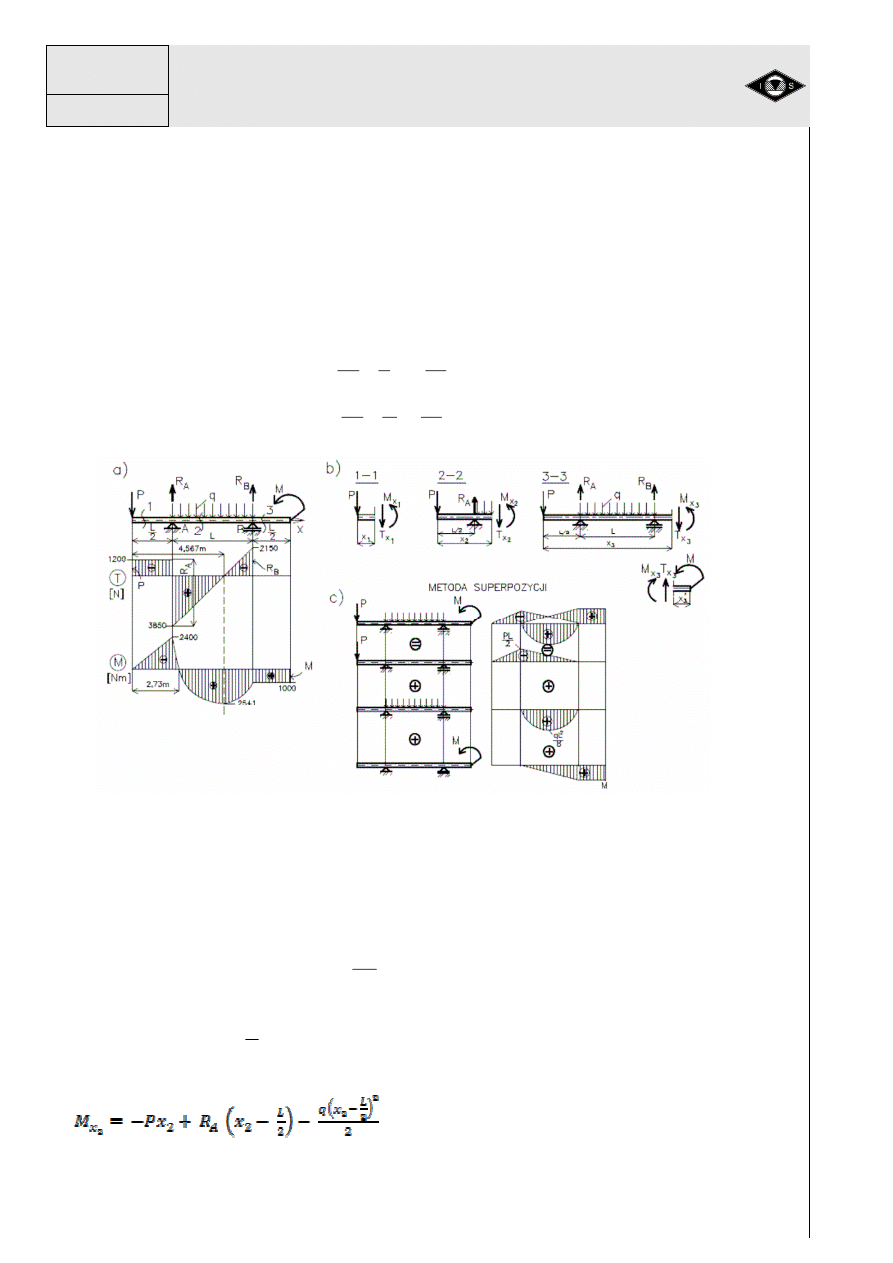
21

Dla belki przedstawionej na rys.31 wykona

ć

wykresy sił wewn

ę

trznych (sił poprzecz-

nych oraz momentów zginaj

ą

cych). Przyj

ąć

dane: P = 1200 N, q = 1500 N/m, M =

1000 Nm, L = 4 m. Wykona

ć

dodatkowo wykres momentów, korzystaj

ą

c z zasady

superpozycji. Na rys. 31 pokazano schemat belki obci

ąż

onej sił

ą

skupion

ą

, siła rów-

nomiernie rozło

ż

on

ą

i momentem skupionym Jak wida

ć

jest to zadanie zbiorcze, w

zakresie którego s

ą

poprzednie sposoby obci

ąż

ania belek.

Reakcje podporowe

N

L

M

P

qL

R

A

5050

2

3

2

=

+

+

=

N

L

M

P

qL

R

B

2150

2

2

=

−

+

=

Rys. 31 Siły wewn

ę

trzne w belce obci

ąż

onej sił

ą

skupion

ą

,

równomiernie rozło

ż

on

ą

i momentem skupionym

Siły wewn

ę

trzne w trzech zało

ż

onych przekrojach (rys. 31 b).

W przedziale 0

≤

x

1

≤

L/2

N

P

T

x

1200

1

−

=

−

=

Nm

PL

M

M

Px

M

L

x

x

x

2100

2

;

0

;

2

/

0

1

2

1

1

−

=

−

=

=

−

=

=

=

W przedziale L/2

≤

x

2

≤

3/2 L













−

−

+

−

=

2

2

2

L

x

q

R

P

T

A

x

N

T

N

T

L

x

L

x

2150

;

3850

2

/

3

2

/

2

2

−

=

=

=

=

Jak wida

ć

z wykresu na rys.31 siła poprzeczna zmieniła swój znak co oznacza,

ż

e

w tym miejscu zerowym (dla równania siły poprzecznej) wyst

ę

puje ekstremum funk-

cji.

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 20

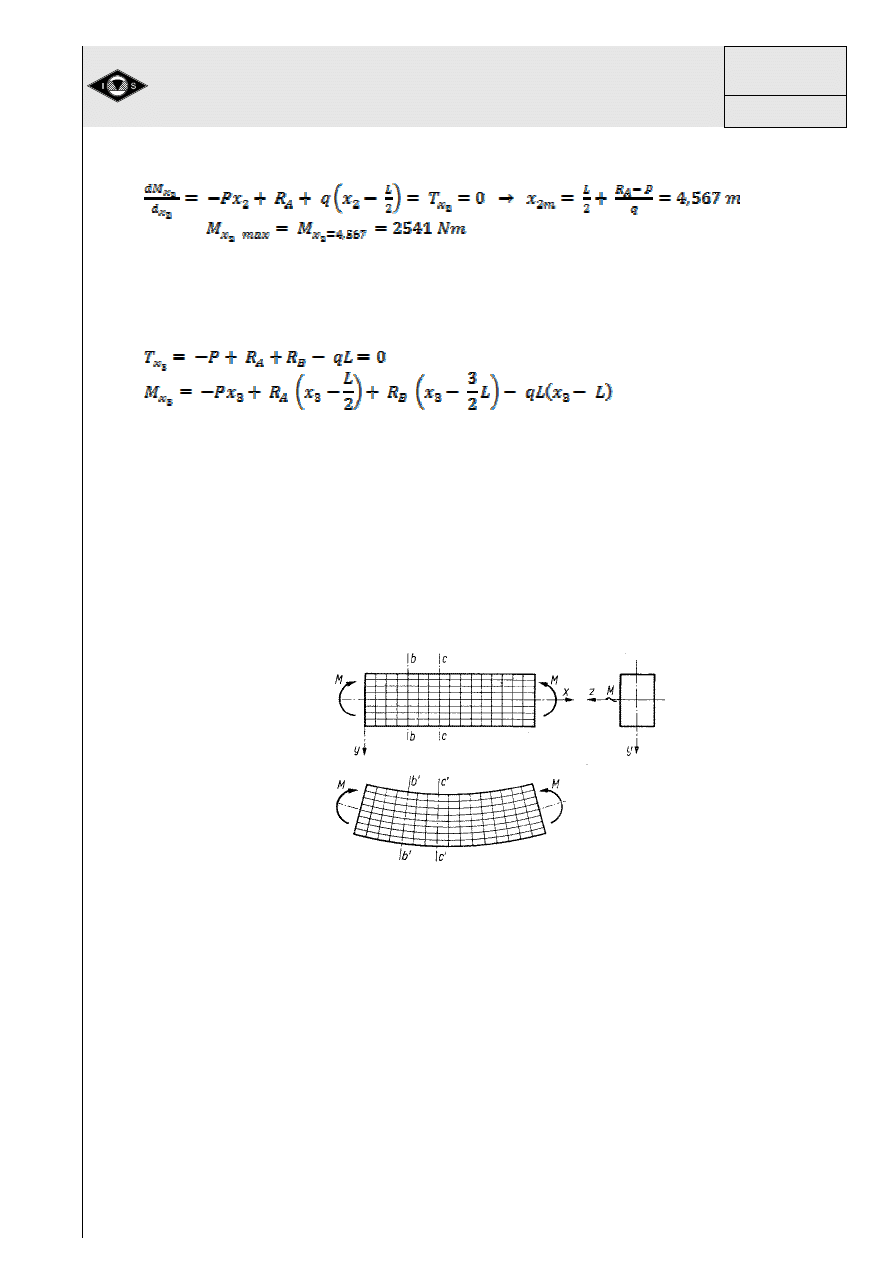
22

i dalej

po rozwi

ą

zaniu równania kwadratowego równania momentów gn

ą

cych w drugim

przedziale i wyznaczeniu jego pierwiastka dodatniego znajduj

ą

cego si

ę

w tym prze-

dziale przekrój wyst

ę

powania maksymalnej warto

ś

ci momentu gn

ą

cego. Przekrój ten

znajduje si

ę

w odległo

ś

ci 2,73 m od pocz

ą

tku układu współrz

ę

dnych.

W przedziale 3/2 L

≤

x

3

≤

2 L

W tym przedziale moment gn

ą

cy przyjmie stał

ą

warto

ść

1000 Nm.

7.2 Napr

ęż

enia przy zginaniu

Przy obci

ąż

enia poprzecznych i momentach skupionych w przekrojach belek

wyst

ą

pi

ą

siły wewn

ę

trzne normalne (momenty gn

ą

ce) styczne (

ś

cinaj

ą

ce). I tutaj siły

wewn

ę

trzne odniesione do przekroju okre

ś

l

ą

stany napr

ęż

e

ń

. Przy zało

ż

eniu płaskich

przekrojów tzn. takich, które pod działaniem sił nie b

ę

d

ą

odkształca

ć

si

ę

w kierunku

prostopadłym. W konsekwencji w przekrojach prostopadłych do osi wzdłu

ż

nej belki

wyst

ą

pi

ą

zró

ż

nicowane napr

ęż

enia. Zjawisko zginania zilustrowano na rys. 23.

Rys. 32 Zginanie belki

Na rys. 32 przedstawiono belk

ę

, na której naniesiono siatk

ę

. Po jej obci

ąż

eniu na

ko

ń

cach momentami M

g

. Odkształcenie pr

ę

ta ujawni si

ę

w postaci zakrzywienia

uprzednio naznaczonych linii podłu

ż

nych i jego osi. Linie prostopadłe do osi b-b i c-c

po odkształceniu zajm

ą

pozycj

ę

b’-b’ i c’-c’ i pozostan

ą

dalej proste , a kontury prze-

krojów nadal płaskie co potwierdzi zasad

ę

płaskich przekrojów. Odkształcenie belki

przedstawione na rys. 32 ujawnia jeszcze jedn

ą

cech

ę

: Istnieje warstwa, która nie

została odkształcona pod wpływem obci

ąż

enia. Jest to warstwa oboj

ę

tna. Je

ś

li w

my

ś

li podzielimy belk

ę

na podłu

ż

ne elementy , które nazwiemy włóknami, to zauwa-

ż

ymy,

ż

e po stronie wkl

ę

słej uległy one skróceniu, a po stronie wypukłej wydłu

ż

eniu.

Przy takich obserwacjach mo

ż

na zało

ż

y

ć

warunki geometryczne (rys.33).

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 21

23

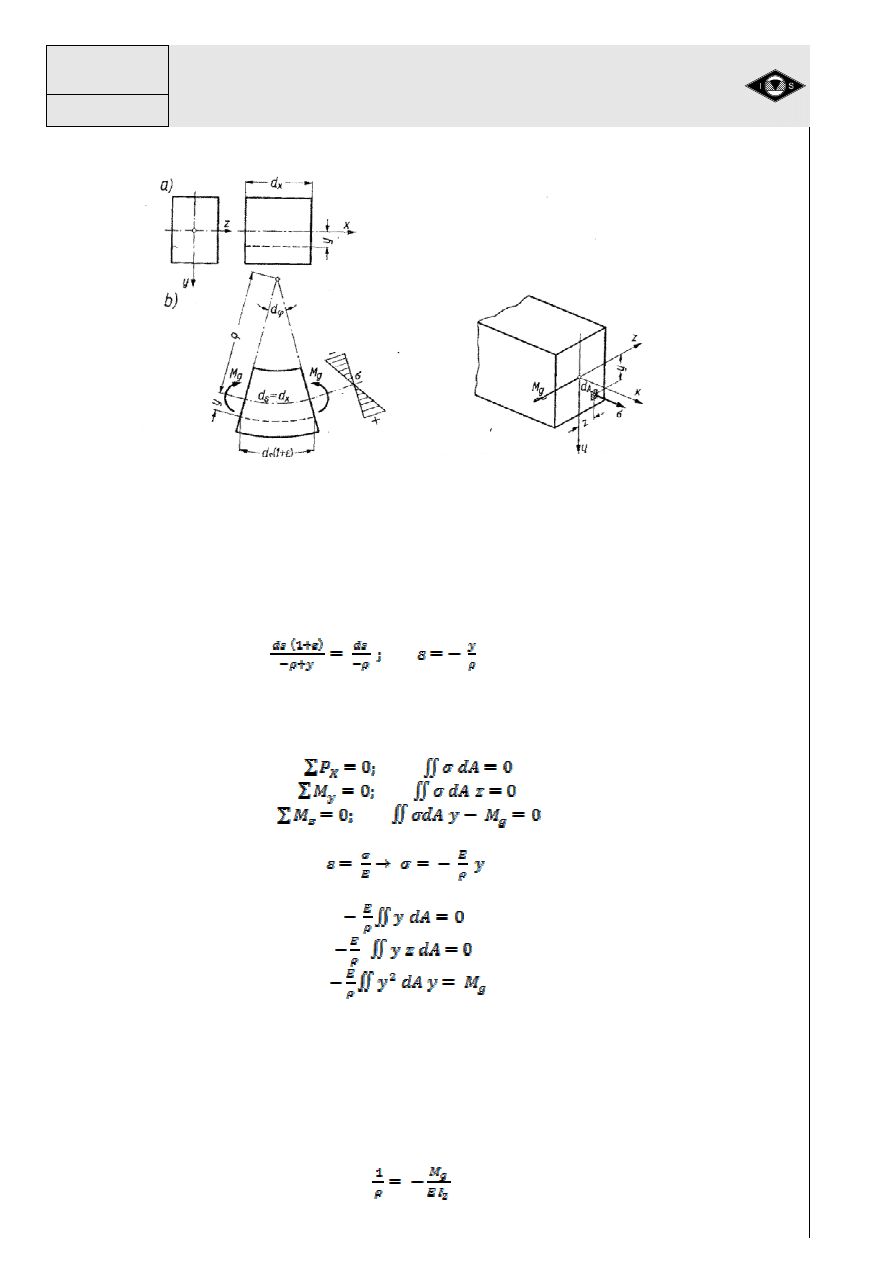
Rys. 33 Warunki geometryczne zginania

Element belki przed odkształceniem o długo

ś

ci dx ma przekrój poprzeczny jak na

rys.33. Po przyło

ż

eniu momentu gn

ą

cego nast

ą

pi jego ugi

ę

cie. We

ź

my pod uwag

ę

włókno odległe od warstwy oboj

ę

tnej o y, długo

ść

którego wynosiła dx = ds, by po

odkształceniu osi

ą

gn

ąć

długo

ść

ds(1+

ε

), gdzie

ε

jest wydłu

ż

eniem wzgl

ę

dnym (rys.

33 b).

(20)

Siły zewn

ę

trzne działaj

ą

ce na cz

ęść

belki po jednej stronie przekroju redukuj

ą

si

ę

do

momentu –M

g

. Uwzgl

ę

dniaj

ą

c wewn

ę

trzne siły elementarne

σ

Da tworz

ą

ce prze-

strzenny układ sił równoległych mo

ż

emy dla odci

ę

tej cz

ęś

ci belki napisa

ć

nast

ę

puj

ą

-

ce warunki równowagi (rys. 33c).

(21)

(22)

(23)

Zakładaj

ą

c ugi

ę

cie spr

ęż

yste jako warunek fizyczny przyjmujemy prawo Hooke’a

(24)

Podstawiaj

ą

c do poprzednich trzech równa

ń

otrzymamy:

(25)

(26)

(27)

Z równania (25) wynika,

ż

e moment statyczny wzgl

ę

dem osin oboj

ę

tnej z jest równy

zeru tzn.,

ż

e o

ś

oboj

ę

tna przekroju przechodzi przez

ś

rodek ci

ęż

ko

ś

ci przekroju. Z

równania (26) wynika,

ż

e moment dewiacji wzgl

ę

dem osi z jest równy zero, co ozna-

cza,

ż

e je

ś

li kierunek wektora M

g

(rys.33) b

ę

dzie pokrywał si

ę

z kierunkiem jednej z

osi centralnych przekroju to wyst

ą

pi zginanie proste. Z kolei równanie (27) pozwala

ustali

ć

podstawow

ą

zale

ż

no

ść

pomi

ę

dzy krzywizn

ą

, momentem gn

ą

cym i napr

ęż

e-

niami. Przyjmuj

ą

c,

ż

e podcałkowe wyra

ż

enie w tym równaniu jest momentem bez-

władno

ś

ci przekroju otrzymamy t

ą

zale

ż

no

ść

w postaci:

(28)

Wykorzystuj

ą

c zale

ż

no

ść

(24) otrzymamy:

c)

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 22

24

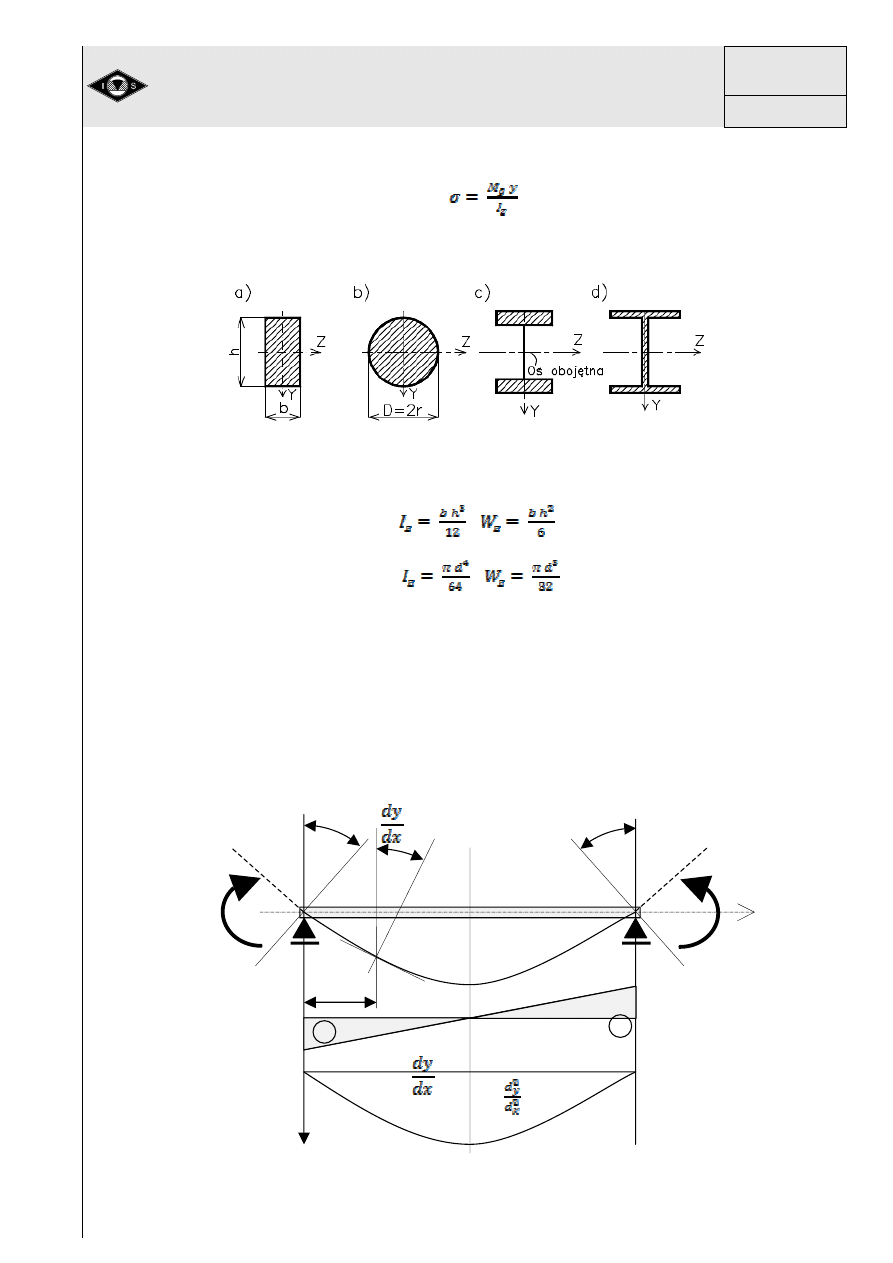
(29)

Wielko

ść

I

z

/y nazywa si

ę

wska

ź

nikiem wytrzymało

ś

ci na zginanie W

z

.

Rys. 34 Podstawowe przekroje figur płaskich

Dla prostok

ą

ta

;

(30)

Dla koła

;

(31)

7.3 Odkształcenia belek

Odkształceniami belki s

ą

:

– ugi

ę

cie belki y, zdefiniowane jako pionowe przemieszczenie

ś

rodka ci

ęż

ko

ś

ci prze-

kroju poprzecznego belki,
– k

ą

t obrotu przekroju dx/dy = tg

Θ

≈

Θ

zdefiniowany jako k

ą

t obrotu normalnej do

przekroju poprzecznego belki lub ze wzgl

ę

dów praktycznych – prostopadłej do nor-

malnej.

Rys.35 Schemat ugi

ę

cia belki

A

B

+

-

M

M

Θ

Θ

y

x

x

y

Θ

< 0

Θ

> 0

linia ugi

ę

cia

K

ą

t obrotu przekroju

poprzecznego belki

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 23

25

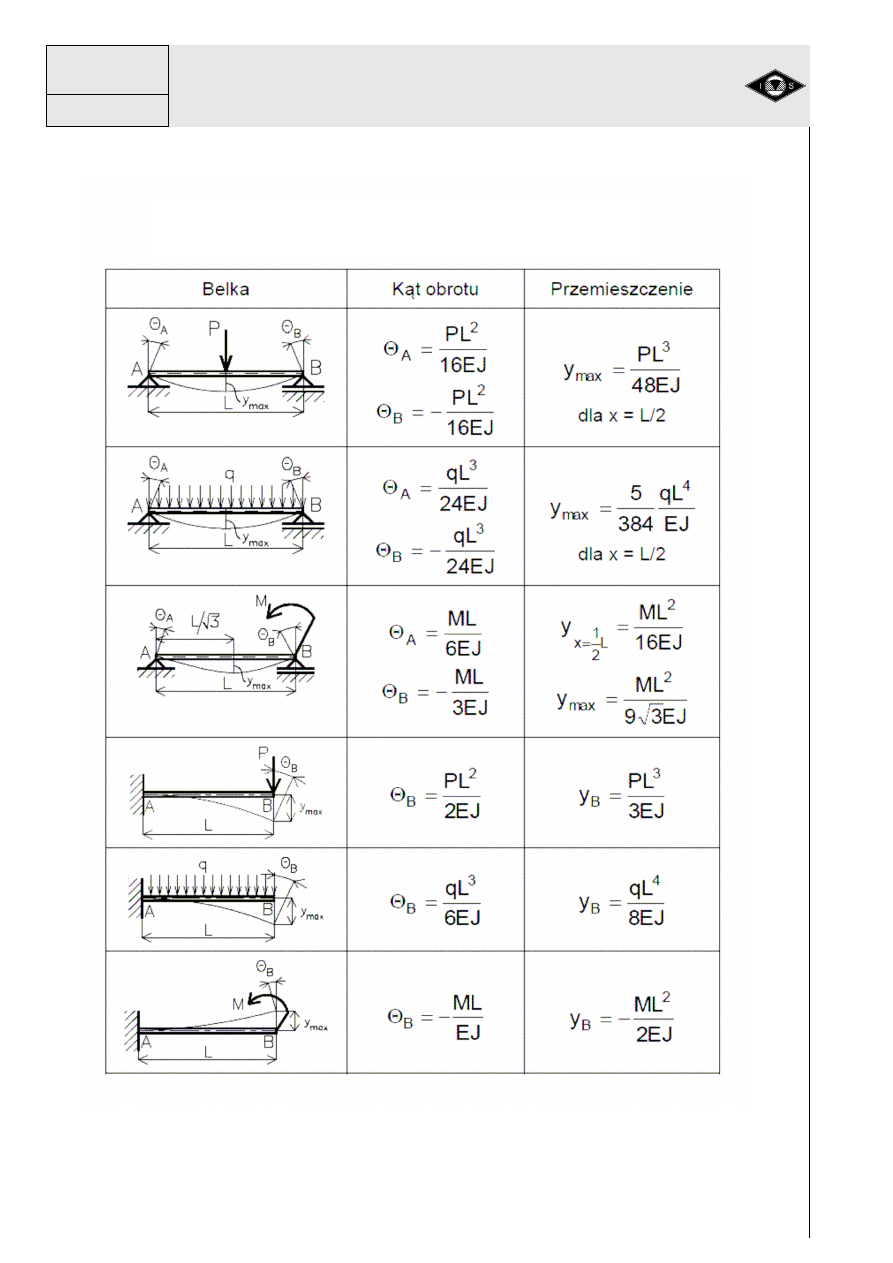
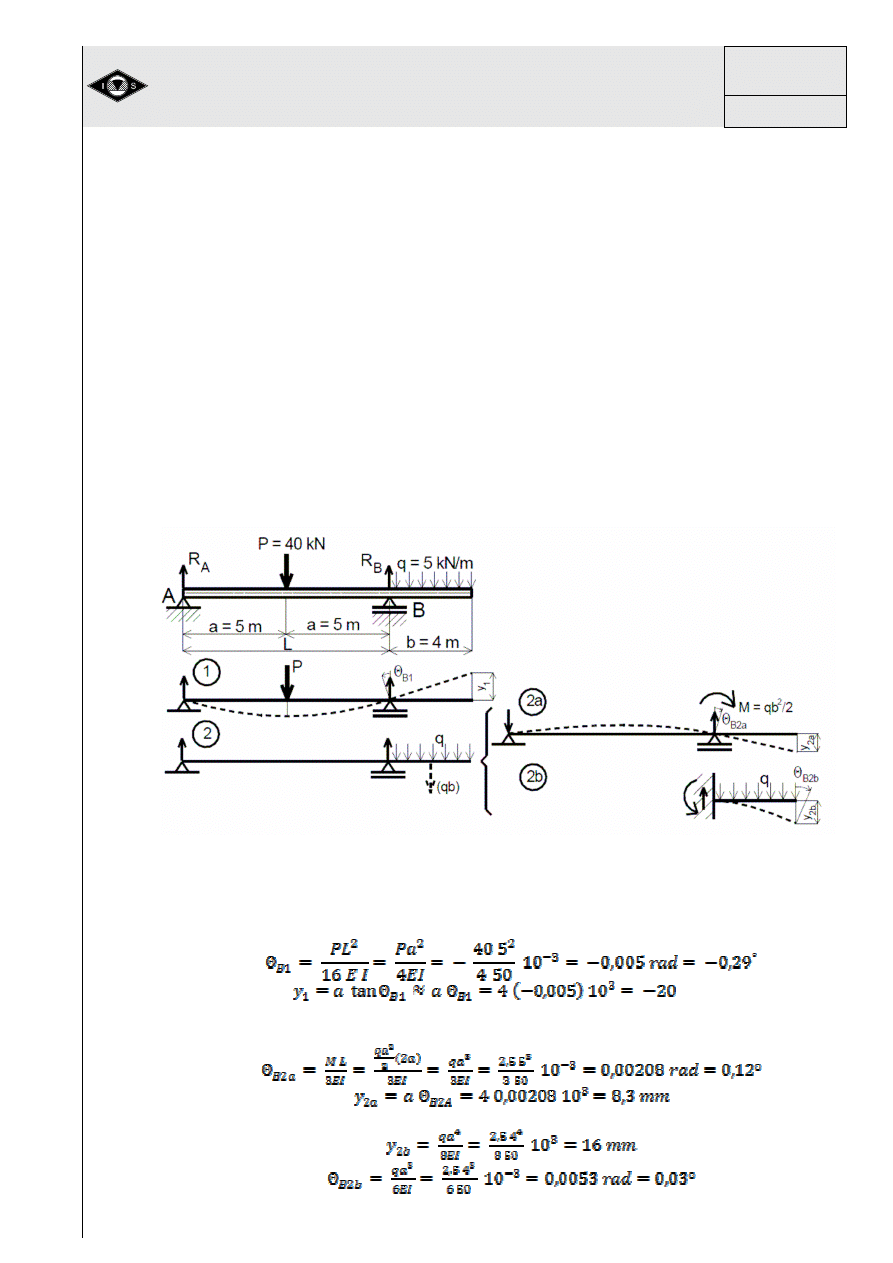
Tablica 1 Przemieszczenia prostych belek

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 24

26

Obliczanie odkształce

ń

belek mo

ż

liwe jest za pomoc

ą

metody całkowania tzw. rów-

nania ró

ż

niczkowego linii ugi

ę

cia belki. Metoda ta pozwala na wyznaczanie ugi

ę

cia

oraz kata obrotu w dowolnym przekroju x. W praktyce in

ż

ynierskiej stosowane s

ą

równie

ż

uproszczone metody wyznaczania odkształce

ń

belek. Jedn

ą

z metod jest

metoda superpozycji

.

Metoda superpozycji pozwala wyznacza

ć

odkształcenia tylko w

wybranych punktach (np. poparcia, ko

ń

ce belki). Dla szybkiego stosowania metody

nale

ż

y korzysta

ć

z gotowych rozwi

ą

za

ń

dla podstawowych typów prostych belek

(patrz tabela).

Przykład 11

Dla belki przedstawionej na rys. 36 obliczy

ć

ugi

ę

cie i k

ą

t obrotu punktu C.

Przyj

ąć

: P = 40 kN, q = 2,5 kN/m, EJ = 50 MNm2.

Aby zastosowa

ć

metod

ę

superpozycji, nale

ż

y rozdzieli

ć

obci

ąż

enia na sił

ę

skupion

ą

P oraz obci

ąż

enia ci

ą

głe q. Poniewa

ż

q działa na cz

ęś

ci cz

ęść

belki znajduj

ą

cej si

ę

poza podporami, nale

ż

y uwzgl

ę

dni

ć

moment M oddziałuj

ą

cy na AB.

Rys. 36 Przykład belki zło

ż

onej

1. Belka obci

ąż

ona sił

ą

P:

2. Belka obci

ąż

ona sił

ą

równomiernie rozło

ż

on

ą

q

2a. Odkształcenie prz

ę

sła AB:

2b. Odkształcenie wspornika BC:

Całkowite ugi

ę

cie ko

ń

ca C:

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 25

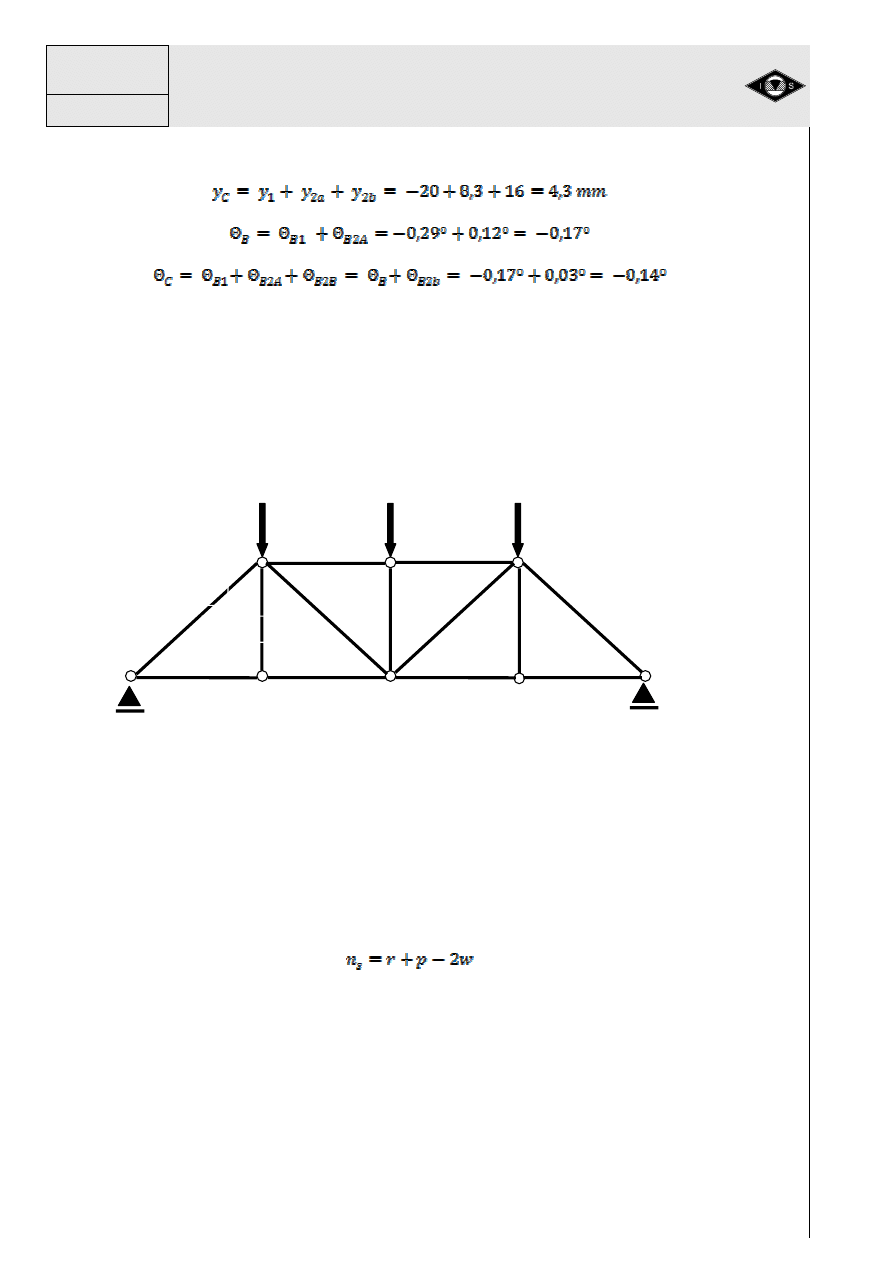
27

K

ą

t obrotu belki na podporze B:

K

ą

t obrotu przekroju belki na ko

ń

cu C:

8. Kratownice

Kratownic

ą

nazywamy układ zło

ż

ony z pr

ę

tów prostych, poł

ą

czonych mi

ę

dzy sob

ą

w w

ę

złach przegubowo (przegubami bez tarcia), obci

ąż

ony siłami skupionymi w

przegubach;
siły przekrojowe w pr

ę

tach kratownicy redukuj

ą

si

ę

do stałej siły podłu

ż

nej.

Rys. 37 Kratownica

Obci

ąż

enia zewn

ę

trzne przekazuje si

ę

na kratownice w postaci sił skupionych

przyło

ż

onych w jej w

ę

złach i działaj

ą

cych w płaszczy

ź

nie kratownicy (w przypadku

kratownic płaskich). Równie

ż

ci

ęż

ar własny kratownicy zast

ę

puje si

ę

siłami skupio-

nymi, zredukowanych i przyło

ż

onych w jej w

ę

złach.

Sprawdzenie stopnia statycznej niewyznaczalno

ś

ci kratownicy

Sprawdzenie stopnia statycznej wyznaczalno

ś

ci kratownicy dokonujemy wzorem

gdzie: n

s

– stopie

ń

statycznej niewyznaczalno

ś

ci,

r – liczba pr

ę

tów reakcyjnych (reakcji podporowych),

p – liczba pr

ę

tów prostych kratownicy,

w – liczba w

ę

złów kratownicy.

Dla kratownicy przedstawionej na rys. 37 stopie

ń

ten wynosi

n

s

= 3 + 13 + - 2 * 8 = 0

gdzie

r = 3, p = 13 (4 pr

ę

ty pasa górnego, 4 pr

ę

ty pasa dolnego, 3 słupki, 2 krzy

ż

ul-

ce), w = 8.

Pr

ę

ty zerowe

W kratownicy mog

ą

wyst

ę

powa

ć

pr

ę

ty, w których pod danym obci

ąż

eniem siły

Pas górny

Pas dolny

Krzy

ż

ulec

Słupek

A

B

(32)

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 26

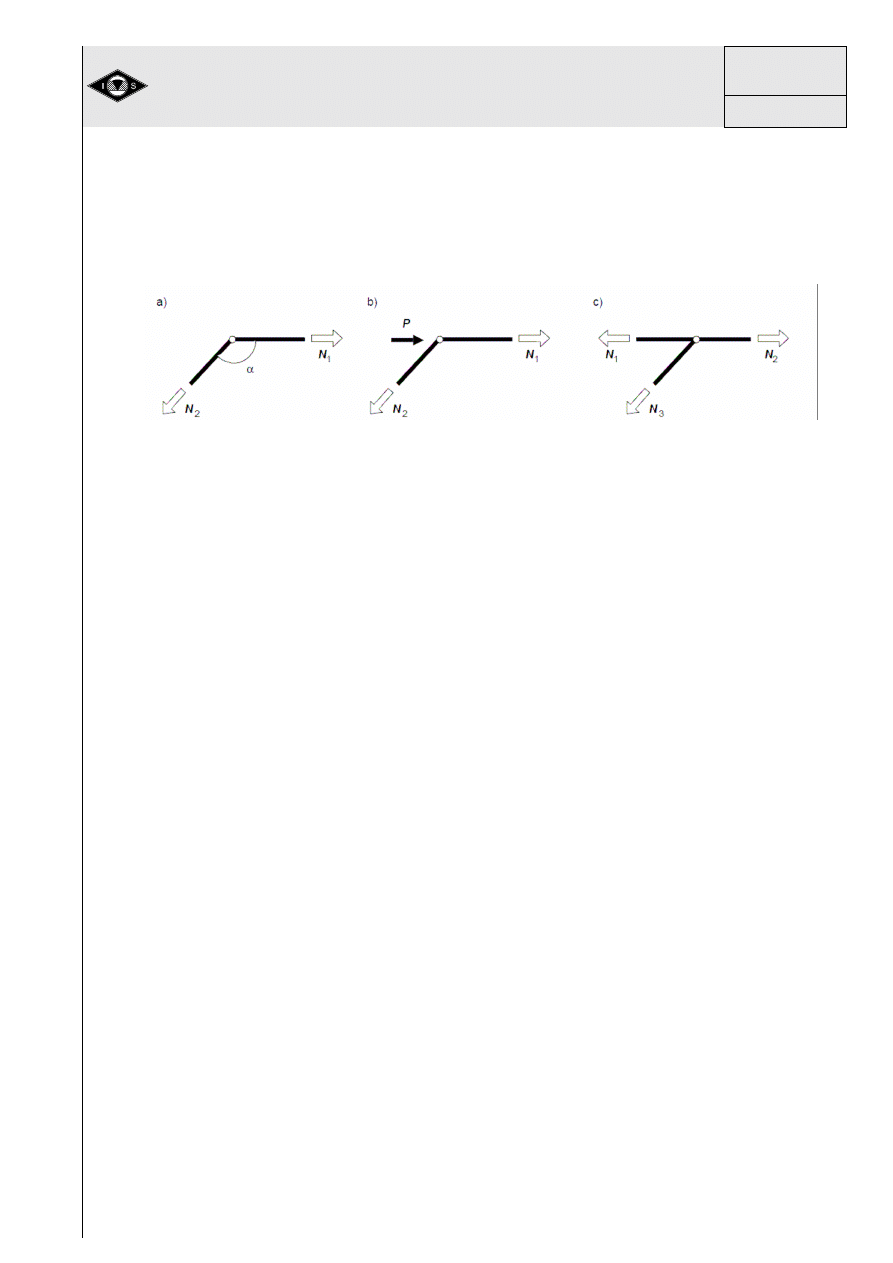
28

podłu

ż

ne s

ą

równe zero, pr

ę

ty te nazywamy pr

ę

tami zerowymi.

Zasady okre

ś

lania tych pr

ę

tów s

ą

nast

ę

puj

ą

ce:

a) je

ś

li w w

ęź

le schodz

ą

si

ę

dwa pr

ę

ty pod pewnym k

ą

tem a i w

ę

zeł jest nieob-

ci

ąż

ony sił

ą

zewn

ę

trzn

ą

, to siły przekrojowe w obu pr

ę

tach s

ą

równe zeru (rys.

38 a),

Rys. 38 Pr

ę

ty zerowe

b) je

ś

li w w

ęź

le schodz

ą

si

ę

dwa pr

ę

ty i w

ę

zeł jest obci

ąż

ony sił

ą

zewn

ę

trzn

ą

,

równoległa do jednego z nich, to w drugim pr

ę

cie siła przekrojowa jest równa

zero (rys. 38 b),

c) je

ś

li w w

ęź

le schodz

ą

si

ę

trzy pr

ę

ty, z których dwa s

ą

równoległe i w

ę

zeł jest

nieobci

ąż

ony sił

ą

zewn

ę

trzn

ą

, to siła przekrojowa w pr

ę

cie trzecim jest równa ze-

ro (rys. 38 c).

8.1 Metody rozwi

ą

zywania kratownic

Metody rozwi

ą

zywania kratownic

- analityczne
- metoda równowa

ż

enia w

ę

złów

- plan sił Cremony
- metoda Rittera
- metoda Culmanna

8.1.1. Metoda równowa

ż

enia w

ę

złów

Metoda ta polega na wypisywaniu równa

ń

równowagi dla ka

ż

dego my

ś

lowo

wyci

ę

tego w

ę

zła kratownicy.

Post

ę

powanie:

1) Z równa

ń

równowagi wyznaczenie składowych reakcji podporowych,

2) W poszczególnych my

ś

lowo wyci

ę

tych w

ę

złach kratownicy zapisuje si

ę

dwa rów-

nania
równowagi:

Σ

P

ix

= 0,

Σ

P

iy

= 0. W tym celu w w

ęź

le zakłada si

ę

odpowiednie zwroty sił

w poszczególnych pr

ę

tach,

3) Z zapisanych równa

ń

równowagi wyznacza si

ę

siły we wszystkich pr

ę

tach kratow-

nicy. Rozwi

ą

zywanie najlepiej zacz

ąć

od w

ę

zła, w którym zbiegaj

ą

si

ę

tylko dwa pr

ę

-

ty o nieznanych siłach, a nast

ę

pnie rozpatrywa

ć

kolejne w

ę

zły spełniaj

ą

ce ten waru-

nek.

8.1.2 Metoda Rittera (metoda przekrojów)

Metoda Rittera, podobnie jak metoda równowa

ż

enia w

ę

złów jest sposobem anali-

tycznym, polega ona na wykorzystaniu twierdzenia o równowadze układu sił ze-
wn

ę

trznych i wewn

ę

trznych przyło

ż

onych do jednej cz

ęś

ci kratownicy. Analitycznych

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 27

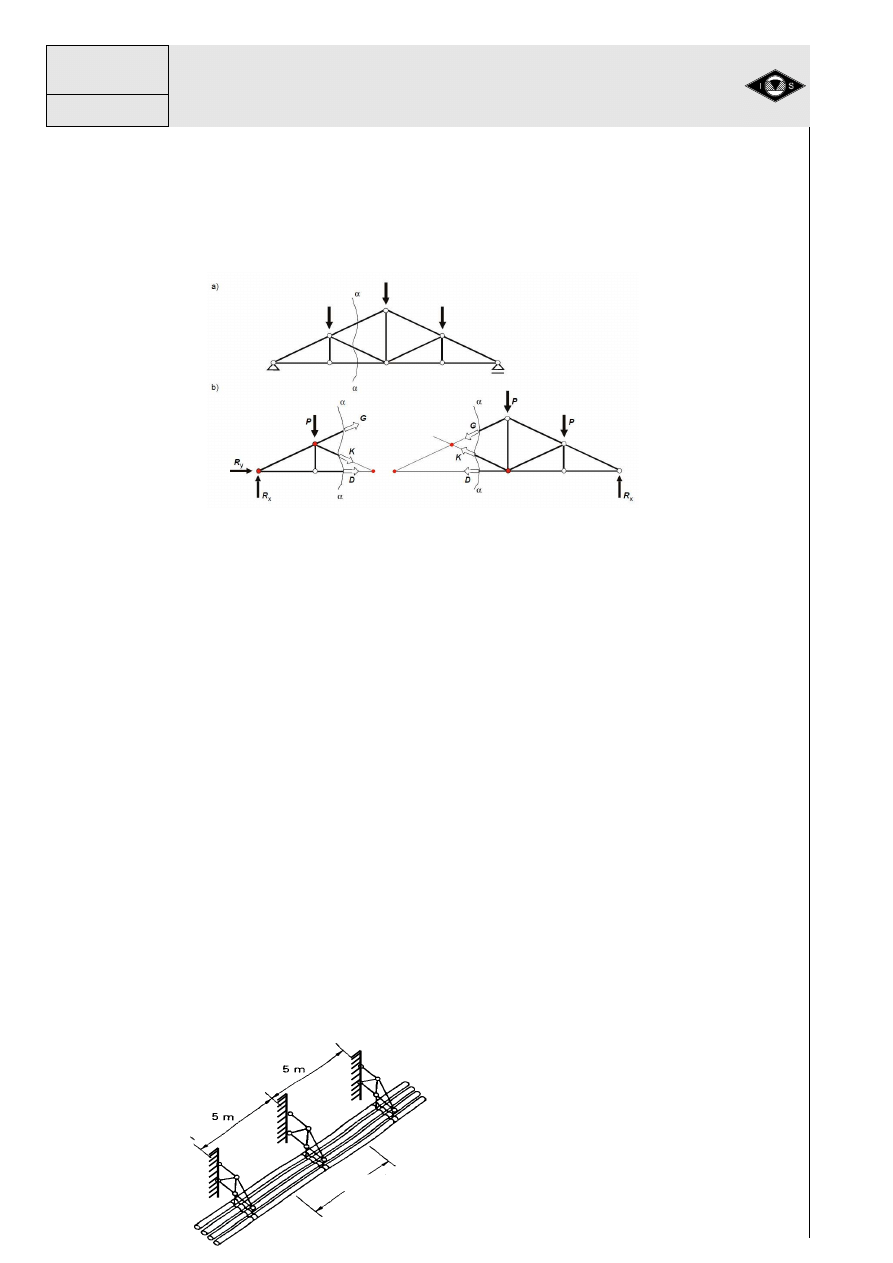
29

równa

ń

równowagi mamy trzy, je

ś

li wi

ę

c kratownice przetniemy przez nie wi

ę

cej ni

ż

trzy pr

ę

ty, to z równa

ń

równowagi mo

ż

emy wyliczy

ć

szukane siły przekrojowe. Meto-

da ta jest wygodniejsza w przypadku, je

ś

li poszukiwane s

ą

siły w konkretnych pr

ę

-

tach kratownicy (rys. 39).

Rys. 39 Metoda Rittera wyznaczania sił w pr

ę

tach

Post

ę

powanie:

1) Z równa

ń

równowagi wyznaczenie składowych reakcji podporowych,

2) Przeprowadza si

ę

przekrój a-a przez trzy pr

ę

ty kratownicy nie zbiegaj

ą

ce si

ę

w

jednym punkcie, w tym przez pr

ę

t (lub pr

ę

ty), w których sił

ę

chcemy wyznaczy

ć

.

Cz

ęść

kratownicy oddzielona przekrojem a-a znajduje si

ę

w równowadze pod działa-

niem sił zewn

ę

trznych, składowych reakcji podpór oraz sił w pr

ę

tach, przez które po-

prowadzono przekrój (rys. 39 b),
3) W odniesieniu do wydzielonej cz

ęś

ci kratownicy zapisuje si

ę

równania sumy mo-

mentów wszystkich sił wzgl

ę

dem trzech punktów, w których przecinaj

ą

si

ę

parami

kierunki poszukiwanych sił w pr

ę

tach. Punkty te s

ą

nazywane punktami Rittera. Je

ś

li

dwa z pr

ę

tów, przez które poprowadzono przekrój, s

ą

do siebie równoległe, to zapi-

suje si

ę

dwa równania sumy momentów wszystkich sił działaj

ą

cych na dan

ą

cz

ęść

kratownicy wzgl

ę

dem punktów, w których trzeci pr

ę

t przecina si

ę

z pr

ę

tami równole-

głymi, oraz trzecie równanie sumy rzutów wszystkich sił na o

ś

prostopadł

ą

do pr

ę

tów

równoległych.

Przykład 12
1. Okre

ś

li

ć

, które pr

ę

ty kratownicy słu

żą

cej do podwieszenia rur instalacji chemicz-

nej s

ą

rozci

ą

gane, a które

ś

ciskane.

2. Okre

ś

li

ć

siły wyst

ę

puj

ą

ce w pr

ę

tach kratownicy, je

ś

li całkowity ci

ęż

ar rur wynosi

3.8 [kN/m].

Rys. 40 Konstrukcja kratowa
podwieszenia zespołu rur

5 m

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 28

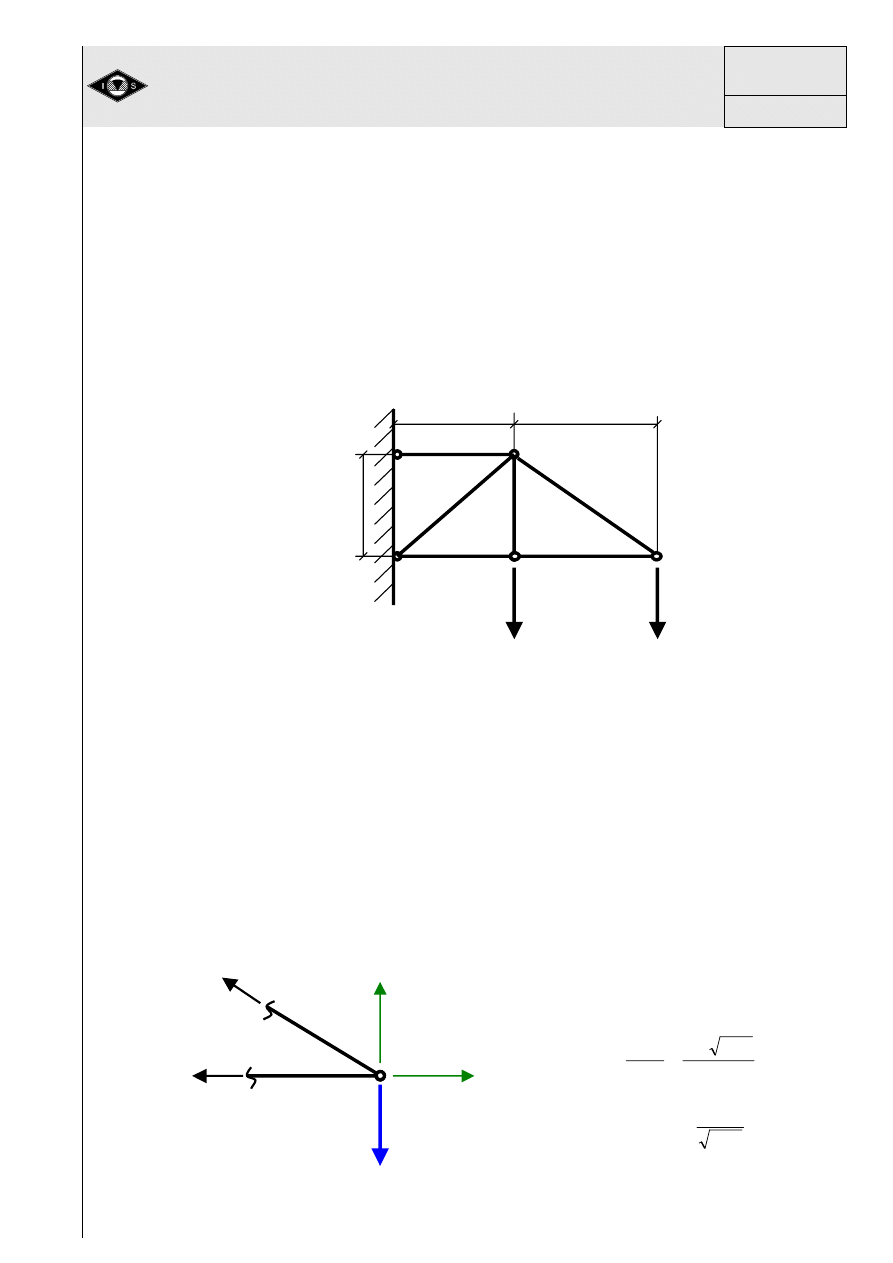
30

Rozwi

ą

zanie

−

Całkowite obci

ąż

enie na jedn

ą

kratownic

ę

:

]

[

19

]

/

[

8

.

3

]

[

5

kN

m

kN

m

P

r

=

⋅

=

−

Obci

ąż

enie jednego w

ę

zła

]

[

5

.

9

2

/

19

2

/

kN

P

P

r

w

=

=

=

−

Uwzgl

ę

dniaj

ą

c ci

ęż

ar kratownicy przyjmiemy ostatecznie obci

ąż

enie w w

ęź

le

]

[

10 kN

P

=

−

Schemat statyczny kratownicy

Rys. 41 Schemat statyczny kratownicy

Warunek statycznej (wewn

ę

trznej) wyznaczalno

ś

ci:

3

2

−

=

w

p

P

L

p

w

=

−

⋅

=

=

+

=

=

3

5

2

7

7

1

6

5

Metoda równowa

ż

enia w

ę

zła

Warunek równowagi w

ę

zła E

]

kN

[

18

1

25

.

3

10

sin

0

sin

0

0

cos

0

=

⋅

=

=

=

+

−

=

=

−

−

=

∑

∑

α

α

α

P

F

F

P

P

F

F

P

EC

EC

iy

EC

ED

ix

- pr

ę

t rozci

ą

gany

[kN]

15

25

.

3

5

.

1

18

cos

−

=

⋅

−

=

−

=

α

EC

ED

F

F

- pr

ę

t

ś

ciskany

Rys. 42 Rozkład sił w w

ęź

le E

A

B

C

D

E

P

P

1.2[m]

1.5[m]

1.0[m]

F

ED

F

EC

E

P=10[kN]

α

y

x

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 29

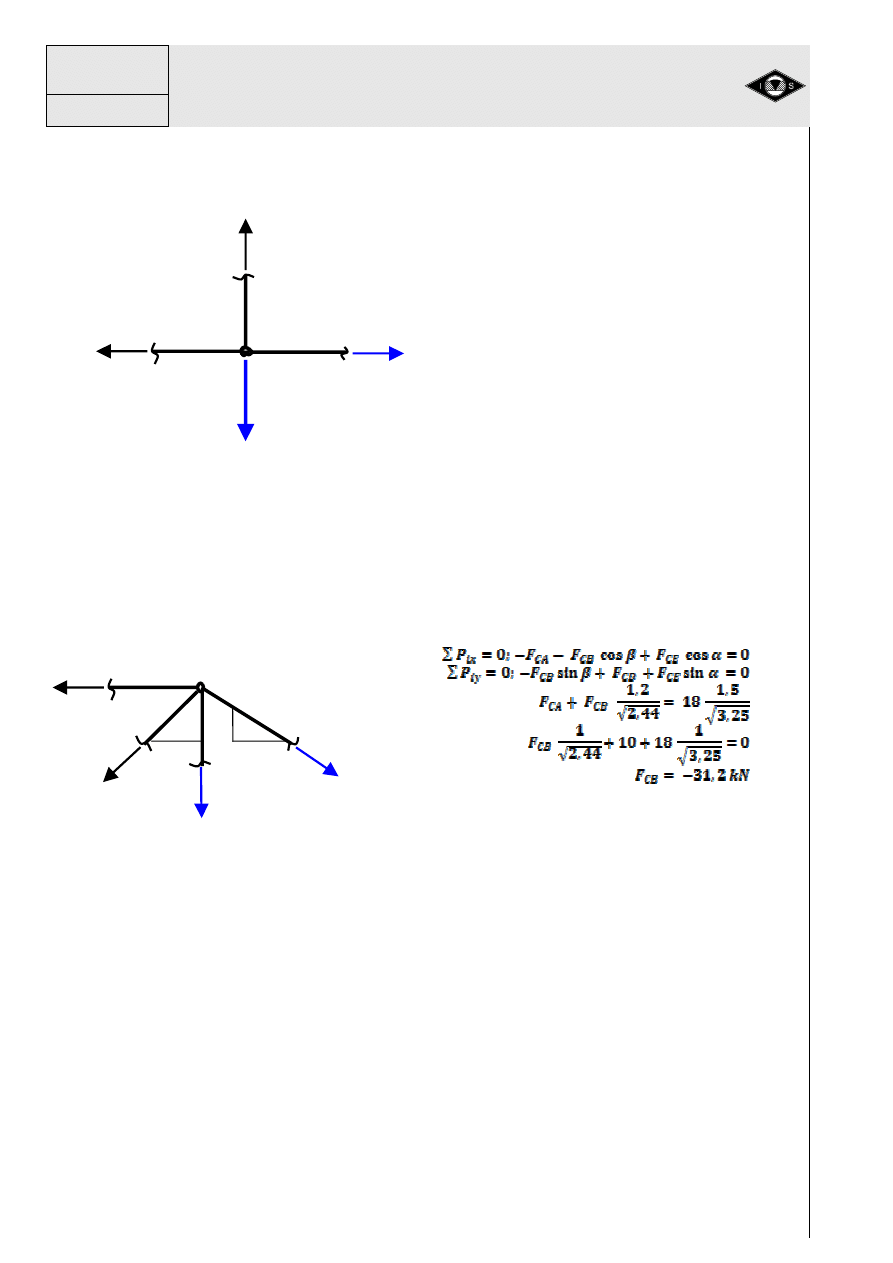
31

Warunek równowagi w

ę

zła D

- pr

ę

t

ś

ciskany

[kN]

10

=

=

P

F

CD

- pr

ę

t rozci

ą

gany

Rys. 43 Rozkład sił w

ęź

le D

Warunek równowagi w

ę

zła C

- pr

ę

t

ś

ciskany

[kN]

9

.

38

=

CA

F

- pr

ę

t rozci

ą

gany

Rozkład sił w w

ęź

le C

[kN]

15

0

0

0

0

−

=

=

=

+

−

=

=

−

=

∑

∑

DB

DB

DC

iy

DB

DE

ix

F

F

F

P

P

F

F

P

P=10[kN]

F

DB

D

F

DC

F

DE

= -15[kN]

F

CA

C

F

CB

F

CE

= 18 [kN]

F

CD

= 10[kN]

α

β

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 30

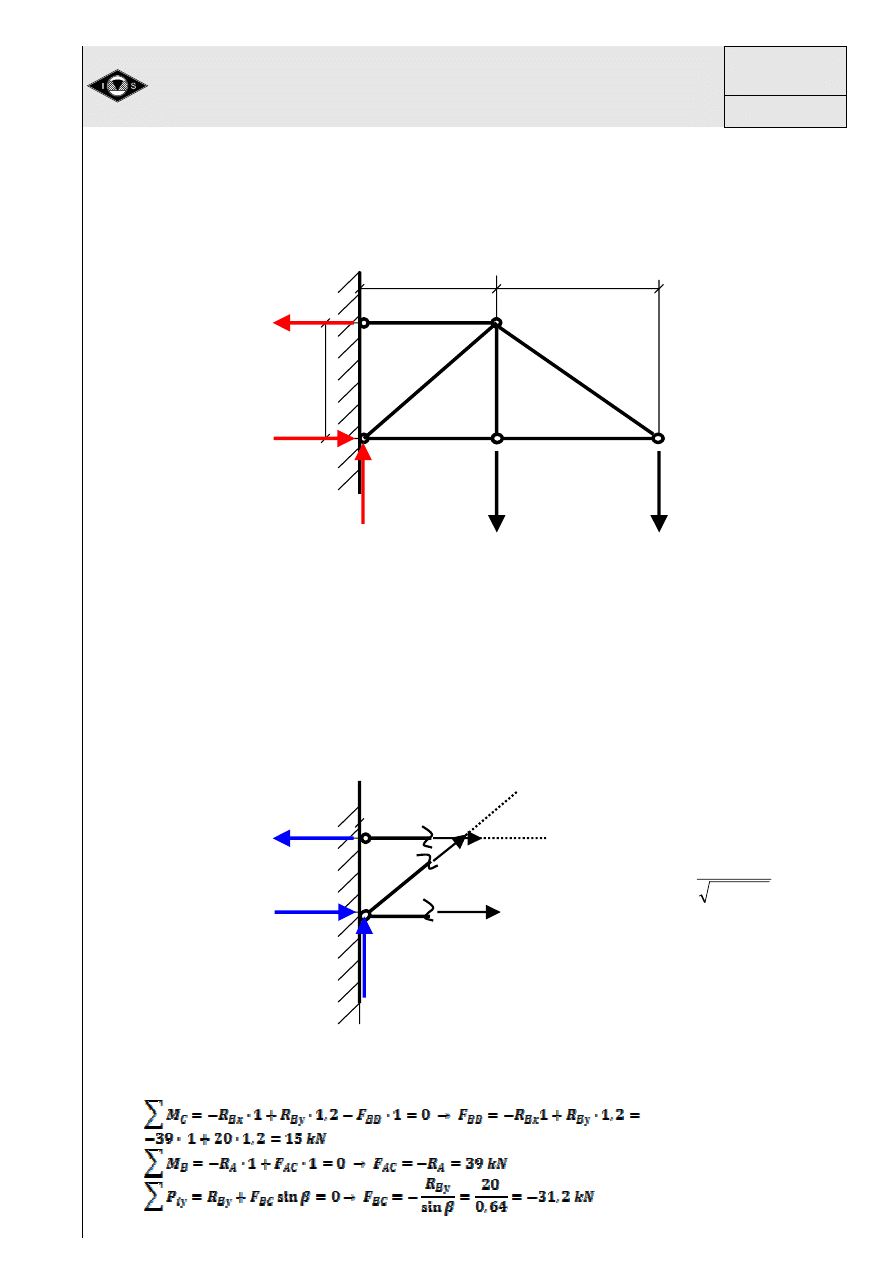
32

Metoda Rittera

1. Równania równowagi

Rys. 45 Reakcje w podporach kratownicy

]

[

39

0

]

[

20

0

]

[

39

0

kN

R

R

M

kN

R

P

kN

R

P

A

Bx

B

By

iy

A

ix

≈

=

=

=

=

≈

=

∑

∑

∑

2. Przeci

ę

cie przez trzy pr

ę

ty nie przechodz

ą

ce przez jeden punkt

64

.

0

1

2

.

1

1

sin

2

2

=

+

=

β

Rys. 46. Przeci

ę

cie pr

ę

tów dla celów metody Rittera

A

R

A

R

Bx

F

AC

F

BC

C

B

R

By

F

BD

B

β

A

B

C

D

E

P

P

1.2[m]

1.5[m]

1.0[m]

R

A

R

Bx

R

By

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 31

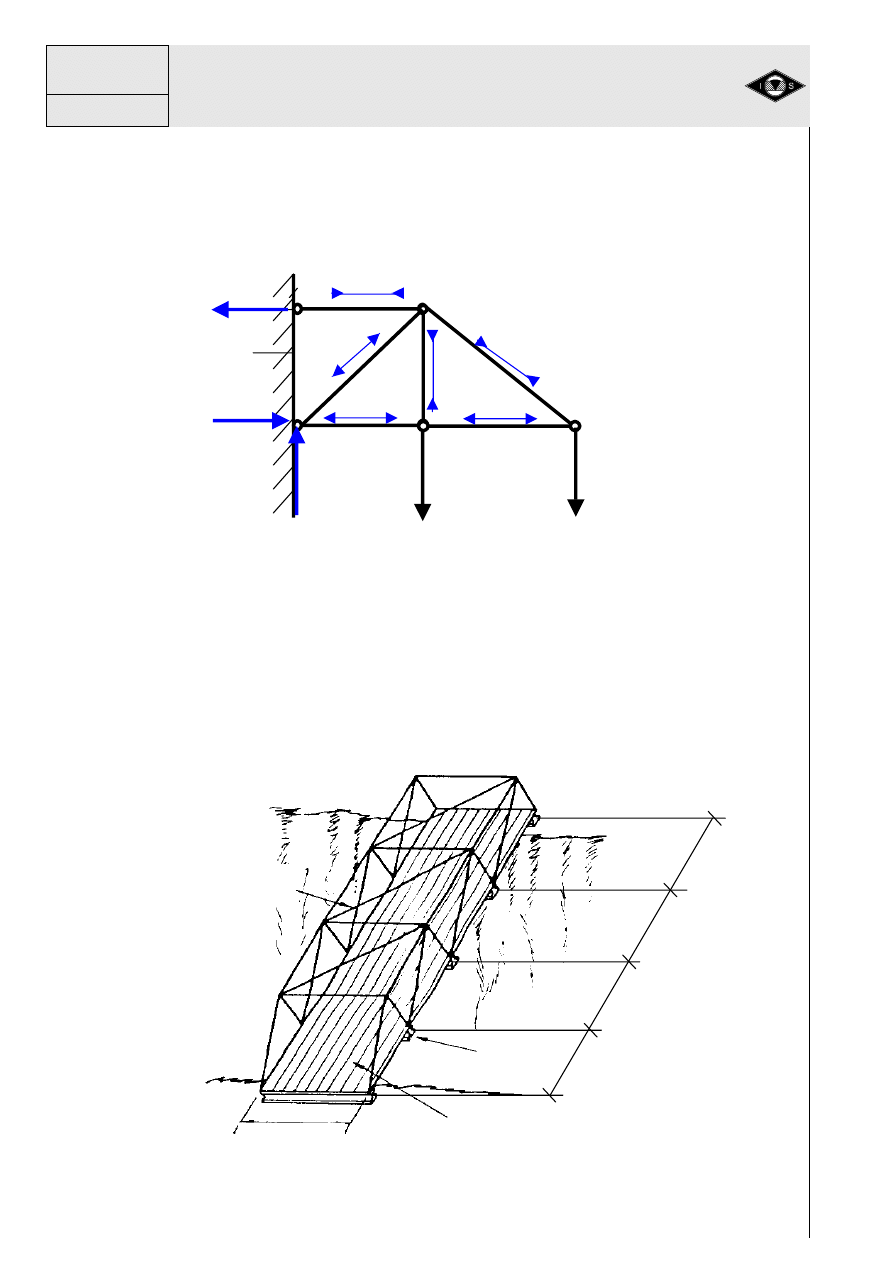
33

Rozwi

ą

zanie

(siły w kN)

Rys. 47 Wyniki oblicze

ń

sił w pr

ę

tach

Przykład 13
Wyznaczy

ć

siły w pr

ę

tach kratownicy przenosz

ą

cej obci

ąż

enie kładk

ą

o rozpi

ę

to

ś

ci

L=12[m]. Ka

ż

dy pr

ę

t – oprócz poprzecznych wzmocnie

ń

– ma długo

ść

l=3[m]. Kładka

ma szeroko

ść

b=2[m], a jej ci

ęż

ar wynosi G=35[kN]. Warto

ść

charakterystyczna ob-

ci

ąż

enia zmiennego Q=4 [kN/m

2

]. Cz

ęś

ciowy współczynnik bezpiecze

ń

stwa obci

ąż

e-

nia statycznego

4

.

1

)

(

=

s

f

γ

, a obci

ąż

enia dynamicznego

6

.

1

)

(

=

d

f

γ

Rys. 48 Widok kładki kratowej

Deski

Poprzeczna belka

4 x l = 3 m

Usztywnienie
poprzeczne

b = 2 m

A

B

E

P=10

P=10

R

A

=39

R

Bx

=39

R

By

=20

39.0

15.0

31.2

10.0

18.0

15.0

C

D

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 32

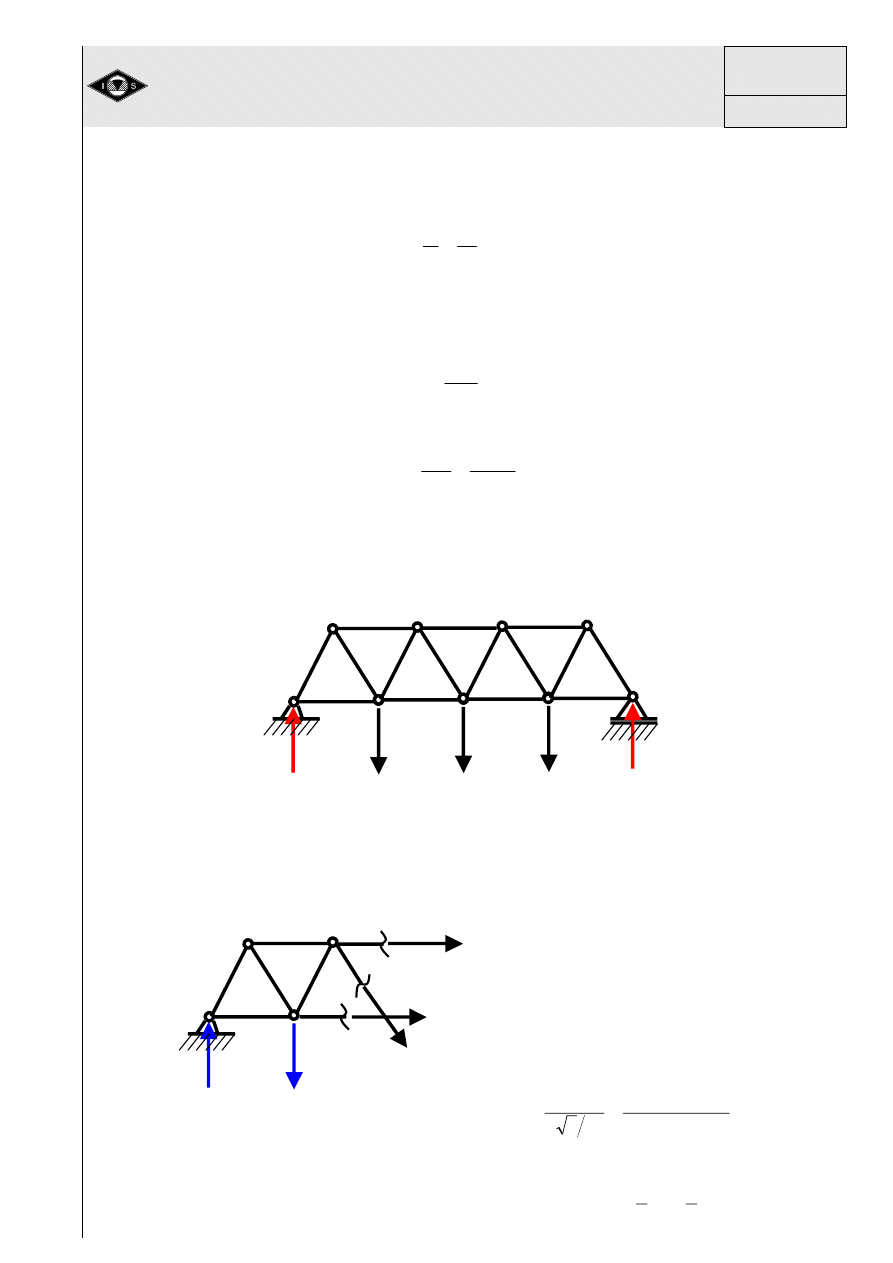
34

Rozwi

ą

zanie

1. Obci

ąż

enie stałe przypadaj

ą

ce na 1 metr mostu

[kN/m]

92

.

2

12

35

1

=

=

=

L

G

q

2. Ka

ż

dy w

ę

zeł dolnego pasa dwóch kratownic (lewej i prawej) obci

ąż

ony jest 3

metrami kładki

]

[

76

.

8

3

92

.

2

2

1

kN

l

q

P

g

=

⋅

=

⋅

=

3. Na jedn

ą

kratownice przypada

]

[

38

.

4

2

76

.

8

kN

P

g

=

=

4. Obci

ąż

enie zmienne pochodzi z cz

ęś

ci kładki o szeroko

ś

ci b=2[m] i długo

ś

ci

l=3[m]. Na jeden w

ę

zeł przypada wi

ę

c

]

[

14

2

3

2

4

2

kN

Qbl

P

d

=

⋅

⋅

=

=

Ostatecznie obci

ąż

enie w

ę

zła wynosi

]

[

3

.

25

6

.

1

12

4

.

1

38

.

4

)

(

)

(

kN

P

P

P

d

f

d

s

f

g

=

⋅

+

⋅

=

+

=

γ

γ

5. Schemat statyczny kratownicy (rys. 49)

Rys. 49 Schemat statyczny kratownicy

Metoda Rittera (rozwi

ą

zanie dla pr

ę

tów DF, DE i CE)

∑

∑

∑

=

=

=

0

)

3

0

)

2

0

)

1

ix

iD

iE

P

M

M

ad. 1)

0

60

sin

2

=

°

+

−

⋅

l

F

Pl

l

R

DF

A

]

[

5

.

58

2

/

73

.

1

95

.

37

2

3

.

25

2

3

2

kN

R

P

F

A

DF

−

=

⋅

−

=

−

=

-

pr

ę

t

ś

ciskany

ad. 2)

0

60

sin

2

2

3

=

°

−

−

⋅

l

F

l

P

l

R

CE

A

P

P

R

J

=37.95[kN]

R

A

=37.95[kN]

G

E

F

H

P

A

B

C

D

P

A

B

C

D

E

F

DE

F

CE

F

DF

R

A

Rys. 50 Przykład przeci

ę

cia kratownicy

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 33

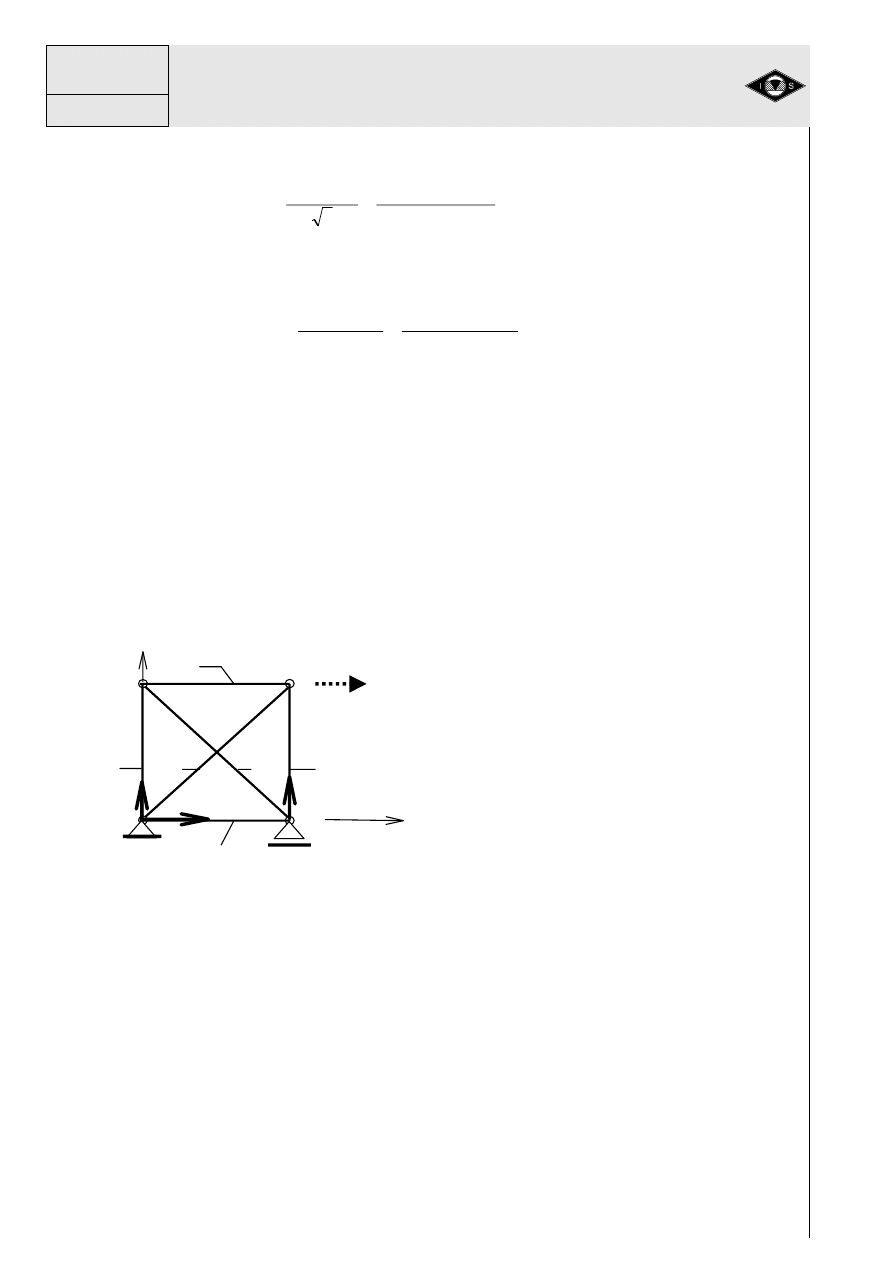
35

]

[

2

.

51

73

.

1

95

.

37

3

3

.

25

3

3

kN

R

P

F

A

CE

=

⋅

+

−

=

+

−

=

-

pr

ę

t rozci

ą

gany

ad. 3)

0

60

cos

=

°

+

+

DE

CE

DF

F

F

F

(

)

6

.

14

5

.

0

2

.

51

5

.

58

5

.

0

=

−

−

−

=

−

−

=

CE

DF

DE

F

F

F

-

pr

ę

t rozci

ą

gany

Przykład 14
Kratownica statycznie niewyznaczalna
Obliczy

ć

warto

ś

ci sił w pr

ę

tach kratownicy przedstawionej na rys.51 .

Kratownica zbudowana jest z 6 pr

ę

tów o identycznym przekroju

2

( )

1cm

F i

=

, oraz z

materiału, którego moduł Younga

5

2 10 MPa

E

= ⋅

. Pr

ę

ty 1, 3, 5, 6 maj

ą

identyczn

ą

długo

ść

( )

100cm

l i

=

.Oraz l(2)=l(4). Kratownica obci

ąż

ona jest sił

ą

poziom

ą

4

10 N

P

=

i podpart

ą

na dwóch podporach w w

ę

złach 1 i 2. Pr

ę

t 3 jest w poziomie. Podpora

przegubowa przesuwna daje reakcj

ę

o kierunku pionowym.

Rozwi

ą

zanie. Z warunku równowagi całej konstrukcji

4

4

4

1

1

2

10 N,

10 N,

10 N

x

y

R

R

R

= −

= −

=

1. Sprawdzenie czy konstrukcja jest statycznie wewn

ę

trznie wyznaczalna

Ilo

ść

w

ę

złów

4

w

=

, ilo

ść

pr

ę

tów

6

p

=

, wzór na sprawdzenie statycznej wyznaczal-

no

ś

ci

2

3,

p

w

=

−

sprawdzenie

1

2 4 3

5

p

= ⋅ − =

. Ró

ż

nica mi

ę

dzy rzeczywist

ą

ilo

ś

ci

ą

pr

ę

tów p a ilo

ś

ci

ą

pr

ę

tów p

1

, przy której kratownica była by statycznie wyznaczalna,

wynosi

1

1

p

p

−

=

. Wniosek kratownica jest jednokrotnie wewn

ę

trznie statycznie nie-

wyznaczalna.
2. Nale

ż

y kratownic

ę

uczyni

ć

statycznie wyznaczaln

ą

np. odcinaj

ą

c my

ś

lowo pr

ę

t 4

od w

ę

zła 3. W miejscu my

ś

lowego przeci

ę

cia w rzeczywistej konstrukcji działa siła X,

która zapewnia,

ż

e w miejscu tym b

ę

dzie ci

ą

gło

ść

konstrukcji czyli

0

δ

=

.

Równanie ci

ą

gło

ś

ci konstrukcji w miejscu przeci

ę

cia

10

11

0

X

δ δ

δ

=

+

=

.(a)

Gdzie

10

δ

jest luk

ą

mi

ę

dzy w

ę

złem 3 a ko

ń

cem pr

ę

ta 4 wywołan

ą

działaniem siły rze-

czywistej P (rys.52).

1

2

3

4

5

6

1

2

3

4

R

1y

R

1x

R

2

y

x

P

Rys.51 Schemat obci

ąż

e

ń

kratownicy

statycznie niewyznaczalnej

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 34

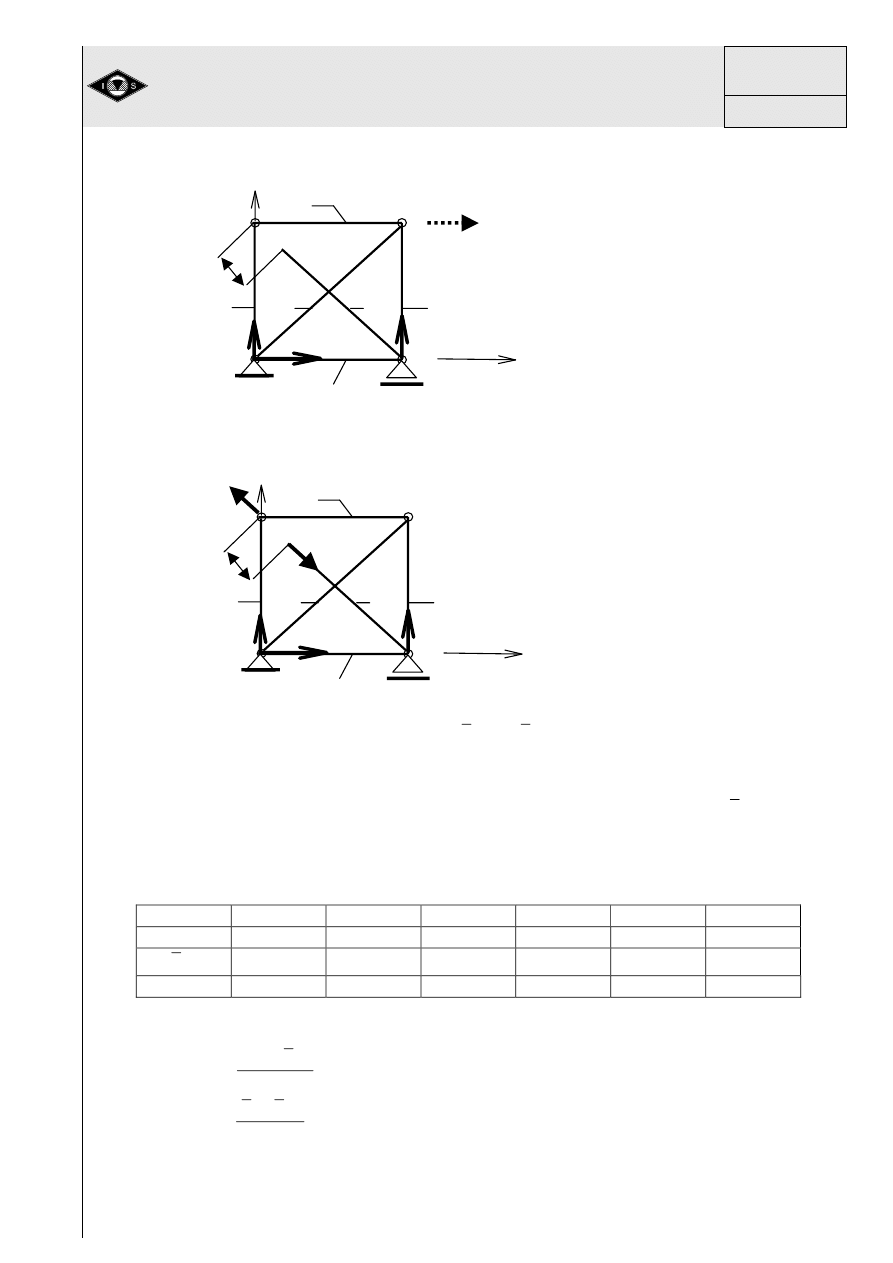
36

Natomiast

δ

11

jest luk

ą

mi

ę

dzy w

ę

złem 3 a ko

ń

cem pr

ę

ta 4 wywołan

ą

wirtualnym ob-

ci

ąż

eniem o warto

ś

ci

1N

X

=

(rys.53).

Z warunku równowagi całej konstrukcji

1

1

2

0,

0,

0

x

y

R

R

R

=

=

=

3. Z warunków równowagi poszczególnych w

ę

złów kratownic zamieszczonych

na rysunkach 2 i 3 obliczamy warto

ś

ci sił działaj

ą

cych w pr

ę

tach. I tak

( )

N i

s

ą

siłami wywołanymi obci

ąż

eniem rzeczywistym (rys.52), natomiast

( )

N i

s

ą

si-

łami powstałymi w wyniku działania obci

ąż

enia wirtualnego (rys.3). Warto

ś

ci

tych sił oraz długo

ś

ci pr

ę

tów zamieszczono w tablicy 2.

Tablica 2

i

1

2

3

4

5

6

N(i)/10

4

0

1,414

0

0

-1

0

( )

N i

0,707

-1

0,707

-1

0,707

0,707

l(i)cm

100

141,4

100

141,4

100

100

4. Warto

ś

ci współczynników

10

δ

i

11

δ

obliczamy ze wzorów:

6

10

1

( )

( )

( )

( ) ( )

i

i

N i

N i

l i

F i E i

δ

=

=

⋅

=

∑

(b)

6

11

1

( ) ( )

( )

( ) ( )

i

i

N i N i

l i

F i E i

δ

=

=

=

∑

(c)

Poniewa

ż

2

( )

1cm

F i

F

= =

oraz

5

( )

2 10 MPa

E i

E

= = ⋅

to wzory (b) i (c) przybior

ą

posta

ć

1

2

3

4

5

6

1

2

3

4

R

1y

R

1x

R

2

y

x

P

δ

10

3

1N

1N

1

2

4

5

6

1

2

3

4

R

1y

R

1x

R

2

y

x

δ

11

Rys. 52 Układ kratownicy
z rozci

ę

tym pr

ę

tem

Rys. 53 Układ kratownicy z zało

ż

onymi

obci

ąż

eniami wirtualnymi

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

3.1

Instytut

Spawalnictwa

w Gliwicach

AW 35

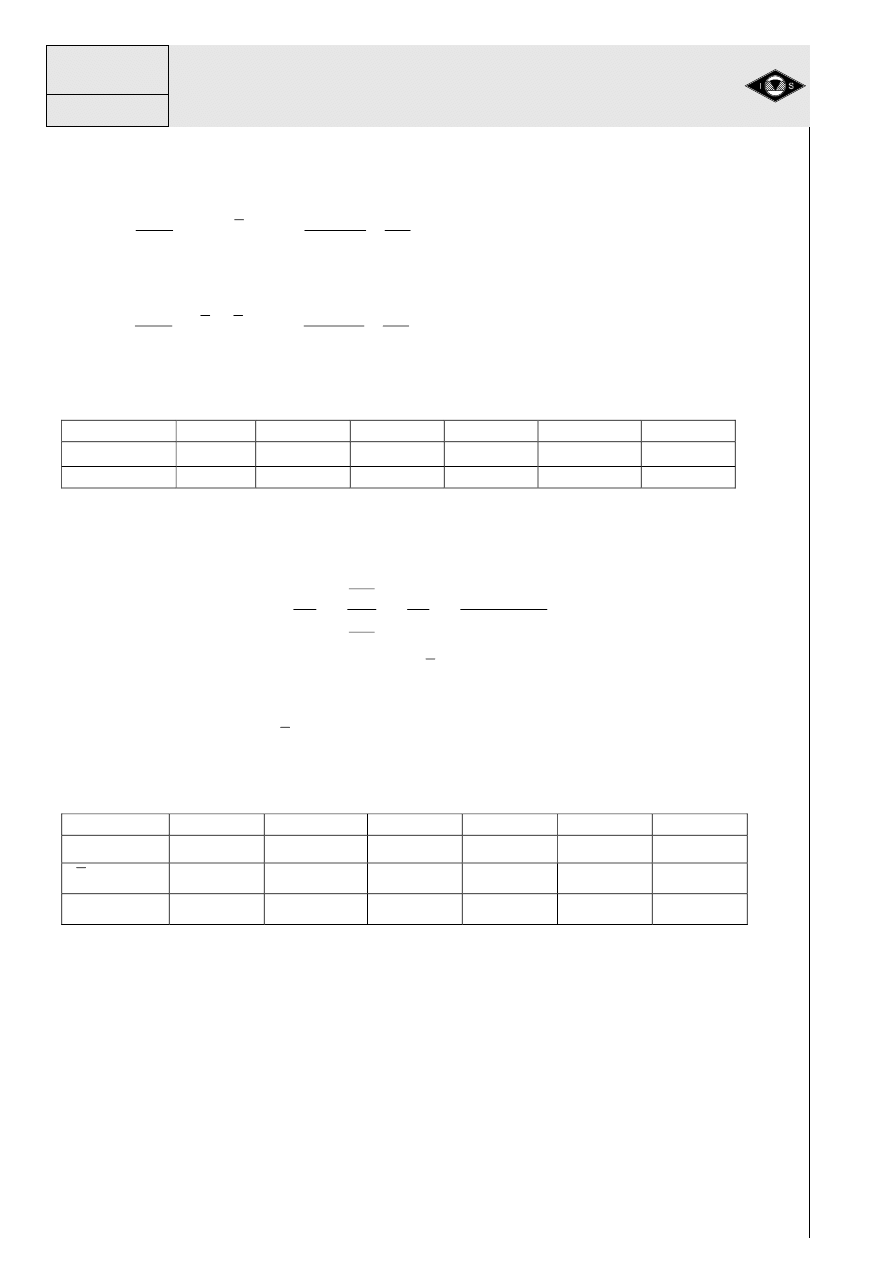
37

6

10

6

1

10

10

1

( )

1

( ) ( ) ( )

i

i

i

i

k

i

k

N i N i l i

F E

FE

FE

δ

=

=

=

=

=

=

=

⋅

∑

∑

(d)

6

11

6

1

11

11

1

( )

1

( ) ( ) ( )

i

i

i

i

k

i

k

N i N i l i

F E

FE

FE

δ

=

=

=

=

=

=

=

⋅

∑

∑

(e)

W tablicy 3 zamieszczono warto

ś

ci

10

( )

k

i

oraz

11

( )

k

i

Tablica 3

i

1

2

3

4

5

6

k

10

(i)[N cm]

0

6

2 10

− ⋅

0

0

6

0.707 10

−

⋅

0

k

11

(i)[N cm]

50,0

141,4

50,0

141,4

50,0

50,0

10

k

obliczamy przez podstawienie danych z tabeli 2 do (d) st

ą

d

6

10

2, 707 10 Ncm

k

= −

⋅

11

k

obliczamy przez podstawienie danych z tabeli 2 do (e) st

ą

d

11

482,8Ncm

k

=

Z równania (a) mamy

10

6

10

10

11

11

11

2, 707 10

5607

482,8

k

k

FE

X

k

k

FE

δ
δ

−

⋅

= −

= −

= −

= −

=

Plus oznacza,

ż

e w rzeczywisto

ś

ci zwrot sił

( )

N i

jest zgodny ze znakiem w tabeli 1.

Warto

ś

ci rzeczywistych sił działaj

ą

cych w konstrukcji przedstawionej na rys.1

maj

ą

posta

ć

( )

( )

( )

rz

N

i

N i

N i

X

=

+

⋅

Warto

ś

ci tych sił przedstawiono w tablicy 4

Tablica 4

i

1

2

3

4

5

6

N(i)[N]

0

4

1, 414 10

⋅

0

0

4

10

−

0

[ ]

( )

N i

X N

⋅

3964

4

0, 561 10

−

⋅

3964

5607

−

3964

3964

[ ]

( )

rz

N

i N

3964

8533

3964

5607

−

6036

−

3964

Literatura

1. W. Siuta Mechanika Techniczna PWSZ Warszawa
2. A. Jakubowicz, Z. Orło

ś

, Wytrzymało

ś

c materiałów WNT Warszawa

Opracowanie Instytut Spawalnictwa - Gliwice.

Wszelkie prawa zastrze

żone. Powielanie lub rozpowszechnianie ca

ło

ści wzgl

ędnie

fragmentu w jakiejkolwiek formie i w jakikolwiek sposób jest zabronione.

KURS MIĘDZYNARODOWEGO

INŻYNIERA / TECHNOLOGA / MISTRZA / INSTRUKTORA SPAWALNIKA

(IWE/IWT/IWS/IWP)

Podstawy teorii układów konstrukcji

Instytut

Spawalnictwa

w Gliwicach

3.1

AW 36