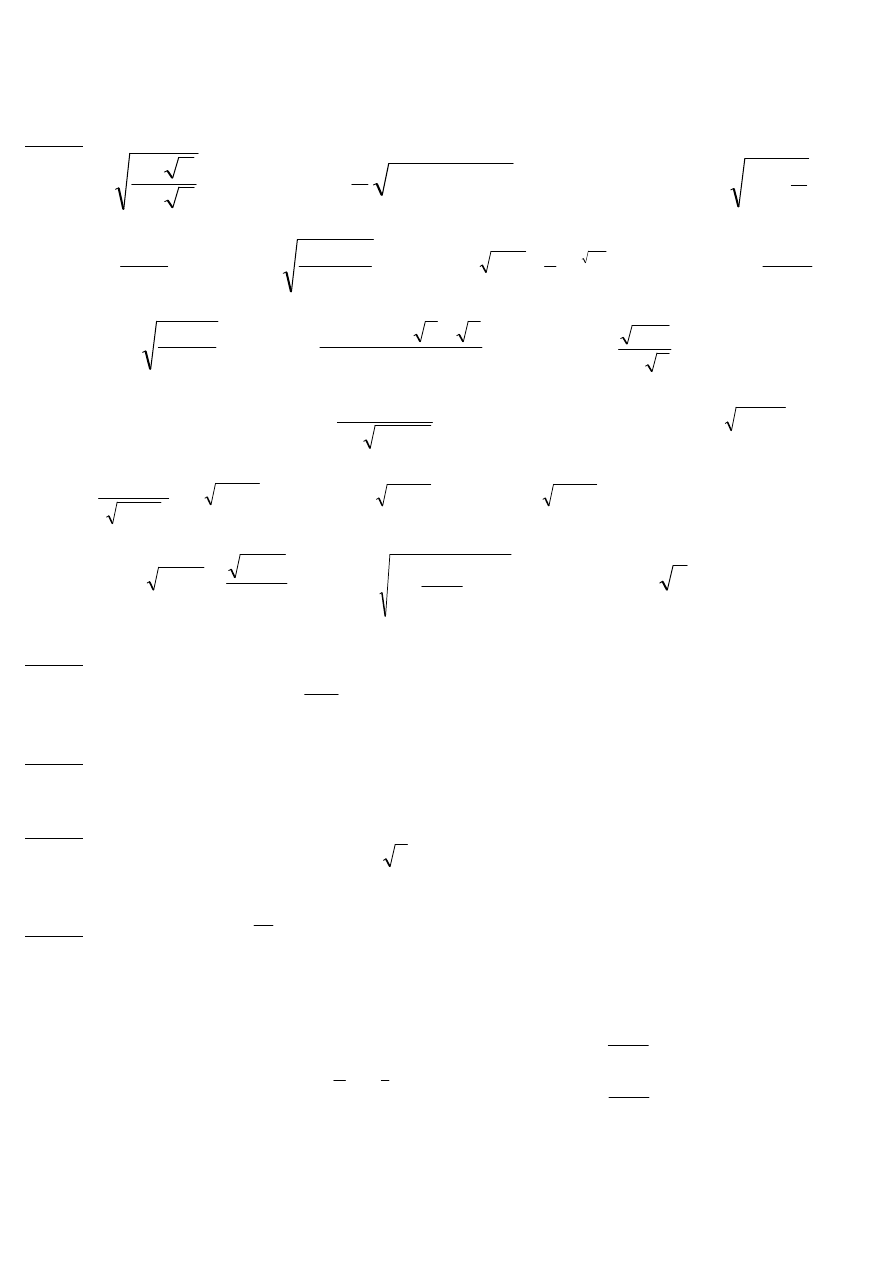
LISTA 3. Pochodna funkcji jednej zmiennej.
Zad. 1: Obliczyć pochodne funkcji:
a.
x
x
x
f
+
−
=
1
1
)
(
b.
(
)
3
)
(
3
2
)
(
x
e
arctg
x
f
=
c.
(
)
5
3
2
1
1
)
(
x
x
x
x
f
+
−
=
d.
x
x
x
f
2
1
2
1
ln
)
(
−
+
=
e.
3
2
)
1
(
1
)
(
−
+
=
x
x
x
f
f.
1
2
2
1
1
)
(
−
−
−
=
x
e
x
x
f
g.
)
2
1
2
3
ln(cos
)
(
x
x
x
f
+
+
=
h.
)
2
1
2
1
ln(
)
(
4
x
x
x
f
−
+
=
i.
x
x
x
arctg
x
x
f
−
+
=
)
1
(
)
(
j.
x
x
arctg
x
f
−
−
=
1
1
)
(
k.
( )
thx
x
x
f
1
)
(
8
+
=
l.
(
)
x
e
x
x
f
5
cos
)
(
=
m.
2
4
1
1
ln
)
(
x
x
x
f
−
+
=
n.
(
)
1
ln
)
arcsin(
)
(
4
2
2
−
+
+
=
−
x
x
x
e
e
e
x
f
o.
2
2
1
ln
1
arcsin
)
(
x
x
x
x
x
f
−
+
−
=
p.
)
1
ln(
1
)
(
2
2
x
x
arctgx
x
x
f
−
+
−
+
=
r.
( )
)
ln(
)
(
tgx
tgx
x
f
=
s.
(
)
x
x
x
x
x
f
2
2
1
1
ln
)
(
+
−
+
+
=
t.
1
2
1
ln
)
(
2
+
+
=
x
e
x
f
u.
( )
x
e
x
x
f
sin
)
(
=
w.
( )
ctgx
e
x
x
f
=
)
(
Zad. 2: Znaleźć równania stycznych i normalnych do danych krzywych we wskazanych punktach:
)
0
;
1
(
,
2
1
arcsin
)
);
0
,
0
(
,
2
)
P
x
y
b
O
x
tg
y
a
−
=
=
;
)
1
;
(
,
ln
)
;
1
,
)
0
1
2
e
P
x
y
d
x
e
y
c
x
=
−
=
=
−
.
Zad. 3: Znaleźć równanie normalnej do krzywej y=xlnx i jednocześnie równoległej do prostej
2x-2y+3=0.
Zad. 4: Znaleźć kąty przecięcia krzywych:
.
2
)
(
,
)
(
.
;
)
(
,
)
(
.
2
3
3
−
=
=
=
=
x
x
e
x
g
e
x
f
b
x
x
g
x
x
f
a
Zad. 5: Obliczyć pochodną
dx
dy
wybranej funkcji określonej równaniami parametrycznymi:
−
=
−
=
=
=
−
=
=
cykloida
t
a
y
t
t
a
x
c
elipsa
t
b
y
t
a
x
b
prosta
linia
t
y
t
x
a
)
cos
1
(
)
sin
(
.
sin
cos
.
)
1
(
8
4
.
a
Kartezjusz
lisc
t
at
y
t
at
x
f
lancuchowa
linia
t
t
a
y
t
a
x
e
asteroida
t
a
y
t
a
x
d
+
=
+
=
+
=
=
=
=
3
2
3
3
3
1
1
.
1
2
ln
.
sin
cos
.
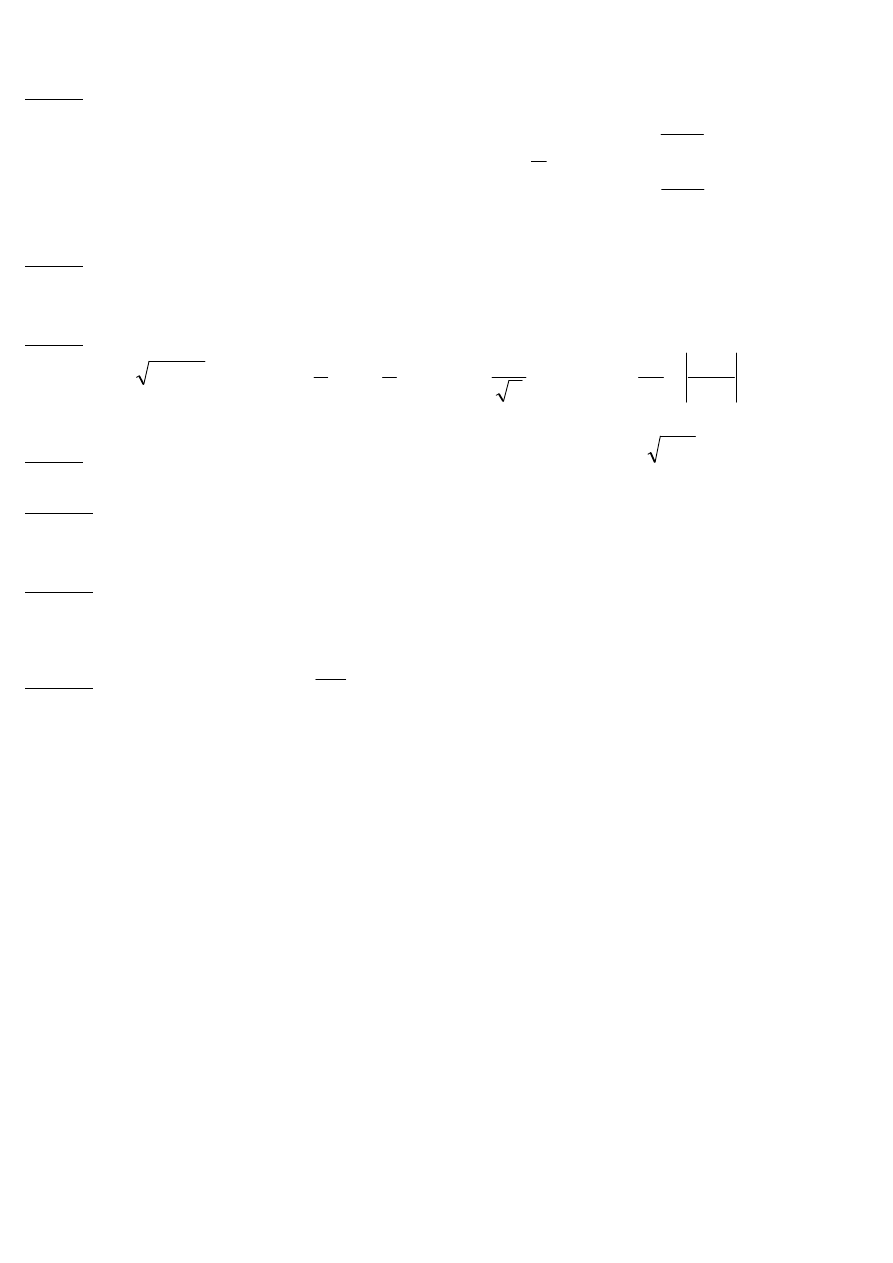
Zad. 6: Napisać równania stycznych i normalnych do linii o równaniu parametrycznym:
2
1
3
1
3
.
;
4
1
)
ln(
2
.
;
0
2
.
0
2
2
2
0
0
=
+
=
+
=
=
+
=
+
=
=
=
=
−
t
t
at
y
t
at
x
c
t
ctgt
tgt
y
ctgt
x
b
t
e
y
e
x
a
t
t
π
.
Zad. 7: Dana jest funkcja f(x)=x
3
-2x+1. Znaleźć liczby
∆f(1) i df(1) dla przyrostów:
.
01
,
0
.
;
1
,
0
.
;
1
.
=
∆
=
∆
=
∆
x
c
x
b
x
a
Zad. 8: Znaleźć wskazane różniczki zupełne dla przyrostu dx:
(
)
(
)
;
1
)
;
ln
)
2
+
+
a
x
arctg
a
d
b
a
x
x
d
a
.
ln
2
1
)
;
ln
)
+
−
a
x
a
x
a
d
d
x
x
d
c
Zad. 9: Wykorzystując różniczkę zupełną obliczyć przybliżenia liczb:
.
05
,
1
.
;
02
,
1
.
3
arctg
b
a
Zad. 10: Wyznaczyć wzór na n-tą pochodną f
(n)
(x), jeżeli:
.
ln
)
(
.
;
2
cos
)
(
.
;
sin
)
(
.
;
)
(
.
;
,
)
(
.
x
x
x
f
e
x
x
f
d
x
x
f
c
xe
x
f
b
R
s
x
x
f
a
x
s
=
=
=
=
∈
=
Zad. 11: Znaleźć wskazane różniczki zupełne rzędu n dla przyrostu dx:
(
)
( )
.
.
;
2
.
2
3
2
sin
2
x
x
e
d
b
d
a
−
Zad. 12: Obliczyć drugą pochodną
2
2
dx
y
d
funkcji określonej równaniami parametrycznymi:
=
=
3
2
.
t
y
t
x
a
;
=
=
spirala
t
e
y
t
e
x
b
t
t
sin
cos
.
;
−
=
=
)
1
ln(
arcsin
.
2
t
y
t
x
c
Wyszukiwarka
Podobne podstrony:
LISTA 1 Podstawowe funkcje 2010
LISTA 1 Podstawowe funkcje 2010
Pochodna funkcji2009 2010
LISTA 4 Twierdzenia Przebieg funkcji 2010
Lista 7 - Zastosowania pochodnych funkcji jednej zmiennej, Studia, Matematyka
2010 12 17 pochodna funkcji
2010 12 17 pochodna funkcji
4 pochodna funkcji jednej zmiennej
10 Pochodna funkcji jednej zmiennej
Pochodne funkcji, IB i IŚ, 2011 12
Przed maturą Zestaw XI Ciągłość i pochodna funkcji
LISTA 5 Calki nieoznaczone 2010
lista nr2 EKONOMETRIA1 2010 11 Nieznany
3 Pochodna funkcji (2)
5 pochodna funkcji
14 Pochodna funkcji odwrotnej i złożonej
4 Pochodna funkcji
pochodne funkcji wzory
więcej podobnych podstron