2014-05-13

1

Bezpieczeństwo i ochrona

danych

Uwierzytelnianie

Grzegorz Kołaczek, Ph.D., Eng.

Agenda

• Zarządzanie kluczami
• Cel uwierzytelniania
• Hasła
• Metoda „challenge-response”

Zarządzanie kluczami

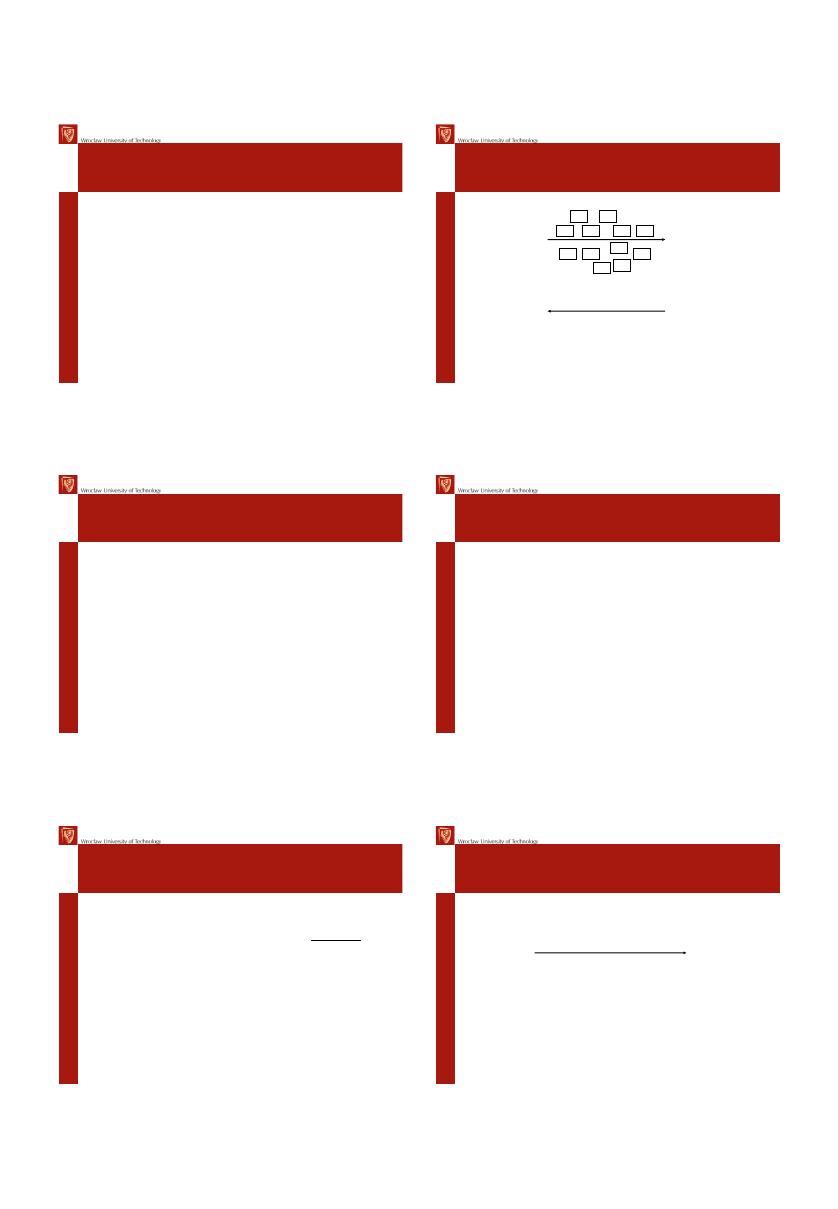
• Dla sieci z algorytmem symetrycznym:

• Alicja, Bob, Carol oraz Dave chcą się komunikować z zachowaniem

poufności

• Aby to osiągnąć, jeżeli jest n osób (podmiotów), potrzeba

n

n(n-1)

2

2

• Zarządzanie i przesyłanie kluczy staje się wyzwaniem.

Alicja

Carol

Bob

Dave

k

ab

k

ac

k

bd

k

cd

k

ad

k

bc

( )

=

różnych kluczy

Definicje

• Ustanowienie klucza

jest to proces, którego celem jest udostępnienie pewnego sekretu,
niezbędnego dla poprawnej realizacji określonego protokołu
kryptograficznego, dwóm lub więcej podmiotom

• Zarządzanie kluczem

jest to zbiór działań i mechanizmów, które wspierają proces
ustanowienia klucza kryptograficznego oraz utrzymanie
istniejących relacji pomiędzy stronami, w skład których wchodzi
m.in. Konieczność odnowienia kluczy, bezpiecznego przekazania
kluczy, itp.

Centrum dystrybucji kluczy

• Podejście naiwne

• Protokół:

(1) Alicja → KDC

: “chce rozmawiać z Bobem”

(2) KDC → Alicja

: KDC wybiera losowo k

ab

, wysyła Ek

a

[k

ab

], Ek

b

[k

ab

, “bilet a-b”]

(3) Alicja → Bob

: Alicja deszyfruje Ek

a

[k

ab

], przesyła bilet do Boba

(4) Bob

: Bob deszyfruje bilet

• Alicja i Bob współdzielą klucz k

ab

.

Alicja

Carol

Bob

Dave

KDC

k

a

k

b

k

c

k

d

Wszystkie strony
współdzielą klucze z KDC

Problemy podejścia naiwnego

• Podejście naiwne:

• Problemy:

– Pojedynczy punkt awarii - KDC (lub cel ataku)
– Brak uwierzytelniania
– Mała skalowalność
– Powolność

Alicja

Carol

Bob

Dave

KDC

k

a

k

b

k

c

k

d

Wszystkie strony
współdzielą klucze z KDC

2014-05-13

2

Puzzle Merklego

• Ralph Merkle (Stanford, 1974)
• Puzzle Merklego pozwalają wymienić klucze Alicji i Bobowi bez

udziału KDC

• Protokół:

(1)

Alicja generuje puzzle P

i

= E

pi

[“To jest puzzle #X

i

”, k

i

]

gdzie i = 1 .. 2

20

, |p

i

| = 20 bit (słaby), |k

i

| = 128 bit (mocny)

X

i

, p

i

oraz k

i

są wybrane losowo oraz są różne dla różnych wartości i.

(2)

Alicja wysyła wszystkie puzzle P

i

do Boba.

(3)

Bob wybiera losowo puzzle j є {1 … 2

20

} i łamie siłowo P

j

(n.p. dla klucza p

j

). Pozwala to odczytać X

j

oraz k

j

z puzzla.

(4)

Bob wysyła X

j

do Alicji tekstem jawnym.

(5) Alicja sprawdza dla indeksu j wartość X

j

(z tablicy) aby otrzymać k

j

.

=>

Alicja oraz Bob teraz współdzielą klucz k

j

.

Puzzle Merklego

Alicja

Bob

P

1

P

6

P

3

P

4

P

12

P

7

P

9

P

2

P

5

P

14

P

11

P

13

Generuje 2

20

puzzli

Alicja sprawdza X

j

Współdzielonym

sekretem jest k

j

Wybiera losowo puzzle
P

j

i łamie je.

Wysyła X

j

do Alicji

Sekretem jest k

j

P

i

= Ep

i

[“To jest puzzle #X

i

”, k

i

]

Intruz ???

Zna jedynie puzzle
oraz X

j

Atak na puzzle Merklego

• Intruz musi złamać około połowę puzzli aby znaleźć

X

j

(bo

k

j

)

– Potrzebny czas dla puzzli 2

20

= 2

19

x 2

19

= 2

38

• Jeżeli Alicja i Bob mogą sprawdzić 10 000 kluczy/sekundę

– realizacja ich kroków zajmie im około minuty (2

19

dla Boba)

– plus dodatkowa minuta aby wymienić puzzle łączem 1.544MB (T1)

• Przy podobnych zasobach Intruzowi złamanie klucza zajmie około

roku.

• Uwaga: Puzzle Merkleego „zapychają” łącza komunikacyjne – mało

praktyczne

Wymiana Diffiego-Helmana

• Diffie-Hellman (Stanford, 1976)
• Ogólnoświatowy standard np. dla smart cards, etc.
• Protokół:

Dla ciała skończonego Z

p

= <0, … p-1> gdzie p jest l.pierwszą (p około 300 cyfrową)

Niech g є Z

p

(generator)

(1)

Alicja

: Alicja wybiera losową dużą wartość a є Z

p

(2)

Bob

: Bob wybiera losową dużą wartość b є Z

p

(3)

Alicja

→

Bob

: Alicja przesyła do Boba g

a

(mod p)

(4)

Bob

→

Alicja

: Bob przesyła do Alicji g

b

(mod p)

(5)

Alicja oraz Bob

: obliczają g

ab

: Alicja oblicza (g

b

)

a

=

g

ab

(mod p)

: Bob oblicza (g

a

)

b

=

g

ab

(mod p)

=> Alicja oraz Bob współdzielą sekret g

ab

Moc protokołu D-H

• Moc protokołu Diffie-Hellman oparta na:

– Znając p, g, g

a

, trudno obliczyć a (problem lograrytmów dyskretnych)

– Znając p, g, g

a

, g

b

trudno Intruzowi obliczyć g

ab

(problem Diffie-Hellman)

– Wiadomo że DL



DH lecz nie wiadomo czy DH



DL.

• W istocie, moc systemu zależy od trudności faktoryzacji liczb

rozmiaru p

• Generator g może być mały

• Nie należy używać wartości g

ab

jako wartości tajnego klucza

– Lepiej obliczyć skrót lub użyć jako ziarno dla algorytmu PRNG – nie

wszystkie bity sekretu mają rozkład jednostajny

Uwierzytelnianie

Alicja

Bob

W jaki sposób Bob może się upewnić, że Alicja jest Alicją?

Kanał niezabezpieczony

Intruz

(

Intruz kontroluje kanał!)

Cześć! Jestem Alicja

2014-05-13

3

Uwierzytelnianie

• Uwierzytelnianie jest sposobem potwierdzenia tożsamości

podmiotów.

• Umożliwia jednej stronie uzyskać pewność odnoście tożsamości

drugiej stronny w komunikacji

• Uwierzytelnienie dostarcza środków umożliwiających osiągnięcie

powyższego celu w sytuacji gdy strony korzystają z
niezabezpieczonego kanału komunikacyjnego, w obecności możliwych
ataków oraz gdy strony nie mają współdzielonego sekretu

• Uwaga: uwierzytelnieniu musi towarzyszyć wymiana kluczy

kryptograficznych w celu uniknięcia przechwycenia sesji (session
hijacking) (po uwierzytelnieniu).

Uwierzytelnienie

• Alicja musi udowodnić swoją tożsamość przed Bobem

– Alicja oraz Bob mogą być ludźmi lub komputerami

• Można również wymagać aby Bob udowodnił swoją

tożsamość (uwierzytelnienie wzajemne)

• Można również oczekiwać ustalenia klucza sesji
• Można również definiować inne wymagania:

– Wykorzystanie tylko kluczy asymetrycznych
– Wykorzystanie tylko algorytmów symetrycznych
– Wykorzystanie tylko kryptograficznych funkcji skrótu
– Zapewnienie anonimowości, niezaprzeczalności, etc., etc.

Czym jest uwierzytelnienie?

• Uwierzytelnienie (authentication):

– powiązanie tożsamości z identyfikatorem

• Jak to osiągnąć?

– Wiedza (podmiot coś wie - sekret)

• ?

– Posiadanie (podmiot coś ma)

• ?

– Stan (podmiot jest czymś)

• ?

– Lokalizacja (podmiot przebywa gdzieś)

• ?

Czym jest uwierzytelnienie?

• Uwierzytelnienie (authentication):

– powiązanie tożsamości z identyfikatorem

• Jak to osiągnąć?

– Wiedza (podmiot coś wie - sekret)

• Hasła, identyfikatory, …

– Posiadanie (podmiot coś ma)

• Karty, znaczniki, …

– Stan (podmiot jest czymś)

• Odcisk palca, …

– Lokalizacja (podmiot przebywa gdzieś)

• IP, GPS, …

Uwierzytelnianie

• Uwierzytelnianie na komputerze

stacjonarnym jest względnie proste

– “bezpieczna ścieżka” - podstawowe
– główny problem – ataki na

oprogramowanie/sprzęt uwierzytelniający

• Uwierzytelniania przez sieć - trudniejsze

– Intruz może obserwować komunikację
– Intruz może powtórzyć przechwycone komunikaty
– Intruz może aktywnie oddziaływać na

komunikację (zmieniając, kasując, …)

Wybór hasła

• Losowe

– Zależne od jakości generatora losowego
– Rozmiar min. 8 znaków: ograniczone możliwości zapamiętania
– Konieczność zapisu

• Złożone i nonsensowne

– 3kstr4m0cn3
– Łatwiejsze do zapamiętania

• Zdefiniowana polityka

– Kontrola dopuszczalności
– Powinno być dobrze:

• Co najmnej 1 cyfra, 1 litera, 1 zank interpunkcyjy, 1 znak kontrolny
• Wierszyki

– S8mnw;@dwnp@t8t

2014-05-13

4

Zarządzanie hasłami

• Starzenie się haseł

– Zmiana hasła po upływie pewnego czasu (na

podstawie średniego czasu poszukiwania/łamania)

– Zabezpieczenie przed użyciem historycznych n haseł

• Problem – ataki przez powtórzenie

– Można ‚nagrać’ i odtworzyć hasło/sekwencje

uwierzytelniającą

– rozwiązanie:

• Uwierzytelnianie realizowane w taki sposób, że

przekazywana informacja za każdym razem jest inna

Sól publiczna

• Dodanie t-bitów soli wzmacnia hasło – utrudnia atak słownikowy

• Sól publiczna (n.p. hasła UNIX)

userA

saltA

h(passwordA | saltA)

userB

saltB

h(passwordB | saltB)

– Sól wybrana losowo
– Atakujący musi obliczyć p*2

t

więcej skrótów aby znaleźć właściwe hasło,

– Skuteczne gdy liczba użytkowników jest zbliżona do liczby możliwych

wartości soli

• np. UNIX korzysta z 4096 możliwych wartości, ale większość systemów nie ma aż

tylu użytkowników

– Nie chroni przed podsłuchem czy rootkitami

Sól ukryta

userA saltA

h(passwordA | saltA | saltA’)

userB saltB

h(passwordB | saltB | saltB’)

• Sól jest mała (~4 bity)
• W celu weryfikacji system podstawia wszystkie możliwe wartości

soli + hasło użytkownika

• Aby znaleźć hasło intruz potrzebuje wykonać 16x obliczeń

– Możliwe rozwiązanie w przypadku małej liczby użytkowników

Hasła jednorazowe

• Każde hasło wykorzystane jest tylko jeden raz

– Zabezpieczenie przed powtórzeniem/odtworzeniem

• Wiele wariantów

– Współdzielona lista hasel jednorazowych

• Usuwane po wykorzystaniu

– Tablica typu „challenge response”

• System ma listę „pytań”, wybiera jedno w losowy sposób

– Aktualizowana lista haseł jednorazowych

• Podczas uwierzytelniania kluczem i, użytkownik generuje i przesyła do systemu

kolejne hasło (i+1)

– Sekwencje jednorazowych haseł generowane z wykorzystaniem funkcji

jednokierunkowych

• np. schemat Lamporta

Schemat Lamporta (s/key)

Konfiguracja:
• Alicja wybiera ziarno g a następnie oblicza sekwencję:

w = h

n

(g) = h(h(h(….h(g))))

• Alicja przesyła w na serwer
• Alicja ustawia licznik count← n-1

Uwierzytelnianie:
• Alicja wysyła x = h

count

(g) na serwer

• Alicja ustawia licznik count ← count - 1
• Serwer weryfikuje h(x) = w
• Serwer ustawia w ← x

Schemat Lamporta (s/key)

• Zalety

– Zabezpiecza przed podsłuchaniem
– Sekret nie jest przechowywany na serwerze

• Problemy

– Ograniczona liczba operacji uwierzytelnienia (konieczność generowania nowej

sekwencji w)

– Podatne na atak typu pre-play gdy niewykorzystane hasło zostało

skompromitowane

w

g

h()

h()

h()

auth 1

auth 2

auth n

2014-05-13

5

Bezpieczne znaczniki

• Implementacja popularna w inteligentnych kartach

• Wymagane jest aby serwer przechowywał sekret (źle)
• Użytkownik wpisuje (słaby) PIN aby aktywować kartę
• Karta musi być odporna na podrabianie

– Trudne do osiągnięcia

• Selekcja klucza może być zależna od czasu

– e.g. SecureID

Alicja (U

żytkownik)

Bob (Server)

k

0

k

1

k

0

k

1

h()

h()

h()

h()

E

k0

(m)

E

k1

(m)

Proste uwierzytelnienie

Alicja

Bob

“jestem Alicja”

Dowiedź tego

Moje hasło to “frank”

• Proste, wygodne, odpowiednie dla systemu

„stand-alone”

• Niebezpieczne dla systemów sieciowych

– Podatne na atak powtórzenia
– Bob musi znać hasło Alicji

Atak na uwierzytelnianie

Alicja

Bob

“jestem Alicja”

Dowiedź tego

Moim hasłem jest “frank”

Intruz

Atak na uwierzytelnianie

Bob

“Jestem Alicja”

Dowiedź tego

Moim hasłem jest “frank”

Intruz

• Atak przez powtórzenie
• Jak zabezpieczyć się?

Proste uwierzytelnianie

Alicja

Bob

Jestem Alicja,

a moim hasłem jest “frank”

• Bardziej wydajne…
• Ale problem pozostaje ten sam

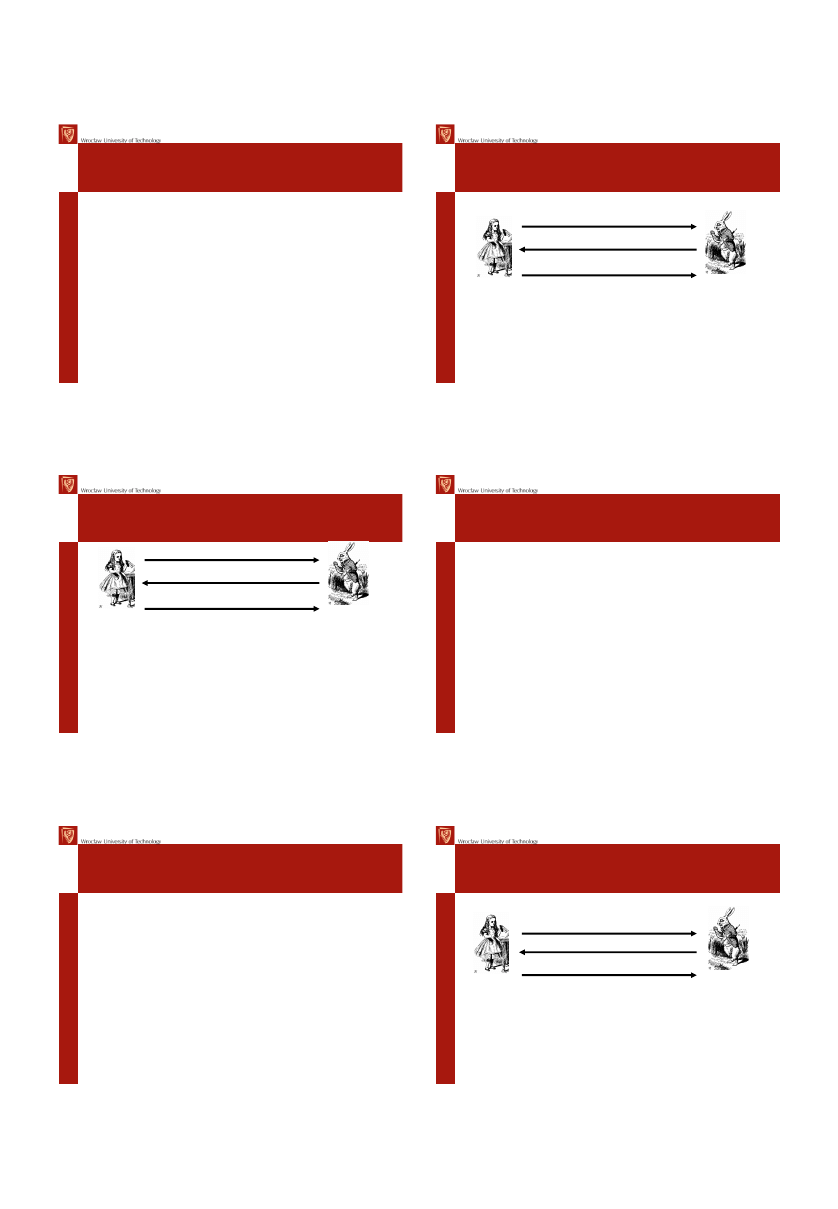
Lepsze uwierzytelnianie

Alicja

Bob

“Jestem Alicja”

Dowiedź tego

h(

hasło Alicji)

• Lepsze bo ukrywa hasło Alicji

– Zarówno względem Boba jak i atakującymi

• Lecz problem pozostaje

2014-05-13

6

Challenge-Response

• W celu zabezpieczenia przed atakami przez powtórzenie

stosuje się schemat „challenge-response”

• Niech Bob chce aby Alicja się uwierzytelniła

– Przesyła pytanie do Alicji (Challenge)
– Tylko Alicja może dostarczyć prawidłowej odpowiedzi (response)
– Pytanie jest wybierane za każdym razem więc nie można go

powtórzyć

• Jak to osiągnąć?

– Hasło jest znane tylko Alicji…
– “number used once” lub

nonce

Challenge-Response

Bob

“Jestem Alicja”

Nonce

Coś co może przesłać jedynie

Alicja

Alicja (oraz Bob

może to zweryfikować)

• Jak to osiągnąć?
• Skrót hasła – dobre, al. Kryptograficzny -

lepsze

Challenge-Response

Bob

“Jestem Alicja”

Nonce

h(

hasło Alicji, Nonce)



Nonce jest

pytaniem (challenge)



skrót jest

odpowiedzią (response)



Nonce

zapobiega powtórzeniom



Hasło jest znane tylko przez Alicję



uwaga - Bob

musi znać hasło Alicji

Alicja

Notacja klucza symetrycznego

• Szyfruj tekst jawny P kluczem K

C = E(P,K)

• Deszyfruj kryptogram C kluczem K

P = D(C,K)

• Rozważamy atak na

protokół

, a nie na algorytm

• Zakładamy bezpieczeństwo algorytmu

Uwierzytelnienie kluczem
symetrycznym

• Alicja oraz Bob współdzielą klucz K

AB

• Klucz K

AB

znany jest tylko przez Alicję

oraz Boba

• Uwierzytelnienie poprzez dowód

znajomości klucza

• Jak to osiągnąć?

– Nie wolno ujawniać klucza
– Nie wolno umożliwić ataku przez

powtórzenie

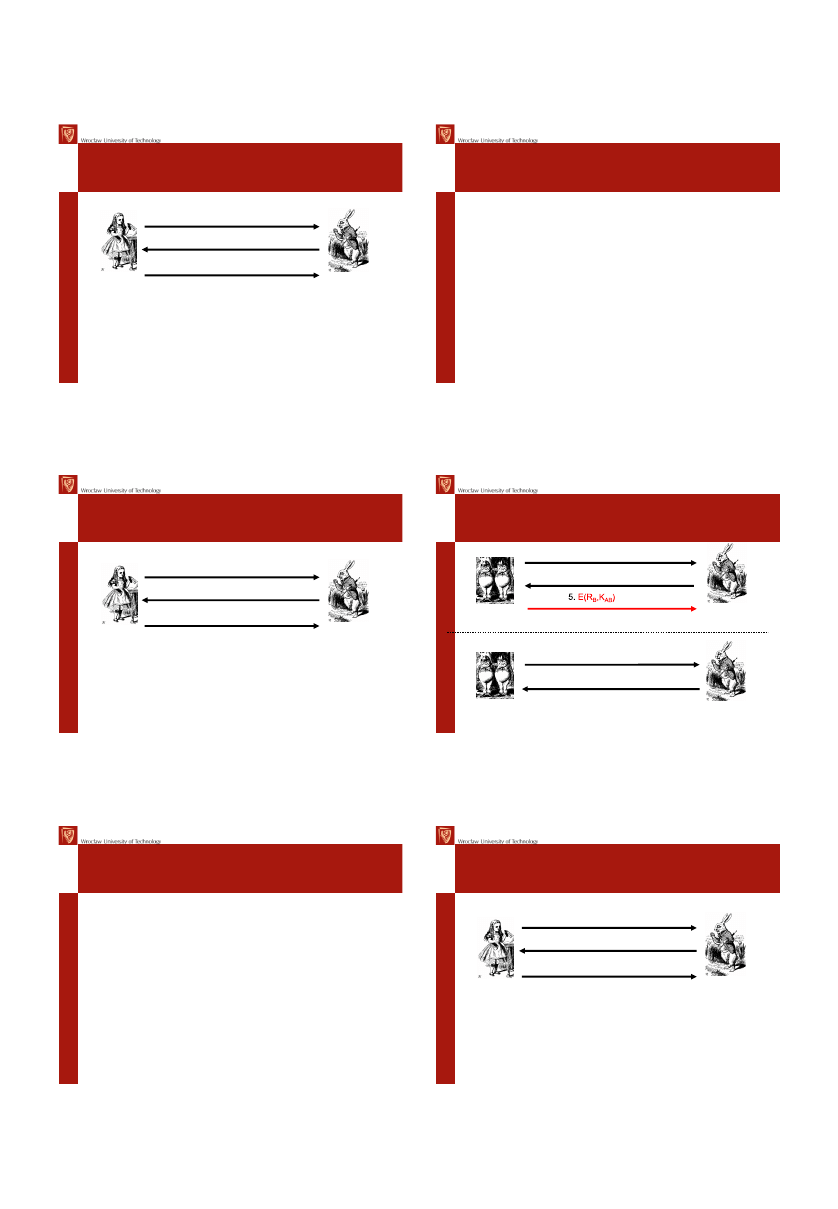
Uwierzytelnienie kluczem
symetrycznym

Alicja, K

AB

Bob, K

AB

“Jestem Alicja”

E(R,K

AB

)



Bezpieczna metoda uwierzytelnienia Alicji przez Boba



Alicja nie uwierzytelnia Boba



Czy można osiągnąć uwierzytelnienie obustronne?

R

2014-05-13

7

Uwierzytelnienie obustronne

Alicja

Bob

“Jestem Alicja”, R

E(R,K

AB

)

E(R,K

AB

)

• Co jest nie tak?
• “Alicja” może być Intruzem

(lub kimkolwiek)!

Uwierzytelnienie obustronne

• Ponieważ mamy dobry protokół

uwierzytelniający jedną stronę…

• Możemy użyć go dwukrotnie

– Raz dla Boba aby uwierzytelnić Alicję
– Raz dla Alicji aby uwierzytelnić Boba

• To musi działać…

Uwierzytelnienie obustronne

Alicja

Bob

“Jestem Alicja”, R

A

R

B

, E(R

A

,K

AB

)

E(R

B

,K

AB

)

• Uwierzytelnienie obustronne…
• …czy na pewno?

Atak na uwierzytelnie obustronne

Bob

1.

“Jestem Alicja”, R

A

2.

R

B

, E(R

A

,K

AB

)

Intruz

Bob

3.

“Jestem Alicja”,

R

B

4. R

C

,

E(R

B

,K

AB

)

Intruz

Uwierzytelnienie obustronne

• Protokół jednokierunkowy nie jest skuteczny dla

uwierzytelnienia w obu kierunkach

• Protokoły są wrażliwe!
• „Oczywiste” rozwiązania nie zawsze prowadzą

do bezpiecznego rezultatu

• Również gdy zmienią się założenia, środowisko,

itp. możemy otrzymać rozwiązanie nie
gwarantujące bezpieczeństwa

– Częste źródło problemów bezpieczeństwa
– Np. protokoły w Internecie

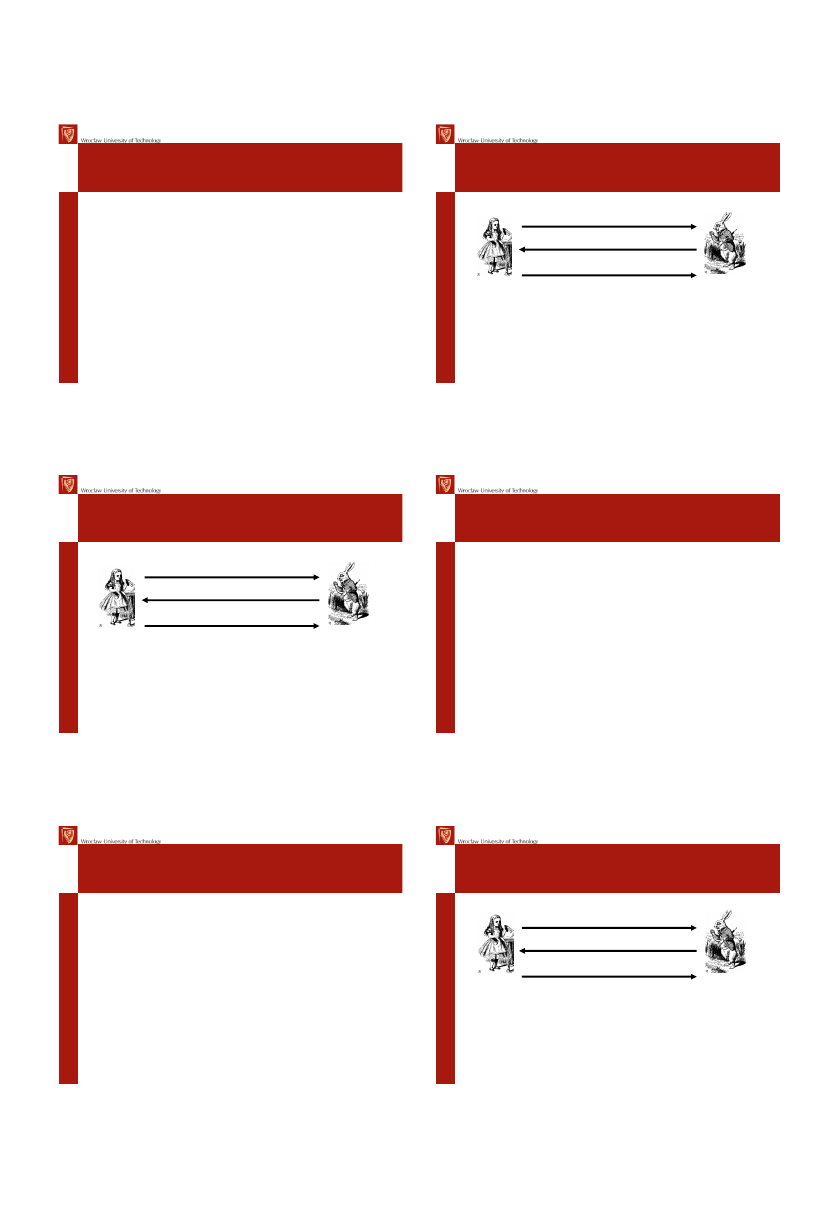
Klucz symetryczny dla
uwierzytelniania obustronnego

Alicja

Bob

“Jestem Alicja”, R

A

R

B

, E(“Bob”,R

A

,K

AB

)

E

(“Alicja”,R

B

,K

AB

)

• Czy ta „nieznacząca” zmiana pomoże?
• Tak!

2014-05-13

8

Notacja klucza publicznego

• Szyfuj M kluczem publicznym Alicji: {M}

Alicja

• Podpisz M kluczem prywatnym Alicji: [M]

Alicja

• Wtedy

– [{M}

Alicja

]

Alicja

= M

– {[M]

Alicja

}

Alicja

= M

• Każdy

może operować

kluczem publicznym

• Tylko

Alicja

może używać

klucza prywatnego

(podpisywać)

Uwierzytelnienie kluczem
publicznym

Alicja

Bob

“Jestem Alicja”

{R}

Alicja

R

• Czy jest to bezpieczne?
• Intruz może „zmusić” Alicję do

odszyfrowania wiadomości!

– Trzeba mieć dwie pary kluczy

Uwierzytelnianie kluczem
publicznym

Alicja

Bob

“Jestem Alicja”

R

[R]

Alicja

• Czy to jest bezpieczne?
• Intruz może „zmusić” Alicję do podpisania

każdego dokumentu!

– Trzeba mieć dwie pary kluczy

Klucze publiczne

• Nigdy nie należy używać tej samej pary

kluczy do szyfrowania i do podpisywania

• Jedna para dla

szyfrowania/deszyfrowania

• Druga para dla

podpisywania/weryfikowania

Klucz sesyjny

• Zazwyczaj korzystamy z odrębnych kluczy

dla każdej sesji

– Klucz symetryczny dla sesji

• Zastosowania:

– Ochrona poufności
– Kontrola integralności

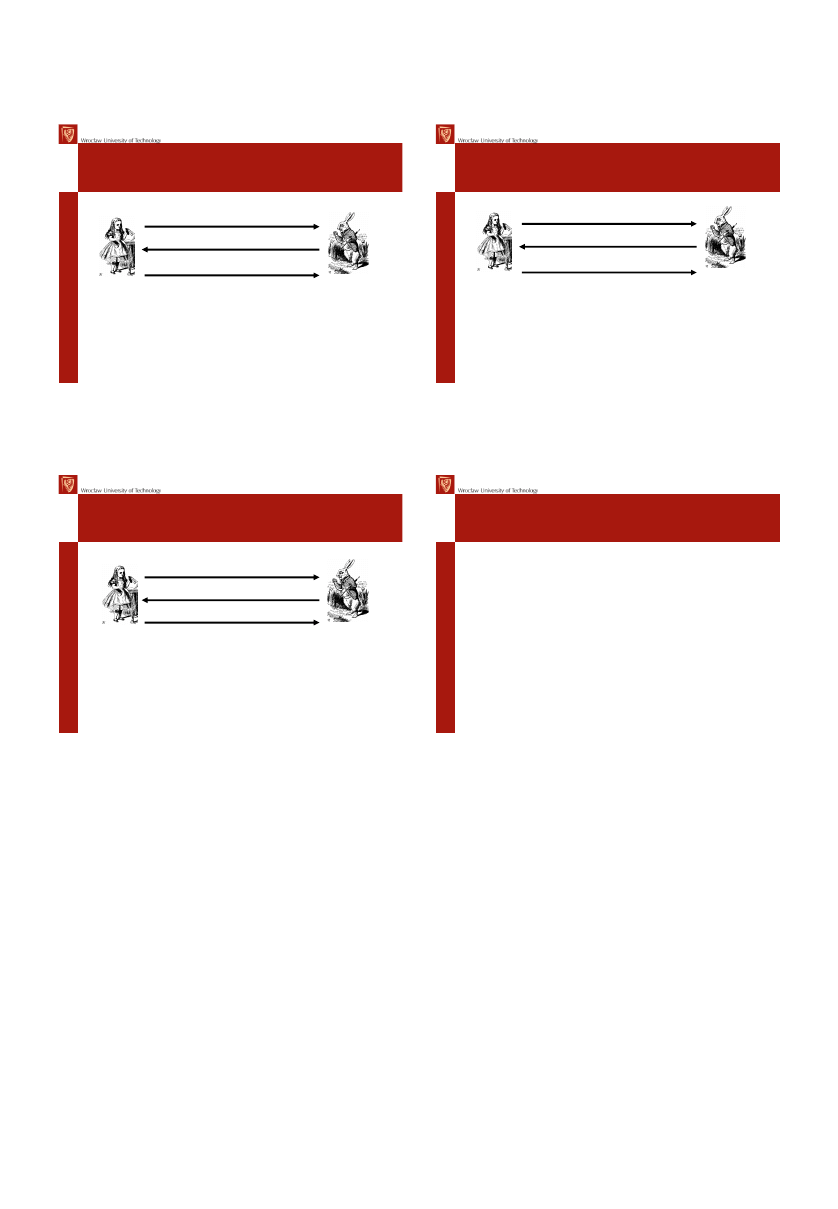
Uwierzytelnianie i klucz sesji

Alicja

Bob

“Jestem Alicja”, R

{R,K}

Alicja

{R +1,K}

Bob

• Czy jest bezpieczne?
• OK dla klucza, lecz nie dla wzajemnego

uwierzytelniania

• Uwaga:

K jest używane jako wartość nonce

Boba

2014-05-13

9

Uwierzytelnienie kluczem
publicznym i klucz sesji

Alicja

Bob

“Jestem Alicja”, R

[R,K]

Bob

[R +1,K]

Alicja

• Czy bezpieczne?
• Obustronne uwierzytelnienie, lecz klucz sesji

nie jest tajny!

Uwierzytelnienie kluczem
publicznym i klucz sesji

Alicja

Bob

“Jestem Alicja”, R

{[R,K]

Bob

}

Alicja

{[R +1,K]

Alicja

}

Bob

• Jest bezpieczne?
• Wygląda OK
• Uwierzytelnienie obustronne i klucz sesji!

Uwierzytelnienie kluczem
publicznym i klucz sesji

Alicja

Bob

“Jestem Alicja”, R

[{R,K}

Alicja

]

Bob

[{R +1,K}

Bob

]

Alicja

• Czy jest bezpieczne?
• Wydaje się być OK

– Każdy może odczytać

{R,K}

Alicja

oraz

{R +1,K}

Bob

Dziękuję za uwagę